Electronic Structure of Mg-, Si-, and Zn-Doped SnO2 Nanowires: Predictions from First Principles
Abstract
:1. Introduction
2. Computational Details
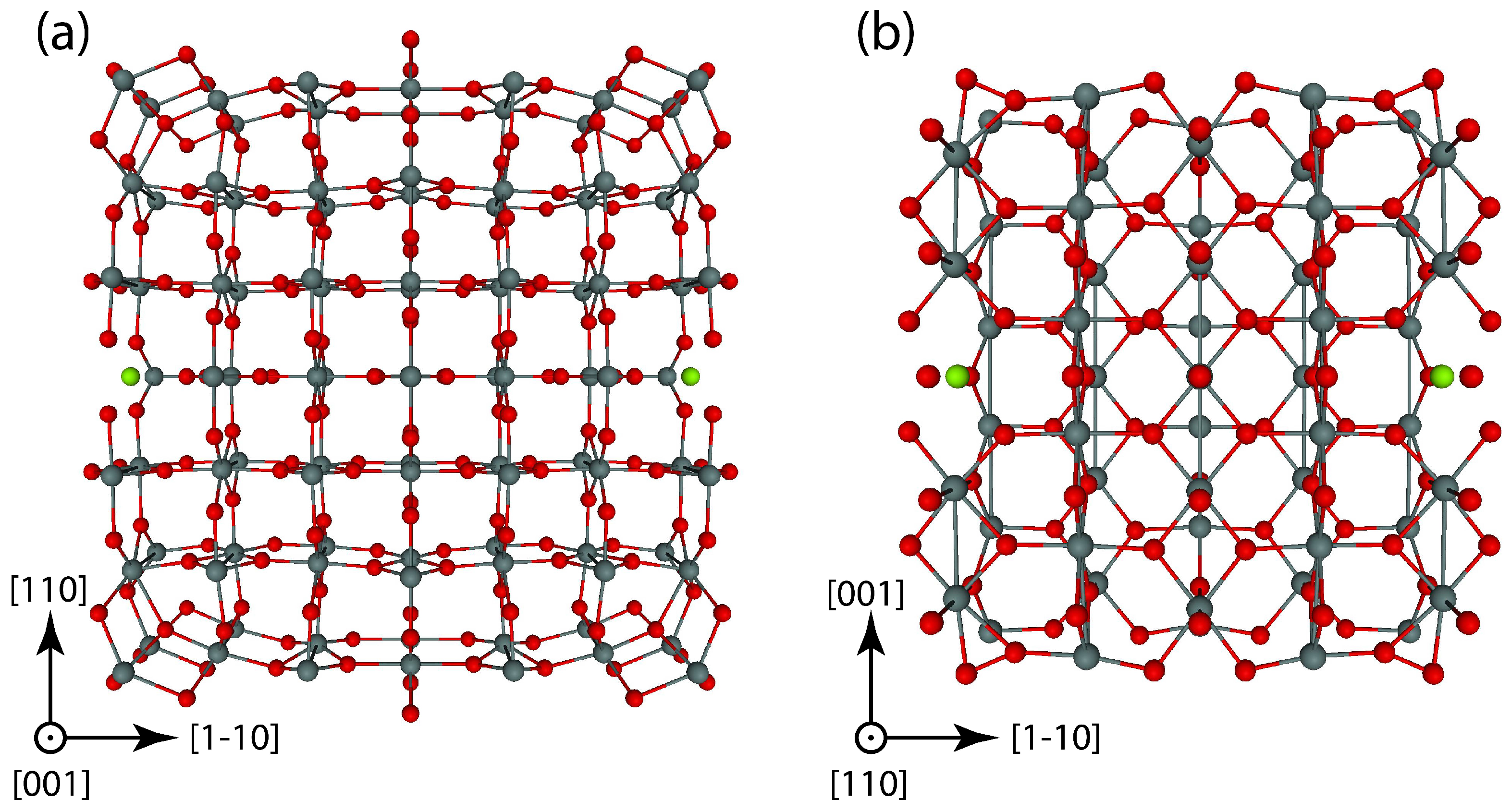
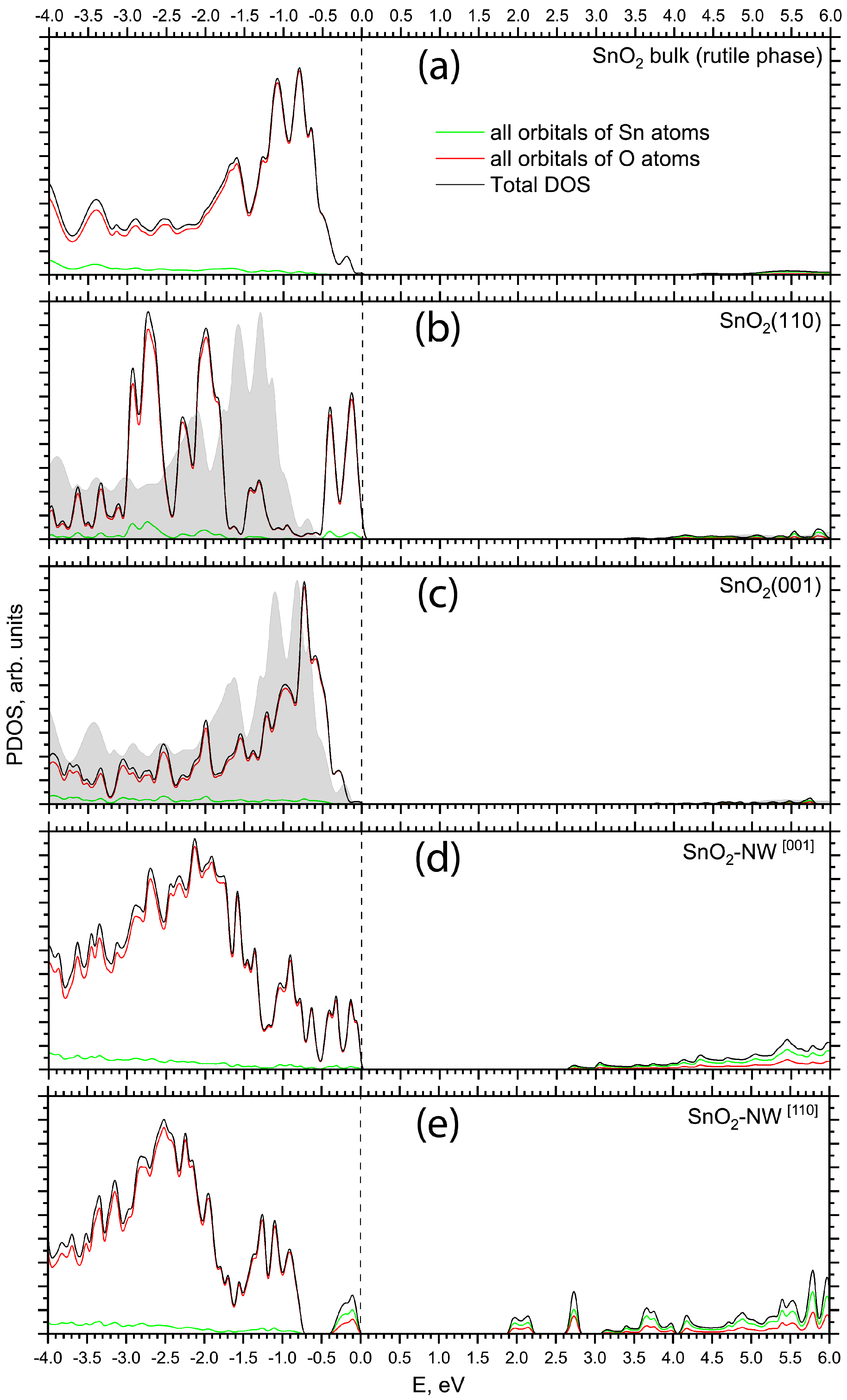
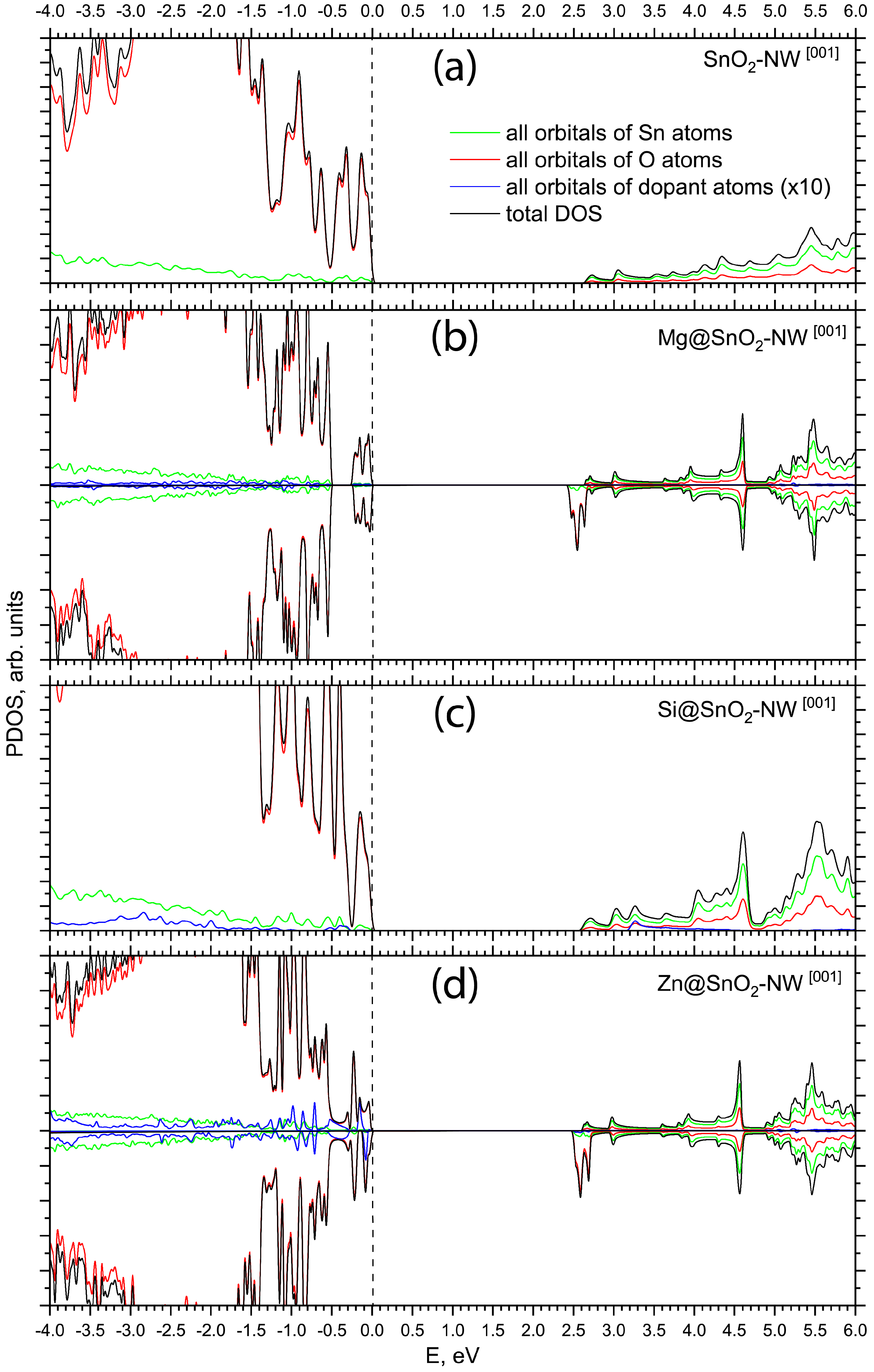
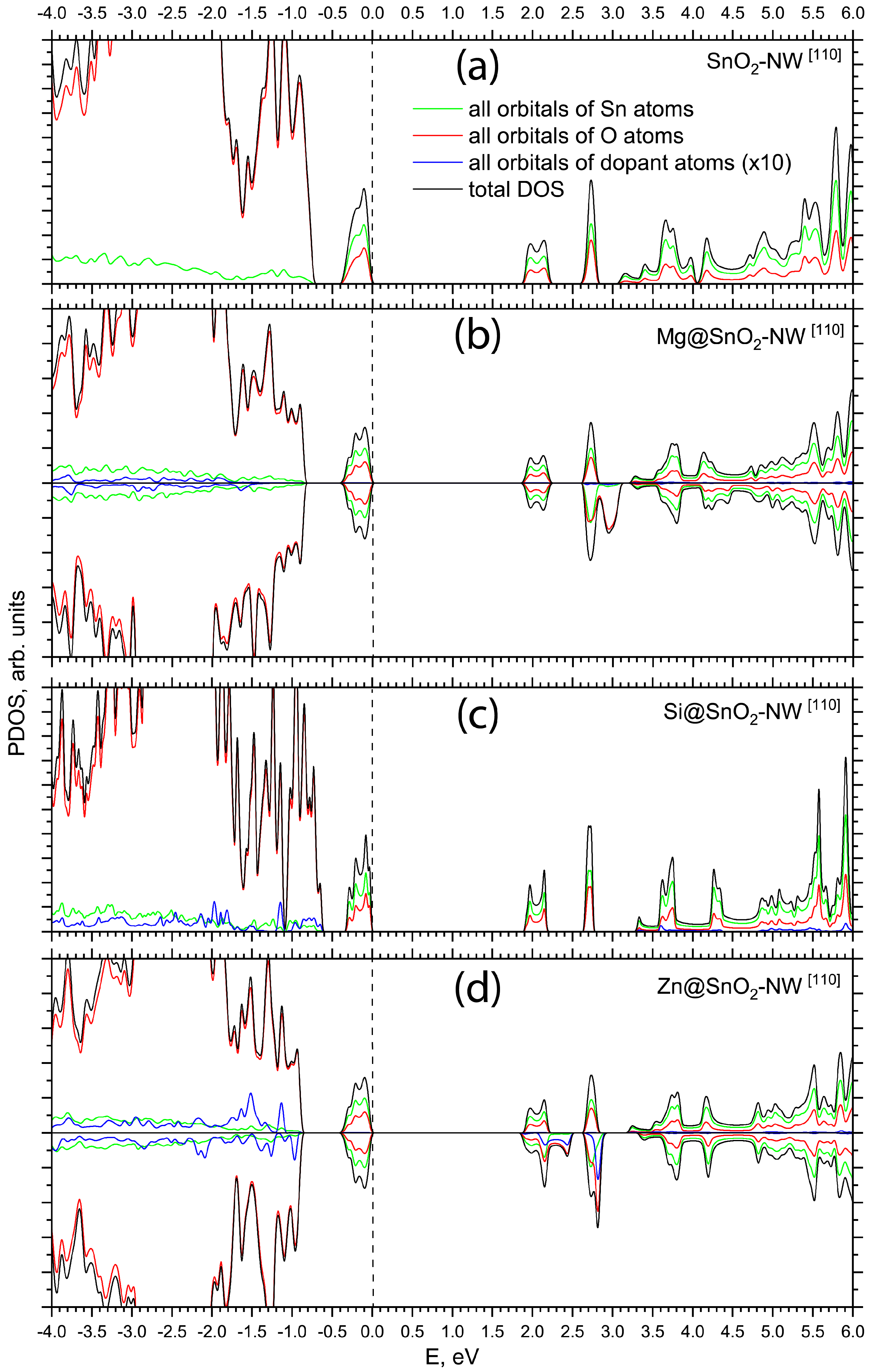
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Batzill, M.; Diebold, U. The surface and materials science of tin oxide. Prog. Surf. Sci. 2005, 79, 47–154. [Google Scholar] [CrossRef]
- Chopra, K.L.; Major, S.; Pandya, D.K. Transparent conductors—A status review. Thin Solid Film. 1983, 102, 1–46. [Google Scholar] [CrossRef]
- Barsan, N.; Schweizer-Berberich, M.; Göpel, W. Fundamental and practical aspects in the design of nanoscaled SnO2 gas sensors: A status report. Fresenius’ J. Anal. Chem. 1999, 365, 287–304. [Google Scholar] [CrossRef]
- Wang, C.F.; Xie, S.Y.; Lin, S.C.; Cheng, X.; Zhang, X.H.; Huang, R.B.; Zheng, L.S. Glow discharge growth of SnO2 nano-needles from SnH4. Chem. Commun. 2004, 15, 1766–1767. [Google Scholar] [CrossRef]
- Almaev, A.V.; Kopyev, V.V.; Novikov, V.A.; Chikiryaka, A.V.; Yakovlev, N.N.; Usseinov, A.B.; Karipbayev, Z.T.; Akilbekov, A.T.; Koishybayeva, Z.K.; Popov, A.I. ITO Thin Films for Low-Resistance Gas Sensors. Materials 2022, 16, 342. [Google Scholar] [CrossRef] [PubMed]
- Cusano, A.; Consales, M.; Pisco, M.; Pilla, P.; Cutolo, A.; Buosciolo, A.; Viter, R.; Smyntyna, V.; Giordano, M. Optochemical sensor for water monitoring based on SnO2 particle layer deposited onto optical fibers by the electrospray pyrolysis method. Appl. Phys. Lett. 2006, 89, 111103. [Google Scholar] [CrossRef]
- Viter, R.; Katoch, A.; Kim, S.S. Grain size dependent bandgap shift of SnO2 nanofibers. Met. Mater. Int. 2014, 20, 163–167. [Google Scholar] [CrossRef]
- Pisco, M.; Consales, M.; Campopiano, S.; Viter, R.; Smyntyna, V.; Giordano, M.; Cusano, A. A Novel Optochemical Sensor Based on SnO2 Sensitive Thin Film for ppm Ammonia Detection in Liquid Environment. J. Light. Technol. 2006, 24, 5000–5007. [Google Scholar] [CrossRef]
- Shabna, S.; Dhas, S.S.J.; Biju, C. Potential progress in SnO2 nanostructures for enhancing photocatalytic degradation of organic pollutants. Catal. Commun. 2023, 177, 106642. [Google Scholar] [CrossRef]
- Zarkov, A.; Stanulis, A.; Mikoliunaite, L.; Salak, A.N.; Kareiva, A. Organic-free synthesis of nanostructured SnO2 thin films by chemical solution deposition. Thin Solid Films 2018, 649, 219–224. [Google Scholar] [CrossRef]
- Dmitriyeva, E.; Lebedev, I.; Bondar, E.; Fedosimova, A.; Temiraliev, A.; Murzalinov, D.; Ibraimova, S.; Nurbaev, B.; Elemesov, K.; Baitimbetova, B. The Influence of Lyophobicity and Lyophilicity of Film-Forming Systems on the Properties of Tin Oxide Films. Coatings 2023, 13, 1990. [Google Scholar] [CrossRef]
- Solomatin, M.A.; Radovic, M.; Petrunin, A.A.; Kirilenko, D.A.; Varezhnikov, A.S.; Dubourg, G.; Vasilkov, M.Y.; Bainyashev, A.M.; Nesterovic, A.; Kiselev, I.; et al. Towards electronic smelling of ketones and alcohols at sub-and low ppms by pinky-sized on-chip sensor array with SnO2 mesoporous layer gradually engineered by near IR-laser. Chem. Eng. J. 2023, 474, 145934. [Google Scholar] [CrossRef]
- Han, J.; Teng, X.; Jia, W.; Liu, P.; Li, Y.; Wang, W. SnO2/Fe2O3/Cu2O composites as catalysts for photoelectrocatalytic degradation of benzotriazoles. Opt. Mater. 2024, 148, 114799. [Google Scholar] [CrossRef]
- Da Silva, L.F.; Lucchini, M.A.; Catto, A.C.; Avansi Jr, W.; Bernardini, S.; Aguir, K.; Niederberger, M.; Longo, E. The Role of Zn Ions in the Structural, Surface, and Gas-Sensing Properties of SnO2:Zn Nanocrystals Synthesized via a Microwave-Assisted Route. Sensors 2023, 24, 140. [Google Scholar] [CrossRef] [PubMed]
- Smok, W.; Zaborowska, M.; Tański, T.; Radoń, A. Novel In2O3/SnO2 heterojunction 1D nanostructure photocatalyst for MB degradation. Opt. Mater. 2023, 139, 113757. [Google Scholar] [CrossRef]
- Panchal, V.; Pampillo, L.; Ferrari, S.; Bilovol, V.; Popescu, C.; Errandonea, D. Pressure-Induced Structural Phase Transition of Co-Doped SnO2 Nanocrystals. Crystals 2023, 13, 900. [Google Scholar] [CrossRef]
- Motevalizadeh, L.; Tahani, M. A Phenomenological Study of Chromium Impurity Effects on Lattice Microstrains of SnO2 Nanoparticles Prepared Using Sol–Gel Technique. Crystals 2023, 13, 919. [Google Scholar] [CrossRef]
- Ma, C.G.; Brik, M.G.; Kiisk, V.; Kangur, T.; Sildos, I. Spectroscopic and crystal-field analysis of energy levels of Eu3+ in SnO2 in comparison with ZrO2 and TiO2. J. Alloy. Compd. 2011, 509, 3441–3451. [Google Scholar] [CrossRef]
- Ivanishcheva, A.P.; Sysoev, V.V.; Abdullin, K.A.; Nesterenko, A.V.; Khubezhov, S.A.; Petrov, V.V. The Application of Combined Visible and Ultraviolet Irradiation to Improve the Functional Characteristics of Gas Sensors Based on ZnO/SnO2 and ZnO/Au Nanorods. Chemosensors 2023, 11, 200. [Google Scholar] [CrossRef]
- Kambar, D.; Seisembekova, T.; Zeinidenov, A.; Aimukhanov, A.; Borodin, Y. Determination of Correlation Between Photoelectric Properties and Structural Features of Nanocomposite Photoelectrode ZnO:SnO2 by Impedance Spectroscopy. In Proceedings of the International Conference «Modern Technologies For Non-Destructive Testing», Tomsk, Russia, 9–11 November 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 187–193. [Google Scholar] [CrossRef]
- Kiani, M.S.; Sadirkhanov, Z.T.; Kakimov, A.G.; Parkhomenko, H.P.; Ng, A.; Jumabekov, A.N. Solution-Processed SnO2 Quantum Dots for the Electron Transport Layer of Flexible and Printed Perovskite Solar Cells. Nanomaterials 2022, 12, 2615. [Google Scholar] [CrossRef]
- Shin, G.; Yoon, C.H.; Bae, M.Y.; Kim, Y.C.; Hong, S.K.; Rogers, J.A.; Ha, J.S. Stretchable Field-Effect-Transistor Array of Suspended SnO2 Nanowires. Small 2011, 7, 1181–1185. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Wu, X.; Ma, Y.; Gong, L.; Qu, F.; Fan, H. Porous SnO2 nanowire bundles for photocatalyst and Li ion battery applications. CrystEngComm 2011, 13, 3506–3510. [Google Scholar] [CrossRef]
- Yuasa, M.; Suematsu, K.; Yamada, K.; Watanabe, K.; Kida, T.; Yamazoe, N.; Shimanoe, K. Thermally stable SnO2 nanocrystals: Synthesis and application to gas sensors. Cryst. Growth Des. 2016, 16, 4203–4208. [Google Scholar] [CrossRef]
- Periyasamy, M.; Kar, A. Modulating the properties of SnO2 nanocrystals: Morphological effects on structural, photoluminescence, photocatalytic, electrochemical and gas sensing properties. J. Mater. Chem. C 2020, 8, 4604–4635. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, X.J.; Ni, J.M.; Tao, H.Z. Structural, electrical and optical properties of p-type transparent conducting SnO2: Al film derived from thermal diffusion of Al/SnO2/Al multilayer thin films. Acta Mater. 2010, 58, 6243–6248. [Google Scholar] [CrossRef]
- Ni, J.; Zhao, X.; Zheng, X.; Zhao, J.; Liu, B. Electrical, structural, photoluminescence and optical properties of p-type conducting, antimony-doped SnO2 thin films. Acta Mater. 2009, 57, 278–285. [Google Scholar] [CrossRef]
- Yuan, H. Structural, electrical and optical properties of Si doped ZnO films grown by atomic layer deposition. J. Mater. Sci. Mater. Electron. 2012, 23, 2075–2081. [Google Scholar] [CrossRef]
- Banyamin, Z.Y.; Kelly, P.J.; West, G.; Boardman, J. Electrical and optical properties of fluorine doped tin oxide thin films prepared by magnetron sputtering. Coatings 2014, 4, 732–746. [Google Scholar] [CrossRef]
- Balakhayeva, R.; Akilbekov, A.; Baimukhanov, Z.; Usseinov, A.; Giniyatova, S.; Zdorovets, M.; Vlasukova, L.; Popov, A.; Dauletbekova, A. CdTe Nanocrystal Synthesis in SiO2/Si Ion-Track Template: The Study of Electronic and Structural Properties. Phys. Status Solidi (A) 2021, 218, 2000231. [Google Scholar] [CrossRef]
- Jang, J.; Yim, H.; Choi, J.W. Exploration of Si-doped SnO2 composition and properties of oxide/Ag/oxide multilayers prepared using continuous composition spread by sputtering. Thin Solid Films 2018, 660, 606–612. [Google Scholar] [CrossRef]
- Thirumurugan, K.; Ravichandran, K. Role of solvent volume on the structural and transparent conducting properties of SnO2:Zn films. J. Mater. Sci. Mater. Electron. 2014, 25, 3594–3600. [Google Scholar] [CrossRef]
- Ni, J.M.; Zhao, X.J.; Zhao, J. Structural, electrical and optical properties of p-type transparent conducting SnO2:Zn film. J. Inorg. Organomet. Polym. Mater. 2012, 22, 21–26. [Google Scholar] [CrossRef]
- Zhang, C.W.; Yan, S.S. First-principles study on ferromagnetism in Mg-doped SnO2. Appl. Phys. Lett. 2009, 95, 232108. [Google Scholar] [CrossRef]
- Korotcenkov, G. Gas response control through structural and chemical modification of metal oxide films: State of the art and approaches. Sens. Actuators B Chem. 2005, 107, 209–232. [Google Scholar] [CrossRef]
- Singh, A.K.; Janotti, A.; Scheffler, M.; Van de Walle, C.G. Sources of electrical conductivity in SnO2. Phys. Rev. Lett. 2008, 101, 055502. [Google Scholar] [CrossRef] [PubMed]
- Falabretti, B.; Robertson, J. Electronic structures and doping of SnO2, CuAlO2, and CuInO2. J. Appl. Phys. 2007, 102, 123703. [Google Scholar] [CrossRef]
- Carrasco, J.; Illas, F.; Lopez, N.; Kotomin, E.A.; Zhukovskii, Y.F.; Piskunov, S.; Maier, J.; Hermansson, K. First principles simulations of F centers in cubic SrTiO3. Phys. Status Solidi (C) 2005, 2, 153–158. [Google Scholar] [CrossRef]
- Piskunov, S.; Gopejenko, A.; Pankratov, V.; Isakoviča, I.; Ma, C.G.; Brik, M.G.; Piasecki, M.; Popov, A.I. First Principles Calculations of Atomic and Electronic Structure of - and -Doped YAlO3. Materials 2021, 14, 5589. [Google Scholar] [CrossRef] [PubMed]
- Piskunov, S.; Spohr, E.; Jacob, T.; Kotomin, E.A.; Ellis, D.E. Electronic and magnetic structure of La0.875Sr0.125MnO3 calculated by means of hybrid density-functional theory. Phys. Rev. B 2007, 76, 012410. [Google Scholar] [CrossRef]
- Gunhold, A.; Beuermann, L.; Gömann, K.; Borchardt, G.; Kempter, V.; Maus-Friedrichs, W.; Piskunov, S.; Kotomin, E.A.; Dorfman, S. Study of the electronic and atomic structure of thermally treated SrTiO3 (110) surfaces. Surf. Interface Anal. Int. J. Devoted Dev. Appl. Tech. Anal. Surfaces Interfaces Thin Film 2003, 35, 998–1003. [Google Scholar] [CrossRef]
- Sokolov, M.; Eglitis, R.I.; Piskunov, S.; Zhukovskii, Y.F. Ab initio hybrid DFT calculations of BaTiO3 bulk and BaO-terminated (001) surface F-centers. Int. J. Mod. Phys. B 2017, 31, 1750251. [Google Scholar] [CrossRef]
- Usseinov, A.; Platonenko, A.; Koishybayeva, Z.; Akilbekov, A.; Zdorovets, M.; Popov, A.I. Pair vacancy defects in β-Ga2O3 crystal: Ab initio study. Opt. Mater. X 2022, 16, 100200. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL23 User’s Manual; University of Torino: Torino, Italy, 2023. [Google Scholar]
- Erba, A.; Desmarais, J.K.; Casassa, S.; Civalleri, B.; Donà, L.; Bush, I.J.; Searle, B.; Maschio, L.; Edith-Daga, L.; Cossard, A.; et al. CRYSTAL23: A Program for Computational Solid State Physics and Chemistry. J. Chem. Theory Comput. 2022, 19, 6891–6932. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Vilela Oliveira, D.; Laun, J.; Peintinger, M.F.; Bredow, T. BSSE-correction scheme for consistent gaussian basis sets of double-and triple-zeta valence with polarization quality for solid-state calculations. J. Comput. Chem. 2019, 40, 2364–2376. [Google Scholar] [CrossRef] [PubMed]
- Laun, J.; Bredow, T. BSSE-corrected consistent Gaussian basis sets of triple-zeta valence with polarization quality of the fifth period for solid-state calculations. J. Comput. Chem. 2022, 43, 839–846. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Balakrishnan, K.; Veerapandy, V.; Fjellvag, H.; Vajeeston, P. First-principles exploration into the physical and chemical properties of certain newly identified SnO2 polymorphs. ACS Omega 2022, 7, 10382–10393. [Google Scholar] [CrossRef] [PubMed]
- Baur, W.H. Über die verfeinerung der kristallstrukturbestimmung einiger vertreter des rutiltyps: TiO2, SnO2, GeO2 und MgF2. Acta Crystallogr. 1956, 9, 515–520. [Google Scholar] [CrossRef]
- Herring, C. Some theorems on the free energies of crystal surfaces. Phys. Rev. 1951, 82, 87. [Google Scholar] [CrossRef]
- Evarestov, R.; Zhukovskii, Y.F. Four-faceted nanowires generated from densely-packed TiO2 rutile surfaces: Ab initio calculations. Surf. Sci. 2013, 608, 226–240. [Google Scholar] [CrossRef]
- Gu, M.; Kushima, A.; Shao, Y.; Zhang, J.G.; Liu, J.; Browning, N.D.; Li, J.; Wang, C. Probing the failure mechanism of SnO2 nanowires for sodium-ion batteries. Nano Lett. 2013, 13, 5203–5211. [Google Scholar] [CrossRef] [PubMed]
- Gao, N.; Li, H.Y.; Zhang, W.; Zhang, Y.; Zeng, Y.; Zhixiang, H.; Liu, J.; Jiang, J.; Miao, L.; Yi, F.; et al. QCM-based humidity sensor and sensing properties employing colloidal SnO2 nanowires. Sens. Actuators B Chem. 2019, 293, 129–135. [Google Scholar] [CrossRef]
- Giniyatova, S.; Dauletbekova, A.; Baimukhanov, Z.; Vlasukova, L.; Akilbekov, A.; Usseinov, A.; Kozlovskiy, A.; Akylbekova, A.; Seitbayev, A.; Karipbayev, Z. Structure, electrical properties and luminescence of ZnO nanocrystals deposited in SiO2/Si track templates. Radiat. Meas. 2019, 125, 52–56. [Google Scholar] [CrossRef]
- Zunger, A.; Malyi, O.I. Understanding doping of quantum materials. Chem. Rev. 2021, 121, 3031–3060. [Google Scholar] [CrossRef]
- Zhang, S. The microscopic origin of the doping limits in semiconductors and wide-gap materials and recent developments in overcoming these limits: A review. J. Phys. Condens. Matter 2002, 14, R881. [Google Scholar] [CrossRef]
| Material | lSn/dop−O | PSn/dop−O | QSn/dop | |||
|---|---|---|---|---|---|---|
| Mg@SnO2-NW[001] | 2.03 | 2.000 | 166 | 1.47 | –1.06 | 2.47 |
| Si@SnO2-NW[001] | 0.72 | 1.730 | 510 | 1.67 | –0.95 | 2.68 |
| Zn@SnO2-NW[001] | 5.07 | 2.020 | 212 | 1.40 | –0.88 | 2.53 |
| Pristine SnO2-NW[001] | 1.967 | 430 | 1.89 | –0.91 | 2.72 | |
| Mg@SnO2-NW[110] | 2.34 | 2.038 | 142 | 1.47 | –0.69 | 3.26 |
| Si@SnO2-NW[110] | 0.32 | 1.698 | 714 | 1.63 | –0.84 | 3.31 |
| Zn@SnO2-NW[110] | 6.09 | 1.933 | 224 | 1.45 | –0.69 | 3.32 |
| Pristine SnO2-NW[110] | 1.970 | 430 | 1.96 | –0.94 | 3.12 | |
| Bulk SnO2 (rutile) | 2.053 | 210 | 2.14 | –1.07 | 3.91 | |
| SnO2 (001) | 1.935 | 556 | 1.81 | –0.89 | 3.46 | |
| SnO2 (110) | 1.964 | 432 | 1.94 | –0.93 | 3.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Platonenko, A.; Piskunov, S.; Yang, T.C.-K.; Juodkazyte, J.; Isakoviča, I.; Popov, A.I.; Junisbekova, D.; Baimukhanov, Z.; Dauletbekova, A. Electronic Structure of Mg-, Si-, and Zn-Doped SnO2 Nanowires: Predictions from First Principles. Materials 2024, 17, 2193. https://doi.org/10.3390/ma17102193
Platonenko A, Piskunov S, Yang TC-K, Juodkazyte J, Isakoviča I, Popov AI, Junisbekova D, Baimukhanov Z, Dauletbekova A. Electronic Structure of Mg-, Si-, and Zn-Doped SnO2 Nanowires: Predictions from First Principles. Materials. 2024; 17(10):2193. https://doi.org/10.3390/ma17102193
Chicago/Turabian StylePlatonenko, Alexander, Sergei Piskunov, Thomas C.-K. Yang, Jurga Juodkazyte, Inta Isakoviča, Anatoli I. Popov, Diana Junisbekova, Zein Baimukhanov, and Alma Dauletbekova. 2024. "Electronic Structure of Mg-, Si-, and Zn-Doped SnO2 Nanowires: Predictions from First Principles" Materials 17, no. 10: 2193. https://doi.org/10.3390/ma17102193
APA StylePlatonenko, A., Piskunov, S., Yang, T. C.-K., Juodkazyte, J., Isakoviča, I., Popov, A. I., Junisbekova, D., Baimukhanov, Z., & Dauletbekova, A. (2024). Electronic Structure of Mg-, Si-, and Zn-Doped SnO2 Nanowires: Predictions from First Principles. Materials, 17(10), 2193. https://doi.org/10.3390/ma17102193







