A Multiphysics Thermoelastoviscoplastic Damage Internal State Variable Constitutive Model including Magnetism
Abstract
1. Introduction
2. Phenomenological Behavior
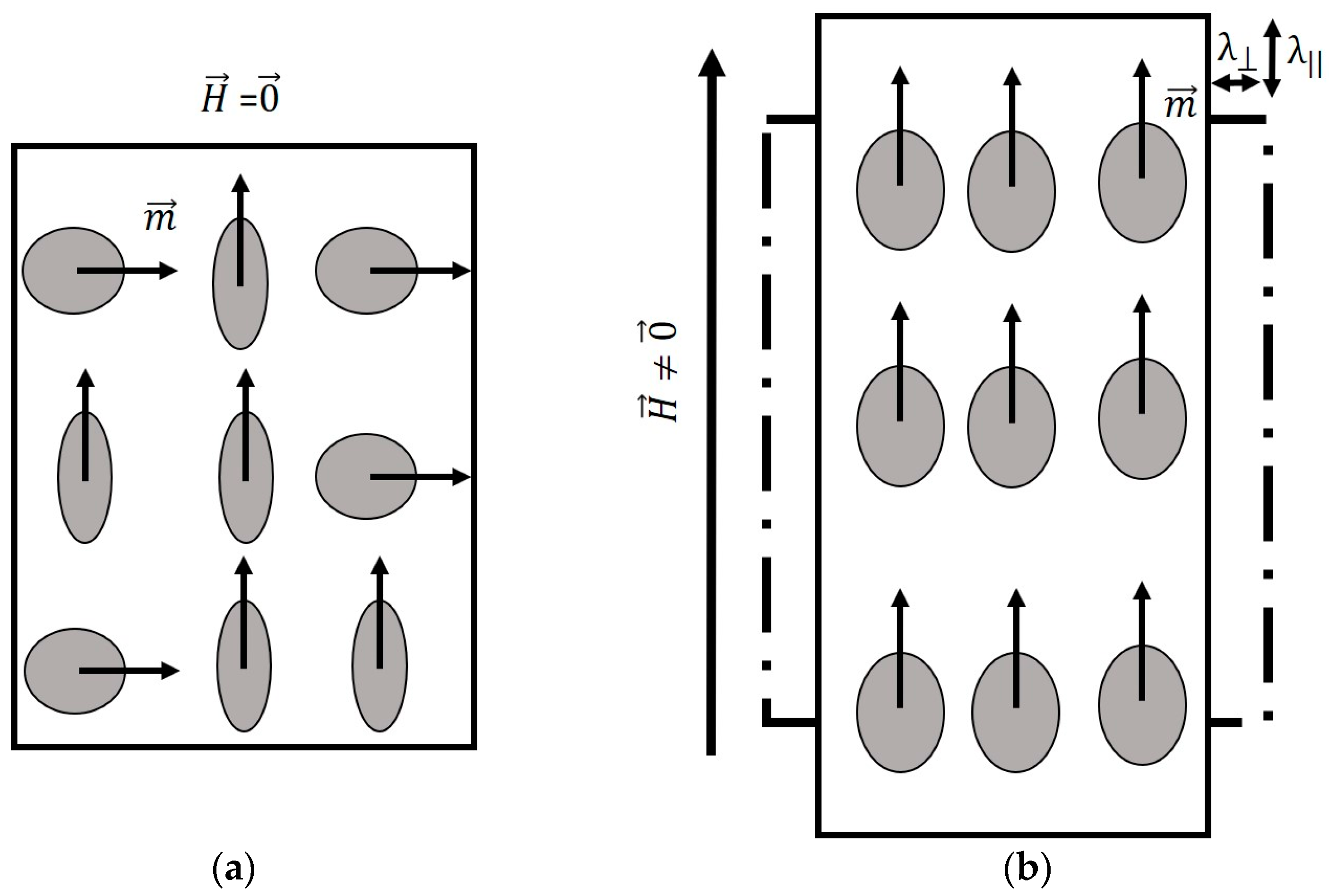
2.1. Macroscale Level: The Magnetostriction Phenomenon
2.2. Mesoscale Level: Domain Wall Motion
2.3. Nanoscale Level: Ising Model
3. Kinematics
4. Thermodynamics
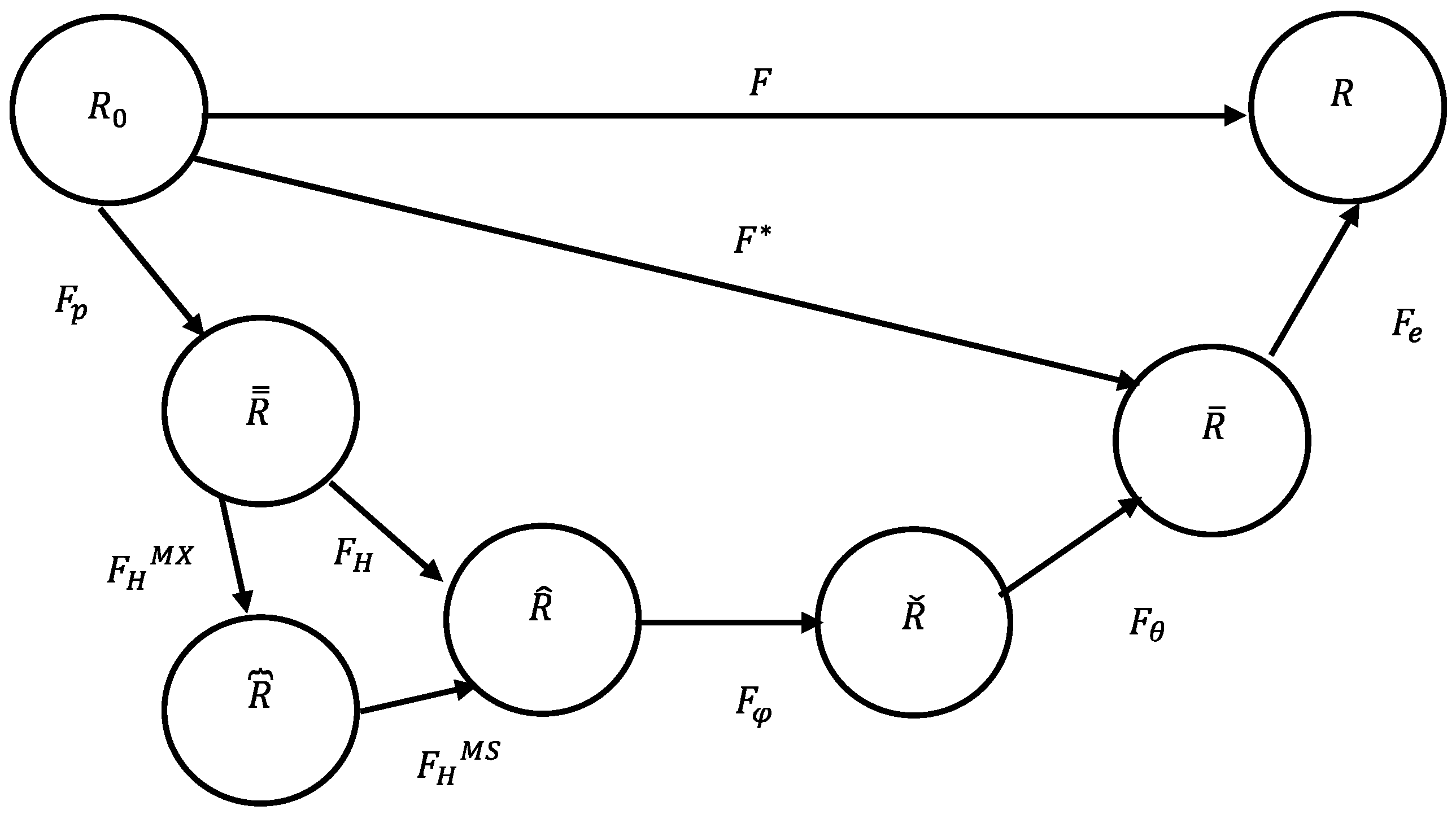
5. Kinetics
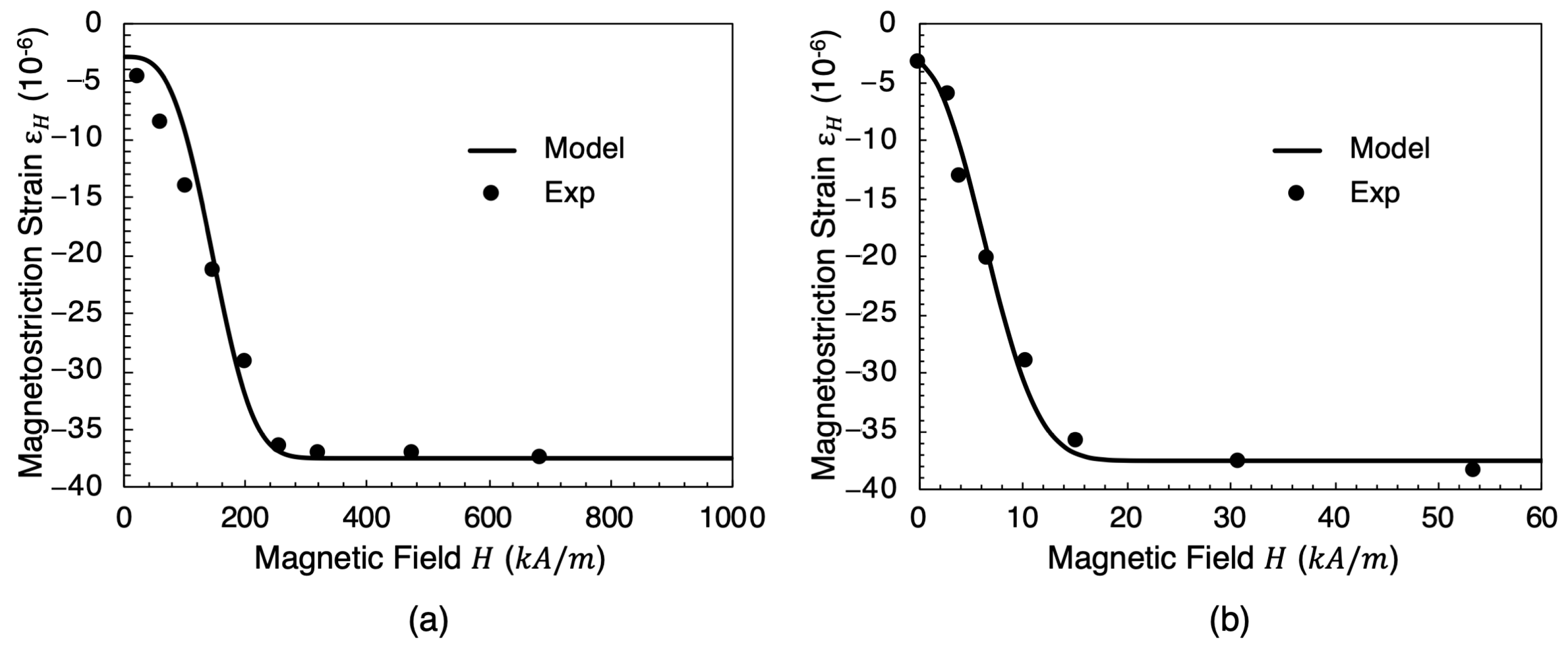
5.1. Experimental Magnetostriction Test
5.2. Cauchy Stress Tensor
5.3. An Internal State Variable for Magnetization
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zakaria, H.A.J.I.; Hamid, M.O.U.N.I.R.; Abdellatif, E.M.; Imane, A.M.A.R.I.R. Recent advancements and developments for electric vehicle technology. In Proceedings of the 2019 International Conference of Computer Science and Renewable Energies (ICCSRE), Agadir, Morocco, 22–24 July 2019; pp. 1–6. [Google Scholar]
- Sacchi, R.; Bauer, C.; Cox, B.; Mutel, C. When, where and how can the electrification of passenger cars reduce greenhouse gas emissions? Renew. Sustain. Energy Rev. 2022, 162, 112475. [Google Scholar] [CrossRef]
- Cui, J.; Kramer, M.; Zhou, L.; Liu, F.; Gabay, A.; Hadjipanayis, G.; Balasubramanian, B.; Sellmyer, D. Current progress and future challenges in rare-earth-free permanent magnets. Acta Mater. 2018, 158, 118–137. [Google Scholar] [CrossRef]
- Avakian, A.; Ricoeur, A. Constitutive modelling of nonlinear reversible and irreversible ferromagnetic behaviors and applictions of multiferroic composites. J. Intell. Mater. Syst. Struct. 2016, 27, 2536–2554. [Google Scholar] [CrossRef]
- Marvalova, B. Modelling of Magnetosensitive Elastomers; Technical University of Liberec: Liberec, Czech Republic, 2008. [Google Scholar]
- Olabi, A.G. A Grunwald, Design and application of magnetostrictive materials. Mater. Design. 2008, 29, 469–483. [Google Scholar] [CrossRef]
- Joule, J. On a new class of magnetic forces. Ann. Electr. Magn. Chem. 1842, 8, 219–224. [Google Scholar]
- Gao, Z.; Zhou, Y. A Magneto-Mechanical Fully Coupled Model for GIANT magnetostriction in High Temperature Superconductor; Key Laboratory of Mechanics on Disaster and Environment in Western China attached to the Ministry of Education of China, Department of Mechanics and Engineering Sciences, College of Civil Engineering and Mechanics, Lanzhou University: Lanzhou, China, 2015. [Google Scholar]
- Bozorth, R.M.; Williams, H.J. Effect of small stresses on magnetic properties. Rev. Mod. Phys. 1945, 17, 72. [Google Scholar] [CrossRef]
- Brown, W.F., Jr. Irreversible magnetic effects of stress. Phys. Rev. 1949, 75, 147. [Google Scholar] [CrossRef]
- Cullity, B.D. Introduction to Magnetic Materials. In Addison Wesley; Mass: Reading, MA, USA, 1972; p. 268. [Google Scholar]
- Sablik, M.J.; Burkhardt, G.L.; Kwun, H.; Jiles, D.C. A model for the effect of stress on the low frequency harmonic content of the magnetic induction in ferromagnetic materials. J. Appl. Phys. 1988, 63, 3930. [Google Scholar] [CrossRef]
- Jiles, D.C. Theory of Magneto-mechanical effect. J. Phys. D Appl. Phys. 1995, 28, 1537. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of Ferromagnetic Hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Joule, J. On the Effects of Magnetism upon the Dimensions of Iron and Steel Bars. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1847, 76–87, 225–241. [Google Scholar]
- Penpeintner, M.; Holländer, R.B.; Seitner, M.J.; Weig, E.M.; Gross, R.; Gönnenwein, S.T.; Huebl, H. A universal platform for magnetostriction measurements in thin films. arXiv 2015, arXiv:1509.00647. [Google Scholar]
- Pislaru-Danescu, L.; Morega, A.M.; Morega, M. A novel magnetostrictive injection actuator based on new giant magnetostrictive materials. In Proceedings of the 2011 7th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 12–14 May 2011. [Google Scholar]
- Zagoruiko, N.V. Effect of an Electrostatic Field and a Pulsed Magnetic Field on the Movements of Dislocations in Sodium Chloride. Sov. Phys. Crystallogr. 1965, 10, 63–67. [Google Scholar]
- Kravchenko, V.Y. Influence of the Magnetic Field on Electronic Deceleration of Dislocations. JEPT Lett. 1970, 12, 551–554. [Google Scholar]
- Al’Shits, V.I.; Liubimov, V.N.; Sarychev, A.V.; Shuvalov, A.L. The topological characteristics of the singular points of an electrical field accompanying the propagation of sound in piezoelectrics. Zhurnal Eksperimentalnoi I Teor. Fiz. 1987, 93, 723–732. [Google Scholar]
- Molotskii, M.I. Theoretical basis for electro-and magnetoplasticity. Mater. Sci. Eng. A 2000, 287, 248–258. [Google Scholar] [CrossRef]
- Müllner, P.; Chernenko, V.A.; Kostorz, G. A microscopic approach to the magnetic-field-induced deformation of martensite (magnetoplasticity). J. Magn. Magn. Mater. 2003, 267, 325–334. [Google Scholar] [CrossRef]
- Klypin, A.A. Effect of magnetic and electric fields on creep. Met. Sci. Heat Treat. 1974, 15, 639–642. [Google Scholar] [CrossRef]
- Gavrilov, G.M. Change in the properties of quenched steel in magnetic field. Met. Sci. Heat Treat. 1977, 19, 442–446. [Google Scholar] [CrossRef]
- Akram, S.; Babutskyi, A.; Chrysanthou, A.; Montalvão, D.; Pizurova, N. Effect of Alternating Magnetic Field on the Fatigue Behaviour of EN8 Steel and 2014-T6 Aluminium Alloy. Metals 2019, 9, 984. [Google Scholar] [CrossRef]
- Li, G.R.; Wang, F.F.; Wang, H.M.; Zheng, R.; Xue, F.; Cheng, J.F. Influence of high pulsed magnetic field on tensile properties of TC4 alloy. Chin. Phys. B 2017, 26, 046201. [Google Scholar] [CrossRef]
- Wang, H.-M.; Zhu, Y.; Li, G.-R.; Zheng, R. Plasticity and microstructure of AZ31 magnesium alloy under coupling action of high pulsed magnetic field and external stress. Acta Phys. Sin. 2016, 65, 146101. [Google Scholar] [CrossRef]
- Choi, K.J.; Yoo, S.C.; Ham, J.; Kim, J.H.; Jeong, S.Y.; Choi, Y.S. Fatigue behavior of AISI 8620 steel exposed to magnetic field. J. Alloys Compd. 2018, 764, 73–79. [Google Scholar] [CrossRef]
- Nawaz, B.; Long, X.; Yang, Z.; Zhao, J.; Zhang, F.; Li, J. Effect of magnetic field on microstructure and mechanical properties of austempered 70Si3MnCr steel. Mater. Sci. Eng. A 2019, 759, 11–18. [Google Scholar] [CrossRef]
- Murase, S.; Kobatake, S.; Tanaka, M.; Tashiro, I.; Horigami, O.; Ogiwara, H.; Shibata, K.; Nagai, K.; Ishikawa, K. Effects of a high magnetic field on fracture toughness at 4.2 K for austenitic stainless steels. Fusion Eng. Des. 1993, 20, 451–454. [Google Scholar] [CrossRef]
- Zhang, Y.; Gey, N.; He, C.; Zhao, X.; Zuo, L.; Esling, C. High temperature tempering behaviors in a structural steel under high magnetic field. Acta Mater. 2004, 52, 3467–3474. [Google Scholar] [CrossRef]
- Kovaleva, T.G.; Shevchuk, A.D. Effect of a magnetic field on the elasticity characteristics for certain steels and alloys. Strength Mater. 1983, 15, 701–703. [Google Scholar] [CrossRef]
- Guo, Y.; Lee, Y.J.; Zhang, Y.; Sorkin, A.; Manzhos, S.; Wang, H. Effect of a weak magnetic field on ductile–brittle transition in micro-cutting of single-crystal calcium fluoride. J. Mater. Sci. Technol. 2022, 112, 96–113. [Google Scholar] [CrossRef]
- Sidhom, A.A.; Sayed, S.A.; Naga, S.A. The influence of magnetic field on the mechanical properties & microstructure of plain carbon steel. Mater. Sci. Eng. A 2017, 682, 636–639. [Google Scholar] [CrossRef]
- Hou, M.; Li, K.; Li, X.; Zhang, X.; Rui, S.; Cai, Z.; Wu, Y. Effects of Pulsed Magnetic Fields of Different Intensities on Dislocation Density, Residual Stress, and Hardness of Cr4Mo4V Steel. Crystals 2020, 10, 115. [Google Scholar] [CrossRef]
- Bose, M.S.C. Effect of saturated magnetic field on fatigue life of carbon steel. Phys. Status Solidi (A) 1984, 86, 649–654. [Google Scholar] [CrossRef]
- Fahmy, Y.; Hare, T.; Tooke, R.; Conrad, H. Effects of a Pulsed Magnetic Treatment on the Fatigue of Low Carbon Steel. Scr. Mater. 1998, 38, 1355–1358. [Google Scholar] [CrossRef]
- Bhat, I.K.; Muju, M.K.; Mazumdar, P.K. Possible effects of magnetic fields in fatigue. Int. J. Fatigue 1993, 15, 193–197. [Google Scholar] [CrossRef]
- Mohin, M.A.; Toofanny, H.; Babutskyi, A.; Lewis, A.; Xu, Y.G. Effect of Electromagnetic Treatment on Fatigue Resistance of 2011 Aluminum Alloy. J. Multiscale Model. 2016, 7, 1650004. [Google Scholar] [CrossRef]
- Gu, Q.; Huang, X.; Xi, J.; Gao, Z. The Influence of Magnetic Field on Fatigue and Mechanical Properties of a 35CrMo Steel. Metals 2021, 11, 542. [Google Scholar] [CrossRef]
- Aksenova, K.; Zaguliaev, D.; Konovalov, S.; Shlyarov, V.; Ivanov, Y. Influence of Constant Magnetic Field upon Fatigue Life of Commercially Pure Titanium. Materials 2022, 15, 6926. [Google Scholar] [CrossRef]
- Skvortsov, A.A.; Pshonkin, D.E.; Luk’Yanov, M.N.; Rybakova, M.R. Influence of permanent magnetic fields on creep and microhardness of iron-containing aluminum alloy. J. Mater. Res. Technol. 2019, 8, 2481–2485. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, H.; Yu, X.; Li, J.; Zhang, B.; Li, T. Research Progress of Magnetic Field Regulated Mechanical Property of Solid Metal Materials. Metals 2022, 12, 1988. [Google Scholar] [CrossRef]
- Zheng, X.J.; Liu, X.E. A nonlinear constitutive model for Terfenol-D rods. J. Appl. Phys. 2005, 97, 053901. [Google Scholar] [CrossRef]
- Li, J.; Xu, M. Modified Jiles-Atherton-Sablik model for asymmetry in magnetomechanical effect under tensile and compressive stress. J. Appl. Phys. 2011, 110, 063918. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis (invited). J. Appl. Phys. 1984, 55, 2115–2120. [Google Scholar] [CrossRef]
- Sablik, M.J. A Model for Asymmetry in Magnetic Property Behavior under Tensile and Compressive Stress in Steel. IEEE Trans. Magn. 1997, 33, 3958–3960. [Google Scholar] [CrossRef]
- Wang, Z.D.; Deng, B.; Yao, K. Physical model of plastic deformation on magnetization in ferromagnetic materials. J. Appl. Phys. 2011, 109, 083928. [Google Scholar] [CrossRef]
- Daniel, L. An analytical model for the magnetostriction strain of ferromagnetic materials subjected to multiaxial stress. Eur. Phys. J. Appl. Phys. 2018, 83, 30904. [Google Scholar] [CrossRef]
- Shi, P.; Bai, P.; Chen, H.-E.; Su, S.; Chen, Z. The magneto-elastoplastic coupling effect on the magnetic flux leakage signal. J. Magn. Magn. Mater. 2020, 504, 166669. [Google Scholar] [CrossRef]
- Shi, P. Magneto-elastoplastic coupling model of ferromagnetic material with plastic deformation under applied stress and magnetic fields. J. Magn. Magn. Mater. 2020, 512, 166980. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. I and II. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Eckart, C. The thermodynamics of irreversible processes. III and IV Relativistic Theory of the Simple Fluid. Phys. Rev. 1948, 58, 919. [Google Scholar] [CrossRef]
- Kroner, E. General continuum theory of dislocations and proper stresses. Arch. Rat. Mech. Anal. 1960, 4, 273–334. [Google Scholar]
- Coleman, B.D.; Gurtin, M.E. Thermodynamics with internal state variables. J. Chem. Phys. 1967, 47, 597–613. [Google Scholar] [CrossRef]
- Cho, H.E.; Hammi, Y.; Francis, D.K.; Stone, T.; Mao, Y.; Sullivan, K.; Wilbanks, J.; Zelinka, R.; Horstemeyer, M.F. Microstructure- Sensitive, History-Dependent Internal State Variable Plasticity-Damage Model for a Sequential Tubing Process. In Integrated Computational Materials Engineering (ICME) for Metals; Wiley: Hoboken, NJ, USA, 2018; pp. 199–234. [Google Scholar]
- Horstemeyer, M.F.; Bammann, D.J. Historical review of internal state variable theory for inelasticity. Int. J. Plast. 2010, 26, 1310–1334. [Google Scholar] [CrossRef]
- Lee, E.H.; Liu, D.T. Finite Strain Elastic-plastic Theory with Application to Plane-Wave, Analysis. J. Appl. Phys. 1967, 38, 391–408. [Google Scholar] [CrossRef]
- Murakami, S. Mechanical modeling of material damage. J. Appl. Mech. 1988, 55, 280–286. [Google Scholar] [CrossRef]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Bammann, D.J.; Aifantis, E.C. A damage model for ductile metals. Nucl. Eng. Des. 1989, 116, 355–362. [Google Scholar] [CrossRef]
- Marin, E.B.; McDowell, D.L. Associative versus non-associative porous viscoplasticity based on internal state variable concepts. Int. J. Plast. 1996, 12, 629–669. [Google Scholar] [CrossRef]
- Steinmann, P.; Carol, I. A framework for geometrically nonlinear continuum damage mechanics. Int. J. Eng. Sci. 1998, 36, 1793–1814. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Park, T. The kinematics of damage for finite-strain elasto-plastic solids. Int. J. Eng. Sci. 1999, 37, 803–830. [Google Scholar] [CrossRef]
- Brünig, M. Numerical analysis and elastic–plastic deformation behavior of anisotropically damaged solids. Int. J. Plast. 2002, 18, 1237–1270. [Google Scholar] [CrossRef]
- Regueiro, R.A.; Bammann, D.J.; Marin, E.B.; Garikipati, K. A nonlocal phenomenological anisotropic finite deformation plasticity model accounting for dislocation defects. J. Eng. Mater. Technol. 2002, 124, 380–387. [Google Scholar] [CrossRef]
- Solanki, K.N. Physically Motivated Internal State Variable Form of a Higher Order Damage Model for Engineering Materials with Uncertainty; Mississippi State University: Starkville, MS, USA, 2008. [Google Scholar]
- Bammann, D.J.; Aifantis, E.C. An anisotropic hardening model of plasticity. Comput. Mech. 1988, 88, 459–462. [Google Scholar]
- Bammann, D.J.; Chiesa, M.; Johnson, G. Modeling large deformation and failure in manufacturing processes. In Theoretical and Applied Mechanics; Tatsumi, T., Watanabe, E., Kambe, T., Eds.; Mathematical Institute SANU: Belgrade, Serbia, 1996; pp. 359–376. [Google Scholar]
- Bammann, D.J.; Chiesa, M.L.; Horstemeyer, M.F.; Weingarten, L.I. Failure in ductile materials using finite element methods. In Structural Crashworthiness and Failure; CRC Press: Boca Raton, FL, USA, 1993; pp. 1–54. [Google Scholar]
- Francis, D.K.; Bouvard, J.L.; Hammi, Y.; Horstemeyer, M.F. Formulation of a damage internal state variable model for amorphous glassy polymers. Int. J. Solids Struct. 2014, 51, 2765–2776. [Google Scholar] [CrossRef]
- Horstemeyer, M.F.; Lathrop, J.; Gokhale, A.M.; Dighe, M. Modelling stress state dependent damage evolution in a cast Al-Si-Mg aluminium alloy. Theor. Appl. Fract. Mech. 2000, 3, 31–47. [Google Scholar] [CrossRef]
- Cho, H.E.; Hammi, Y.; Bowman, A.L.; Karato, S.; Baumgardner, J.R.; Horstemeyer, M.F. A unified static and dynamic recrystallization Internal State Variable (ISV) constitutive model coupled with grain size evolution for metals and mineral aggregates. Int. J. Plast. 2019, 112, 123–157. [Google Scholar] [CrossRef]
- Dimitrov, N.; Liu, Y.; Horstemeyer, M.F. An electroplastic internal state variable (ISV) model for nonferromagnetic ductile metals. Mech. Adv. Mater. Struct. 2020, 29, 761–772. [Google Scholar] [CrossRef]
- Cho, H.E.; Zbib, H.M.; Horstemeyer, M.F. An Internal State Variable Elastoviscoplasticity-Damage Model for Irradiated Metals. J. Eng. Mater. Technol. 2022, 144, 1–44. [Google Scholar] [CrossRef]
- Brugmans, A. Magnetismus, seu de affinitatibus magneticis observationes academicae. In Apud Luzac & Van Damme; Lugduni Batavorum: Leiden, The Netherlands, 1778. [Google Scholar]
- Stoner, E.C. Collective Electron Specific Heat and Spin Paramagnetism in Metals. R. Soc. Publ. 1935, 154, 656–678. [Google Scholar]
- Nunez, A.S.; Duine, R.A.; Haney, P.; MacDonald, A.H. Theory of spin torques and giant magnetoresistance in antiferromagnetic metals. Phys. Rev. 2006, 73, 214426. [Google Scholar] [CrossRef]
- Linnemann, K.; Klinkel, S.; Wagner, W. A constitutive model for magnetostrictive and piezoelectric materials. Int. J. Solids Struct. 2009, 46, 1149–1166. [Google Scholar] [CrossRef]
- Dapino, M.J.; Smith, R.C.; Flatau, A.B. A structural magnetic strain model for magnetostrictive transducers. IEEE Trans. Magn. 2000, 36, 545–556. [Google Scholar] [CrossRef]
- Burgoyne, J.W.; Daniels, D.; Timms, K.W.; Vale, S.H. Advances in superconducting magnets for commercial and industrial applications. IEEE Trans. Appl. Supercond. 2000, 10, 703–709. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Kwon, Y.E. Review of magnetostrictive patch transducers and applications in ultrasonic nondestructive testing of waveguides. Ultrasonics 2015, 62, 3–19. [Google Scholar] [CrossRef] [PubMed]
- Calkins, F.T.; Flatau, A.B.; Dapino, M.J. Overview of magnetostrictive sensor technology. J. Intell. Mater. Syst. Struct. 2007, 18, 1057–1066. [Google Scholar] [CrossRef]
- Ekreem, N.B.; Olabi, A.G.; Prescott, T.; Rafferty, A.; Hashmi, M.S.J. An overview of magnetostriction, its use and methods to measure these properties. J. Mater. Process Technol. 2007, 191, 96–101. [Google Scholar] [CrossRef]
- Bieńkowski, A.; Kulikowski, J. The magneto-elastic Villari effect in ferrites. J. Magn. Magn. Mater. 1980, 19, 120–122. [Google Scholar] [CrossRef]
- Skomski, R.; Sellmyer, D.J. Curie temperature of multiphase nanostructures. J. Appl. Phys. 2000, 87, 4756–4758. [Google Scholar] [CrossRef]
- Arrott, A. Criterion for ferromagnetism from observations of magnetic isotherms. Phys. Rev. 1957, 108, 1394. [Google Scholar] [CrossRef]
- Dey, P.; Roy, J.N. Magnetic Domain Wall Motion. Spintronics 2021, 145–161. [Google Scholar] [CrossRef] [PubMed]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Yang, C.N. The spontaneous magnetization of a two-dimensional Ising model. Phys. Rev. 1952, 85, 808. [Google Scholar] [CrossRef]
- McCoy, B.M.; Wu, T.T. The Two-Dimensional Ising Model; Courier Corporation: North Chelmsford, MA, USA, 2014. [Google Scholar]
- Bammann, D.J.; Johnson, G.C. On the kinematics of finite-deformation plasticity. Acta Mech. 1987, 70, 1–13. [Google Scholar] [CrossRef]
- Hashiguchi, K. Nonlinear Continuum Mechanics for Finite Elasticity-Plasticity: Multiplicative Decomposition with Subloading Surface Model; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Sun, Q.C.; Song, T.; Anderson, E.; Brunner, A.; Förster, J.; Shalomayeva, T.; Taniguchi, T.; Watanabe, K.; Gräfe, J.; Stöhr, R.; et al. Magnetic domains and domain wall pinning in atomically thin CrBr3 revealed by nanoscale imaging. Nat. Commun. 2021, 12, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Fiorillo, F.; Küpferling, M.; Appino, C. Magnetic Hysteresis and Barkausen Noise in Plastically Deformed Steel Sheets. Metals 2018, 8, 15. [Google Scholar] [CrossRef]
- Hammi, Y.; Horstemeyer, M.F.; Bammann, D.J. An anisotropic damage model for ductile metals. Int. J. Damage Mech. 2003, 12, 245–262. [Google Scholar] [CrossRef]
- Bammann, D.J.; Solanki, K. On kinematic, thermodynamic, and kinetic coupling of a damage theory of polycrystalline material. Int. J. Solids Struct. 2010, 26, 775–924. [Google Scholar] [CrossRef]
- Dafalias, F. The plastic spin in viscoplasticity. Int. J. Solids Struct. 1989, 26, 149–163. [Google Scholar] [CrossRef]
- Bammann, D.J. Modeling temperature and strain rate dependent large deformations of metals. Appl. Mech. Rev. 1990, 43, S312–S319. [Google Scholar] [CrossRef]
- Horstemeyer, M. Integrated Computational Materials Engineering (ICME) for Metals: Using Multiscale Modeling to Invigorate Engineering Design with Science; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hanson, R.; Witkamp, B.; Vandersypen, L.M.K.; van Beveren, L.W.; Elzerman, J.M.; Kouwenhoven, L. Zeeman energy and spin relaxation in a one-electron quantum dot. Phys. Rev. Lett. 2003, 91, 196802. [Google Scholar] [CrossRef]
- Gaskell, D.R.; Laughlin, D.E. Introduction to the Thermodynamics of Materials; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Feinberg, M.; Lavine, R. Thermodynamics based on the Hahn-Banach theorem: The Clausius inequality. Arch. Ration. Mech. Anal. 1983, 82, 203–293. [Google Scholar] [CrossRef]
- Salehghaffari, S.; Rais-Rohani, M.; Marin, E.; Bammann, D. A new approach for determination of material constants of internal state variable based plasticity models and their uncertainty quantification. Comput. Mater. Sci. 2011, 55, 237–244. [Google Scholar] [CrossRef]
- Dimitrov, N.; Liu, Y.; Horstemeyer, M.F. On the thermo-mechanical coupling of the Bammann plasticity-damage internal state variable model. Acta Mech. 2019, 230, 1855–1868. [Google Scholar] [CrossRef]
- Clark, A.E.; DeSavage, B.F.; Bozorth, R. Anomalous thermal expansion and magnetostriction of single-crystal dysprosium. Phys. Rev. 1965, 138, A216. [Google Scholar] [CrossRef]
- Kratochvil, J.; Dillon, O.W., Jr. Thermodynamics of elastic-plastic materials as a theory with internal state variables. J. Appl. Phys. 1969, 40, 3207–3218. [Google Scholar] [CrossRef]
- Paulo, V.I.M.; Neves-Araujo, J.; Revoredo, F.A.; Padrón-Hernández, E. Magnetization curves of electrodeposited Ni, Fe and Co nanotubes. Mater. Lett. 2018, 223, 78–81. [Google Scholar] [CrossRef]
- Horstemeyer, M.F.; Gokhale, A.M. A void-crack nucleation model for ductile metals. Int. J. Solids Struct. 1999, 36, 5029–5055. [Google Scholar] [CrossRef]
- Horstemeyer, M.; Matalanis, M.; Sieber, A.; Botos, M. Micromechanical finite element calculations of temperature and void configuration effects on void growth and coalescence. Int. J. Plast. 2000, 16, 979–1015. [Google Scholar] [CrossRef]
- Tucker, M.T.; Horstemeyer, M.F.; Whittington, W.R.; Solanki, K.N. Structure/property Relations of Aluminum under Varying Rates and Stress States; No. LA-UR-10-07799; LA-UR-10-7799; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2010. [Google Scholar]
- McClintock, F.A. A criterion for ductile fracture by the growth of holes. J. Appl. Mech. 1964, 35, 363–371. [Google Scholar] [CrossRef]
- Wang, X.; Thomas, D.W.P.; Sumner, M.; Paul, J.; Cabral, S.H.L. Characteristics of Jiles-Atherton Model Parameters and Their Application to Transformer Inrush Current Simulation. IEEE Trans. Magn. 2008, 44, 340–345. [Google Scholar] [CrossRef]




| Type | Spin Alignment | Spin Illustrated in Simplified Plot | Examples |
|---|---|---|---|
| Ferromagnets | Electron spins align parallel to one another, resulting in a spontaneous magnetization. | 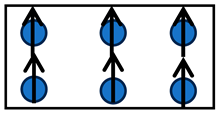 | Fe, Co, Ni |
| Ferrimagnets | Majority of electron’s spins parallel to one another, some spins are antiparallel, resulting in spontaneous magnetization. |  | Magnetite (), yttrium iron garnet (YIG) |
| Antiferromagnets | Electron spins align antiparallel to each other, resulting in a null net magnetization. | 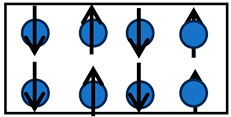 | Cr |
| Paramagnets | Electron spins tend to align parallel when an external magnetic field is applied. |  | Oxygen, sodium, aluminum, calcium, uranium |
| Diamagnets | Electron spins tend to align antiparallel to an external magnetic field. |  | Copper, silver, gold, nitrogen |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malki, M.; Horstemeyer, M.F.; Cho, H.E.; Peterson, L.A.; Dickel, D.; Capolungo, L.; Baskes, M.I. A Multiphysics Thermoelastoviscoplastic Damage Internal State Variable Constitutive Model including Magnetism. Materials 2024, 17, 2412. https://doi.org/10.3390/ma17102412
Malki M, Horstemeyer MF, Cho HE, Peterson LA, Dickel D, Capolungo L, Baskes MI. A Multiphysics Thermoelastoviscoplastic Damage Internal State Variable Constitutive Model including Magnetism. Materials. 2024; 17(10):2412. https://doi.org/10.3390/ma17102412
Chicago/Turabian StyleMalki, M., M. F. Horstemeyer, H. E. Cho, L. A. Peterson, D. Dickel, L. Capolungo, and M. I. Baskes. 2024. "A Multiphysics Thermoelastoviscoplastic Damage Internal State Variable Constitutive Model including Magnetism" Materials 17, no. 10: 2412. https://doi.org/10.3390/ma17102412
APA StyleMalki, M., Horstemeyer, M. F., Cho, H. E., Peterson, L. A., Dickel, D., Capolungo, L., & Baskes, M. I. (2024). A Multiphysics Thermoelastoviscoplastic Damage Internal State Variable Constitutive Model including Magnetism. Materials, 17(10), 2412. https://doi.org/10.3390/ma17102412









