Quasi-Static Penetration Properties of 3D-Printed Composite Plates
Abstract
:1. Introduction
2. Materials and Methods
2.1. 3D Printing Equipment
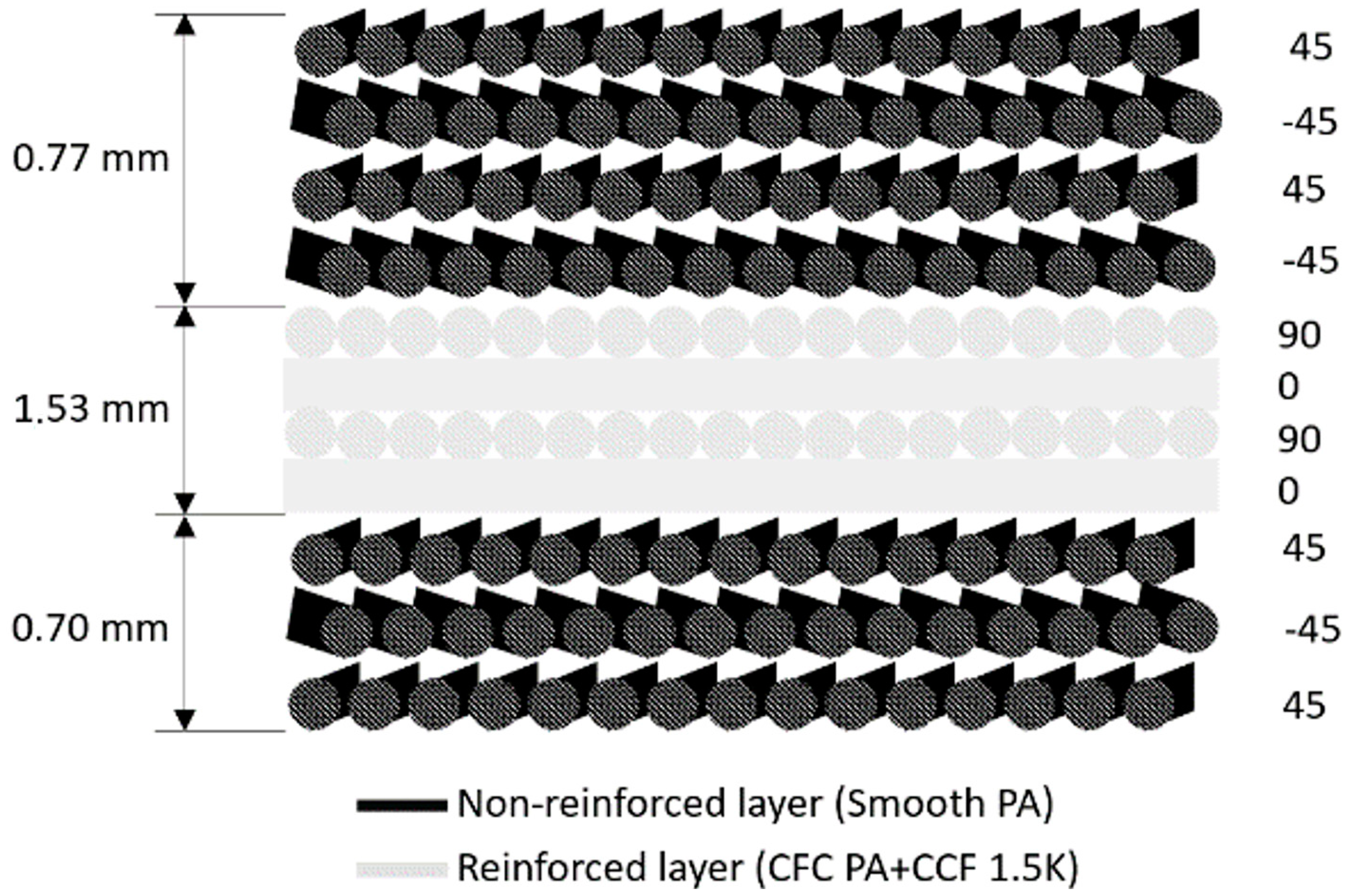
2.2. Plate Specimens
2.3. Quasi-Static Indentation Test Equipment
2.4. Quasi-Static Penetration Model (QSPM)
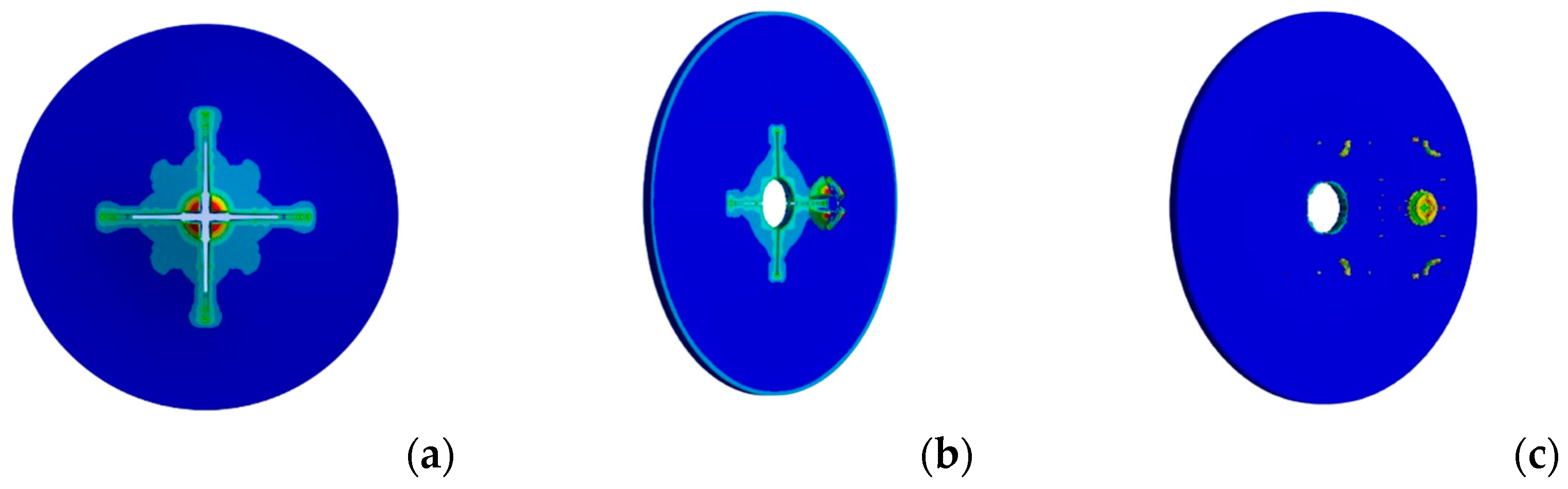
2.5. Preliminary Dynamic FEM Analysis of Short-Fiber-Reinforced Plates
3. Results and Discussion
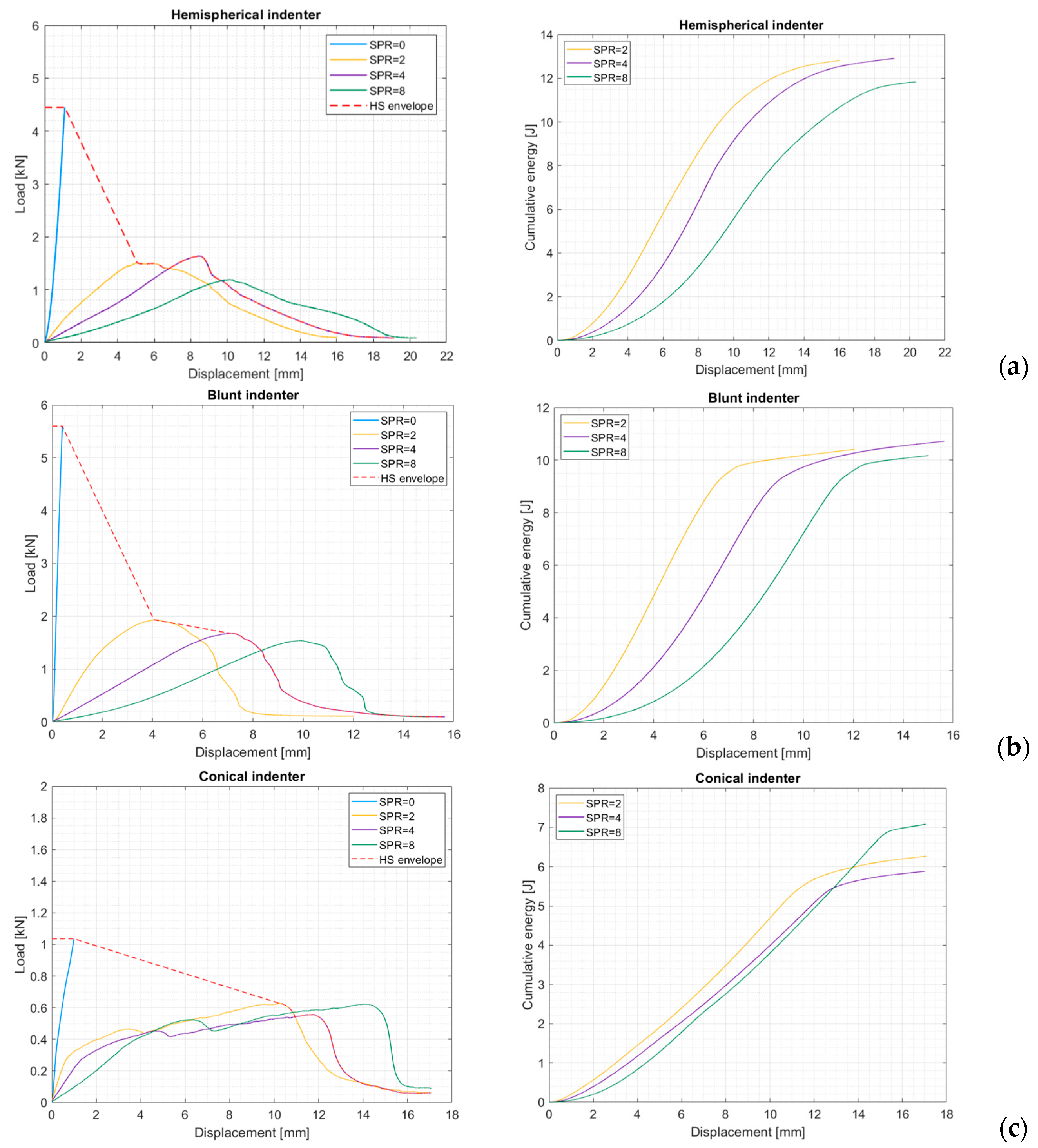
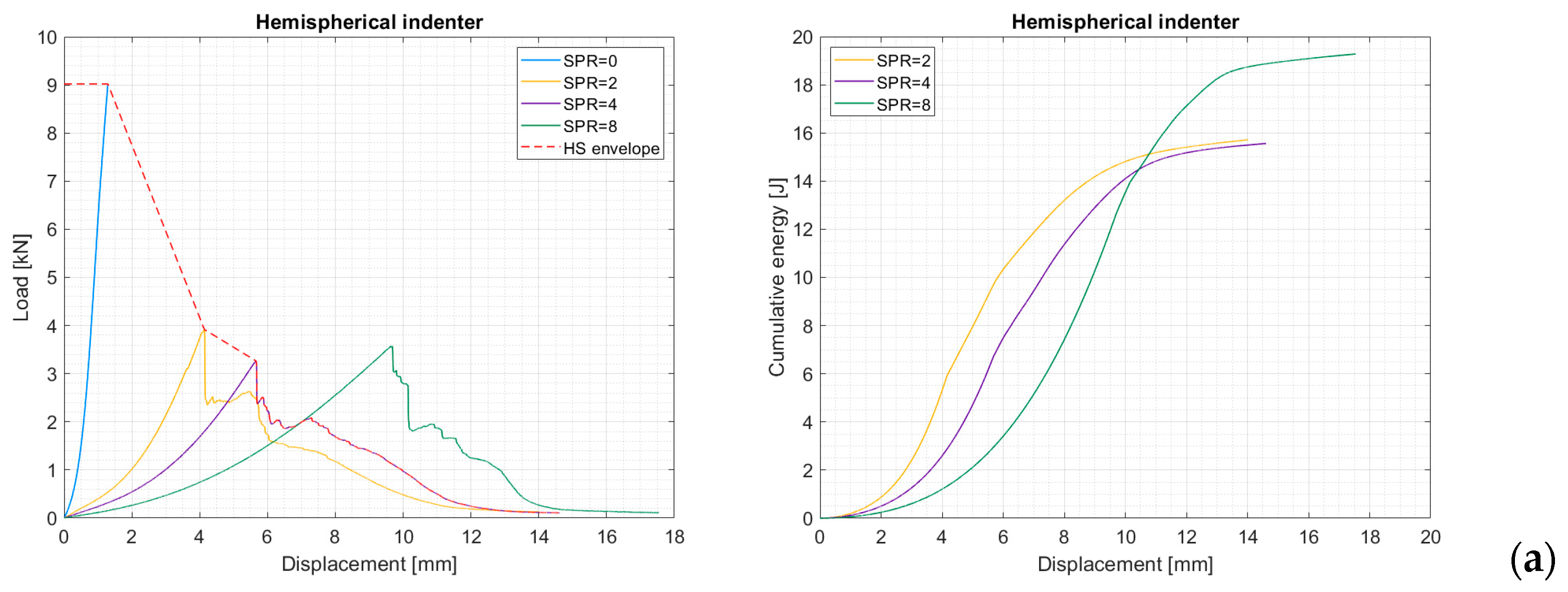
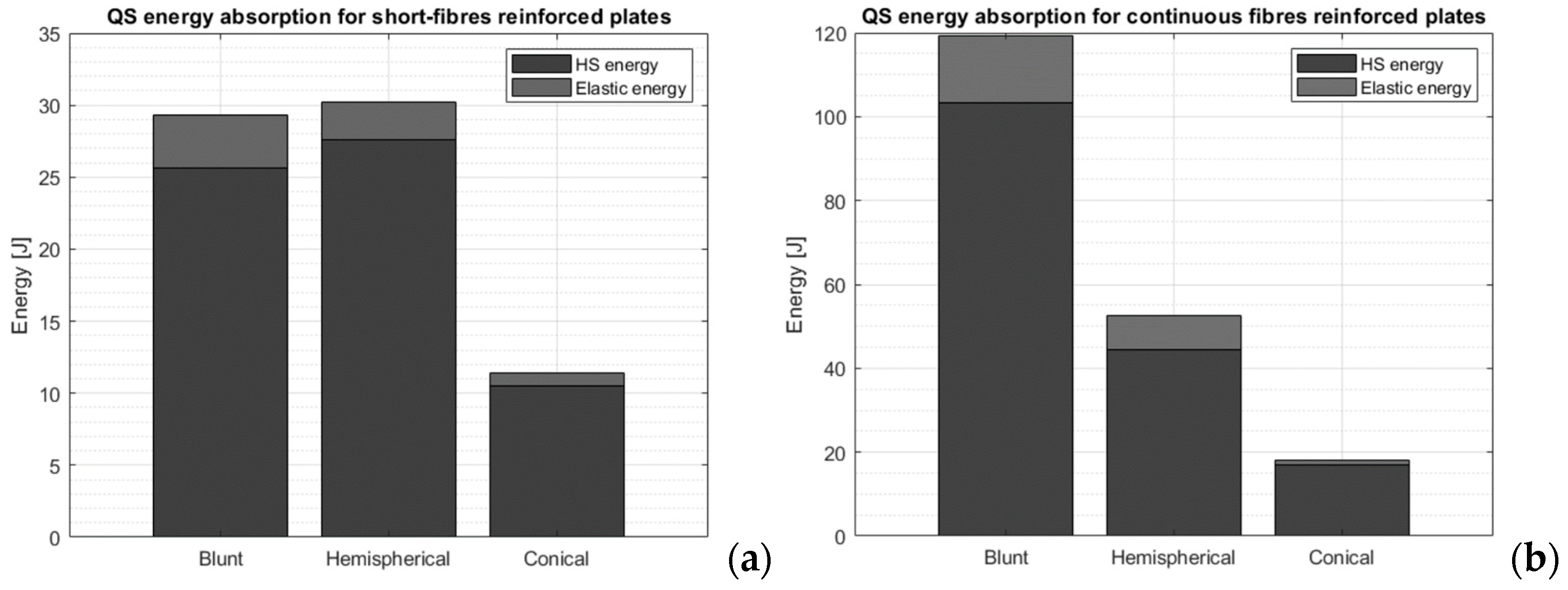
3.1. Quasi-Static Punch Model Applied to Short-Fiber-Reinforced Plates
3.2. Quasi-Static Punch Model Applied to Continuous-Fiber-Reinforced Plates
3.3. Plate Strengthening through Addition of Continuous Fibers
3.4. Plate Strengthening through Addition of Continuous Fibers
3.5. Traditional vs. FFF-Printed Plates: Quasi-Static Loading
4. Discussion
4.1. Uncertainty in the Quasi-Static Punch Model
4.2. Performance Increase through Addition of Continuous Fibers
4.3. Overall Performance of FFF Plates Reinforced with Continuous Fibers
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kabir, S.M.F.; Mathur, K.; Seyam, A.-F.M. A Critical Review on 3D Printed Continuous Fiber-Reinforced Composites: History, Mechanism, Materials and Properties. Compos. Struct. 2020, 232, 111476. [Google Scholar] [CrossRef]
- Safari, F.; Kami, A.; Abedini, V. 3D Printing of Continuous Fiber Reinforced Composites: A Review of the Processing, Pre-and Post-Processing Effects on Mechanical Properties. Polym. Polym. Compos. 2022, 30, 09673911221098734. [Google Scholar] [CrossRef]
- Taghizadeh, S.; Niknejad, A.; Concli, F. Mechanical Behavior of Novel Bio Composite Sandwich Structures Under Quasi-Static Compressive Loading Condition. In Towards a Smart, Resilient and Sustainable Industry, Proceedings of the International Symposium on Industrial Engineering and Automation, Bozen-Bolzano, Italy, 22–23 June 2023; Springer: Cham, Switzerland, 2023; pp. 544–551. [Google Scholar]
- Wang, K.; Zhu, W.; Li, S.; Peng, Y.; Ahzi, S. Investigations of Quasi-Static Indentation Properties of 3D Printed Polyamide/Continuous Kevlar/Continuous Carbon Fiber Composites. J. Appl. Polym. Sci. 2022, 139, e52758. [Google Scholar] [CrossRef]
- Goh, G.D.; Dikshit, V.; Nagalingam, A.P.; Goh, G.L.; Agarwala, S.; Sing, S.L.; Wei, J.; Yeong, W.Y. Characterization of Mechanical Properties and Fracture Mode of Additively Manufactured Carbon Fiber and Glass Fiber Reinforced Thermoplastics. Mater. Des. 2018, 137, 79–89. [Google Scholar] [CrossRef]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.-F.M. Maximizing the Performance of 3D Printed Fiber-Reinforced Composites. J. Compos. Sci. 2021, 5, 136. [Google Scholar] [CrossRef]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.-F.M. Impact Resistance and Failure Mechanism of 3D Printed Continuous Fiber-Reinforced Cellular Composites. J. Text. Inst. 2021, 112, 752–766. [Google Scholar] [CrossRef]
- Caminero, M.A.; Chacón, J.M.; García-Moreno, I.; Rodríguez, G.P. Impact Damage Resistance of 3D Printed Continuous Fibre Reinforced Thermoplastic Composites Using Fused Deposition Modelling. Compos. B Eng. 2018, 148, 93–103. [Google Scholar] [CrossRef]
- Li, L.; Liu, W.; Sun, L. Mechanical Characterization of 3D Printed Continuous Carbon Fiber Reinforced Thermoplastic Composites. Compos. Sci. Technol. 2022, 227, 109618. [Google Scholar] [CrossRef]
- Fraccaroli, L.; Concli, F. Introduction of Open-Source Engineering Tools for the Structural Modeling of a Multilayer Mountaineering Ski under Operation. Appl. Sci. 2020, 10, 5310. [Google Scholar] [CrossRef]
- Cersoli, T.; Yelamanchi, B.; MacDonald, E.; Carrillo, J.G.; Cortes, P. 3D Printing of a Continuous Fiber-Reinforced Composite Based on a Coaxial Kevlar/PLA Filament. Compos. Adv. Mater. 2021, 30, 26349833211000058. [Google Scholar] [CrossRef]
- Cheng, P.; Peng, Y.; Wang, K.; Le Duigou, A.; Yao, S.; Chen, C. Quasi-Static Penetration Property of 3D Printed Woven-like Ramie Fiber Reinforced Biocomposites. Compos. Struct. 2023, 303, 116313. [Google Scholar] [CrossRef]
- Taghizadeh, S.; Concli, F. Numerical Investigation of the Mechanical Performance of Multilayer Composite Laminates under Low Velocity Impact Loading Condition. In Towards a Smart, Resilient and Sustainable Industry, Proceedings of the International Symposium on Industrial Engineering and Automation, Bozen-Bolzano, Italy, 22–23 June 2023; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 745 LNNS, pp. 745600–745608. [Google Scholar] [CrossRef]
- Gama, B.A.; Gillespie, J.W., Jr. Punch Shear Based Penetration Model of Ballistic Impact of Thick-Section Composites. Compos. Struct. 2008, 86, 356–369. [Google Scholar] [CrossRef]
- Potti, S.V.; Sun, C.T. Prediction of Impact Induced Penetration and Delamination in Thick Composite Laminates. Int. J. Impact Eng. 1997, 19, 31–48. [Google Scholar] [CrossRef]
- Taghizadeh, S.A.; Liaghat, G.; Niknejad, A.; Pedram, E. Experimental Study on Quasi-Static Penetration Process of Cylindrical Indenters with Different Nose Shapes into the Hybrid Composite Panels. J. Compos. Mater. 2019, 53, 107–123. [Google Scholar] [CrossRef]
- Gellert, E.P.; Cimpoeru, S.J.; Woodward, R.L. A Study of the Effect of Target Thickness on the Ballistic Perforation of Glass-Fibre-Reinforced Plastic Composites. Int. J. Impact Eng. 2000, 24, 445–456. [Google Scholar] [CrossRef]
- Concli, F.; Gonzalez-Jimenez, A.; Manes, A.; Giglio, M. Experimental Testing and Numerical Modelling of a Kevlar Woven–Epoxy Matrix Composite Subjected to a Punch Test. Procedia Struct. Integr. 2019, 24, 3–10. [Google Scholar] [CrossRef]
- Liu, F.; Ferraris, E.; Ivens, J. Mechanical Investigation and Microstructure Performance of a Two-Matrix Continuous Carbon Fibre Composite Fabricated by 3D Printing. J. Manuf. Process 2022, 79, 383–393. [Google Scholar] [CrossRef]
- Parker, M.; Ezeokeke, N.; Matsuzaki, R.; Arola, D. Strength and Its Variability in 3D Printing of Polymer Composites with Continuous Fibers. Mater. Des. 2023, 225, 111505. [Google Scholar] [CrossRef]
- Nalli, F.; Cortese, L.; Concli, F. Ductile Damage Assessment of Ti6Al4V, 17–4PH and AlSi10Mg for Additive Manufacturing. Eng. Fract. Mech. 2021, 241, 107395. [Google Scholar] [CrossRef]
- Ojoc, G.G.; Pirvu, C.; Badea, S.; Deleanu, L. Friction modeling in simulating ballistic impact. A review. Proc. Eng. Sci. 2019, 1, 154–167. [Google Scholar] [CrossRef]
- Islam, M.N.; Baxevanakis, K.P.; Silberschmidt, V. V Dynamic Fracture Behaviour of Additively Manufactured Polymers and Composites under Ballistic Impact. Procedia Struct. Integr. 2022, 37, 217–224. [Google Scholar] [CrossRef]
- Scrocco, M.; Chamberlain, T.; Chow, C.; Weinreber, L.; Elks, E.; Halford, C.; Cortes, P.; Conner, B.P. Impact Testing of 3D Printed Kevlar-Reinforced Onyx Material. In Proceedings of the 29th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2018; University of Texas at Austin: Austin, TX, USA, 2018. [Google Scholar]
- Yelamanchi, B.; MacDonald, E.; Gonzalez-Canche, N.G.; Carrillo, J.G.; Cortes, P. The Mechanical Properties of Fiber Metal Laminates Based on 3D Printed Composites. Materials 2020, 13, 5264. [Google Scholar] [CrossRef] [PubMed]
- Papa, I.; Manco, E.; Epasto, G.; Lopresto, V.; Squillace, A. Impact Behaviour and Non Destructive Evaluation of 3D Printed Reinforced Composites. Compos. Struct. 2022, 281, 115112. [Google Scholar] [CrossRef]
- Ulven, C.; Vaidya, U.K.; Hosur, M. V Effect of Projectile Shape during Ballistic Perforation of VARTM Carbon/Epoxy Composite Panels. Compos. Struct. 2003, 61, 143–150. [Google Scholar] [CrossRef]
- Hosur, M.V.; Vaidya, U.K.; Ulven, C.; Jeelani, S. Performance of Stitched/Unstitched Woven Carbon/Epoxy Composites under High Velocity Impact Loading. Compos. Struct. 2004, 64, 455–466. [Google Scholar] [CrossRef]
- Goldsmith, W.; Dharan, C.K.H.; Chang, H. Quasi-Static and Ballistic Perforation of Carbon Fiber Laminates. Int. J. Solids Struct. 1995, 32, 89–103. [Google Scholar] [CrossRef]






| Material | Properties * | |||
|---|---|---|---|---|
| Diameter [mm] | Vf [−] | UTS [MPa] | E [GPa] | |
| Smooth PA | 1.75 | - | 71.8 | 5.82 |
| CFC PA | 1.75 | - | 41 | 1.25 |
| CCF-1.5K | 0.36 | 0.6 | 2206 | 149 |
| Parameter | Selection |
|---|---|
| Print speed | 10 mm/s |
| Layer thickness | 0.36 mm |
| Hatch spacing | 0.65 mm |
| Nozzle temperature | 250 °C |
| Fiber layout | 0°/90° |
| Property | Value |
|---|---|
| Elastic modulus | 3 GPa |
| Poisson’s ratio | 0.4 |
| Yield strength | 30 MPa |
| Ultimate tensile strength (UTS) | 50 MPa |
| Equivalent Plastic Strain at Failure (EQPS) | 0.035 |
| Study | Test | Material | SPR | Impact Velocity [m/s] | Areal Density [kg/m2] | Impact Energy [J] | Normalized Impact Energy [J/(kg/m2)] |
|---|---|---|---|---|---|---|---|
| [23] | Ballistic | Nylon—short fibers | 11.1 | 95 | 2.925 | 14 | 4.8 |
| [24] | Ballistic | Nylon—short fibers | 12.6 | 208 | 4.204 | 44.5 | 10.6 |
| [25] | Ballistic | Nylon—short fibers | 12.6 | 21 | 0.870 | 0.5 | 0.5 |
| [25] | Drop test | Nylon—short fibers | 5.1 | 2.7 | 0.870 | 5.0 | 4.4 |
| [26] | Drop test | Nylon—short fibers | 3.0 | 4 | 3.000 | 8.7 | 2.9 |
| FEM | N/A | Smooth PA | 8.0 | 16 | 3.150 | 2.54 | 0.9 |
| QSPM | Quasi-static | Smooth PA | 8.0 | N/A | 2.880 | 30.2 | 10.5 |
| Study | Test | Material | Vf [−] | SPR | Impact Velocity [m/s] | Areal Density [kg/m2] | Impact Energy [J] | Normalized Impact Energy [J/(kg/m2)] |
|---|---|---|---|---|---|---|---|---|
| [6] | Drop test | Nylon and glass fibers | 0.32 | 4.7 | 3.88 | 4.09 | 99.2 | 24.6 |
| [26] | Drop test | Nylon and glass fibers | 0.54 | 3.0 | 4 | 3.000 | 79.2 | 23.3 |
| QSPM | Quasi-static | Reinforced nylon and carbon fibers | 0.23 | 8.0 | N/A | 2.909 | 52.6 | 18.1 |
| Study | Test | Projectile Shape | SPR | Impact Velocity [m/s] | Areal Density [kg/m2] | Impact Energy [J] | Normalized Impact Energy [J/(kg/m2)] |
|---|---|---|---|---|---|---|---|
| [27] | Ballistic | Blunt | 8.0 | 82 | 3.660 | 47 | 12.8 |
| [27] | Ballistic | Hemis. | 8.0 | 79 | 3.660 | 44 | 12.0 |
| [27] | Ballistic | Conical | 8.0 | 83 | 3.660 | 48 | 13.1 |
| [15] | Ballistic | Blunt | 8.0 | 80 | 6.355 | 96 | 15.0 |
| [28] | Ballistic | Blunt | N/A | 114 | 5.250 | 87 | 16.6 |
| [29] | Ballistic | Conical | N/A | 44 | 3.506 | 29 | 8.3 |
| QSPM | Quasi-static | Blunt | 8.0 | N/A | 2.909 | 119.4 | 41.0 |
| QSPM | Quasi-static | Hemis. | 8.0 | N/A | 2.909 | 52.6 | 18.1 |
| QSPM | Quasi-static | Conical | 8.0 | N/A | 2.909 | 18.2 | 6.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baruscotti, A.; Borgianni, Y.; Concli, F. Quasi-Static Penetration Properties of 3D-Printed Composite Plates. Materials 2024, 17, 2536. https://doi.org/10.3390/ma17112536
Baruscotti A, Borgianni Y, Concli F. Quasi-Static Penetration Properties of 3D-Printed Composite Plates. Materials. 2024; 17(11):2536. https://doi.org/10.3390/ma17112536
Chicago/Turabian StyleBaruscotti, Axel, Yuri Borgianni, and Franco Concli. 2024. "Quasi-Static Penetration Properties of 3D-Printed Composite Plates" Materials 17, no. 11: 2536. https://doi.org/10.3390/ma17112536





