The Influence of Microstructural Arrangement on the Failure Characteristics of 3D-Printed Polymers: Exploring Damage Behaviour in Acrylonitrile Butadiene Styrene
Abstract
:1. Introduction
2. Experimental Layout
3. Modelling Technique
4. Results and Discussion
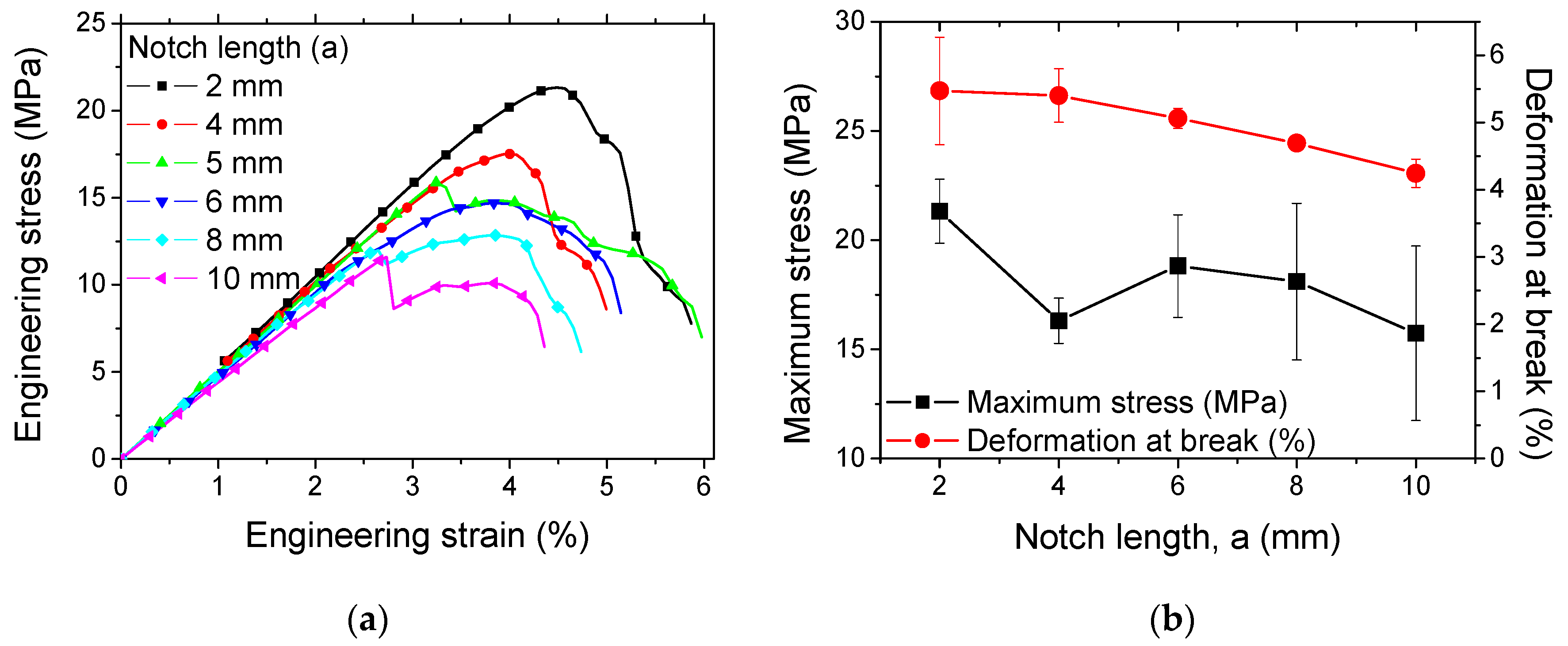
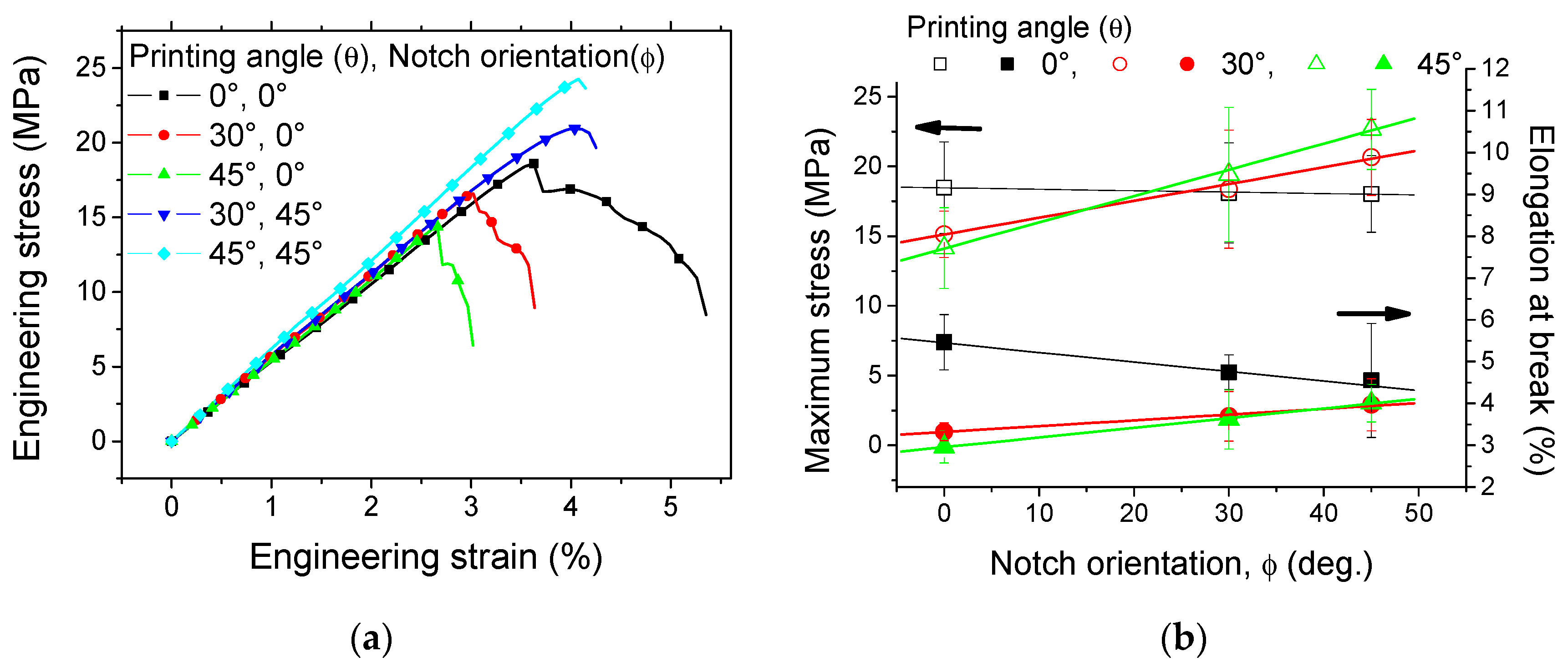
4.1. Experimental Results
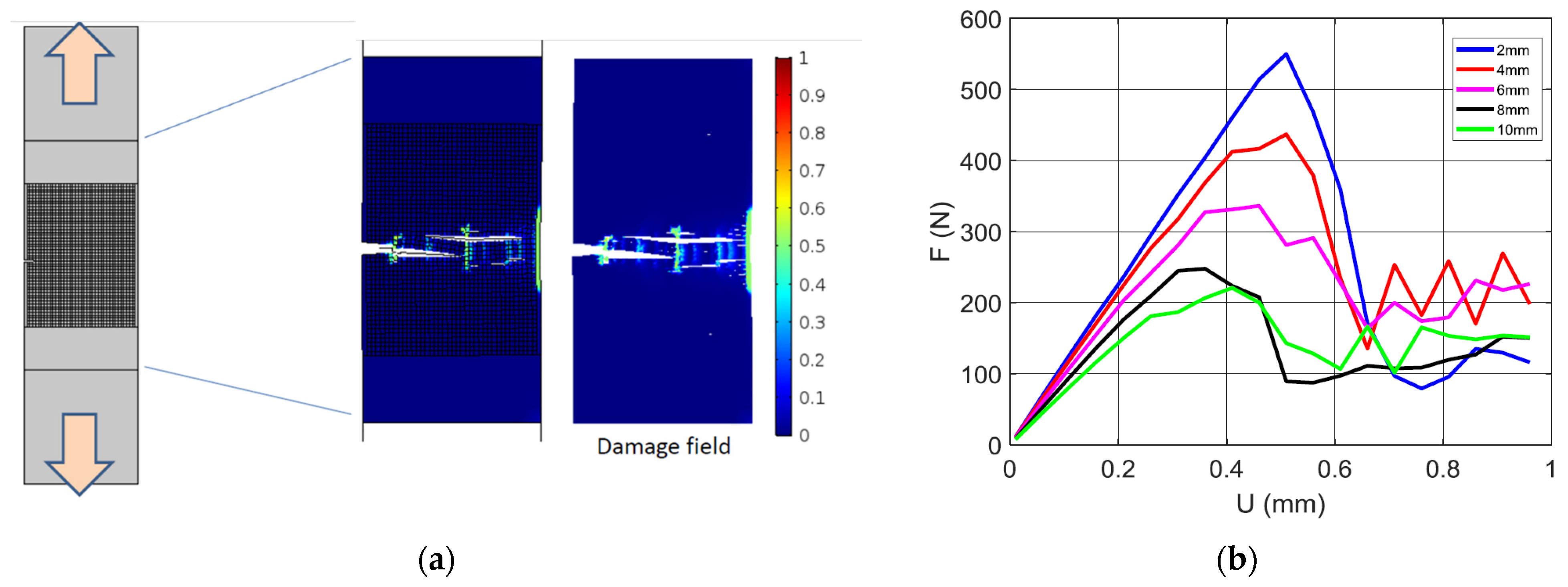
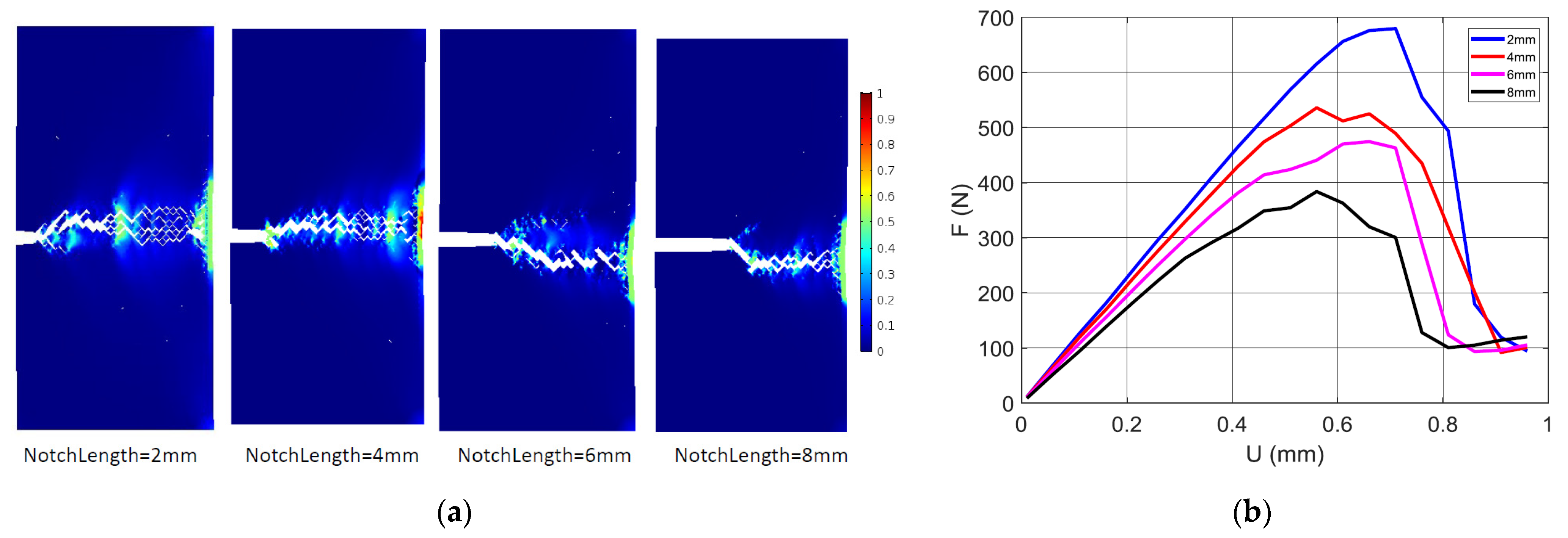
4.2. Numerical Results
4.3. Validity of the Cracking Behaviour for Other Feedstock Polymers
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Y.; Fang, J.; Wu, C.; Li, C.; Sun, G.; Li, Q. Additively manufactured materials and structures: A state-of-the-art review on their mechanical characteristics and energy absorption. Int. J. Mech. Sci. 2023, 246, 108102. [Google Scholar] [CrossRef]
- Vyavahare, S.; Mahesh, V.; Mahesh, V.; Harursampath, D. Additively manufactured meta-biomaterials: A state-of-the-art review. Compos. Struct. 2023, 305, 116491. [Google Scholar] [CrossRef]
- Hu, Z.; Ma, Z.; Yu, L.; Liu, Y. Functionally graded materials with grain-size gradients and heterogeneous microstructures achieved by additive manufacturing. Scr. Mater. 2023, 226, 115197. [Google Scholar] [CrossRef]
- Miki, T. Self-support topology optimization considering distortion for metal additive manufacturing. Comput. Methods Appl. Mech. Eng. 2023, 404, 115821. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Song, B.; Zhang, Z.; Zhang, J.; Fan, J.; Wei, S.; Han, Q.; Shi, Y. Tunable mechanical performance of additively manufactured plate lattice metamaterials with half-open-cell topology. Compos. Struct. 2022, 300, 116172. [Google Scholar] [CrossRef]
- Esfarjani, S.M.; Dadashi, A.; Azadi, M. Topology optimization of additive-manufactured metamaterial structures: A review focused on multi-material types. Forces Mech. 2022, 7, 100100. [Google Scholar] [CrossRef]
- Monteiro, H.; Carmona-Aparicio, G.; Lei, I.; Despeisse, M. Energy and material efficiency strategies enabled by metal additive manufacturing—A review for the aeronautic and aerospace sectors. Energy Rep. 2022, 8, 298–305. [Google Scholar] [CrossRef]
- Germaini, M.-M.; Belhabib, S.; Guessasma, S.; Deterre, R.; Corre, P.; Weiss, P. Additive manufacturing of biomaterials for bone tissue engineering—A critical review of the state of the art and new concepts. Prog. Mater. Sci. 2022, 130, 100963. [Google Scholar] [CrossRef]
- Dörfler, K.; Dielemans, G.; Lachmayer, L.; Recker, T.; Raatz, A.; Lowke, D.; Gerke, M. Additive Manufacturing using mobile robots: Opportunities and challenges for building construction. Cem. Concr. Res. 2022, 158, 106772. [Google Scholar] [CrossRef]
- Siacor, F.D.C.; Chen, Q.; Zhao, J.Y.; Han, L.; Valino, A.D.; Taboada, E.B.; Caldona, E.B.; Advincula, R.C. On the additive manufacturing (3D printing) of viscoelastic materials and flow behavior: From composites to food manufacturing. Addit. Manuf. 2021, 45, 102043. [Google Scholar] [CrossRef]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. Towards Large Parts Manufacturing in Additive Technologies for Aerospace and Automotive applications. Procedia Comput. Sci. 2022, 200, 1113–1124. [Google Scholar] [CrossRef]
- Lakkala, P.; Munnangi, S.R.; Bandari, S.; Repka, M. Additive manufacturing technologies with emphasis on stereolithography 3D printing in pharmaceutical and medical applications: A review. Int. J. Pharm. X 2023, 5, 100159. [Google Scholar] [CrossRef]
- Gay, P.; Blanco, D.; Pelayo, F.; Noriega, A.; Fernández, P. Analysis of Factors Influencing the Mechanical Properties of Flat PolyJet Manufactured Parts. Procedia Eng. 2015, 132, 70–77. [Google Scholar] [CrossRef]
- Grossin, D.; Montón, A.; Navarrete-Segado, P.; Özmen, E.; Urruth, G.; Maury, F.; Maury, D.; Frances, C.; Tourbin, M.; Lenormand, P.; et al. A review of additive manufacturing of ceramics by powder bed selective laser processing (sintering/melting): Calcium phosphate, silicon carbide, zirconia, alumina, and their composites. Open Ceram. 2021, 5, 100073. [Google Scholar] [CrossRef]
- Gunasekaran, J.; Sevvel, P.; John Solomon, I.; Tanushkumaar, P. A brief review on the manufacturing of metal components using selective laser melting. Mater. Today Proc. 2022, 64, 173–180. [Google Scholar] [CrossRef]
- Hu, K.; Zhao, P.; Li, J.; Lu, Z. High-resolution multiceramic additive manufacturing based on digital light processing. Addit. Manuf. 2022, 54, 102732. [Google Scholar] [CrossRef]
- Vayre, B.; Vignat, F.; Villeneuve, F. Identification on Some Design Key Parameters for Additive Manufacturing: Application on Electron Beam Melting. Procedia CIRP 2013, 7, 264–269. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Lu, J.; Xu, L.; Lin, Y.; Chen, P.; Sheng, Q.; Chen, F. Additive manufacturing and mechanical properties of martensite/austenite functionally graded materials by laser engineered net shaping. J. Mater. Res. Technol. 2022, 17, 1570–1581. [Google Scholar] [CrossRef]
- Sola, A.; Chong, W.J.; Pejak Simunec, D.; Li, Y.; Trinchi, A.; Kyratzis, I.; Wen, C. Open challenges in tensile testing of additively manufactured polymers: A literature survey and a case study in fused filament fabrication. Polym. Test. 2023, 117, 107859. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S.; Altin, A. On the Tensile Behaviour of Bio-Sourced 3D-Printed Structures from a Microstructural Perspective. Polymers 2020, 12, 1060. [Google Scholar] [CrossRef]
- Al-Ghamdi, K.A. Sustainable FDM additive manufacturing of ABS components with emphasis on energy minimized and time efficient lightweight construction. Int. J. Lightweight Mater. Manuf. 2019, 2, 338–345. [Google Scholar] [CrossRef]
- Liu, Z.; Lei, Q.; Xing, S. Mechanical characteristics of wood, ceramic, metal and carbon fiber-based PLA composites fabricated by FDM. J. Mater. Res. Technol. 2019, 8, 3741–3751. [Google Scholar] [CrossRef]
- Mogan, J.; Sandanamsamy, L.; Harun, W.S.W.; Ishak, I.; Romlay, F.R.M.; Kadirgama, K.; Ramasamy, D. Thermo-mechanical properties of ABS/stainless steel composite using FDM. Mater. Today: Proc. 2024; in press. [Google Scholar] [CrossRef]
- Golubovic, Z.; Bojovic, B.; Petrov, L.; Sedmak, A.; Milovanović, A.; Mišković, Ž.; Milošević, M. Comparative analysis of ABS materials mechanical properties. Procedia Struct. Integr. 2024, 56, 153–159. [Google Scholar] [CrossRef]
- Rodríguez-Reyna, S.L.; Mata, C.; Díaz-Aguilera, J.H.; Acevedo-Parra, H.R.; Tapia, F. Mechanical properties optimization for PLA, ABS and Nylon + CF manufactured by 3D FDM printing. Mater. Today Commun. 2022, 33, 104774. [Google Scholar] [CrossRef]
- Dusanapudi, S.; Krupakaran, R.L.; Srinivas, A.; Nikhil, K.S.; Vamshi, T. Optimization and experimental analysis of mechanical properties and porosity on FDM based 3D printed ABS sample. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- He, F.; Alshammari, Y.L.A.; Khan, M. The Effect of Printing Parameters on Crack Growth Rate of FDM ABS Cantilever Beam under Thermo-mechanical Loads. Procedia Struct. Integr. 2021, 34, 59–64. [Google Scholar] [CrossRef]
- Andrés, M.S.; Chércoles, R.; Navarro, E.; de la Roja, J.M.; Gorostiza, J.; Higueras, M.; Blanch, E. Use of 3D printing PLA and ABS materials for fine art. Analysis of composition and long-term behaviour of raw filament and printed parts. J. Cult. Herit. 2023, 59, 181–189. [Google Scholar] [CrossRef]
- Żur, P.; Kołodziej, A.; Baier, A.; Kokot, G. Optimization of Abs 3D-Printing Method and Parameters. Eur. J. Eng. Sci. Technol. 1970, 3, 44–51. [Google Scholar] [CrossRef]
- Angelopoulos, P.M.; Kenanakis, G.; Viskadourakis, Z.; Tsakiridis, P.; Vasilopoulos, K.C.; Karakassides, M.A.; Taxiarchou, M. Manufacturing of ABS/expanded perlite filament for 3D printing of lightweight components through fused deposition modeling. Mater. Today Proc. 2022, 54, 14–21. [Google Scholar] [CrossRef]
- Foltuţ, D.; Vălean, E.; Dzitac, V.; Marşavina, L. The influence of temperature on the mechanical properties of 3D printed and injection molded ABS. Mater. Today Proc. 2023, 78, 210–213. [Google Scholar] [CrossRef]
- Aw, Y.Y.; Yeoh, C.K.; Idris, M.A.; Amali, H.K.; Aqzna, S.S.; Teh, P.L. A study of tensile and thermal properties of 3D printed conductive ABS–ZnO composite. AIP Conf. Proc. 2017, 1835, 020008. [Google Scholar]
- Aravind, D.; Krishnasamy, S.; Rajini, N.; Siengchin, S.; Kumar, T.S.M.; Chandrasekar, M.; Yorseng, K. Thermal and tensile properties of 3D printed ABS-glass fibre, ABS-glass fibre-carbon fibre hybrid composites made by novel hybrid manufacturing technique. J. Thermoplast. Compos. Mater. 2023, 37, 206–225. [Google Scholar] [CrossRef]
- Hassana, O.B.; Guessasma, S.; Belhabib, S.; Nouri, H. Explaining the Difference Between Real Part and Virtual Design of 3D Printed Porous Polymer at the Microstructural Level. Macromol. Mater. Eng. 2016, 301, 566–576. [Google Scholar] [CrossRef]
- Belarbi, Y.E.; Guessasma, S.; Belhabib, S.; Benmahiddine, F.; Hamami, A.E.A. Effect of Printing Parameters on Mechanical Behaviour of PLA-Flax Printed Structures by Fused Deposition Modelling. Materials 2021, 14, 5883. [Google Scholar] [CrossRef]
- Olongal, M.; Mohamed Nainar, M.A.; Marakkattupurathe, M.; Muslim Veettil Asharaf, S.; Athiyanathil, S. Effect of poly(ethylene-co-vinyl acetate) additive on mechanical properties of maleic anhydride-grafted acrylonitrile butadiene styrene for coating applications. J. Vinyl Addit. Technol. 2018, 25, 287–295. [Google Scholar] [CrossRef]
- Mastorakis, N.; Stoklasek, P.; Navratil, M.; Bednarik, M.; Hudec, I.; Petrzelka, D.; Mladenov, V.; Bulucea, A. Flexural behaviour of ABS 3D printed parts on professional printer Stratasys Fortus 900mc. MATEC Web Conf. 2018, 210, 04048. [Google Scholar]
- Croccolo, D.; De Agostinis, M.; Olmi, G. Experimental characterization and analytical modelling of the mechanical behaviour of fused deposition processed parts made of ABS-M30. Comput. Mater. Sci. 2013, 79, 506–518. [Google Scholar] [CrossRef]
- ISO 13934-1:2013; Textiles—Tensile Properties of Fabrics—Part 1: Determination of Maximum Force and Elongation at Maximum Force by the Belt Method. International Organization for Standardization: Geneva, Switzerland, 2013.
- Lv, N.; Ouyang, X.; Qiao, Y. Adaptive Layering Algorithm for FDM-3D Printing Based on Optimal Volume Error. Micromachines 2022, 13, 836. [Google Scholar] [CrossRef]
- Eryildiz, M. Effect of Build Orientation on Mechanical Behaviour and Build Time of FDM 3D-Printed PLA Parts: An Experimental Investigation. Eur. Mech. Sci. 2021, 5, 116–120. [Google Scholar] [CrossRef]
- Tanoto, Y.Y.; Anggono, J.; Siahaan, I.H.; Budiman, W. The effect of orientation difference in fused deposition modeling of ABS polymer on the processing time, dimension accuracy, and strength. AIP Conf. Proc. 2017, 1788, 030051. [Google Scholar]
- Mohd Yasin, S.B.; Terry, J.S.; Taylor, A.C. Fracture and mechanical properties of an impact toughened polypropylene composite: Modification for automotive dashboard-airbag application. RSC Adv. 2023, 13, 27461–27475. [Google Scholar] [CrossRef] [PubMed]
- ASTM F 1473; Standard Test Method for Notch Tensile Test to Measure the Resistance to Slow Crack Growth of Polyethylene Pipes and Resins. ASTM International: West Conshohocken, PA, USA, 2023. [CrossRef]
- ISO 16241:2005; Notch Tensile Test to Measure the Resistance to Slow Crack Propagation of Polyethylenes for Tubes and Fittings (PENT). International Organization for Standardization: Geneva, Switzerland, 2005.
- ASTM E602-03; Standard Test Method for Sharp-Notch Tension Testing with Cylindrical Specimens. ASTM International: West Conshohocken, PA, USA, 2010.
- Guessasma, S.; Belhabib, S.; Nouri, H.; Ben Hassana, O. Anisotropic damage inferred to 3D printed polymers using fused deposition modelling and subject to severe compression. Eur. Polym. J. 2016, 85, 324–340. [Google Scholar] [CrossRef]
- Ahmad, M.N.; Yahya, A. Effects of 3D Printing Parameters on Mechanical Properties of ABS Samples. Designs 2023, 7, 136. [Google Scholar] [CrossRef]
- Dvorak, K.; Dvorakova, J.; Zarybnicka, L.; Horak, Z. Influence of 3D Printing Topology by DMLS Method on Crack Propagation. Materials 2021, 14, 7483. [Google Scholar] [CrossRef] [PubMed]
- Aourik, O.; Othmani, M.; Saadouki, B.; Abouzaid, K.; Chouaf, A. Fracture toughness of ABS additively manufactured by FDM process. J. Achiev. Mater. Manuf. Eng. 2021, 109, 49–58. [Google Scholar] [CrossRef]
- Marsavina, L.; Negru, R.; Serban, D.; Marghitas, M.; Popa, C. The notch effect on additive manufactured polymers. Procedia Struct. Integr. 2023, 47, 744–748. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Khosravani, M.R.; Kaynak, A. Fracture Resistance Analysis of 3D-Printed Polymers. Polymers 2020, 12, 302. [Google Scholar] [CrossRef]
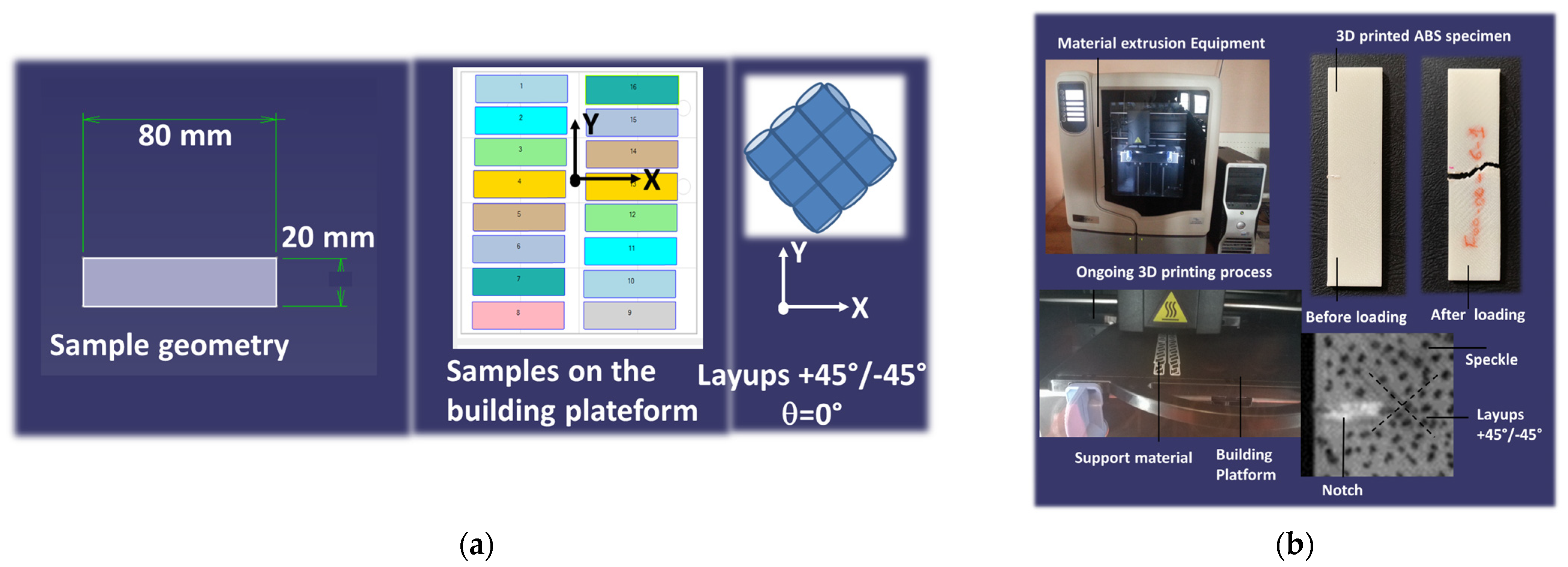

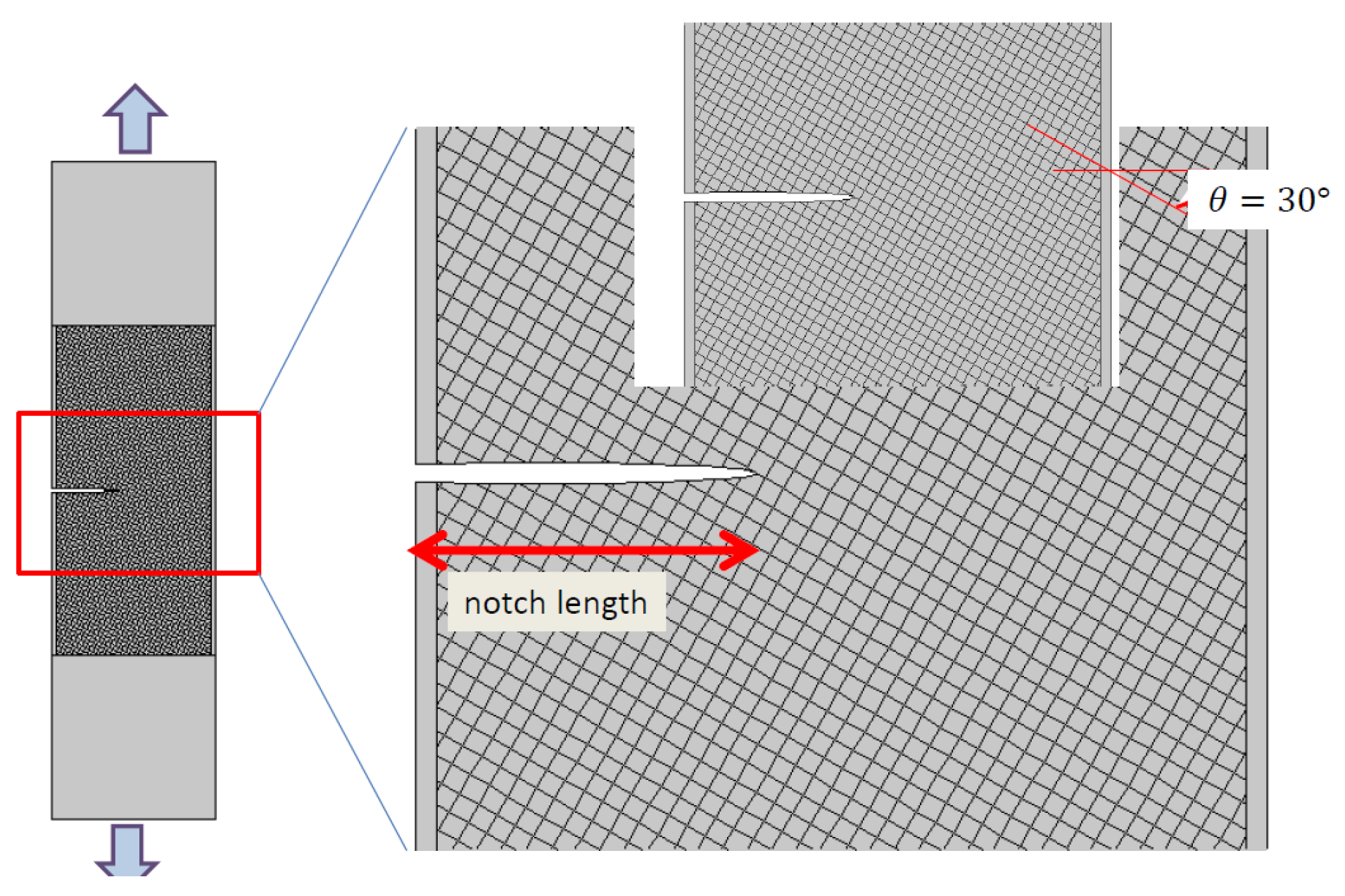





| Sample | θ (deg.) | ϕ (deg.) | a (mm) |
|---|---|---|---|
| F00-00-02 | 0 | 0 | 2 |
| F00-00-04 | 0 | 0 | 4 |
| F00-00-05 | 0 | 0 | 5 |
| F00-00-06 | 0 | 0 | 6 |
| F00-00-08 | 0 | 0 | 8 |
| F00-00-10 | 0 | 0 | 10 |
| F00-30-05 | 0 | 30 | 5 |
| F00-45-05 | 0 | 30 | 5 |
| F30-00-05 | 30 | 0 | 5 |
| F30-30-05 | 30 | 30 | 5 |
| F30-45-05 | 30 | 45 | 5 |
| F45-00-05 | 45 | 0 | 5 |
| F45-30-05 | 45 | 30 | 5 |
| F45-45-05 | 45 | 45 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guessasma, S.; Belhabib, S. The Influence of Microstructural Arrangement on the Failure Characteristics of 3D-Printed Polymers: Exploring Damage Behaviour in Acrylonitrile Butadiene Styrene. Materials 2024, 17, 2699. https://doi.org/10.3390/ma17112699
Guessasma S, Belhabib S. The Influence of Microstructural Arrangement on the Failure Characteristics of 3D-Printed Polymers: Exploring Damage Behaviour in Acrylonitrile Butadiene Styrene. Materials. 2024; 17(11):2699. https://doi.org/10.3390/ma17112699
Chicago/Turabian StyleGuessasma, Sofiane, and Sofiane Belhabib. 2024. "The Influence of Microstructural Arrangement on the Failure Characteristics of 3D-Printed Polymers: Exploring Damage Behaviour in Acrylonitrile Butadiene Styrene" Materials 17, no. 11: 2699. https://doi.org/10.3390/ma17112699





