Numerical and Experimental Analysis of Buckling and Post-Buckling Behaviour of TWCFS Lipped Channel Section Members Subjected to Eccentric Compression
Abstract
:1. Introduction
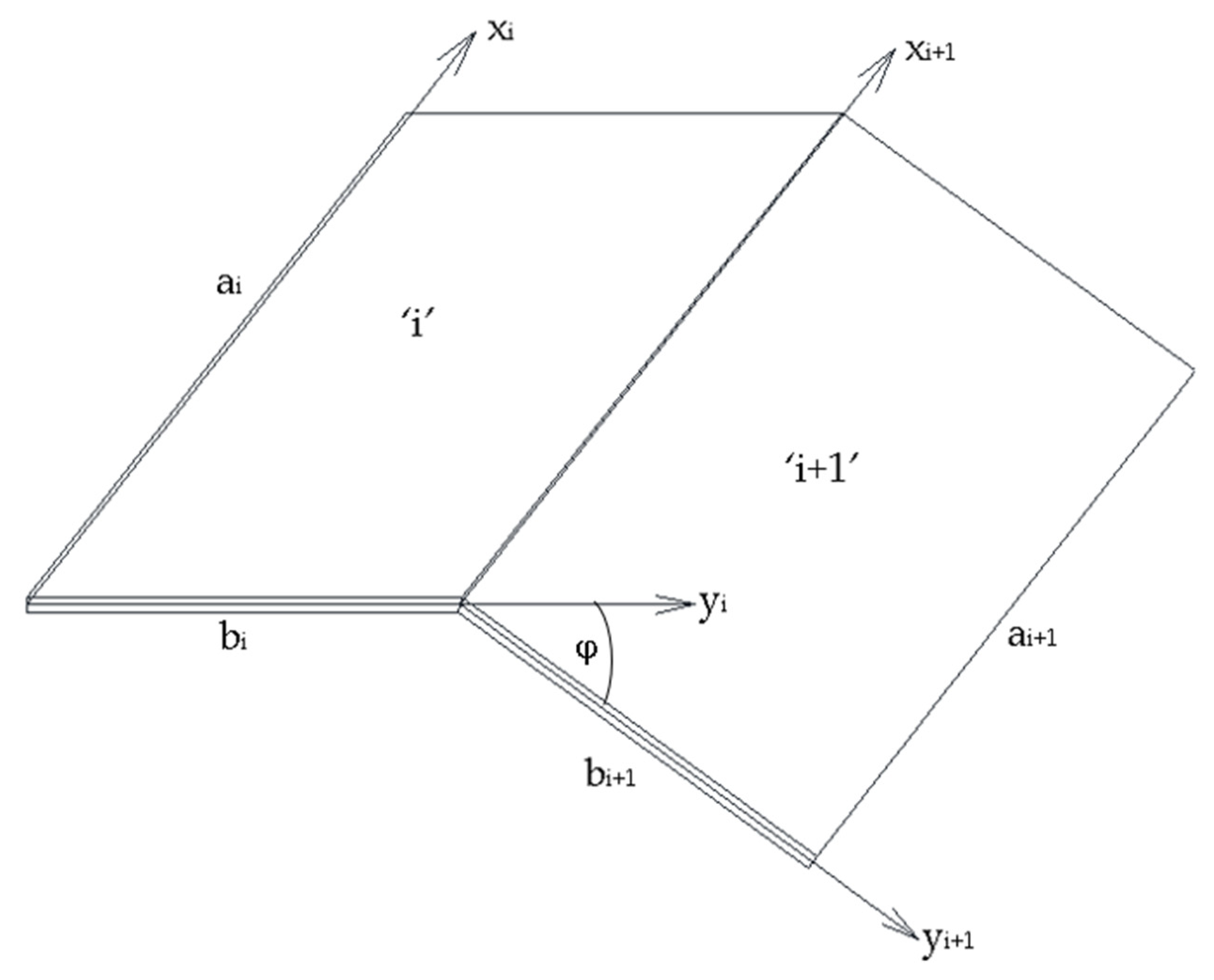
2. Basics of the Numerical Solution of the Problem
2.1. General Formulations
2.1.1. Boundary Conditions for Buckling Problem
- For x = 0, L:
- For y = 0, (b.c. concern only lips):
2.1.2. Boundary Conditions for Post-Buckling Problem
- For x = 0, L:
- For y = 0, (boundary conditions concern only lips):
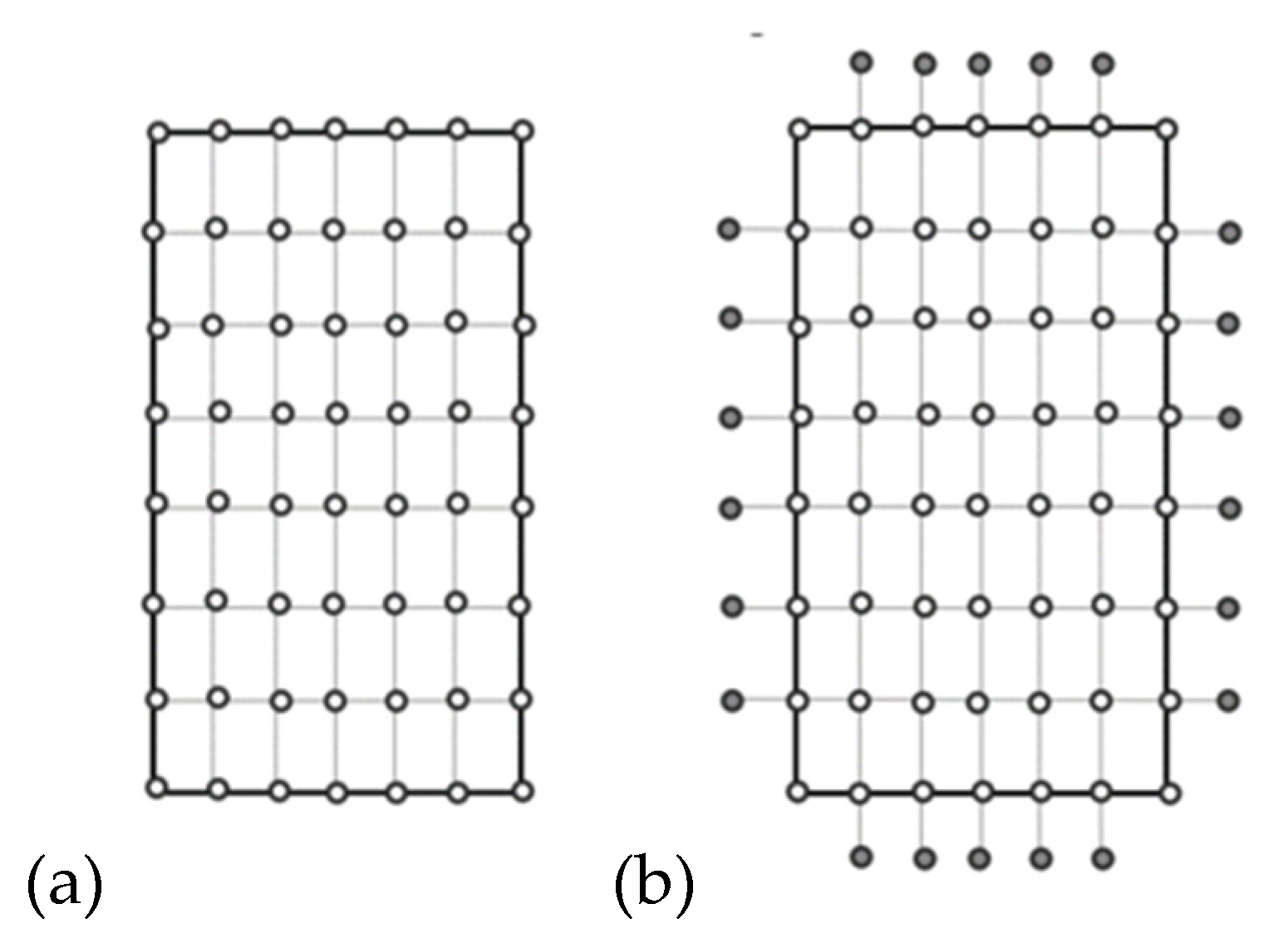
2.2. Finite Difference Method
2.2.1. Solution of the Linear Buckling Problem
- For x = 0, L (or i = 0 or imax):
- For y = 0, (it concerns only two lips—j = 0 or jmax):
- For x = 0:
- For x = L:
- For y = 0, (it concerns only two lips—j = 0 or jmax):
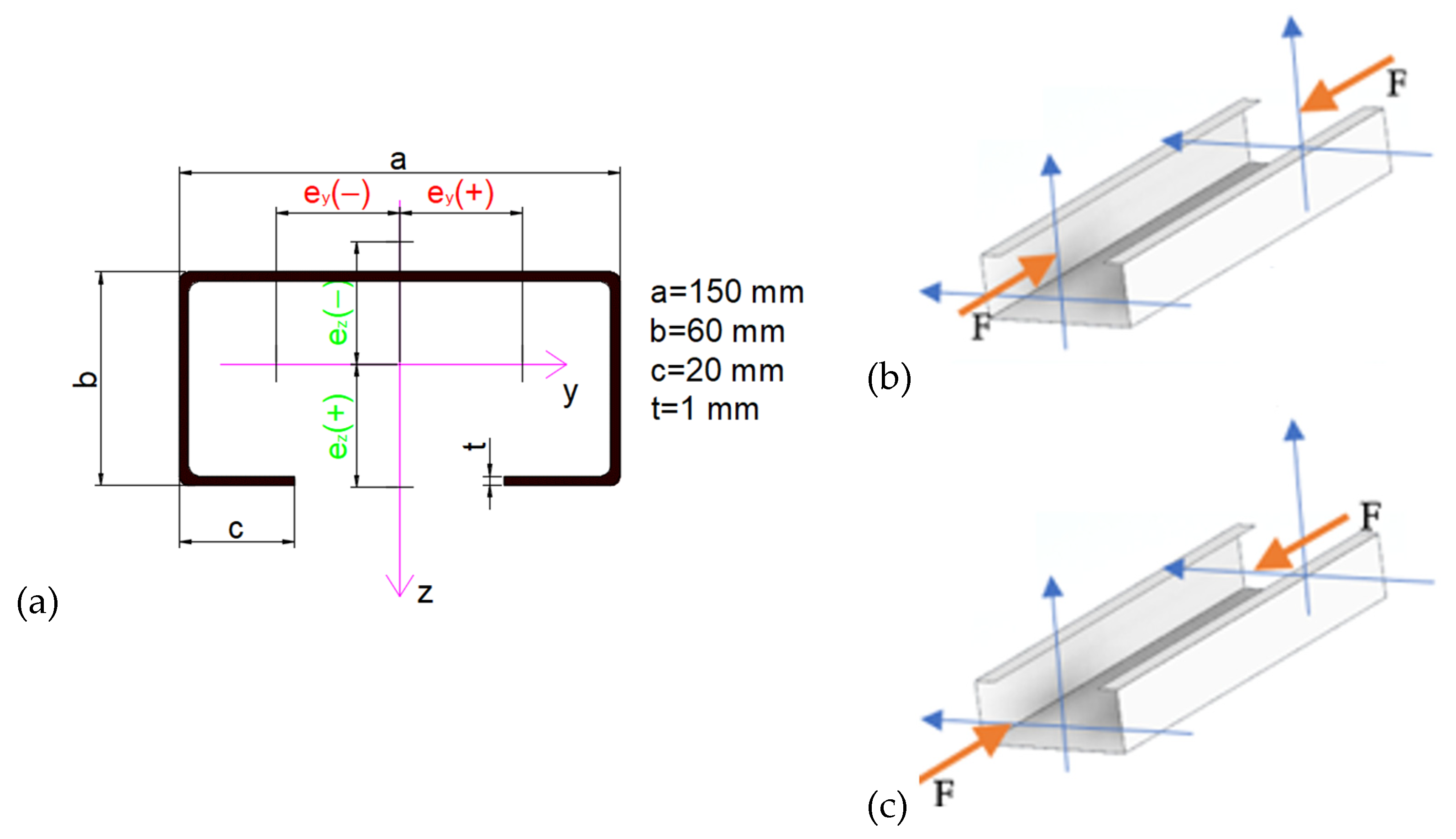
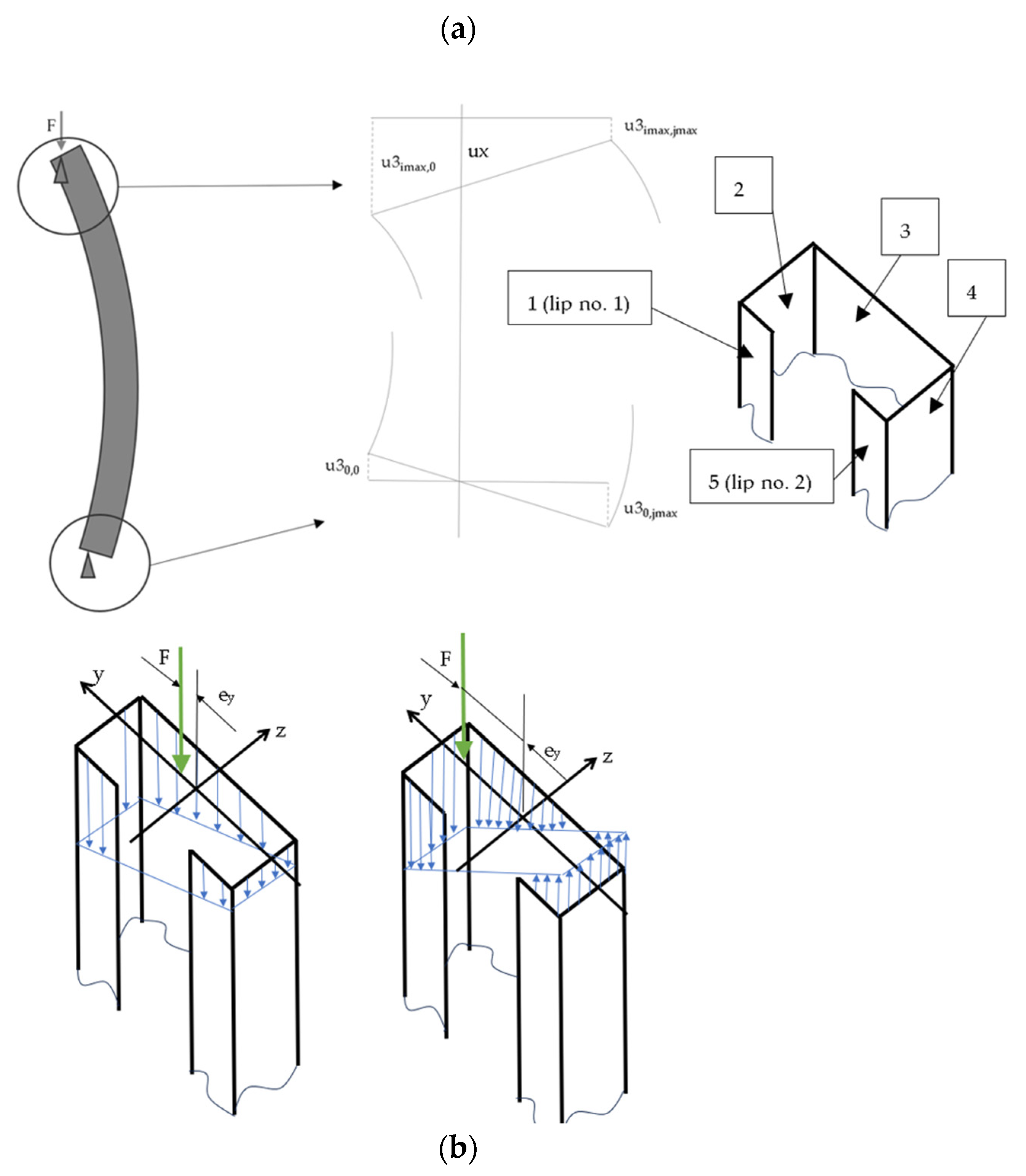
- u1, u2, u3, u4, u5 are the mean displacements in x directions for plates no. 1,2,3,4,5 corresponding to eccentricity about the major axis (see Figure 4);
- u11, u12, u13, u14, u15 are the mean displacements in x direction for plates no. 1,2,3,4,5 corresponding to eccentricity about the minor axis (see Figure 4);
- M1, M2, M3, M4, M5 are the bending moments at the edges of plates no. 1,2,3,4,5.
2.2.2. Solution of the Nonlinear Post-Buckling Problem
- For x = L (top of member—i = imax):
- For x = 0 (bottom of member—i = 0):
- For y = 0 (lip 1 (wall 1)—free edge):
- For y = b5 (lip 2 (wall 5)—free edge):
- For x = 0:
- For x = L:
- For y = 0 (lip 1 (wall 1)—free edge):
- For y = b5 (lip 2 (wall 5)—free edge):
2.2.3. Equilibrium Equations and Definition of Internal, Sectional Pre-Buckling Forces—Major Axis
2.3. Solution of Nonlinear Algebraic Equations
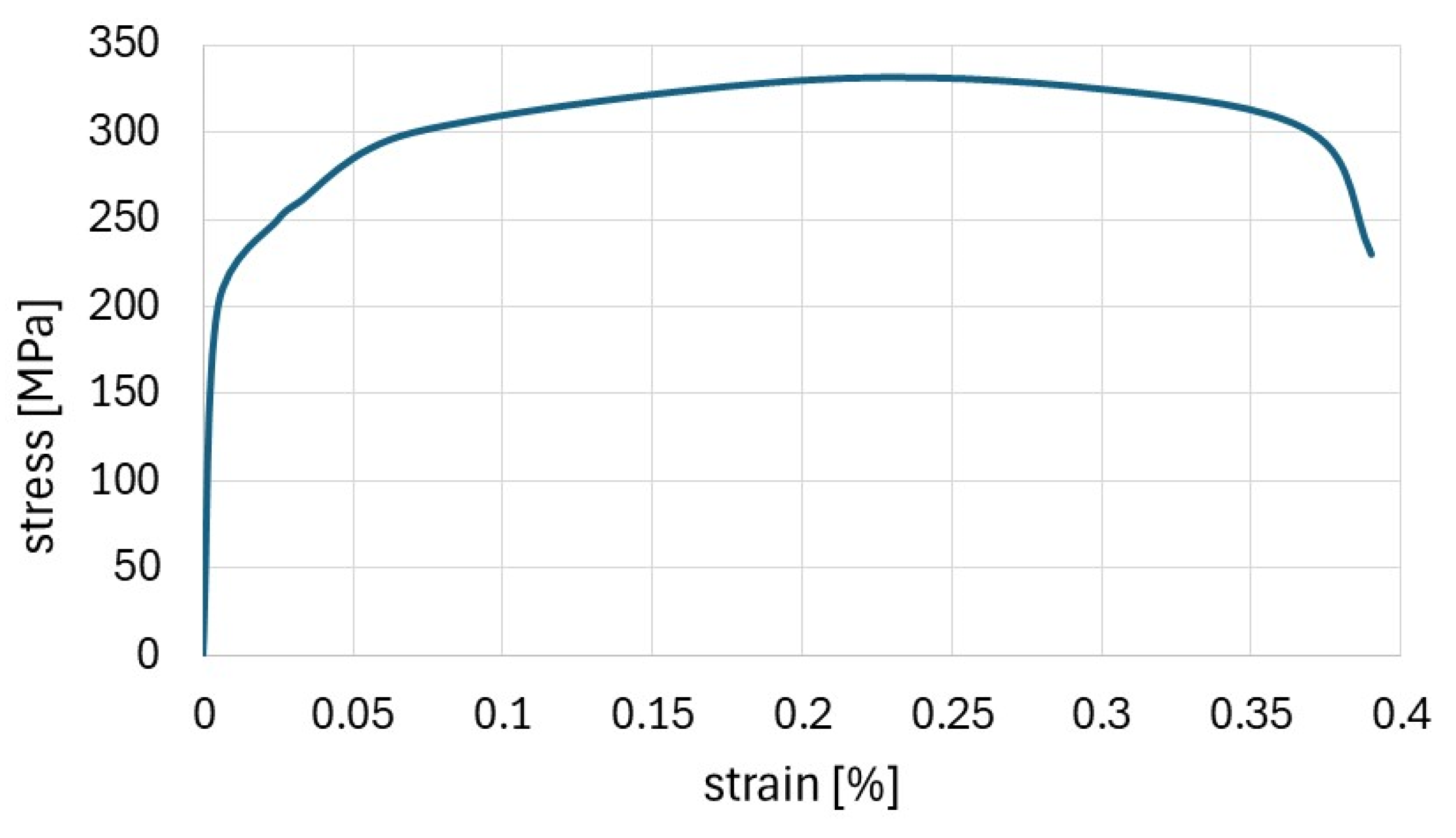
3. Experimental Study
4. Numerical and Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Central difference quotients:
- Left-sided difference quotients:
- Right-sided difference quotients:
Appendix B
- First equation:
| (K133∙(u11[i,−1 + j] − 2∙u11[i,j] + u11[i,1 + j]))/Power(hy1,2) + | (A4) |
| (K133∙(v11[−1 + i,−1 + j] − v11[−1 + i,1 + j] − v11[1 + i,−1 + j] + v11[1 + i,1 + j]))/(4∙hx1∙hy1) + | |
| (K133∙(w11[i,−1 + j] − 2∙w11[i,j] + w11[i,1 + j])∙(−w11[−1 + i,j] + | |
| + w11[1 + i,j]))/(2∙hx1∙Power(hy1,2)) + (K133∙(−w11[i,−1 + j] + w11[i,1 + j])∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(8∙hx1∙Power(hy1,2)) + ((2∙K111∙(u11[−1 + i,j] − 2∙u11[i,j] + u11[1 + i,j]))/Power(hx1,2) + (K112∙(v11[−1 + i,−1 + j] − v11[−1 + i,1 + j] − v11[1 + i,−1 + j] + v11[1 + i,1 + j]))/(2∙hx1∙hy1) + (K112∙(−v11[i,−1 + j] + v11[i,1 + j])∙(v11[−1 + i,−1 + j] − v11[−1 + i,1 + j] − v11[1 + i,−1 + j] + v11[1 + i,1 + j]))/(4∙hx1∙Power(hy1,2)) + (K111∙(−w11[−1 + i,j] + w11[1 + i,j])∙(w11[−1 + i,j] − 2∙w11[i,j] + w11[1 + i,j]))/Power(hx1,3) + (K112∙(−w11[i,−1 + j] + w11[i,1 + j])∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(4∙hx1∙Power(hy1,2)))/2 |
- Second equation:
| (K133∙(u11[−1 + i,−1 + j] − u11[−1 + i,1 + j] − u11[1 + i,−1 + j] + u11[1 + i,1 + j]))/(4∙hx1∙hy1) +(K133∙(v11[−1 + i,j] − 2∙v11[i,j] + v11[1 + i,j]))/Power(hx1,2) + (K133∙(−w11[i,−1 + j] + w11[i,1 + j]) ∙(w11[−1 + i,j] − 2∙w11[i,j] + w11[1 + i,j]))/(2∙Power(hx1,2)∙hy1) + ((v11[i,−1 + j] − 2∙v11[i,j] + v11[i,1 + j])∙((K121∙(−u11[−1 + i,j] + u11[1 + i,j]))/hx1 + (K122∙(−v11[i,1 + j] + v11[i,1 + j]))/hy1 + (K122∙Power(−v11[i,−1 + j] + v11[i,1 + j],2))/(4∙Power(hy1,2)) + (K122∙Power(−w11[i,−1 + j] + w11[i,1 + j],2))/(4∙Power(hy1,2)) + (K121∙Power(−w11[−1 + i,j] + w11[1 + i,j],2))/(4∙Power(hx1,2))))/(2∙Power(hy1,2)) +(K133∙ (−w11[−1 + i,j] + w11[1 + i,j])∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(8∙Power(hx1,2) ∙hy1) + ((K121∙ (u11[−1 + i,−1 + j] − u11[−1 + i,1 + j] − u11[1 + i,−1 + j] + u11[1 + i,1 + j]))/(2∙hx1∙hy1) + (2∙K122∙ (v11[i,−1 + j] − 2∙v11[i,j] + v11[i,1 + j]))/Power(hy1,2) + (K122∙(−v11[i,−1 + j] + v11[i,1 + j]) ∙ (v11[i,−1 + j] − 2∙v11[i,j] ++ v11[i,1 + j]))/Power(hy1,3) + (K122∙(−w11[i,−1 + j] + w11[i,1 + j]) ∙ (w11[i,−1 + j] − 2∙w11[i,j] + w11[i,1 + j]))/Power(hy1,3) + (K121∙(−w11[−1 + i,j] + w11[1 + i,j]) ∙ (w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(4∙Power(hx1,2) ∙hy1))/2. + ((−v11[i,−1 + j] + v11[i,1 + j])∙((K121∙ (u11[−1 + i,−1 + j] − u11[−1 + i,1 + j] − u11[1 + i,−1 + j] + u11[1 + i,1 + j]))/(2∙hx1∙hy1) + (2∙K122∙(v11[i,−1 + j] − 2∙v11[i,j] + v11[i,1 + j]))/Power(hy1,2) + (K122∙(−v11[i,−1 + j] + v11[i,1 + j])∙(v11[i,−1 + j] − 2∙v11[i,j] + v11[i,1 + j]))/Power(hy1,3) + (K122∙(−w11[i,−1 + j] + w11[i,1 + j])∙(w11[i,−1 + j] − 2∙w11[i,j] + w11[i,1 + j]))/Power(hy1,3) + (K121∙(−w11[−1 + i,j] + w11[1 + i,j])∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(4∙Power(hx1,2)∙hy1)))/(4∙hy1) | (A5) |
- Third equation:
| −(L122∙(w11[i,−2 + j] − 4∙w11[i,−1 + j] + 6∙w11[i,j] − 4∙w11[i,1 + j] + w11[i,2 + j]))/Power(hy1,4) + ((w11[−1 + i,j] − 2∙w11[i,j] + w11[1 + i,j])∙(−2∙Nx10[j] + (K111∙(−u11[−1 + i,j] + u11[1 + i,j]))/hx1 + (K112∙(−v11[i,−1 + j] + v11[i,1 + j]))/hy1 + (K112∙Power(−v11[i,−1 + j] + v11[i,1 + j],2))/(4∙Power(hy1,2)) + (K112∙Power(−w11[i,−1 + j] + w11[i,1 + j],2))/(4∙Power(hy1,2)) + (K111∙Power(−w11[−1 + i,j] + w11[1 + i,j],2))/(4∙Power(hx1,2))))/(2∙Power(hx1,2)) + ((w11[i,−1 + j] − 2∙w11[i,j] + w11[i,1 + j])∙((K121∙(−u11[−1 + i,j] + u11[1 + i,j]))/hx1 + (K122∙(−v11[i,−1 + j] + v11[i,1 + j]))/hy1 + (K122∙Power(−v11[i,−1 + j] + v11[i,1 + j],2))/(4∙Power(hy1,2)) + (K122∙Power(−w11[i,−1 + j] + w11[i,1 + j],2))/(4∙Power(hy1,2)) + (K121∙Power(−w11[−1 + i,j] + w11[1 + i,j],2))/(4∙Power(hx1,2))))/(2∙Power(hy1,2)) + (((K133∙(−u11[i,−1 + j] + u11[i,1 + j]))/(2∙hy1) + (K133∙(−v11[−1 + i,j] + v11[1 + i,j]))/(2∙hx1) + (K133∙(−w11[i,−1 + j] + w11[i,1 + j])∙(−w11[−1 + i,j] + w11[1 + i,j]))/(4∙hx1∙hy1))∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(2∙hx1∙hy1) + znak1∙(L112∙(w11[−1 + i,−1 + j] + w11[−1 + i,1 + j] + 4∙w11[i,j] + w11[1 + i,−1 + j] − 2∙(w11[−1 + i,j] + w11[i,−1 + j] + w11[i,1 + j] + w11[1 + i,j]) + w11[1 + i,1 + j]))/(Power(hx1,2)∙Power(hy1,2)) + znak1∙(L121∙(w11[−1 + i,−1 + j] + w11[−1 + i,1 + j] + 4∙w11[i,j] + w11[1 + i,−1 + j] − 2∙(w11[−1 + i,j] + w11[i,−1 + j] + w11[i,1 + j] + w11[1 + i,j]) + w11[1 + i,1 + j]))/(Power(hx1,2)∙Power(hy1,2)) −(4∙L133∙(w11[−1 + i,−1 + j] + w11[−1 + i,1 + j] + 4∙w11[i,j] + w11[1 + i,−1 + j] − 2∙(w11[−1 + i,j] + w11[i,−1 + j] + w11[i,1 + j] + w11[1 + i,j]) + w11[1 + i,1 + j]))/(Power(hx1,2)∙Power(hy1,2)) + ((−w11[−1 + i,j] + w11[1 + i,j])∙((2∙K111∙(u11[−1 + i,j] − 2∙u11[i,j] + u11[1 + i,j]))/Power(hx1,2) + (K112∙(v11[−1 + i,−1 + j] − v11[−1 + i,1 + j] − v11[1 + i,−1 + j] + v11[1 + i,1 + j]))/(2∙hx1∙hy1) + (K112∙(−v11[i,−1 + j] + v11[i,1 + j])∙(v11[−1 + i,−1 + j] − v11[−1 + i,1 + j] − v11[1 + i,−1 + j] + v11[1 + i,1 + j]))/(4∙hx1∙Power(hy1,2)) + (K111∙(−w11[−1 + i,j] + w11[1 + i,j])∙(w11[−1 + i,j] − 2∙w11[i,j] + w11[1 + i,j]))/Power(hx1,3) + (K112∙(−w11[i,−1 + j] + w11[i,1 + j])∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(4.∙hx1∙Power(hy1,2))))/(4.∙hx1) + ((−w11[−1 + i,j] + w11[1 + i,j])∙((K133∙(u11[i,−1 + j] − 2∙u11[i,j] + u11[i,1 + j]))/Power(hy1,2) + (K133∙(v11[−1 + i,−1 + j] − v11[−1 + i,1 + j] − v11[1 + i,−1 + j] + v11[1 + i,1 + j]))/(4∙hx1∙hy1) + (K133∙(w11[i,−1 + j] − 2∙w11[i,j] + w11[i,1 + j])∙(−w11[−1 + i,j] + w11[1 + i,j]))/(2.∙hx1∙Power(hy1,2)) + (K133∙(−w11[i,−1 + j] + w11[i,1 + j])∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(8∙hx1∙Power(hy1,2))))/(2∙hx1) + ((−w11[i,−1 + j] + w11[i,1 + j])∙((K121∙(u11[−1 + i,−1 + j] − u11[−1 + i,1 + j] − u11[1 + i,−1 + j] + u11[1 + i,1 + j]))/(2∙hx1∙hy1) + (2∙K122∙(v11[i,−1 + j] − 2∙v11[i,j] + v11[i,1 + j]))/Power(hy1,2) + (K122∙(−v11[i,−1 + j] + v11[i,1 + j])∙(v11[i,−1 + j] − 2∙v11[i,j] + v11[i,1 + j]))/Power(hy1,3) + (K122∙(−w11[i,−1 + j] + w11[i,1 + j])∙(w11[i,−1 + j] − 2∙w11[i,j] + w11[i,1 + j]))/Power(hy1,3) + (K121∙(−w11[−1 + i,j] + w11[1 + i,j])∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(4∙Power(hx1,2)∙hy1)))/(4∙hy1) + ((−w11[i,−1 + j] + w11[i,1 + j])∙((K133∙(u11[−1 + i,−1 + j] − u11[−1 + i,1 + j] − u11[1 + i,−1 + j] + u11[1 + i,1 + j]))/(4∙hx1∙hy1) + (K133∙(v11[−1 + i,j] − 2∙v11[i,j] + v11[1 + i,j]))/Power(hx1,2) + (K133∙(−w11[i,−1 + j] + w11[i,1 + j])∙(w11[−1 + i,j] − 2∙w11[i,j] + w11[1 + i,j]))/(2.∙Power(hx1,2)∙hy1) + (K133∙(−w11[−1 + i,j] + w11[1 + i,j])∙(w11[−1 + i,−1 + j] − w11[−1 + i,1 + j] − w11[1 + i,−1 + j] + w11[1 + i,1 + j]))/(8∙Power(hx1,2)∙hy1)))/(2∙hy1) −(L111∙(w11[−2 + i,j] − 4∙w11[−1 + i,j] + 6∙w11[i,j] − 4∙w11[1 + i,j] + w11[2 + i,j]))/Power(hx1,4) | (A6) |
Appendix C

Appendix D
Nx30(j) = Nx20(j) − j hy3/b3(Nx20(j) − Nx40(j))
Nx50(j) = Nx40(j) − (hy1 j (− Nx20(j) + Nx40(j)))/b3
Appendix E
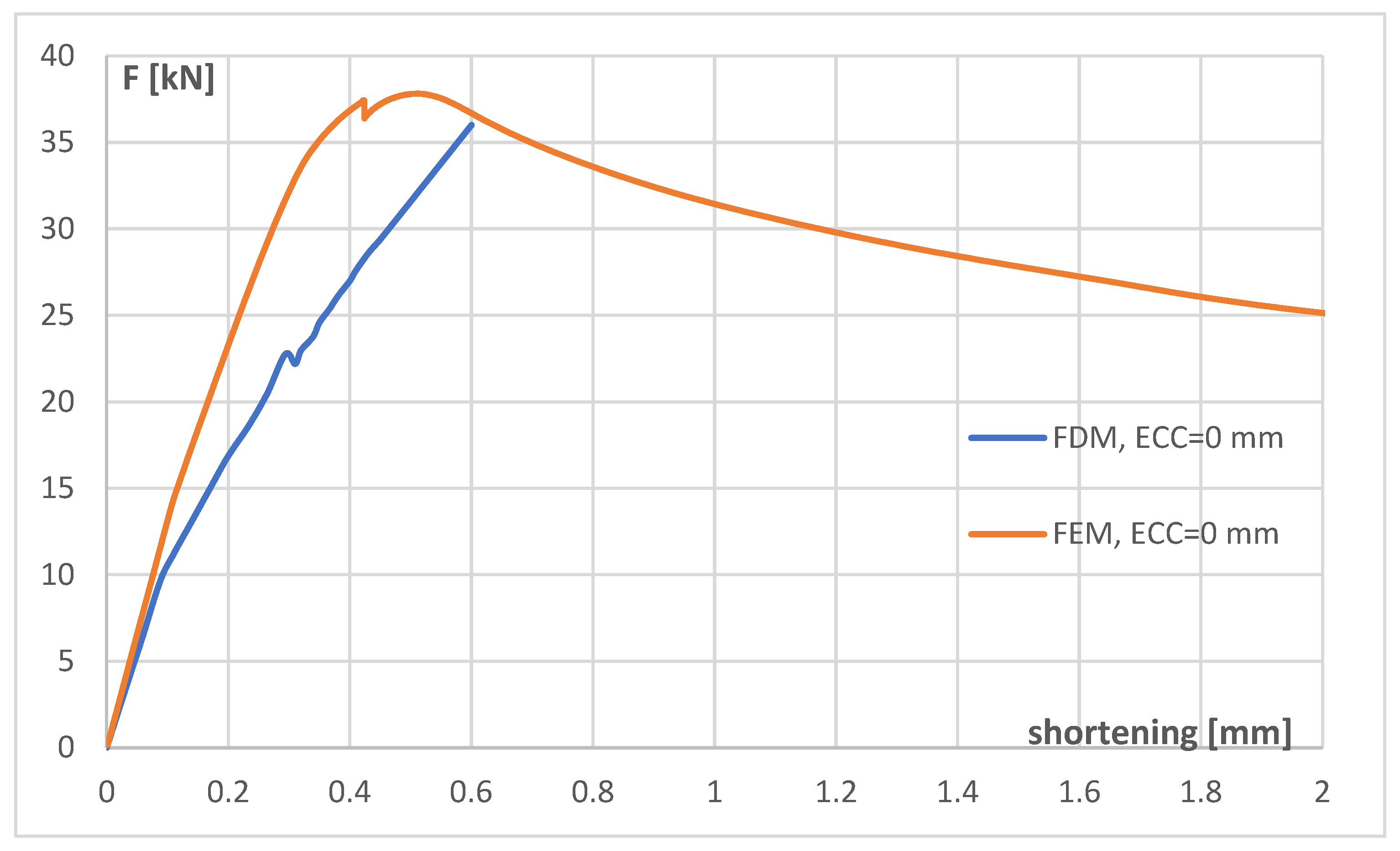
References
- EN 1993-1-3; Eurocode 3: Design of Steel Structures, Part 1.3: General Rules, Supplementary Rules for Cold-Formed Thin Gauge Members and Sheeting. CEN: Brussels, Belgium, 2006.
- He, Z.; Peng, S.; Zhou, X.; Li, Z.; Yang, G.; Zhang, Z. Design recommendation of cold-formed steel built-up sections under concentric and eccentric compression. J. Constr. Steel Res. 2023, 212, 108255. [Google Scholar] [CrossRef]
- Zhao, J.; He, J.; Chen, B.; Zhang, W.; Yu, S. Test and direct strength method on slotted perforated cold-formed steel channels subjected to eccentric compression. Eng. Struct. 2023, 285, 116082. [Google Scholar] [CrossRef]
- Ozturuk, F.; Mojtabaei, S.M.; Şentürk, M.; Pul, P.; Hajirasouliha, I. Buckling behaviour of cold-formed sigma and lipped channel beam-column members. J. Thin-Walled Struct. 2022, 173, 108963. [Google Scholar] [CrossRef]
- Guo, Y.L.; Fukumoto, Y. Theoretical study of ultimate load locally buckled stub columns loaded eccentrically. J. Constr. Steel Res. 1996, 38, 239–255. [Google Scholar] [CrossRef]
- Kotełko, M.; Grudziecki, J.; Ungureanu, V.; Dubina, D. Ultimate and post-ultimate behaviour of thin-walled cold-formed steel open-section members under eccentric compression. Part I: Collapse mechanisms database (theoretical study). Thin-Walled Struct. 2021, 169, 108366. [Google Scholar] [CrossRef]
- Borkowski, Ł.; Grudziecki, J.; Kotełko, M.; Ungureanu, V.; Dubina, D. Ultimate and post-ultimate behaviour of thin-walled cold-formed steel open-section members under eccentric compression. Part II: Experimental study. Thin-Walled Struct. 2022, 171, 108802. [Google Scholar] [CrossRef]
- Ungureanu, V.; Both, I.; Kotełko, M.; Czechowski, L.; Bodea, F.; Dubina, D. Buckling strength and post-ultimate behaviour of lipped channel section members under eccentric compression. Thin-Walled Struct. 2022, 181, 110085. [Google Scholar] [CrossRef]
- Ungureanu, V.; Kotełko, M.; Bodea, F.; Both, I.; Czechowski, L. Failure mechanisms of TWCFS members considering various eccentricities. Steel Constr. 2023, 16, 44–55. [Google Scholar] [CrossRef]
- Rajkannu, J.S.; Arul Jayachandran, S. Experimental evaluation of DSM beam-column strength of cold-formed steel members under uniaxial eccentric compression. Thin-Walled Struct. 2022, 174, 109096. [Google Scholar] [CrossRef]
- Peiris, M.; Mahendran, M. Behaviour of cold-formed steel lipped channel sections subject to eccentric axial compression. J. Constr. Steel Res. 2021, 184, 106808. [Google Scholar] [CrossRef]
- Zhang, L.; Zhong, Y.; Zhao, O. Press-braked stainless steel channel sections under major axis combined loading: Tests, simulations and design. J. Constr. Steel Res. 2021, 187, 106932. [Google Scholar] [CrossRef]
- Liang, Y.; Zhao, O.; Long, Y.-L.; Gardner, L. Stainless steel channel sections under combined compression and minor axis bending—Part 1: Experimental study and numerical modelling. J. Constr. Steel Res. 2019, 152, 154–161. [Google Scholar] [CrossRef]
- Liang, Y.; Zhao, O.; Long, Y.-L.; Gardner, L. Stainless steel channel sections under combined compression and minor axis bending—Part 2: Parametric studies and design. J. Constr. Steel Res. 2019, 152, 162–172. [Google Scholar] [CrossRef]
- Liang, Y.; Zhao, O.; Long, Y.-L.; Gardner, L. Experimental and numerical studies of laser-welded stainless steel channel sections under combined compression and major axis bending moment. Thin-Walled Struct. 2020, 157, 107035. [Google Scholar] [CrossRef]
- Craveiro, H.D.; Rahnavard, R.; Laím, L.; Simões, R.A.; Santiago, A. Buckling behavior of closed built-up cold-formed steel columns under compression. Thin-Walled Struct. 2022, 179, 109493. [Google Scholar] [CrossRef]
- An, J.; Wang, A.; Zhang, K.; Zhang, W.; Song, L.; Xiao, B.; Wang, R. Bending and buckling analysis of functionally graded graphene origami metamaterial irregular plates using generalized finite difference method. Results Phys. 2023, 53, 106945. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Kowal-Michalska, K. Selected Problems of Instabilities in Composite Structures, 1st ed.; TUŁ: Lodz, Poland, 1999. [Google Scholar]
- Baron, B.; Pasierbek, A.; Maciążek, M. The Numerical Algorithms in Delphi, 1st ed.; Helion: Gliwice, Poland, 2005. (In Polish) [Google Scholar]
- Czechowski, L.; Kotełko, M.; Jankowski, J.; Ungureanu, V.; Sanduly, A. Strength analysis of eccentrically loaded thin-walled steel lipped C-profile columns. J. Arch. Civ. Eng. 2023, 69, 301–314. [Google Scholar]
- Schafer, B.W.; Hiriyur, B.K.J. Yield-line Analysis of Cold-Formed Steel Members. Steel Struct. 2005, 5, 43–54. [Google Scholar]
- Ungureanu, V.; Kotełko, M.; Dubina, D. Ultimate limit capacity of thin-walled cold-formed steel members. Rom. J. Tech. Sci. Appl. Mech. 2018, 63, 183–206. [Google Scholar]



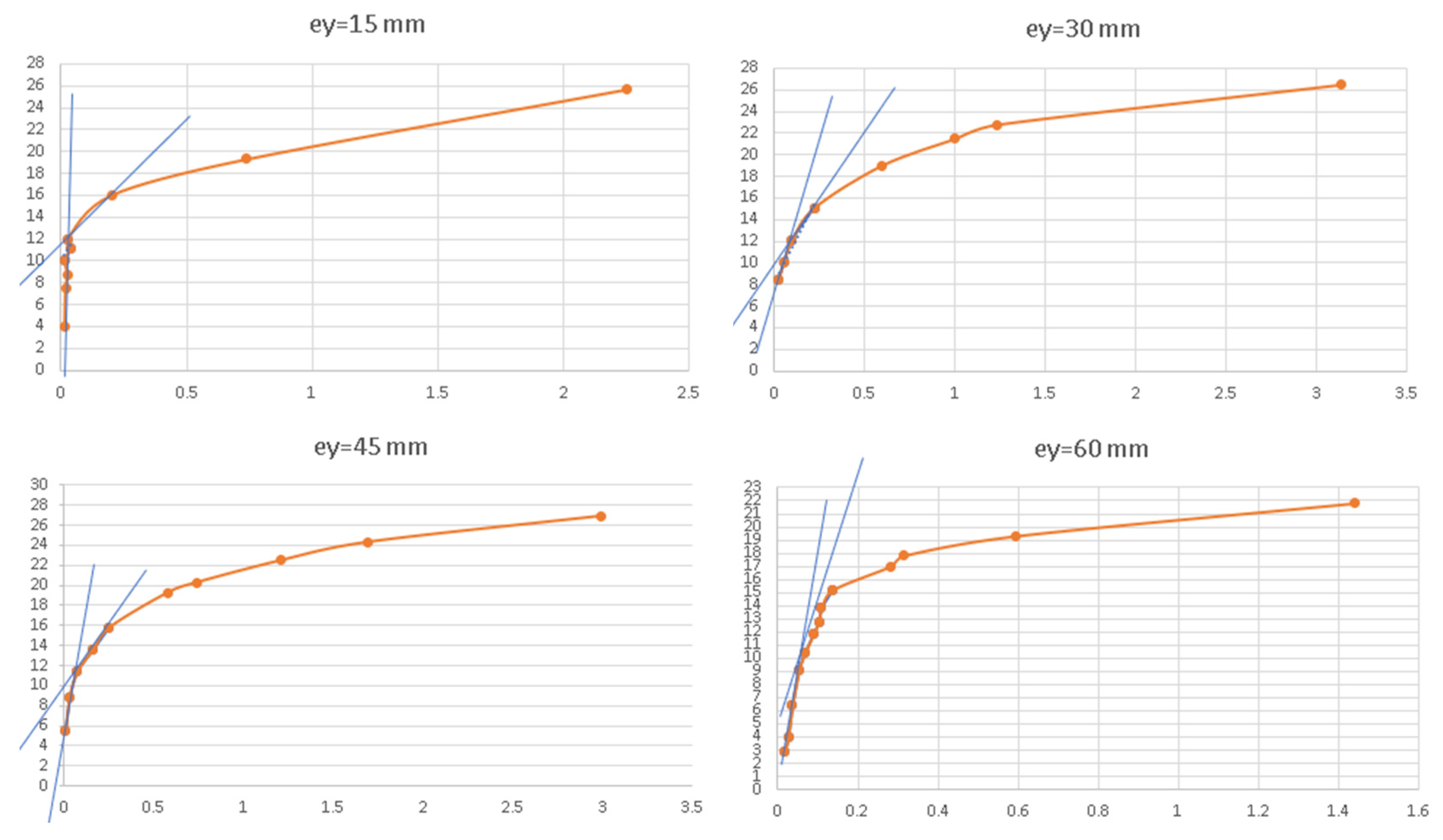
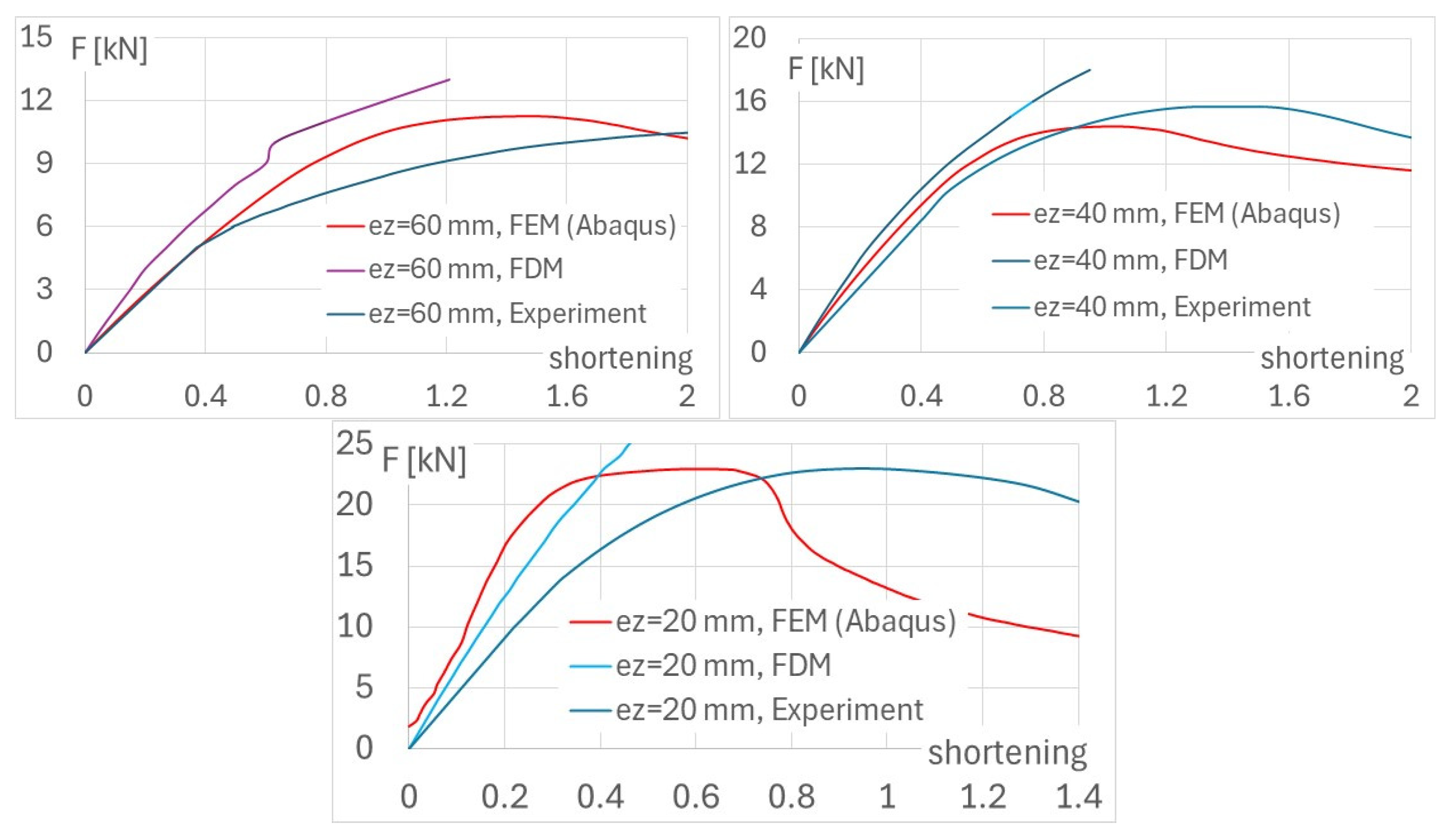
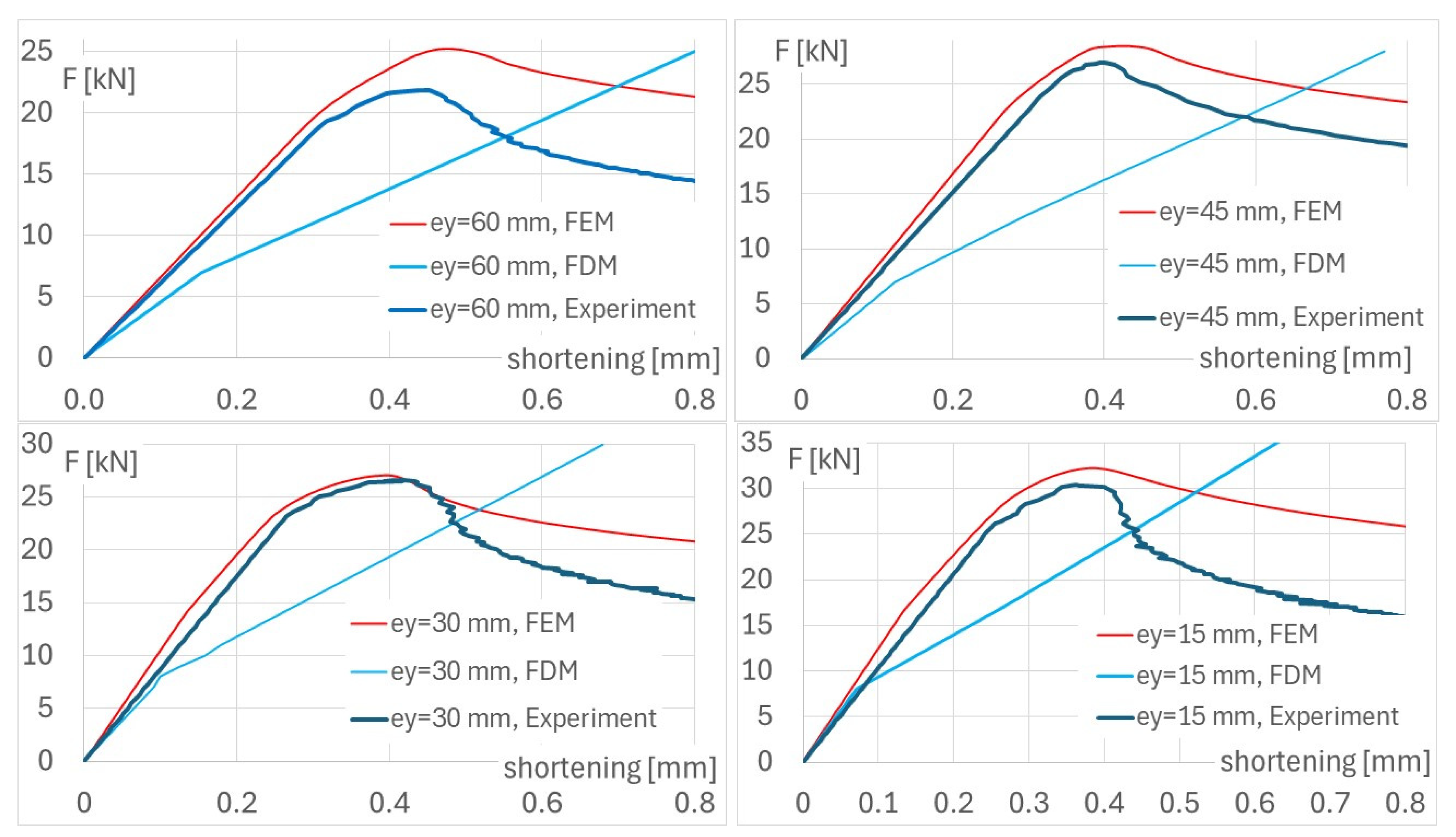
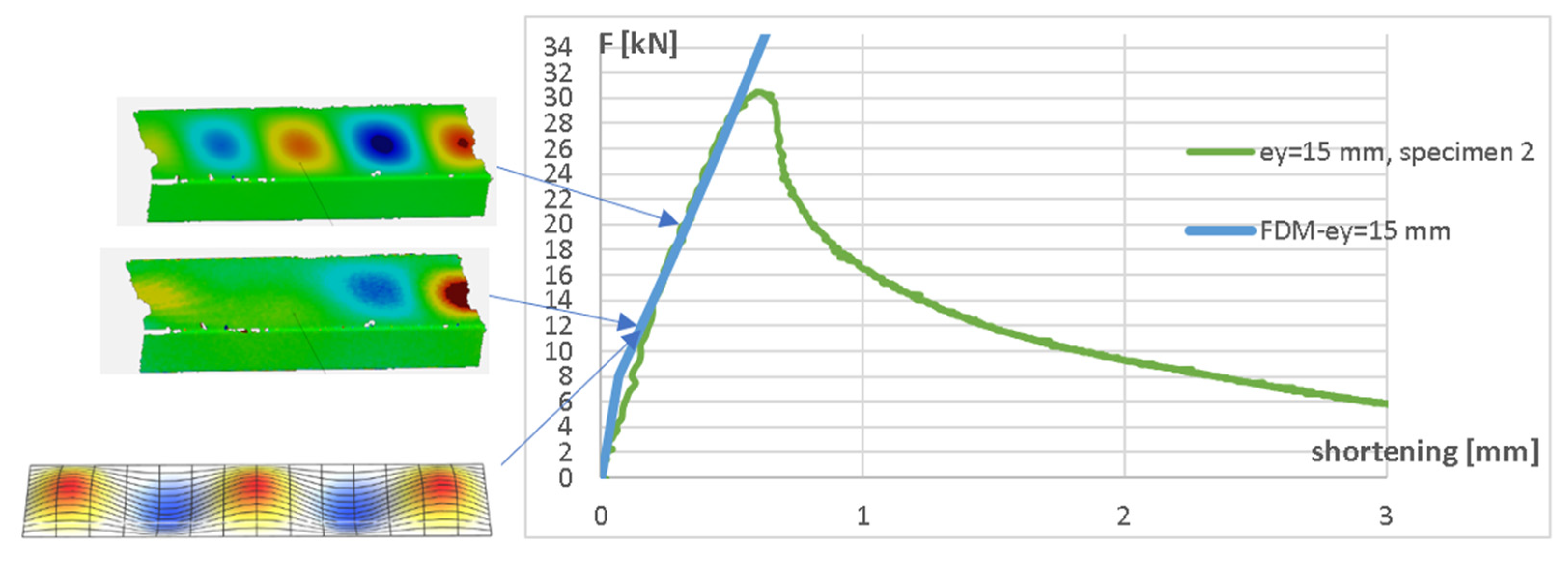

| Eccentricity [mm] | Fey,L [kN] | Fey,NL [kN] | Fey,E [kN] |
|---|---|---|---|
| 15 | 13.1 | 8.1 | 12.5 |
| 30 | 13.0 | 8.0 | 11.9 |
| 45 | 12.8 | 7.5 | 11.5 |
| 60 | 12.5 | 7.0 | 9.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jankowski, J.; Kotełko, M.; Ungureanu, V. Numerical and Experimental Analysis of Buckling and Post-Buckling Behaviour of TWCFS Lipped Channel Section Members Subjected to Eccentric Compression. Materials 2024, 17, 2874. https://doi.org/10.3390/ma17122874
Jankowski J, Kotełko M, Ungureanu V. Numerical and Experimental Analysis of Buckling and Post-Buckling Behaviour of TWCFS Lipped Channel Section Members Subjected to Eccentric Compression. Materials. 2024; 17(12):2874. https://doi.org/10.3390/ma17122874
Chicago/Turabian StyleJankowski, Jacek, Maria Kotełko, and Viorel Ungureanu. 2024. "Numerical and Experimental Analysis of Buckling and Post-Buckling Behaviour of TWCFS Lipped Channel Section Members Subjected to Eccentric Compression" Materials 17, no. 12: 2874. https://doi.org/10.3390/ma17122874





