Preparation and Modeling of Graphene Bubbles to Obtain Strain-Induced Pseudomagnetic Fields
Abstract
1. Introduction
2. A Brief Overview of Bubbling Methods
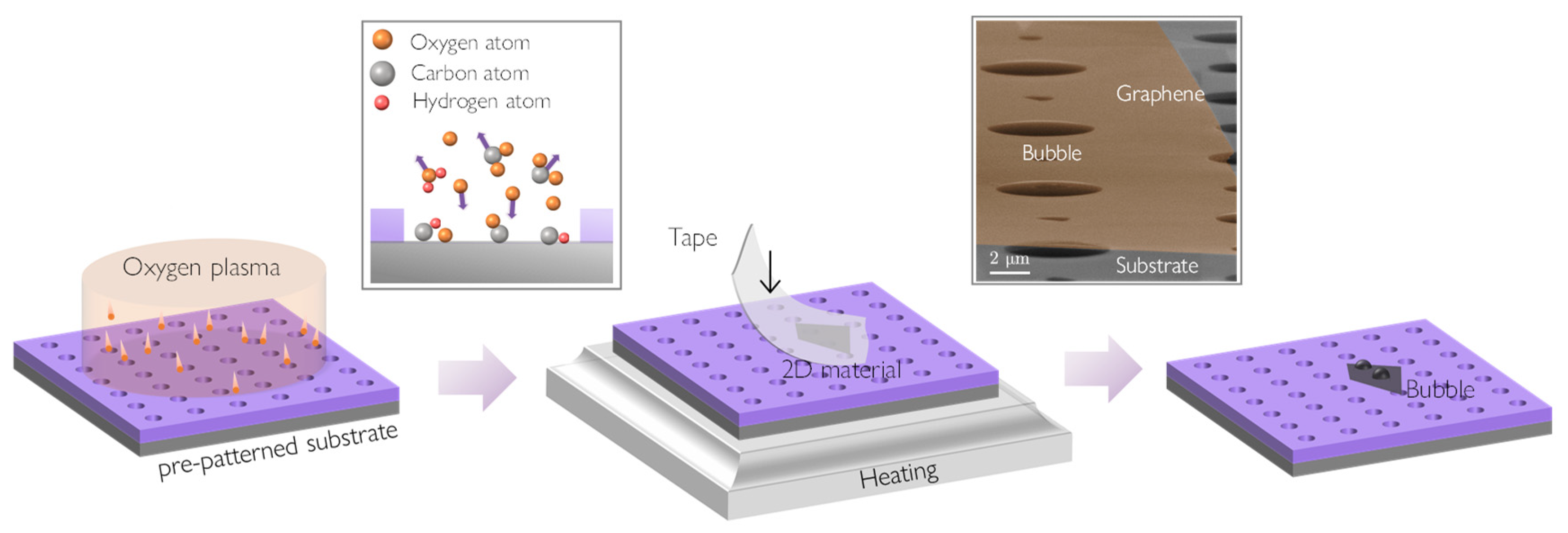
3. Experimental Method
4. Results and Discussion
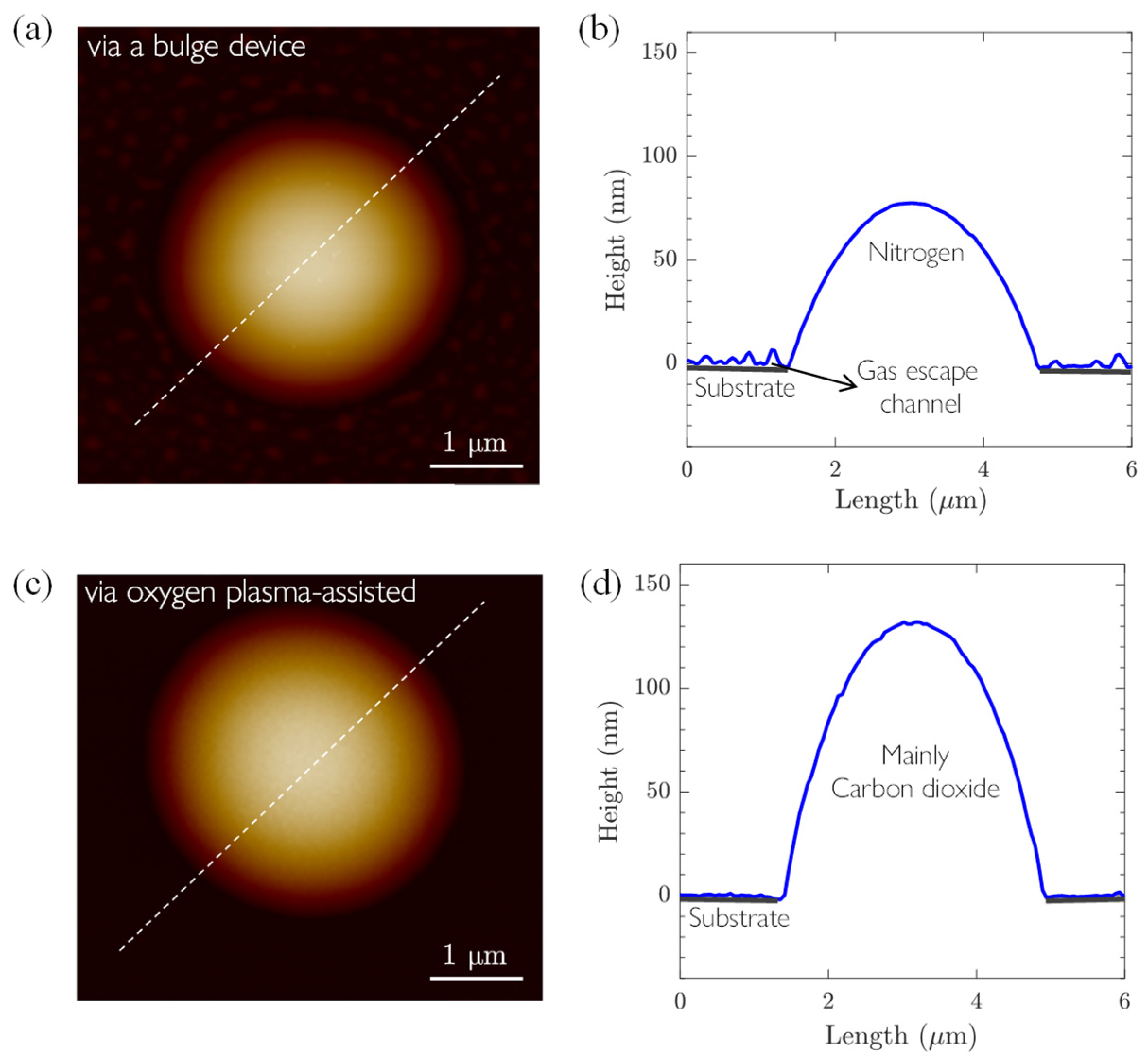
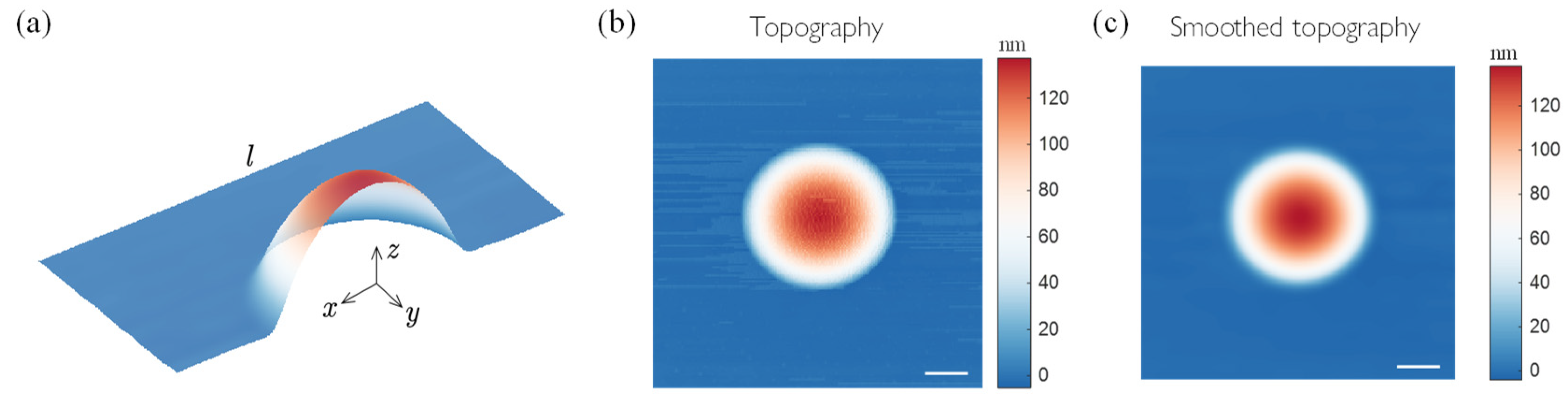
4.1. Surface Topography
4.2. Deflating Behavior
5. Calculation of Strain and Pseudomagnetic Fields
5.1. Numerical Scheme
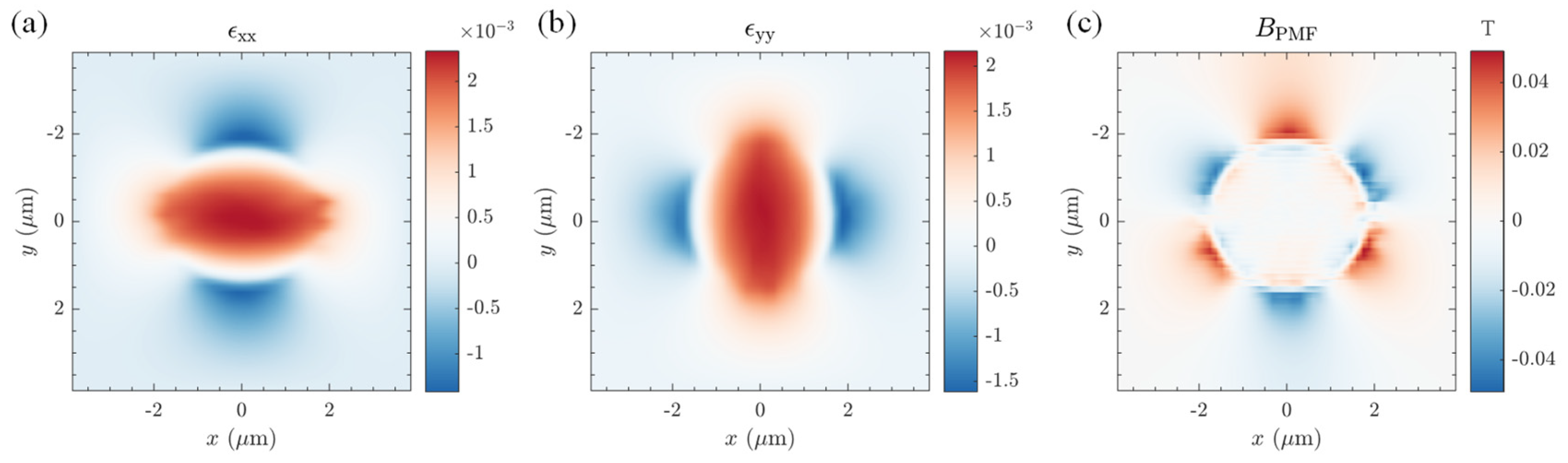
5.2. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Schaibley, J.R.; Yu, H.; Clark, G.; Rivera, P.; Ross, J.S.; Seyler, K.L.; Yao, W.; Xu, X. Valleytronics in 2D materials. Nat. Rev. Mater. 2016, 1, 16055. [Google Scholar] [CrossRef]
- Hu, H.; Chen, N.; Teng, H.; Yu, R.; Xue, M.; Chen, K.; Xiao, Y.; Qu, Y.; Hu, D.; Chen, J.; et al. Gate-tunable negative refraction of mid-infrared polaritons. Science 2023, 379, 558–561. [Google Scholar] [CrossRef]
- Levy, N.; Burke, S.A.; Meaker, K.L.; Panlasigui, M.; Zettl, A.; Guinea, F.; Neto, A.H.C.; Crommie, M.F. Strain-Induced Pseudo–Magnetic Fields Greater Than 300 Tesla in Graphene Nanobubbles. Science 2010, 329, 544–547. [Google Scholar] [CrossRef] [PubMed]
- Androulidakis, C.; Koukaras, E.N.; Paterakis, G.; Trakakis, G.; Galiotis, C. Tunable macroscale structural superlubricity in two-layer graphene via strain engineering. Nat. Commun. 2020, 11, 1595. [Google Scholar] [CrossRef]
- Si, C.; Sun, Z.; Liu, F. Strain engineering of graphene: A review. Nanoscale 2016, 8, 3207–3217. [Google Scholar] [CrossRef]
- Wang, B.; Li, J.; Fang, Z.; Jiang, Y.; Li, S.; Zhan, F.; Dai, Z.; Chen, Q.; Wei, X. Large and Pressure-Dependent c-Axis Piezoresistivity of Highly Oriented Pyrolytic Graphite near Zero Pressure. Nano Lett. 2024, 24, 4965–4971. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Dai, Z.; Wang, B.; Tian, Z.; Yu, C.; Chen, Q.; Wei, X. Pull-to-Peel of Two-Dimensional Materials for the Simultaneous Determination of Elasticity and Adhesion. Nano Lett. 2023, 23, 742–749. [Google Scholar] [CrossRef] [PubMed]
- Stegmann, T.; Szpak, N. Current flow paths in deformed graphene: From quantum transport to classical trajectories in curved space. New J. Phys. 2016, 18, 53016. [Google Scholar] [CrossRef]
- Stegmann, T.; Szpak, N. Current splitting and valley polarization in elastically deformed graphene. 2D Mater. 2019, 6, 015024. [Google Scholar] [CrossRef]
- Low, T.; Guinea, F. Strain-Induced Pseudomagnetic Field for Novel Graphene Electronics. Nano Lett. 2010, 10, 3551–3554. [Google Scholar] [CrossRef] [PubMed]
- Rechtsman, M.C.; Zeuner, J.M.; Tünnermann, A.; Nolte, S.; Segev, M.; Szameit, A. Strain-induced pseudomagnetic field and photonic Landau levels in dielectric structures. Nat. Photon. 2013, 7, 153–158. [Google Scholar] [CrossRef]
- Zhang, D.-B.; Seifert, G.; Chang, K. Strain-Induced Pseudomagnetic Fields in Twisted Graphene Nanoribbons. Phys. Rev. Lett. 2014, 112, 096805. [Google Scholar] [CrossRef] [PubMed]
- Settnes, M.; Power, S.R.; Brandbyge, M.; Jauho, A.-P. Graphene Nanobubbles as Valley Filters and Beam Splitters. Phys. Rev. Lett. 2016, 117, 276801. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Huang, Y.; Klimov, N.N.; Newell, D.B.; Zhitenev, N.B.; Stroscio, J.A.; Solares, S.D.; Li, T. Pseudomagnetic fields in a locally strained graphene drumhead. Phys. Rev. B 2014, 90, 075426. [Google Scholar] [CrossRef]
- Dai, Z.; Liu, L.; Zhang, Z. Strain Engineering of 2D Materials: Issues and Opportunities at the Interface. Adv. Mater. 2019, 31, e1805417. [Google Scholar] [CrossRef] [PubMed]
- Deng, S.; Sumant, A.V.; Berry, V. Strain engineering in two-dimensional nanomaterials beyond graphene. Nano Today 2018, 22, 14–35. [Google Scholar] [CrossRef]
- Qi, Y.; Sadi, M.A.; Hu, D.; Zheng, M.; Wu, Z.; Jiang, Y.; Chen, Y.P. Recent Progress in Strain Engineering on Van der Waals 2D Materials: Tunable Electrical, Electrochemical, Magnetic, and Optical Properties. Adv. Mater. 2023, 35, e2205714. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, R.; Shi, Z.; Zhang, L.; Shi, D.; Wang, E.; Zhang, G. Super-Elastic Graphene Ripples for Flexible Strain Sensors. ACS Nano 2011, 5, 3645–3650. [Google Scholar] [CrossRef]
- Zhao, Q.; Frisenda, R.; Wang, T.; Castellanos-Gomez, A. InSe: A two-dimensional semiconductor with superior flexibility. Nanoscale 2019, 11, 9845–9850. [Google Scholar] [CrossRef]
- Islam, A.; Akker, A.v.D.; Feng, P.X.-L. Anisotropic Thermal Conductivity of Suspended Black Phosphorus Probed by Opto-Thermomechanical Resonance Spectromicroscopy. Nano Lett. 2018, 18, 7683–7691. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhou, B.; Sun, H.; Cui, A.; Jiang, T.; Xu, L.; Jiang, K.; Shang, L.; Hu, Z.; Chu, J. Difference analysis model for the mismatch effect and substrate-induced lattice deformation in atomically thin materials. Phys. Rev. B 2018, 98, 245403. [Google Scholar] [CrossRef]
- Mohiuddin, T.M.G.; Lombardo, A.; Nair, R.R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.M.; Galiotis, C.; Marzari, N.; et al. Uniaxial strain in graphene by Raman spectroscopy:Gpeak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 2009, 79, 205433. [Google Scholar] [CrossRef]
- Raju, A.P.A.; Lewis, A.; Derby, B.; Young, R.J.; Kinloch, I.A.; Zan, R.; Novoselov, K.S. Wide-Area Strain Sensors based upon Graphene-Polymer Composite Coatings Probed by Raman Spectroscopy. Adv. Funct. Mater. 2014, 24, 2865–2874. [Google Scholar] [CrossRef]
- Hou, Y.; Zhou, J.; Xue, M.; Yu, M.; Han, Y.; Zhang, Z.; Lu, Y. Strain Engineering of Twisted Bilayer Graphene: The Rise of Strain-Twistronics. Small 2024, e2311185. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; He, J.; Rao, Y.; Dai, Z.; Ye, H.; Tanir, J.C.; Li, Y.; Lu, N. Conformability of flexible sheets on spherical surfaces. Sci. Adv. 2023, 9, eadf2709. [Google Scholar] [CrossRef] [PubMed]
- Castellanos-Gomez, A.; Roldán, R.; Cappelluti, E.; Buscema, M.; Guinea, F.; van der Zant, H.S.J.; Steele, G.A. Local Strain Engineering in Atomically Thin MoS2. Nano Lett. 2013, 13, 5361–5366. [Google Scholar] [CrossRef]
- Quereda, J.; San-Jose, P.; Parente, V.; Vaquero-Garzon, L.; Molina-Mendoza, A.J.; Agraït, N.; Rubio-Bollinger, G.; Guinea, F.; Roldán, R.; Castellanos-Gomez, A. Strong Modulation of Optical Properties in Black Phosphorus through Strain-Engineered Rippling. Nano Lett. 2016, 16, 2931–2937. [Google Scholar] [CrossRef] [PubMed]
- Martella, C.; Mennucci, C.; Cinquanta, E.; Lamperti, A.; Cappelluti, E.; de Mongeot, F.B.; Molle, A. Anisotropic MoS2 Nanosheets Grown on Self-Organized Nanopatterned Substrates. Adv. Mater. 2017, 29, 1605785. [Google Scholar] [CrossRef]
- Mangu, V.S.; Zamiri, M.; Brueck, S.R.J.; Cavallo, F. Strain engineering, efficient excitonic photoluminescence, and exciton funnelling in unmodified MoS2 nanosheets. Nanoscale 2017, 9, 16602–16606. [Google Scholar] [CrossRef]
- Chen, Z.; Leng, K.; Zhao, X.; Malkhandi, S.; Tang, W.; Tian, B.; Dong, L.; Zheng, L.; Lin, M.; Yeo, B.S.; et al. Interface confined hydrogen evolution reaction in zero valent metal nanoparticles-intercalated molybdenum disulfide. Nat. Commun. 2017, 8, 14548. [Google Scholar] [CrossRef]
- Zhang, Y.; Heiranian, M.; Janicek, B.; Budrikis, Z.; Zapperi, S.; Huang, P.Y.; Johnson, H.T.; Aluru, N.R.; Lyding, J.W.; Mason, N. Strain Modulation of Graphene by Nanoscale Substrate Curvatures: A Molecular View. Nano Lett. 2018, 18, 2098–2104. [Google Scholar] [CrossRef]
- Yang, S.; Chen, Y.; Jiang, C. Strain engineering of two-dimensional materials: Methods, properties, and applications. InfoMat 2021, 3, 397–420. [Google Scholar] [CrossRef]
- Chen, E.; Dai, Z. Axisymmetric Peeling of Thin Elastic Films: A Perturbation Solution. J. Appl. Mech. 2023, 90, 101011. [Google Scholar] [CrossRef]
- Cui, X.; Liu, L.; Dong, W.; Zhou, Y.; Zhang, Z. Mechanics of 2D material bubbles. Nano Res. 2023, 16, 13434–13449. [Google Scholar] [CrossRef]
- Darlington, T.P.; Carmesin, C.; Florian, M.; Yanev, E.; Ajayi, O.; Ardelean, J.; Rhodes, D.A.; Ghiotto, A.; Krayev, A.; Watanabe, K.; et al. Imaging strain-localized excitons in nanoscale bubbles of monolayer WSe2 at room temperature. Nat. Nanotechnol. 2020, 15, 854–860. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Dong, W.; Feng, S.; Wang, G.; Wang, C.; Wang, S.; Zhou, Y.; Qiu, X.; Liu, L.; Xu, Z.; et al. Extra-High Mechanical and Phononic Anisotropy in Black Phosphorus Blisters. Small 2023, 19, e2301959. [Google Scholar] [CrossRef]
- Sanchez, D.A.; Dai, Z.; Lu, N. 2D Material Bubbles: Fabrication, Characterization, and Applications. Trends Chem. 2021, 3, 204–217. [Google Scholar] [CrossRef]
- Dai, Z.; Lu, N.; Liechti, K.M.; Huang, R. Mechanics at the interfaces of 2D materials: Challenges and opportunities. Curr. Opin. Solid State Mater. Sci. 2020, 24, 100837. [Google Scholar] [CrossRef]
- Wang, G.; Dai, Z.; Xiao, J.; Feng, S.; Weng, C.; Liu, L.; Xu, Z.; Huang, R.; Zhang, Z. Bending of Multilayer van der Waals Materials. Phys. Rev. Lett. 2019, 123, 116101. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Shen, W.; Wu, M.; Li, B.; Zhang, Q.; Liu, S.; Hu, C.; Yang, S.; Gao, Y.; et al. Strain and Interference Synergistically Modulated Optical and Electrical Properties in ReS2/Graphene Heterojunction Bubbles. ACS Nano 2022, 16, 16271–16280. [Google Scholar] [CrossRef] [PubMed]
- Tedeschi, D.; Blundo, E.; Felici, M.; Pettinari, G.; Liu, B.; Yildrim, T.; Petroni, E.; Zhang, C.; Zhu, Y.; Sennato, S.; et al. Controlled Micro/Nanodome Formation in Proton-Irradiated Bulk Transition-Metal Dichalcogenides. Adv. Mater. 2019, 31, e1903795. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Wang, H.; Chen, L.; Wang, X.; Xie, H.; Jiang, C.; Li, C.; Elibol, K.; Meyer, J.; Watanabe, K.; et al. Isolating hydrogen in hexagonal boron nitride bubbles by a plasma treatment. Nat. Commun. 2019, 10, 2815. [Google Scholar] [CrossRef] [PubMed]
- Yasuda, S.; Tamura, K.; Terasawa, T.-O.; Yano, M.; Nakajima, H.; Morimoto, T.; Okazaki, T.; Agari, R.; Takahashi, Y.; Kato, M.; et al. Confinement of Hydrogen Molecules at Graphene-Metal Interface by Electrochemical Hydrogen Evolution Reaction. J. Phys. Chem. C 2020, 124, 5300–5307. [Google Scholar] [CrossRef]
- Wang, J.; Sorescu, D.C.; Jeon, S.; Belianinov, A.; Kalinin, S.V.; Baddorf, A.P.; Maksymovych, P. Atomic intercalation to measure adhesion of graphene on graphite. Nat. Commun. 2016, 7, 13263. [Google Scholar] [CrossRef] [PubMed]
- Larciprete, R.; Colonna, S.; Ronci, F.; Flammini, R.; Lacovig, P.; Apostol, N.; Politano, A.; Feulner, P.; Menzel, D.; Lizzit, S. Self-Assembly of Graphene Nanoblisters Sealed to a Bare Metal Surface. Nano Lett. 2016, 16, 1808–1817. [Google Scholar] [CrossRef] [PubMed]
- Villarreal, R.; Lin, P.-C.; Faraji, F.; Hassani, N.; Bana, H.; Zarkua, Z.; Nair, M.N.; Tsai, H.-C.; Auge, M.; Junge, F.; et al. Breakdown of Universal Scaling for Nanometer-Sized Bubbles in Graphene. Nano Lett. 2021, 21, 8103–8110. [Google Scholar] [CrossRef] [PubMed]
- Blundo, E.; Surrente, A.; Spirito, D.; Pettinari, G.; Yildirim, T.; Chavarin, C.A.; Baldassarre, L.; Felici, M.; Polimeni, A. Vibrational Properties in Highly Strained Hexagonal Boron Nitride Bubbles. Nano Lett. 2022, 22, 1525–1533. [Google Scholar] [CrossRef]
- Blundo, E.; Felici, M.; Yildirim, T.; Pettinari, G.; Tedeschi, D.; Miriametro, A.; Liu, B.; Ma, W.; Lu, Y.; Polimeni, A. Evidence of the direct-to-indirect band gap transition in strained two-dimensional WS2, MoS2, and WSe2. Phys. Rev. Res. 2020, 2, 012024. [Google Scholar] [CrossRef]
- Blundo, E.; Di Giorgio, C.; Pettinari, G.; Yildirim, T.; Felici, M.; Lu, Y.; Bobba, F.; Polimeni, A. Engineered Creation of Periodic Giant, Nonuniform Strains in MoS2 Monolayers. Adv. Mater. Interfaces 2020, 7, 2000621. [Google Scholar] [CrossRef]
- Di Giorgio, C.; Blundo, E.; Pettinari, G.; Felici, M.; Lu, Y.; Cucolo, A.M.; Polimeni, A.; Bobba, F. Nanoscale Measurements of Elastic Properties and Hydrostatic Pressure in H2-Bulged MoS2Membranes. Adv. Mater. Interfaces 2020, 7, 2001024. [Google Scholar] [CrossRef]
- Jain, A.; Bharadwaj, P.; Heeg, S.; Parzefall, M.; Taniguchi, T.; Watanabe, K.; Novotny, L. Minimizing residues and strain in 2D materials transferred from PDMS. Nanotechnology 2018, 29, 265203. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Ren, X.; Fan, J.; Wang, G.; Dai, Z.; Jin, C.; Wang, W.; Zhu, Y.; Zhang, S.; Liu, L.; et al. Preparation of Twisted Bilayer Graphene via the Wetting Transfer Method. ACS Appl. Mater. Interfaces 2020, 12, 40958–40967. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, D.A.; Dai, Z.; Wang, P.; Cantu-Chavez, A.; Brennan, C.J.; Huang, R.; Lu, N. Mechanics of spontaneously formed nanoblisters trapped by transferred 2D crystals. Proc. Natl. Acad. Sci. USA 2018, 115, 7884–7889. [Google Scholar] [CrossRef] [PubMed]
- Pizzocchero, F.; Gammelgaard, L.; Jessen, B.S.; Caridad, J.M.; Wang, L.; Hone, J.; Bøggild, P.; Booth, T.J. The hot pick-up technique for batch assembly of van der Waals heterostructures. Nat. Commun. 2016, 7, 11894. [Google Scholar] [CrossRef] [PubMed]
- Purdie, D.G.; Pugno, N.M.; Taniguchi, T.; Watanabe, K.; Ferrari, A.C.; Lombardo, A. Cleaning interfaces in layered materials heterostructures. Nat. Commun. 2018, 9, 5387. [Google Scholar] [CrossRef] [PubMed]
- Haigh, S.J.; Gholinia, A.; Jalil, R.; Romani, S.; Britnell, L.; Elias, D.C.; Novoselov, K.S.; Ponomarenko, L.A.; Geim, A.K.; Gorbachev, R. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat. Mater. 2012, 11, 764–767. [Google Scholar] [CrossRef] [PubMed]
- Gasparutti, I.; Song, S.H.; Neumann, M.; Wei, X.; Watanabe, K.; Taniguchi, T.; Lee, Y.H. How Clean Is Clean? Recipes for van der Waals Heterostructure Cleanliness Assessment. ACS Appl. Mater. Interfaces 2020, 12, 7701–7709. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Dai, Z.; Zhang, S.; Feng, S.; Wang, G.; Liu, L.; Xu, Z.; Li, Q.; Zhang, Z. Elastocapillary cleaning of twisted bilayer graphene interfaces. Nat. Commun. 2021, 12, 5069. [Google Scholar] [CrossRef]
- Khestanova, E.; Guinea, F.; Fumagalli, L.; Geim, A.K.; Grigorieva, I.V. Universal shape and pressure inside bubbles appearing in van der Waals heterostructures. Nat. Commun. 2016, 7, 12587. [Google Scholar] [CrossRef]
- Rao, Y.; Kim, E.; Dai, Z.; He, J.; Li, Y.; Lu, N. Size-dependent shape characteristics of 2D crystal blisters. J. Mech. Phys. Solids 2023, 175, 105286. [Google Scholar] [CrossRef]
- Dong, W.; Dai, Z.; Liu, L.; Zhang, Z. Toward Clean 2D Materials and Devices: Recent Progress in Transfer and Cleaning Methods. Adv. Mater. 2023, 36, e2303014. [Google Scholar] [CrossRef]
- Kretinin, A.V.; Cao, Y.; Tu, J.S.; Yu, G.L.; Jalil, R.; Novoselov, K.S.; Haigh, S.J.; Gholinia, A.; Mishchenko, A.; Lozada, M.; et al. Electronic Properties of Graphene Encapsulated with Different Two-Dimensional Atomic Crystals. Nano Lett. 2014, 14, 3270–3276. [Google Scholar] [CrossRef]
- Xu, K.; Cao, P.; Heath, J.R. Graphene Visualizes the First Water Adlayers on Mica at Ambient Conditions. Science 2010, 329, 1188–1191. [Google Scholar] [CrossRef]
- Wu, S.; He, F.; Xie, G.; Bian, Z.; Ren, Y.; Liu, X.; Yang, H.; Guo, D.; Zhang, L.; Wen, S.; et al. Super-Slippery Degraded Black Phosphorus/Silicon Dioxide Interface. ACS Appl. Mater. Interfaces 2020, 12, 7717–7726. [Google Scholar] [CrossRef]
- Wood, J.D.; Wells, S.A.; Jariwala, D.; Chen, K.-S.; Cho, E.; Sangwan, V.K.; Liu, X.; Lauhon, L.J.; Marks, T.J.; Hersam, M.C. Effective Passivation of Exfoliated Black Phosphorus Transistors against Ambient Degradation. Nano Lett. 2014, 14, 6964–6970. [Google Scholar] [CrossRef]
- Budania, P.; Baine, P.; Montgomery, J.; McGeough, C.; Cafolla, T.; Modreanu, M.; McNeill, D.; Mitchell, N.; Hughes, G.; Hurley, P. Long-term stability of mechanically exfoliated MoS2 flakes. MRS Commun. 2017, 7, 813–818. [Google Scholar] [CrossRef]
- Mirabelli, G.; McGeough, C.; Schmidt, M.; McCarthy, E.K.; Monaghan, S.; Povey, I.M.; McCarthy, M.; Gity, F.; Nagle, R.; Hughes, G.; et al. Air sensitivity of MoS2, MoSe2, MoTe2, HfS2, and HfSe2. J. Appl. Phys. 2016, 120, 125102. [Google Scholar] [CrossRef]
- Kim, H.H.; Yang, J.W.; Jo, S.B.; Kang, B.; Lee, S.K.; Bong, H.; Lee, G.; Kim, K.S.; Cho, K. Substrate-Induced Solvent Intercalation for Stable Graphene Doping. ACS Nano 2013, 7, 1155–1162. [Google Scholar] [CrossRef]
- Li, Y.; Wang, B.; Li, W.; Xu, K. Dynamic, Spontaneous Blistering of Substrate-Supported Graphene in Acidic Solutions. ACS Nano 2022, 16, 6145–6152. [Google Scholar] [CrossRef]
- Zong, Z.; Chen, C.-L.; Dokmeci, M.R.; Wan, K.-T. Direct measurement of graphene adhesion on silicon surface by intercalation of nanoparticles. J. Appl. Phys. 2010, 107, 026104. [Google Scholar] [CrossRef]
- Gao, X.; Yu, X.; Li, B.; Fan, S.; Li, C. Measuring Graphene Adhesion on Silicon Substrate by Single and Dual Nanoparticle-Loaded Blister. Adv. Mater. Interfaces 2017, 4, 1601023. [Google Scholar] [CrossRef]
- Dai, Z.; Hou, Y.; Sanchez, D.A.; Wang, G.; Brennan, C.J.; Zhang, Z.; Liu, L.; Lu, N. Interface-Governed Deformation of Nanobubbles and Nanotents Formed by Two-Dimensional Materials. Phys. Rev. Lett. 2018, 121, 266101. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Shokuhfar, T.; Klie, R.F. Precise In Situ Modulation of Local Liquid Chemistry via Electron Irradiation in Nanoreactors Based on Graphene Liquid Cells. Adv. Mater. 2016, 28, 7716–7722. [Google Scholar] [CrossRef] [PubMed]
- Binder, J.; Dabrowska, A.K.; Tokarczyk, M.; Ludwiczak, K.; Bozek, R.; Kowalski, G.; Stepniewski, R.; Wysmolek, A. Epitaxial Hexagonal Boron Nitride for Hydrogen Generation by Radiolysis of Interfacial Water. Nano Lett. 2023, 23, 1267–1272. [Google Scholar] [CrossRef] [PubMed]
- Stolyarova, E.; Stolyarov, D.; Bolotin, K.; Ryu, S.; Liu, L.; Rim, K.T.; Klima, M.; Hybertsen, M.; Pogorelsky, I.; Pavlishin, I.; et al. Observation of Graphene Bubbles and Effective Mass Transport under Graphene Films. Nano Lett. 2009, 9, 332–337. [Google Scholar] [CrossRef] [PubMed]
- An, H.; Tan, B.H.; Moo, J.G.S.; Liu, S.; Pumera, M.; Ohl, C.-D. Graphene Nanobubbles Produced by Water Splitting. Nano Lett. 2017, 17, 2833–2838. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Chen, W.; Qiao, J.; Zhang, M.; Zheng, X.; Xue, Z.; Liang, R.; Tian, C.; He, L.; Di, Z.; et al. Programmable graphene nanobubbles with three-fold symmetric pseudo-magnetic fields. Nat. Commun. 2019, 10, 3127. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Tan, J.Y.; Toh, C.-T.; Koenig, S.P.; Fedorov, V.E.; Neto, A.H.C.; Özyilmaz, B. Nanometer Thick Elastic Graphene Engine. Nano Lett. 2014, 14, 2677–2680. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Cao, S.; Zhang, N.; Jin, B.; Zong, Z.; Li, Z.; Chen, X. Construction of Position-Controllable Graphene Bubbles in Liquid Nitrogen with Assistance of Low-Power Laser. ACS Appl. Mater. Interfaces 2020, 12, 56260–56268. [Google Scholar] [CrossRef]
- Bampoulis, P.; Teernstra, V.J.; Lohse, D.; Zandvliet, H.J.W.; Poelsema, B. Hydrophobic Ice Confined between Graphene and MoS2. J. Phys. Chem. C 2016, 120, 27079–27084. [Google Scholar] [CrossRef]
- Pandey, M.; Kumar, R. Polymer curing assisted formation of optically visible sub-micron blisters of multilayer graphene for local strain engineering. J. Phys. Condens. Matter 2022, 34, 245401. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Dai, Z. Characterizing the wetting behavior of 2D materials: A review. J. Mater. Informatics 2023, 3, 20. [Google Scholar] [CrossRef]
- Vasu, K.S.; Prestat, E.; Abraham, J.; Dix, J.; Kashtiban, R.J.; Beheshtian, J.; Sloan, J.; Carbone, P.; Neek-Amal, M.; Haigh, S.J.; et al. Van der Waals pressure and its effect on trapped interlayer molecules. Nat. Commun. 2016, 7, 12168. [Google Scholar] [CrossRef] [PubMed]
- Bunch, J.S.; Verbridge, S.S.; Alden, J.S.; Van Der Zande, A.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Impermeable atomic membranes from graphene sheets. Nano Lett. 2008, 8, 2458–2462. [Google Scholar] [CrossRef] [PubMed]
- Koenig, S.P.; Boddeti, N.G.; Dunn, M.L.; Bunch, J.S. Ultrastrong adhesion of graphene membranes. Nat. Nanotechnol. 2011, 6, 543–546. [Google Scholar] [CrossRef] [PubMed]
- Yin, P.; Ma, M. Efficient and Robust Fabrication of Microscale Graphene Drums. ACS Appl. Nano Mater. 2018, 1, 6596–6602. [Google Scholar] [CrossRef]
- Wang, G.; Dai, Z.; Wang, Y.; Tan, P.; Liu, L.; Xu, Z.; Wei, Y.; Huang, R.; Zhang, Z. Measuring Interlayer Shear Stress in Bilayer Graphene. Phys. Rev. Lett. 2017, 119, 036101. [Google Scholar] [CrossRef]
- Lloyd, D.A.-O.; Liu, X.; Boddeti, N.; Cantley, L.; Long, R.; Dunn, M.L.; Bunch, J.S. Adhesion, Stiffness, and Instability in Atomically Thin MoS(2) Bubbles. Nano Lett. 2017, 17, 5329–5334. [Google Scholar] [CrossRef]
- Sun, P.Z.; Yang, Q.; Kuang, W.J.; Stebunov, Y.V.; Xiong, W.Q.; Yu, J.; Nair, R.R.; Katsnelson, M.I.; Yuan, S.J.; Grigorieva, I.V.; et al. Limits on gas impermeability of graphene. Nature 2020, 579, 229–232. [Google Scholar] [CrossRef]
- Sun, P.Z.; Yagmurcukardes, M.; Zhang, R.; Kuang, W.J.; Lozada-Hidalgo, M.; Liu, B.L.; Cheng, H.-M.; Wang, F.C.; Peeters, F.M.; Grigorieva, I.V.; et al. Exponentially selective molecular sieving through angstrom pores. Nat. Commun. 2021, 12, 7170. [Google Scholar] [CrossRef] [PubMed]
- Nicholl, R.J.; Conley, H.J.; Lavrik, N.V.; Vlassiouk, I.; Puzyrev, Y.S.; Sreenivas, V.P.; Pantelides, S.T.; Bolotin, K.I. The effect of intrinsic crumpling on the mechanics of free-standing graphene. Nat. Commun. 2015, 6, 8789. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, V.O.; Kalappattil, V.; Eggers, T.; Bonilla, M.; Kolekar, S.; Huy, P.T.; Batzill, M.; Phan, M.-H. A magnetic sensor using a 2D van der Waals ferromagnetic material. Sci. Rep. 2020, 10, 4789. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Zheng, L.; Liu, Z.; Wang, X. Two-dimensional materials: From mechanical properties to flexible mechanical sensors. InfoMat 2020, 2, 1077–1094. [Google Scholar] [CrossRef]
- Lemme, M.C.; Wagner, S.; Lee, K.; Fan, X.; Verbiest, G.J.; Wittmann, S.; Lukas, S.; Dolleman, R.J.; Niklaus, F.; van der Zant, H.S.J.; et al. Nanoelectromechanical Sensors Based on Suspended 2D Materials. Research 2020, 2020, 8748602. [Google Scholar] [CrossRef] [PubMed]
- Khan, Z.H.; Kermany, A.R.; Öchsner, A.; Iacopi, F. Mechanical and electromechanical properties of graphene and their potential application in MEMS. J. Phys. D Appl. Phys. 2017, 50, 053003. [Google Scholar] [CrossRef]
- Fonash, S.J. An Overview of Dry Etching Damage and Contamination Effects. J. Electrochem. Soc. 1990, 137, 3885. [Google Scholar] [CrossRef]
- Saga, K.; Hattori, T. Identification and Removal of Trace Organic Contamination on Silicon Wafers Stared in Plastic Boxes. J. Electrochem. Soc. 1996, 143, 3279. [Google Scholar] [CrossRef]
- Lee, C.; Kim, H.W.; Kim, S. Organic contaminants removal by oxygen ECR plasma. Appl. Surf. Sci. 2007, 253, 3658–3663. [Google Scholar] [CrossRef]
- Boddeti, N.G.; Koenig, S.P.; Long, R.; Xiao, J.; Bunch, J.S.; Dunn, M.L. Mechanics of Adhered, Pressurized Graphene Blisters. J. Appl. Mech. 2013, 80, 040909. [Google Scholar] [CrossRef]
- Boddeti, N.G.; Liu, X.; Long, R.; Xiao, J.; Bunch, J.S.; Dunn, M.L. Graphene blisters with switchable shapes controlled by pressure and adhesion. Nano Lett. 2013, 13, 6216–6221. [Google Scholar] [CrossRef] [PubMed]
- Darlington, T.P.; Krayev, A.; Venkatesh, V.; Saxena, R.; Kysar, J.W.; Borys, N.J.; Jariwala, D.; Schuck, P.J. Facile and quantitative estimation of strain in nanobubbles with arbitrary symmetry in 2D semiconductors verified using hyperspectral nano-optical imaging. J. Chem. Phys. 2020, 153, 024702. [Google Scholar] [CrossRef] [PubMed]
- Guinea, F.; Katsnelson, M.I.; Geim, A.K. Energy gaps and a zero-field quantum Hall effect in graphene by strain engineering. Nat. Phys. 2010, 6, 30–33. [Google Scholar] [CrossRef]
- Mansfield, E.H. The Bending and Stretching of Plates; Cambridge University Press: Cambridge, UK, 1989; p. 240. [Google Scholar]
- Dai, Z.; Rao, Y.; Lu, N. Two-dimensional crystals on adhesive substrates subjected to uniform transverse pressure. Int. J. Solids Struct. 2022, 257, 111829. [Google Scholar] [CrossRef]
- Qi, Z.; Kitt, A.L.; Park, H.S.; Pereira, V.M.; Campbell, D.K.; Neto, A.H.C. Pseudomagnetic fields in graphene nanobubbles of constrained geometry: A molecular dynamics study. Phys. Rev. B 2014, 90, 125419. [Google Scholar] [CrossRef]
- Dai, Z. Analytical Solutions for Circular Elastic Membranes Under Pressure. J. Appl. Mech. 2024, 91, 1–16. [Google Scholar] [CrossRef]


| Methods | Reference | Max. Height (nm) | Max. Lateral Size (nm) | Shape | Position | Durability |
|---|---|---|---|---|---|---|
| Proton irradiation-assisted | [42] | ~500 | ~3000 | Circular | Controlled | >2 years |
| [43] | ~200 | ~9600 | Near-circular | Uncontrolled | >40 weeks | |
| [46] | ~0.3 | ~12 | Irregular | Uncontrolled | NA (Not applicable) | |
| [48] | 267 | 4540 | Near-circular | Uncontrolled | >23 months | |
| [49] | 482 | 6300 | Circular | Uncontrolled | NA | |
| [50] | 422 | 5140 | Circular | Uncontrolled | >2 years | |
| Spontaneous formation | [67] | ~60 | ~1000 | Irregular | Uncontrolled | NA |
| [70] | ~100 | Micron | Irregular | Uncontrolled | NA | |
| Water splitting | [77] | ~100 | ~2000 | Nearly circular | Uncontrolled | NA |
| Hydrogen desorption | [78] | 25 | ~400 | Nearly circular | Controlled | NA |
| Laser irradiation | [79] | 325 | 5600 | Nearly circular | Controlled | NA |
| [80] | ~3.6 | ~68 | Nearly circular | Uncontrolled | <12 days | |
| Liquid introduction | [81] | ~130 | ~450 | Irregular | Uncontrolled | NA |
| [82] | ~850 | ~30,000 | Irregular | Uncontrolled | >58 days | |
| Direct bulging | [37] | ~130 | 9000 | Rectangular | Controlled | NA |
| [85] | 175 | 4750 | Square | Controlled | <10 h | |
| [86] | ~580 | ~7300 | Circular | Controlled | >20 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Cao, J.; Zhu, S.; Dai, Z. Preparation and Modeling of Graphene Bubbles to Obtain Strain-Induced Pseudomagnetic Fields. Materials 2024, 17, 2889. https://doi.org/10.3390/ma17122889
Yu C, Cao J, Zhu S, Dai Z. Preparation and Modeling of Graphene Bubbles to Obtain Strain-Induced Pseudomagnetic Fields. Materials. 2024; 17(12):2889. https://doi.org/10.3390/ma17122889
Chicago/Turabian StyleYu, Chuanli, Jiacong Cao, Shuze Zhu, and Zhaohe Dai. 2024. "Preparation and Modeling of Graphene Bubbles to Obtain Strain-Induced Pseudomagnetic Fields" Materials 17, no. 12: 2889. https://doi.org/10.3390/ma17122889
APA StyleYu, C., Cao, J., Zhu, S., & Dai, Z. (2024). Preparation and Modeling of Graphene Bubbles to Obtain Strain-Induced Pseudomagnetic Fields. Materials, 17(12), 2889. https://doi.org/10.3390/ma17122889







