Reactive Infiltration: Effects of Different Parameters
Abstract
:1. Introduction
2. Theoretical Background
- Diffusion
- Chemical reactions
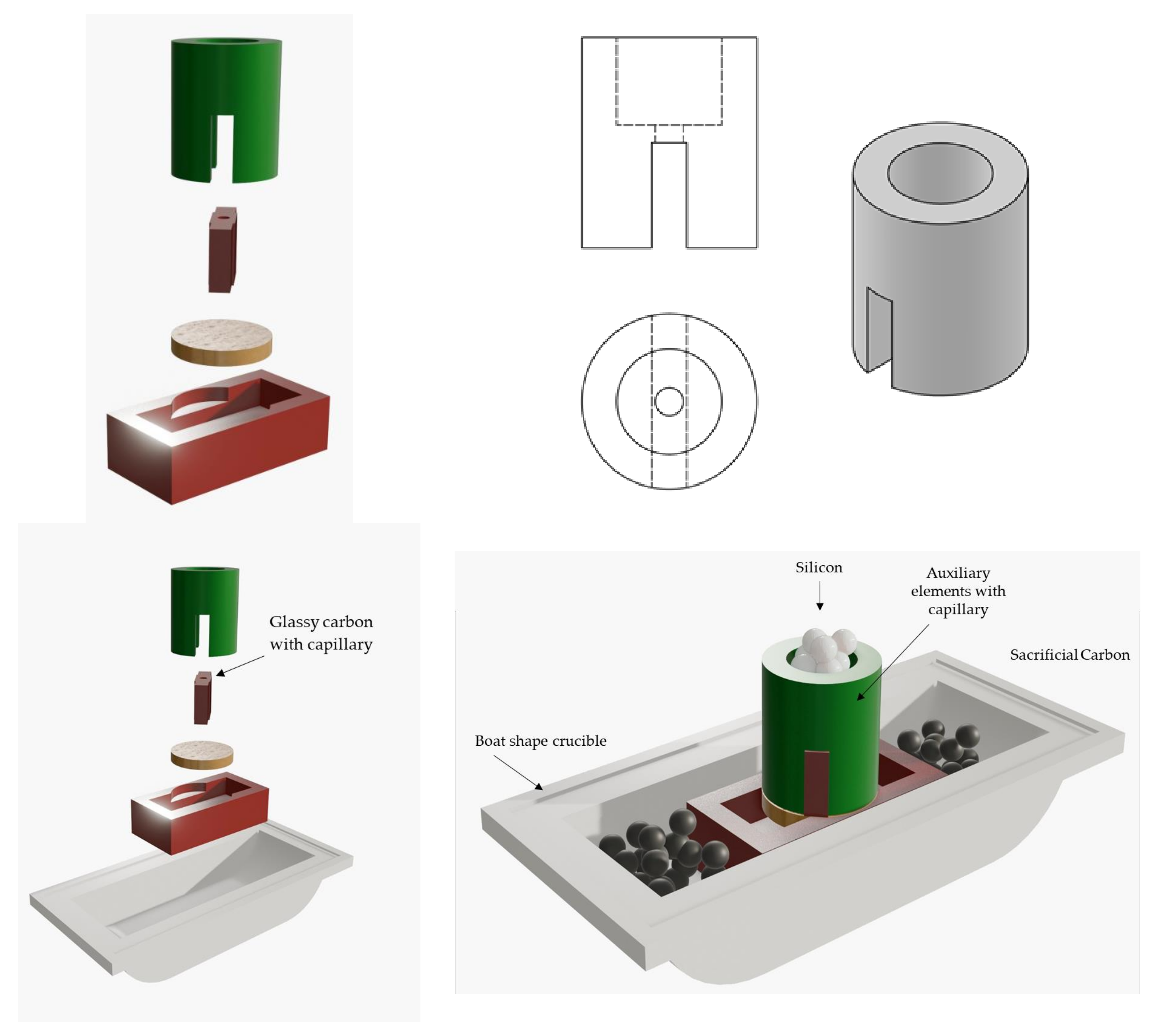
3. Experimental
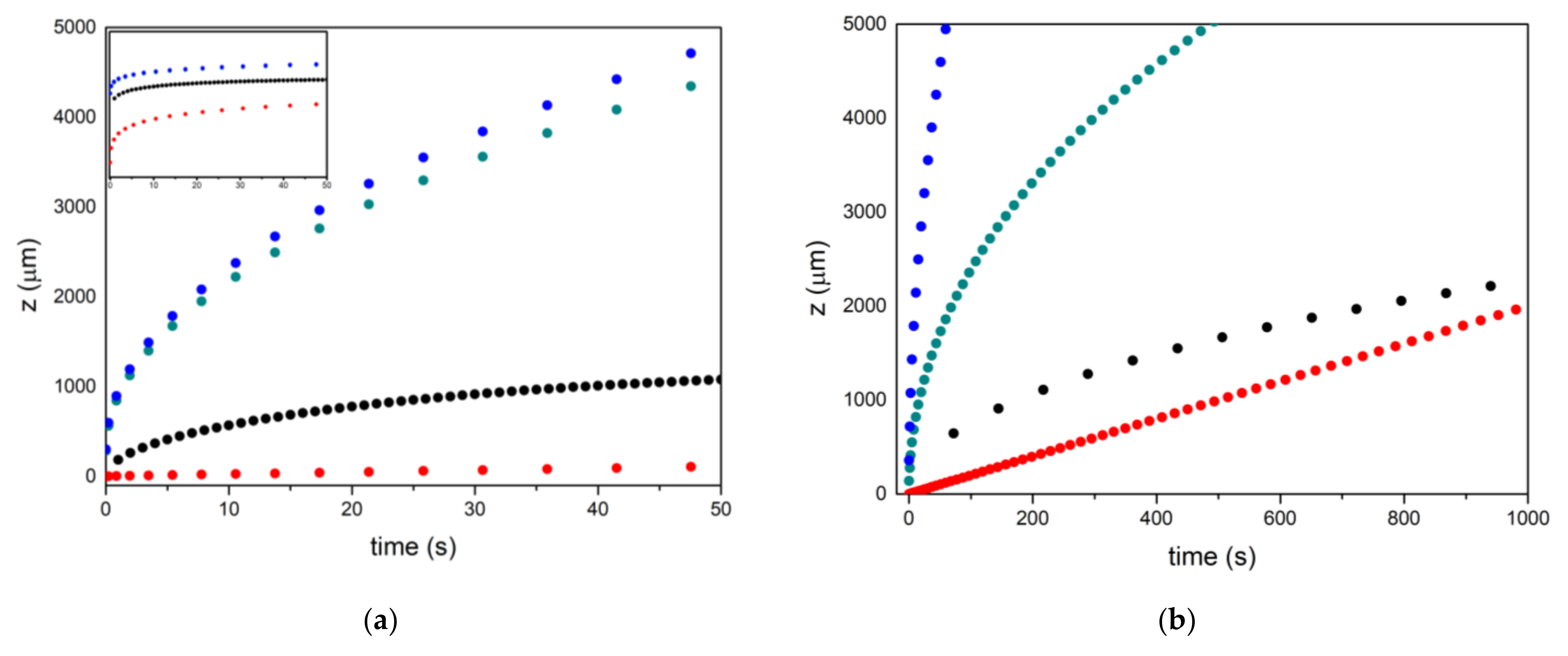
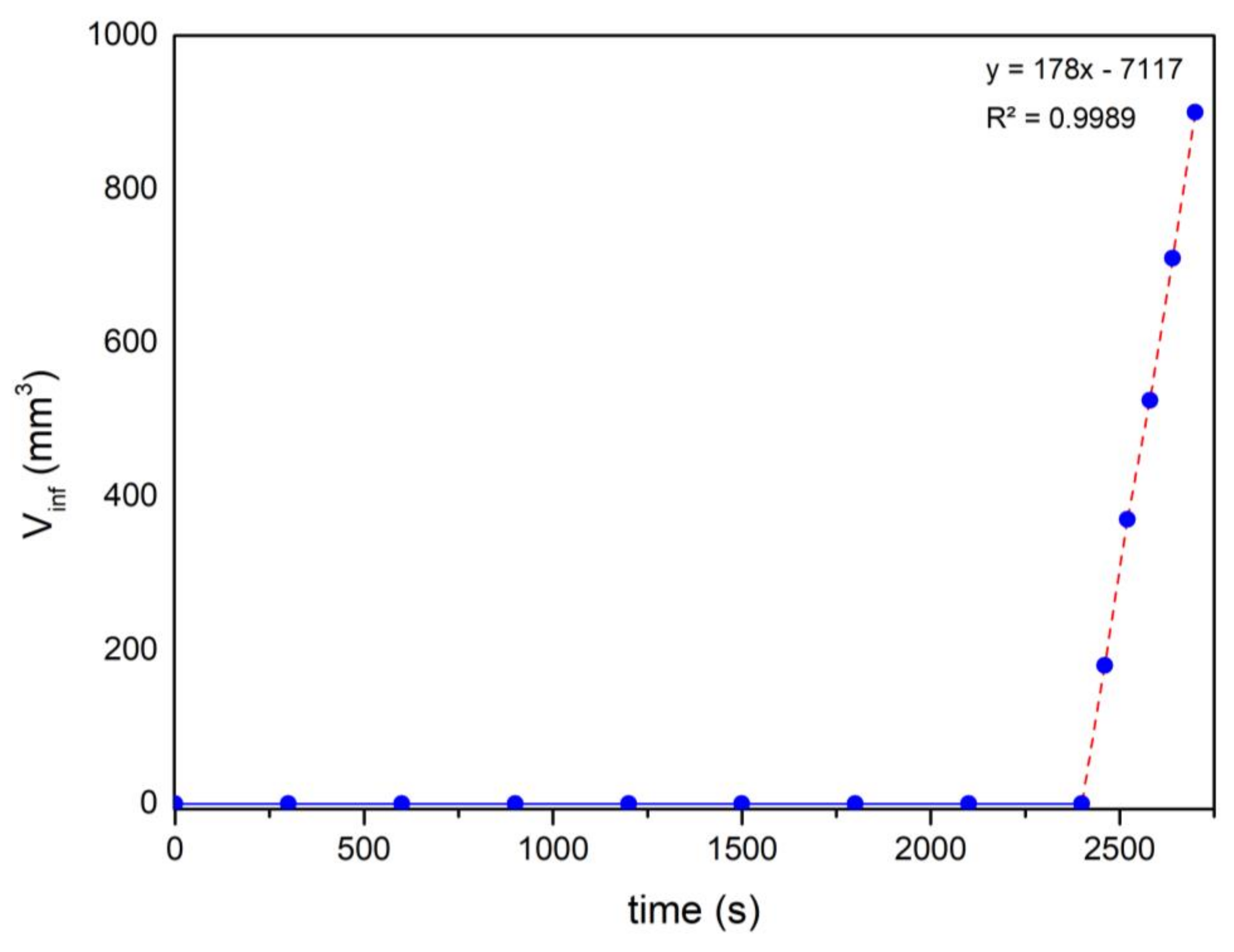
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Calderon, N.R.; Martinez-Escandell, M.; Narciso, J.; Rodríguez-Reinoso, F. The role of carbon biotemplate density in mechanical properties of biomorphic SiC. J. Eur. Ceram. Soc. 2009, 29, 465–472. [Google Scholar] [CrossRef]
- Calderon, N.R.; Martinez-Escandell, M.; Narciso, J.; Rodríguez-Reinoso, F. Manufacture of Biomorphic SiC Components with Homogeneous Properties from Sawdust by Reactive Infiltration with Liquid Silicon. J. Am. Ceram. Soc. 2010, 93, 1003–1009. [Google Scholar] [CrossRef]
- Wu, R.; Zhou, K.; Yue, C.Y.; Wei, J.; Pan, Y. Recent progress in synthesis, properties and potential applications of SiC nanomaterials. Prog. Mater. Sci. 2015, 72, 1–60. [Google Scholar] [CrossRef]
- Choyke, W.J.; Pensl, G. Physical Properties of SiC. MRS Bull. 1997, 22, 25–29. [Google Scholar] [CrossRef]
- Mortensen, A.; Llorca, J. Metal Matrix Composites. Annu. Rev. Mater. Res. 2010, 40, 243–270. [Google Scholar] [CrossRef]
- Mussatto, A.; Ahad, I.U.; Mousavian, R.T.; Delaure, Y.; Brabazon, D. Advanced production routes for metal matrix composites. Eng. Rep. 2021, 3, e12330. [Google Scholar] [CrossRef]
- Ozpineci, B.; Tolbert, L.M. Characterization of SiC Schottky Diodes at Different Temperatures. IEEE Power Electron. Lett. 2003, 1, 54–57. [Google Scholar] [CrossRef]
- Rupp, R.; Treu, M.; Voss, S.; Bjork, F.; Reimann, T. “2nd Generation” SiC Schottky diodes: A new benchmark in SiC device ruggedness. In Proceedings of the 18th International Symposium on Power Semiconductor Devices & IC’s, Naples, Italy, 4–8 June 2006. [Google Scholar] [CrossRef]
- Neudeck, P.G. Progress in silicon carbide semiconductor electronics technology. J. Electron. Mater. 1995, 24, 283–288. [Google Scholar] [CrossRef]
- Lara-Avila, S.; Danilov, A.; Golubev, D.; He, H.; Kim, K.H.; Yakimova, R.; Lombardi, F.; Bauch, T.; Cherednichenko, S.; Kubatkin, S. Towards quantum-limited coherent detection of terahertz waves in charge-neutral graphene. Nat. Astron. 2019, 3, 983–988. [Google Scholar] [CrossRef]
- Cacccia, M.; Molina-Jordá, J.M.; Moral, M.; Nowak, R.; Ricci, E.; Sobczak, N.; Narciso, J.; Fernández-Sanz, J. Graphene Translucency and Interfacial Interactions in the Gold/Graphene/SiC System. J. Phys. Chem. Lett. 2018, 9, 3850–3855. [Google Scholar] [CrossRef] [PubMed]
- Katoh, Y.; Snead, L.L.; Szlufarska, I.; Weber, W.J. Radiation effects in SiC for nuclear structural applications. Curr. Opin. Solid State Mater. Sci. 2012, 16, 143–152. [Google Scholar] [CrossRef]
- Koyanagi, T.; Katoh, Y.; Nozawa, T.; Snead, L.L.; Kondo, S.; Henager, C.H.; Ferraris, M.; Hinoki, T.; Huang, Q. Recent progress in the development of SiC composites for nuclear fusion applications. J. Nucl. Mater. 2018, 511, 544–555. [Google Scholar] [CrossRef]
- Katoh, Y.; Ozawa, K.; Shih, C.; Nozawa, T.; Shinavski, R.J.; Hasegawa, A.; Snead, L.L. Continuous SiC fiber, CVI SiC matrix composites for nuclear applications: Properties and irradiation effects. J. Nucl. Mater. 2014, 511, 448–476. [Google Scholar] [CrossRef]
- Gnesin, G.G.; Dyban, Y.P.; Osovitskii, E.J. Development of a high-density silicon carbide material for heating elements using a planning method. Powder Metall. Met. Ceram. 1975, 14, 632–636. [Google Scholar] [CrossRef]
- Ramesh, P.D.; Vaidhyanathan, B.; Ganguli, M.; Rao, K.J. Synthesis of β-SiC powder by use of microwave radiation. J. Mater. Res. 1994, 9, 3025–3027. [Google Scholar] [CrossRef]
- Li, X.; Zhang, G.; Tronstad, R.; Ostrvski, O. Synthesis of SiC whiskers by VLS and VS process. Ceram. Int. 2016, 42, 5668–5676. [Google Scholar] [CrossRef]
- Chiew, Y.L.; Cheong, K.Y. A review on the synthesis of SiC from plant-based biomasses. Mater. Sci. Eng. B 2011, 176, 951–964. [Google Scholar] [CrossRef]
- El-Eskandarany, M.S.; Sumiyama, K.; Suzuki, K. Mechanical solid state reaction for synthesis of β—Sic powders. J. Mater. Res. 1995, 10, 659–667. [Google Scholar] [CrossRef]
- Chaira, D.; Mishra, B.K.; Sangal, S. Synthesis and characterization of silicon carbide by reaction milling in a dual-drive planetary mill. Mater. Sci. Eng. A 2008, 460–446, 111–120. [Google Scholar] [CrossRef]
- Chavda, M.A.; Ojovan, M.I.; Zhang, S. Immobilization of Nuclear Waste Graphite Using the SiC Synthesis Route. In Proceedings of the WM’11 Conference, Phoenix, AZ, USA, 27 February–3 March 2011. [Google Scholar]
- Ellison, A.; Zhang, J.; Peterson, J.; Henry, A.; Wahab, Q.; Bergman, J.P.; Makarov, Y.N.; Vorob’ev, A.; Vehanen, A.; Janzén, E. High temperature CVD growth of SiC. Mater. Sci. Eng. B 1999, 61–62, 113–120. [Google Scholar] [CrossRef]
- Kordina, O.; Hallin, C.; Henry, A.; Bergman, J.P.; Ivanov, I.; Ellison, A.; Son, N.T.; Janzén, E. Growth of SiC by “Hot-Wall” CVD and HTCVD. PSS B 1997, 202, 321–3344. [Google Scholar] [CrossRef]
- Pedersen, H.; Leone, S.; Kordina, O.; Henry, A.; Nishizawa, S.; Koshka, Y.; Janzén, E. Chloride-Based CVD Growth of Silicon Carbide for Electronic Applications. Chem. Rev. 2012, 112, 2434–2453. [Google Scholar] [CrossRef]
- Kuo, D.H.; Cheng, D.J.; Shyy, W.J.; Hon, M.H. The Effect of CH 4 on CVD β-SiC Growth. J. Electrochem. Soc. 1990, 137, 3688. [Google Scholar] [CrossRef]
- Shi, J.; Guo, J.; Jiang, D. Hot isostatic pressing of α-silicon carbide ceramics. Ceram. Int. 1993, 19, 347–351. [Google Scholar] [CrossRef]
- Watson, G.K.; Moore, T.J.; Millard, M.L. Effect of hot isostatic pressing on the properties of sintered alpha silicon carbide. Am. Ceram. Soc. Bull. 1985, 64, 1985006606. [Google Scholar]
- Lange, F.F. Hot-pressing behaviour of silicon carbide powders with additions of aluminium oxide. J. Mater. Sci. 1975, 10, 314–320. [Google Scholar] [CrossRef]
- Singhal, S.C.; Lange, F.F. Effect of Alumina Content on the Oxidation of Hot-Pressed Silicon Carbide. J. Am. Ceram. Soc. 1975, 58, 433–435. [Google Scholar] [CrossRef]
- Popper, P.; Davies, D.G.S. The preparation and properties of self-bonded silicon carbide. Powder Met. 1961, 4, 113–127. [Google Scholar] [CrossRef]
- Aroati, S.; Cafri, M.; Dilman, H.; Dariel, M.P.; Frage, N. Preparation of reaction bonded silicon carbide (RBSC) using boron carbide as an alternative source of carbón. J. Eur. Ceram. Soc. 2011, 31, 841–845. [Google Scholar] [CrossRef]
- Jepps, N.W.; Page, T.F. Polytypic transformations in silicon carbide. Prog. Cryst. Growth Charact. 1983, 7, 259–307. [Google Scholar] [CrossRef]
- Ness, J.N.; Page, T.F. Microstructural evolution in reaction-bonded silicon carbide. J. Mater. Sci. 1986, 21, 1377–1397. [Google Scholar] [CrossRef]
- Ramos-Fernández, E.; Narciso, J. Manufacture of SiC: Effect of Carbon Precursor. Materials 2023, 16, 2034. [Google Scholar] [CrossRef] [PubMed]
- Caccia, M.; Narciso, J. Key Parameters in the Manufacture of SiC-Based Composite Materials by Reactive Melt Infiltration. Materials 2019, 12, 2425. [Google Scholar] [CrossRef] [PubMed]
- Naslain, R.; Christin, F. Ultrahigh-Temperature Materials for Jet Engines. MRS Bull. 2003, 28, 654–658. [Google Scholar] [CrossRef]
- Ohnabe, H.; Masaki, S.; Onozuka, M.; Miyahara, K.; Sasa, T. Potential application of ceramic matrix composites to aero-engine components. Compos. Part A Appl. Sci. Manuf. 1999, 30, 489–496. [Google Scholar] [CrossRef]
- Krenkel, W.; Heidenreich, B.; Renz, R. C/C-SiC Composites for Advanced Friction Systems. Adv. Eng. Mater. 2002, 4, 427–436. [Google Scholar] [CrossRef]
- Krenkel, W.; Berndt, F. C/C–SiC composites for space applications and advanced friction systems. Mater. Sci. Eng. A 2005, 412, 177–181. [Google Scholar] [CrossRef]
- Einset, E.O. Capillary Infiltration Rates into Porous Media with Applications to Silcomp Processing. J. Am. Ceram. Soc. 1996, 79, 333–338. [Google Scholar] [CrossRef]
- Einset, E.O. Analysis of reactive melt infiltration in the processing of ceramics and ceramic composites. Chem. Eng. Sci. 1998, 53, 1027–1039. [Google Scholar] [CrossRef]
- Roger, J.; Chollon, G. Mechanisms and kinetics during reactive infiltration of molten silicon in porous graphite. Ceram. Int. 2019, 45, 8690–8699. [Google Scholar] [CrossRef]
- Sangsuwan, P.; Tewari, S.N.; Gatica, J.E.; Singh, M.; Dickerson, R. Reactive infiltration of silicon melt through microporous amorphous carbon preforms. Met. Mater. Trans. B 1999, 30, 933–944. [Google Scholar] [CrossRef]
- Dezellus, O.; Jacques, S.; Hodaj, F.; Eustathopoulos, N. Wetting and infiltration of carbon by liquid silicon. J. Mater. Sci. 2005, 40, 2307–2311. [Google Scholar] [CrossRef]
- Eustathopoulos, N.; Nicholas, M.G.; Drevet, B. Wettability at High Temperatures: Volume 3 (Pergamon Materials Series); Elsevier: Oxford, UK, 1999. [Google Scholar]
- Eustathopoulos, N. Progress in understanding and modeling reactive wetting of metals on ceramics. Curr. Opin. Solid State Mater. Sci. 2005, 9, 152–160. [Google Scholar] [CrossRef]
- Landry, K.; Rado, C.; Voitivich, R.; Eustathopulos, N. Mechanisms of reactive wetting: The question of triple line configuration. Acta Mater. 1997, 45, 3079–3085. [Google Scholar] [CrossRef]
- Caccia, M.; Amore, S.; Giuranno, D.; Novakovic, R.; Ricci, E.; Narciso, J. Towards optimization of SiC/CoSi2 composite material manufacture via reactive infiltration: Wetting study of Si–Co alloys on carbon materials. Eur. Ceram. Soc. 2015, 35, 4099–4106. [Google Scholar] [CrossRef]
- Calderon, N.R.; Voytovych, R.; Narciso, J.; Eustathopoulos, N. Pressureless infiltration versus wetting in AlSi/graphite system. J. Mater. Sci. 2010, 45, 4345–4350. [Google Scholar] [CrossRef]
- Bougiouri, V.; Voytovych, R.; Rojo-Calderon, N.; Narciso, J.; Eustathopoulos, N. The role of the chemical reaction in the infiltration of porous carbon by NiSi alloys. Scr. Mater. 2006, 54, 1875–1878. [Google Scholar] [CrossRef]
- Sergi, D.; Camarano, A.; Molina, J.M.; Ortona, A.; Narciso, J. Surface growth for molten silicon infiltration into carbon millimeter-sized channels: Lattice–Boltzmann simulations, experiments and models. Int. J. Mod. Phys. C 2016, 27, 1650062. [Google Scholar] [CrossRef]
- Caccia, M.R.; Camarano, A.; Sergi, D.; Ortona, A.; Narciso, J. Wetting and Navier-Stokes Equation—The Manufacture of Composites Materials. In Wetting and Wettability; Aliofkhazraei, M., Ed.; BoD–Books on Demand: London, UK, 2015. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application des Principes a Suivre et des Formulesa Employer dans les Questions de Distribution d’Eau; Dalmont, V., Ed.; Victor Dalmont: Paris, France, 1856; 647p. [Google Scholar]
- Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Garcia-Cordovilla, C.; Louis, E.; Narciso, J. Pressure infiltration of packed ceramic particulates by liquid metals. Acta Mater. 1999, 47, 4461–4479. [Google Scholar] [CrossRef]
- Alonso, A.; Pamies, A.; Narciso, J.; Garcia-Cordovilla, C.; Louis, E. Evaluation of the wettability of liquid aluminum with ceramic particulates (SiC, TiC, AI2O3) by means of pressure infiltration. Metall. Trans. A 1993, 24, 1423–1432. [Google Scholar] [CrossRef]
- De Arellano-Lopez, A.R.; Martinez-Fernandez, J.J.; Gonzalez, P.; Dominguez, C.; Fernandez-Quero, V.; Singh, M. Biomorphic SiC: A new engineering ceramic material. Appl. Ceram. Technol. 2004, 1, 56–57. [Google Scholar] [CrossRef]
- Amore, S.; Giuranno, D.; Novakovic, R.; Ricci, E.; Nowak, R.; Sobczak, N. Thermodynamic and surface properties of liquid Ge-Si alloys. Calphad 2014, 44, 95–101. [Google Scholar] [CrossRef]
- Novakovic, R.; Ricci, E.; Gnecco, F.; Giuranno, D.; Borzone, G. Surface and transport properties of Au-Sn liquid alloys. Surf. Sci. 2005, 599, 230–247. [Google Scholar] [CrossRef]
- Egry, I.; Ricci, E.; Novakovic, R.; Ozawa, S. Surface tension of liquid metals and alloys—Recent developments. Adv. Colloid Interface Sci. 2010, 159, 198–212. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; Wiley India Pvt. Limited: Hoboken, NJ, USA, 2006; ISBN 8126510005/9788126510009. [Google Scholar]
- Levenspiel, O. Chemical Reaction Omnibook; Oregon State University Bookstores: Corvallis, OR, USA, 2010; ISBN 13: 9780882461731. [Google Scholar]
- Hofbauer, P. In-Situ Measurement and Simulation of the Liquid Silicon Infiltration Process. Ph.D. Thesis, University of Ilmenau, Ilmenau, Germany, 2019. [Google Scholar]
- Hofbauer, P.J.; Rädlein, E.; Raether, F. Fundamental Mechanisms with Reactive Infiltration of Silicon Melt Into Carbon Capillaries. Adv. Eng. Mater. 2018, 21, 1900184–1900194. [Google Scholar] [CrossRef]
- Naikade, M.; Hain, C.; Kastelik, K.; Parrilli, A.; Graule, T.; Weber, L.; Ortona, A. Liquid metal infiltration of silicon based alloys into porous carbonaceous materials Part-III: Experimental verification of conversion products and infiltration depth by infiltration of Si-Zr alloy into mixed SiC/graphite preforms. J. Eur. Ceram. Soc. 2023, 43, 47–53. [Google Scholar] [CrossRef]
- Naikade, M.; Ortona, A.; Graule, T.; Weber, L. Liquid metal infiltration of silicon based alloys into porous carbonaceous materials. Part I: Modelling of channel filling and reaction phase formation. J. Eur. Ceram. Soc. 2022, 42, 1971–1983. [Google Scholar] [CrossRef]
- Naikade, M.; Hain, C.; Kastelik, K.; Brönnimann, R.; Bianchi, G.; Ortona, A.; Graule, T.; Weber, L. Liquid metal infiltration of silicon based alloys into porous carbonaceous materials. Part II: Experimental verification of modelling approaches by infiltration of Si-Zr alloy into idealized microchannels. J. Eur. Ceram. Soc. 2022, 42, 1984–1994. [Google Scholar] [CrossRef]
- Sergi, D.; Grossi, L.; Leidi, T. Simulation of capillary infiltration into packing structures for the optimization of ceramic materials using the lattice Boltzmann method. Eng. Appl. Comput. Fluid Mech. 2016, 10, 485–499. [Google Scholar] [CrossRef]

| Symbol | Magnitude | Value | SI Units | References |
|---|---|---|---|---|
| λ | Geometrical factor | 2 | - | [52,55,56] |
| a | Proportionality constant | 4 × 10−4 | - | [57] |
| γLV | Surface tension | 0.750 | N/m | [58,59,60] |
| θ | Contact angle of Si on C | 40 | ° | [45] |
| μ | Viscosity of liquid Si | 6.05 × 10−2 | Pa·s | [58] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-González, M.K.; Figueroa-Quintero, L.; Villalgordo-Hernández, D.; Ramos Fernández, E.V.; Narciso, J. Reactive Infiltration: Effects of Different Parameters. Materials 2024, 17, 3063. https://doi.org/10.3390/ma17133063
López-González MK, Figueroa-Quintero L, Villalgordo-Hernández D, Ramos Fernández EV, Narciso J. Reactive Infiltration: Effects of Different Parameters. Materials. 2024; 17(13):3063. https://doi.org/10.3390/ma17133063
Chicago/Turabian StyleLópez-González, M. Karla, Leidy Figueroa-Quintero, David Villalgordo-Hernández, Enrique V. Ramos Fernández, and Javier Narciso. 2024. "Reactive Infiltration: Effects of Different Parameters" Materials 17, no. 13: 3063. https://doi.org/10.3390/ma17133063
APA StyleLópez-González, M. K., Figueroa-Quintero, L., Villalgordo-Hernández, D., Ramos Fernández, E. V., & Narciso, J. (2024). Reactive Infiltration: Effects of Different Parameters. Materials, 17(13), 3063. https://doi.org/10.3390/ma17133063







