Mechanical Property Analysis of a Boom–Membrane Structure Used for Aerospace Technologies
Abstract
:1. Introduction and Literature Review
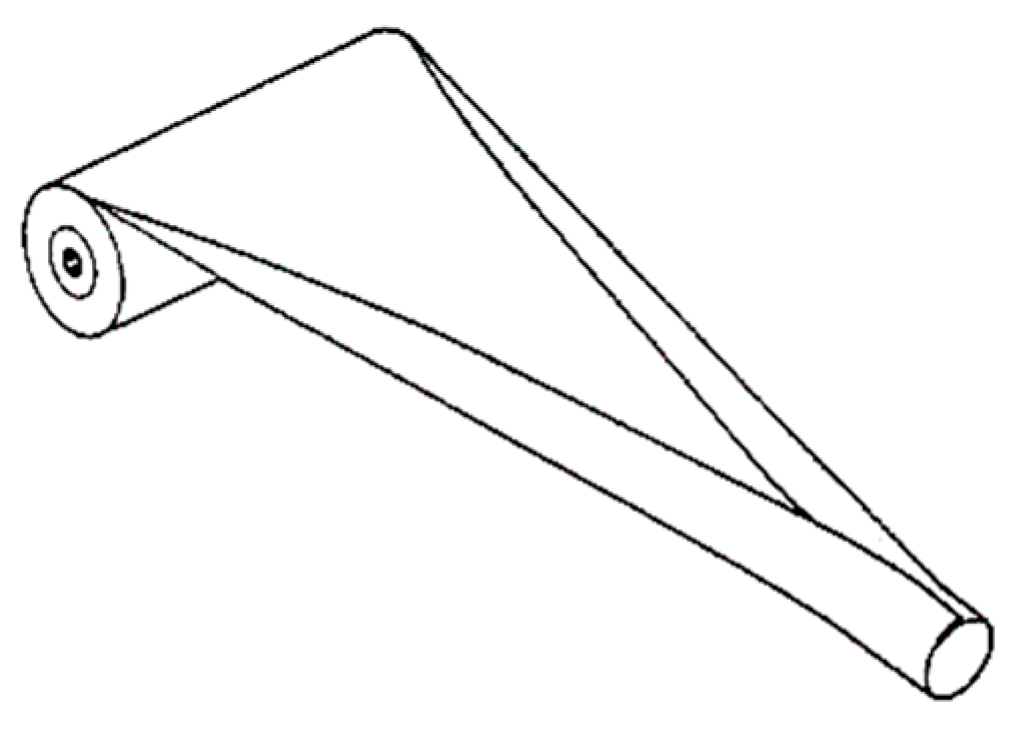
2. Analytical Model Establishment of a Boom–Membrane Structure
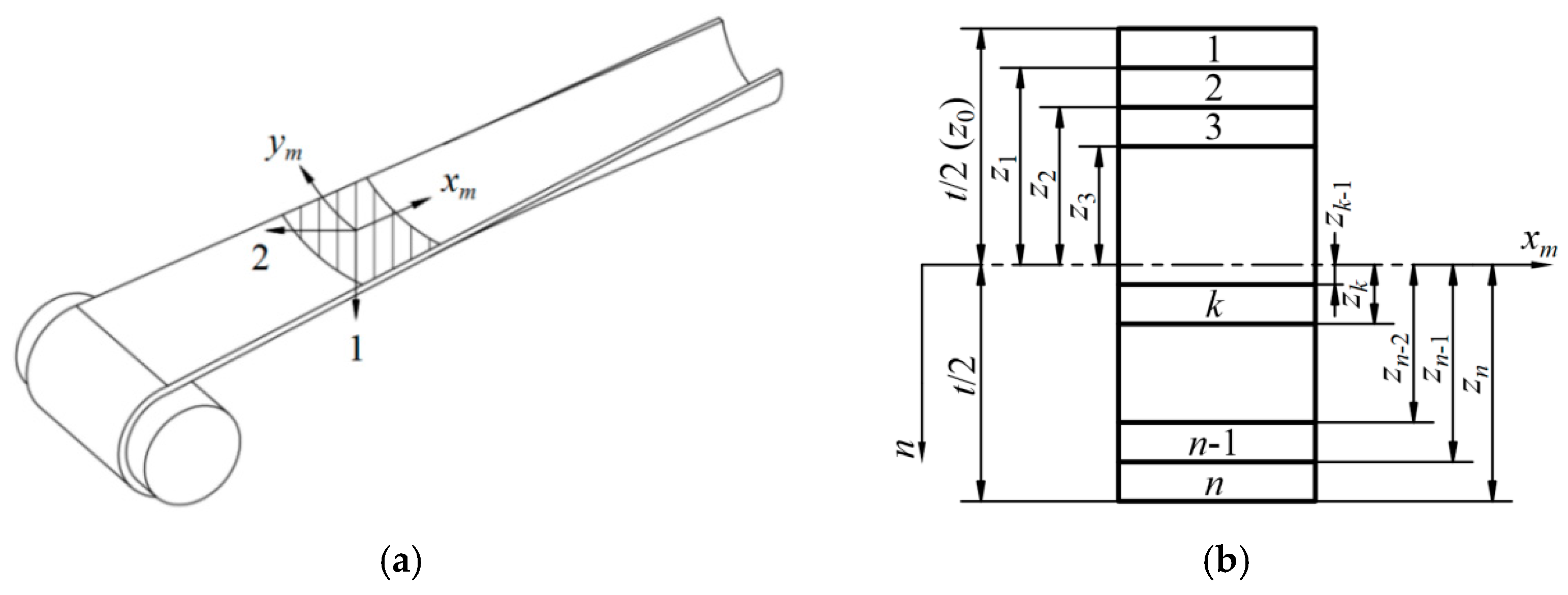
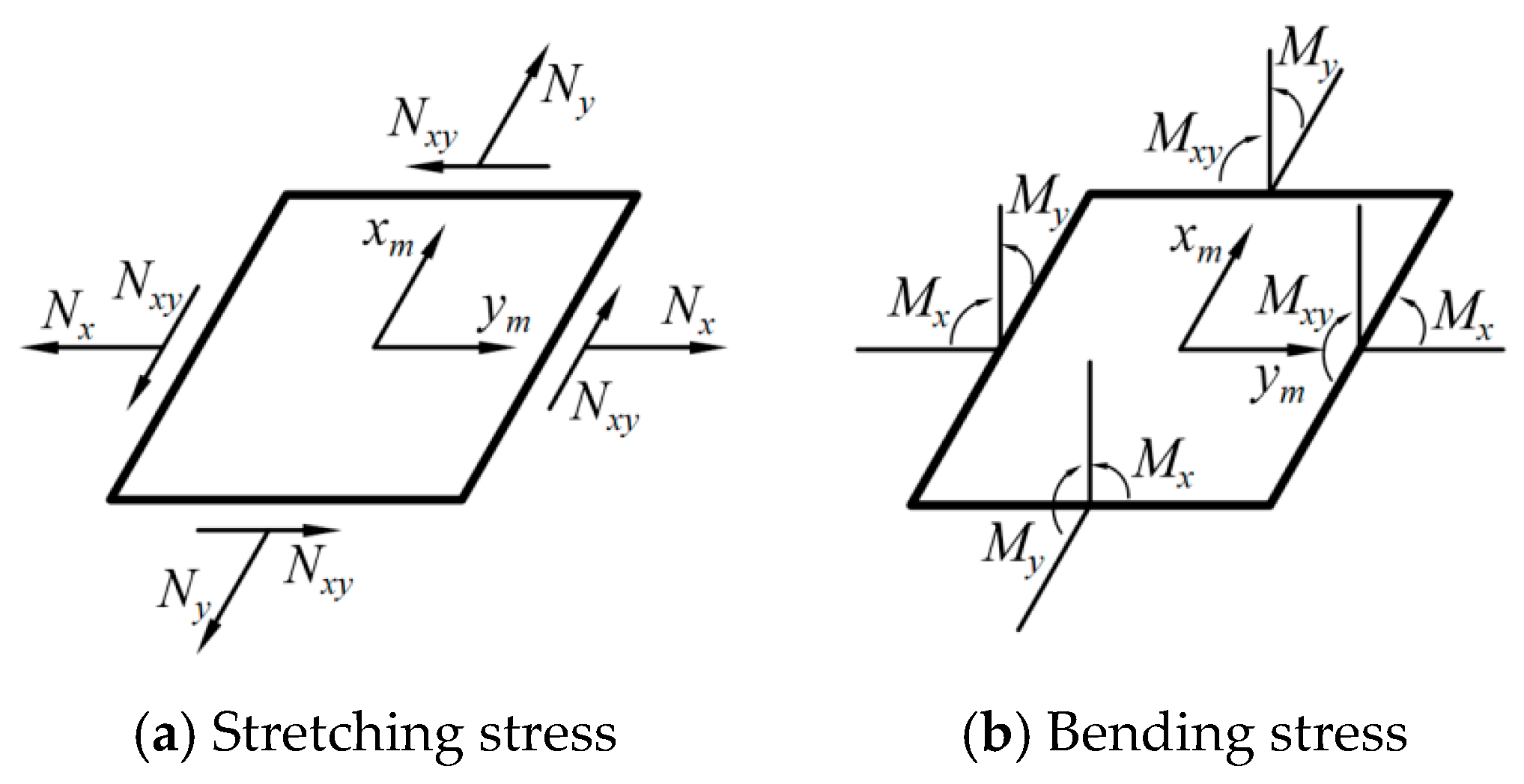
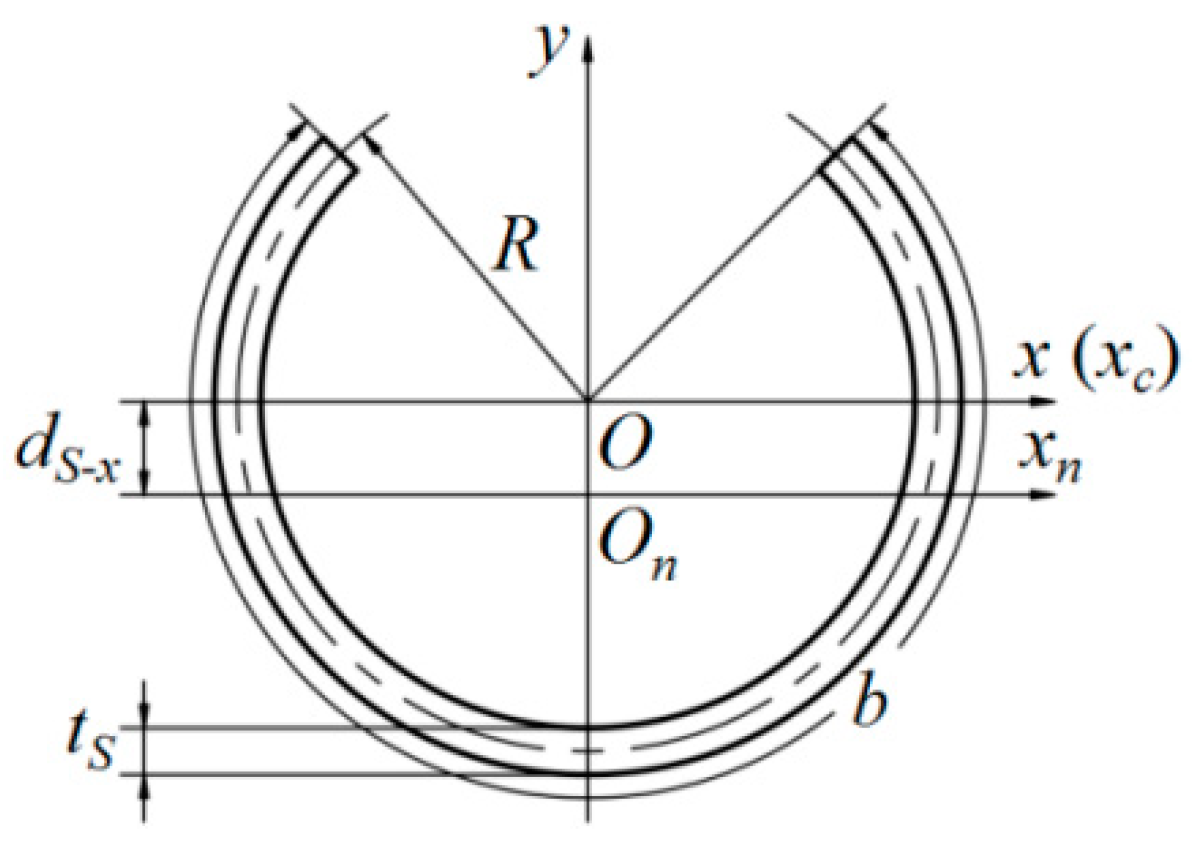
2.1. Mathematical Model Establishment
2.2. Boom Bending Property Calculation
2.3. Boom Buckling Load Calculation
2.4. Fundamental Frequency Calculation of Boom–Membrane Structures
3. Parametric Study of Tape Spring Booms and Boom–Membrane Structures
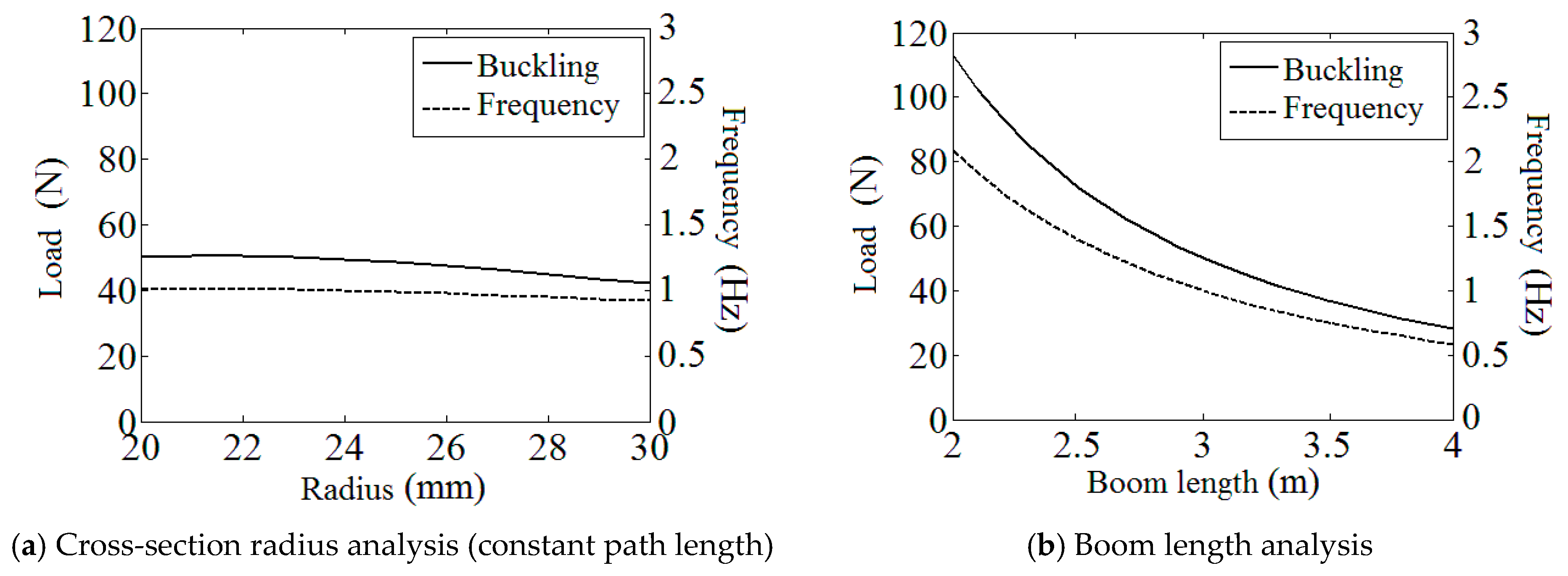
3.1. Study of Boom Geometric Parameters
3.2. Study of Boom Laminate Parameters
4. Experimental Study
4.1. Boom Bending Stiffness Experiment
4.2. Fundamental Frequency Experiment of Boom–Membrane Structure
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sim, A.; Santer, M. Analysis of a segmented dompliant deployable boom for CubeSat magnetometer missions. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 12–15 April 2010; p. 2581. [Google Scholar]
- Leclerc, C.; Pedivellano, A.; Pellegrino, S. Stress concentration and material failure during doiling of ultra-thin TRAC booms. In Proceedings of the 2018 AIAA Spacecraft Structures Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 690. [Google Scholar]
- Bourgeois-Doyle, R.; Klein, G. The Great Inventor: NRC Press Biography Series; NRC Research Press: Ottawa, ON, Canada, 2004; No. 2. [Google Scholar]
- Suliga, A.; Jakubczyk, E.; Hamerton, I.; Viquerat, A. Analysis of atomic oxygen and ultraviolet exposure effects on cycloaliphatic epoxy resins reinforced with octa-functional POSS. Acta Astronaut. 2018, 142, 103–111. [Google Scholar] [CrossRef]
- Cox, K.; Davis, B.; VanHalle, R.; Francis, W. Flight build of a furled high strain composite antenna for CubeSats. In Proceedings of the 2018 AIAA Spacecraft Structures Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 1678. [Google Scholar]
- Martin, E.; Hassan, R. Comparing the N-branch genetic algorithm and the multi-objective genetic algorithm. AIAA J. 2004, 42, 1496–1500. [Google Scholar] [CrossRef]
- Santer, M.; Pellegrino, S. An asymmetrically-bistable monolithic energy-storing structure. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004; p. 1527. [Google Scholar]
- Zhang, Z.; Yang, L.; Yu, X.; Li, X.; Wu, H.; Wu, H.; Jiang, S.; Chai, G. Bistable morphing composite structures: A review. Thin-Walled Struct. 2019, 142, 74–97. [Google Scholar] [CrossRef]
- Pellegrino, S. Bistable Shell Structures. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; p. 1934. [Google Scholar]
- Sickinger, C.; Herbeck, L.; Breitbach, E. Structural engineering on deployable CFRP booms for a solar propelled sailcraft. In Proceedings of the 54th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law, Bremen, Germany, 29 September–3 October 2003; Volume 58, pp. 185–196. [Google Scholar]
- Murphy, D. MegaFlex—The scaling potential of UltraFlex technology. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; p. 1581. [Google Scholar]
- Costa, M. A spaceborne small SAR design with reflector antenna associated with compact polarimetry. In Proceedings of the AIAA SPACE, Long Beach, CA, USA, 13–16 September 2016; p. 5499. [Google Scholar]
- Mallol, P.; Tibert, G. Deployment modeling and experimental testing of a bi-stable composite boom for small satellites. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, CA, USA, 8–11 April 2013; p. 1672. [Google Scholar]
- Mao, H.; Sinn, T.; Vasile, M.; Tibert, G. Simulation and control of a space web deployed by centrifugal forces in a sounding rocket experiment. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Washington, DC, USA, 13–17 June 2016; p. 4421. [Google Scholar]
- Santer, M.; Sim, A.; Stafford, J. Testing of a segmented compliant deployable boom for CubeSat magnetometer Missions. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, CO, USA, 4–7 April 2011; p. 1732. [Google Scholar]
- Chu, Z.; Lei, Y. Design theory and dynamic analysis of a deployable boom. Mech. Mach. Theory 2014, 71, 126–141. [Google Scholar] [CrossRef]
- Pellegrino, S. Large retractable appendages in spacecraft. J. Spacecr. Rocket. 1995, 32, 1006–1014. [Google Scholar] [CrossRef]
- Roybal, F.; Banik, J.; Murphey, T. Development of an elastically deployable boom for tensioned planar structures. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 1838. [Google Scholar]
- Banik, J.; Murphey, T. Performance validation of the Triangular Rollable And Collapsible mast. In Proceedings of the 24th Annual AIAA/USU Conference on Small Stallites, Logan, Utah, USA, 9–12 August 2010; p. 2159. [Google Scholar]
- Wang, S.; Schenk, M.; Jiang, S.; Viquerat, A. Blossoming analysis of composites deployable booms. Thin-Walled Struct. 2020, 157, 107098. [Google Scholar] [CrossRef]
- Wang, S.; Schenk, M.; Guo, H.; Viquerat, A. Tip force and pressure distribution analysis of a deployable boom during blossoming. Int. J. Solids Struct. 2020, 194, 141–151. [Google Scholar] [CrossRef]
- Underwood, C.; Viquerat, A.; Schenk, M.; Taylor, B.; Massimiani, C.; Duke, R.; Stewart, B.; Fellowes, S.; Bridges, C.; Aglietti, G.; et al. Inflatesail de-orbit flight demonstration results and follow-on drag-sail applications. Acta Astronaut. 2019, 162, 344–358. [Google Scholar] [CrossRef]
- Viquerat, A.; Schenk, M.; Lappas, V.; Sanders, B. Functional and qualification testing of the InflateSail technology demonstrator. In Proceedings of the 2nd AIAA Spacecraft Structures Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 1627. [Google Scholar]
- Wu, C.; Viquerat, A. Natural frequency optimization of braided bi-stable carbon/epoxy tubes: Analysis of braid angles and stacking sequences. Compos. Struct. 2017, 159, 528–537. [Google Scholar] [CrossRef]
- Wu, C.; Viquerat, A.; Aglietti, G. Optimization of the natural frequency and buckling analysis of bi-stable carbon fiber reinforced plastic booms for space applications. In Proceedings of the 3rd AIAA Spacecraft Structures Conference, San Diego, CA, USA, 4–8 January 2016; pp. 156–168. [Google Scholar]




| R (mm) | b (mm) | Em (GPa) | Gm (GPa) | νm | Ef (GPa) |
| 20 | 110 | 4 | 2.7 | 0.35 | 240 |
| Gf (GPa) | νf | tUD (mm) | VUD (%) | ϕUD (%) | tf (mm) |
| 95 | 0.22 | 0.057 | 31 | 15 | 0.096 |
| Vf (%) | ϕf (%) | μ | Eh (GPa) | Er (GPa) | Lay out |
| 53 | 15 | 0.1 | 205 | 205 | [±50°F/0°]s * |
| Membrane Size pm × qm | Membrane Areal Density ρma | Boom Length l | Boom Distance qm | Boom Density (On Average) ρb | Tip Beam Length lr | Tip Beam Linear Density ρrl |
|---|---|---|---|---|---|---|
| 2950 × 900 mm2 | 0.3 kg/m2 | 3000 mm | 1000 mm | 1500 kg/m3 | 1100 mm | 0.1 kg/m |
| Weight (g) | 5 | 10 | 15 | 20 | ||
| Corresponding torque (N∙m) | 0.98 | 1.96 | 2.94 | 3.92 | ||
| Around x-axis | Displacement (mm) | 11.46 | 22.92 | 34.39 | 45.88 | |
| Bending stiffness | Test (N∙m4) | 349.0 | 349.0 | 348.9 | 348.7 | |
| Theory (N∙m4) | 343.4 | |||||
| Error (%) | −1.63 | −1.63 | −1.60 | −1.54 | ||
| Around y-axis | Displacement (mm) | 8.12 | 16.29 | 24.56 | 32.98 | |
| Bending stiffness | Test (N∙m4) | 492.6 | 491.1 | 488.6 | 485.1 | |
| Theory (N∙m4) | 484.3 | |||||
| Error (%) | −1.71 | −1.40 | −0.98 | −0.17 | ||
| Membrane size pm × qm | Membrane areal density ρma | Boom length l | Boom distance qm |
| 1980 × 450 mm2 | 0.15 kg/m2 | 2000 mm | 570 mm |
| Boom density (on average) ρb | Tip beam length lr | Tip beam linear density ρrl | Membrane tension Tm |
| 1500 kg/m3 | 620 mm | 0.05 kg/m | 10 N |
| Test 1 | Test 2 | Test 3 | Test 4 | |
|---|---|---|---|---|
| Experiment (Hz) | 3.08 | 3.26 | 3.10 | 3.15 |
| Theory (Hz) | 3.32 | |||
| Error (%) | +7.8 | +1.8 | +7.1 | +5.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Yu, X.; Gao, Y.; Wang, S.; Sun, L. Mechanical Property Analysis of a Boom–Membrane Structure Used for Aerospace Technologies. Materials 2024, 17, 3204. https://doi.org/10.3390/ma17133204
Xu S, Yu X, Gao Y, Wang S, Sun L. Mechanical Property Analysis of a Boom–Membrane Structure Used for Aerospace Technologies. Materials. 2024; 17(13):3204. https://doi.org/10.3390/ma17133204
Chicago/Turabian StyleXu, Shuhong, Xiaojiao Yu, Yue Gao, Sicong Wang, and Lining Sun. 2024. "Mechanical Property Analysis of a Boom–Membrane Structure Used for Aerospace Technologies" Materials 17, no. 13: 3204. https://doi.org/10.3390/ma17133204
APA StyleXu, S., Yu, X., Gao, Y., Wang, S., & Sun, L. (2024). Mechanical Property Analysis of a Boom–Membrane Structure Used for Aerospace Technologies. Materials, 17(13), 3204. https://doi.org/10.3390/ma17133204






