Analysis of Bending Deformation and Stress of 6063-T5 Aluminum Alloy Multi-Cavity Tube Filled with Liquid
Abstract
1. Introduction
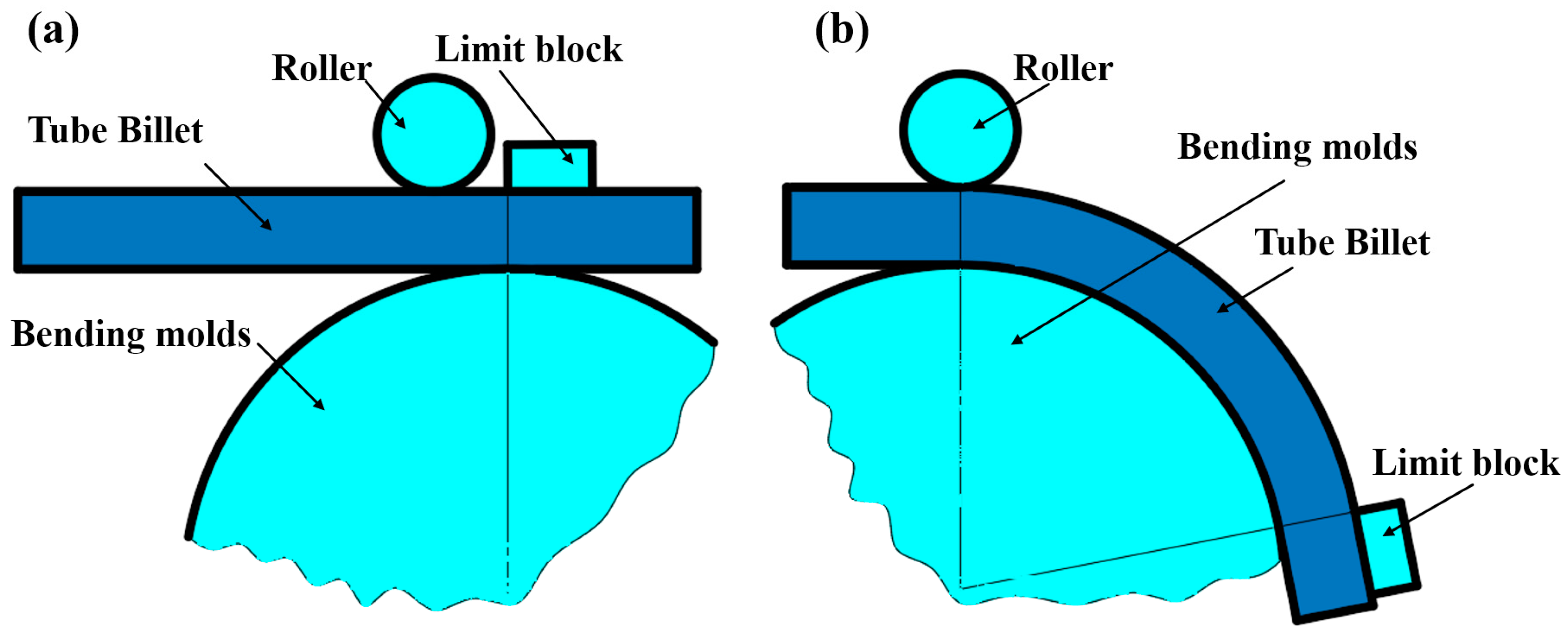
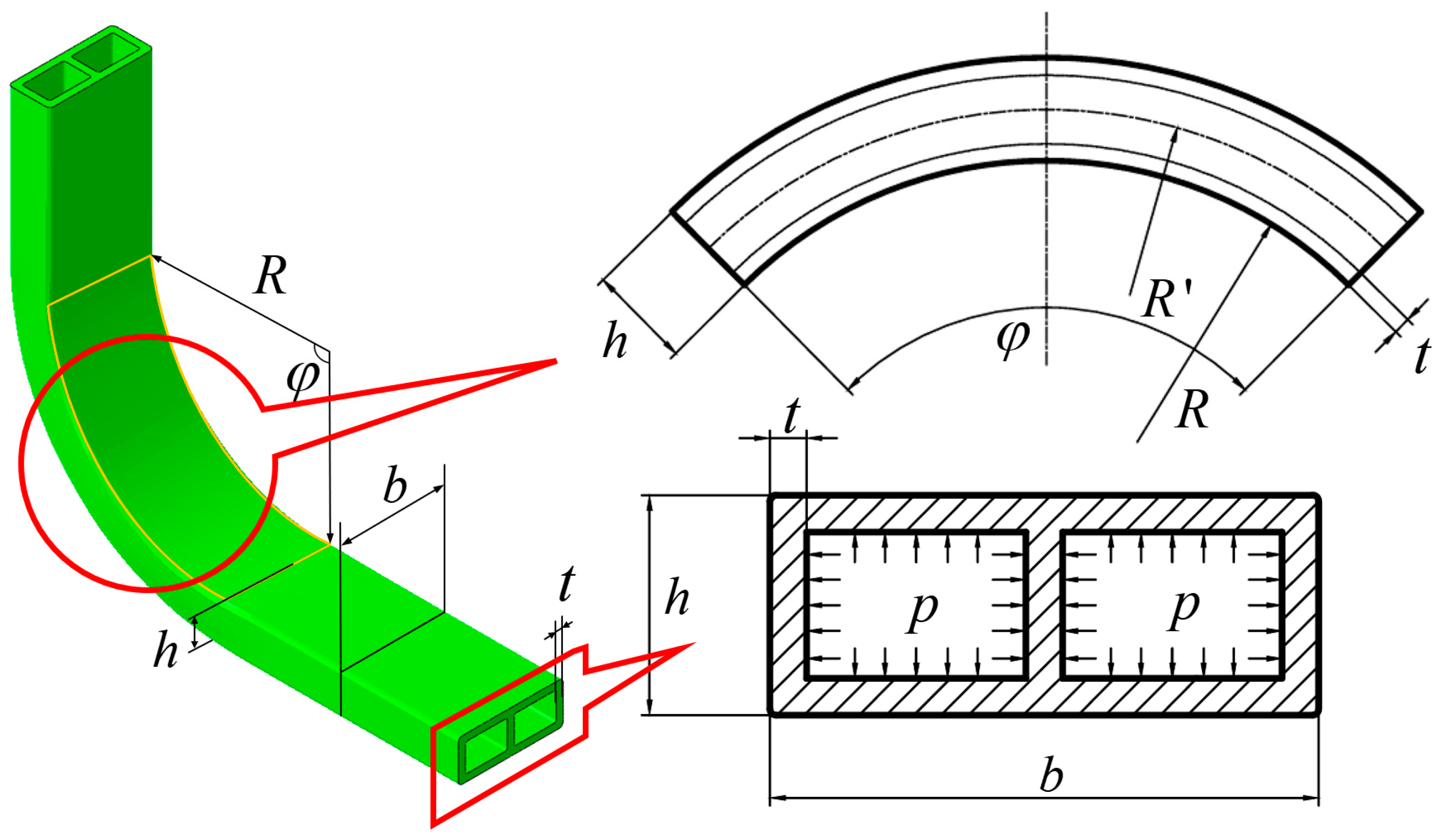
2. Liquid-Filled Bending Principle for Reinforced Profiles
3. Experimental
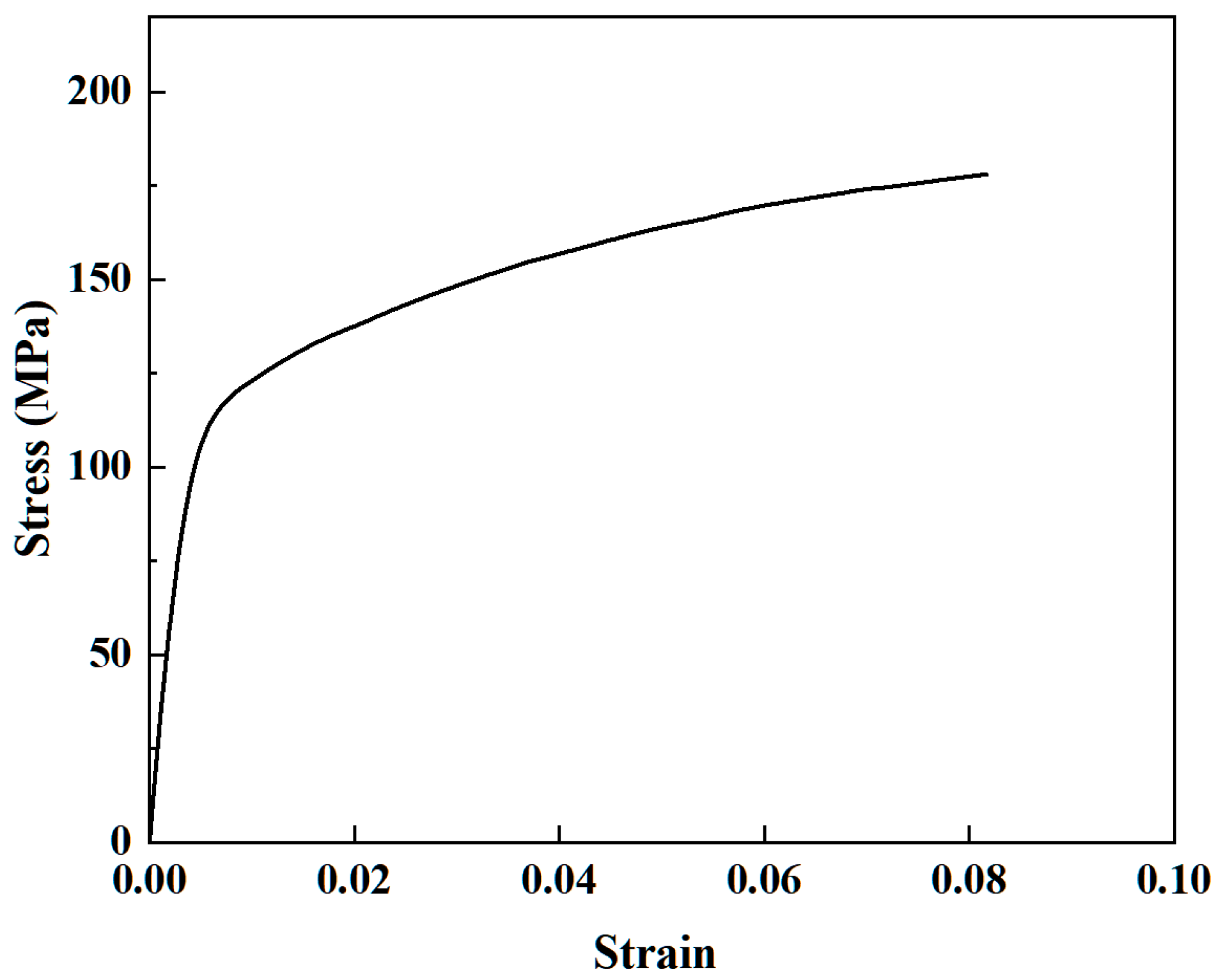
3.1. Experimental Materials
3.2. Experimental Devices
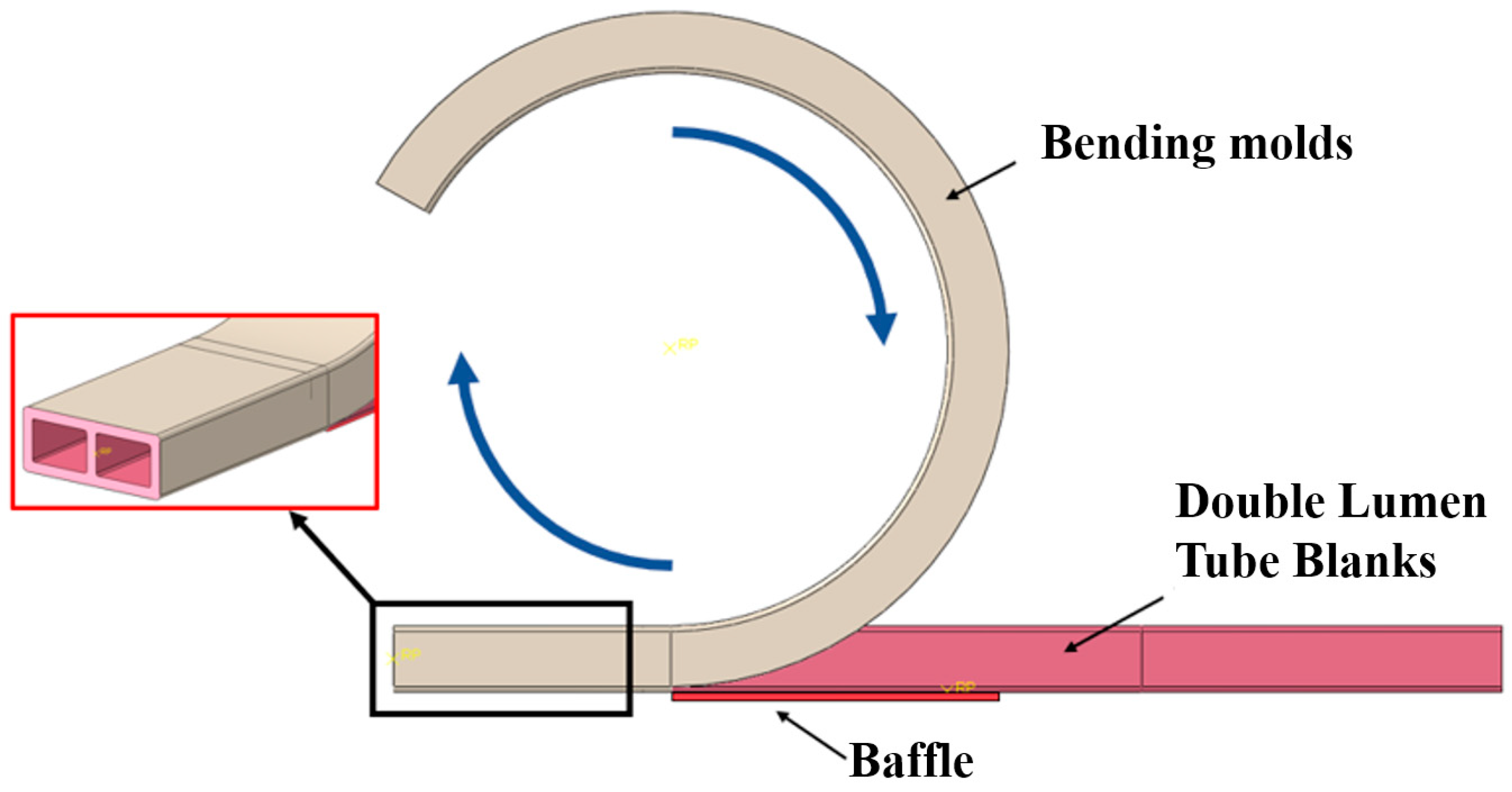
3.3. Experimental Program
4. Theoretical Analysis
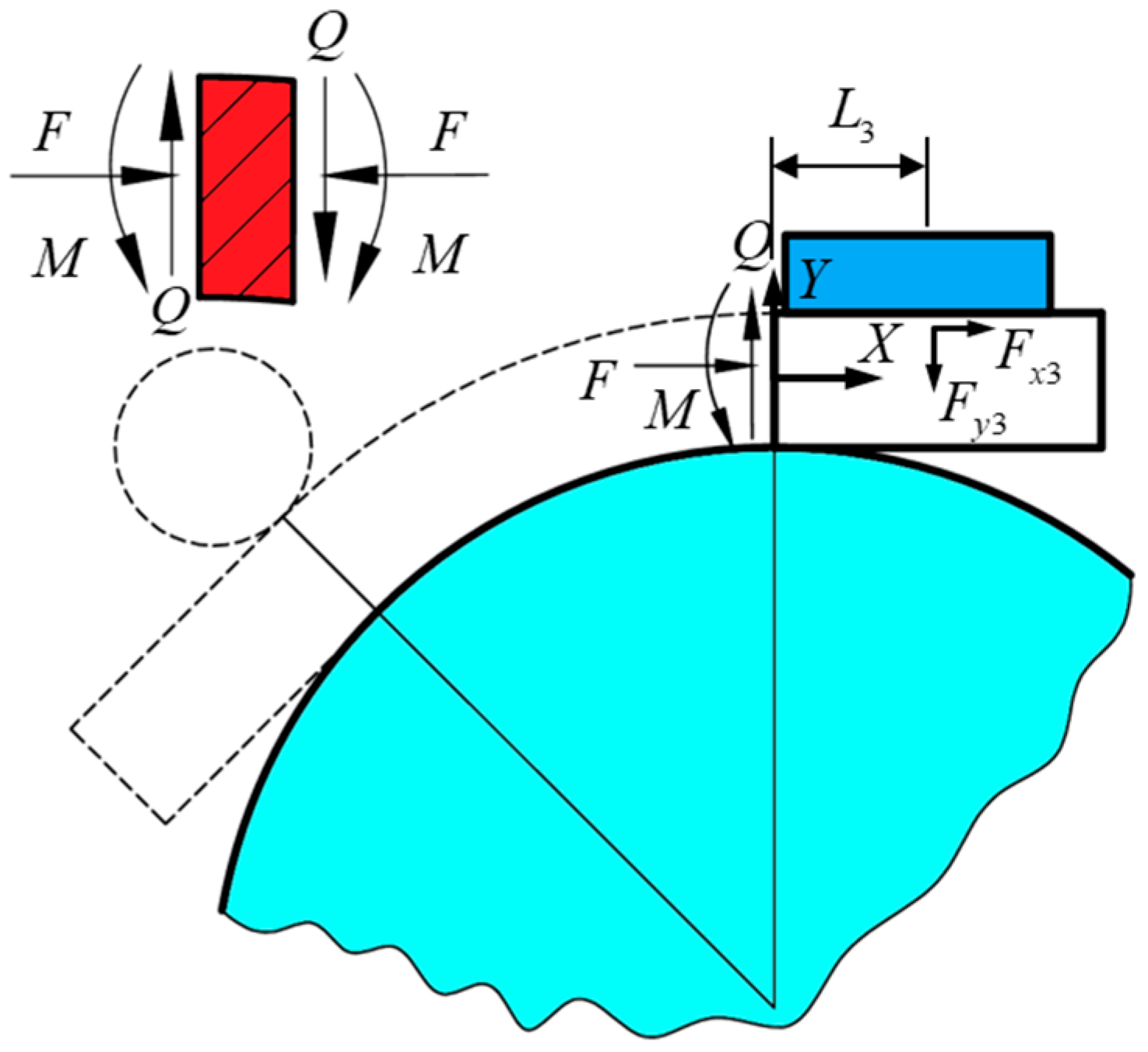
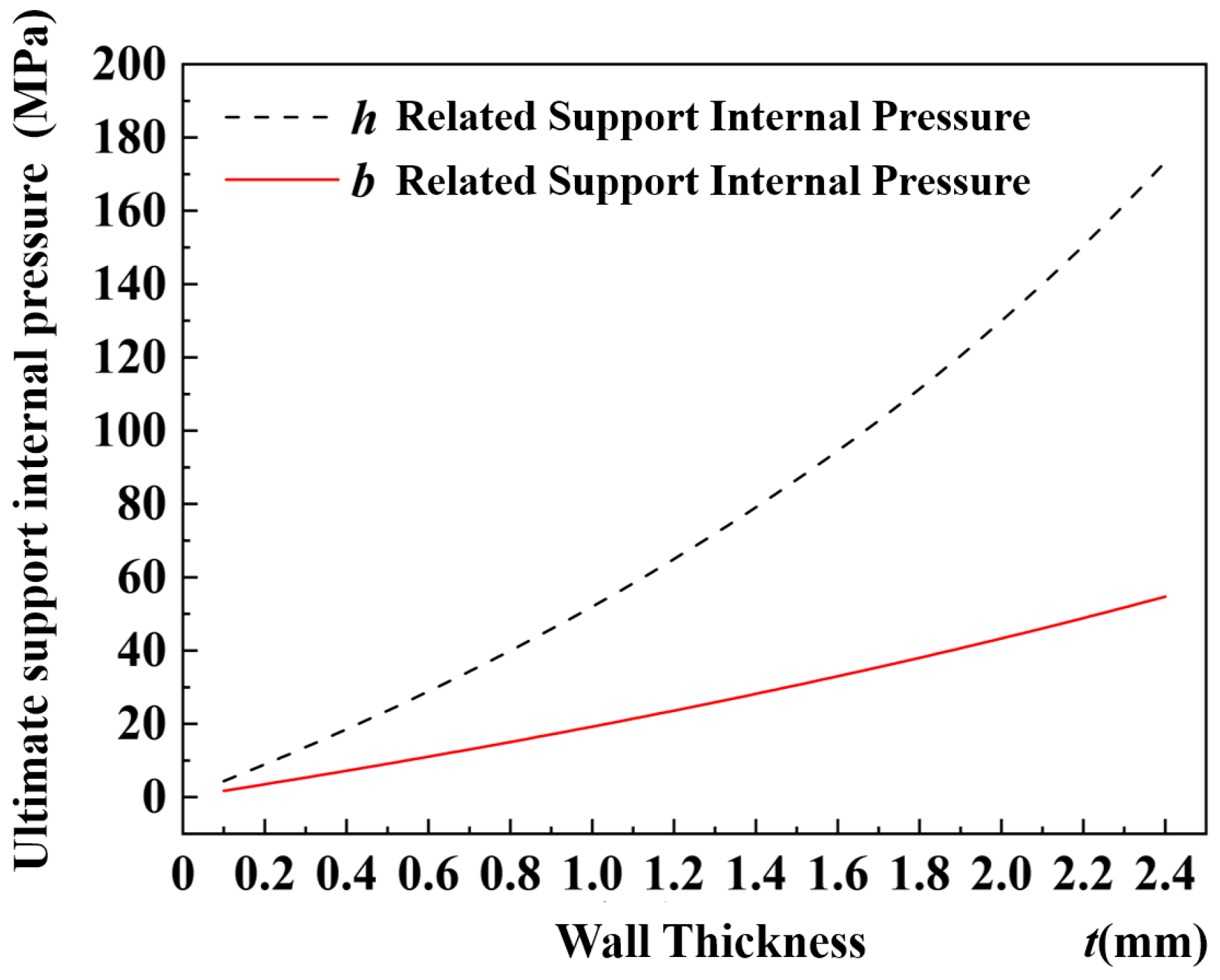
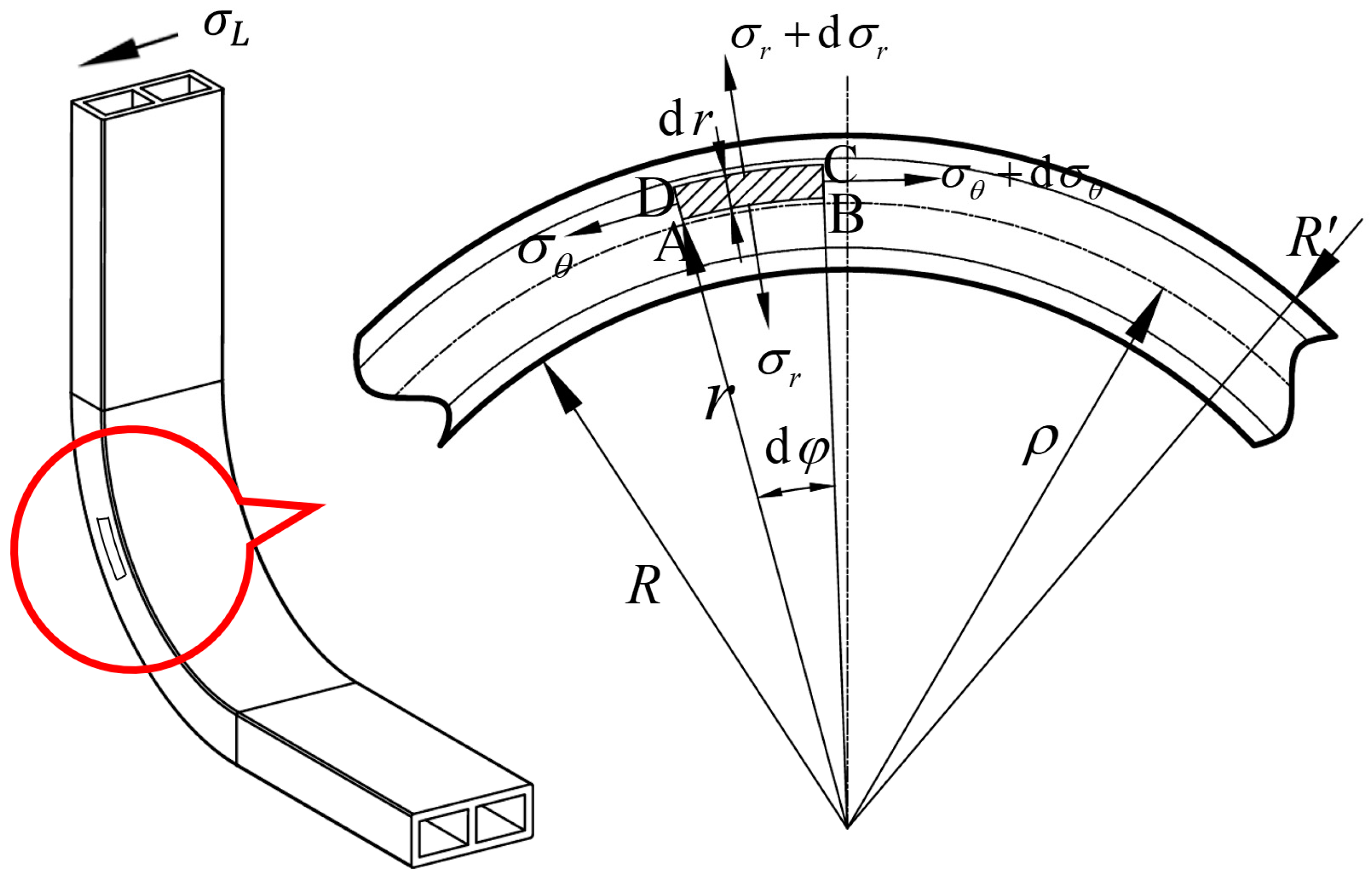
4.1. Force Analysis
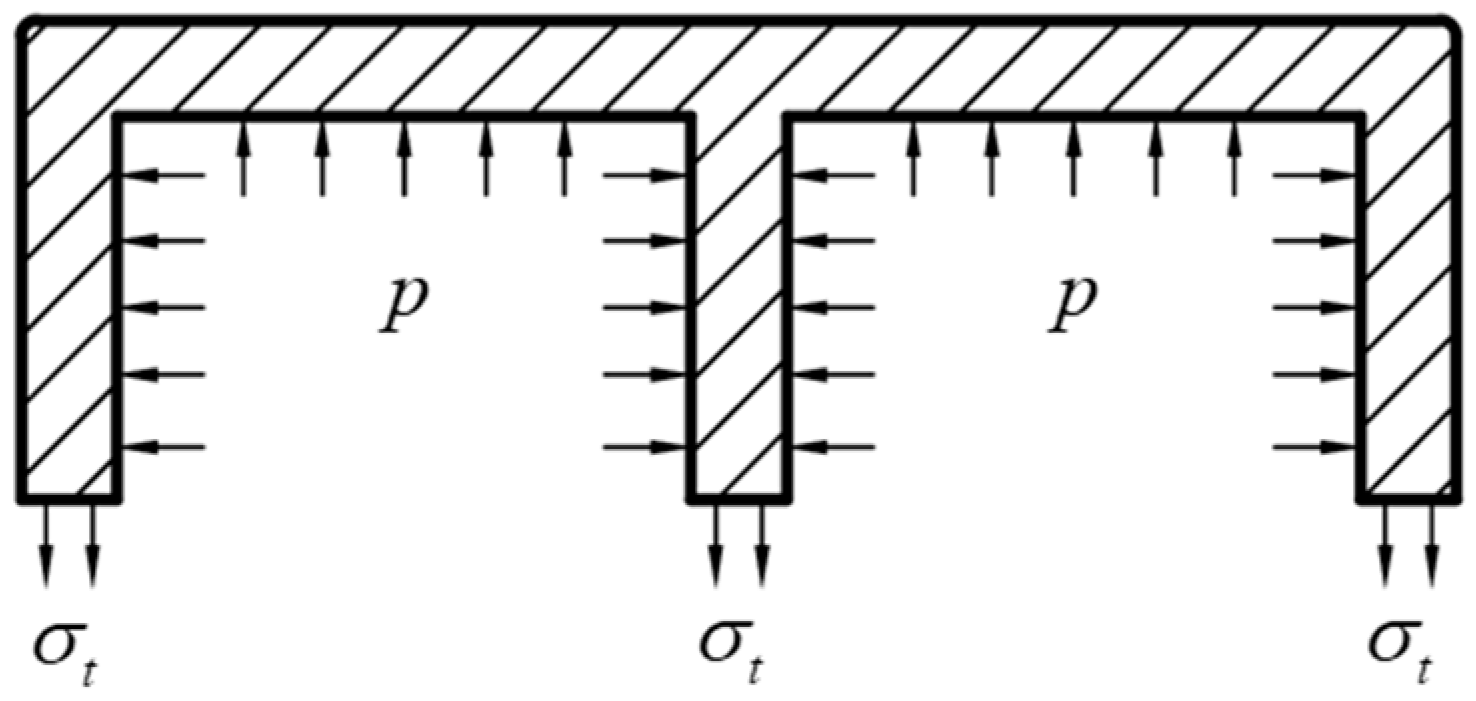
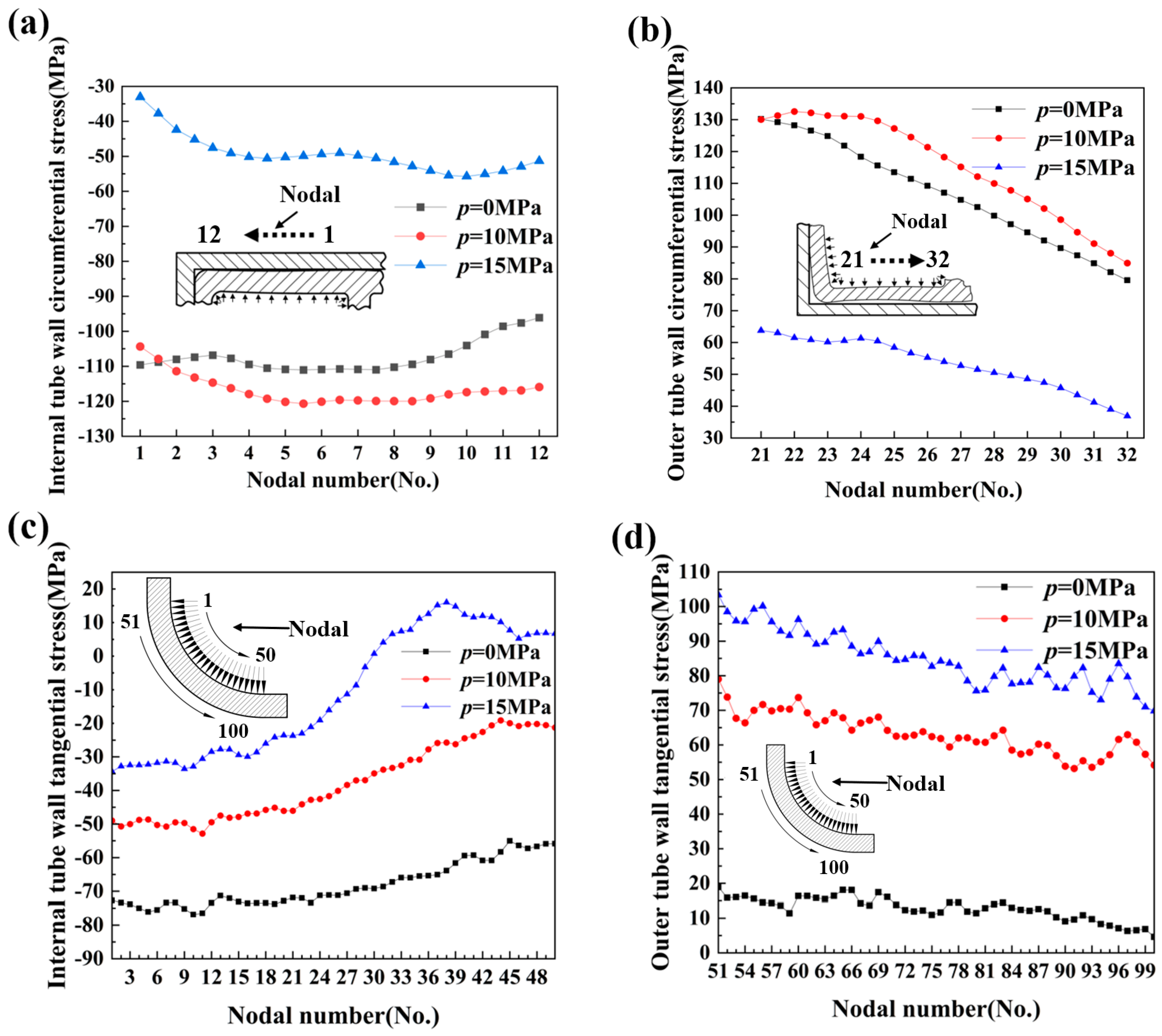
4.2. Stress Analysis
5. Finite Element Model
6. Results Analysis
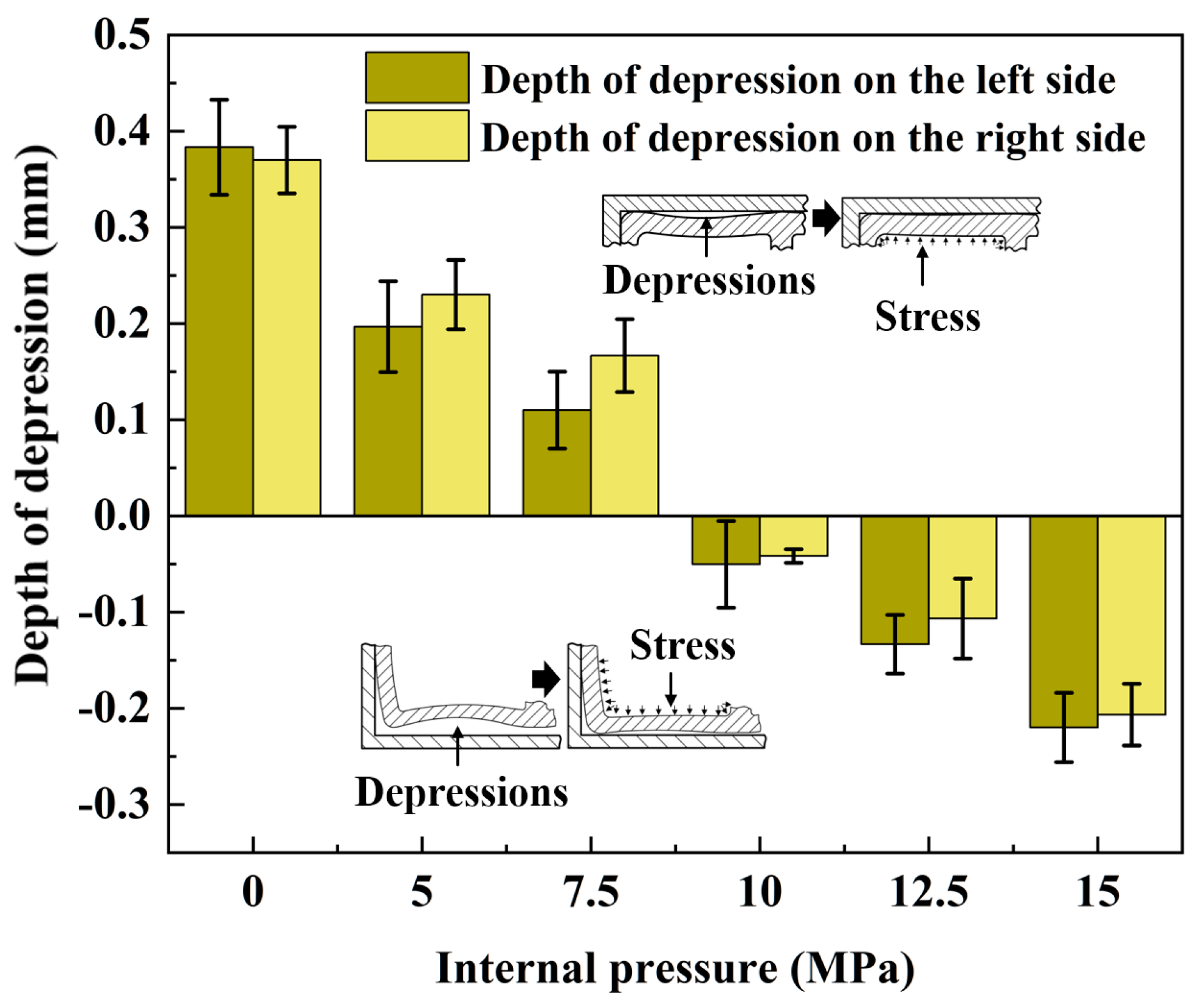
6.1. Validation of FEA Model
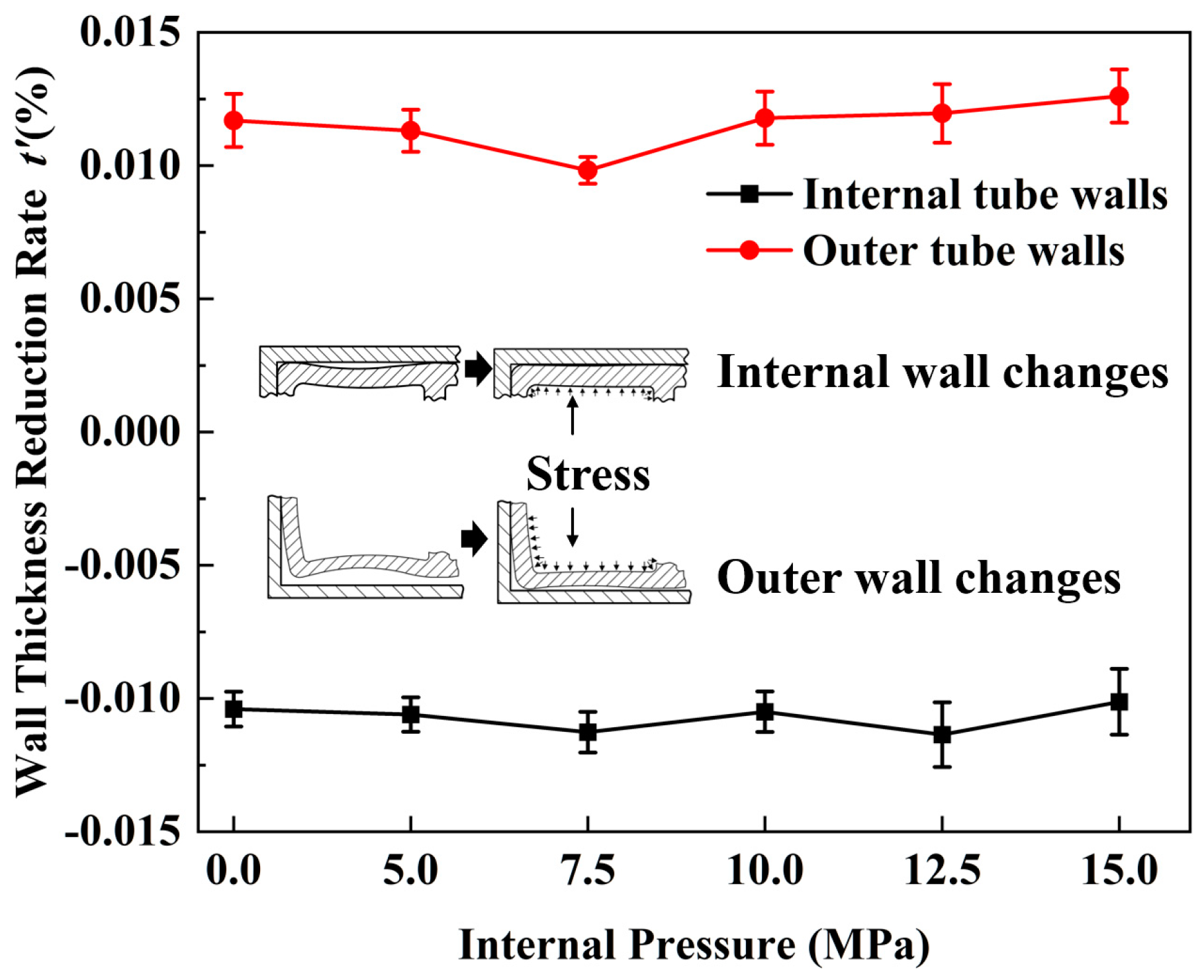
6.2. Experimental Study of Cross-Sectional Distortion of Tubing under Different Internal Pressures
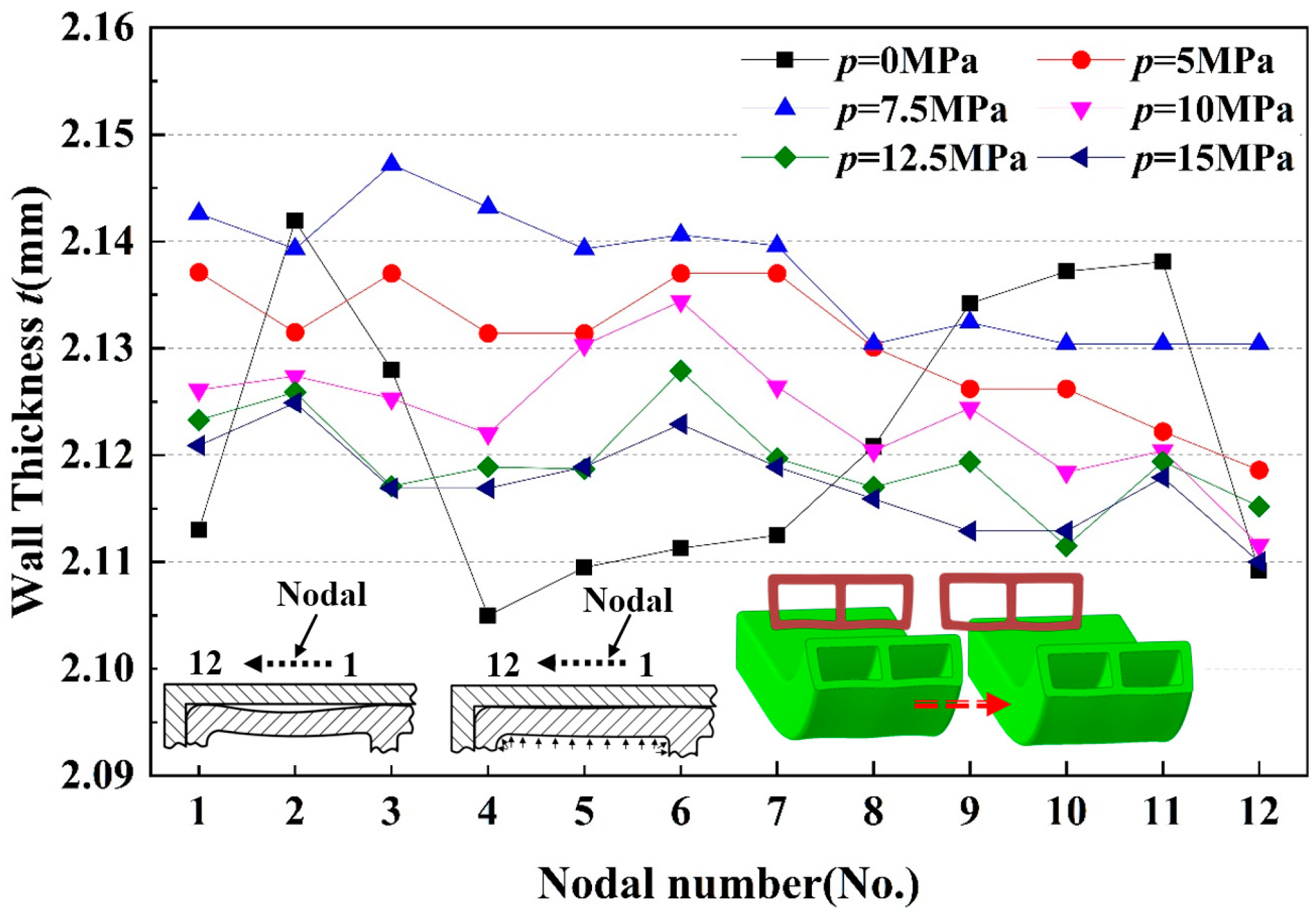
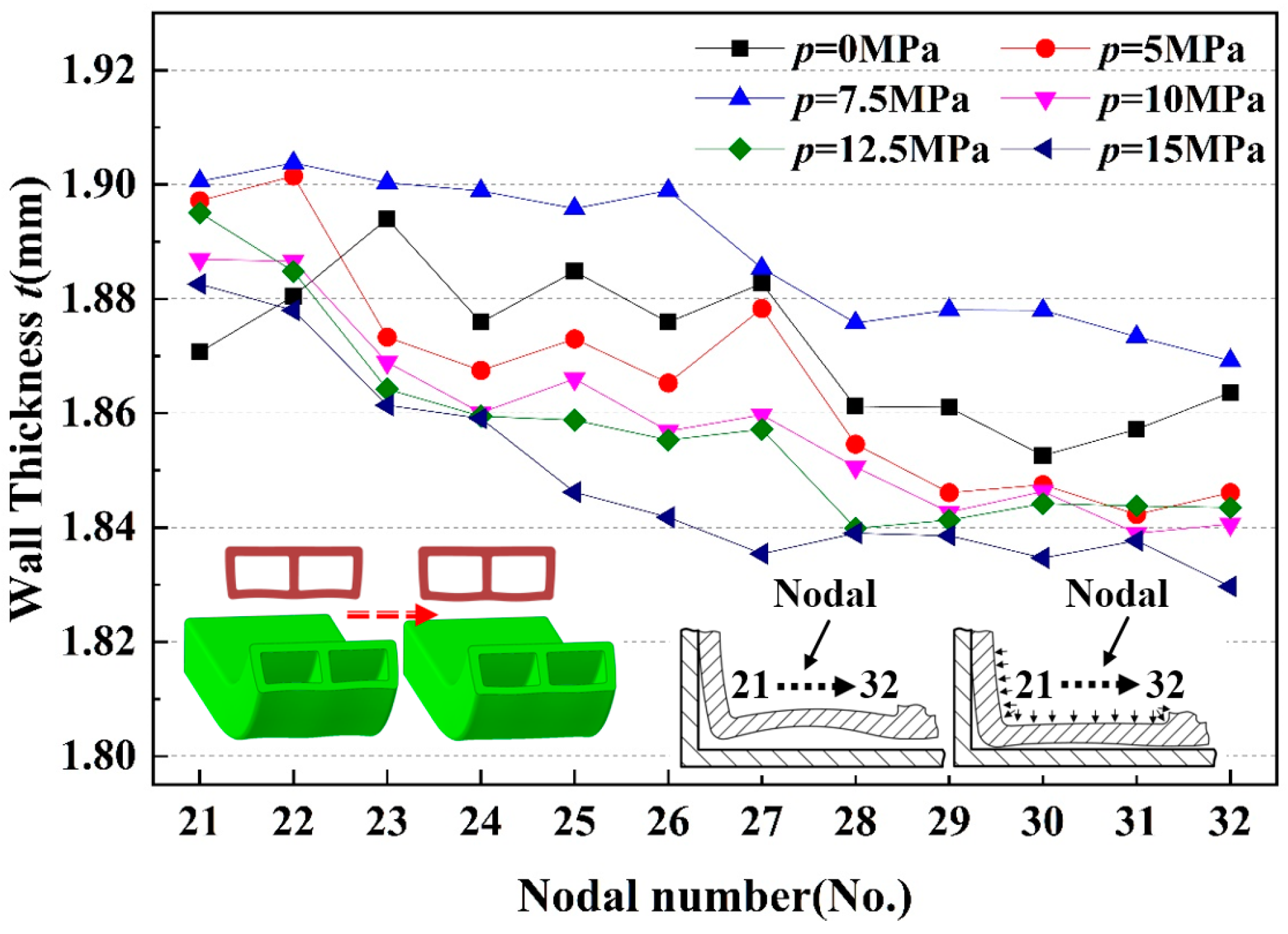
6.3. Numerical Simulation of Wall Thickness Distribution in Bending of Tubing under Different Internal Pressures
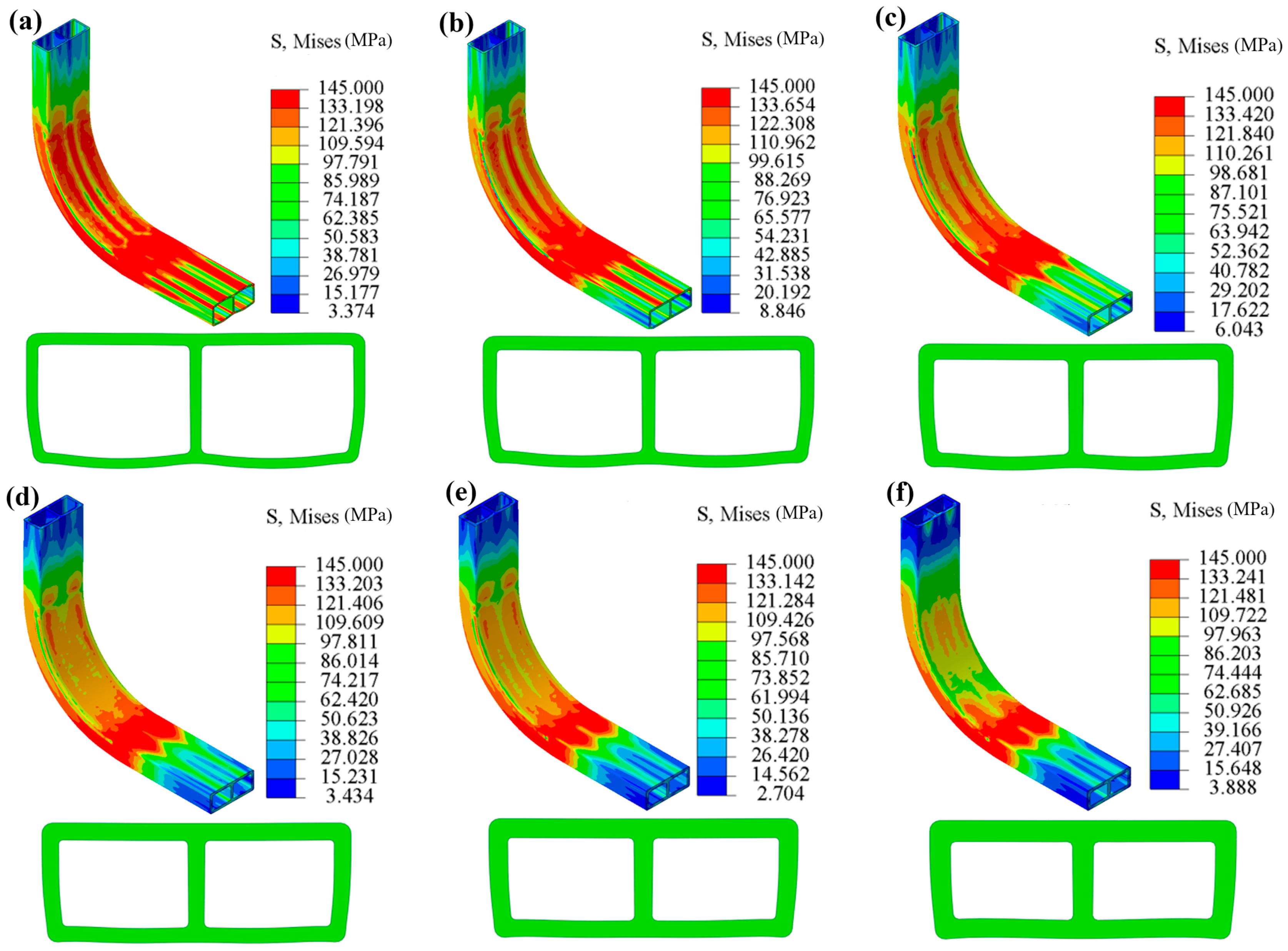
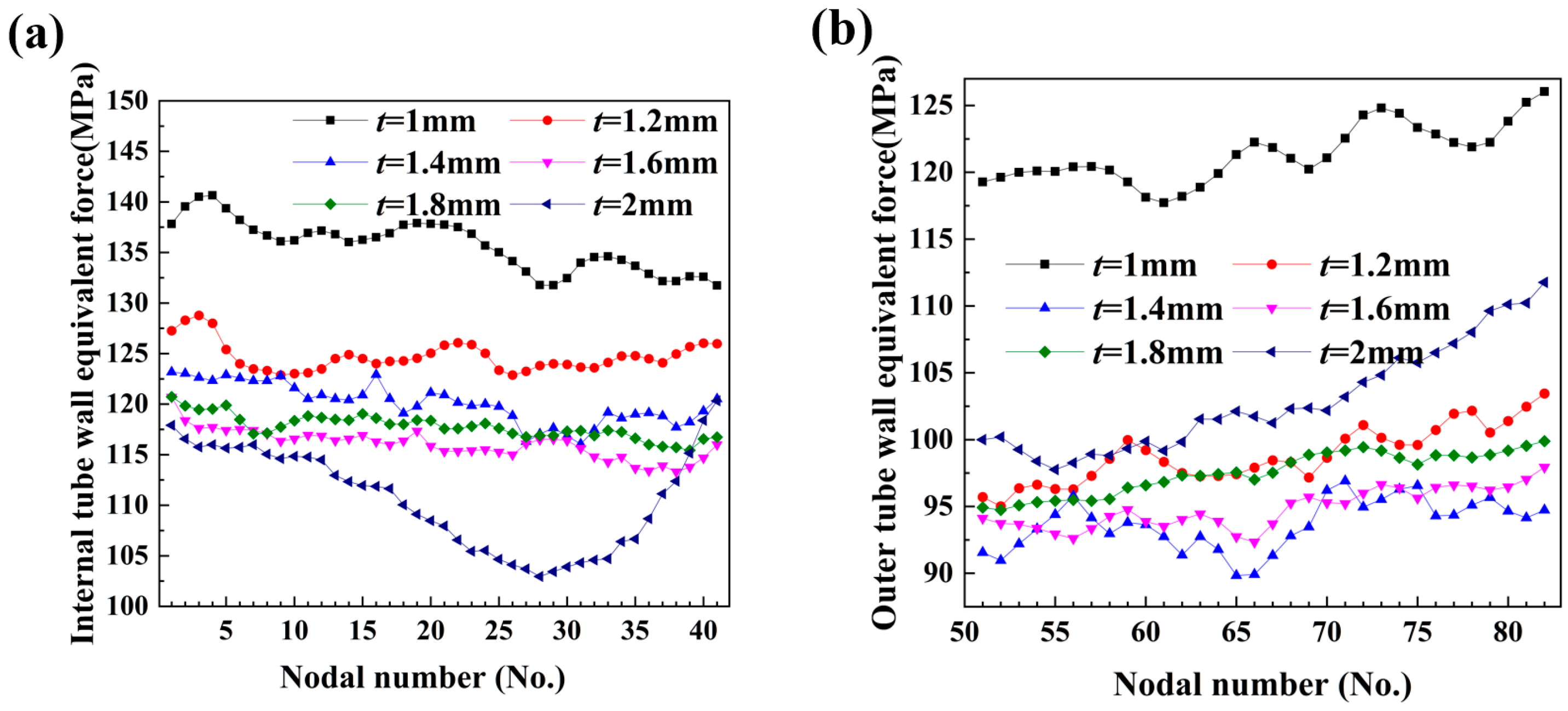
6.4. Simulation of Bending Behavior in Tubing with Variable Wall Thicknesses
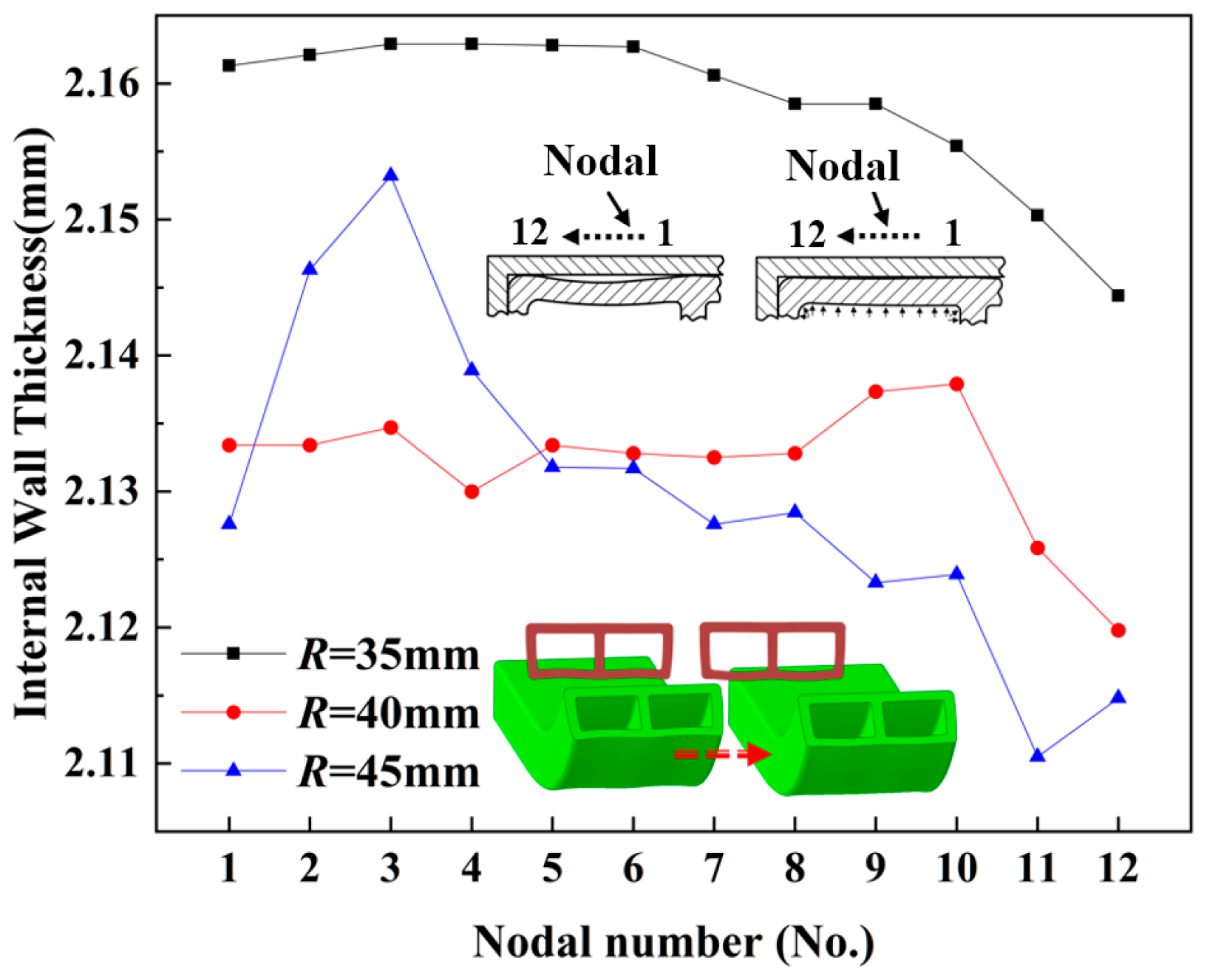
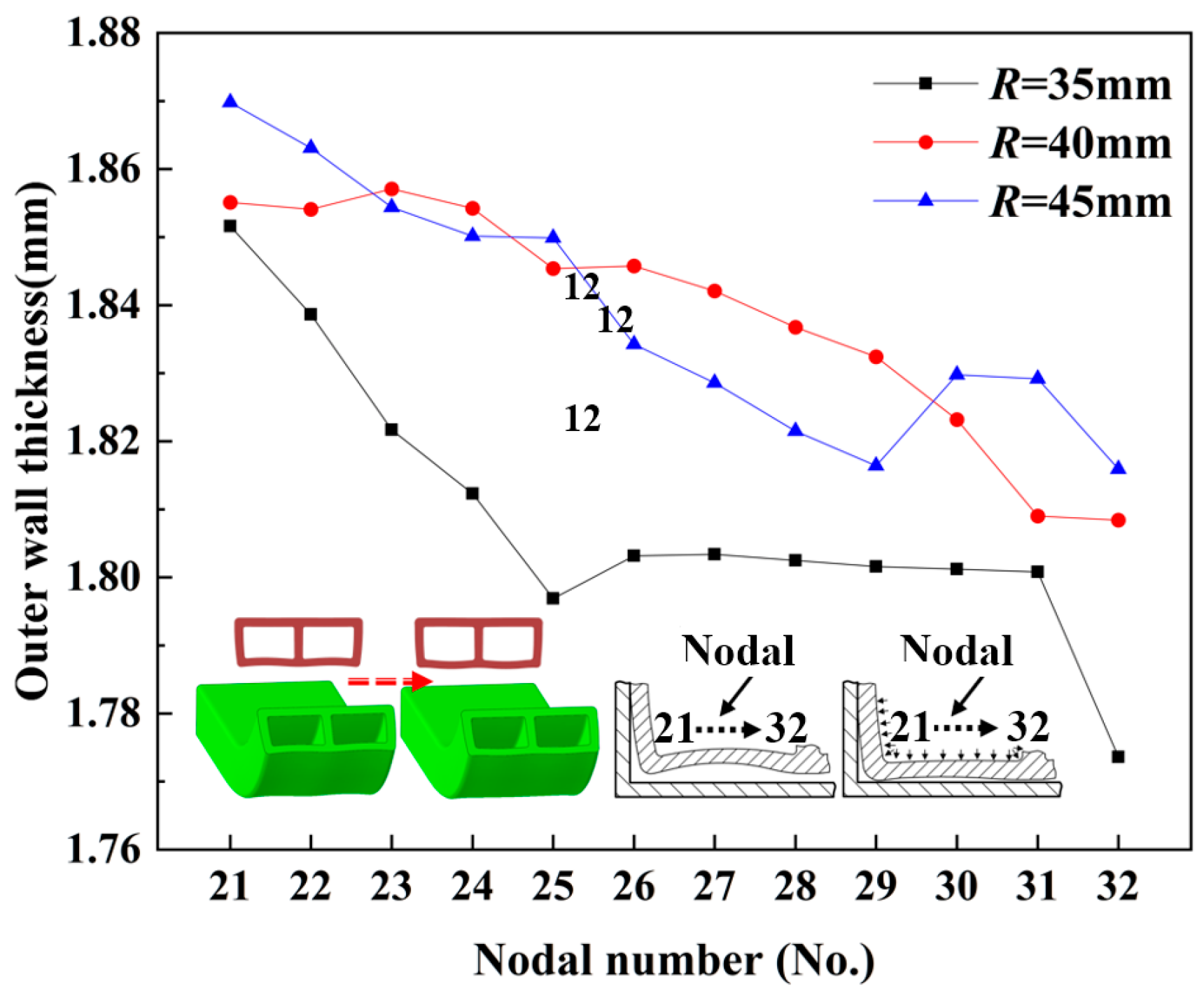
6.5. Effect of Different Bending Radii on the Wall Thickness of Tube Fittings
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dursun, T.; Soutis, C. Recent developments in advanced aircraft aluminum alloys. Mater. Des. 2014, 56, 862–871. [Google Scholar] [CrossRef]
- Yang, S.; Bao, Z.; He, Z.; Zheng, K.; Yuan, S. The hot gas forming process of ultra-large aluminum tubular parts with irregular cross-sections: Experimentation and application. J. Manuf. Process. 2023, 93, 239–252. [Google Scholar] [CrossRef]
- Wang, D.; Xu, F.; Yuan, L.; Zhang, D.; Liu, J.; Hu, Y.; Kang, H.; Ma, Q.; Tong, Y.; Han, W. Brief introduction and recent development on the manufacture of aluminum alloy integral panels in aerospace applications. Int. J. Mater. Struct. Integr. 2021, 14, 299–318. [Google Scholar] [CrossRef]
- Liu, P.; Xie, S.; Cheng, L. Die structure optimization for a large, multi-cavity aluminum profile using numerical simulation and experiments. Mater. Des. 2012, 36, 152–160. [Google Scholar] [CrossRef]
- Wang, X.-S.; Yuan, S.-J.; Song, P.; Xie, W.-C. Plastic deformation on hydroforming of aluminum alloy tube with rectangular sections. Trans. Nonferrous Met. Soc. China 2012, 22, s350–s356. [Google Scholar] [CrossRef]
- Cui, X.L.; Guo, J.; Zhao, Y.; Lin, P. Hydroforming process of thin-walled tubular components with multiple local bulges. Arch. Civ. Mech. Eng. 2023, 23, 169. [Google Scholar] [CrossRef]
- Liu, C.; El-Aty, A.A.; Lee, M.-G.; Hou, Y.; Xu, Y.; Hu, S.; Cheng, C.; Tao, J.; Guo, X. Predicting the forming limits in the tube hydroforming process by coupling the cyclic plasticity model with ductile fracture criteria. J. Mater. Res. Technol. 2023, 26, 109–120. [Google Scholar] [CrossRef]
- Nikhare, C.P. Effect of Thickness on Tube Deformation Mechanics during Low Pressure Tube Hydroforming Process Sequence Variation. In Proceedings of the ASME 2020 International Mechanical Engineering Congress and Exposition, Virtual, 16–19 November 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84485, p. V02AT02A019. [Google Scholar]
- Khalfallah, A.; Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Constitutive parameter identification of CB2001 yield function and its experimental verification using tube hydroforming tests. Int. J. Mech. Sci. 2020, 185, 105868. [Google Scholar] [CrossRef]
- Zhang, X.; He, J.; Chu, G.; Yuan, S. Experimental research on deformation and dimensional accuracy of rectangular-section tubular part during open die hydro-pressing process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 705–714. [Google Scholar] [CrossRef]
- Chen, G.; Yao, S.J.; Chen, B.G.; Chu, G.N. Research on tube hydro-forging process of trapezoid-sectional parts. Int. J. Adv. Manuf. Technol. 2020, 107, 1901–1908. [Google Scholar] [CrossRef]
- Hu, J.M.; Zhang, Y.X.; Luo, J.; Li, J.J.; Yang, Y.F.; Wan, Y.C.; Li, Y.C. Hydro-pressing process for complex three-dimensional twisted hollow blade. Forg. Stamp. Technol. 2023, 48, 90–95. [Google Scholar] [CrossRef]
- Marlapalle, B.G.; Hingole, R.S. Numerical and experimental predictions of formability parameters in tube hydroforming process. Aust. J. Mech. Eng. 2023, 21, 991–1007. [Google Scholar] [CrossRef]
- Marlapalle, B.G.; Hingole, R.S. Predictions of formability parameters in tube hydroforming process. SN Appl. Sci. 2021, 3, 606. [Google Scholar] [CrossRef]
- Raut, S.V.; Ramesh, A.; Arun, A.; Sumesh, C.S. Finite element analysis and optimization of tube hydroforming process. Mater. Today Proc. 2021, 46, 5008–5016. [Google Scholar] [CrossRef]
- Weber, F.; Hahn, M.; Tekkaya, A.E. Joining by die-less hydroforming with outer pressurization. J. Adv. Join. Process. 2020, 1, 100014. [Google Scholar] [CrossRef]
- Cui, X.L.; Yan, Y.; He, J.; Han, C. Dimensional Accuracy Enhancement in Hydroforming of Tubular Components with Rectangular Cross-Sections. JOM 2024, 76, 1788–1798. [Google Scholar] [CrossRef]
- Song, P.; Wang, X.S.; Xu, Y.C.; Yuan, S.J. Influence of internal pressure on hydro-bending of thin-walled aluminum alloy tube. Chin. J. Nonferrous Met. 2011, 21, 311–317. [Google Scholar]
- Xie, W.C.; Lin, J.F.; Hu, L. Research on deformation law of hydroforming steel/aluminum double-layered tubes. J. Plast. Eng. 2013, 20, 25–30. [Google Scholar] [CrossRef]
- Cui, X.L.; Han, C.; He, J.; Xu, W.; Yuan, S. Springback behavior and control strategy for dimensional accuracy of hydroformed tubular parts. Int. J. Mater. Form. 2023, 16, 15. [Google Scholar] [CrossRef]
- Chu, G.N.; Chen, G.; Lin, C.Y.; Fan, Z.G.; Li, H. Analytical model for tube hydro-forging: Prediction of die closing force, wall thickness and contact stress. J. Mater. Process. Technol. 2020, 275, 116310. [Google Scholar] [CrossRef]
- Ma, J.; Yang, L.; Huang, J.; Chen, Z.; He, Y.; Jiang, J. Residual contact pressure and elastic recovery of an assembled camshaft using tube hydroforming. CIRP J. Manuf. Sci. Technol. 2021, 32, 287–298. [Google Scholar] [CrossRef]
- Zhang, B.; Endelt, B.; Lihui, L.A.; Yang, Z.H.; Shu, Y.A.; Nielsen, K.B. An inverse strategy to determine constitutive parameters of tubular materials for hydroforming processes. Chin. J. Aeronaut. 2022, 35, 379–390. [Google Scholar] [CrossRef]
- Limam, A.; Lee, L.-H.; Corona, E.; Kyriakides, S. Inelastic wrinkling and collapse of tubes under combined bending and internal pressure. Int. J. Mech. Sci. 2010, 52, 637–647. [Google Scholar] [CrossRef]
- Xu, Y.; Xia, L.L.; Li, M.; Zhang, S.H. Research progress on hydro-mechanical forming technology for tube. Forg. Stamp. Technol. 2021, 46, 29–35. [Google Scholar] [CrossRef]
- Lin, C.Y.; Zhao, Q.; Chu, G.N. Hydroforming for bimetallic composite tube. J. Netshape Form. Eng. 2018, 10, 38–44. [Google Scholar]
- Available online: https://www.3ds.com/products/simulia/abaqus (accessed on 27 June 2024).





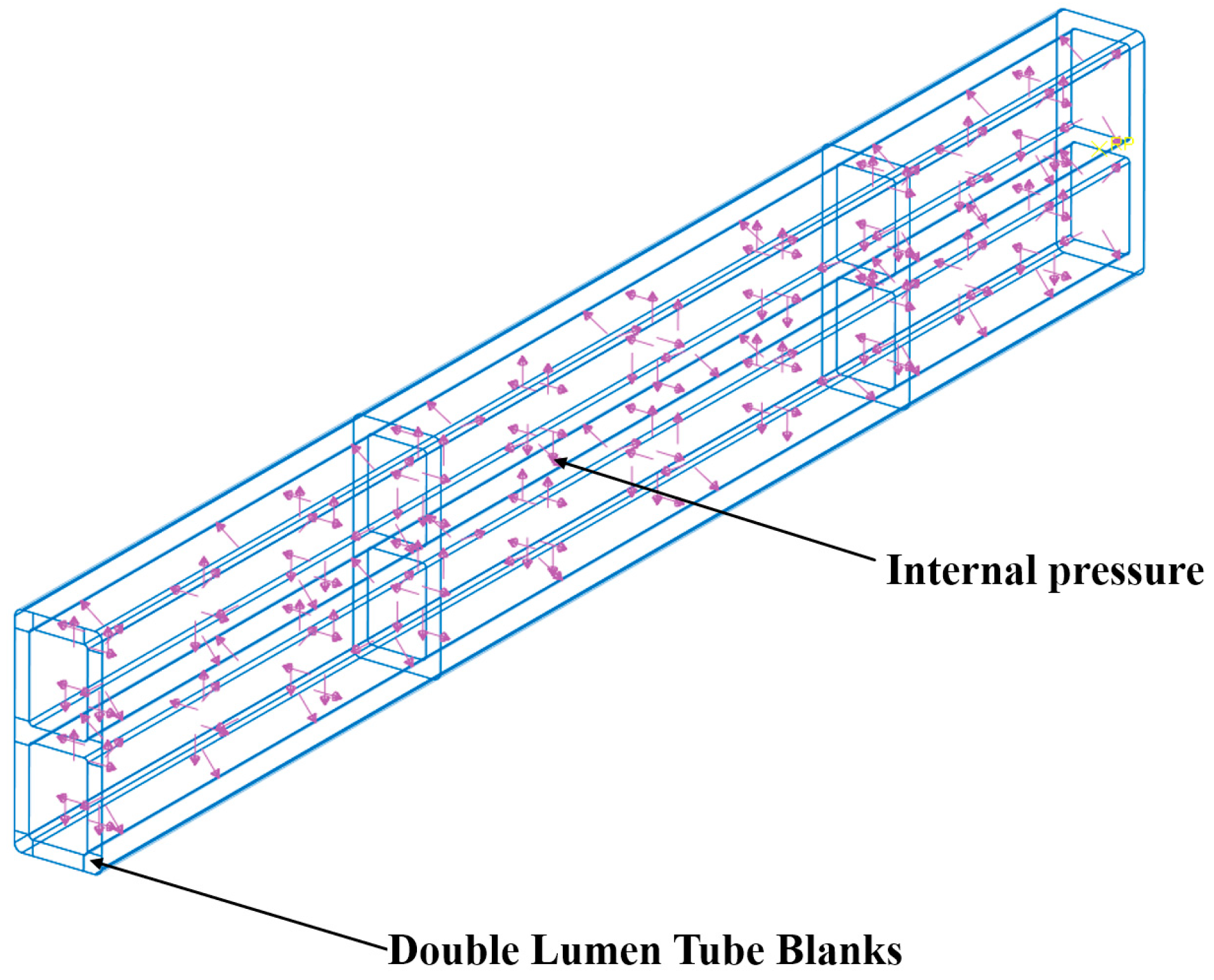



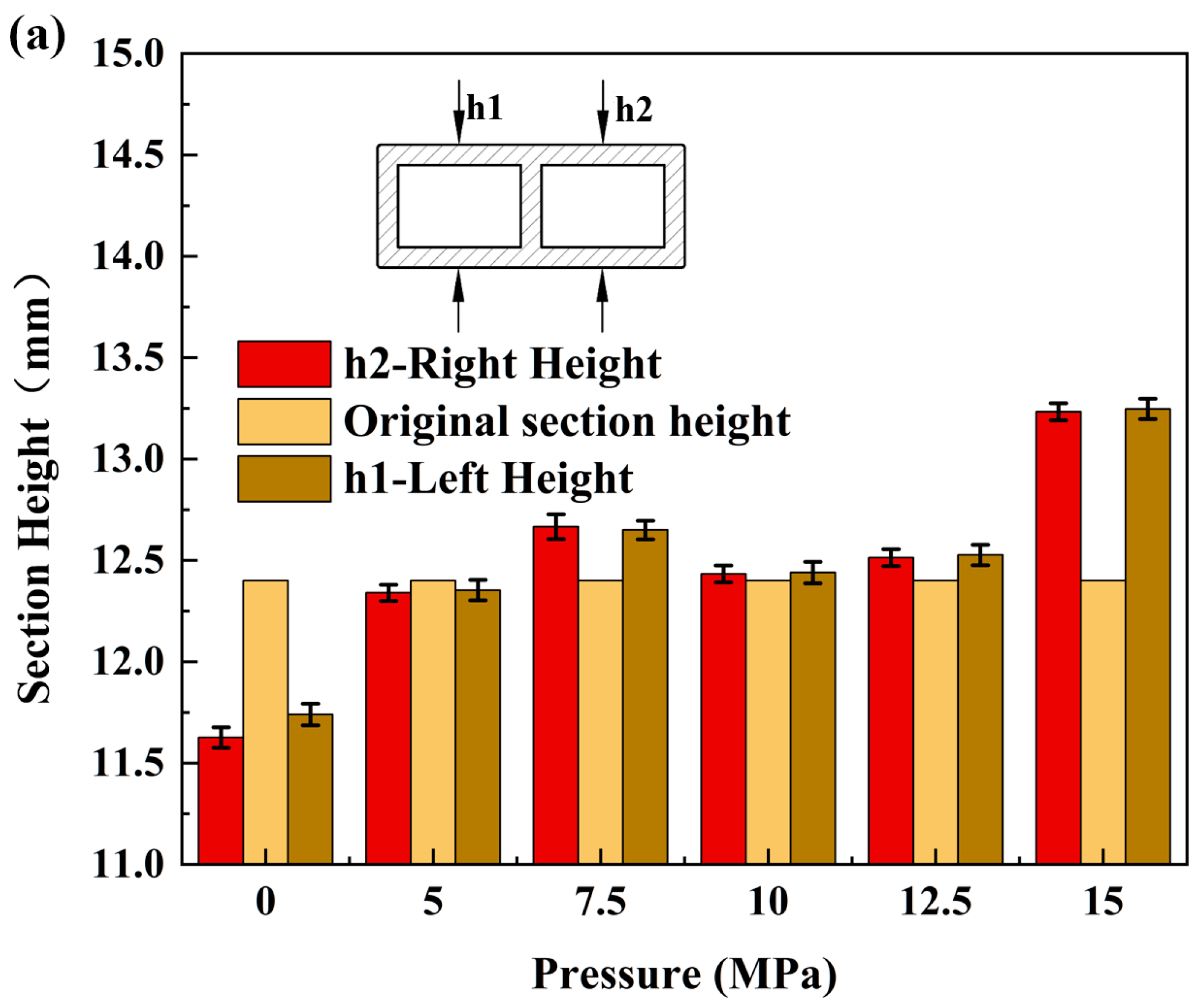
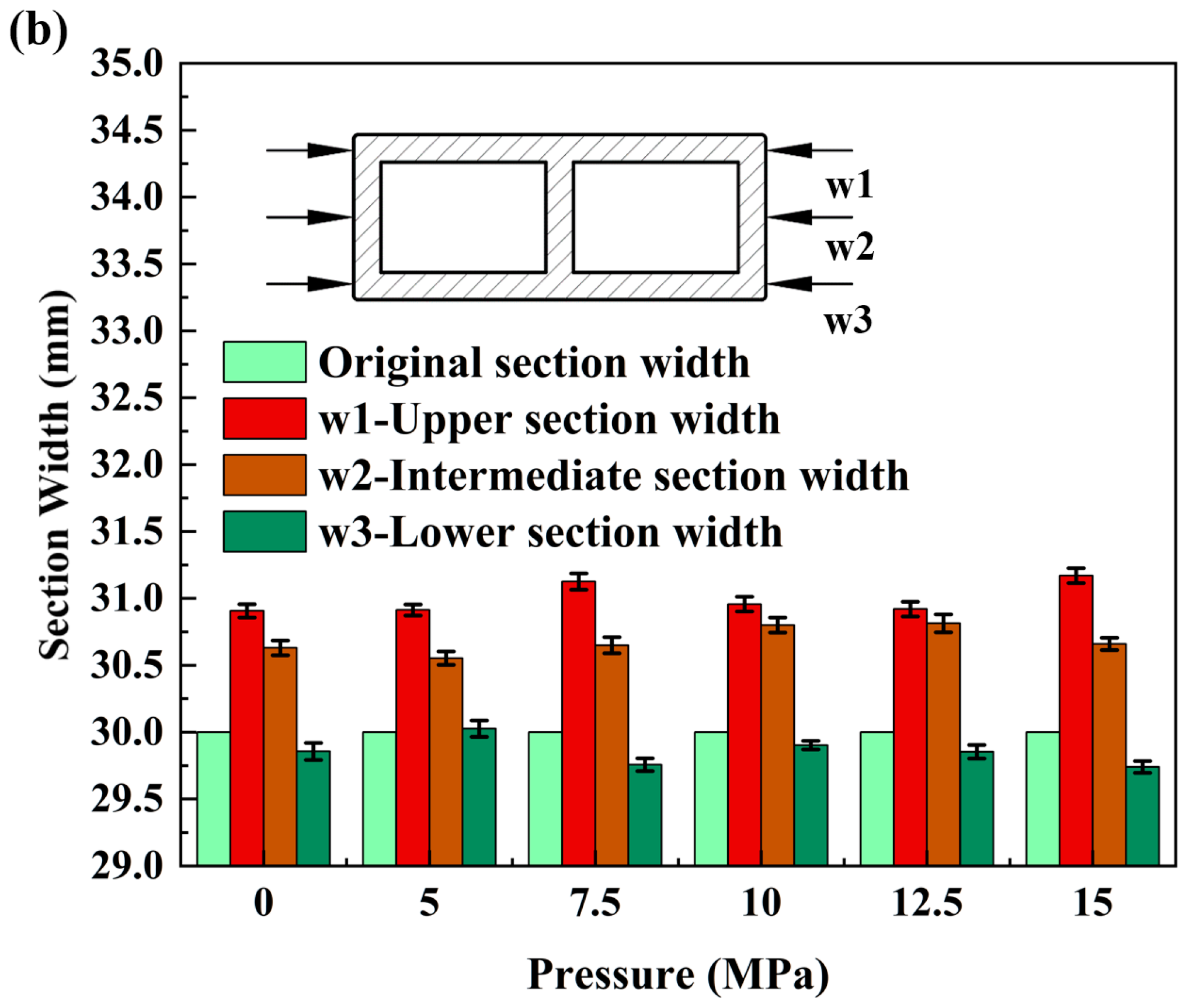


| Elements | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|
| Quantity contained (wt.%) | 0.35 | 0.10 | 0.10 | 0.51 | 0.10 | 0.10 | 0.10 | Balance |
| Material | (MPa) | (MPa) | Strain Hardening Index n | Strength Coefficient K (MPa) | (%) |
|---|---|---|---|---|---|
| 6063-T5 | 130 | 175 | 0.15 | 259.2 | 8 |
| Groups | Fixed Parameter | Variation Parameters |
|---|---|---|
| Group 1 | Bend radius R = 50 mm Wall thickness t = 2 mm | Internal pressure (MPa) p = 0, 5, 7.5, 10, 12.5, 15 |
| Group 2 | Internal pressure p = 5 MPa Wall thickness t = 2 mm | Bend radius (mm) R = 35, 40, 45 |
| Group 3 | Internal pressure p = 5 MPa Bend radius R = 50 mm | Wall thickness (mm) t = 1, 1.2, 1.4, 1.6, 1.8, 2 |
| Group | Pressure (MPa) | Depth of Depression (mm) | Relative Error | ||
|---|---|---|---|---|---|
| Exp. | Num. | Max | Min | ||
| 1 | p = 0 MPa | 0.36 | 0.39 | 8.3% | 2.6% |
| 0.42 | |||||
| 0.38 | |||||
| 2 | p = 5 MPa | 0.18 | 0.195 | 8.3% | 2.5% |
| 0.20 | |||||
| 0.185 | |||||
| 3 | p = 7.5 MPa | 0.11 | 0.113 | 5.8% | 2.7% |
| 0.118 | |||||
| 0.12 | |||||
| 4 | p = 10 MPa | −0.045 | −0.04 | 12.5% | 2.4% |
| −0.041 | |||||
| −0.043 | |||||
| 5 | p = 12.5 MPa | −0.14 | −0.13 | 13% | 7.1% |
| −0.12 | |||||
| −0.115 | |||||
| 6 | p = 15 MPa | −0.25 | −0.24 | 4% | 3.2% |
| −0.26 | |||||
| −0.248 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Jiang, Z.; Zhao, S.; Xie, X.; Xiao, J.; Liu, X.; Wu, Z.; Zhang, Y. Analysis of Bending Deformation and Stress of 6063-T5 Aluminum Alloy Multi-Cavity Tube Filled with Liquid. Materials 2024, 17, 3230. https://doi.org/10.3390/ma17133230
Zhang X, Jiang Z, Zhao S, Xie X, Xiao J, Liu X, Wu Z, Zhang Y. Analysis of Bending Deformation and Stress of 6063-T5 Aluminum Alloy Multi-Cavity Tube Filled with Liquid. Materials. 2024; 17(13):3230. https://doi.org/10.3390/ma17133230
Chicago/Turabian StyleZhang, Xinlong, Zhaosong Jiang, Shuang Zhao, Xiaodong Xie, Jiang Xiao, Xueyan Liu, Zhe Wu, and Yang Zhang. 2024. "Analysis of Bending Deformation and Stress of 6063-T5 Aluminum Alloy Multi-Cavity Tube Filled with Liquid" Materials 17, no. 13: 3230. https://doi.org/10.3390/ma17133230
APA StyleZhang, X., Jiang, Z., Zhao, S., Xie, X., Xiao, J., Liu, X., Wu, Z., & Zhang, Y. (2024). Analysis of Bending Deformation and Stress of 6063-T5 Aluminum Alloy Multi-Cavity Tube Filled with Liquid. Materials, 17(13), 3230. https://doi.org/10.3390/ma17133230






