Resistance Analysis of Crack Propagation in Concrete Subjected to Hydraulic Pressure
Abstract
:1. Introduction
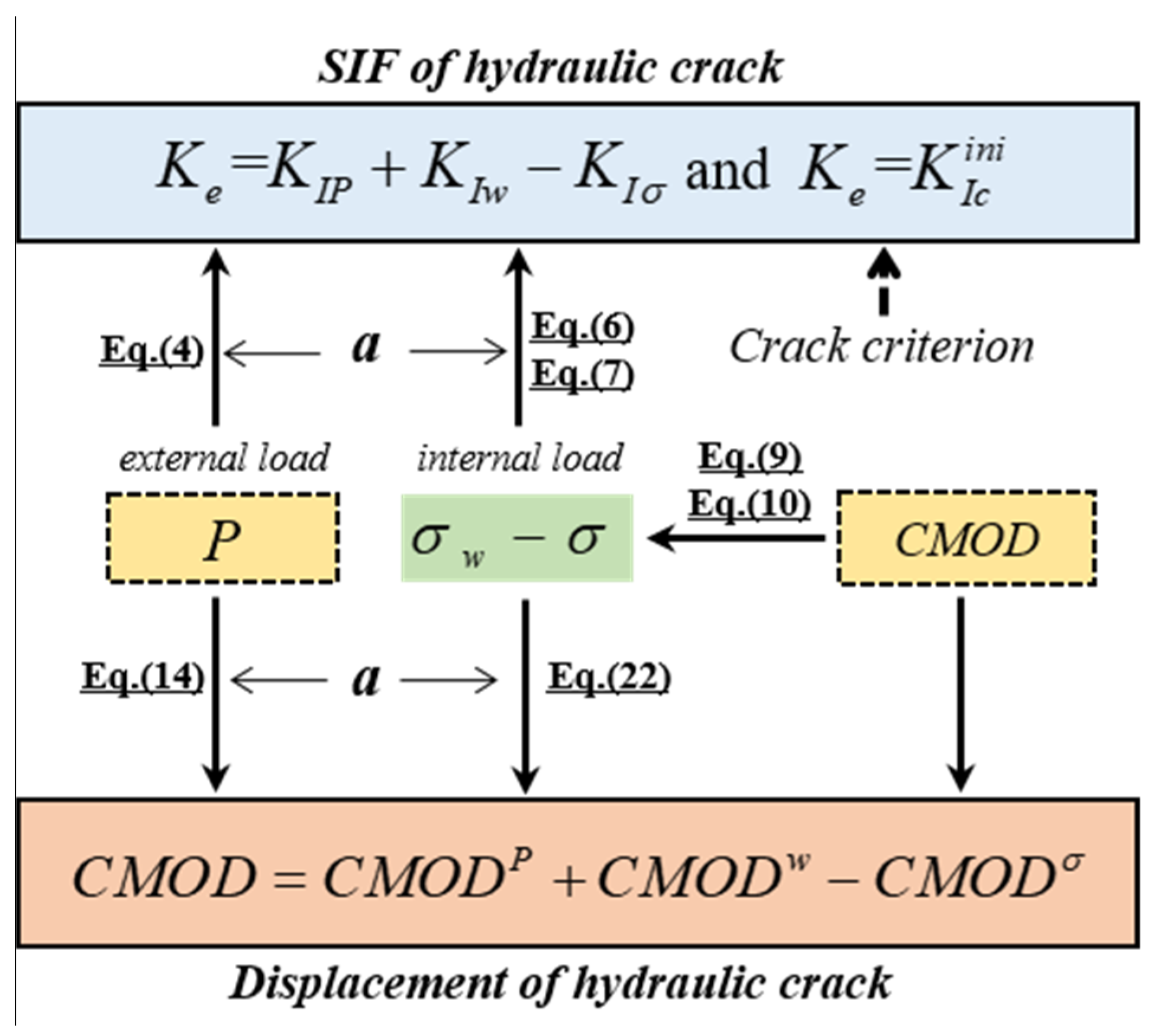
2. Analysis of Hydraulic Crack Propagation in Concrete Beam
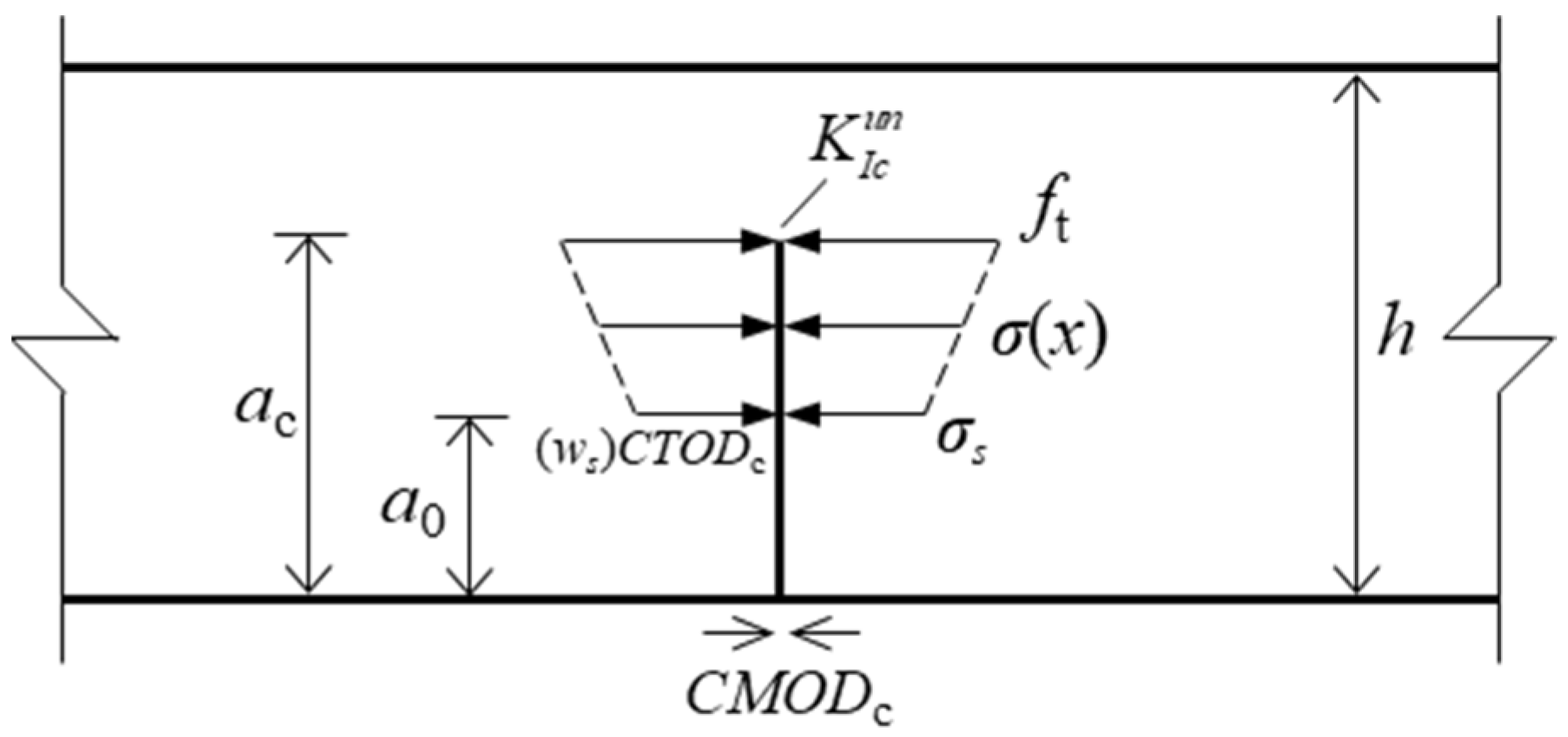
2.1. Criterion of Hydraulic Crack Propagation in Concrete
2.2. Determination of Hydraulic Crack Width in Concrete
2.3. Calculation of Hydraulic Crack Propagation
- (1)
- Input the parameters required for the calculation, including the geometrical dimensions (span S, width B, height h, and initial notch length a0) of the test beam and the material parameters (Young’s modulus E, tensile strength ft, fracture energy GF, and initial fracturing toughness ) of the concrete.
- (2)
- Specify the expansion of the crack length increment, Δa = a + Δa, Δa = 0.0001 m; employ the increment of crack mouth opening displacement, CMOD = CMOD + ΔCMOD, ΔCMOD = 0.00002m; apply the increment of external load, P = P + ΔP, ΔP = 0.0001 kN.
- (3)
- Calculate , , , , , and by increasing P and CMOD until and are satisfied. This iterative process is terminated until the increase in applied load P cannot satisfy the , and the maximum load Pmax and the critical crack mouth opening displacement CMODc are determined.
- (4)
- Calculate , , , , , and by decreasing P and increasing CMOD until and are satisfied. This iterative process is terminated when the crack tip reaches the boundary of the concrete. P < 0 is used in the calculation of satisfying , but P = 0 stands in the calculation of satisfying .
- (5)
- Output the calculated results of the characteristic curves of the hydraulic crack propagation process of the test concrete, including the P-CMOD curve, the KR curve, the KIP curve, and the KIw curve.
3. Hydraulic Fracturing Test of Concrete Beams
3.1. Experiment Program
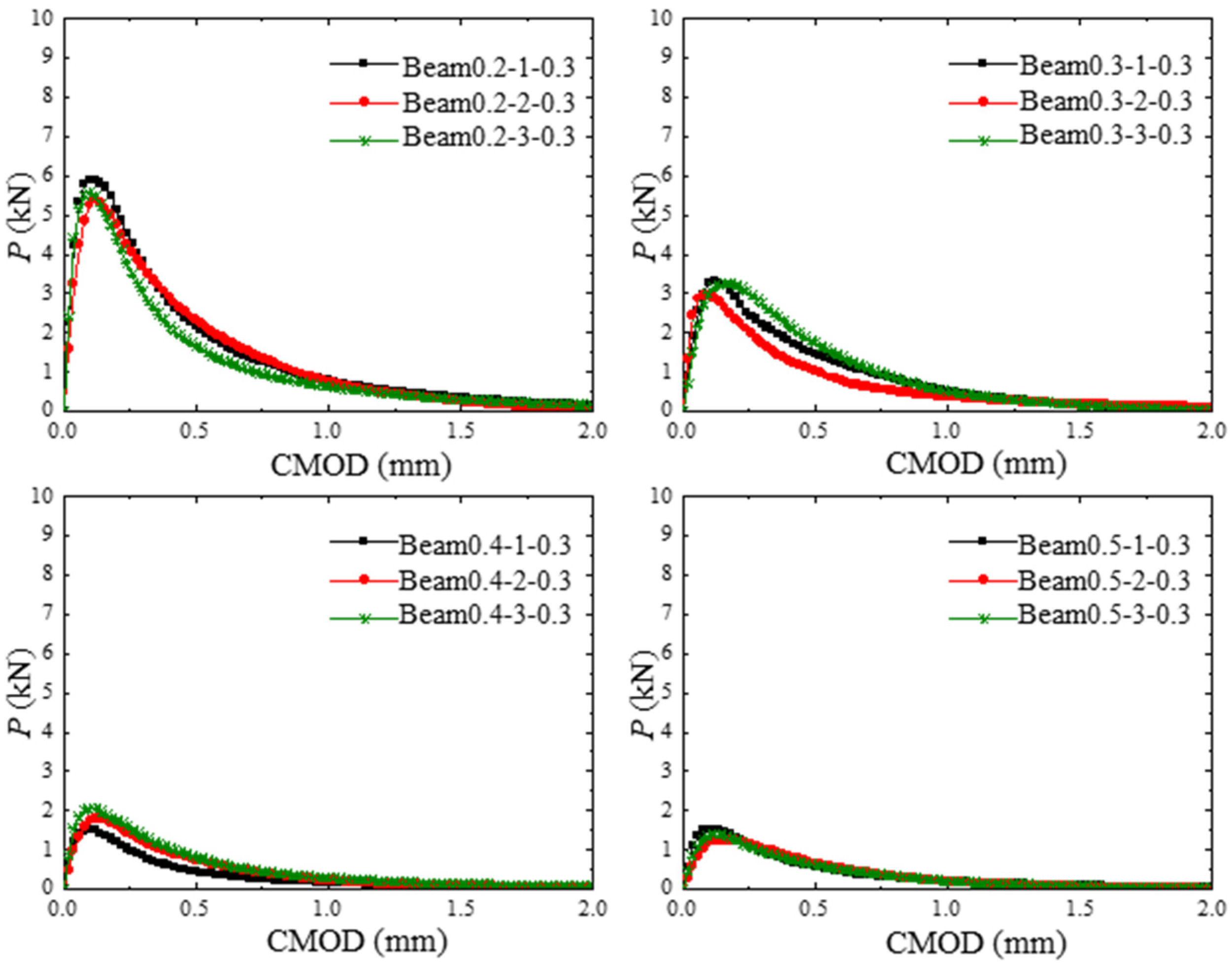
3.2. Experiment Results
4. Results and Discussion
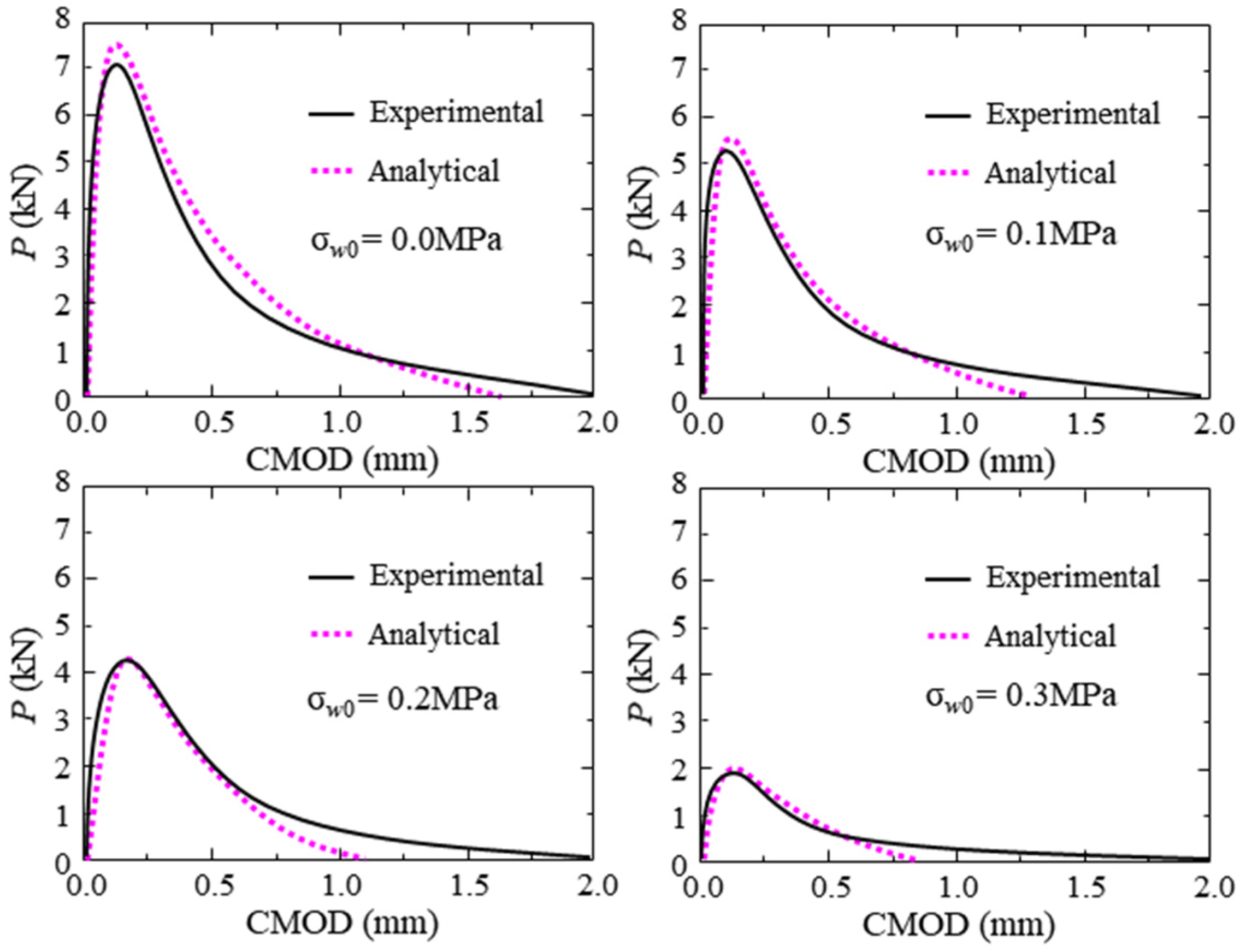
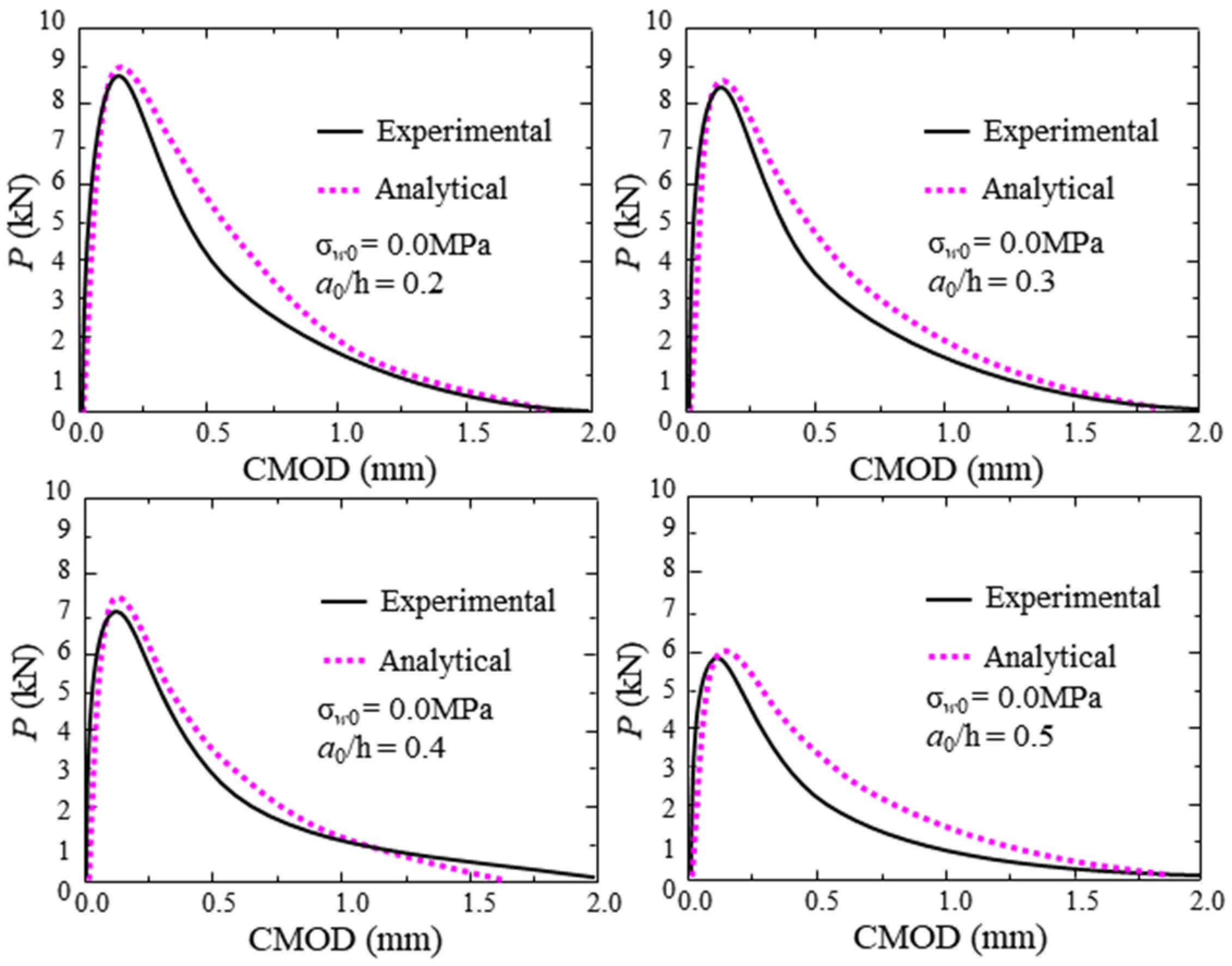
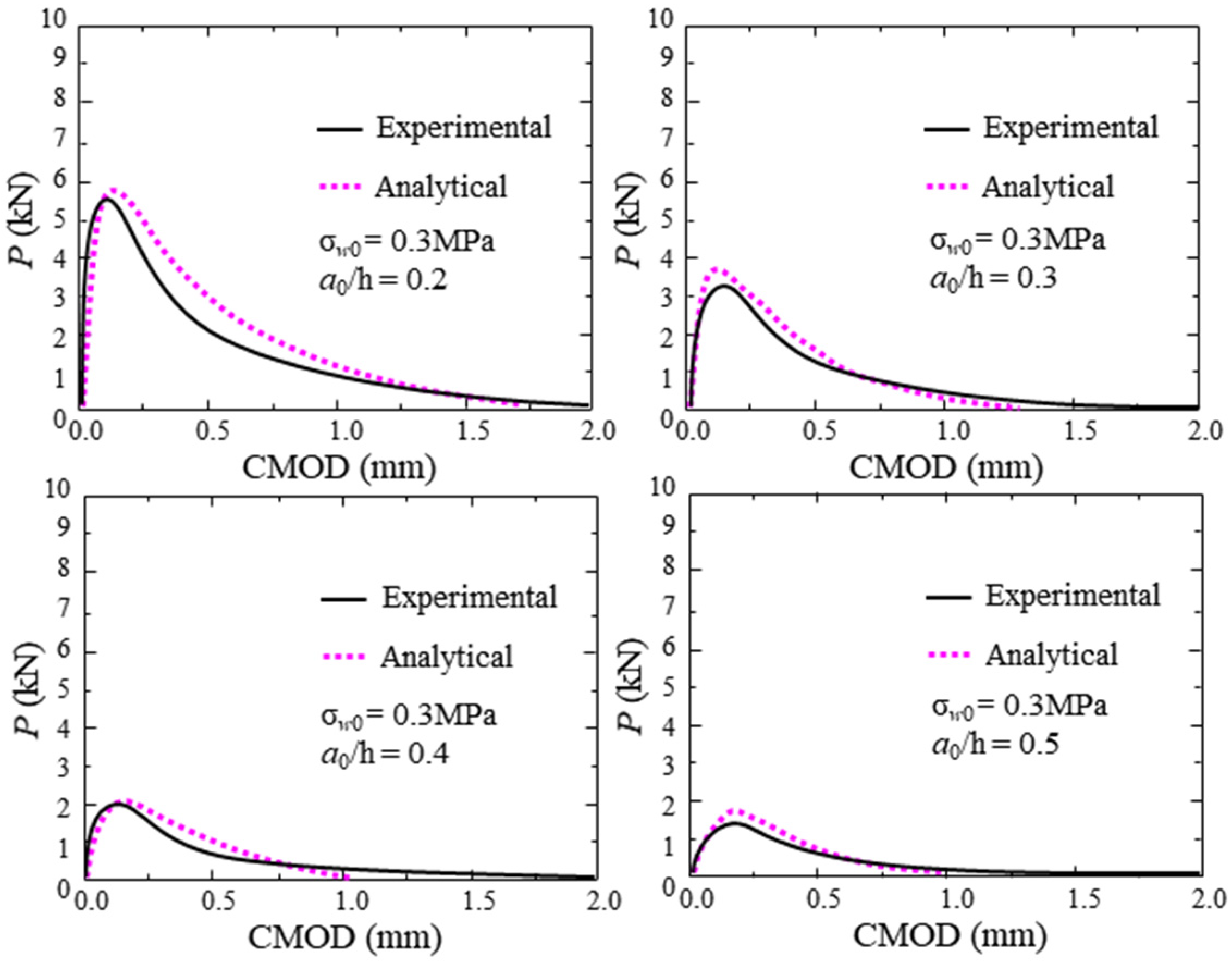
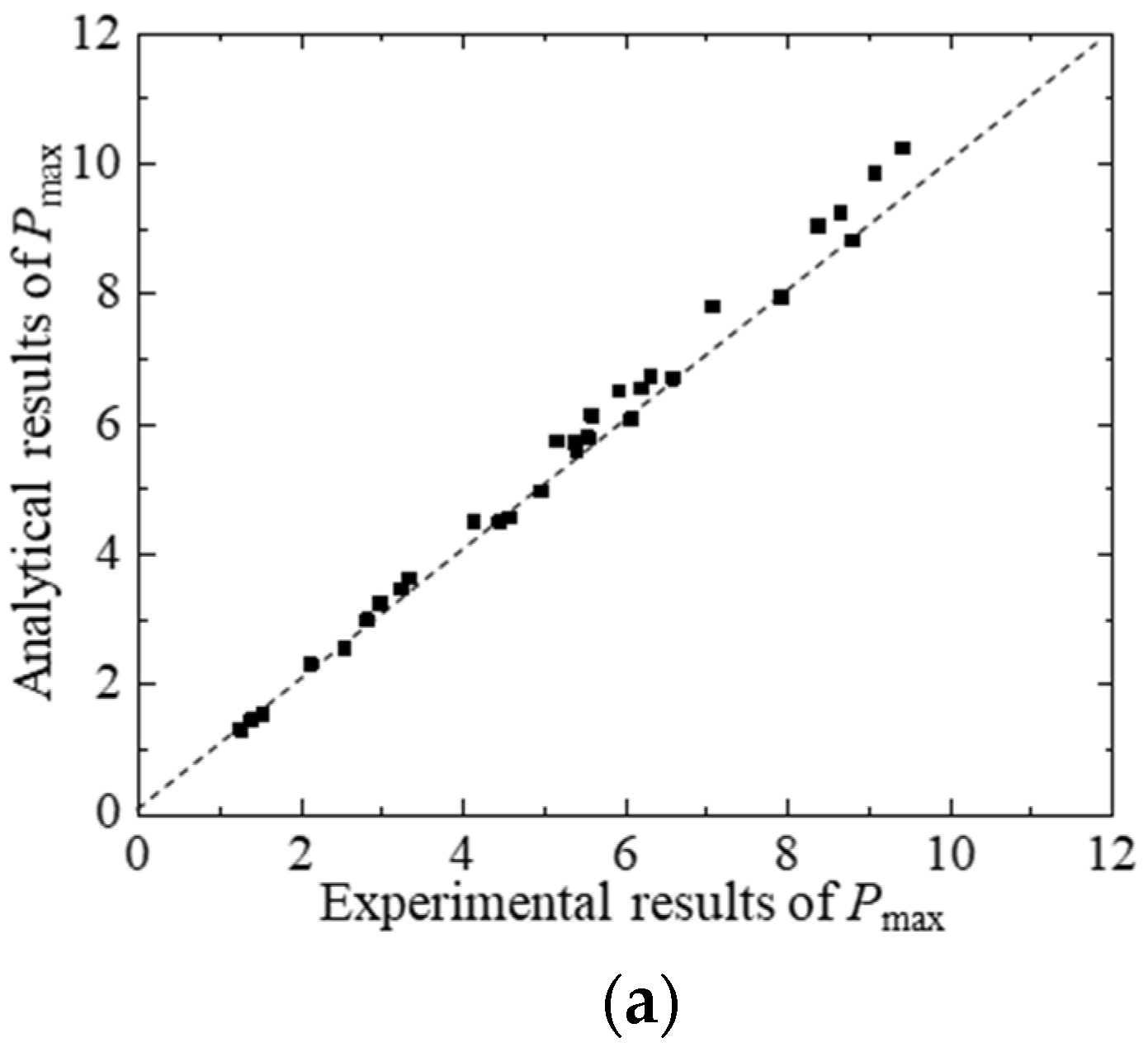
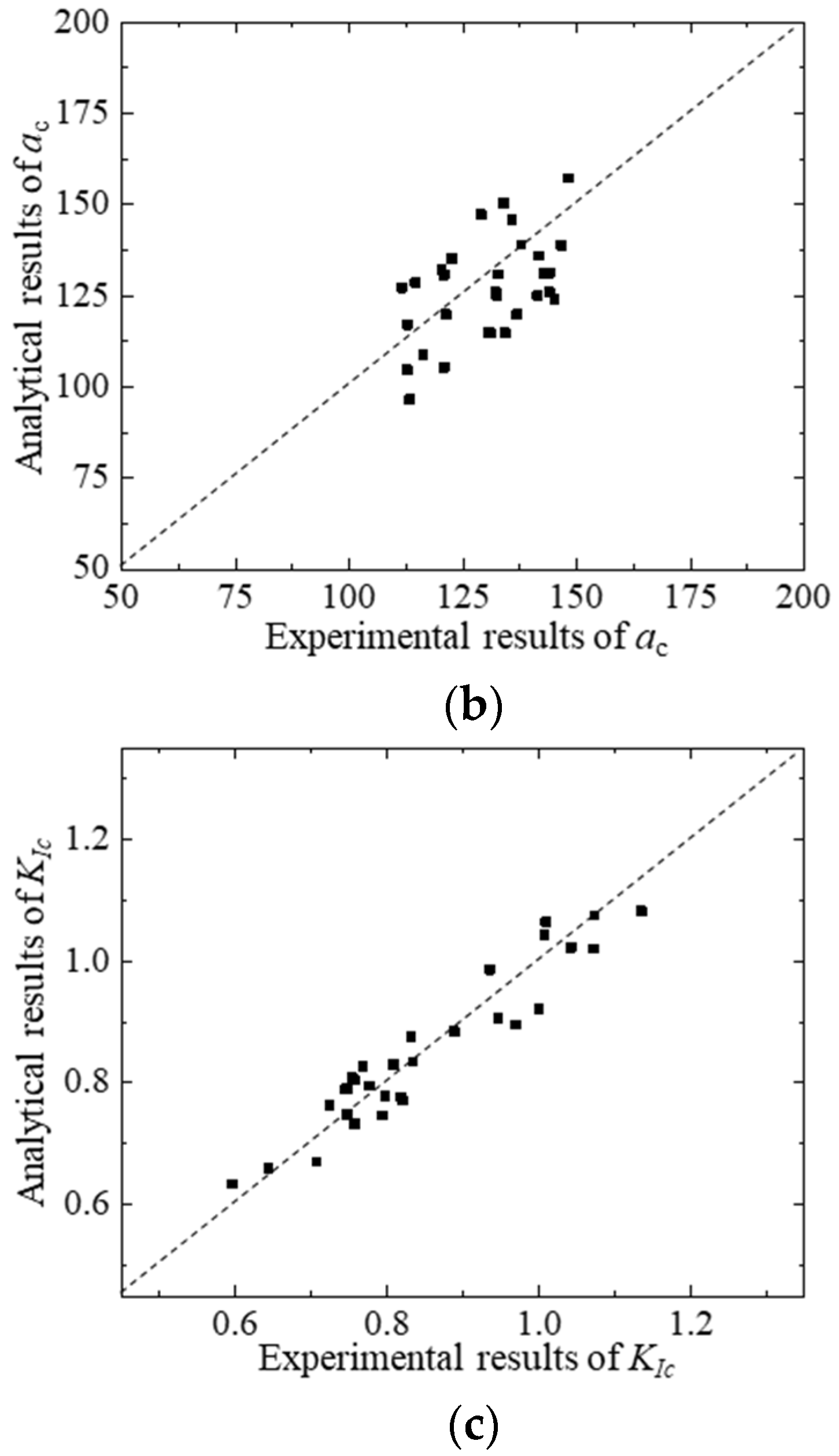
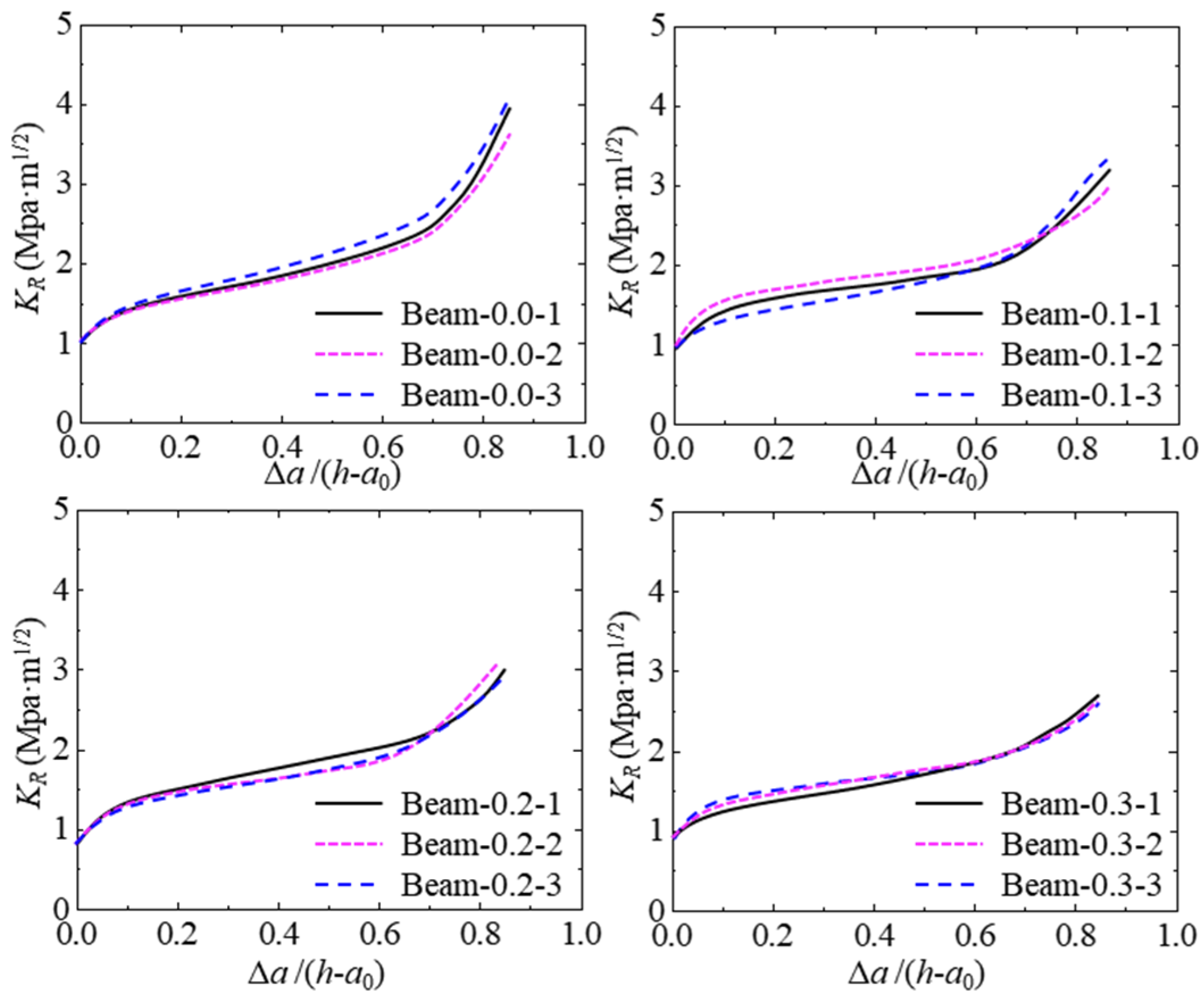
4.1. Verification of Proposed Theoretical Model
4.2. Effect of Hydraulic Pressure on KR Resistance Curve
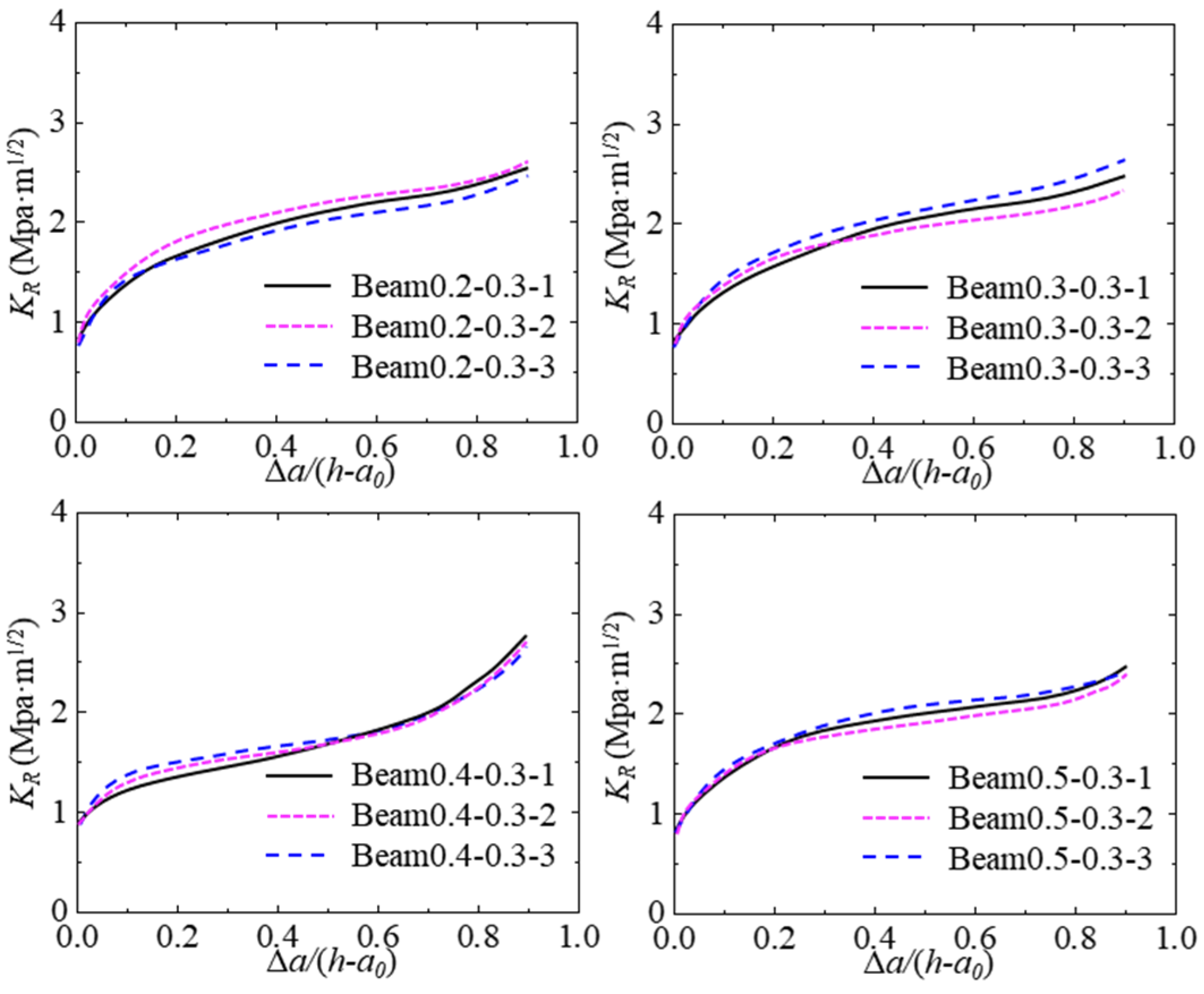
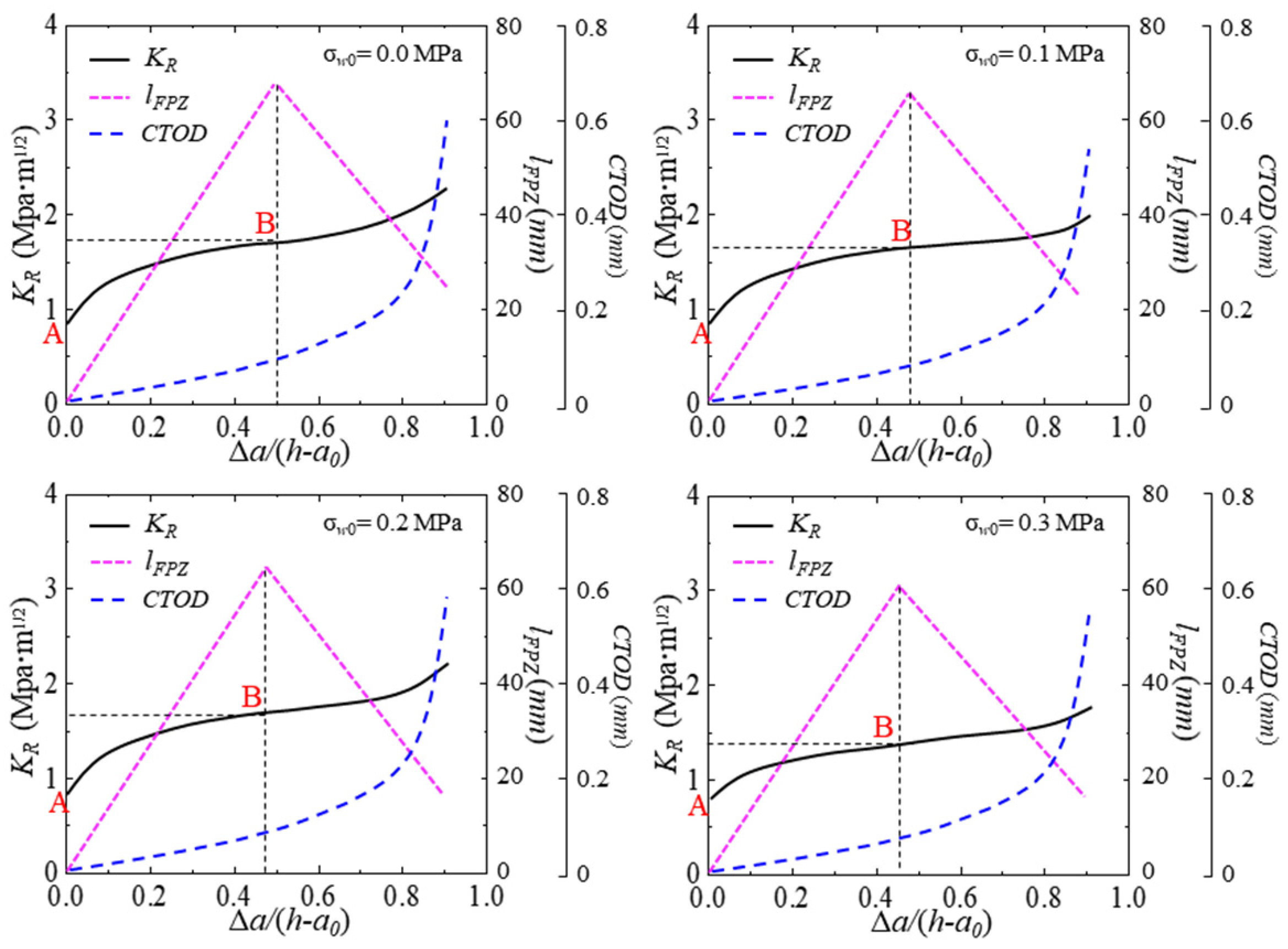
4.3. Effect of Fracture Process Zone Length on KR Resistance Curve
- When , there is stable crack propagation;
- When , there is unstable crack propagation.
4.4. Analysis of Hydraulic Crack Propagation in Concrete
- When , there is stable crack propagation;
- When , there is unstable crack propagation;
- When , hydraulic crack propagation accelerates.
5. Conclusions
- (1)
- Through the deformation relationship and crack initiation criterion, an analytical method for the hydraulic fracture propagation in concrete is proposed. Based on this analytical method, given the geometry and material information of the test concrete beam, the P-CMOD curve, FPZ length, and SIF curves induced by different loads can be calculated. The accuracy of the proposed analytical method is verified by comparing the theoretical results with the experimental results.
- (2)
- Increasing the internal hydraulic pressure decreases the carrying capacity of the test beam, the crack resistance of concrete, and the length of the FPZ of the hydraulic crack. As the applied hydraulic pressure increases from 0.0 MPa to 0.3 MPa, the peak load decreases by 60%, the cohesion fracture toughness decreases by 30%, and the maximum FPZ length decreases by 10%.
- (3)
- Increasing the initial crack depth ratio decreases the initial cracking load and peak load of the test beam, but it has less influence on the crack resistance of concrete and the length of the FPZ of the hydraulic crack. As a0/h increases from 0.2 to 0.5, the initial cracking load and the peak load incur a substantial percentage reduction of 30%.
- (4)
- The stability of crack propagation in concrete subjected to hydraulic fracturing decreases as the internal hydraulic pressure increases, but it is less affected by the initial crack depth ratio. Furthermore, crack propagation, which is primarily driven by hydraulic pressure, occurs earlier with the increase in internal hydraulic pressure. The values of Δa/(h − a0) at the collapse of the concrete beam under hydraulic pressures of 0.1, 0.2, and 0.3 MPa are 0.74, 0.52, and 0.38, respectively.
- (5)
- In this analytical method for hydraulic crack propagation in concrete, the softening curve parameters are determined based on the measured CTODc, which may compromise the computational accuracy of the proposed analysis model. Consequently, a more reliable theoretical approach to determining softening curve parameters using this method requires further investigation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feltrin, G.; Wepf, D.; Bachmann, H. Seismic cracking of concrete gravity dams. Dam. Eng. 1990, 1, 279–289. [Google Scholar]
- Bucher, K.; Stober, I.; Seelig, U. Water deep inside the mountains: Unique water samples from the Gotthard rail base tunnel, Switzerland. Chem. Geol. 2012, 12, 240–253. [Google Scholar] [CrossRef]
- Duan, K.M.; Zhang, G.F.; Sun, H. Construction practice of water conveyance tunnel among complex geotechnical conditions: A case study. Sci. Rep. 2023, 13, 715–736. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Tao, M.M.; Wang, Z.K. Effect of leaching behavior on the geometric and hydraulic characteristics of concrete fracture. Materials 2022, 15, 4584. [Google Scholar] [CrossRef]
- He, J.X.; Ding, X.Y.; Liu, L. Predicting the effect of the loading rate on the fracture toughness of hydraulic asphalt concrete based on the weibull distribution. Materials 2024, 17, 803. [Google Scholar] [CrossRef]
- Ouyang, C.S.; Mobasher, B.; Shah, S.P. An R-curve approach for fracture of quasi-brittle materials. Eng. Fract. Mech. 1990, 37, 901–913. [Google Scholar]
- Bažant, Z.P.; Jirásek, M. R-curve modeling of rate and size effects in quasi brittle fracture. Int. J. Fract. 1993, 62, 355–373. [Google Scholar] [CrossRef]
- Reinhardt, H.W.; Xu, S.L. Crack extension resistance based on the cohesive force in concrete. Eng. Fract. Mech. 1999, 64, 563–587. [Google Scholar] [CrossRef]
- Xu, S.L.; Reinhardt, H.W. Determination of double-K criterion for crack propagation in quasi-brittle fracture, Part I: Experimental investigation of crack propagation. Int. J. Fract. 1999, 98, 111–149. [Google Scholar] [CrossRef]
- Kumar, S.; Barai, S. Influence of specimen geometry and size-effect on the KR-curve based on the cohesive stress in concrete. Int. J. Fract. 2008, 152, 127–148. [Google Scholar] [CrossRef]
- Wang, H.W.; Wu, Z.M.; Wang, Y.J.; Yu, R.C. An analytical method for predicting mode-I crack propagation process and resistance curve of rock and concrete materials. Theor. Appl. Fract. Mech. 2019, 100, 328–341. [Google Scholar] [CrossRef]
- Hu, S.W.; Fan, B. Crack extension resistance of concrete at low temperatures. Mag. Concr. Res. 2020, 72, 837–851. [Google Scholar] [CrossRef]
- Li, Z.H. A numerical method for applying cohesive stress on fracture process zone in concrete using nonlinear spring element. Materials 2022, 5, 1251. [Google Scholar] [CrossRef]
- Bruhwiler, E.; Saouma, V.E. Water fracture interaction in concrete-part I: Fracture properties. ACI Mater. J. 1995, 92, 296–303. [Google Scholar]
- Bruhwiler, E.; Saouma, V.E. Water fracture interaction in concrete-part II: Hydrostatic pressure in cracks. ACI Mater. J. 1995, 92, 383–390. [Google Scholar]
- Xu, S.; Wang, J. Crack propagation in a concrete dam under water pressure and determination of the double-K fracture parameters. China Civ. Eng. J. 2009, 42, 121–125. [Google Scholar]
- Xu, S.; Wang, J. Experimental determination of double-K fracture parameters of concrete under water pressure. J. Hydraul. Eng. 2007, 38, 972–978. [Google Scholar]
- Forth, J.P.; Higgins, L.; Neville, A.; Hodgson, T. Response of reinforced concrete beams to hydrostatic pressure acting within primary cracks. Mater. Struct. 2014, 47, 1545–1557. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, J. Experimental study on the influence of hydraulic fracturing on high concrete gravity dams. Eng. Struct. 2017, 132, 508–517. [Google Scholar] [CrossRef]
- Jia, J.; Wang, Y.; Wei, F. Simulation method of hydraulic fracturing and discussions on design criteria for super high gravity dams. J. Hydraul. Eng. 2013, 44, 127–133. [Google Scholar]
- Du, C.; Chen, X.; Chen, Y. Experimental research on hydraulic fracture of concrete. J. Hydraul. Eng. 2017, 48, 1–8. [Google Scholar]
- Chen, X.; Du, C.; You, M.; Jiang, S.; Sun, L. Experimental study on water fracture interactions in concrete. Eng. Fract. Mech. 2017, 179, 314–327. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, S.; Fan, X.; Lu, J. Effect of water pressure on fracture parameters of concrete. Constr. Build. Mater. 2019, 199, 613–623. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, S.; Lu, J.; Qiao, Y. A note on the fracture behavior of concrete beams within water pressure under different loading rates. KSCE J. Civ. Eng. 2019, 23, 3993–3999. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, W.; Hu, S.; Wang, G.; Chen, M.; Yan, P. Study on the influence of hydraulic pressure on the bilinear softening curve of concrete. Theor. Appl. Fract. Mech. 2022, 119, 103351. [Google Scholar] [CrossRef]
- Wu, Z.M.; Dong, W.; Liu, K.; Yang, S.T. Mode-I crack propagation criterion of concrete and numerical simulation for the complete crack propagation process. J. Hydraul. Eng. 2007, 12, 1453–1507. [Google Scholar]
- Dong, W.; Wu, Z.M.; Zhou, X.M. Calculating crack extension resistance of concrete based on a new crack propagation criterion. Constr. Build. Mater. 2013, 38, 879–889. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook, 3rd ed.; ASME Press: New York, USA, 2000. [Google Scholar]
- Jenq, Y.S.; Shah, S.P. A fracture toughness criterion for concrete. Eng. Fract. Mech. 1985, 21, 1055–1069. [Google Scholar] [CrossRef]
- Foote, R.M.L.; Mai, Y.W.; Cotterell, B. Crack growth resistance curves in strain softening materials. J. Mech. Phys. Solids 1986, 34, 593–607. [Google Scholar] [CrossRef]







| Water | Cement | Sand | Gravel (5–12.5 mm) | Gravel (12.5–25 mm) |
|---|---|---|---|---|
| 182 | 350 | 761 | 614 | 538 |
| Beams | a0 (mm) | a0/h | σw0 (MPa) | Amounts | Sources |
|---|---|---|---|---|---|
| Beam-0.0-X | 80 | 0.4 | 0.0 | 3 | Ref. [23] |
| Beam-0.1-X | 80 | 0.4 | 0.1 | 3 | |
| Beam-0.2-X | 80 | 0.4 | 0.2 | 3 | |
| Beam-0.3-X | 80 | 0.4 | 0.3 | 3 | |
| Beam0.2-X-0.0 | 40 | 0.2 | 0.0 | 3 | This work |
| Beam0.3-X-0.0 | 60 | 0.3 | 0.0 | 3 | |
| Beam0.4-X-0.0 | 80 | 0.4 | 0.0 | 3 | |
| Beam0.5-X-0.0 | 100 | 0.5 | 0.0 | 3 | |
| Beam0.2-X-0.3 | 40 | 0.2 | 0.3 | 3 | |
| Beam0.3-X-0.3 | 60 | 0.3 | 0.3 | 3 | |
| Beam0.4-X-0.3 | 80 | 0.4 | 0.3 | 3 | |
| Beam0.5-X-0.3 | 100 | 0.5 | 0.3 | 3 |
| Number | ac (mm) | Pini (kN) | Pmax (kN) | Fracture Toughness (MPa·m1/2) | |
|---|---|---|---|---|---|
| TPB-0.0-1 | 135.7 | 3.69 | 6.31 | 0.883 | 1.714 |
| TPB-0.0-2 | 137.7 | 3.82 | 7.08 | 0.914 | 1.923 |
| TPB-0.0-3 | 133.8 | 3.56 | 6.58 | 0.852 | 1.787 |
| Average | 135.7 | 3.69 | 6.66 | 0.883 | 1.808 |
| TPB-0.1-1 | 141.5 | 2.58 | 4.96 | 0.854 | 1.601 |
| TPB-0.1-2 | 132.7 | 2.83 | 5.53 | 0.922 | 1.756 |
| TPB-0.1-3 | 136.8 | 2.76 | 5.16 | 0.903 | 1.657 |
| Average | 137.0 | 2.72 | 5.22 | 0.893 | 1.671 |
| TPB-0.2-1 | 134.2 | 2.01 | 4.44 | 0.939 | 1.715 |
| TPB-0.2-2 | 130.5 | 2.12 | 4.56 | 0.974 | 1.742 |
| TPB-0.2-3 | 141.3 | 1.82 | 4.13 | 0.878 | 1.623 |
| Average | 135.3 | 1.98 | 4.38 | 0.93 | 1.693 |
| TPB-0.3-1 | 132.3 | 1.42 | 2.12 | 0.789 | 1.385 |
| TPB-0.3-2 | 130.9 | 1.31 | 2.81 | 0.757 | 1.575 |
| TPB-0.3-3 | 132.2 | 1.15 | 2.53 | 0.745 | 1.502 |
| Average | 131.8 | 1.29 | 2.49 | 0.764 | 1.487 |
| Number | σw0 (MPa) | Hydraulic Pressure Curve | Softening Stress Curve | |||||
|---|---|---|---|---|---|---|---|---|
| A | B | CODw (μm) | (MPa) | (MPa) | (μm) | (μm) | ||
| TPB-0.1-1 | 0.1 | −1.21 | 2.07 | 81 | 3.12 | 1.04 | 32.45 | 146.03 |
| TPB-0.1-2 | −0.76 | 1.84 | 76 | 3.12 | 1.04 | 32.01 | 144.05 | |
| TPB-0.1-3 | −0.94 | 1.98 | 104 | 3.12 | 1.04 | 31.42 | 141.39 | |
| Average | −0.97 | 1.96 | 87 | 3.12 | 1.04 | 31.96 | 143.82 | |
| TPB-0.2-1 | 0.2 | −1.53 | 2.55 | 60 | 3.12 | 1.04 | 28.49 | 128.21 |
| TPB-0.2-2 | −1.21 | 2.23 | 76 | 3.12 | 1.04 | 28.67 | 129.02 | |
| TPB-0.2-3 | −0.82 | 1.91 | 67 | 3.12 | 1.04 | 28.55 | 128.48 | |
| Average | −1.18 | 2.23 | 68 | 3.12 | 1.04 | 28.57 | 128.57 | |
| TPB-0.3-1 | 0.3 | −0.94 | 2.01 | 51 | 3.12 | 1.04 | 27.99 | 125.96 |
| TPB-0.3-2 | −1.55 | 2.56 | 57 | 3.12 | 1.04 | 28.01 | 126.05 | |
| TPB-0.3-3 | −1.13 | 2.15 | 60 | 3.12 | 1.04 | 27.49 | 123.71 | |
| Average | −1.21 | 2.24 | 56 | 3.12 | 1.04 | 27.83 | 125.24 | |
| Number | ac (mm) | Pini (kN) | Pmax (kN) | Fracture Toughness (MPa·m1/2) | ||
|---|---|---|---|---|---|---|
| TPB0.2-1-0.0 | 114.5 | 5.13 | 8.78 | 0.932 | 1.878 | 0.946 |
| TPB0.2-2-0.0 | 112.7 | 5.08 | 9.41 | 0.917 | 2.042 | 1.135 |
| TPB0.2-3-0.0 | 116.2 | 4.91 | 9.07 | 0.891 | 1.891 | 1.000 |
| Average | 114.5 | 5.03 | 9.08 | 0.913 | 1.937 | 1.038 |
| TPB0.3-1-0.0 | 121.2 | 4.89 | 8.37 | 0.953 | 1.995 | 1.042 |
| TPB0.3-2-0.0 | 120.8 | 4.67 | 8.65 | 0.911 | 1.983 | 1.072 |
| TPB0.3-3-0.0 | 122.5 | 4.28 | 7.91 | 0.945 | 1.942 | 1.007 |
| Average | 121.2 | 4.61 | 8.31 | 0.933 | 1.973 | 1.042 |
| TPB0.4-1-0.0 | 135.7 | 3.69 | 6.31 | 0.883 | 1.714 | 0.831 |
| TPB0.4-2-0.0 | 137.7 | 3.82 | 7.08 | 0.914 | 1.923 | 1.009 |
| TPB0.4-3-0.0 | 133.8 | 3.56 | 6.58 | 0.852 | 1.787 | 0.935 |
| Average | 135.7 | 3.69 | 6.66 | 0.883 | 1.808 | 0.925 |
| TPB0.5-1-0.0 | 146.5 | 3.13 | 5.36 | 0.914 | 1.792 | 0.888 |
| TPB0.5-2-0.0 | 148.1 | 3.34 | 6.19 | 0.909 | 1.982 | 1.073 |
| TPB0.5-3-0.0 | 145.1 | 3.28 | 6.07 | 0.871 | 1.841 | 0.970 |
| Average | 146.5 | 3.25 | 5.87 | 0.891 | 1.874 | 0.983 |
| TPB0.2-1-0.3 | 111.5 | 4.23 | 5.91 | 0.807 | 1.554 | 0.747 |
| TPB0.2-2-0.3 | 113.3 | 3.86 | 5.39 | 0.755 | 1.512 | 0.757 |
| TPB0.2-3-0.3 | 112.7 | 3.98 | 5.58 | 0.785 | 1.593 | 0.808 |
| Average | 112.5 | 4.02 | 5.62 | 0.781 | 1.554 | 0.773 |
| TPB0.3-1-0.3 | 128.9 | 2.38 | 3.32 | 0.801 | 1.444 | 0.643 |
| TPB0.3-2-0.3 | 120.3 | 2.13 | 2.97 | 0.736 | 1.556 | 0.820 |
| TPB0.3-3-0.3 | 120.8 | 2.32 | 3.24 | 0.728 | 1.525 | 0.797 |
| Average | 123.7 | 2.27 | 3.18 | 0.759 | 1.520 | 0.761 |
| TPB0.4-1-0.3 | 132.3 | 1.42 | 2.12 | 0.789 | 1.385 | 0.596 |
| TPB0.4-2-0.3 | 130.9 | 1.31 | 2.81 | 0.757 | 1.575 | 0.818 |
| TPB0.4-3-0.3 | 132.2 | 1.15 | 2.53 | 0.745 | 1.502 | 0.757 |
| Average | 131.8 | 1.29 | 2.49 | 0.764 | 1.487 | 0.723 |
| TPB0.5-1-0.3 | 143.9 | 1.088 | 1.52 | 0.792 | 1.516 | 0.724 |
| TPB0.5-2-0.3 | 142.7 | 0.895 | 1.25 | 0.736 | 1.529 | 0.793 |
| TPB0.5-3-0.3 | 143.9 | 0.988 | 1.38 | 0.801 | 1.508 | 0.707 |
| Average | 143.6 | 0.988 | 1.38 | 0.773 | 1.518 | 0.745 |
| Number | ac (mm) | Pini (kN) | Pmax (kN) | Fracture Toughness (MPa·m1/2) | ||
|---|---|---|---|---|---|---|
| TPB-0.0-X | Experiment | 135.7 | 3.69 | 6.66 | 0.883 | 1.808 |
| Calculation | 135.9 | 3.62 | 7.36 | 0.831 | 1.925 | |
| Error | 0.1% | 1.9% | 9.5% | 6.25% | 6.1% | |
| TPB-0.1-X | Experiment | 137.0 | 2.72 | 5.22 | 0.893 | 1.671 |
| Calculation | 138.5 | 2.61 | 5.63 | 0.832 | 1.754 | |
| Error | 1.1% | 4.2% | 7.3% | 7.3% | 4.7% | |
| TPB-0.2-X | Experiment | 135.3 | 1.98 | 4.38 | 0.93 | 1.693 |
| Calculation | 135.0 | 1.82 | 4.37 | 0.88 | 1.689 | |
| Error | 0.2% | 8.8% | 0.2% | 5.7% | 0.2% | |
| TPB-0.3-X | Experiment | 131.8 | 1.29 | 2.09 | 0.764 | 1.487 |
| Calculation | 130.9 | 1.22 | 2.10 | 0.732 | 1.443 | |
| Error | 0.7% | 5.7% | 0.5% | 4.4% | 3.0% | |
| TPB0.2-X-0.0 | Experiment | 114.5 | 5.03 | 9.08 | 0.913 | 1.937 |
| Calculation | 114.0 | 5.00 | 9.10 | 0.909 | 1.989 | |
| Error | 0.4% | 0.6% | 0.2% | 0.4% | 2.6% | |
| TPB0.3-X-0.0 | Experiment | 121.2 | 4.61 | 8.31 | 0.933 | 1.973 |
| Calculation | 120.8 | 4.58 | 8.46 | 0.920 | 1.987 | |
| Error | 0.3% | 0.6% | 1.8% | 1.4% | 0.7% | |
| TPB0.4-X-0.0 | Experiment | 135.7 | 3.69 | 7.06 | 0.883 | 1.808 |
| Calculation | 134.2 | 3.63 | 7.53 | 0.868 | 1.897 | |
| Error | 1.1% | 1.7% | 6.2% | 1.7% | 4.7% | |
| TPB0.5-X-0.0 | Experiment | 146.5 | 3.25 | 5.87 | 0.891 | 1.874 |
| Calculation | 140.9 | 3.28 | 5.99 | 0.887 | 1.901 | |
| Error | 4.0% | 0.9% | 2.0% | 0.5% | 1.4% | |
| TPB0.2-X-0.3 | Experiment | 112.5 | 4.02 | 5.62 | 0.781 | 1.554 |
| Calculation | 112.7 | 3.98 | 5.68 | 0.780 | 1.567 | |
| Error | 0.2% | 1.0% | 1.1% | 0.1% | 0.8% | |
| TPB0.3-X-0.3 | Experiment | 123.7 | 2.27 | 3.18 | 0.759 | 1.520 |
| Calculation | 124.0 | 2.20 | 3.21 | 0.750 | 1.531 | |
| Error | 0.2% | 3.2% | 0.9% | 1.2% | 0.7% | |
| TPB0.4-X-0.3 | Experiment | 131.8 | 1.29 | 2.49 | 0.764 | 1.487 |
| Calculation | 130.9 | 1.27 | 2.58 | 0.759 | 1.499 | |
| Error | 0.7% | 1.6% | 3.5% | 0.7% | 0.8% | |
| TPB0.5-X-0.3 | Experiment | 143.6 | 0.988 | 1.38 | 0.773 | 1.518 |
| Calculation | 142.8 | 0.972 | 1.45 | 0.780 | 1.529 | |
| Error | 0.6% | 1.6% | 4.8% | 0.9% | 0.7% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Sun, J.; Wang, G.; Li, Y.; Xiong, W. Resistance Analysis of Crack Propagation in Concrete Subjected to Hydraulic Pressure. Materials 2024, 17, 3243. https://doi.org/10.3390/ma17133243
Wang Y, Sun J, Wang G, Li Y, Xiong W. Resistance Analysis of Crack Propagation in Concrete Subjected to Hydraulic Pressure. Materials. 2024; 17(13):3243. https://doi.org/10.3390/ma17133243
Chicago/Turabian StyleWang, Yang, Jingshan Sun, Gaohui Wang, Yongzhen Li, and Weiqi Xiong. 2024. "Resistance Analysis of Crack Propagation in Concrete Subjected to Hydraulic Pressure" Materials 17, no. 13: 3243. https://doi.org/10.3390/ma17133243
APA StyleWang, Y., Sun, J., Wang, G., Li, Y., & Xiong, W. (2024). Resistance Analysis of Crack Propagation in Concrete Subjected to Hydraulic Pressure. Materials, 17(13), 3243. https://doi.org/10.3390/ma17133243






