Optimization Design and Performance Study of Wearable Thermoelectric Device Using Phase Change Material as Heat Sink
Abstract
:1. Introduction
2. Structural Description and Material Properties
2.1. TED (Thermoelectric Devices) Structure of a Compact PCM Heat Sink
2.2. Properties of Materials
3. Methods
3.1. Heat Transfer between Solids and Fluids
3.2. Thermal Resistance Model and Formula
3.3. Electric Current
3.4. Thermal and Electrical Coupling Modules
3.5. Boundary Condition
- (a)
- Steady-state operation is assumed;
- (b)
- Thin encapsulation materials surrounding the thermoelectric generator are neglected;
- (c)
- Heat flux exists only at the boundary of the encapsulation materials, with heat conduction occurring only along the height direction of the thermoelectric leg. The lateral surfaces of the thermoelectric leg are insulated;
- (d)
- Extremely weak thermal radiation and thermal resistance between different materials are ignored;
- (e)
- It is assumed that all materials exhibit isotropic and constant thermal characteristics.
3.6. Model Verification
4. Results and Discussion
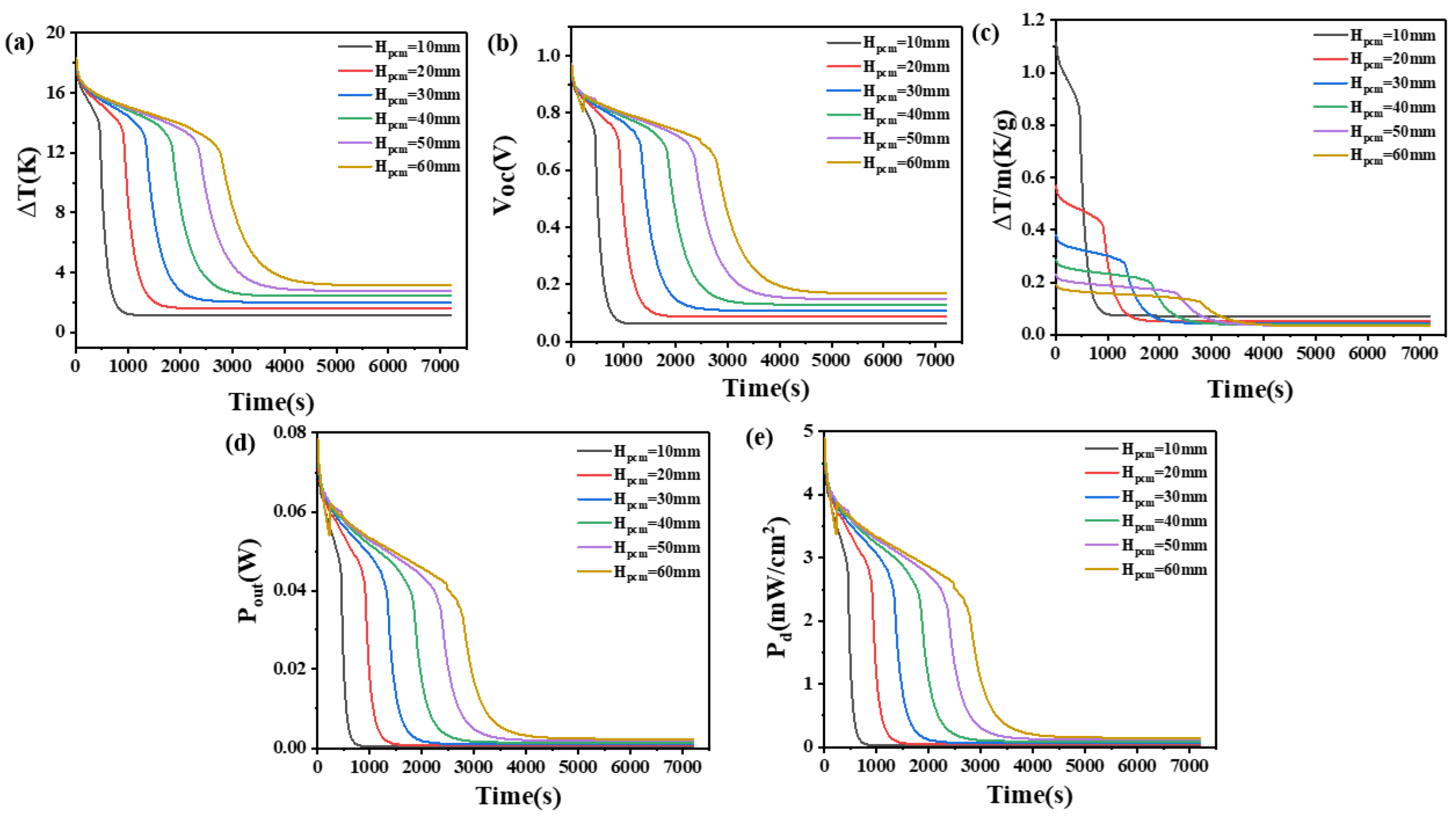
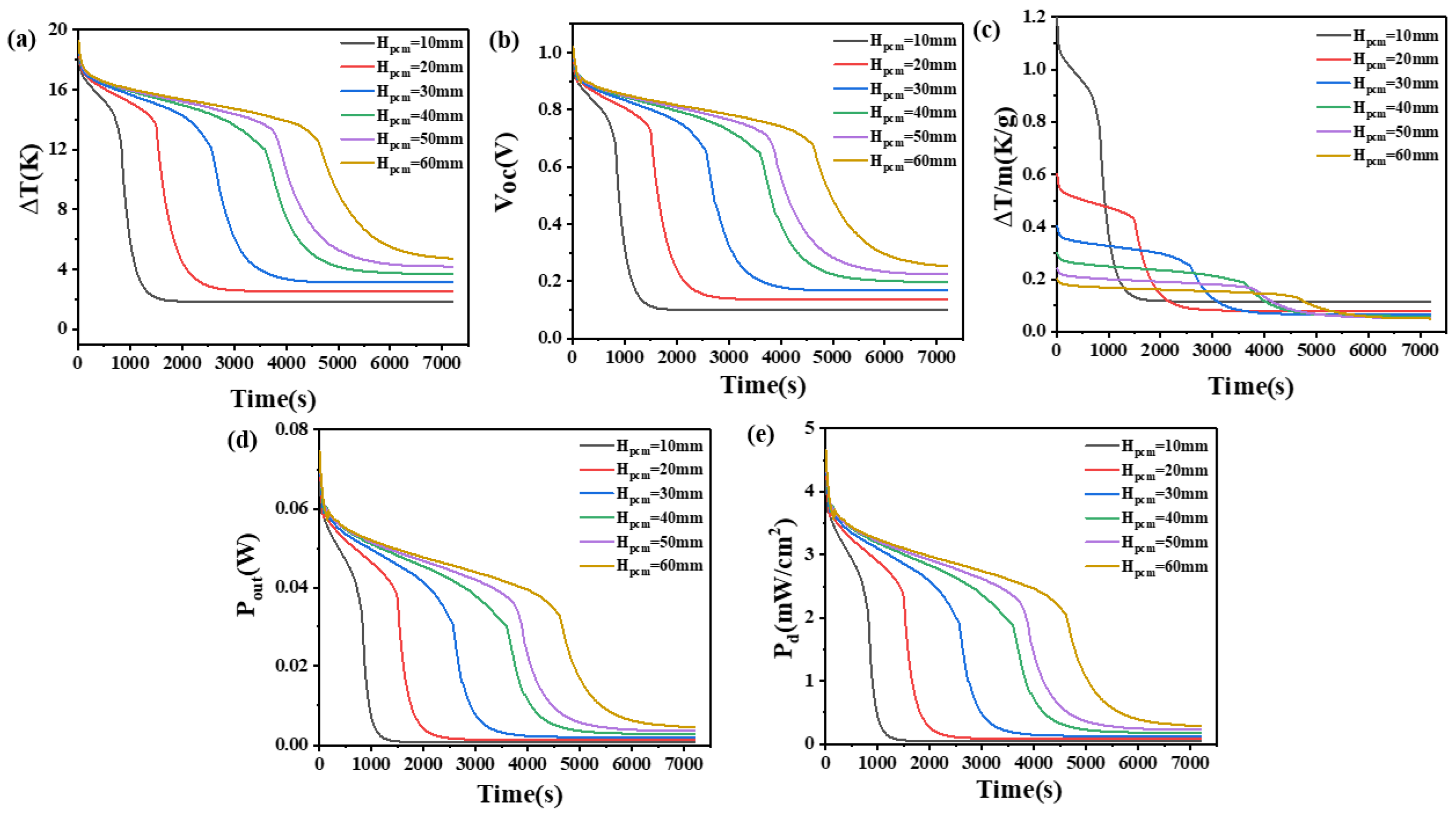
4.1. The Effect of the Quantity of Phase Change Materials
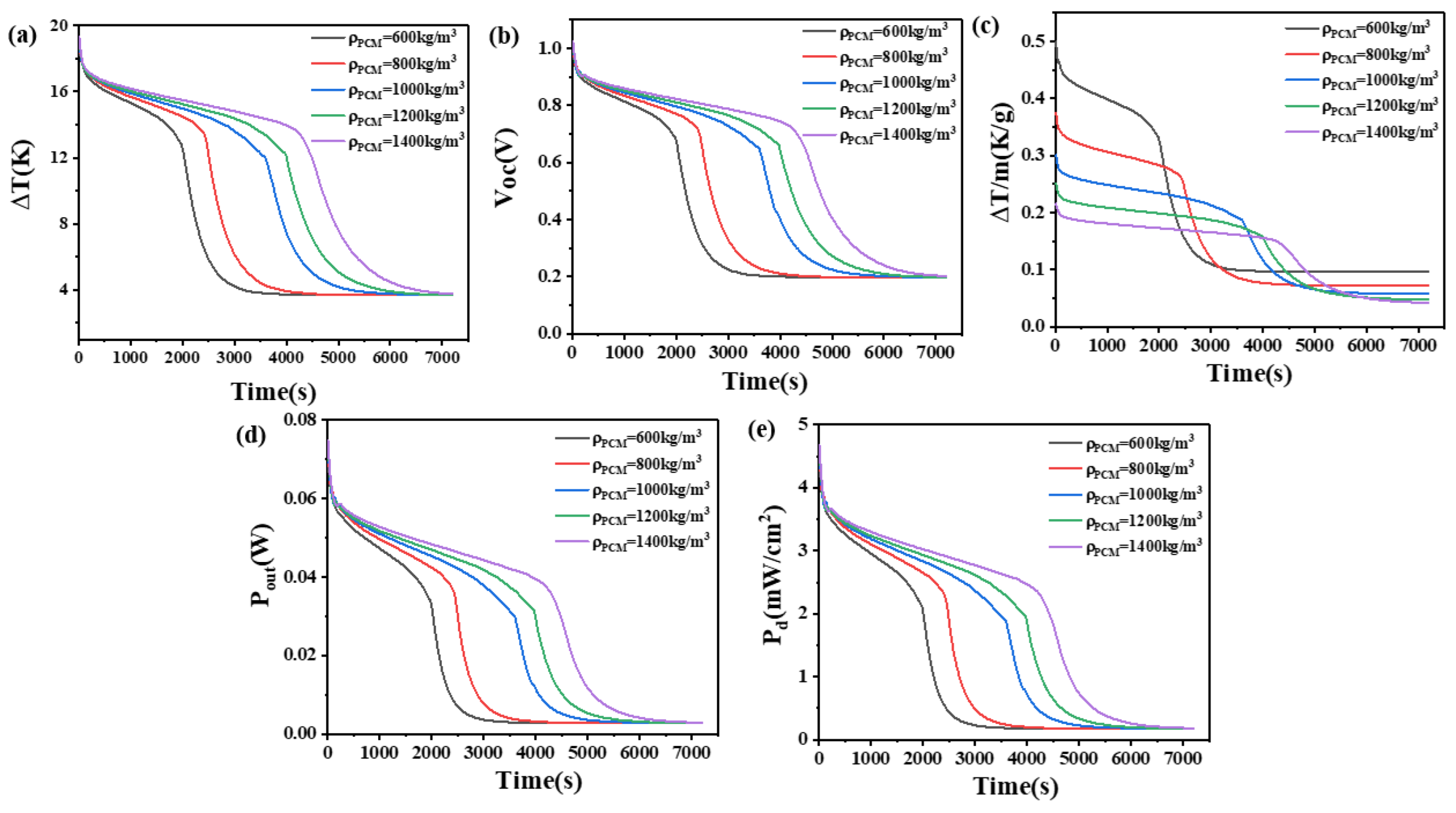
4.2. The Effect of Density of Phase Change Materials
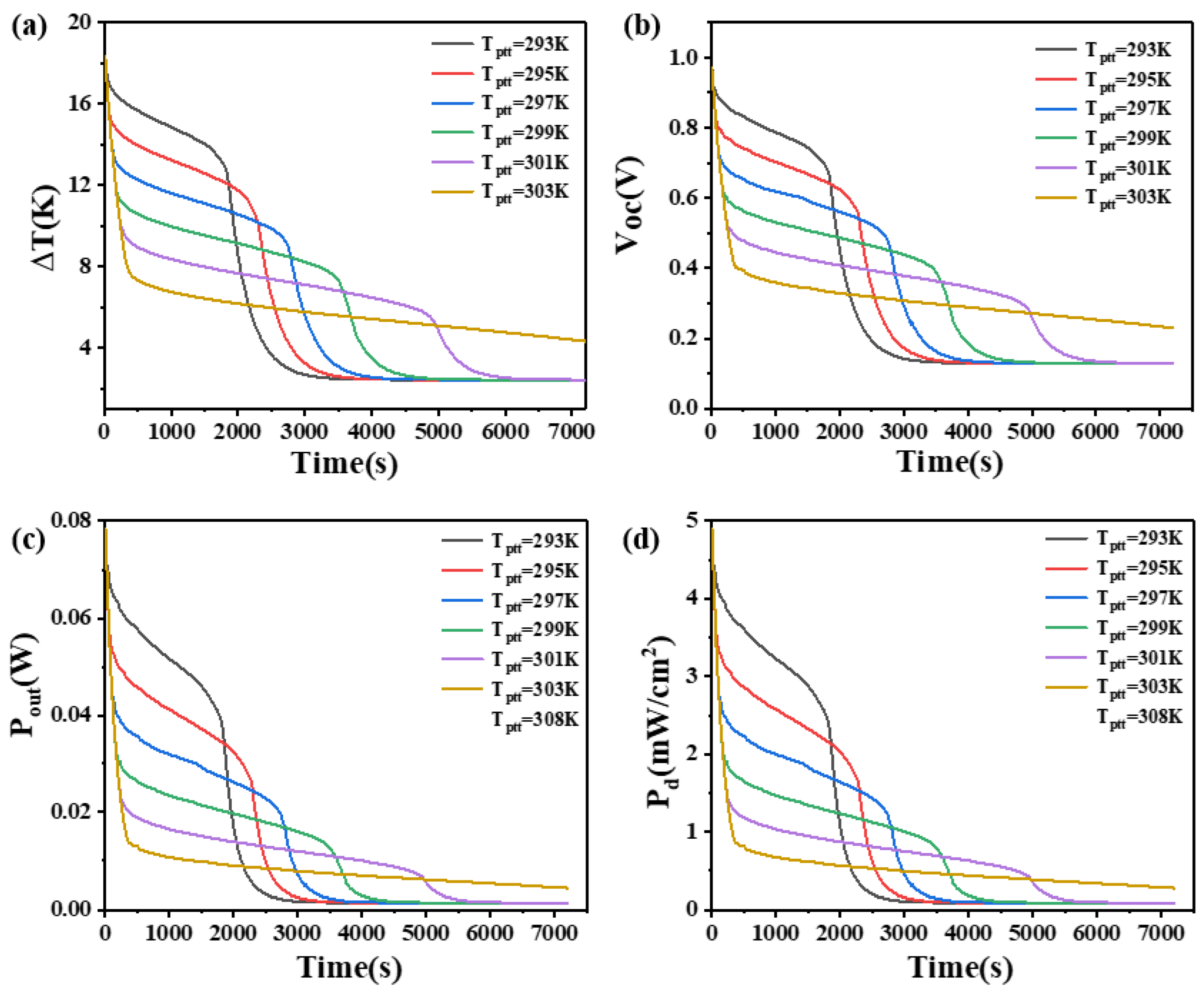
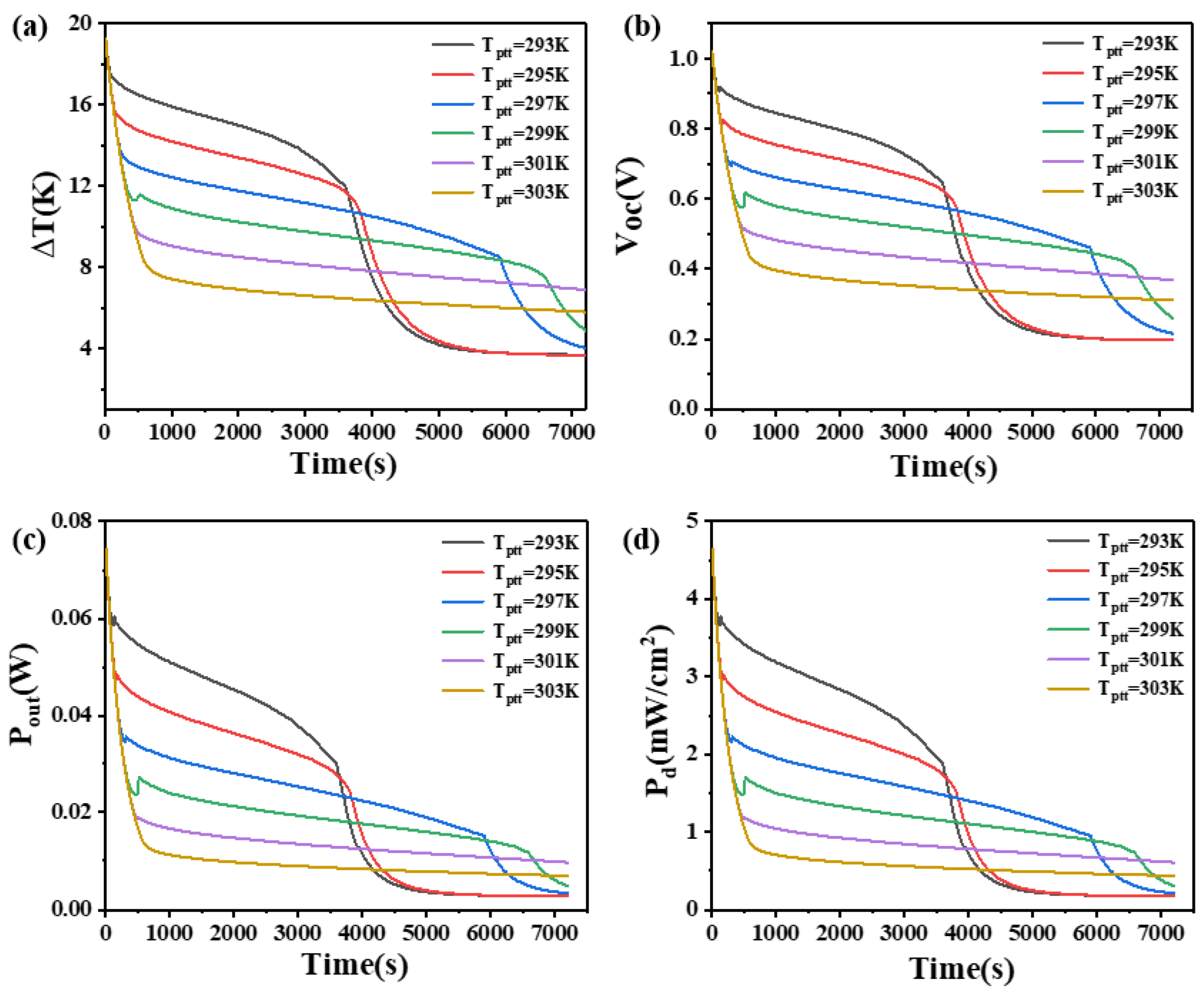
4.3. The Effect of Phase Transition Temperature on Phase Change Materials
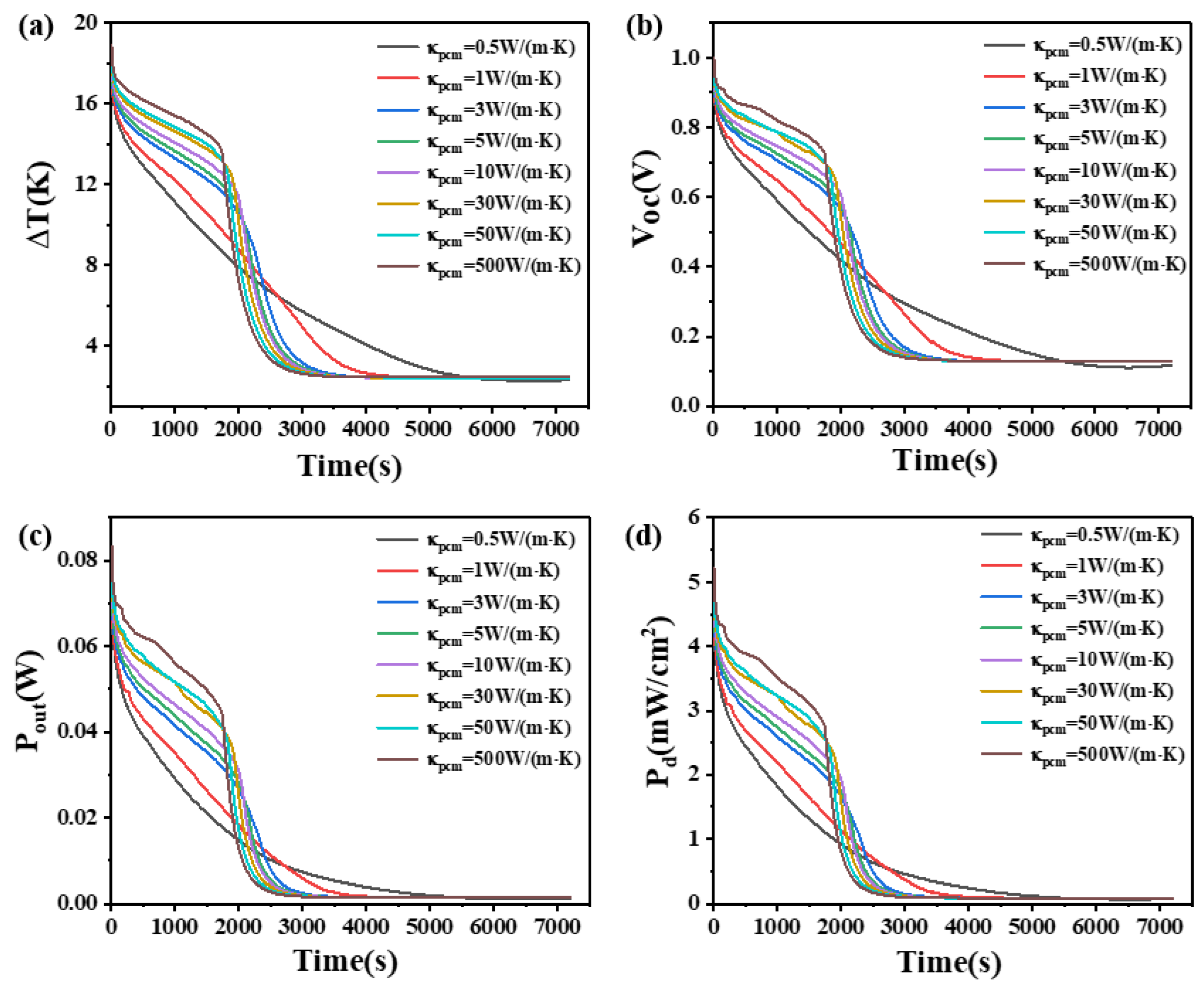
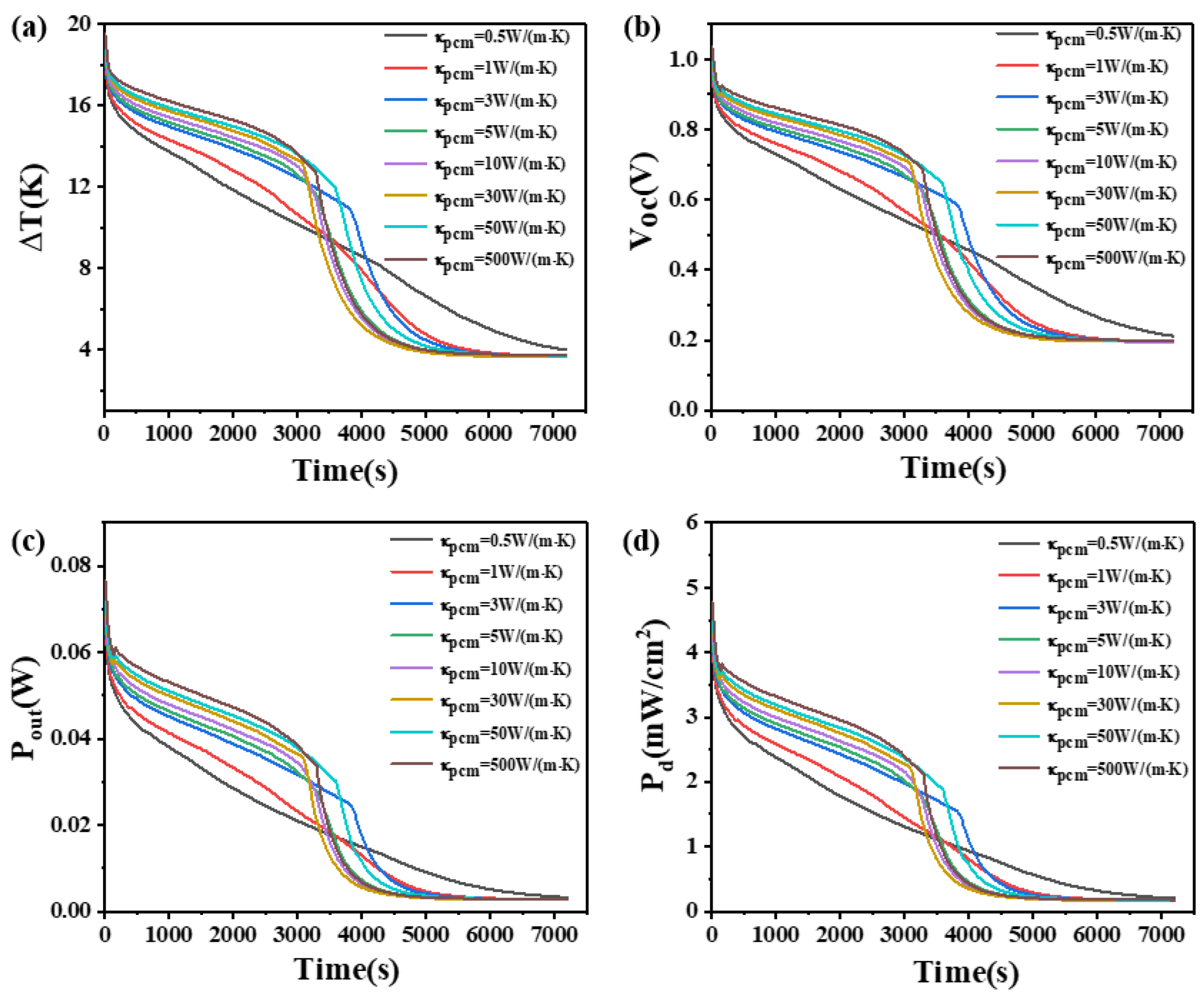
4.4. The Effect of Thermal Conductivity of Phase Change Materials
4.5. The Effect of Phase Transition Temperature Interval of Phase Change Materials
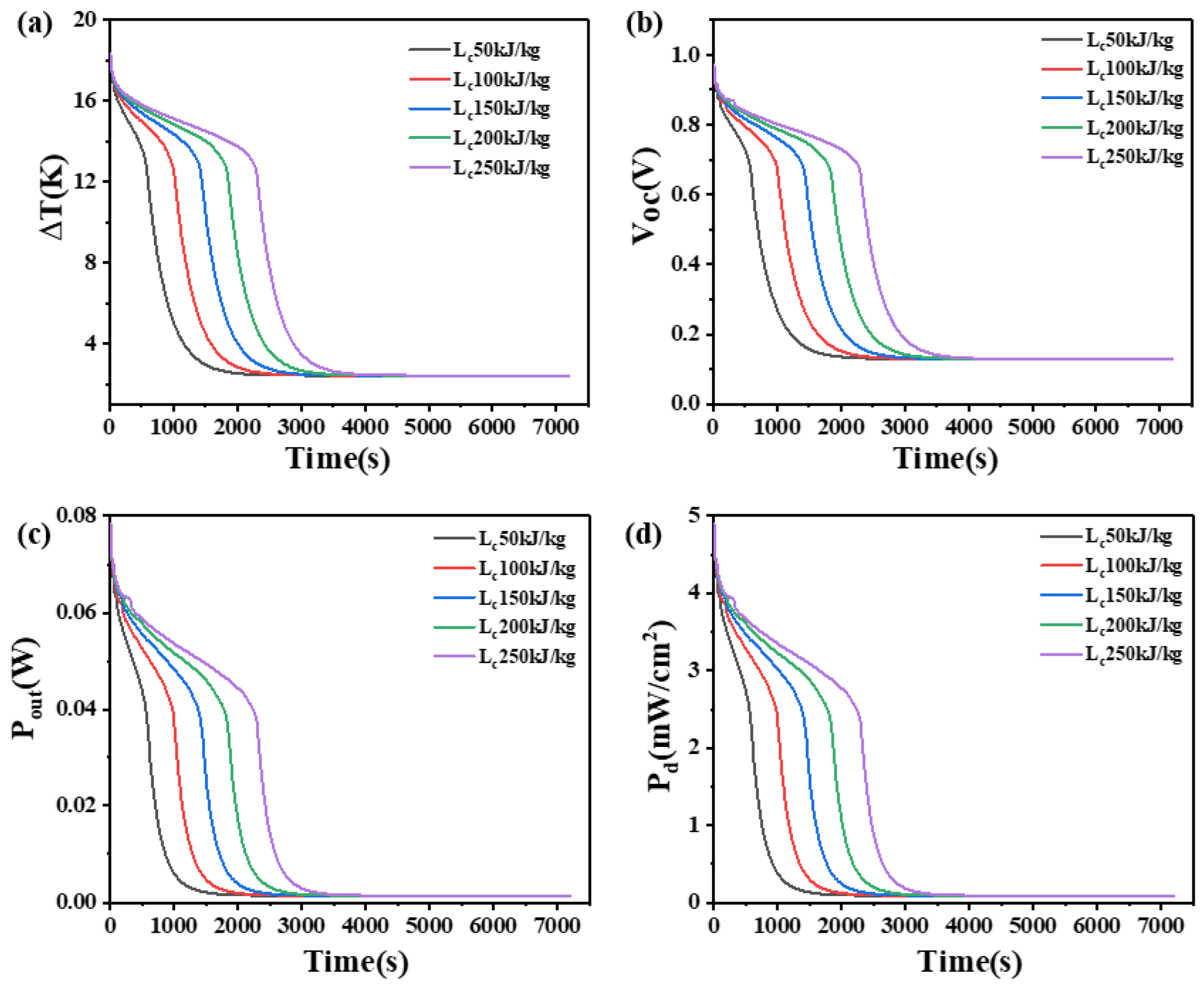
4.6. The Effect of Latent Heat on Phase Change Materials
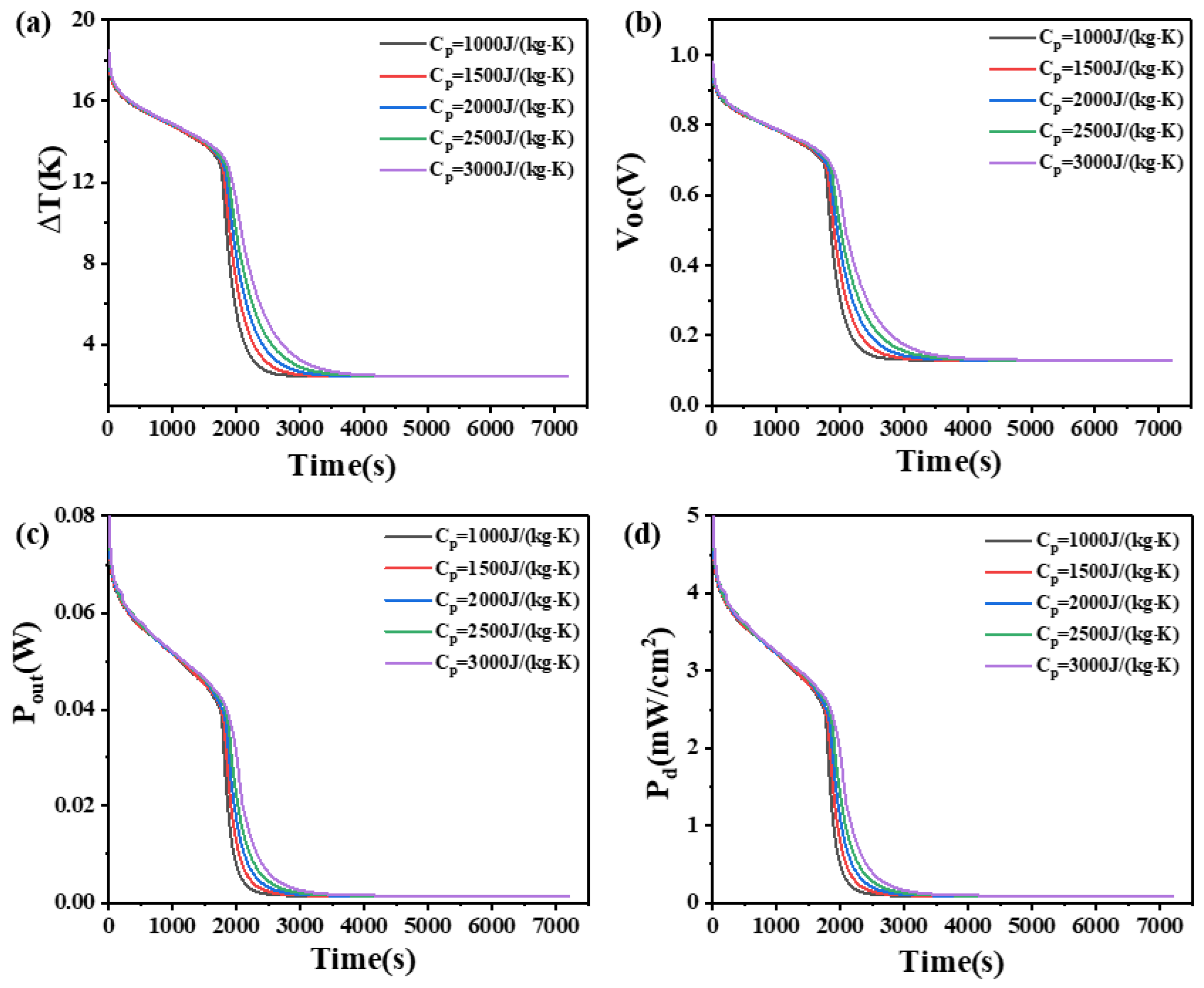
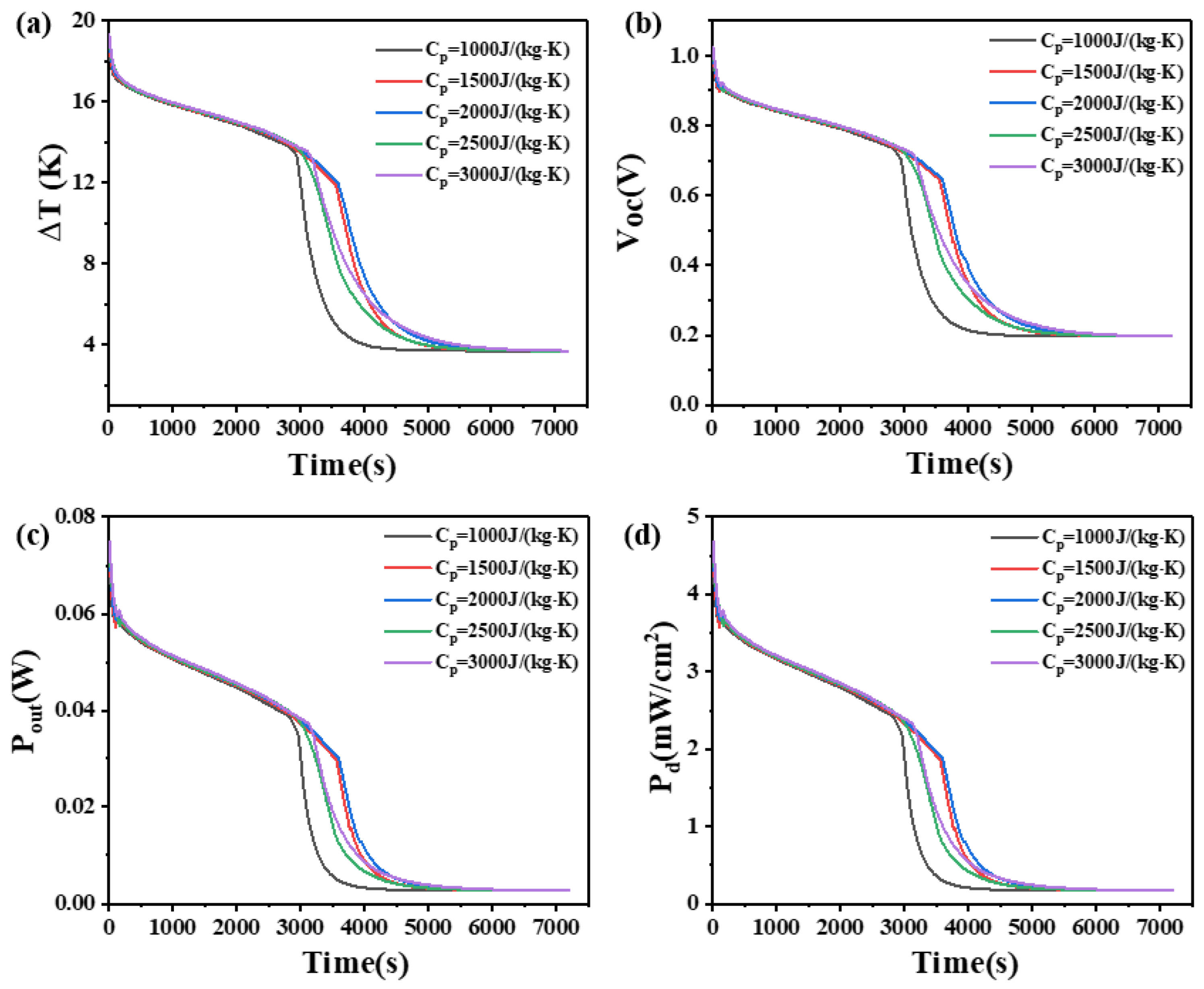
4.7. The Effect of Isobaric Heat Capacity on Phase Change Materials
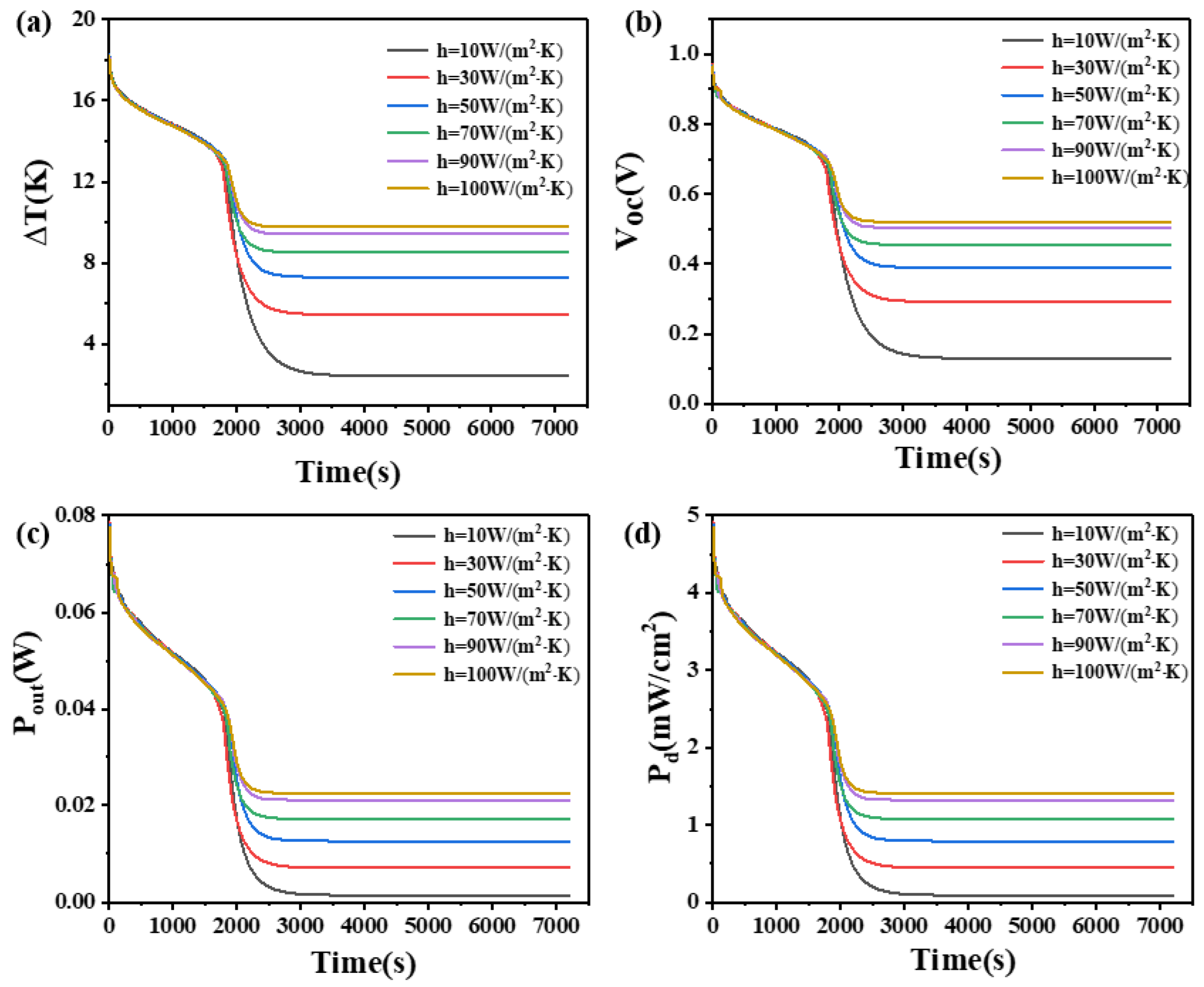
4.8. The Effect of Convective Heat Transfer Coefficient
5. Conclusions
- (1)
- The more the quantity of phase change materials, the greater the density, the greater the latent heat, the greater the height of the thermoelectric leg, and the greater the convective heat transfer coefficient, the better the performance of the heat sink. The height of the thermoelectric leg should be given priority in the selection.
- (2)
- The phase change temperature of the PCMs determines the maximum temperature difference that can be maintained. PCMs with lower phase transition temperatures can maintain higher temperature differences in a short period, while those with higher phase transition temperatures can maintain a relatively stable temperature difference over a longer period. However, different heights of the thermoelectric leg require different phase transition temperatures. Alternatively, employing multiple PCMs can optimize their combined performance.
- (3)
- The influence of thermal conductivity on PCMs resembles that of the phase transition temperature.
- (4)
- When the height of the thermoelectric leg is 1.6 mm, the greater the isobaric heat capacity of the phase change material used, the better the output performance of the device. When the height of the thermoelectric leg is 2.7 mm, the isobaric heat capacity of the phase change material used is 2000 J/(kg·K), the better the output performance of the device.
- (5)
- When the thermoelectric leg height is 1.6 mm, a PCM with a phase transition temperature interval of 9 K maintains the largest temperature difference, along with the greatest average temperature difference over the entire duration. However, when the thermoelectric leg height is 2.7 mm, a PCM with a phase transition temperature interval of 1 K should be selected because it can maintain a temperature difference of at least 13 K for the first 4700 s.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | boundary area, m2 |
| αab | the Seebeck coefficient difference between the two materials, V/K |
| Cp | heat capacity at constant pressure, J/(kg·K) |
| h | convective heat transfer coefficient, W/(m2·K) |
| H | height, m |
| kc | thermal conductivity of composite phase change materials, W/(m·K) |
| kg | thermal conductivity of graphene, W/(m·K) |
| L | length, m |
| Lc | latent heat of composite phase change material, J/kg |
| Lpcm | latent heat of phase change material, J/kg |
| latent heat, J/kg | |
| n | unit vector |
| Pb | heat rate, W |
| Pd | theoretical output power density, W/m2 |
| Pout | theoretical output power, W |
| Q | heat source, W/m3 |
| q | heat flux density, W/m2 |
| Qb | heat rate per unit area, W |
| Qc | heat of the cold end of the thermoelectric generator, W |
| Qh | heat of the hot end of the thermoelectric generator, W |
| q0 | the heat flux density in a certain direction, W/m2 |
| Re | the internal resistance of thermoelectric generator, Ω |
| RL | load resistance, Ω |
| t | time, s |
| T | temperature, K |
| Tc | cold end temperature, K |
| Th | hot end temperature, K |
| V | voltage, V |
| Vg | the volume fraction of graphene |
| w | the mass fraction of graphene |
| W | width, m |
| ΔT | temperature difference, K |
| ΔV | seebeck voltage, V/K |
| Greek symbols | |
| α | electrical conductivity, S/m |
| η | efficiency |
| κ | thermal conductivity, W/m/K |
| density, kg/m3 | |
| μ | velocity field, m/s |
| θ | content of a certain phase |
| Abbreviations | |
| Bi2Te3 | bismuth telluride |
| EG | expanded graphite |
| PCM | phase change material |
| TEG | thermoelectric generator |
| TED | thermoelectric device |
| TL | thermoelectric leg |
| Subscripts | |
| ext | exterior |
| oc | open circuit |
| pti | phase transition temperature interval |
| ptt | phase transition temperature |
| ted | thermoelastic damping |
References
- Ko, J.; Cheon, S.-Y.; Kang, Y.-K.; Jeong, J.-W. Design of a thermoelectric generator-assisted energy harvesting block considering melting temperature of phase change materials. Renew. Energy 2022, 193, 89–112. [Google Scholar] [CrossRef]
- Ebling, D.; Jaegle, M.; Bartel, M.; Jacquot, A.; Böttner, H. Multiphysics Simulation of Thermoelectric Systems for Comparison with Experimental Device Performance. J. Electron. Mater. 2009, 38, 1456–1461. [Google Scholar] [CrossRef]
- Byon, Y.; Jeong, J. Phase change material-integrated thermoelectric energy harvesting block as an independent power source for sensors in buildings. Renew. Sustain. Energy Rev. 2020, 128, 109921. [Google Scholar] [CrossRef]
- El-Adl, A.S.; Mousa, M.G.; Hegazi, A.A. Performance analysis of a passively cooled thermoelectric generator. Energy Convers. Manag. 2018, 173, 399–411. [Google Scholar] [CrossRef]
- Ming, T.; Yang, W.; Huang, X.; Wu, Y.; Li, X.; Liu, J. Analytical and numerical investigation on a new compact thermoelectric generator. Energy Convers. Manag. 2017, 132, 261–271. [Google Scholar] [CrossRef]
- Mohammadi, A.; Jianu, O.A. Novel thermoelectric generator heat exchanger for indirect heat recovery from molten CuCl in the thermochemical Cu–Cl cycle of hydrogen production. Int. J. Hydrogen Energy 2023, 48, 5001–5017. [Google Scholar] [CrossRef]
- Ruan, H.; Xie, H.; Wang, J.; Liao, J.; Sun, L.; Gao, M.; Li, C. Numerical investigation and comparative analysis of nanofluid cooling enhancement for TEG and TEC systems. Case Stud. Therm. Eng. 2021, 27, 101331. [Google Scholar] [CrossRef]
- Chen, X.; Gao, H.; Tang, Z.; Dong, W.; Li, A.; Wang, G. Optimization strategies of composite phase change materials for thermal energy storage, transfer, conversion and utilization. Energy Environ. Sci. 2020, 13, 4498–4535. [Google Scholar] [CrossRef]
- Gulfam, R.; Zhang, P.; Meng, Z. Advanced thermal systems driven by paraffin-based phase changematerials—A review. Appl. Energy 2019, 238, 582–611. [Google Scholar] [CrossRef]
- Liu, A.; Zou, J.; Wu, Z.; Wang, Y.; Tian, Y.; Xie, H. Enhancing the performance of TEG system coupled with PCMs by regulating the interfacial thermal conduction. Energy Rep. 2020, 6, 1942–1949. [Google Scholar] [CrossRef]
- Shaikh, S.; Lafdi, K. Effect of multiple phase change materials (PCMs) slab configurations on thermal energy storage. Energy Convers. Manag. 2006, 47, 2103–2117. [Google Scholar] [CrossRef]
- Lee, G.; Kim, C.S.; Kim, S.; Kim, Y.J.; Choi, H.; Cho, B.J. Flexible Heatsink Based on a Phase-change Material for a Wearable Thermoelectric Generator. Energy 2019, 179, 12–18. [Google Scholar] [CrossRef]
- Jame, L.; Kumar, J.R.; Perumal, S.; Jeyashree; Moorthy, M. Experimental Investigation of Thermoelectric Power Generator Using D-Mannitol Phase Change Material for Transient Heat Recovery. ECS J. Solid State Sci. Technol. 2021, 10, 61005. [Google Scholar] [CrossRef]
- Jaworski, M.; Bednarczyk, M.; Czachor, M. Experimental investigation of thermoelectric generator (TEG) with PCM module. Appl. Therm. Eng. 2016, 96, 527–533. [Google Scholar] [CrossRef]
- Tuoi, T.T.K.; Toan, N.V.; Ono, T. Theoretical and experimental investigation of a thermoelectric generator (TEG) integrated with a phase change material (PCM) for harvesting energy from ambient temperature changes. Energy Rep. 2020, 6, 2022–2029. [Google Scholar] [CrossRef]
- Ahmadi Atouei, S.; Ranjbar, A.A.; Rezania, A. Experimental Investigation of Two-stage Thermoelectric Generator System Integrated with Phase Change Materials. Appl. Energy 2017, 208, 332–343. [Google Scholar] [CrossRef]
- Atouei, S.A.; Rezania, A.; Ranjbar, A.A.; Rosendahl, L. Protection and thermal management of thermoelectric generator system using phase change materials: An experimental investigation. Energy 2018, 156, 311–318. [Google Scholar] [CrossRef]
- Meng, J.; Gao, D.; Liu, Y.; Zhang, K.; Lu, G. Heat transfer mechanism and structure design of phase change materials to improve thermoelectric device performance. Energy 2022, 245, 123332. [Google Scholar] [CrossRef]
- Hassan, F.; Jamil, F.; Hussain, A.; Ali, H.M.; Janjua, M.M.; Khushnood, S.; Farhan, M.; Altaf, K.; Said, Z.; Li, C. Recent advancements in latent heat phase change materials and their applications for thermal energy storage and buildings: A state of the art review. Sustain. Energy Technol. Assess. 2022, 49, 101646. [Google Scholar] [CrossRef]
- He, D.; Ou, D.; Gao, H.; Jiao, F. Performance evaluation of a thermoelectric generator-coupled composite phase change material for intermittent aerodynamic heat sources. Int. J. Energy Res. 2022, 46, 2698–2708. [Google Scholar] [CrossRef]
- Borhani, S.M.; Hosseini, M.J.; Pakrouh, R.; Ranjbar, A.; Nourian, A. Performance enhancement of a thermoelectric harvester with a PCM/Metal foam composite. Renew. Energy 2021, 168, 1122–1140. [Google Scholar] [CrossRef]
- Selvam, C.; Manikandan, S.; Krishna, N.V.; Lamba, R.; Kaushik, S.; Mahian, O. Enhanced thermal performance of a thermoelectric generator with phase change materials. Int. Commun. Heat Mass Transf. 2020, 114, 104561. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Li, W. Design and test of phase change radiator for thermoelectric power generation device. For. Eng. 2020, 36, 85–91. [Google Scholar]
- Liu, Y.; Shi, Y.; Li, J.; Guo, X.; Wang, Y.; Xiang, Q.; Guo, S.; Ze, R.; Zeng, J.; Xiang, Y.; et al. Comprehensive performance prediction and power promotion for wearable thermoelectric generator with flexible encapsulation in practical application. Energy Convers. Manag. 2020, 220, 113080. [Google Scholar] [CrossRef]
- Chen, K. Research on a New Type of Human Cooling Suit Based on Thermoelectric Refrigeration; Shandong University: Jinan, China, 2020. [Google Scholar]
- Zhou, W. Performance Evaluation and Comfortable Inlet Water Temperature Prediction Model of Temperature-Adjustable Whole-Body Water-Cooled Clothing; Jiangnan University: Wuxi, China, 2022. [Google Scholar]
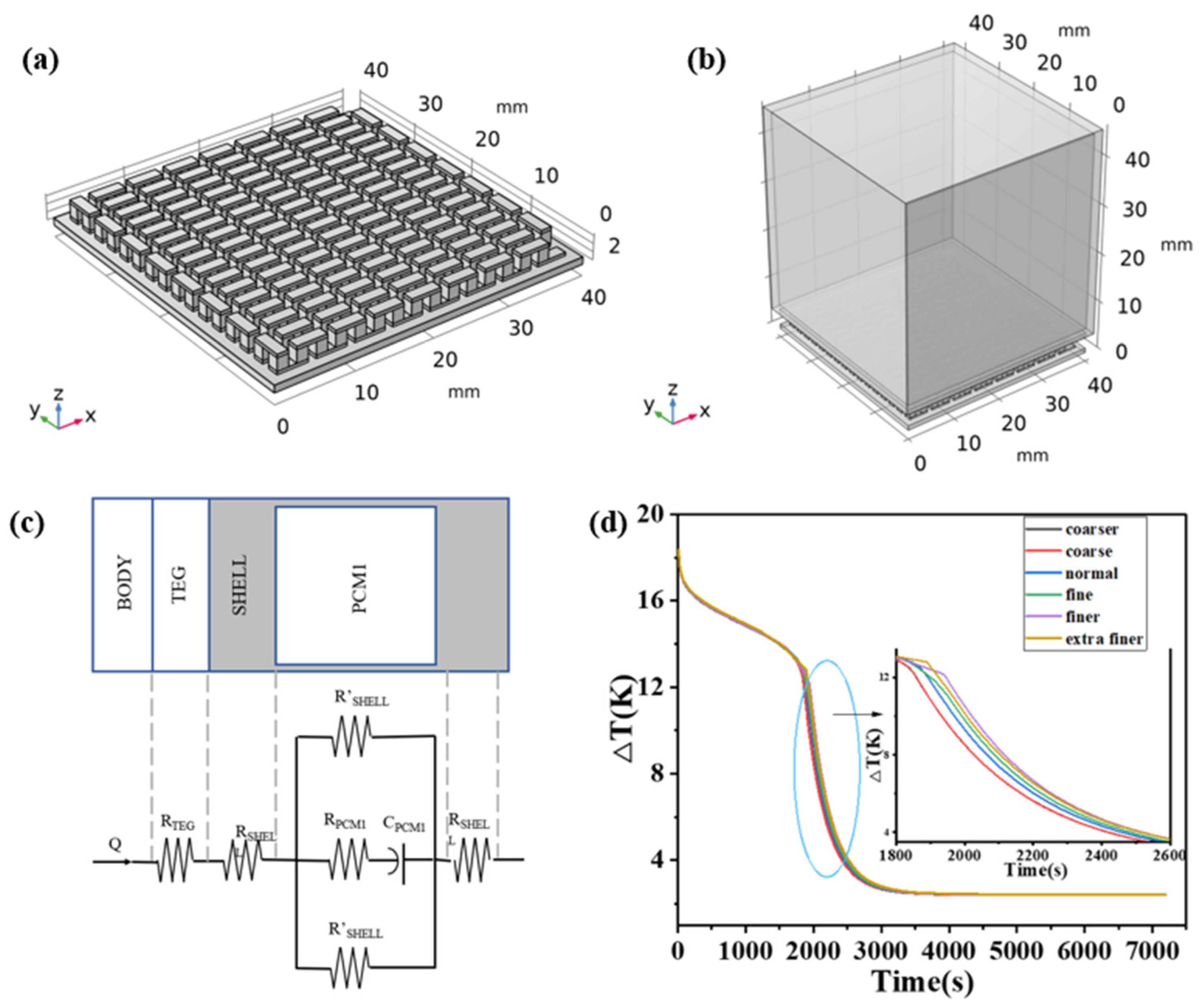






| Material | Length [mm] | Width [mm] | Height [mm] |
|---|---|---|---|
| Alumina | 40 | 40 | 0.9 |
| Thermoelectric legs | 1.4 | 1.4 | 1.6/2.7 |
| Copper guide strip | 1.4 | 3.8 | 0.4 |
| Wall of phase change material container | 42 | 42 | 1 |
| Phase change material | 40 | 40 | 40 |
| P-Type Material | N-Type Material | Copper | Alumina | Phase Change Material | Thermoelectric Module | |
|---|---|---|---|---|---|---|
| Isobaric heat Capacity (J/kg K) | 154 | 154 | 385 | 900 | 2000 | - |
| Density (kg/m3) | 7700 | 7700 | 8960 | 2700 | 1000 | - |
| Electrical conductivity (S/m) | σ (T) | σ (T) | 5.998 × 107 | 0 | - | 1/3(HTL = 1.6 mm) 2/7(HTL = 2.7 mm) |
| Seebeck coefficient (V/K) | α(T) | −α(T) | - | - | - | - |
| Thermal conductivity, (W/m2 K) | k(T) | k(T) | 400 | 2 | 50 | - |
| Relative permittivity | 1 | 1 | 1 | 1 | - | - |
| Number of Elements | Average Cell Quality | Voc (t = 7200 s; V) | (t = 7200 s; V) | |
|---|---|---|---|---|
| extra fine | 644,050 | 0.6647 | 0.12953 | 2.414 |
| finer | 331,144 | 0.651 | 0.12952 | 2.418 |
| fine | 179,556 | 0.6462 | 0.12949 | 2.422 |
| normal | 127,270 | 0.6321 | 0.12948 | 2.422 |
| coarse | 79,767 | 0.5843 | 0.12948 | 2.425 |
| coarser | 35,391 | 0.4929 | 0.12945 | 2.429 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, J.; Xu, G.; Guo, T.; Nan, B. Optimization Design and Performance Study of Wearable Thermoelectric Device Using Phase Change Material as Heat Sink. Materials 2024, 17, 3266. https://doi.org/10.3390/ma17133266
Xin J, Xu G, Guo T, Nan B. Optimization Design and Performance Study of Wearable Thermoelectric Device Using Phase Change Material as Heat Sink. Materials. 2024; 17(13):3266. https://doi.org/10.3390/ma17133266
Chicago/Turabian StyleXin, Jiakai, Guiying Xu, Tao Guo, and Bohang Nan. 2024. "Optimization Design and Performance Study of Wearable Thermoelectric Device Using Phase Change Material as Heat Sink" Materials 17, no. 13: 3266. https://doi.org/10.3390/ma17133266
APA StyleXin, J., Xu, G., Guo, T., & Nan, B. (2024). Optimization Design and Performance Study of Wearable Thermoelectric Device Using Phase Change Material as Heat Sink. Materials, 17(13), 3266. https://doi.org/10.3390/ma17133266






