The Influence of Measurement Conditions on the Electrocaloric Effect in Ferroelectric Ceramics of Modified Barium Titanate
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Microstructural Characterization
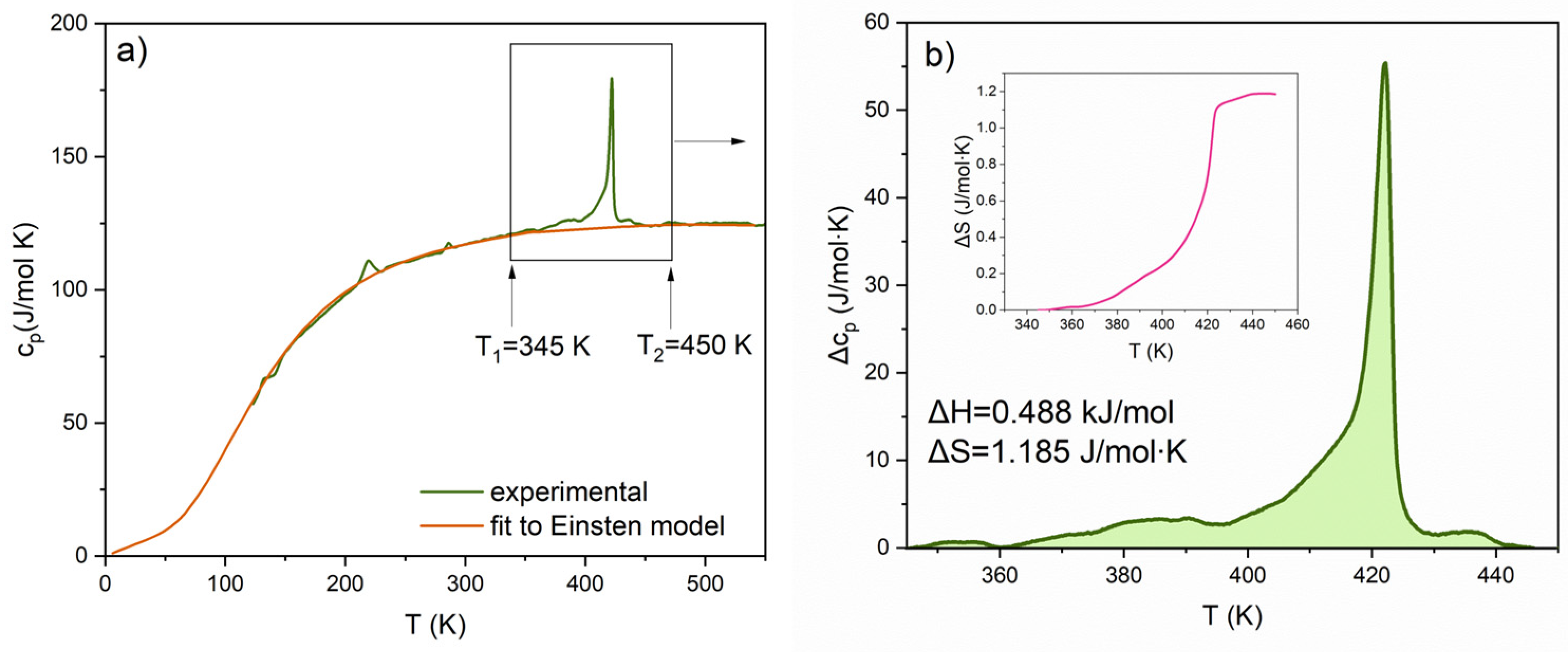
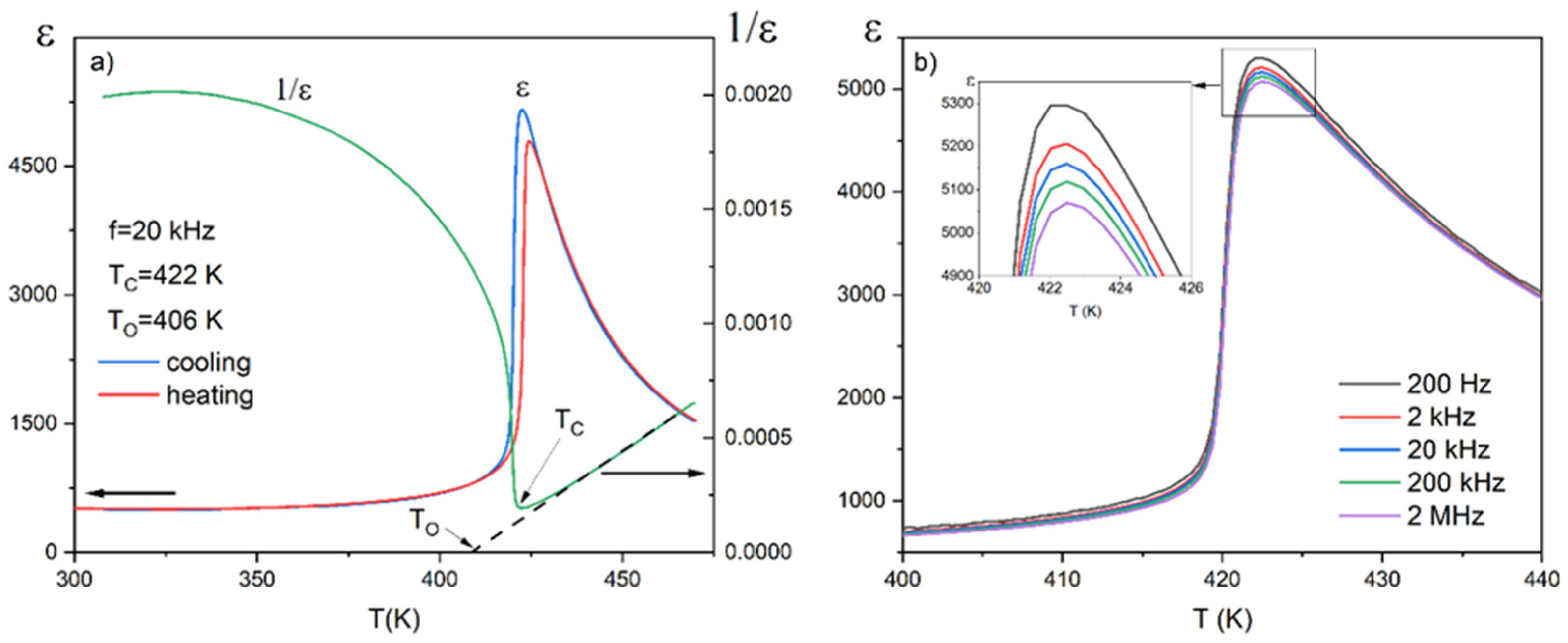
3.2. Identification of the Phase Transitions
3.3. Ferroelectric and ECE Measurements
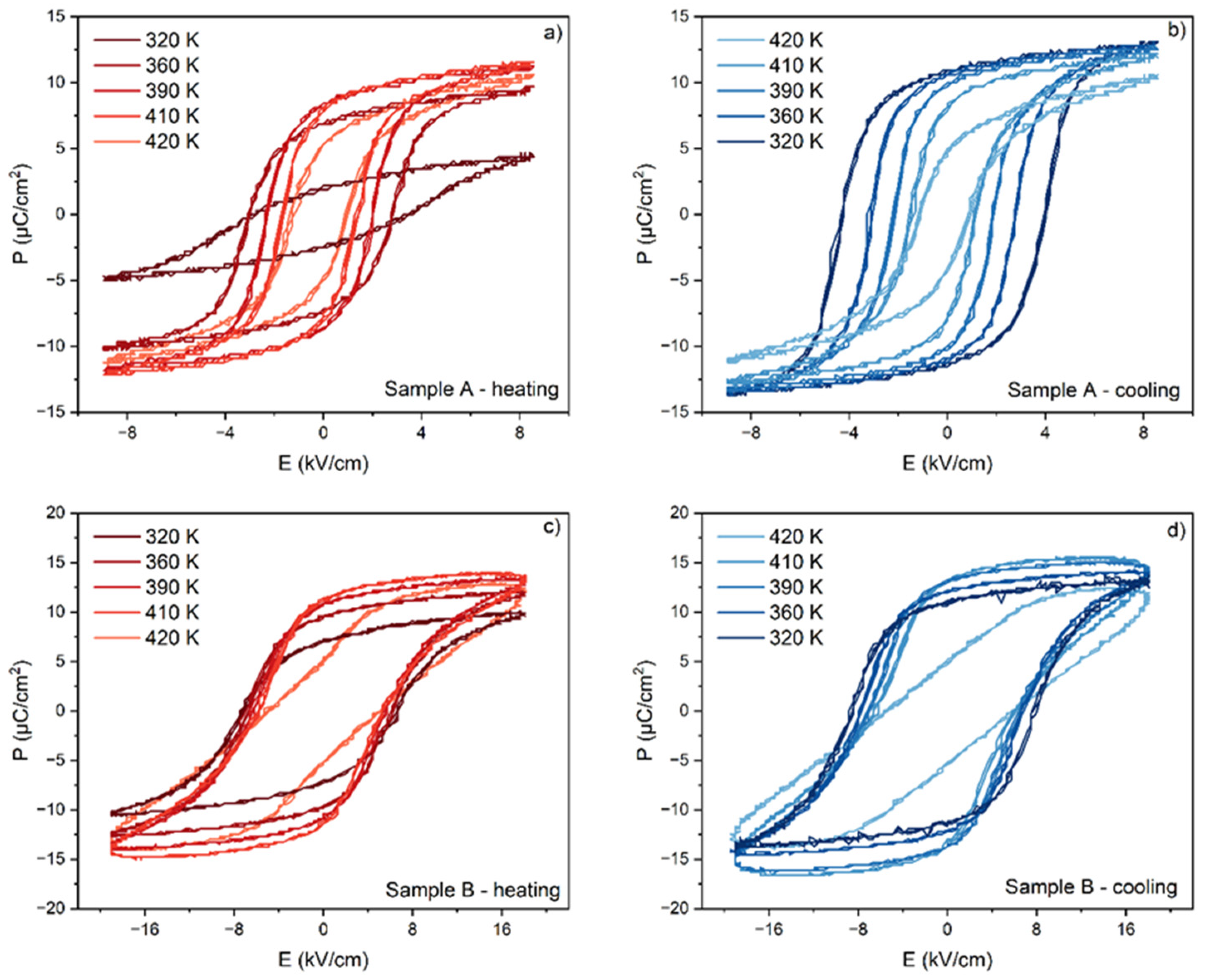
3.4. Influence of Measuring Conditions on the ECE Effect
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, J.; Liu, W.; Zhang, L.; Kong, F.; Zhao, Y.; Li, S. Enhanced dielectric and ferroelectric properties of the hybrid-doped BaTiO3 ceramics by the semi-solution method. Ceram. Int. 2021, 47, 15661–15667. [Google Scholar] [CrossRef]
- Shirane, G.; Suzuki, K. On the phase transition in Barium Lead Titanate. J. Phys. Soc. Jpn. 1951, 6, 265–270. [Google Scholar] [CrossRef]
- Butee, S.; Kambale, K.R.; Ghorpade, A.; Halikar, A.; Gaikwad, R.; Panda, H. Significant improvement in Curie temperature and piezoelectric properties of BaTiO3 with minimum Pb addition. J. Asian Ceram. Soc. 2019, 7, 407–416. [Google Scholar] [CrossRef]
- Amin, R.; Khatun, N.; Sen, S. Optimization of Pb content in enhancing ferroelectricity and shifting the Tc of BaTiO3 to a higher temperature. J. Appl. Phys. 2019, 126, 174105. [Google Scholar] [CrossRef]
- Jaffari, G.H.; Zafar, A.; Tanvir, J.; Ali, W.; Ali, A.; Yuan, G. Identification of the consequences of Pb-O chemical bond modification, Pb lone pair and Pb volatilization on the intrinsic and extrinsic physical properties of Ba1−xPbxTiO3 (x ≤ 0–0.5). J. Alloys Compd. 2021, 865, 158977. [Google Scholar] [CrossRef]
- Arshad, M.; Abushad, M.; Azhar, M.; Ahmed, H.; Nadeem, M.; Ansari, A.; Chakradhary, V.K.; Husain, S.; Khan, W. Origin of enhanced dielectric and multiferroic properties in Pb-doped BaTiO3 ceramics. Appl. Phys. A 2022, 128, 1123. [Google Scholar] [CrossRef]
- Lai, C.H.; Tseng, T.Y. Preparation and ac electrical response analysis for (Ba,Pb)TiO3, PTCR Ceramics. J. Am. Ceramic. Soc. 1993, 76, 781–787. [Google Scholar] [CrossRef]
- Kuwabara, M.; Suemure, S.; Kawahara, M. Preparation of High-Curie-Point Barium Lead Titanates and Their PTCR Characteristics. Am. Ceram. Soc. Bull. 1985, 6, 1394–1398. [Google Scholar]
- Moya, X.; Stern-Taulats, E.; Crossley, S.; González-Alonso, D.; Kar-Narayan, S.; Planes, A.; Mañosa, L.; Mathur, N.D. Giant electrocaloric strength in single-crystal BaTiO3. Adv. Mater. 2013, 25, 1360. [Google Scholar] [CrossRef]
- Singh, G.; Bhaumik, I.; Ganesamoorthy, S.; Bhatt, R.; Karnal, A.K.; Tiwari, V.S.; Gupta, P.K. Electro-caloric effect in 0.45BaZr0.2Ti0.8O3-0.55Ba0.7Ca0.3TiO3 single crystal. Appl. Phys. Lett. 2013, 102, 082902. [Google Scholar] [CrossRef]
- Bai, Y.; Han, X.; Qiao, L. Optimized electrocaloric refrigeration capacity in lead-free (1−x)BaZr0.2Ti0.8O3−xBa0.7Ca0.3TiO3 ceramics. Appl. Phys. Lett. 2013, 102, 252904. [Google Scholar] [CrossRef]
- Maiwa, H. Temperature dependences of the electromechanical and electrocaloric properties of Ba(Zr,Ti)O3 and (Ba,Sr)TiO3 ceramics. Ferroelectrics 2013, 450, 84. [Google Scholar] [CrossRef]
- Ye, H.J.; Qian, X.S.; Jeong, D.Y.; Zhang, S.; Zhou, Y.; Shao, W.Z.; Zhen, L.; Zhang, Q.M. Giant electrocaloric effect in BaZr0.2Ti0.8O3 thick film. Appl. Phys. Lett. 2014, 105, 152908. [Google Scholar] [CrossRef]
- Ren, X. Large electric-field-induced strain in ferroelectric crystals by point-defect-mediated reversible domain switching. Nat. Mater. 2004, 3, 91. [Google Scholar] [CrossRef]
- Erhart, P.; Träskelin, P.; Albe, K. Formation and switching of defect dipoles in acceptor-doped lead titanate: A kinetic model based on first-principles calculations. Phys. Rev. B 2013, 88, 024107. [Google Scholar] [CrossRef]
- Van Vechten, J. Dielectic Refrigerator Using Orientable Defect Dipoles. U.S. Patent US4136525A, 30 January 1979. [Google Scholar]
- Ponomareva, I.; Lisenkov, S. Bridging the Macroscopic and Atomistic Descriptions of the Electrocaloric Effect. Phys. Rev. Lett. 2012, 108, 167604. [Google Scholar] [CrossRef]
- Li, B.; Wang, J.B.; Zhong, X.L.; Wang, F.; Zeng, Y.K.; Zhou, Y.C. The coexistence of the negative and positive electrocaloric effect in ferroelectric thin films for solid-state refrigeration. Europhys. Lett. 2013, 102, 47004. [Google Scholar] [CrossRef]
- Wu, M.; Zhu, Q.; Li, J.; Song, D.; Wu, H.; Guo, M.; Gao, J.; Bai, Y.; Feng, Y.; Pennycook, S.J.; et al. Electrocaloric effect in ferroelectric ceramics with point defects. Appl. Phys. Lett. 2019, 114, 142901. [Google Scholar] [CrossRef]
- Ma, Y.B.; Grünebohm, A.; Meyer, K.C.; Albe, K.; Xu, B.X. Positive and negative electrocaloric effect in BaTiO3 in the presence of defect dipoles. Phys. Rev. B 2016, 94, 094113. [Google Scholar] [CrossRef]
- Han, F.; Bai, Y.; Qiao, L.J.; Guo, D. A systematic modification of the large electrocaloric effect within a broad temperature range in rare-earth doped BaTiO3 ceramics. J. Mater. Chem. C 2016, 4, 1842–1849. [Google Scholar] [CrossRef]
- PI Ceramic. Available online: https://www.piceramic.de/de/ (accessed on 2 July 2024).
- Liu, Y.; Scott, J.F.; Dkhil, B. Direct and indirect measurements on electrocaloric effect: Recent developments and perspectives. Appl. Phys. Rev. 2016, 3, 031102. [Google Scholar] [CrossRef]
- Kutnjak, Z.; Rožič, B. Electrocaloric Effect: Theory, Measurements, and Applications. In Electrocaloric Materials: New Generation of Coolers; Correia, T., Zhang, Q., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 147–182. [Google Scholar]
- Pecherskaya, E.A. The use of the Sawyer-Tower method and its modifications to measure the electrical parameters of ferroelectric materials. Meas. Tech. 2007, 50, 1101–1107. [Google Scholar] [CrossRef]
- Shu, Y.C.; Bhattacharya, K. Domain patterns and macroscopic behaviour of ferroelectric materials. Philos. Mag. B 2001, 81, 2021–2054. [Google Scholar] [CrossRef]
- Bachulska, U.; Jankowska-Sumara, J.; Majchrowski, A.; Chrunik, M.; Zasada, D.; Soszyński, A. Thermal and dielectric properties of ferroelectric lead germanate single crystals doped with chromium ions (Pb5Ge3O11:Cr3+). Phase Transit. 2018, 91, 923–931. [Google Scholar] [CrossRef]
- Nomura, S.; Sawada, S. Dielectric and Thermal Properties of Barium Lead Titanates. J. Phys. Soc. Jpn. 1951, 6, 36–39. [Google Scholar] [CrossRef]
- Krupska-Klimczak, M.; Gwizd, P.; Jankowska-Sumara, I.; Sitko, D.; Jeleń, P. An Overview of Some Nonpiezoelectric Properties of BaTiO3 Ceramics Doped by Eu Ions. Materials 2022, 15, 5363. [Google Scholar] [CrossRef] [PubMed]
- Krupska-Klimczak, M.; Jankowska-Sumara, I.; Sowa, S. Positive and Negative Electrocaloric Effect in soft- and hard-doped commercial PZT ceramics. Ceram. Int. 2023, 49, 36807–36815. [Google Scholar] [CrossRef]
- Lv, Z.; Wei, J.; Yang, T.; Sun, Z.; Xu, Z. Manipulation of Curie temperature and ferroelectric polarization for large electrocaloric strength in BaTiO3-based ceramics. Ceram. Int. 2020, 46, 14978–14984. [Google Scholar] [CrossRef]
- Grünebohm, A.; Ma, Y.B.; Marathe, M.; Xu, B.X.; Albe, K.; Kalcher, C.; Meyer, K.C.; Shvartsman, V.V.; Lupascu, D.C.; Ederer, C. On the origins of the inverse electrocaloric effect. Energy Technol. 2018, 6, 1491–1511. [Google Scholar] [CrossRef]

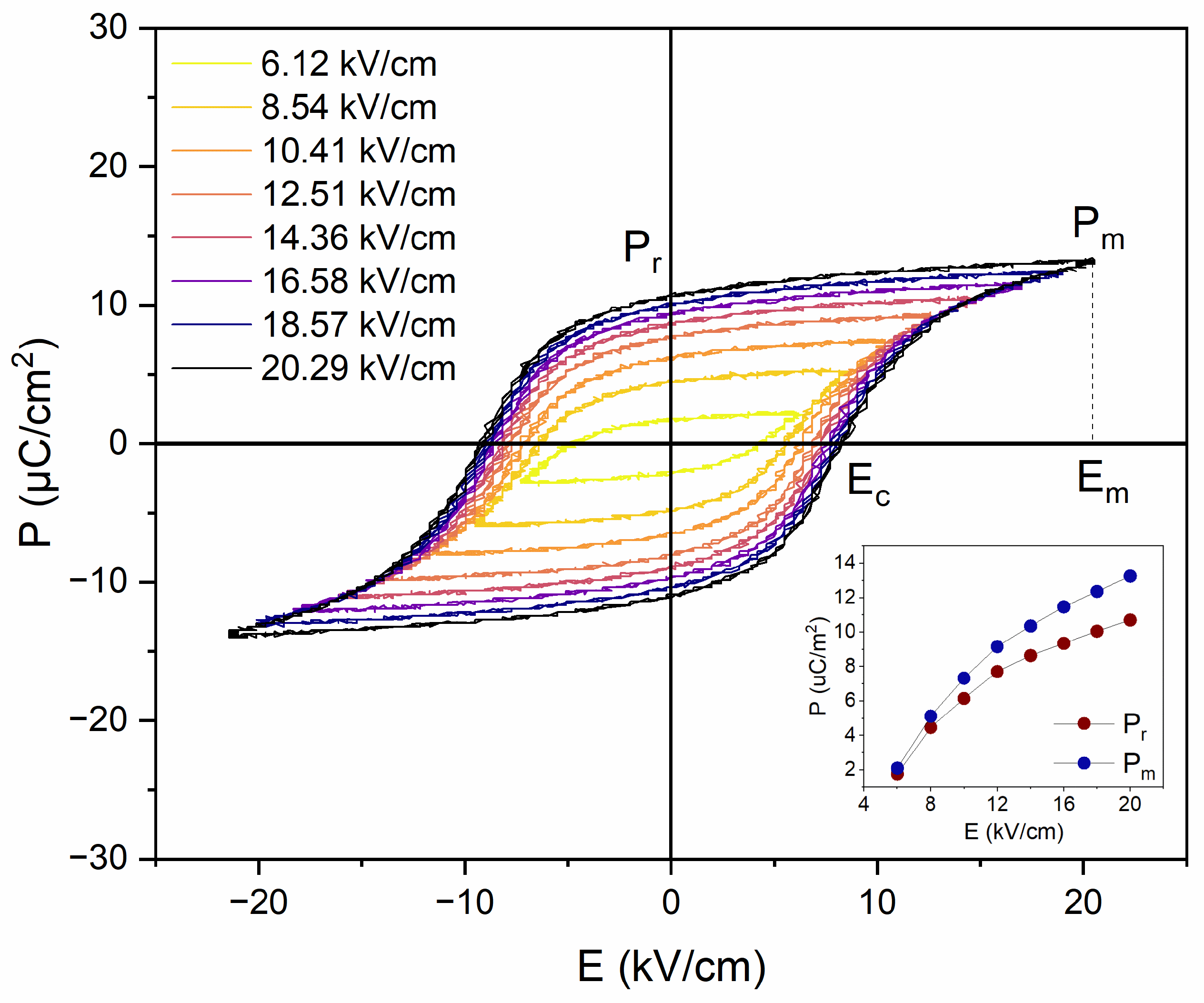
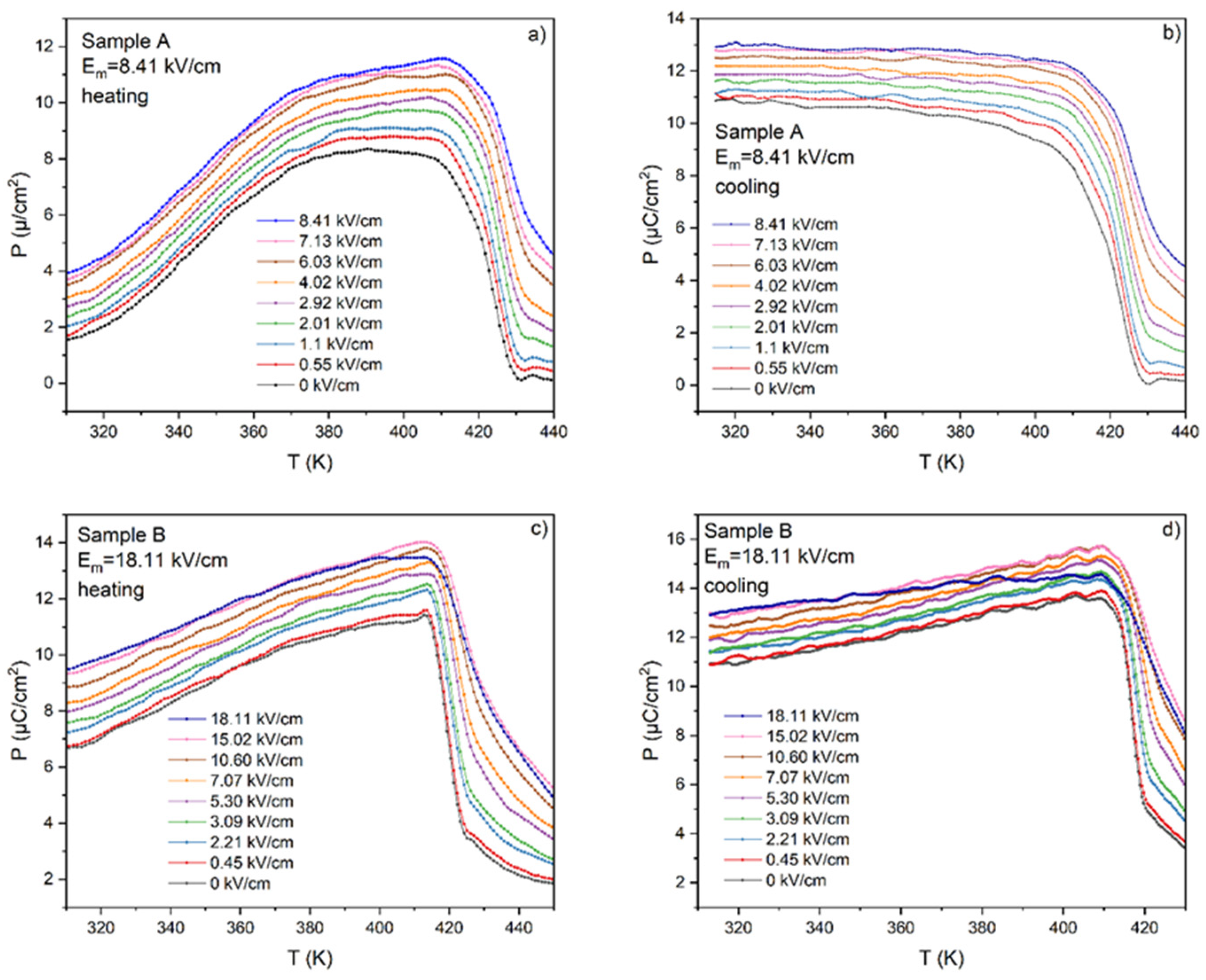

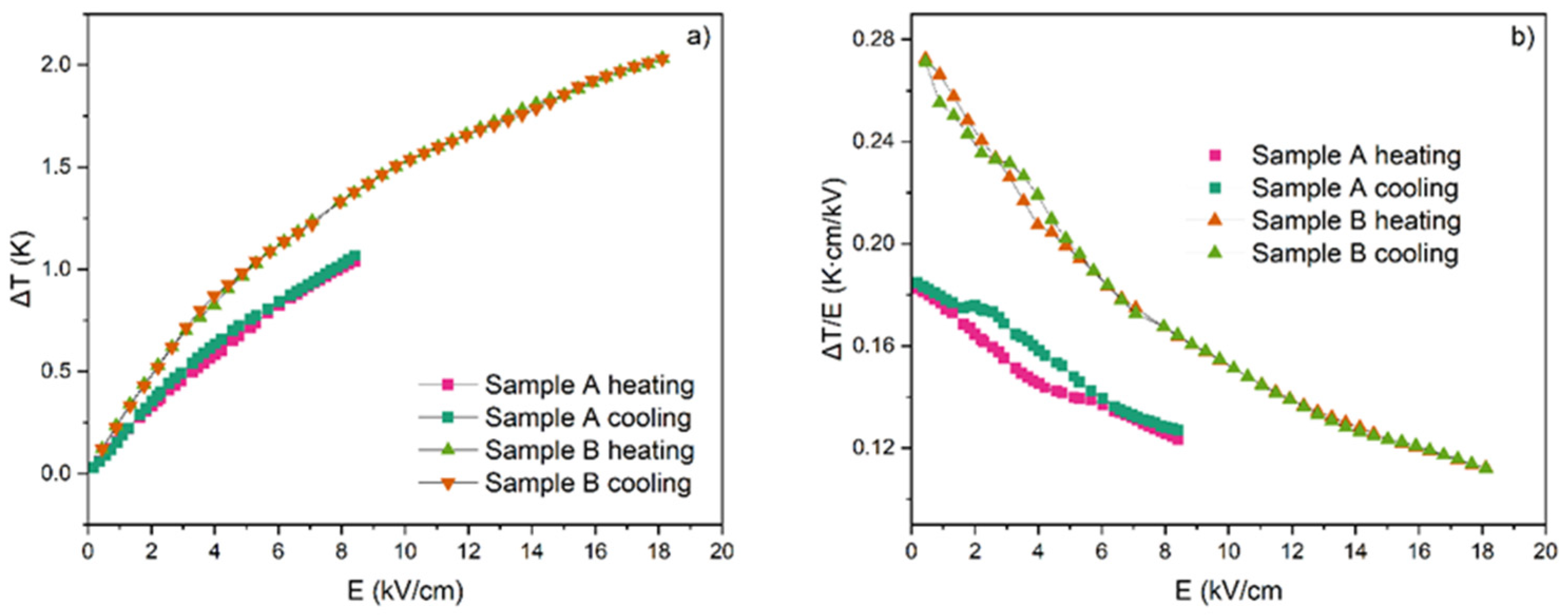
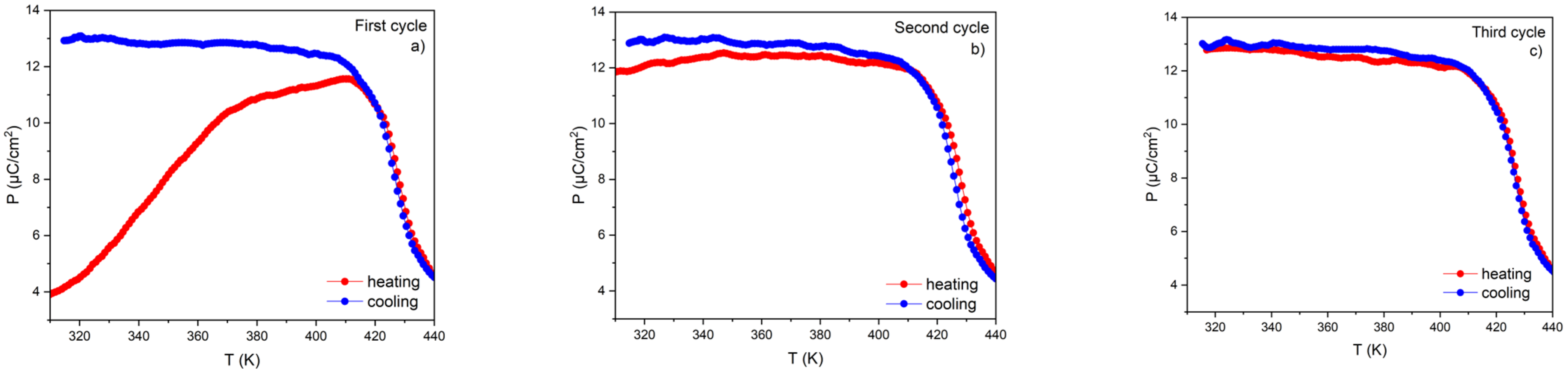
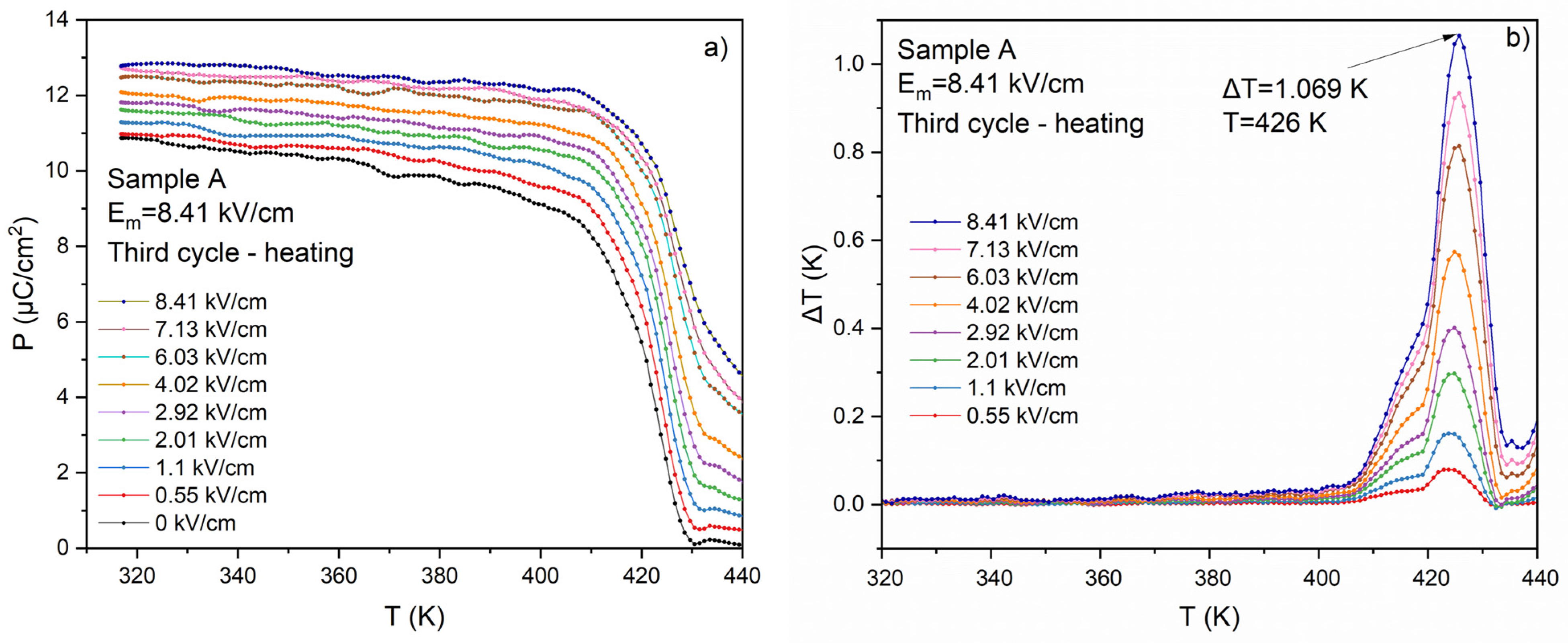
| Em (kV/cm) | Ec (kV/cm) | Pr (μC/cm2) | Pm (μC/cm2) |
|---|---|---|---|
| 6.12 | 4.23 | 1.77 | 2.10 |
| 8.54 | 5.57 | 4.47 | 5.12 |
| 10.41 | 6.38 | 6.15 | 7.33 |
| 12.51 | 6.89 | 7.71 | 9.16 |
| 14.36 | 7.32 | 8.64 | 10.36 |
| 16.58 | 7.71 | 9.35 | 11.47 |
| 18.57 | 7.93 | 10.06 | 12.37 |
| 20.29 | 8.24 | 10.71 | 13.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krupska-Klimczak, M.; Ziewiec, K.; Jankowska-Sumara, I. The Influence of Measurement Conditions on the Electrocaloric Effect in Ferroelectric Ceramics of Modified Barium Titanate. Materials 2024, 17, 3329. https://doi.org/10.3390/ma17133329
Krupska-Klimczak M, Ziewiec K, Jankowska-Sumara I. The Influence of Measurement Conditions on the Electrocaloric Effect in Ferroelectric Ceramics of Modified Barium Titanate. Materials. 2024; 17(13):3329. https://doi.org/10.3390/ma17133329
Chicago/Turabian StyleKrupska-Klimczak, Magdalena, Krzysztof Ziewiec, and Irena Jankowska-Sumara. 2024. "The Influence of Measurement Conditions on the Electrocaloric Effect in Ferroelectric Ceramics of Modified Barium Titanate" Materials 17, no. 13: 3329. https://doi.org/10.3390/ma17133329
APA StyleKrupska-Klimczak, M., Ziewiec, K., & Jankowska-Sumara, I. (2024). The Influence of Measurement Conditions on the Electrocaloric Effect in Ferroelectric Ceramics of Modified Barium Titanate. Materials, 17(13), 3329. https://doi.org/10.3390/ma17133329







