Energy Filtering in Doping Modulated Nanoengineered Thermoelectric Materials: A Monte Carlo Simulation Approach
Abstract
1. Introduction
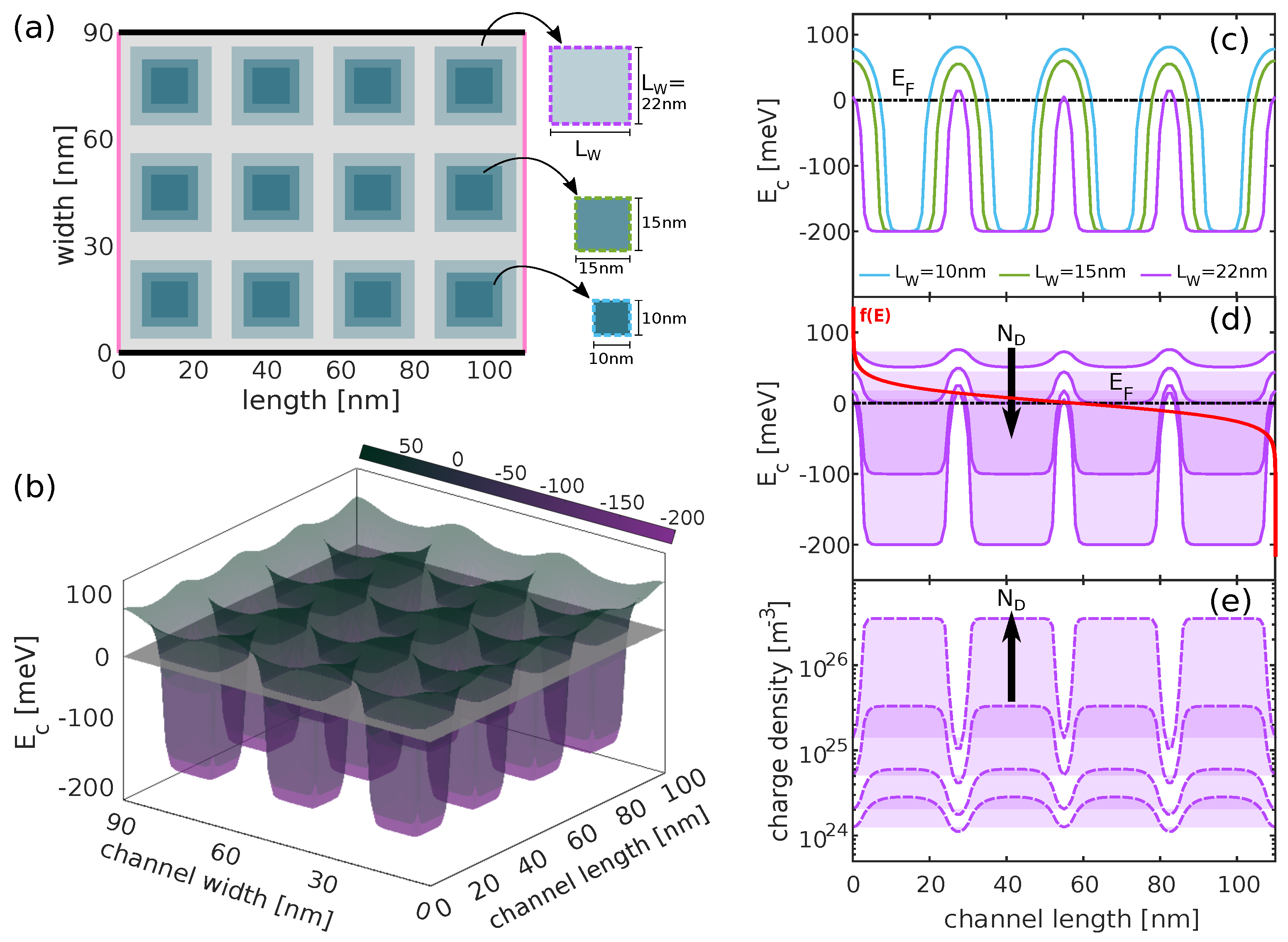
2. Method and Approach
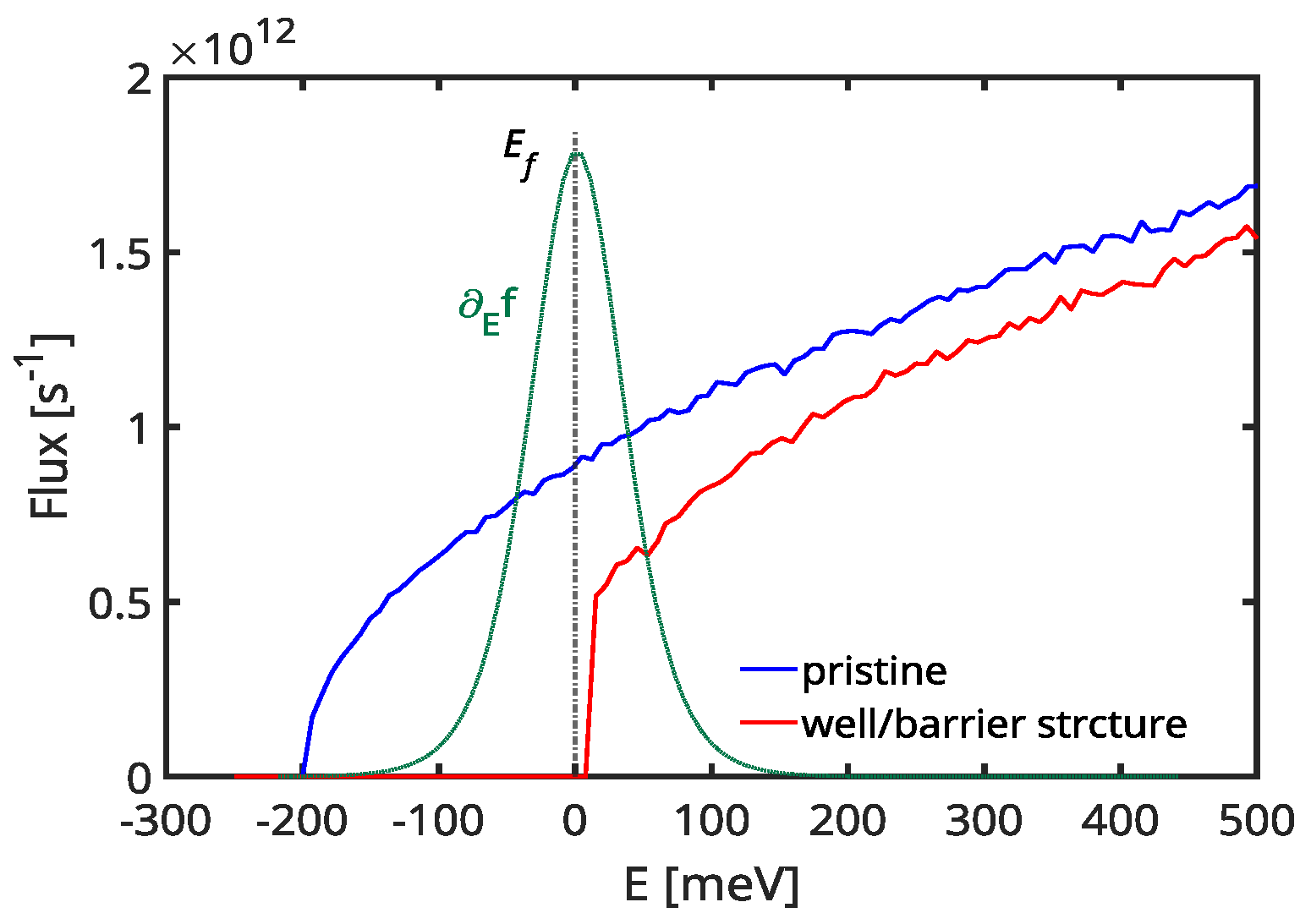
3. Power Factor in a Structure with Doped/Intrinsic Regions
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beretta, D.; Neophytou, N.; Hodges, J.; Kanatzidis, M.; Narducci, D.; Martin-Gonzalez, M.; Beekman, M.; Balke, B.; Cerretti, G.; Tremel, W.; et al. Thermoelectrics: From history, a window to the future. Mater. Sci. Eng. R Rep. 2019, 138, 100501. [Google Scholar] [CrossRef]
- Shi, X.L.; Zou, J.; Chen, Z.G. Advanced Thermoelectric Design: From Materials and Structures to Devices. Chem. Rev. 2020, 120, 7399–7515. [Google Scholar] [CrossRef] [PubMed]
- Shankar, M.R.; Prabhu, A.N. A review on structural characteristics and thermoelectric properties of mid-temperature range Chalcogenide-based thermoelectric materials. J. Mater. Sci. 2023, 58, 16591–16633. [Google Scholar] [CrossRef]
- Artini, C.; Pennelli, G.; Graziosi, P.; Li, Z.; Neophytou, N.; Melis, C.; Colombo, L.; Isotta, E.; Lohani, K.; Scardi, P.; et al. Roadmap on thermoelectricity. Nanotechnology 2023, 34, 292001. [Google Scholar] [CrossRef]
- Wu, H.J.; Zhao, L.D.; Zheng, F.S.; Wu, D.; Pei, Y.L.; Tong, X.; Kanatzidis, M.G.; He, J.Q. Broad temperature plateau for thermoelectric figure of merit ZT>2 in phase-separated PbTe0.7S0.3. Nat. Commun. 2014, 5, 4515. [Google Scholar] [CrossRef]
- Biswas, K.; He, J.; Blum, I.; Wu, C.; Hogan, T.; Seidman, D.; Dravid, V.; Kanatzidis, M. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 2012, 489, 414–418. [Google Scholar] [CrossRef]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef]
- Fu, T.; Yue, X.; Wu, H.; Fu, C.; Zhu, T.; Liu, X.; Hu, L.; Ying, P.; He, J.; Zhao, X. Enhanced thermoelectric performance of PbTe bulk materials with figure of merit zT >2 by multi-functional alloying. J. Mater. 2016, 2, 141–149. [Google Scholar] [CrossRef]
- Liu, H.; Shi, X.; Xu, F.; Zhang, L.; Zhang, W.; Chen, L.; Li, Q.; Uher, C.; Day, T.; Snyder, G.J. Copper ion liquid-like thermoelectrics. Nat. Mater. 2012, 11, 422–425. [Google Scholar] [CrossRef]
- Kim, S.; Lee, K.; Mun, H.; Kim, H.; Hwang, S.; Roh, J.; Yang, D.; Shin, W.; Li, X.; Lee, Y.; et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 2015, 348, 109–114. [Google Scholar] [CrossRef]
- Olvera, A.A.; Moroz, N.A.; Sahoo, P.; Ren, P.; Bailey, T.P.; Page, A.A.; Uher, C.; Poudeu, P.F.P. Partial indium solubility induces chemical stability and colossal thermoelectric figure of merit in Cu2Se. Energy Environ. Sci. 2017, 10, 1668–1676. [Google Scholar] [CrossRef]
- Rogl, G.; Grytsiv, A.; Rogl, P.; Peranio, N.; Bauer, E.; Zehetbauer, M.; Eibl, O. n-Type skutterudites (R,Ba,Yb)yCo4Sb12 (R = Sr, La, Mm, DD, SrMm, SrDD) approaching ZT≈2.0. Acta Mater. 2014, 63, 30–43. [Google Scholar] [CrossRef]
- Hao, S.; Dravid, V.P.; Kanatzidis, M.G.; Wolverton, C. Computational strategies for design and discovery of nanostructured thermoelectrics. Npj Comput. Mater. 2019, 5, 58. [Google Scholar] [CrossRef]
- Fiorentini, V.; Farris, R.; Argiolas, E.; Maccioni, M.B. High thermoelectric figure of merit and thermopower in layered perovskite oxides. Phys. Rev. Mater. 2019, 3, 022401. [Google Scholar] [CrossRef]
- Finn, P.A.; Asker, C.; Wan, K.; Bilotti, E.; Fenwick, O.; Nielsen, C.B. Thermoelectric Materials: Current Status and Future Challenges. Front. Electron. Mater. 2021, 1, 677845. [Google Scholar] [CrossRef]
- Wei, J.; Yang, L.; Ma, Z.; Song, P.; Zhang, M.; Ma, J.; Yang, F.; Wang, X. Review of current high-ZT thermoelectric materials. J. Mater. Sci. 2020, 55, 12642–12704. [Google Scholar] [CrossRef]
- Wolf, M.; Hinterding, R.; Feldhoff, A. High Power Factor vs. High zT—A Review of Thermoelectric Materials for High-Temperature Application. Entropy 2019, 21, 1058. [Google Scholar] [CrossRef]
- Nakamura, Y.; Taniguchi, T.; Terada, T. Enhancement of Phonon Scattering in Epitaxial Hierarchical Nanodot Structures for Thermoelectric Application. Vac. Surf. Sci. 2018, 61, 296–301. [Google Scholar] [CrossRef][Green Version]
- Perez-Taborda, J.A.; Muñoz Rojo, M.; Maiz, J.; Neophytou, N.; Martin-Gonzalez, M. Ultra-low thermal conductivities in large-area Si-Ge nanomeshes for thermoelectric applications. Sci. Rep. 2016, 6, 32778. [Google Scholar] [CrossRef]
- Lee, J.; Lee, W.; Wehmeyer, G.; Dhuey, S.; Olynick, D.L.; Cabrini, S.; Dames, C.; Urban, J.J.; Yang, P. Investigation of phonon coherence and backscattering using silicon nanomeshes. Nat. Commun. 2017, 8, 14054. [Google Scholar] [CrossRef]
- Ohnishi, M.; Shiomi, J. Towards ultimate impedance of phonon transport by nanostructure interface. APL Mater. 2019, 7, 013102. [Google Scholar] [CrossRef]
- Kearney, B.T.; Jugdersuren, B.; Queen, D.R.; Metcalf, T.H.; Culbertson, J.C.; Desario, P.A.; Stroud, R.M.; Nemeth, W.; Wang, Q.; Liu, X. From amorphous to nanocrystalline: The effect of nanograins in an amorphous matrix on the thermal conductivity of hot-wire chemical-vapor deposited silicon films. J. Phys. Condens. Matter 2018, 30, 085301. [Google Scholar] [CrossRef]
- Hashemi, A.; Babaei, H.; Lee, S. Effects of medium range order on propagon thermal conductivity in amorphous silicon. J. Appl. Phys. 2020, 127, 045109. [Google Scholar] [CrossRef]
- Braun, J.L.; Baker, C.H.; Giri, A.; Elahi, M.; Artyushkova, K.; Beechem, T.E.; Norris, P.M.; Leseman, Z.C.; Gaskins, J.T.; Hopkins, P.E. Size effects on the thermal conductivity of amorphous silicon thin films. Phys. Rev. B 2016, 93, 140201. [Google Scholar] [CrossRef]
- Sojo Gordillo, J.M.; Morata, A.; Sierra, C.D.; Salleras, M.; Fonseca, L.; Tarancón, A. Recent advances in silicon-based nanostructures for thermoelectric applications. APL Mater. 2023, 11, 040702. [Google Scholar] [CrossRef]
- Bahk, J.H.; Bian, Z.; Shakouri, A. Electron transport modeling and energy filtering for efficient thermoelectric Mg2Si1−xSnx solid solutions. Phys. Rev. B 2014, 89, 075204. [Google Scholar] [CrossRef]
- Bahk, J.H.; Shakouri, A. Minority carrier blocking to enhance the thermoelectric figure of merit in narrow-band-gap semiconductors. Phys. Rev. B 2016, 93, 165209. [Google Scholar] [CrossRef]
- Neophytou, N.; Kosina, H. Optimizing thermoelectric power factor by means of a potential barrier. J. Appl. Phys. 2013, 114, 044315. [Google Scholar] [CrossRef]
- Vargiamidis, V.; Neophytou, N. Hierarchical nanostructuring approaches for thermoelectric materials with high power factors. Phys. Rev. B 2019, 99, 045405. [Google Scholar] [CrossRef]
- Kim, R.; Lundstrom, M.S. Computational study of energy filtering effects in one-dimensional composite nano-structures. J. Appl. Phys. 2012, 111, 024508. [Google Scholar] [CrossRef]
- Gayner, C.; Amouyal, Y. Energy Filtering of Charge Carriers: Current Trends, Challenges, and Prospects for Thermoelectric Materials. Adv. Funct. Mater. 2020, 30, 1901789. [Google Scholar] [CrossRef]
- Sakane, S.; Ishibe, T.; Taniguchi, T.; Naruse, N.; Mera, Y.; Fujita, T.; Alam, M.M.; Sawano, K.; Mori, N.; Nakamura, Y. Thermoelectric power factor enhancement based on carrier transport physics in ultimately phonon-controlled Si nanostructures. Mater. Today Energy 2019, 13, 56–63. [Google Scholar] [CrossRef]
- Ishibe, T.; Tomeda, A.; Watanabe, K.; Kamakura, Y.; Mori, N.; Naruse, N.; Mera, Y.; Yamashita, Y.; Nakamura, Y. Methodology of Thermoelectric Power Factor Enhancement by Controlling Nanowire Interface. ACS Appl. Mater. Interfaces 2018, 10, 37709–37716. [Google Scholar] [CrossRef]
- Liang, S.; Shi, Y.; Hu, D.; Zhu, H.; Yue, S. Significantly improved thermoelectric performance of Ag-doped Bi0.5Sb1.5Te3 films deriving from high-efficient carrier filtering effect. Ceram. Int. 2023, 49, 35309–35315. [Google Scholar] [CrossRef]
- Vashaee, D.; Shakouri, A. Improved Thermoelectric Power Factor in Metal-Based Superlattices. Phys. Rev. Lett. 2004, 92, 106103. [Google Scholar] [CrossRef]
- Neophytou, N.; Zianni, X.; Kosina, H.; Frabboni, S.; Lorenzi, B.; Narducci, D. Simultaneous increase in electrical conductivity and Seebeck coefficient in highly boron-doped nanocrystalline Si. Nanotechnology 2013, 24, 205402. [Google Scholar] [CrossRef]
- Narducci, D.; Zulian, L.; Lorenzi, B.; Giulio, F.; Villa, E. Exceptional thermoelectric power factors in hyperdoped, fully dehydrogenated nanocrystalline silicon thin films. Appl. Phys. Lett. 2021, 119, 263903. [Google Scholar] [CrossRef]
- Bennett, N.S.; Byrne, D.; Cowley, A.; Neophytou, N. Dislocation loops as a mechanism for thermoelectric power factor enhancement in silicon nano-layers. Appl. Phys. Lett. 2016, 109, 173905. [Google Scholar] [CrossRef]
- Neophytou, N.; Foster, S.; Vargiamidis, V.; Pennelli, G.; Narducci, D. Nanostructured potential well/barrier engineering for realizing unprecedentedly large thermoelectric power factors. Mater. Today Phys. 2019, 11, 100159. [Google Scholar] [CrossRef]
- Priyadarshi, P.; Neophytou, N. Computationally efficient Monte Carlo electron transport algorithm for nanostructured thermoelectric material configurations. J. Appl. Phys. 2023, 133, 054301. [Google Scholar] [CrossRef]
- Fischetti, M.V.; Laux, S.E. Monte carlo analysis of electron transport in small semiconductor devices including band-structure and space-charge effects. Phys. Rev. B 1988, 38, 9721–9745. [Google Scholar] [CrossRef]
- Jacoboni, C.; Reggiani, L. The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials. Rev. Mod. Phys. 1983, 55, 645–705. [Google Scholar] [CrossRef]
- Lundstrom, M.S. Fundamentals of Carrier Transport; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Chakraborty, D.; Foster, S.; Neophytou, N. Monte Carlo phonon transport simulations in hierarchically disordered silicon nanostructures. Phys. Rev. B 2018, 98, 115435. [Google Scholar] [CrossRef]
- Neophytou, N. Theory and Simulation Methods for Electronic and Phononic Transport in Thermoelectric Materials; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Lorenzi, B.; Narducci, D.; Tonini, R.; Frabboni, S.; Gazzadi, G.C.; Ottaviani, G.; Neophytou, N.; Zianni, X. Paradoxical Enhancement of the Power Factor of Polycrystalline Silicon as a Result of the Formation of Nanovoids. J. Electron. Mater. 2014, 43, 3812–3816. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Priyadarshi, P.; Vargiamidis, V.; Neophytou, N. Energy Filtering in Doping Modulated Nanoengineered Thermoelectric Materials: A Monte Carlo Simulation Approach. Materials 2024, 17, 3522. https://doi.org/10.3390/ma17143522
Priyadarshi P, Vargiamidis V, Neophytou N. Energy Filtering in Doping Modulated Nanoengineered Thermoelectric Materials: A Monte Carlo Simulation Approach. Materials. 2024; 17(14):3522. https://doi.org/10.3390/ma17143522
Chicago/Turabian StylePriyadarshi, Pankaj, Vassilios Vargiamidis, and Neophytos Neophytou. 2024. "Energy Filtering in Doping Modulated Nanoengineered Thermoelectric Materials: A Monte Carlo Simulation Approach" Materials 17, no. 14: 3522. https://doi.org/10.3390/ma17143522
APA StylePriyadarshi, P., Vargiamidis, V., & Neophytou, N. (2024). Energy Filtering in Doping Modulated Nanoengineered Thermoelectric Materials: A Monte Carlo Simulation Approach. Materials, 17(14), 3522. https://doi.org/10.3390/ma17143522







