Simulation of Frost-Heave Failure of Air-Entrained Concrete Based on Thermal–Hydraulic–Mechanical Coupling Model
Abstract
:1. Introduction
2. Estimation of Effective Properties of Cement Mortar and Average Pore Pressure
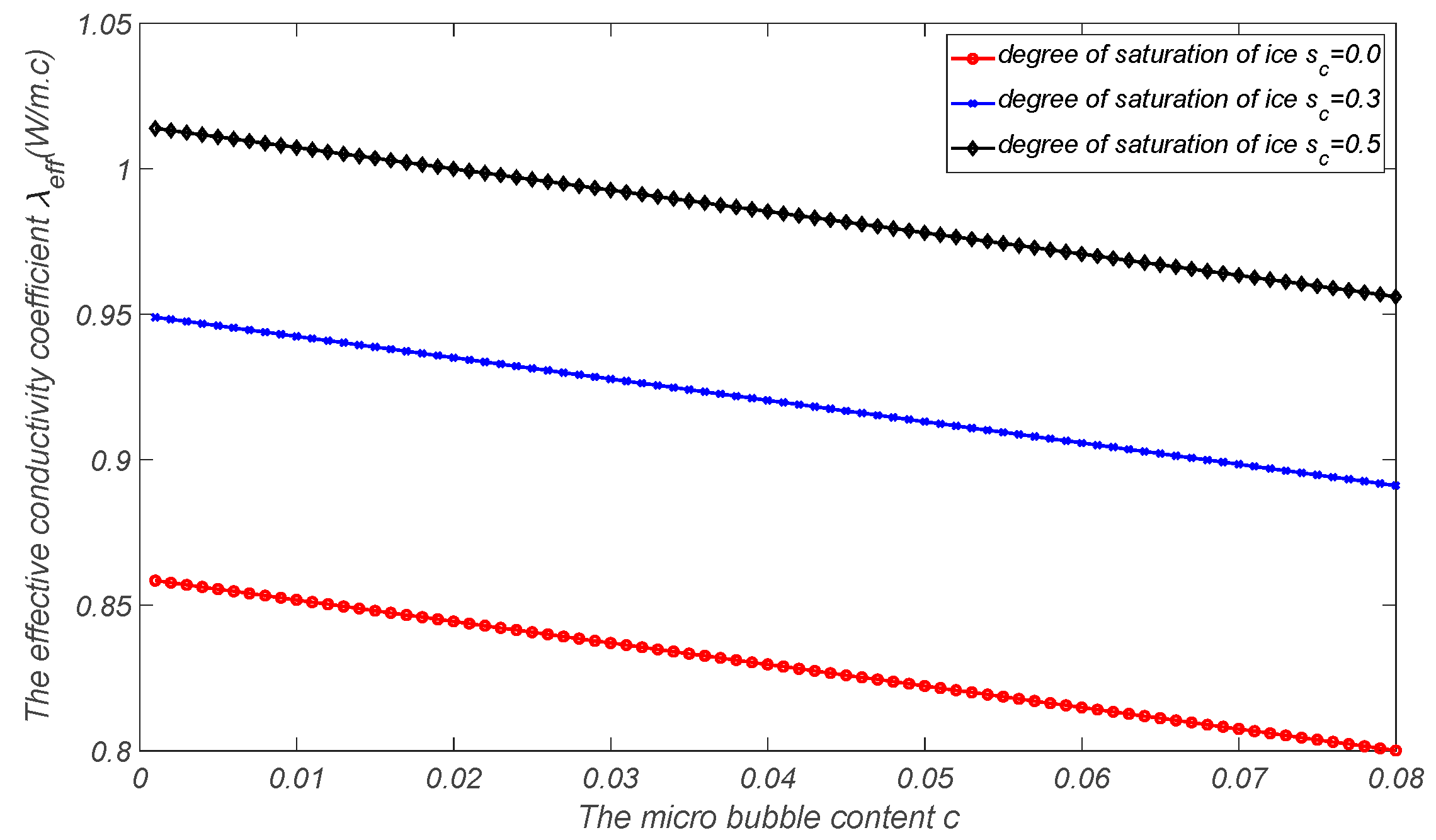
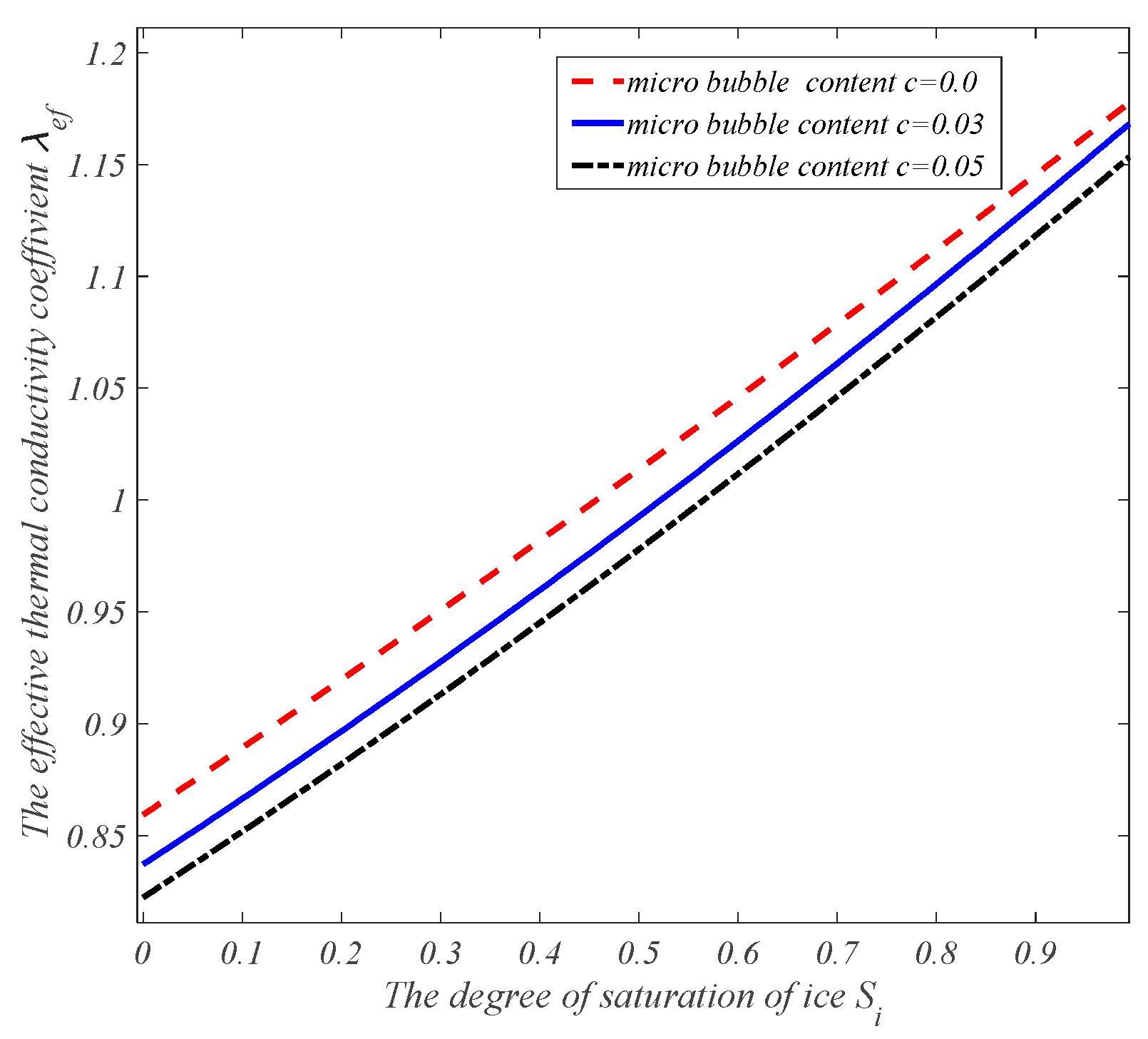
2.1. Effective Thermal Conductivity of Air-Entrained Mortar
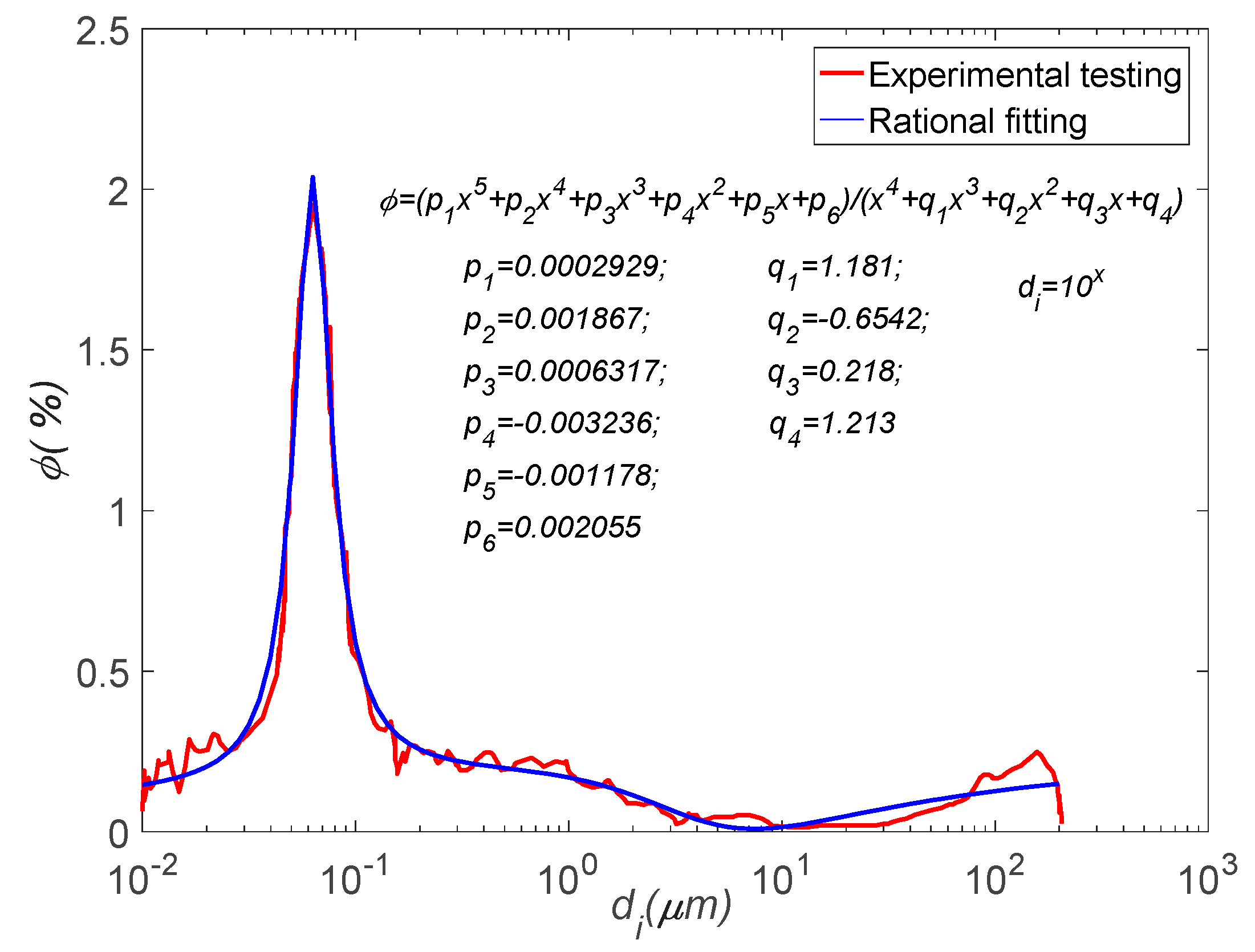
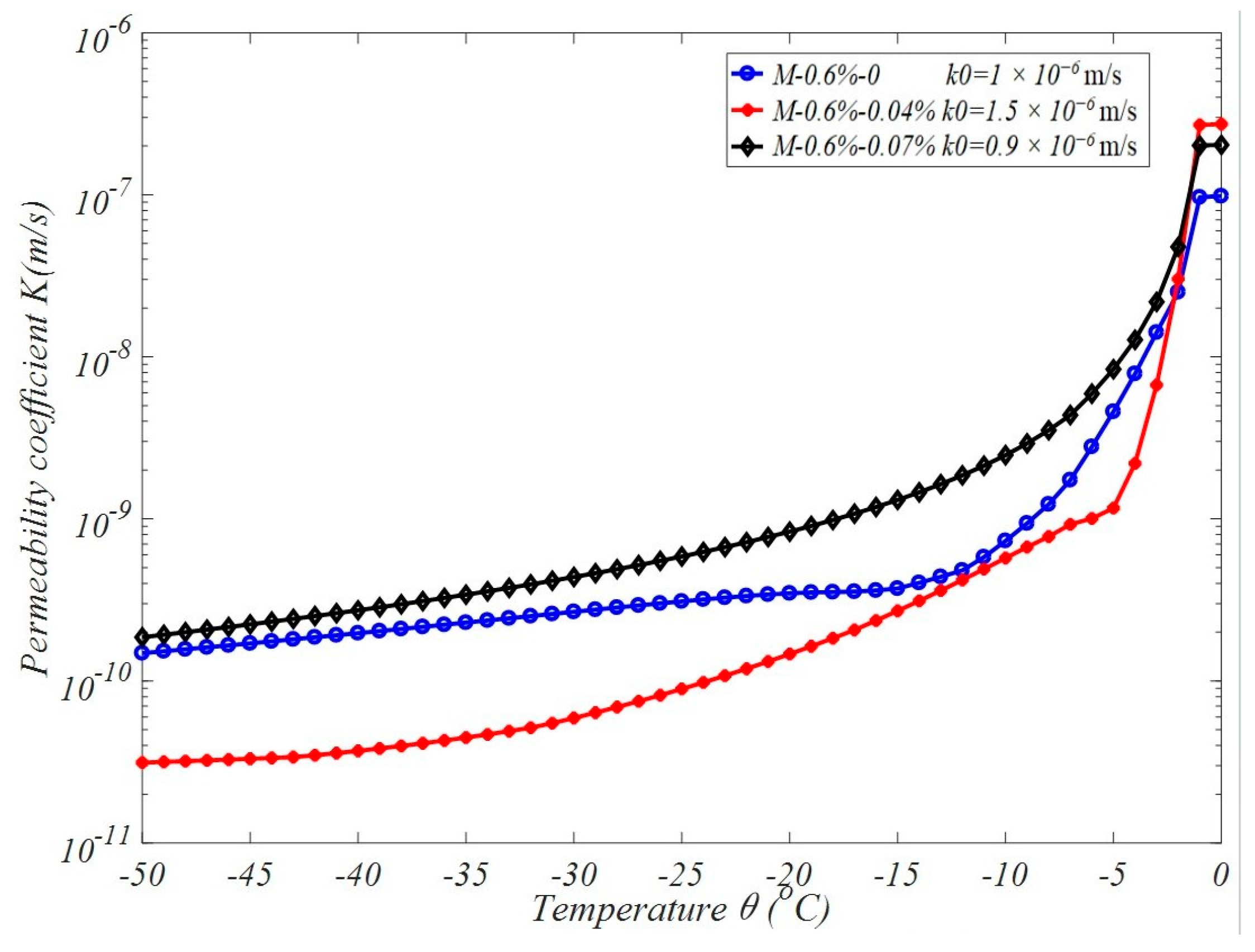
2.2. Effective Permeability Coefficient of Air-Entrained Mortar
2.3. Pore Pressure
3. Fracture Phase-Field Method
3.1. Brittle Fracture Theory
3.2. Phase-Field Approximation of Fracture Energy
3.3. Governing Equation
4. Thermal–Hydraulic–Mechanical Coupling Model for Frost Damage Process in Concrete
4.1. Stress Field
4.2. Seepage Flow Field in Porous Systems
4.3. Temperature Field
5. Simulation of Frost Damage in Concrete Specimens
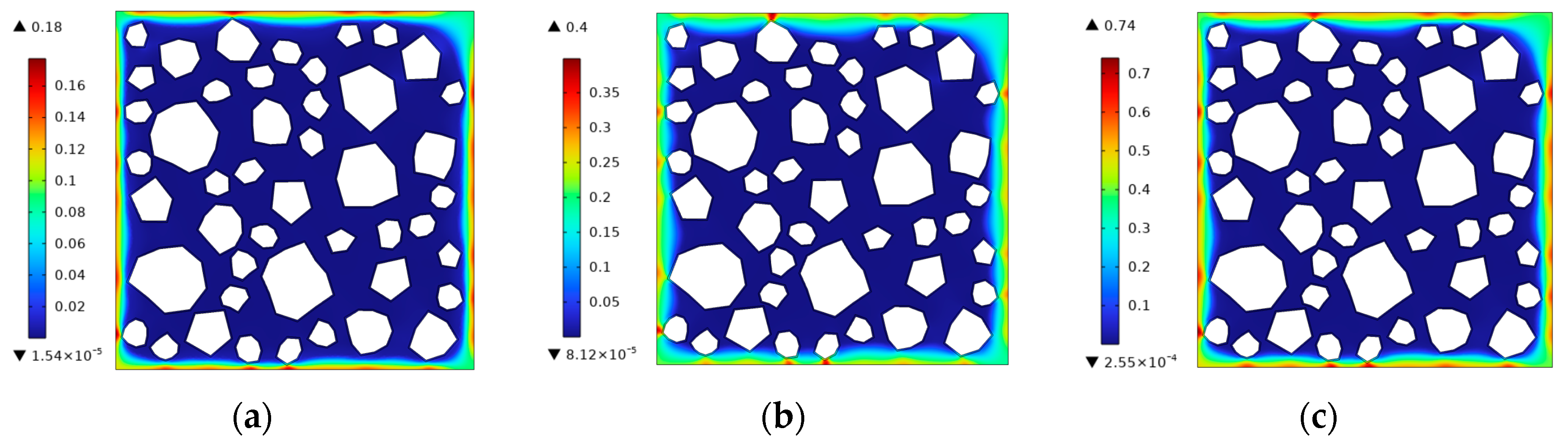
5.1. Frost Damage in Ordinary Concrete Specimens
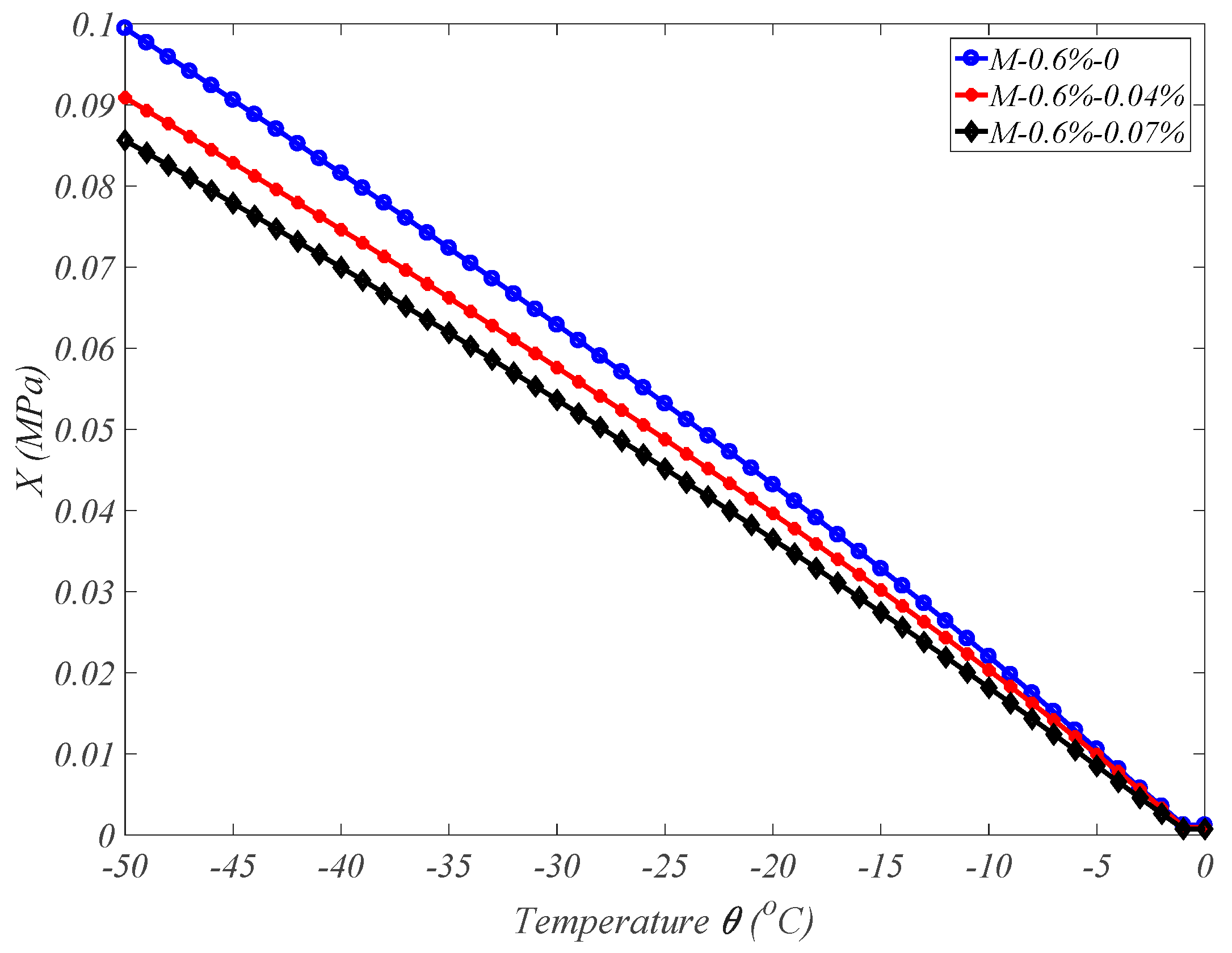
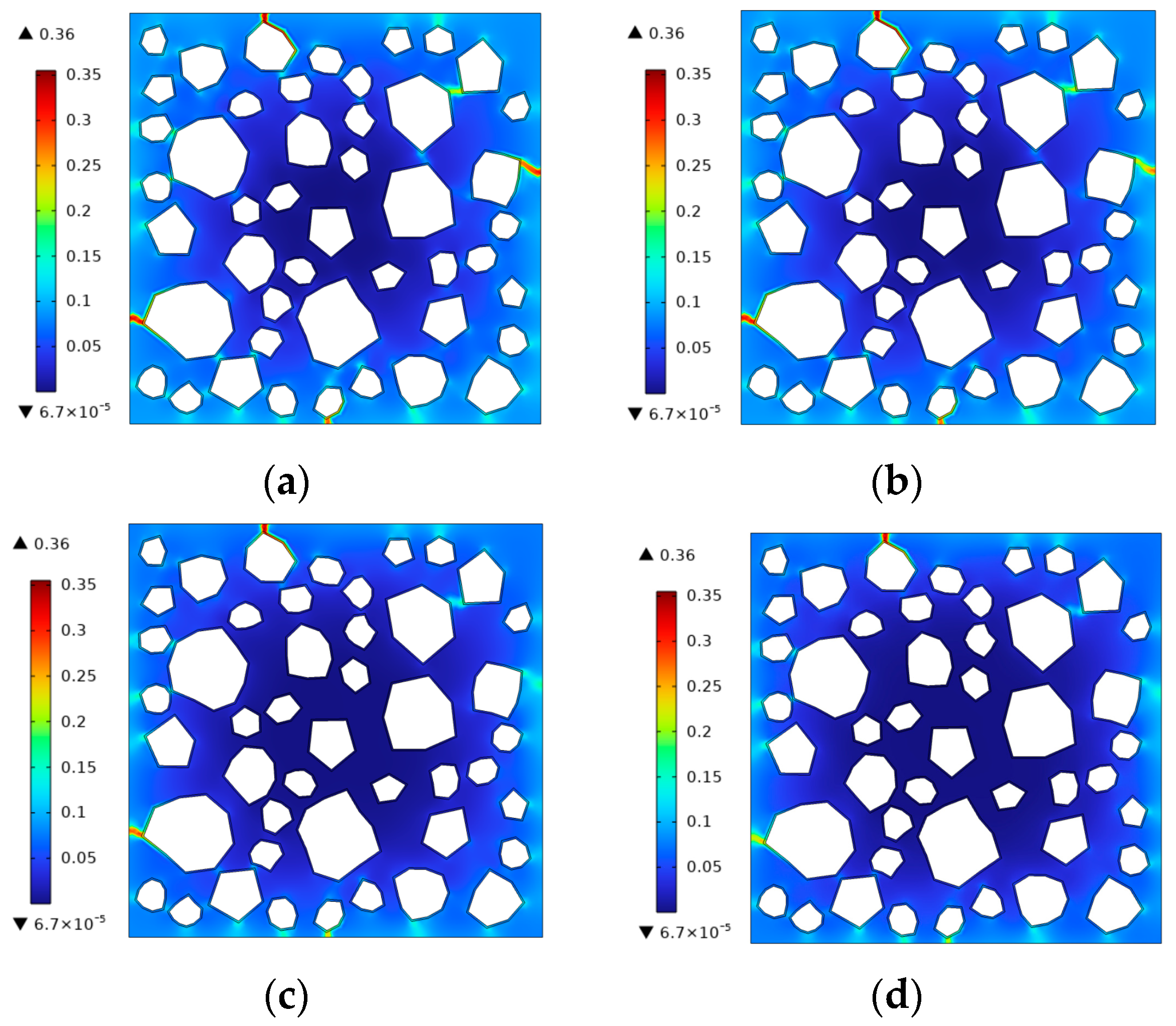
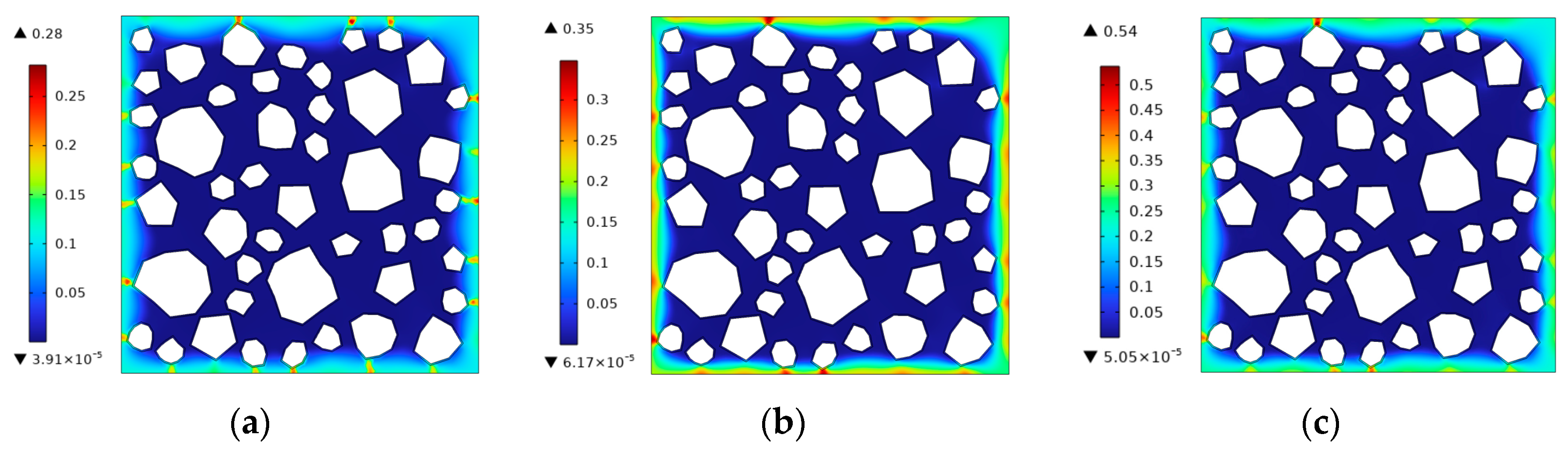
5.2. Frost Damage in Concrete with Different Microbubble Contents
5.3. Frost Damage in Concrete with Different Cooling Rates
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Powers, T.C. The air requirement frost-resistant concrete. Proc. Highw. Res. Board 1949, 29, 184–211. [Google Scholar]
- Scherer, G. Crystallization in pores. Cem. Concr. Res. 1999, 29, 1347–1358. [Google Scholar] [CrossRef]
- Sun, Z.H.; Scherer, G. Effect of air voids on salt scaling and internal freezing. Cem. Concr. Res. 2010, 40, 260–270. [Google Scholar] [CrossRef]
- Mayercsik, N.P.; Vandamme, M. Assessing the efficiency of entrained air voids for freeze-thaw durability through modeling. Cem. Concr. Res. 2016, 88, 43–59. [Google Scholar] [CrossRef]
- Gong, F.Y.; Jacobsen, S. Modeling of water transport in highly saturated concrete with wet surface during freeze/thaw. Cem. Concr. Res. 2019, 115, 294–307. [Google Scholar] [CrossRef]
- Wei, X.; Huai, Z.S.; Chen, F.S.; Sen, Z. Numerical Analysis and Poromechanics Calculation for Saturated Mortar Involved with Sub-Freezing Temperature. Materials 2022, 15, 7885. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Su, C.; Qiao, P.; Sun, L. A thermal-hydraulic-mechanical coupling model for freezing process simulation of cementitious materials with entrained air voids. Constr. Build. Mater. 2020, 243, 118253. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, C.; Liu, X.; Chang, X.; Feng, C. Mesoscopic simulation of thermo-mechanical behaviors in concrete under frost action. Constr. Build. Mater. 2017, 157, 117–131. [Google Scholar] [CrossRef]
- Xie, Y.L. Numerical Simulation of Freeze-Thaw Damage of Concrete; Harbin Institute of Technology: Harbin, China, 2018. [Google Scholar]
- Ng, K.; Dai, Q. Numerical investigation of internal frost damage of digital cement paste samples with cohesive zone modeling and SEM microstructure characterization. Constr. Build. Mater. 2014, 50, 266–275. [Google Scholar] [CrossRef]
- Koniorczyk, M.; Gawin, D.; Schrefler, B.A. Modeling evolution of frost damage in fully saturated porous materials exposed to variable hygro-thermal conditions. Comput. Methods Appl. Mech. Eng. 2015, 297, 38–61. [Google Scholar] [CrossRef]
- Coussy, O.; Monteiro, P.J.M. Poroelastic model for concrete exposed to freezing temperatures. Cem. Concr. Res. 2008, 38, 40–48. [Google Scholar] [CrossRef]
- Wills, J.R. Bounds and self-consistent estimates for the overall properties of anisotropic composite. J. Mech. Phys. Solids 1977, 25, 185–202. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Norris, A.N. A differential scheme for the effective moduli of composites. Mech. Mater. 1985, 4, 1–16. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, K.X.; Chandra, A. A generalized self-consistent mechanics method for composite materials with multiphase inclusions. J. Mech. Phys. Solids 1994, 42, 491–504. [Google Scholar] [CrossRef]
- Olsen, M. Mathematical modeling of the freezing process of concrete and aggregates. Cem. Concr. Res. 1984, 14, 113–122. [Google Scholar] [CrossRef]
- Ortiz, M.; Pandolfi, A. Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int. J. Numer. Methods Eng. 1999, 44, 1267–1282. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Xia, X.Z.; Wu, Z.; Zhang, Q. The effect of initial defects on overall mechanical properties of concrete material. Comput. Mater. Contin. 2020, 62, 413–442. [Google Scholar] [CrossRef]
- Sanz, B.; Planas, J.; Sancho, J.M. An experimental and numerical study of the pattern of cracking of concrete due to steel reinforcement corrosion. Eng. Fract. Mech. 2013, 114, 26–41. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Qiaoyan, G.; Mengyu, Y.; Ke, S.; Tao, Z. Experimental Study and Finite Element Analysis on the Flexural Behavior of Steel Fiber Reinforced Recycled Aggregate Concrete Beams. Materials 2022, 15, 8210. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.C.; Teng, J.G.; Tang, C.A. Mesomechanical model for concrete. Part I: Model development. Mag. Concr. Res. 2004, 56, 313–330. [Google Scholar] [CrossRef]
- Teng, J.G.; Zhu, W.C.; Tang, C.A. Mesomechanical model for concrete. Part II: Application. Mag. Concr. Res. 2004, 56, 331–345. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Lin, F.B. Nonlocal smeared cracking model for concrete fracture. J. Struct. Eng. 1988, 114, 2493–2510. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Pijaudier-Cabot, G. Nonlocal continuum damage localization instability and convergence. J. Appl. Mech. Trans. ASME 1988, 55, 287–293. [Google Scholar] [CrossRef]
- Jirasek, M. Nonlocal models for damage and fracture: Comparison of approaches. Int. J. Solids Struct. 1998, 35, 4133–4145. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Jirásek, M. Nonlocal integral formulations of plasticity and damage: Survey of progress. J. Eng. Mech. 2002, 128, 1119–1149. [Google Scholar] [CrossRef]
- Li, X.; Gu, X.; Xia, X.; Madenci, E.; Chen, A.; Zhang, Q. Peridynamic simulation of micro-internal damage and macro-mechanical properties of cement paste under freeze-thaw cycles. J. Build. Eng. 2024, 31, 109759. [Google Scholar] [CrossRef]
- Wu, P.; Liu, Y.; Peng, X.; Chen, Z. Peridynamic modeling of freeze-thaw damage in concrete structures. Mech. Adv. Mater. Struct. 2023, 30, 2826–2837. [Google Scholar] [CrossRef]
- Nikolaev, P.; Jivkov, A.P.; Margetts, L.; Sedighi, M. Non-local modelling of freezing and thawing of unsaturated soils. Adv. Water Resour. 2024, 184, 104614. [Google Scholar] [CrossRef]
- Bobaru, F.; Zhang, G. Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. Int. J. Fract. 2015, 196, 59–98. [Google Scholar] [CrossRef]
- Breitenfeld, M.S.; Geubelle, P.H.; Weckner, O.; Silling, S. Non-ordinary state-based peridynamic analysis of stationary crack problems. Comput. Methods Appl. Mech. Eng. 2014, 272, 233–250. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Xia, X.Z. Voronoi-based peridynamics and cracking analysis with adaptive refinement. Int. J. Numer. Methods Eng. 2017, 112, 2087–2109. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q. A modified conjugated bond-based peridynamic analysis of impact failure for concrete gravity dam. Meccanica 2020, 55, 547–566. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Z.; Mehrmashhadi, J.; Bobaru, F. A stochastic multiscale peridynamic model for corrosion-induced fracture in reinforced concrete. Eng. Fract. Mech. 2020, 229, 106969. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, L. Peridynamics simulation of shotcrete lining damage characteristics under freeze-thaw cycles in cold region tunnels. Eng. Anal. Bound. Elem. 2022, 141, 17–35. [Google Scholar] [CrossRef]
- Karma, A.; Kessler, D.A.; Levine, H. Phase-field model of mode III dynamic fracture. Phys. Rev. Lett. 2001, 87, 045501. [Google Scholar] [CrossRef] [PubMed]
- Hakim, V.; Karma, A. Laws of crack motion and phase-field models of fracture. J. Mech. Phys. Solids 2009, 57, 342–368. [Google Scholar] [CrossRef]
- Hofacker, M.; Miehe, C. A phase field model of dynamic fracture: Robust field updates for the analysis of complex crack patterns. Int. J. Numer. Methods Eng. 2013, 93, 276–301. [Google Scholar] [CrossRef]
- Wu, J.Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure. J. Mech. Phys. Solids 2017, 103, 72–99. [Google Scholar] [CrossRef]
- Fei, F.; Choo, J. A phase-field model of frictional shear fracture in geologic materials. Comput. Methods Appl. Mech. Eng. 2020, 369, 113265. [Google Scholar] [CrossRef]
- Wu, J.Y.; Nguyen, V.P.; Nguyen, C.T.; Sutula, D.; Sinaie, S.; Bordas, S.P. Phase-field modeling of fracture. Adv. Appl. Mech. 2020, 53, 1–183. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Tanné, E.; Li, T.; Bourdin, B.; Marigo, J.J.; Maurini, C. Crack nucleation in variational phase-field models of brittle fracture. J. Mech. Phys. Solids 2018, 110, 80–99. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A. Past and present of variational fracture. Siam News 2019, 52, 104. [Google Scholar]
- Mandal, T.K.; Nguyen, V.P.; Wu, J.Y. Evaluation of variational phase-field models for dynamic brittle fracture. Eng. Fract. Mech. 2020, 235, 107169. [Google Scholar] [CrossRef]
- Wu, J.Y.; Huang, Y.; Zhou, H.; Nguyen, V.P. Three-dimensional phase-field modeling of mode I+ II/III failure in solids. Comput. Methods Appl. Mech. Eng. 2021, 373, 113537. [Google Scholar] [CrossRef]
- Xia, X.Z.; Qin, C.S.; Lu, G.D.; Gu, X.; Zhang, Z. Simulation of CorrosionInduced Cracking of Reinforced Concrete Based on Fracture Phase Field Method. Comput. Model. Eng. Sci. 2022, 138, 2257–2276. [Google Scholar]
- Fang, X.; Pan, Z.; Chen, A.R.; Tian, H.; Ma, R.J. Phase-field method for modeling non-uniform corrosion-induced cracking in concrete. Eng. Fract. Mech. 2023, 281, 109131. [Google Scholar] [CrossRef]
- Bazant, Z.P. Mathematical model for freeze-thaw durability of concrete. J. Am. Ceram. Soc. 1988, 77, 776–783. [Google Scholar] [CrossRef]
- Penttala, V. Freezing-induced strains and pressures in wet porous materials and especially in concrete mortar. Adv. Cem. Based Mater. 1988, 7, 8–19. [Google Scholar] [CrossRef]
- Fagerlund, G. Determination of pore-size distribution from freezing-point depression. Mater. Struct. 1973, 6, 215–225. [Google Scholar] [CrossRef]
- Romero, E.; Simms, P.H. Microstructure investigation in unsaturated soils: A review with special attention to contribution of Mercury Intrusion Porosimetry and environmental scanning electron microscopy. Geotech. Geol. Eng. 2008, 26, 705–727. [Google Scholar] [CrossRef]
- Chen, Y.J.; Al-Neshawy, F.; Punkki, J. Investigation on the effect of entrained air on pore structure in hardened concrete using MIP. Constr. Build. Mater. 2021, 292, 123441. [Google Scholar] [CrossRef]
- Zuber, B.; Machand, J. Predicting the volume instability of hydrated cement systems upon freezing using poro-mechanics and local phase equilibria. Mater. Struct. 2004, 37, 257–270. [Google Scholar] [CrossRef]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217, 77–95. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Duan, A. Research on Constitutive Relationship of Frozen-Thawed Concrete and Mathematical Modeling of Freeze-Thaw Process; Tsinghua University: Beijing, China, 2009. [Google Scholar]
- Gao, F. Experimental Study on Physical Mechanics of Aerated Concrete and Its Engineering Application; Shenyang Jianzhu University: Shenyang, China, 2019. [Google Scholar]

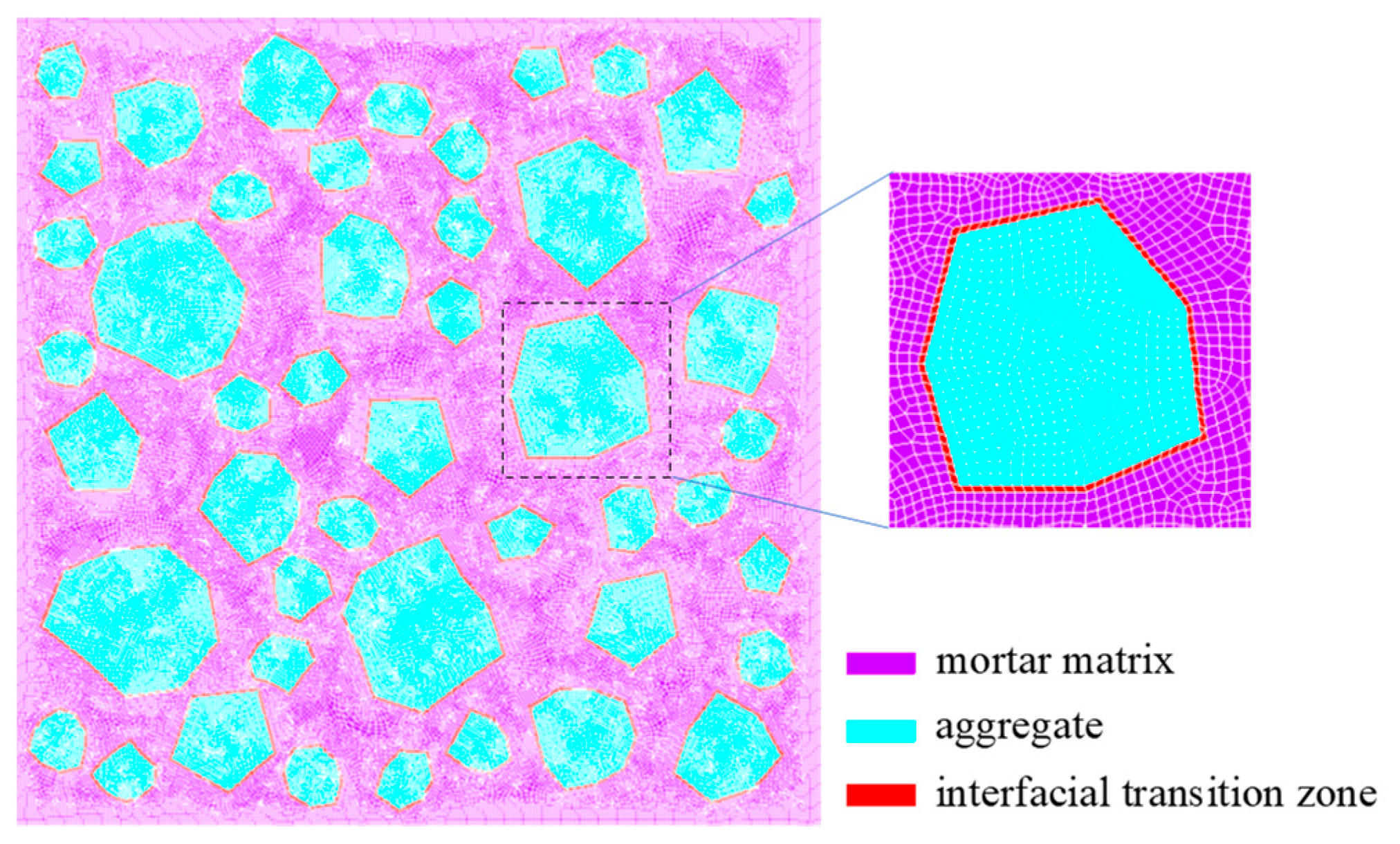


| Component in Concrete | Density (kg/m3) | (GPa) | Poisson’s | (mm) | (J/m2) |
|---|---|---|---|---|---|
| Aggregate | 2600 | 70.0 | 0.2 | ||
| Mortar matrix | 2140 | 10.1 | 0.2 | 0.45 | 15.0 |
| ITZ | 2140 | 7.0 | 0.2 | 0.3 | 10.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xue, F.; Gu, X.; Xia, X. Simulation of Frost-Heave Failure of Air-Entrained Concrete Based on Thermal–Hydraulic–Mechanical Coupling Model. Materials 2024, 17, 3727. https://doi.org/10.3390/ma17153727
Wang X, Xue F, Gu X, Xia X. Simulation of Frost-Heave Failure of Air-Entrained Concrete Based on Thermal–Hydraulic–Mechanical Coupling Model. Materials. 2024; 17(15):3727. https://doi.org/10.3390/ma17153727
Chicago/Turabian StyleWang, Xinmiao, Feng Xue, Xin Gu, and Xiaozhou Xia. 2024. "Simulation of Frost-Heave Failure of Air-Entrained Concrete Based on Thermal–Hydraulic–Mechanical Coupling Model" Materials 17, no. 15: 3727. https://doi.org/10.3390/ma17153727






