Examining Shape Dependence on Small Mild Steel Specimens during Heating Processes
Abstract
:1. Introduction
2. Materials and Methods
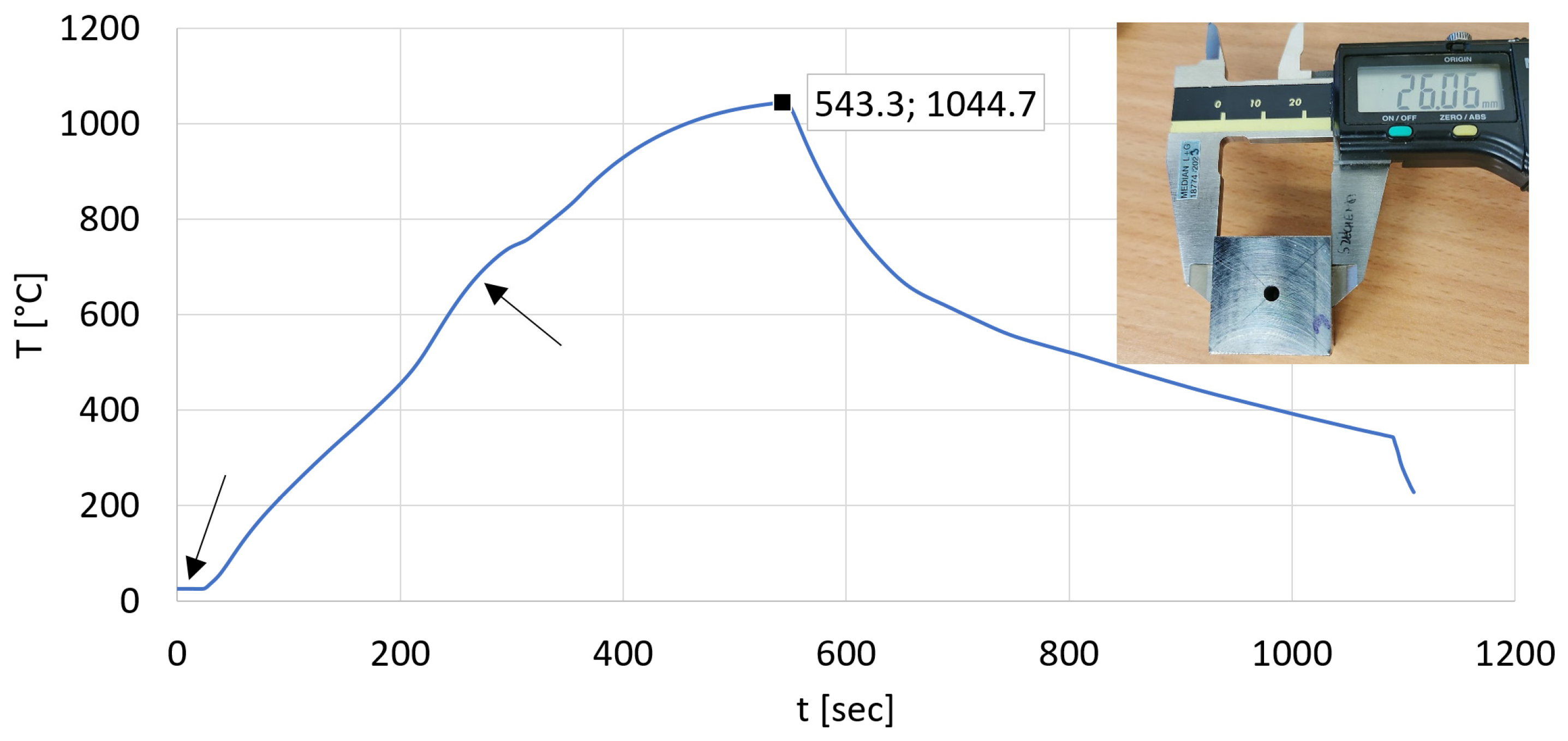
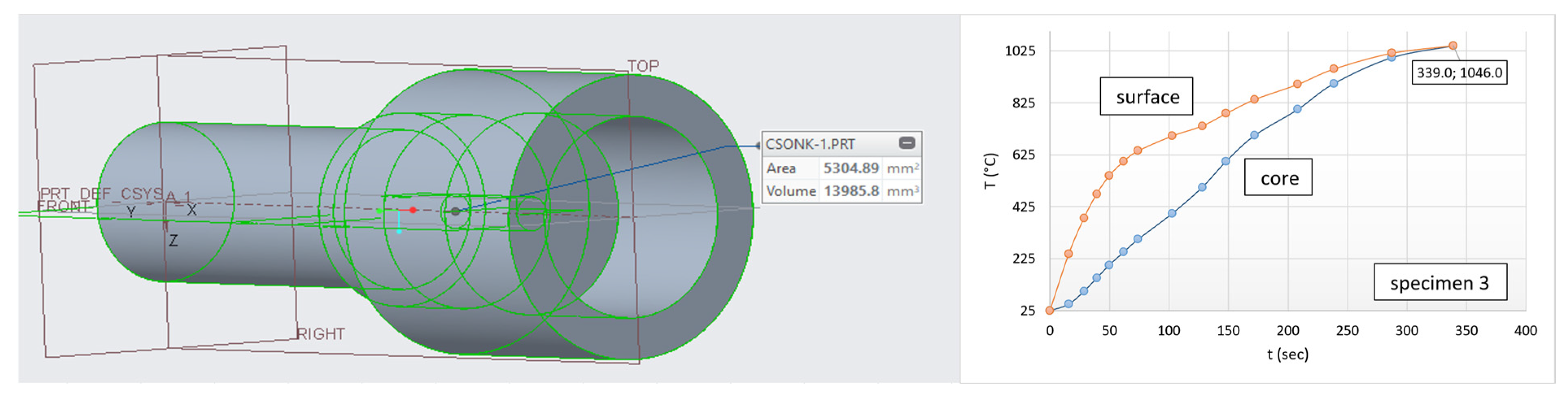
2.1. Data Collection
2.2. The Biot Number
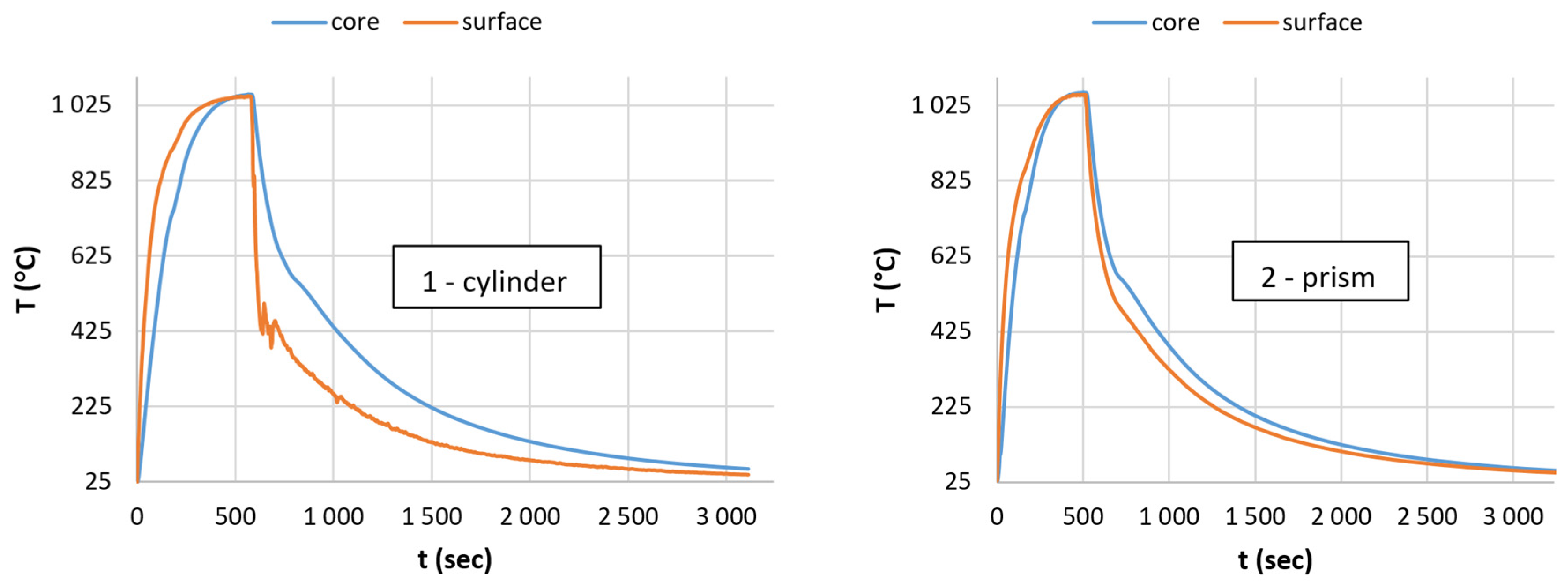
3. Results
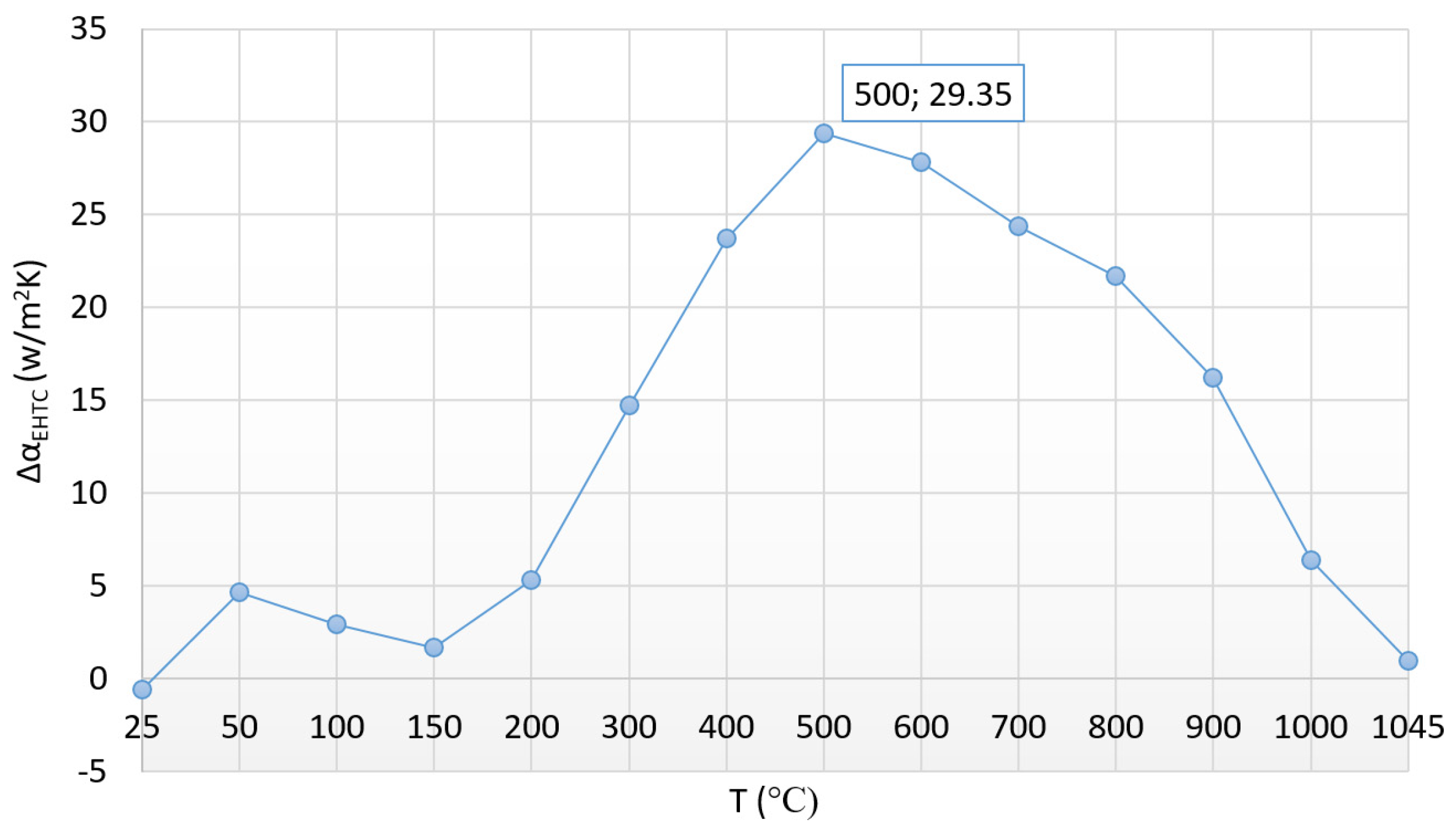
3.1. The Heat Transfer Factors
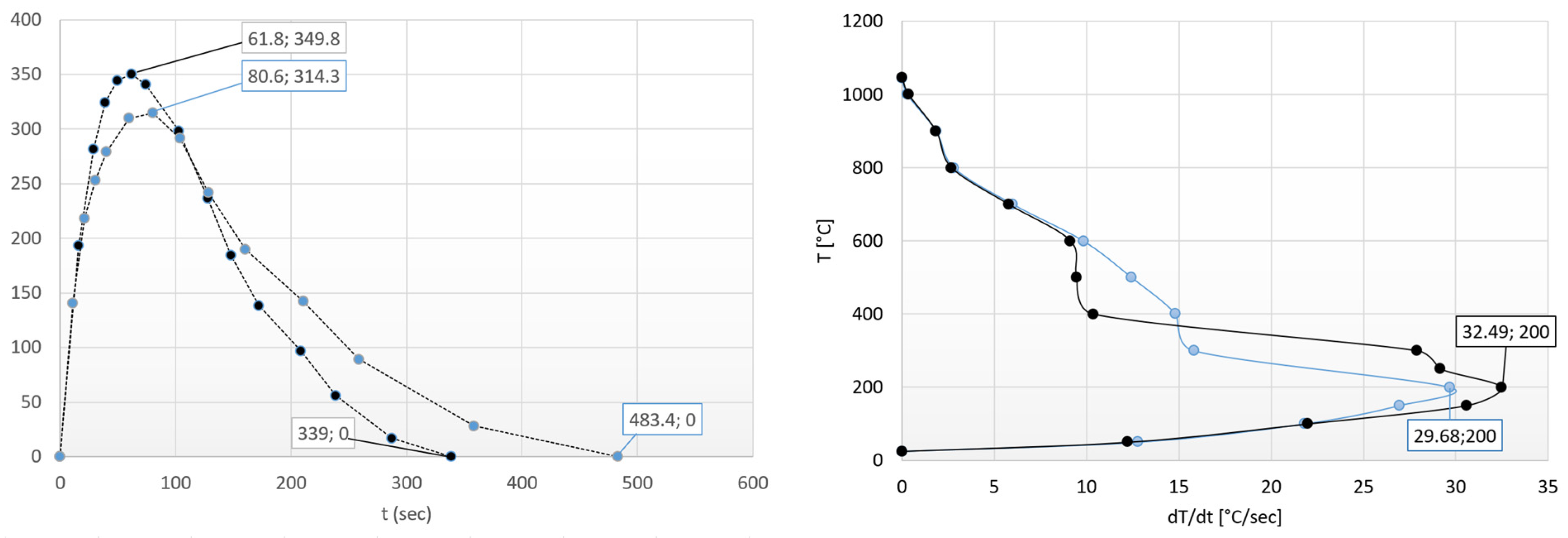
3.2. The Heat Equalization Process
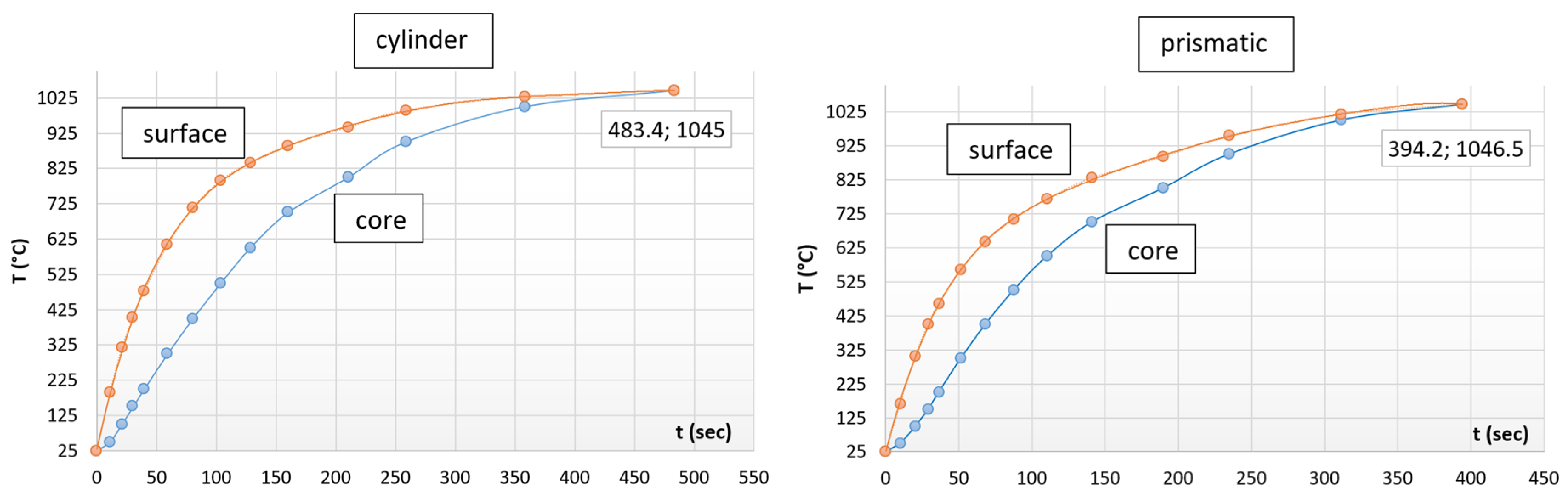
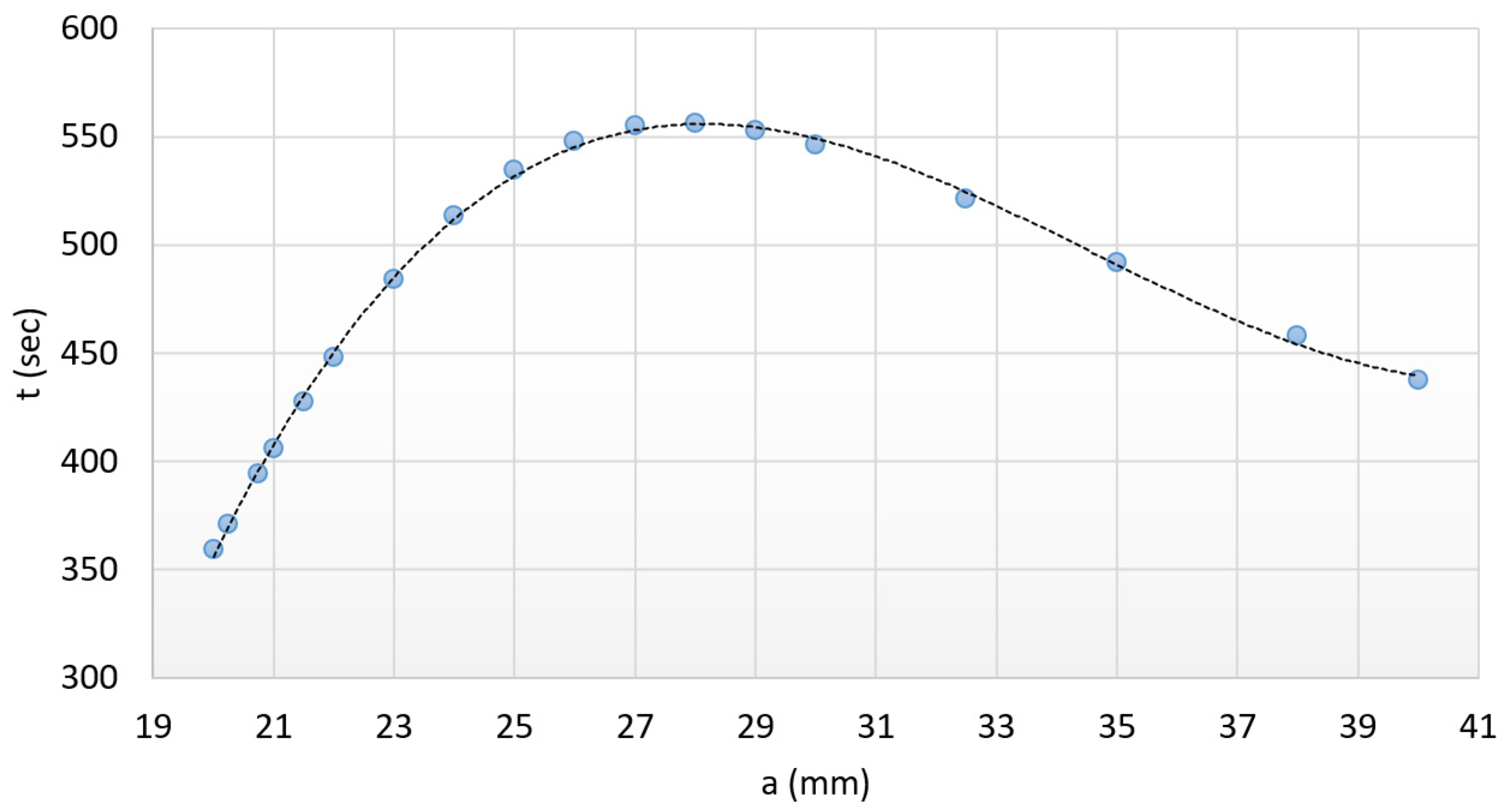
3.3. The Optimal Heating Time
- -
- The nature of heat transfer must be similar to the above-investigated system; consequently, only the size of the active surfaces can affect the required heating time.
- -
- .
3.4. The Applicability of Heating Time
- -
- Thermocouple made by TC Direct (Uxbridge, UK), N type, 1.5 mm and 3 mm diameter, Class 2: at a temperature of 1060 °C, the permissible deviation is 8 °C.
- -
- Furnace space PID control unit: permissible deviation at a temperature of 1060 °C is 10.6 °C.
4. Discussion
5. Conclusions
- -
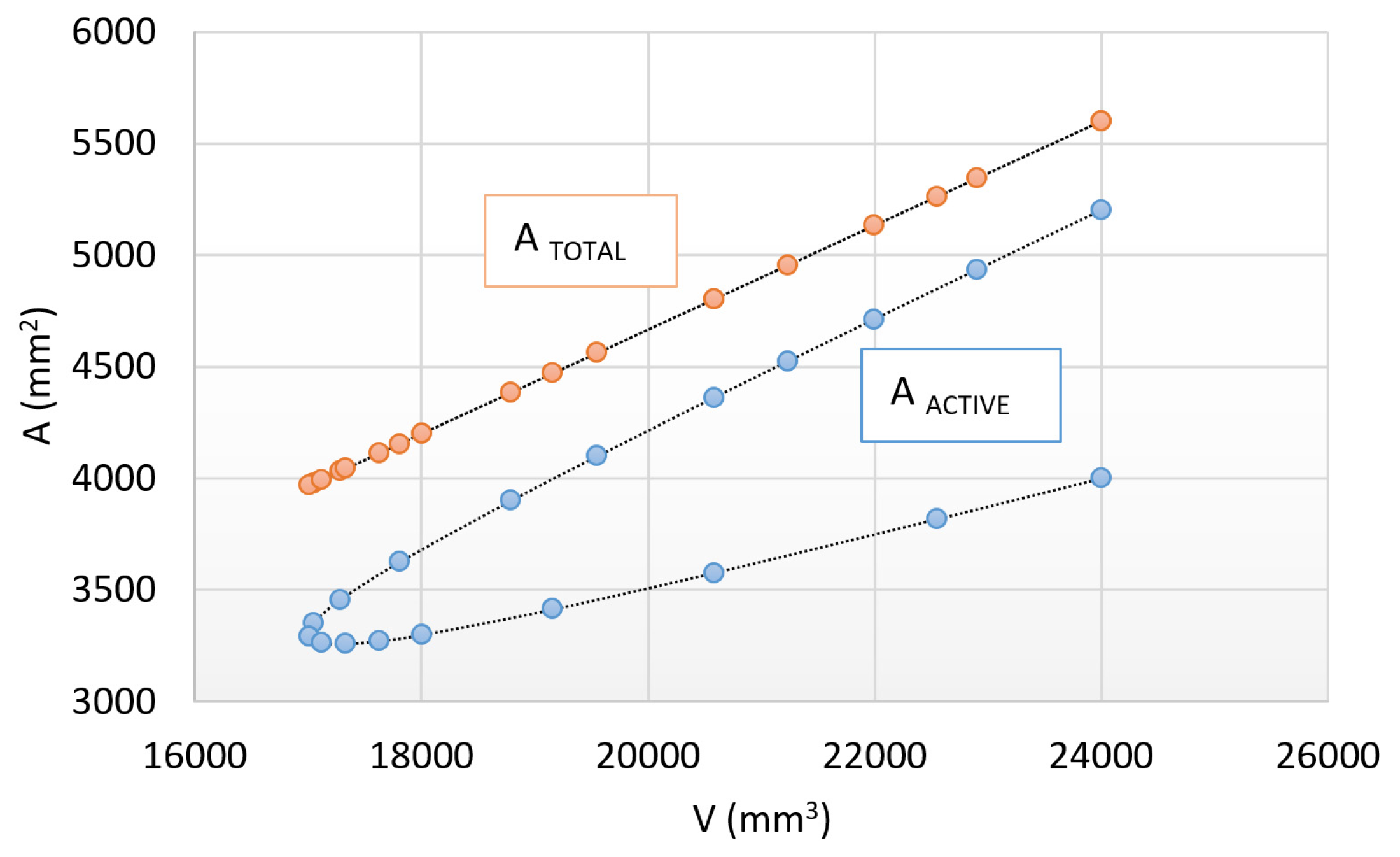
- Complex geometric shapes can be characterized by a larger surface area and a lower heat transfer coefficient, which can lead to a shorter heating time in the case of the same surface-to-volume ratio.
- -
- Heating time is basically determined by the size and shape of the active surfaces; therefore, in the case of the same shape, volume and total surface, the larger active surface can be associated with a shorter heating time of up to 20%.
- -
- As a result of the experiments, a shape factor between the cylinder and the prismatic-shaped specimen was established, which equals 1.125.
- -
- The mathematical relationship between the amount of heat that can be stored in the body during heat equalization and the complexity of the shape is established, which is characterized through ratios depending on heating times and active surfaces in the function of total surface-to-volume ratio.
- -
- The mathematical relationship between the rate of heat equalization and the surface-to-volume ratio is established. These results point out that in the case of a larger surface-to-volume ratio, which means a smaller cross-section, heat equalization occurs sooner; consequently, the heating time will be shorter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| the dimensionless Biot number (-) | |
| the effective heat transfer coefficient (sum up convection and radiation) (W/m2·K) | |
| the effective thermal conductivity of scaled specimen (W/m·K) | |
| the characteristic length (ratio of the volume and the surface) (m) | |
| the radiation heat transfer coefficient (W/m2·K) | |
| the convective heat transfer coefficient (W/m2·K) | |
| dimensionless emissivity constant (henceforth, its value is 0.8) | |
| the Stefan–Boltzmann constant (5.67 × 10−8 W/m2·K4) | |
| the surface temperature of the specimen (K) | |
| the furnace space temperature inside (K) | |
| the radiation heat transfer coefficient (W/m2·K) | |
| the dimensionless Nusselt number (-) | |
| the crucial length of the specimen (m) | |
| the effective thermal conductivity of the air film near the surface (W/m·K) | |
| the dimensionless Rayleigh number (-) | |
| the diameter of the specimen (m) | |
| the dimensionless Prandtl number (-) | |
| the dynamic viscosity of dry air near the specimen surface (kg/m·s) | |
| the specific heat of dry air near the specimen surface (J/kg·K) | |
| the thermal conductivity of dry air near the specimen surface (W/m·K) | |
| the dimensionless Grashof number (-) | |
| the gravitational acceleration (9.81 m/s2) | |
| the dry air thermal expansion coefficient a good approximation for gases is the reciprocal of the air temperature in Kelvin: (1/K) | |
| the dry air film temperature that surrounds the specimen, which is the average of the surface temperature of the furnace space and test specimen (K) | |
| the kinematic viscosity of dry air near the specimen surface (m2/s) | |
| the scale thickness at a given moment (μm) | |
| the universal gas constant (8.314 J/K·mol) | |
| the heating temperature which is equal to the surface temperature (K) | |
| the heating time of specimen (s) | |
| the specific heat of the specimen considering the scaled surface at 1045 °C (611.585 J/kg °C) | |
| the density of the specimen considering the scaled surface at 1045 °C (7481.43 kg/m3) | |
| the perpendicular distance between the surface and the core referring to the radius of cylinder (m) | |
| the heat conduction of S460N steel at 1050 °C (−28.35 W/m °C) | |
| the aggregated heat transfer coefficient of the cylindrical specimen at 1045 °C (427.5 W/m2 °C) | |
| the value of the entire surface-to-volume ratio expressed in meters (m−1) | |
| all heating time of the cylindrical-shaped specimen (s) | |
| all heating time of the prismatic-shaped specimen (s) | |
| the active surface of the prismatic-shaped specimen (m2) | |
| the active surface of the cylindrical specimen (m2) | |
| all heating time of the new prismatic-shaped specimen (s) | |
| the active surface of the new prismatic-shaped specimen (m2) | |
| the side distance of prismatic specimen (m) | |
| the height of the specimen (m) | |
| the average diameter of the specimen (m) | |
| the heat capacity matrix (J/K) | |
| the time derivative of the temperature (K/s) | |
| the thermal conductivity matrix (W/m·K) | |
| the nodal temperature vector (m·K) | |
| the thermal load vector (W) | |
| all heating time of the spindle-shaped specimen (s) | |
| the total surface of the cylindrical specimen (m2) | |
| the total surface of the spindle-shaped specimen (m2) |
References
- Adamczyk, J.; Grajcar, A. Heat treatment and mechanical properties of low-carbon steel with dual-phase microstructure. J. Achiev. Mater. Manuf. Eng. 2007, 22, 13–20. [Google Scholar]
- Gaggiotti, M.; Albini, L.; Nunzio, P.E.; Schino, A.; Stornelli, G.; Tiracorrendo, G. Ultrafast Heating Heat Treatment Effect on the Microstructure and Properties of Steels. Metals 2022, 12, 1313. [Google Scholar] [CrossRef]
- Santofimia, M.J.; Zhao, L.; Sietsma, J. Microstructural Evolution of a Low-Carbon Steel during Application of Quenching and Partitioning Heat Treatments after Partial Austenitization. Metall. Mater. Trans. A 2009, 40A, 46–57. [Google Scholar] [CrossRef]
- Phoumiphon, N.; Othman, R.; Ismail, A.B. Improment in Mechanical Properties Plain Low Carbon Steel Via Cold Rolling and Intercritical Annealing. Proc. Chem. 2016, 19, 822–827. [Google Scholar] [CrossRef]
- Zurnadzhy, V.; Stavrovskaia, V.; Chabak, Y.; Petryshynets, I.; Efremenko, B.; Wu, K.; Efremenko, V.; Brykov, M. Enhancing the Tensile Properties and Ductile-Brittle Transition Behavior of the EN S355 Grade Rolled Steel via Cost-Saving Processing Routes. Materials 2024, 17, 1958. [Google Scholar] [CrossRef] [PubMed]
- Maciejewski, K.; Sun, Y.; Gregory, O.; Ghonem, H. Time-Dependent Deformation of Low Carbon Steel at Elevated Temperatures. Mater. Sci. Eng. 2012, 534, 147–156. [Google Scholar] [CrossRef]
- Charles, M.; Deskevich, N.; Varkey, V.; Voigt, R.; Wollenburg, A. Heat Treatment Procedure Qualification for Steel Castings; The Pennsylvania State University: University Park, PA, USA, 2004. [Google Scholar]
- Steinboeck, A.; Graichen, K.; Kugi, A. Dynamic optimization of a slab reheating furnace with consistent approximation of control variables. IEEE Trans. Control. Syst. Technol. 2011, 19, 1444–1456. [Google Scholar] [CrossRef]
- Hirbodi, K.; Jafarpur, K. A simple and accurate model for conduction shape factor of hollow cylinders. Int. J. Therm. Sci. 2020, 153, 106362. [Google Scholar] [CrossRef]
- Uhm, S.; Moon, J.; Lee, C.; Yoon, J.; Lee, B. Prediction Model for the Austenite Grain Size in the Coarse-Grained Heat Affected Zone of Fe–C–Mn Steels: Considering the Effect of Initial Grain Size on Isothermal Growth Behavior. ISIJ Int. 2004, 44, 1230–1237. [Google Scholar] [CrossRef]
- Hwang, J.K. Comparison of Thermal Behaviors of Carbon and Stainless-Steel Billets during the Heating Process. Materials 2024, 17, 183. [Google Scholar] [CrossRef] [PubMed]
- Hofmeister, A.M. Dependence of Heat Transport in Solids on Length-Scale, Pressure, and Temperature: Implications for Mechanisms and Thermodynamics. Materials 2021, 14, 449. [Google Scholar] [CrossRef] [PubMed]
- ASTM E112-13(2021); Standard Test Methods for Determining Average Grain Size. ASTM International: West Conshohocken, PA, USA, 2021.
- EN 1011-2:2001; Welding-Recommendations for welding of metallic materials-Part 2: Arc welding of ferritic steels. CEN-Europen Comittee for Standardization: Brussels, Belgium, 2001.
- Lienhard, J.H., IV; Lienhard, J.H., V. A Heat Transfer Textbook, 3rd ed.; Phlogiston Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Gono, R.; Hradílek, Z.; Král, V. Electro Thermal Technology; Technical University of Ostrava: Ostrava, Czech Republic, 2015. [Google Scholar]
- Wickström, U. Adiabatic Surface Temperature and the Plate Thermometer for Calculating Heat Transfer and Controlling Fire Resistance Furnaces, Fire Safety Science. In Proceedings of the 9th International Symposium, University of Karlsruhe, Karlsruhe, Germany, 21–26 September 2008. [Google Scholar]
- Narang, V.A. Heat Transfer Analysis in Steel Structures; Worcester Polytechnic Institute, Civil and Environmental Engineering: Worcester, MA, USA, 2005. [Google Scholar]
- Day, J.C.; Zemler, M.K.; Traum, M.J.; Boetcher, S.K. Laminar Natural Convection from Isothermal Vertical Cylinders: Revisiting a Classical Subject. J. Heat Transf. 2013, 135, 1–9. [Google Scholar] [CrossRef]
- Roncati, D. Iterative Calculation of the Heat Transfer Coefficient; Progettazione Ottica Roncati: Ferrara, Italy, 2022. [Google Scholar]
- Tancsics, F.; Ibriksz, T. Determining the optimum heating time of small sized test specimen made from weldable mild steel. Mat. Sci. Eng. 2020, 903, 012033. [Google Scholar] [CrossRef]
- Raudensky, M.; Chabicovsky, M.; Hrabovsky, J. Impact of Oxide Scale on Heat Treatment of Steels. In Proceedings of the 23rd International Conference on Metallurgy and Materials, Brno, Czech Republic, 21–23 May 2014. [Google Scholar]
- Kawahara, T.; Hidaka, S.; Nishiyama, T.; Takahashi, K.; Takata, Y. Thermal Conductivity Measurement of Iron Scale at High Temperature by Laser Flash Method. In Proceedings of the Asian Conference on Thermal Sciences 2017, 1st ACTS, Jeju Island, Republic of Korea, 26–30 March 2017. [Google Scholar]
- Endo, R.; Yagi, T.; Ueda, M.; Susa, M. Thermal Diffusivity Measurement of Oxide Scale Formed on Steel during Hot-rolling Process. ISIJ Int. 2014, 54, 2084–2088. [Google Scholar] [CrossRef]
- Li, M.; Endo, R.; Akoshima, M.; Susa, M. Temperature Dependence of Thermal Diffusivity and Conductivity of FeO Scale Produced on Iron by Thermal Oxidation. ISIJ Int. 2017, 57, 2097–2106. [Google Scholar] [CrossRef]
- Czinege, I.; Harangozó, D. Application of artificial neural networks for characterization of formability properties of sheet meals. Int. J. Lightweight Mat. Manufact. 2024, 7, 37–44. [Google Scholar]







| Parameters | Input |
|---|---|
| FEM software | Simufact Forming 15.0 |
| Simulation type | 2D |
| Cylinder geometry | Ø20 × 60 mm |
| Material model | S460 |
| Workpiece initial temperature | 25 °C |
| Heat transfer coefficient on average value | 299.3 W/m2 °C |
| Emissivity of heat radiation for cold workpiece | automatic |
| Mesher type | 2D-FE Quadtree |
| Element edge length | 0.8 mm |
| Heating time | 483.4 s |
| Furnace temperature | 1046.5 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibriksz, T.; Fekete, G.; Tancsics, F. Examining Shape Dependence on Small Mild Steel Specimens during Heating Processes. Materials 2024, 17, 3912. https://doi.org/10.3390/ma17163912
Ibriksz T, Fekete G, Tancsics F. Examining Shape Dependence on Small Mild Steel Specimens during Heating Processes. Materials. 2024; 17(16):3912. https://doi.org/10.3390/ma17163912
Chicago/Turabian StyleIbriksz, Tamás, Gusztáv Fekete, and Ferenc Tancsics. 2024. "Examining Shape Dependence on Small Mild Steel Specimens during Heating Processes" Materials 17, no. 16: 3912. https://doi.org/10.3390/ma17163912







