Inverse Method to Determine Parameters for Time-Dependent and Cyclic Plastic Material Behavior from Instrumented Indentation Tests
Abstract
:1. Introduction
2. Material and Experiments
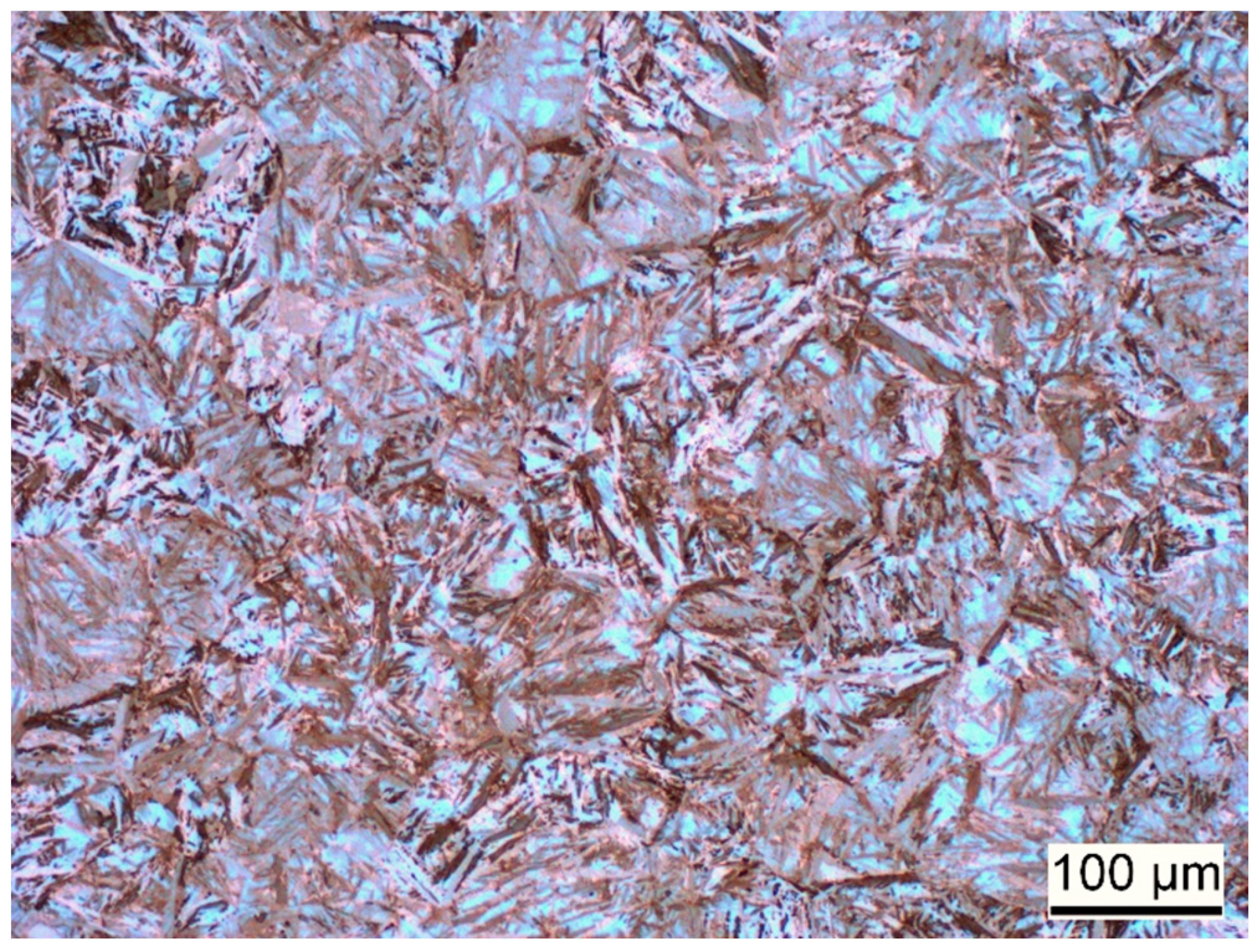
2.1. Material Specifications
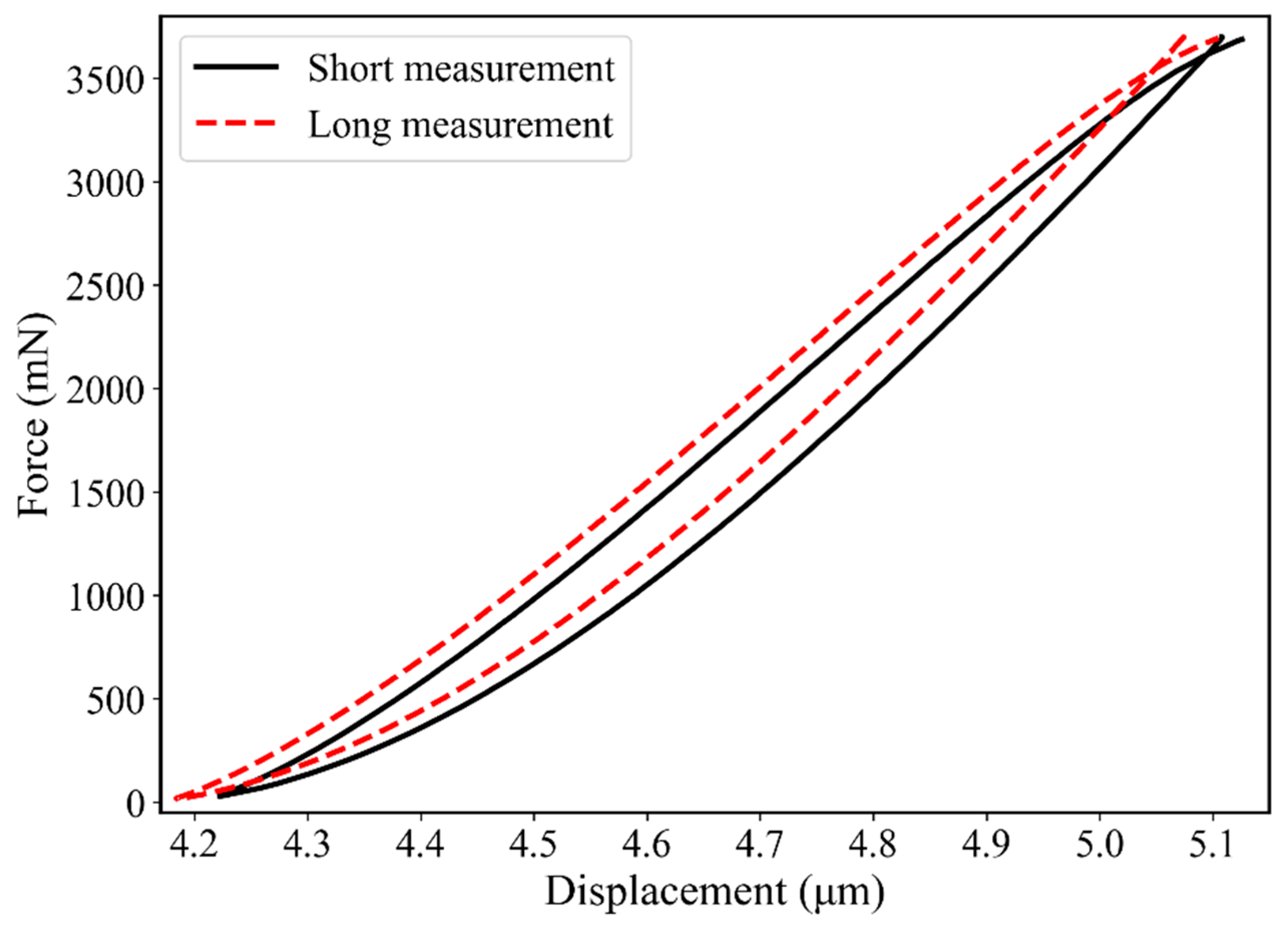
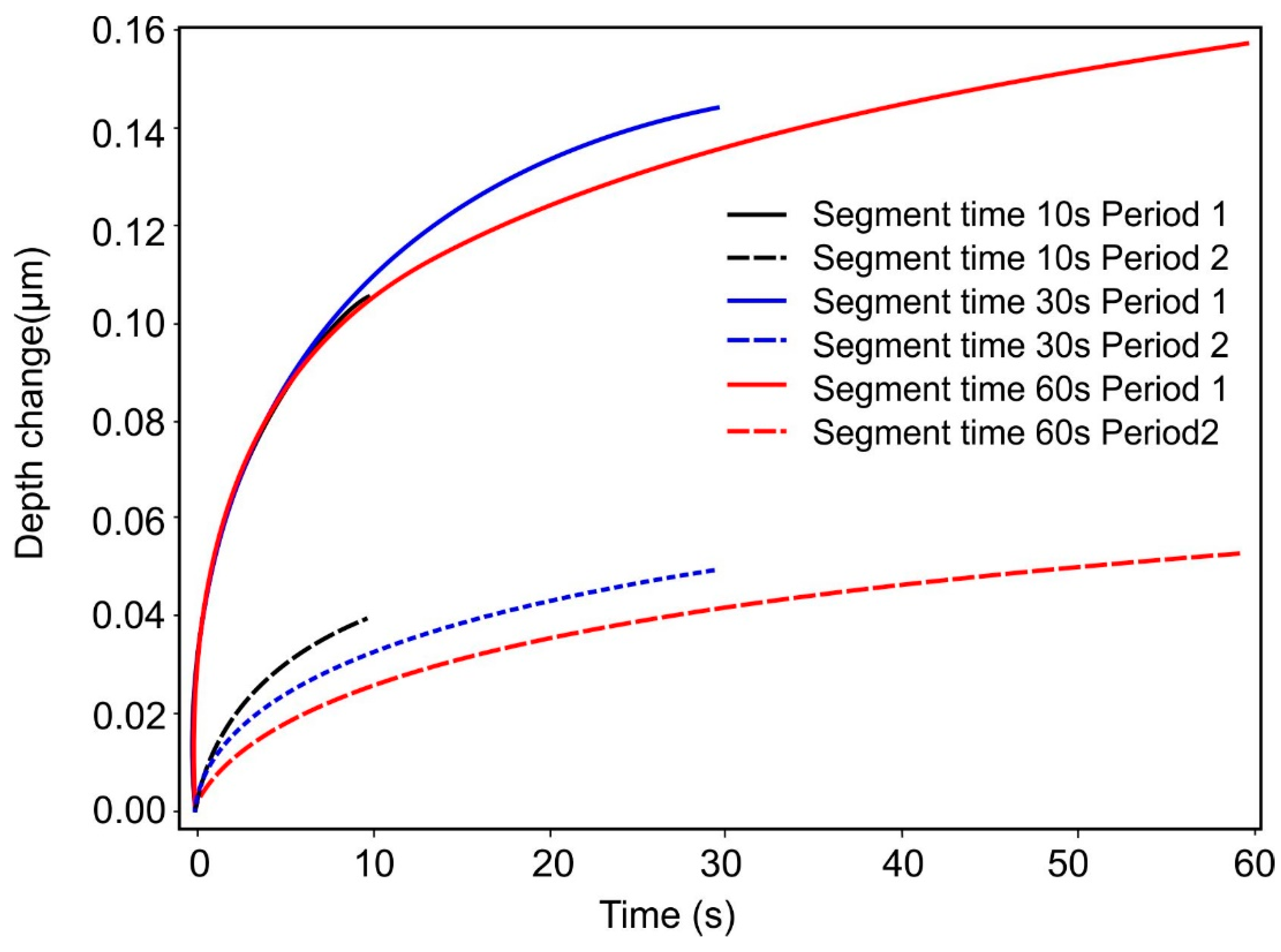
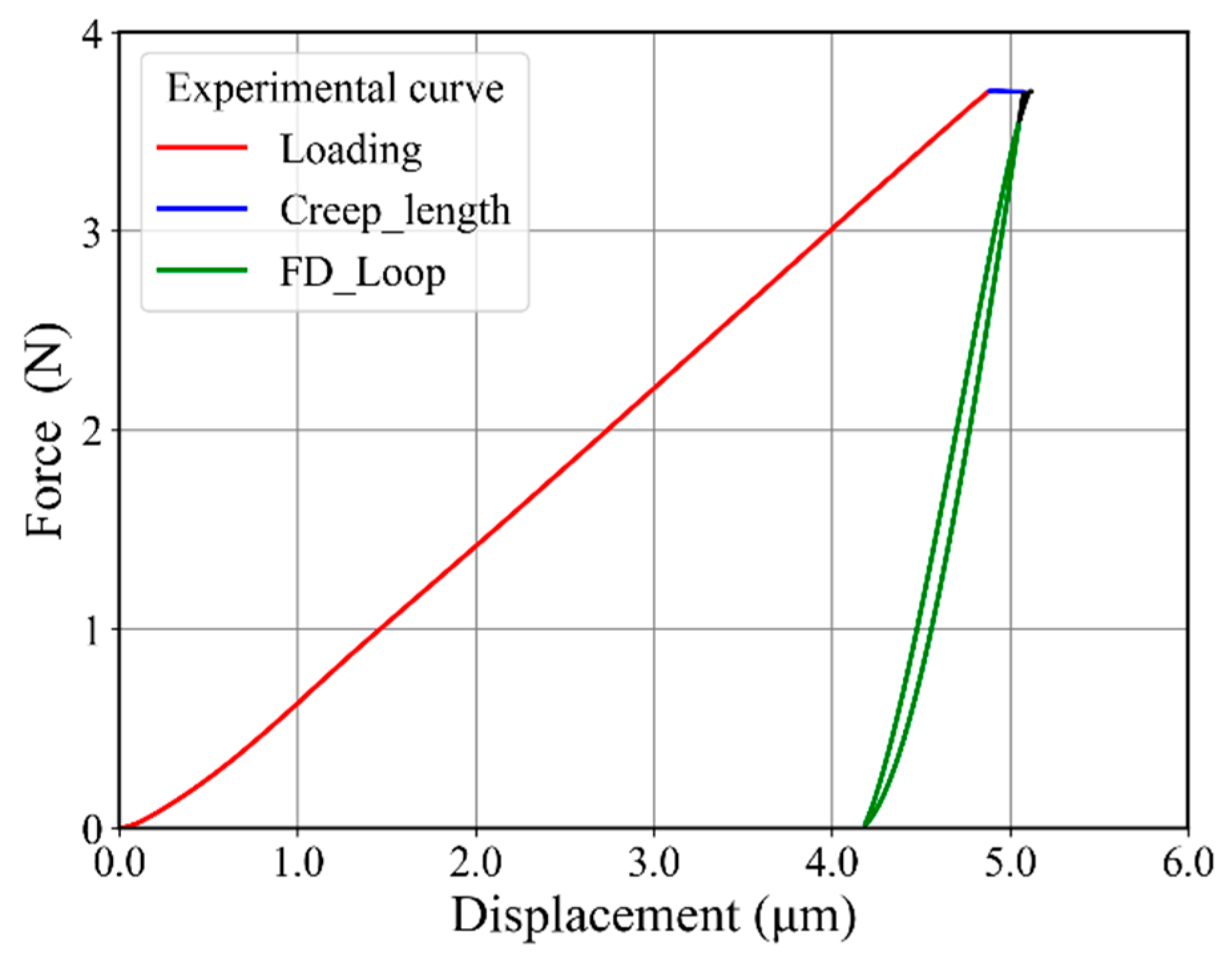
2.2. Experimental Procedure
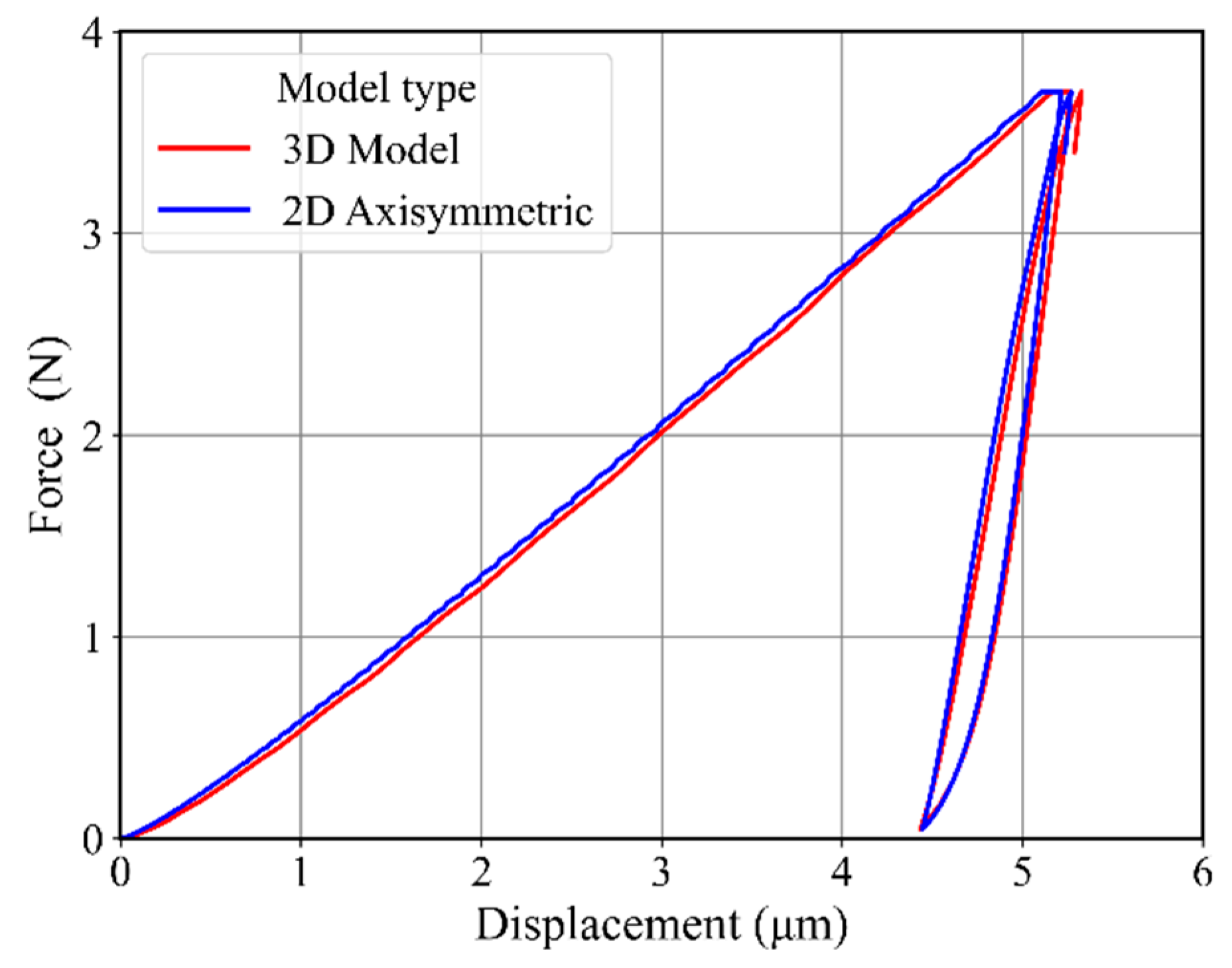
3. Numerical Model
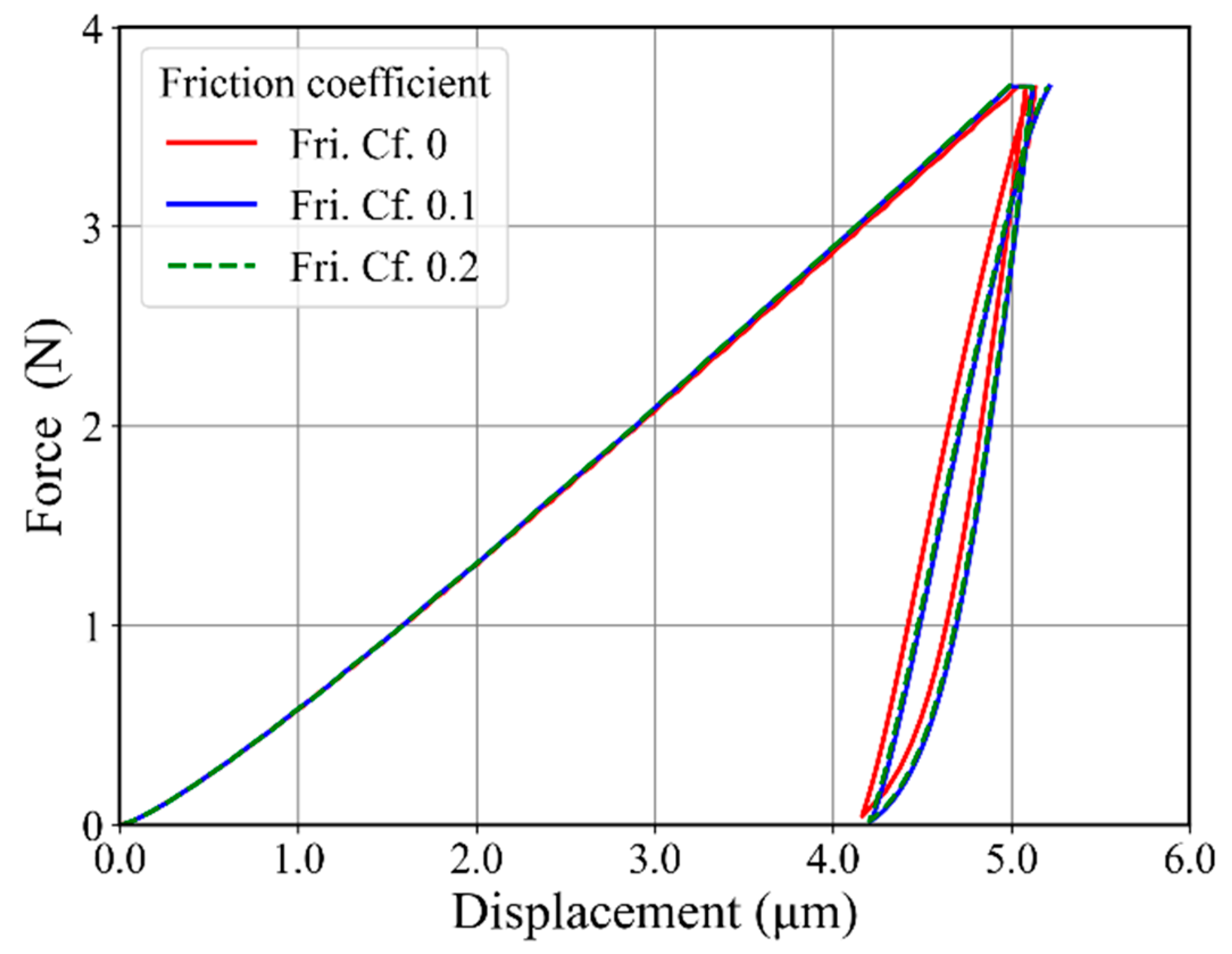
3.1. Friction Effect
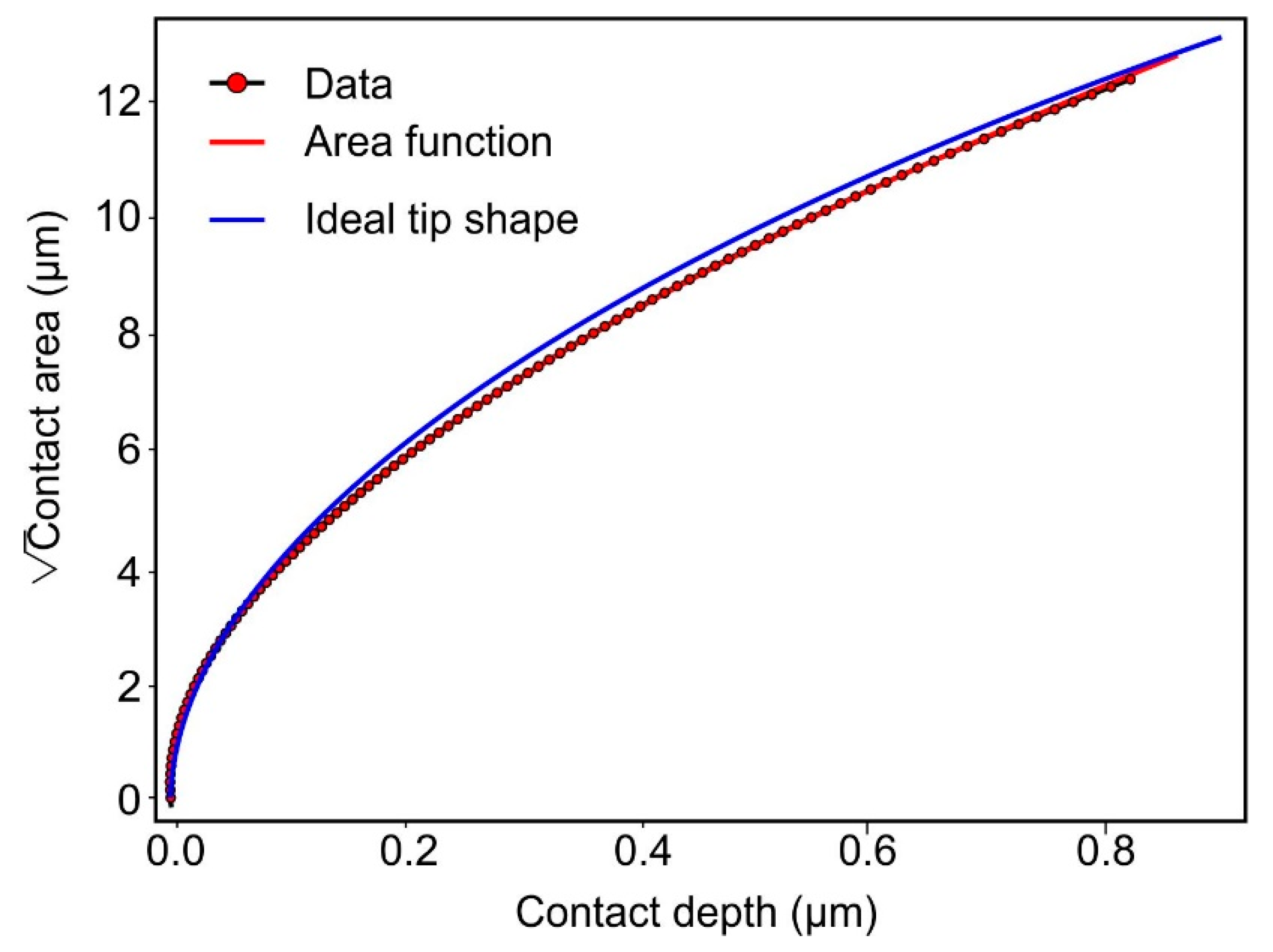
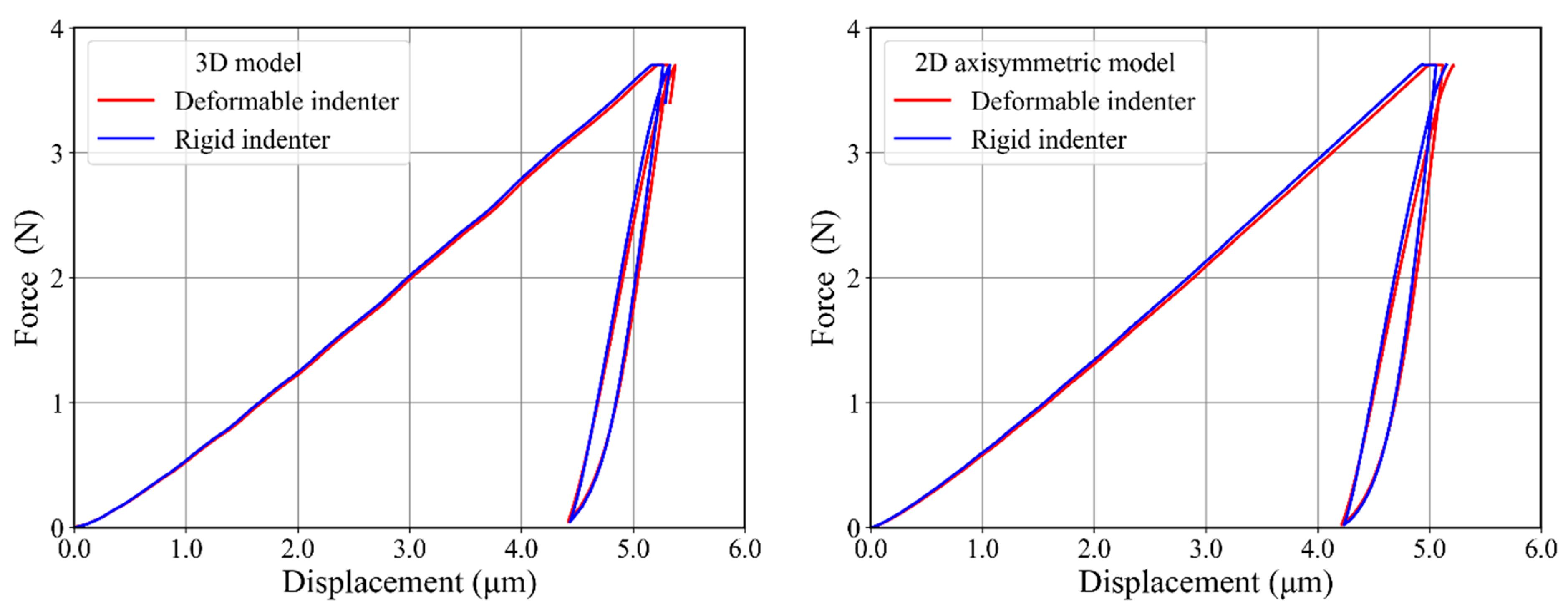
3.2. Rigid and Deformable Indenter
3.3. Constitutive Model
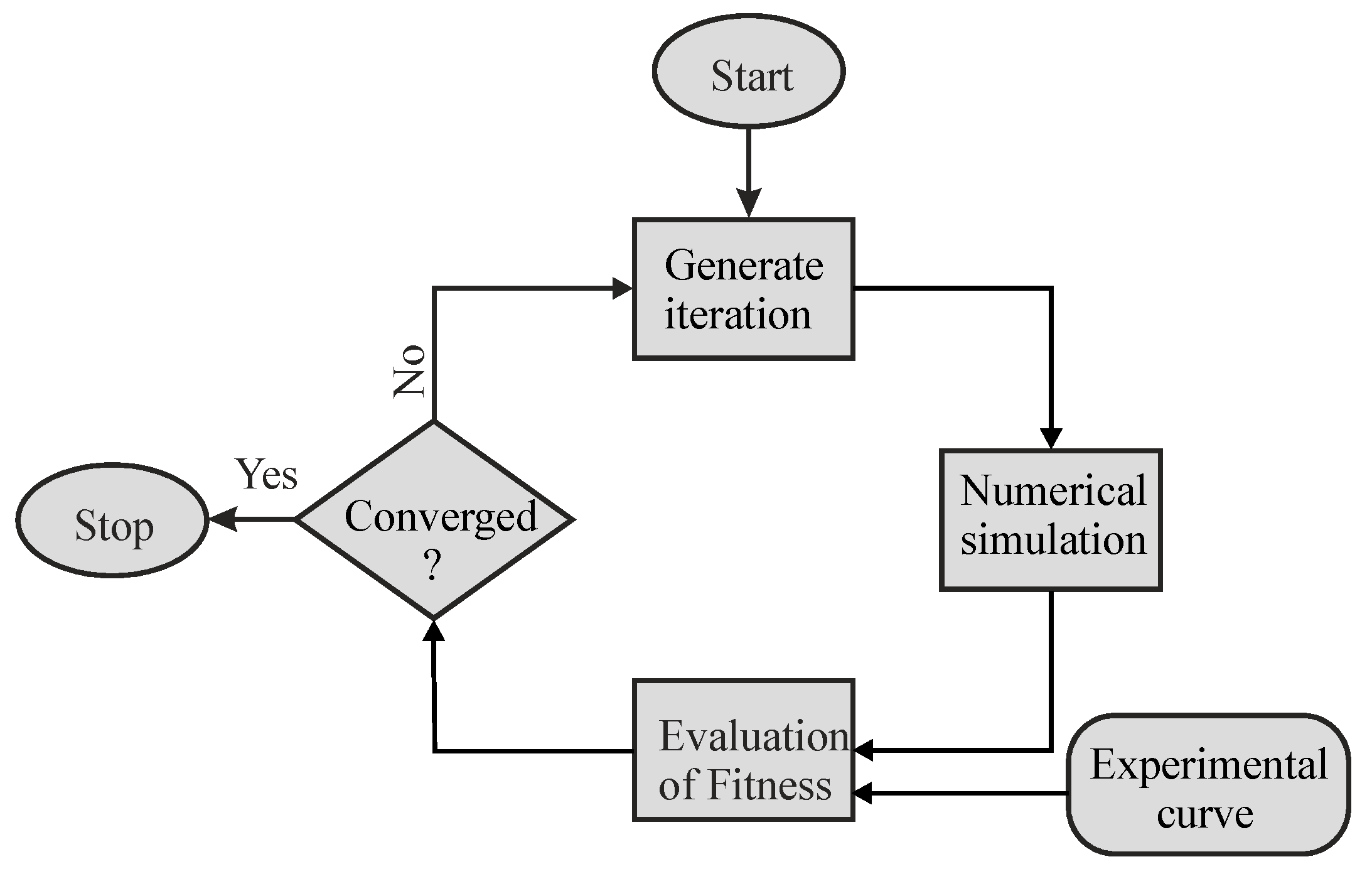
4. Optimization Procedure for Material Parameter Identification
4.1. Parameter Identification by the Inverse Method
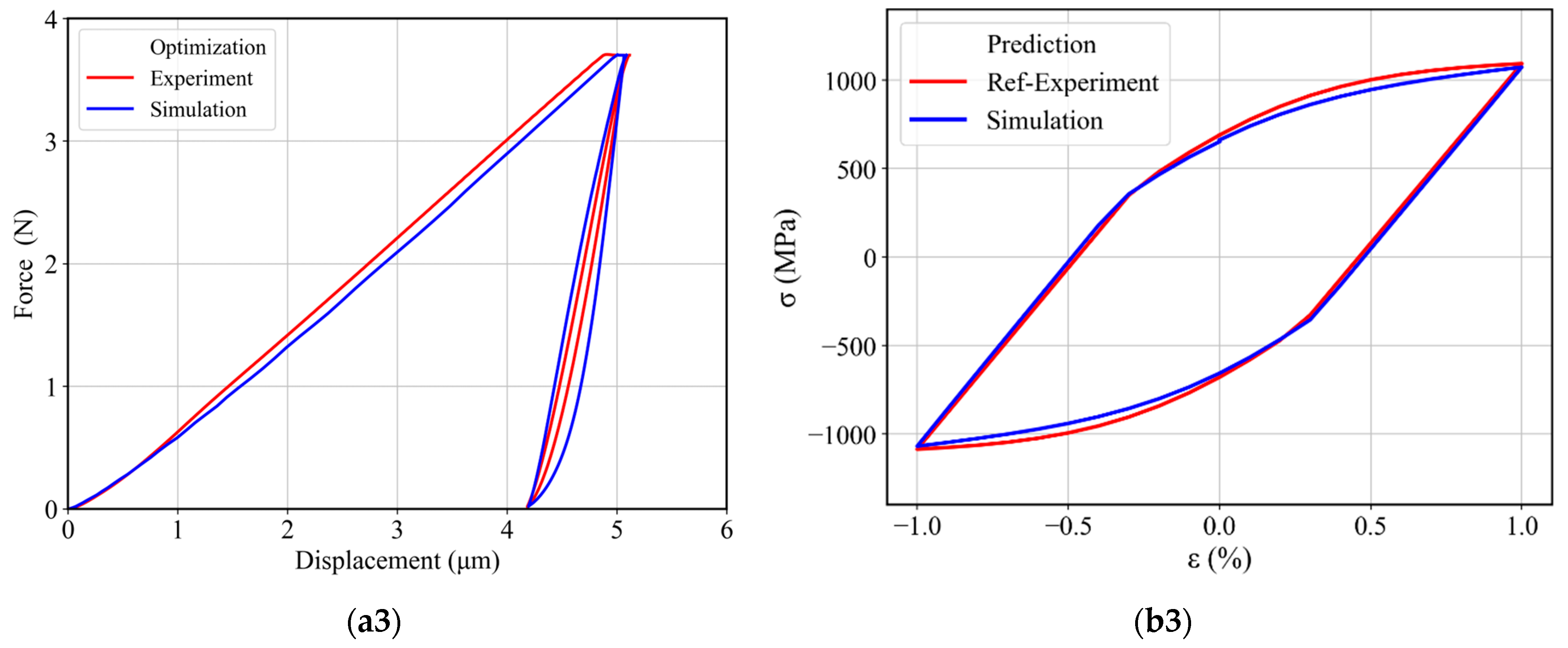
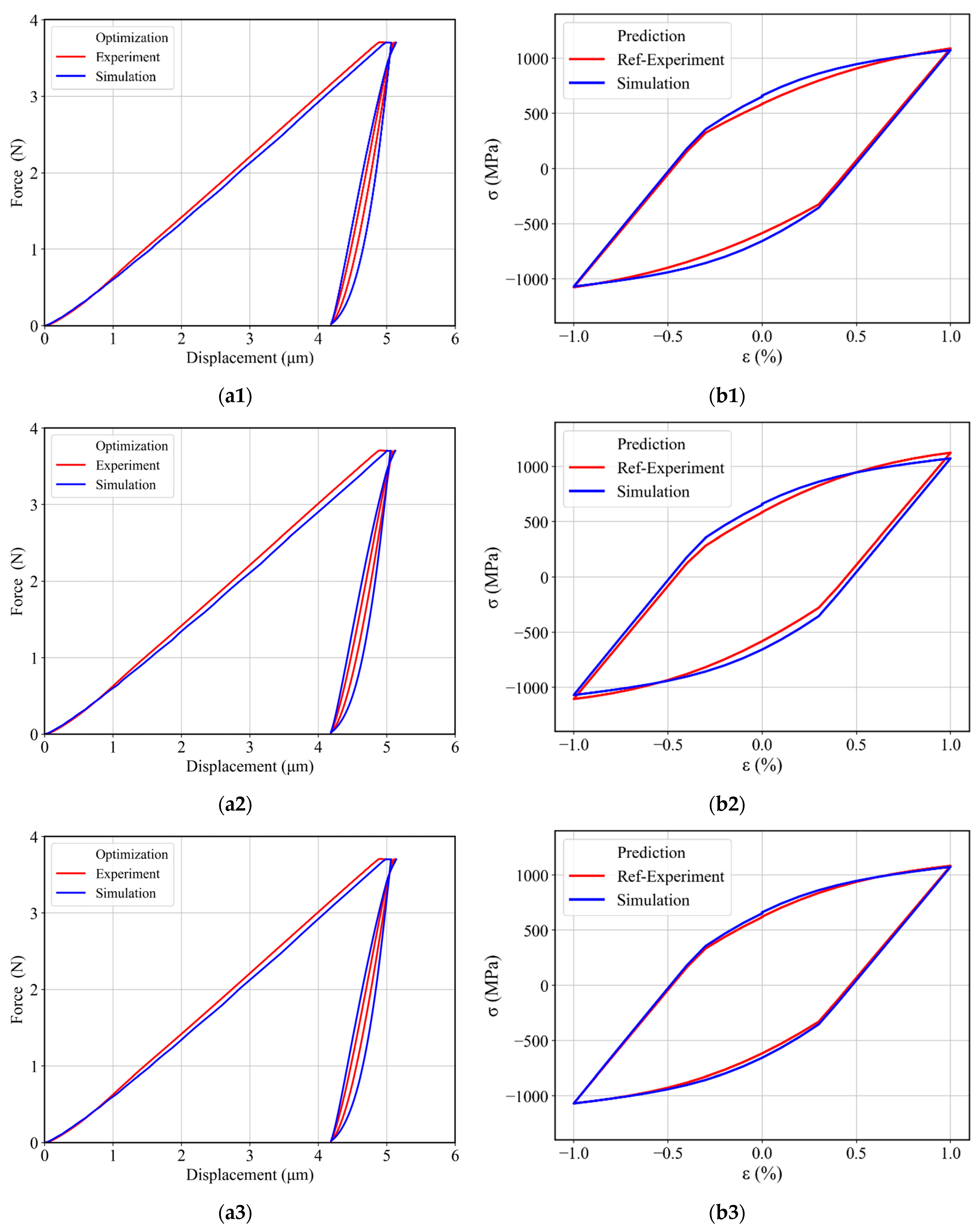
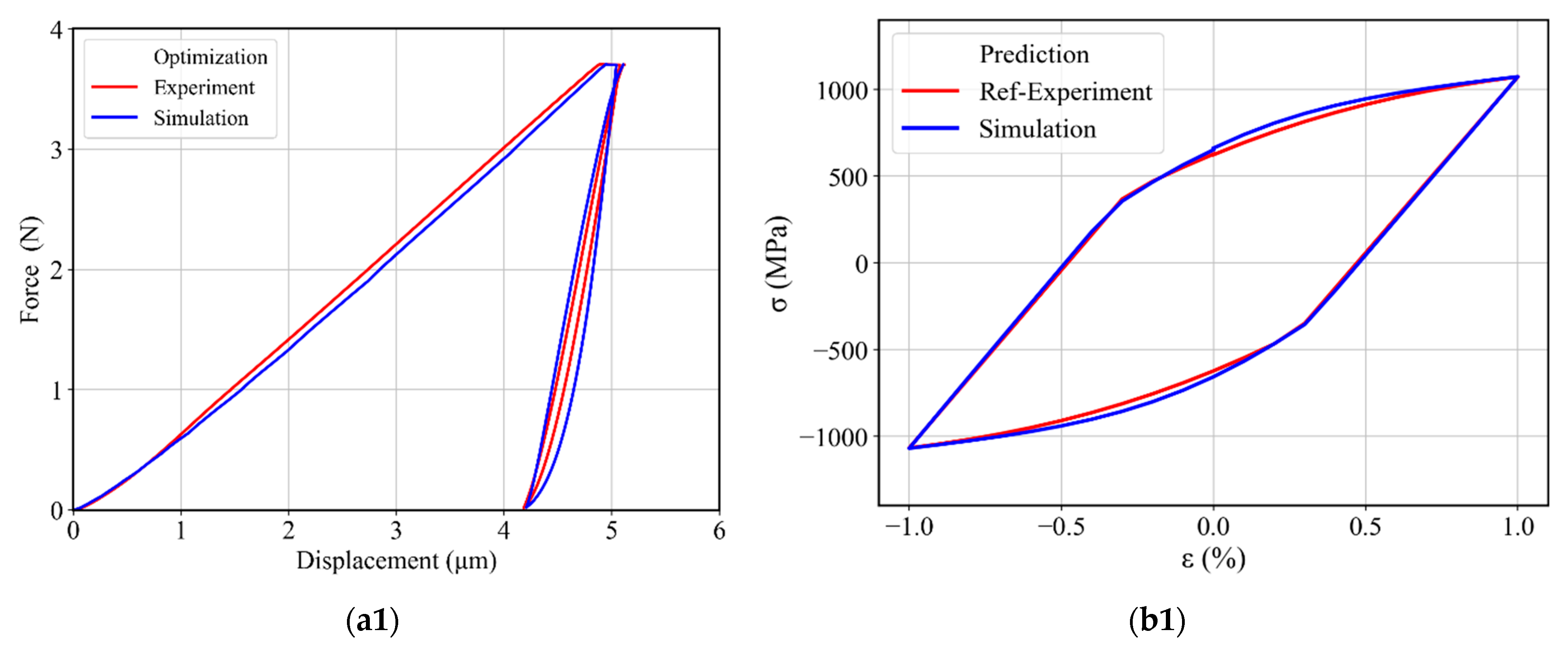
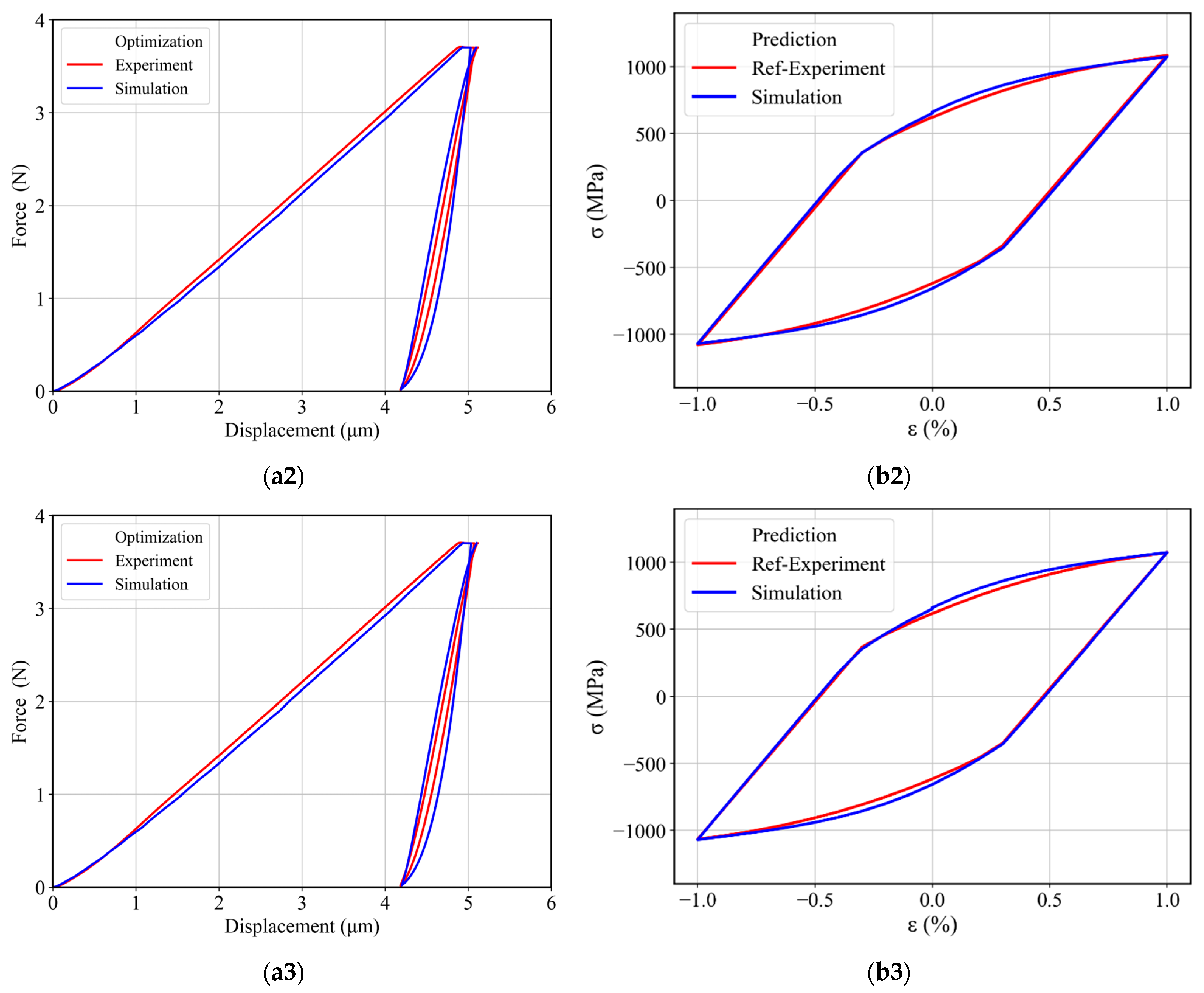
4.2. Combined Parameter Identification with Two Back-Stress Terms
4.3. Combined Parameter Identification with Three Back-Stress Terms
4.4. Two-Stage Material Parameter Determination
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Midawi, A.R.H.; Simha, C.H.M.; Gerlich, A.P. Novel Techniques for Estimating Yield Strength from Loads Measured Using Nearly-Flat Instrumented Indenters. Mater. Sci. Eng. A 2016, 675, 449–453. [Google Scholar] [CrossRef]
- Casagrande, A.; Cammarota, G.P.; Micele, L. Relationship between Fatigue Limit and Vickers Hardness in Steels. Mater. Sci. Eng. A 2011, 528, 3468–3473. [Google Scholar] [CrossRef]
- Kramer, H.S.; Starke, P.; Klein, M.; Eifler, D. Cyclic Hardness Test PHYBALCHT—Short-Time Procedure to Evaluate Fatigue Properties of Metallic Materials. Int. J. Fatigue 2014, 63, 78–84. [Google Scholar] [CrossRef]
- Frydrych, K.; Papanikolaou, S. Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation. Crystals 2022, 12, 1341. [Google Scholar] [CrossRef]
- Broitman, E. Indentation Hardness Measurements at Macro-, Micro-, and Nanoscale: A Critical Overview. Tribol. Lett. 2017, 65, 23. [Google Scholar] [CrossRef]
- Schmaling, B. Determination of Plastic Material Properties on Different Length Scales by Indentation Techniques and Inverse Analyses. Ph.D. Thesis, Ruhr University of Bochum, Bochum, Germany, 2012. [Google Scholar]
- Faisal, N.H.; Ahmed, R.; Prathuru, A.K.; Spence, S.; Hossain, M.; Steel, J.A. An Improved Vickers Indentation Fracture Toughness Model to Assess the Quality of Thermally Sprayed Coatings. Eng. Fract. Mech. 2014, 128, 189–204. [Google Scholar] [CrossRef]
- Khodabakhshi, F.; Haghshenas, M.; Eskandari, H.; Koohbor, B. Hardness-Strength Relationships in Fine and Ultra-Fine Grained Metals Processed through Constrained Groove Pressing. Mater. Sci. Eng. A 2015, 636, 331–339. [Google Scholar] [CrossRef]
- Sanders, P.G.; Youngdahl, C.J.; Weertman, J.R. The Strength of Nanocrystalline Metals with and without Flaws. Mater. Sci. Eng. A 1997, 234–236, 77–82. [Google Scholar] [CrossRef]
- Zhang, P.; Li, S.X.; Zhang, Z.F. General Relationship between Strength and Hardness. Mater. Sci. Eng. A 2011, 529, 62–73. [Google Scholar] [CrossRef]
- Roessle, M.L.; Fatemi, A. Strain-Controlled Fatigue Properties of Steels and Some Simple Approximations. Int. J. Fatigue 2000, 22, 495–511. [Google Scholar] [CrossRef]
- ASTM E-140-02 (2002); Standard Hardness Conversion Tables for Metals Relationship among Brinell Hardness, Vickers Hardness, Rockwell Hardness, Superficial Hardness, Knoop Hardness, and Scleroscope Hardness. ASTM International: West Conshohocken, PA, USA, 2002.
- ISO 20795-1; Denture Base Polymers. International Organization for Standardization: Geneva, Switzerland, 2008.
- Strzelecki, P. Analytical Method for Determining Fatigue Properties of Materials and Construction Elements in High Cycle Life. Ph.D. Thesis, Uniwersytet Technologiczno-Przyrodniczy w Bydgoszczy, Bydgoszcz, Poland, 2014. [Google Scholar]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions; Elsevier Science: Amsterdam, The Netherlands, 2002; ISBN 9780080496566. [Google Scholar]
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I.; Dissanayake, R. Developing a Full Range S-N Curve and Estimating Cumulative Fatigue Damage of Steel Elements. Comput. Mater. Sci. 2015, 96, 96–101. [Google Scholar] [CrossRef]
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I. Ranjith Dissanayake Hardness-Based Non-Destructive Method for Developing Location Specific S-N Curves for Fatigue Life Evaluation. J. Civ. Eng. Arch. 2016, 10, 183–191. [Google Scholar] [CrossRef]
- Lyamkin, V.; Starke, P.; Boller, C. Cyclic Indentation as an Alternative to Classic Fatigue Evaluation. In Proceedings of the 7th International Symposium on Aircraft Materialsno, Compiegne, France, 24–26 April 2018. [Google Scholar]
- Sajjad, H.M.; Hassan, H.; Kuntz, M.; Schäfer, B.J.; Sonnweber-Ribic, P.; Hartmaier, A. Inverse Method to Determine Fatigue Properties of Materials by Combining Cyclic Indentation and Numerical Simulation. J. Mater. 2020, 13, 3126. [Google Scholar] [CrossRef] [PubMed]
- Huber, N.; Tsakmakis, C. A Finite Element Analysis of the Effect of Hardening Rules on the Indentation Test. J. Eng. Mater. Technol. 1998, 120, 143–148. [Google Scholar] [CrossRef]
- Faisal, N.H.; Prathuru, A.K.; Goel, S.; Ahmed, R.; Droubi, M.G.; Beake, B.D.; Fu, Y.Q. Cyclic Nanoindentation and Nano-Impact Fatigue Mechanisms of Functionally Graded TiN/TiNi Film. Shape Mem. Superelasticity 2017, 3, 149–167. [Google Scholar] [CrossRef]
- Sajjad, H.M.; Hanke, S.; Güler, S.; ul Hassan, H.; Fischer, A.; Hartmaier, A. Modelling Cyclic Behaviour of Martensitic Steel with J2 Plasticity and Crystal Plasticity. Materials 2019, 12, 1767. [Google Scholar] [CrossRef] [PubMed]
- Mises, R.v. Mechanik Der Festen Körper Im Plastisch-Deformablen Zustand. Nachrichten Ges. Wiss. Göttingen Math. Kl. 1913, 1913, 582–592. [Google Scholar]
- Bažant, Z.P. Mechanics of Solid Materials. Can. J. Civ. Eng. 1992, 19, 197. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.-D. Kinematic Hardening Rules with Critical State of Dynamic Recovery, Part I: Formulation and Basic Features for Ratchetting Behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Schäfer, B.; Song, X.; Sonnweber-Ribic, P.; ul Hassan, H.; Hartmaier, A. Micromechanical Modelling of the Cyclic Deformation Behavior of Martensitic SAE 4150—A Comparison of Different Kinematic Hardening Models. Metals 2019, 9, 368. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Nielen, S. LS-OPT User’s Manual: A Desing Optimization and Probabilistic Analysis Tool for the Engineering Analyst; Livermore Software Technology Corporation: Livermore, CA, USA, 2014. [Google Scholar]






| Element | Cr | Mo | Si | Mn | N | C | Ni | P | Al | V | Ti | Cu | S |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| wt.% | 15.3 | 1.0 | 0.7 | 0.4 | 0.4 | 0.3 | 0.2 | 0.02 | 0.01 | 0.03 | 0.003 | 0.05 | 0.001 |
| Parameter | Minimum | Middle | Maximum |
|---|---|---|---|
| C1 (MPa) | 25,000 | 125,000 | 225,000 |
| γ1 | 100 | 425 | 750 |
| C2 (MPa) | 2000 | 3500 | 5000 |
| γ2 | 0 | 0 | 0 |
| C3 (MPa) | 5000 | 77,500 | 150,000 |
| γ3 | 10 | 255 | 500 |
| Q (MPa) | −350 | −187 | −25 |
| b | 0.1 | 6 | 12 |
| (s−1) | 1 × 10−7 | 5 × 10−4 | 1 × 10−3 |
| n | 3 | 7.5 | 12 |
| m | −0.99 | −0.5 | −0.01 |
| 2 Back-Stress Terms | 3 Back-Stress Terms | |||||
|---|---|---|---|---|---|---|
| Parameter | Min | Mid | Max | Min | Mid | Max |
| C1 (MPa) | 64,193 | 87,366 | 148,784 | 68,783 | 107,437 | 110,187 |
| γ1 | 138 | 171 | 434 | 229 | 253 | 336 |
| C2 (MPa) | 3722 | 3616 | 4227 | 3660 | 3628 | 3567 |
| γ2 | 0 | 0 | 0 | 0 | 0 | 0 |
| C3 (MPa) | -- | -- | -- | 34,543 | 29,012 | 14,582 |
| γ3 | -- | -- | -- | 165 | 355 | 75 |
| Q (MPa) | −252 | −251 | −55 | −276 | −275 | −247 |
| b | 3.31 | 8.39 | 7.87 | 7.97 | 11.09 | 9.54 |
| (s−1) | 1.54 × 10−6 | 9.46 × 10−7 | 2.87 × 10−7 | 1.86 × 10−6 | 8.39 × 10−6 | 7.67 × 10−6 |
| n | 10 | 11 | 9.8 | 8 | 6.5 | 7.7 |
| m | −0.96 | −0.92 | −0.67 | −0.58 | −0.82 | −0.91 |
| NMSE | 9.73 × 10−5 | 1.10 × 10−4 | 1.27 × 10−4 | 9.73 × 10−5 | 9.57 × 10−5 | 9.88 × 10−5 |
| Two-Stage Optimization | Combined Optimization | |||||
|---|---|---|---|---|---|---|
| Parameters | Min | Mid | Max | Min | Mid | Max |
| C1 (MPa) | 87,646 | 94,140 | 90,260 | 64,193 | 87,366 | 148,784 |
| γ1 | 210 | 221 | 210 | 138 | 171 | 434 |
| C2 (MPa) | 4000 | 4005 | 4011 | 3722 | 3616 | 4227 |
| γ2 | 0 | 0 | 0 | 0 | 0 | 0 |
| Q (MPa) | −136 | −189 | −107 | −252 | −251 | −55 |
| b | 4.12 | 3.19 | 8.92 | 3.31 | 8.39 | 7.87 |
| (s−1) | 7.96 × 10−7 | 1.38 × 10−6 | 1.23 × 10−6 | 1.54 × 10−6 | 9.46 × 10−7 | 2.87 × 10−7 |
| n | 11.83 | 10.7 | 10.95 | 10 | 11 | 9.8 |
| m | −0.99 | −0.99 | −0.99 | −0.96 | −0.92 | −0.67 |
| NMSE | 1.02 × 10−4 | 1.16 × 10−4 | 1.01 × 10−4 | 9.73 × 10−5 | 1.10 × 10−4 | 1.27 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajjad, H.M.; Chudoba, T.; Hartmaier, A. Inverse Method to Determine Parameters for Time-Dependent and Cyclic Plastic Material Behavior from Instrumented Indentation Tests. Materials 2024, 17, 3938. https://doi.org/10.3390/ma17163938
Sajjad HM, Chudoba T, Hartmaier A. Inverse Method to Determine Parameters for Time-Dependent and Cyclic Plastic Material Behavior from Instrumented Indentation Tests. Materials. 2024; 17(16):3938. https://doi.org/10.3390/ma17163938
Chicago/Turabian StyleSajjad, Hafiz Muhammad, Thomas Chudoba, and Alexander Hartmaier. 2024. "Inverse Method to Determine Parameters for Time-Dependent and Cyclic Plastic Material Behavior from Instrumented Indentation Tests" Materials 17, no. 16: 3938. https://doi.org/10.3390/ma17163938







