Bending Collapse and Energy Absorption of Dual-Phase Lattice Structures
Abstract
:1. Introduction
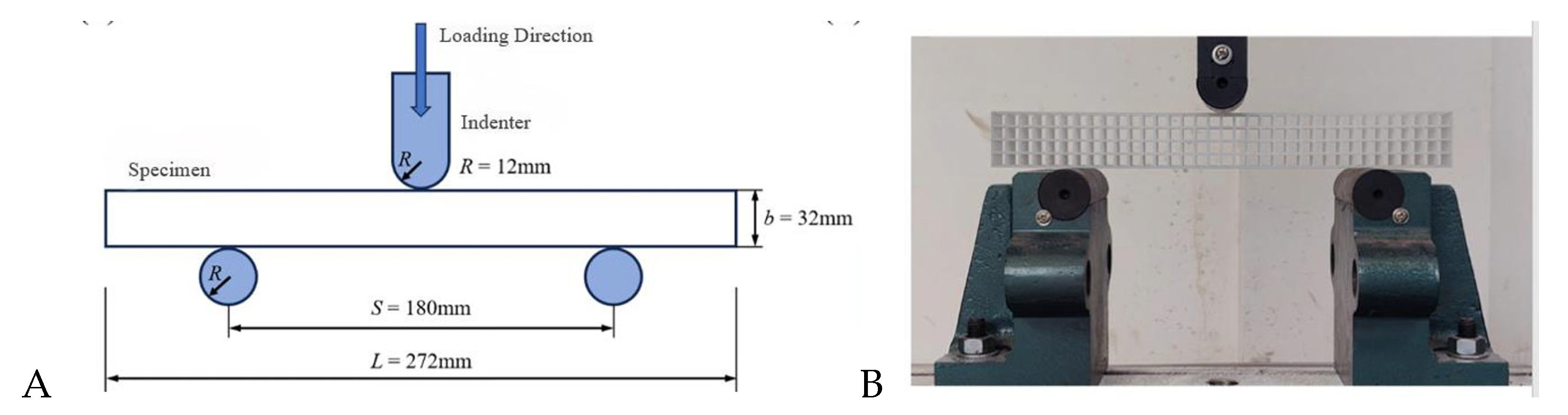
2. Specimen Preparation
3. Experimental Setup
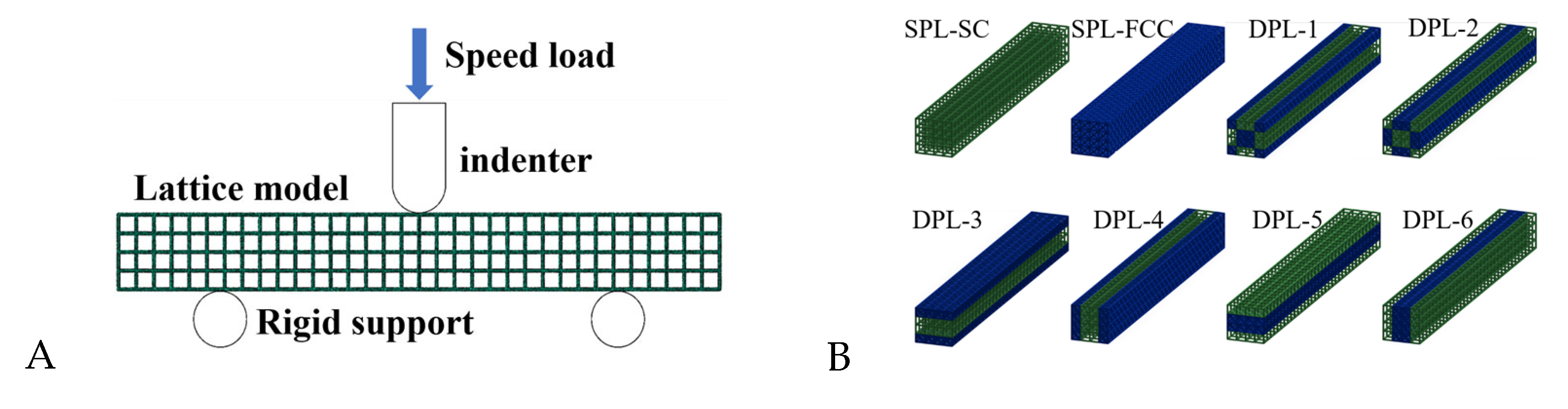
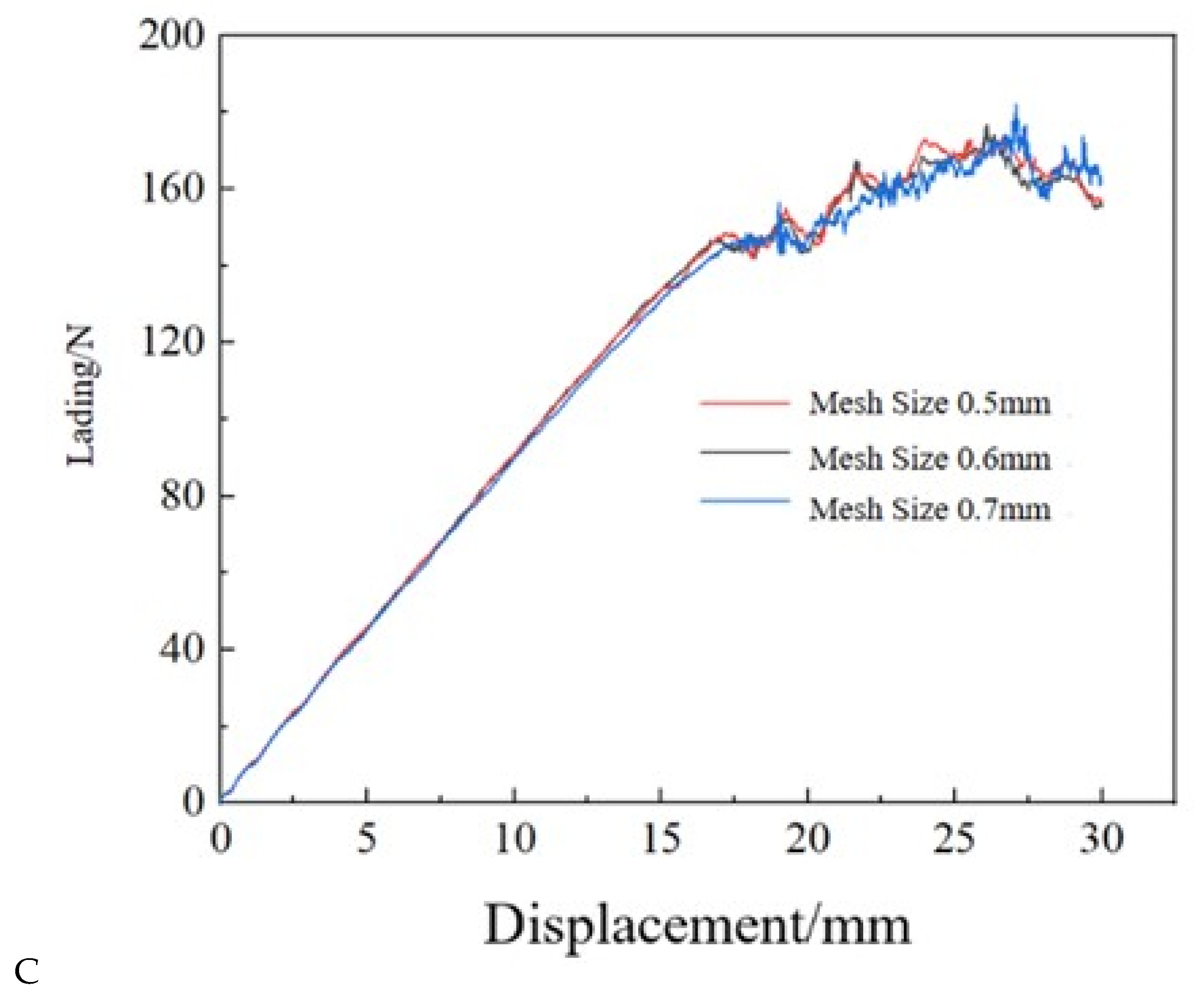
4. Finite Element Modeling
5. Experimental and Numerical Simulation Results
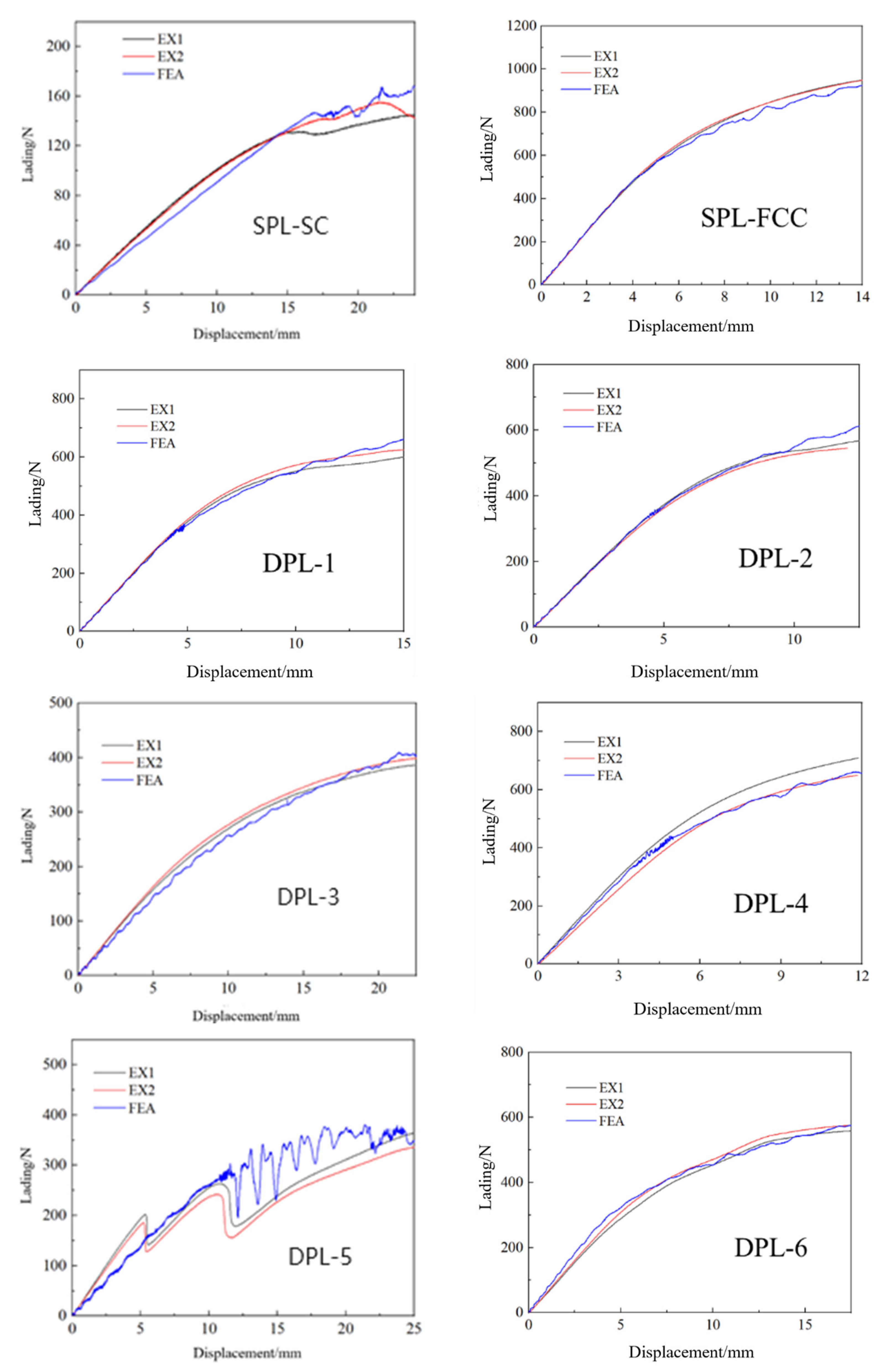
5.1. Load Response and Deformation Process
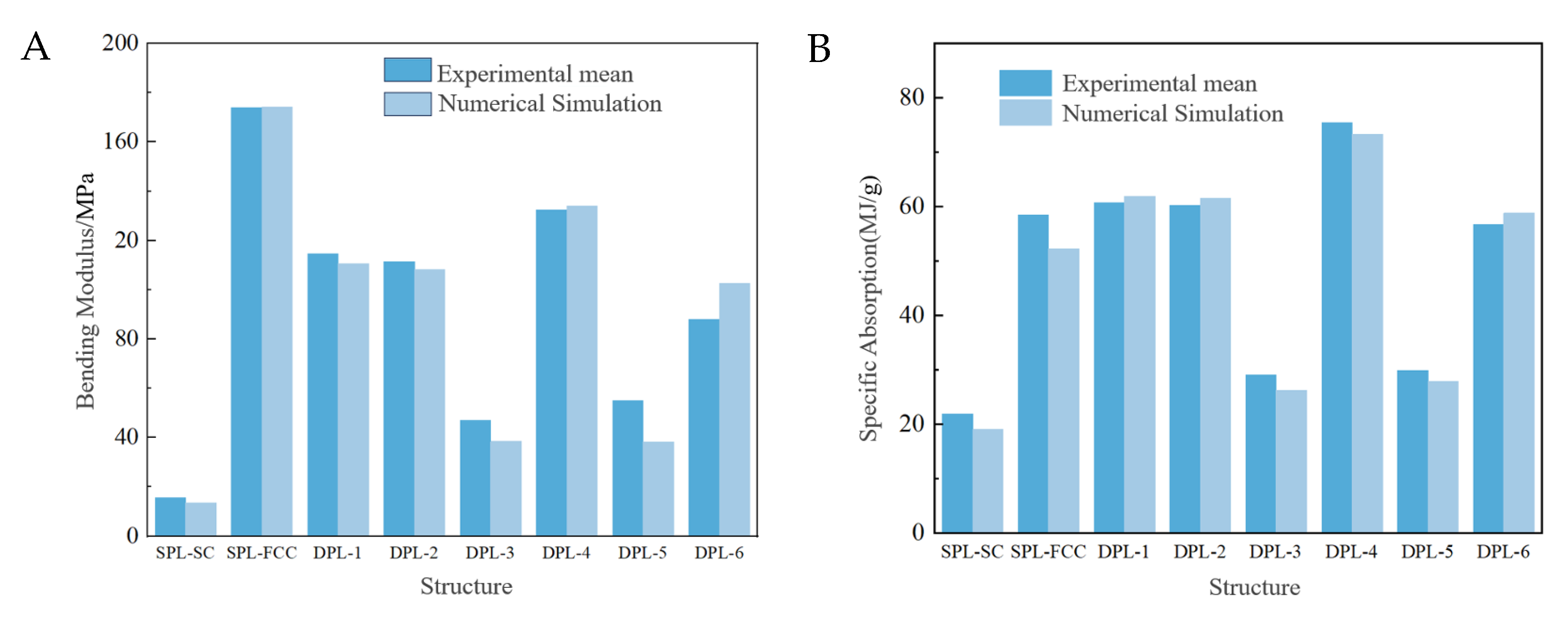
5.2. Bending Modulus
5.3. Energy Absorption Characteristics
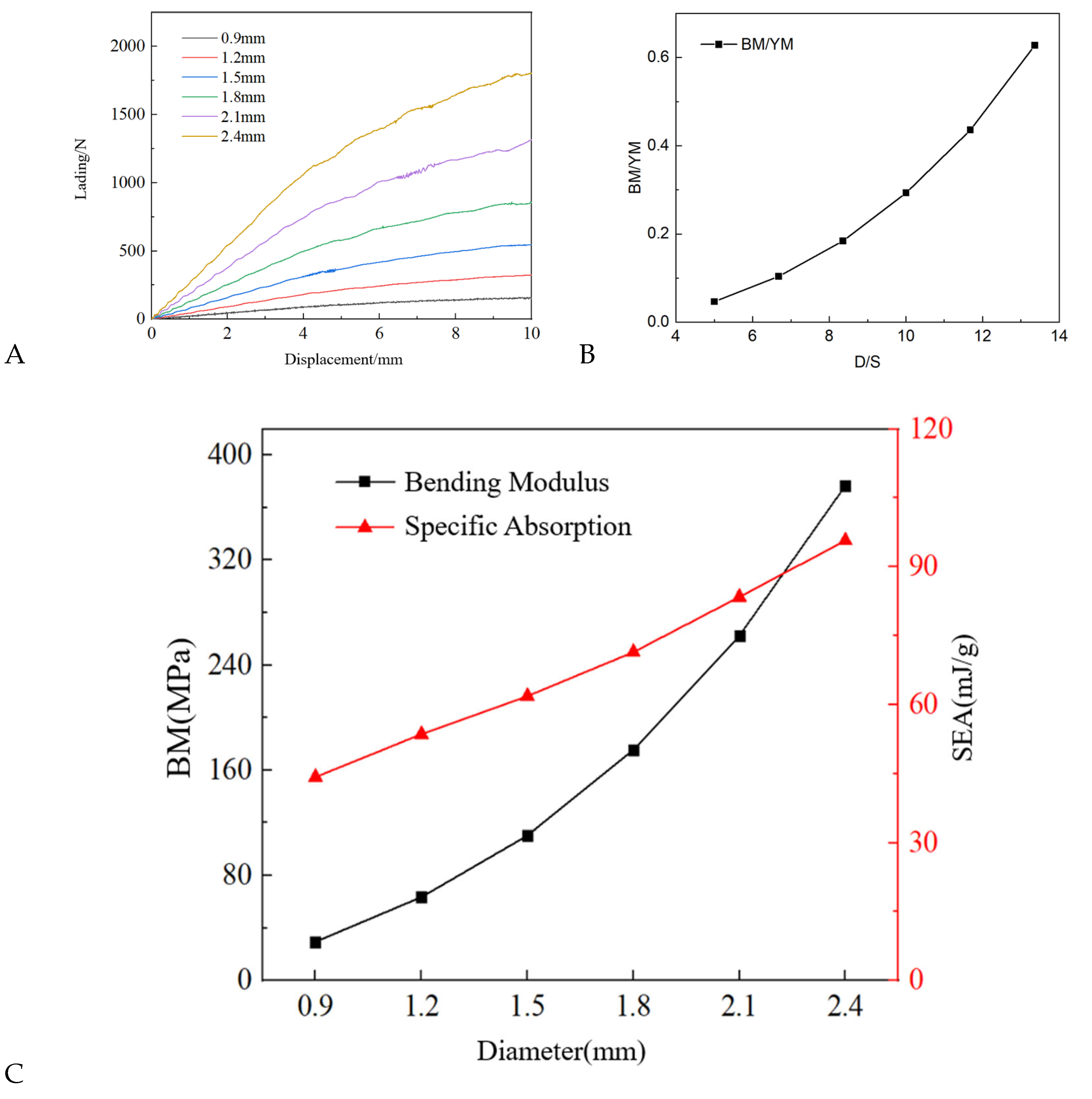
6. The Effect of Rod Diameter
7. Conclusions
- (1)
- In quasi-static three-point bending experiments, both single and dual-phase lattice structures undergo overall bending deformation, and local rod buckling occurs in the contact part with the indenter. The magnitude of buckling is related to the type of contact cell, with the matrix phase cell showing more flexible characteristics.
- (2)
- The bending resistance and energy absorption level of the matrix-phase single-phase lattice structure are relatively low. The introduction of reinforced phase cell elements in the dual-phase lattice structure can achieve a significant improvement in mechanical properties, with a maximum increase in bending modulus of 744.7% and a maximum increase in specific energy absorption of 243.5%. In addition, the specific energy absorption of some biphasic lattice structures even exceeds that of enhanced phase lattice structures, which means that the combination of soft and hard lattice designs can better achieve energy absorption under lateral loads.
- (3)
- The results of numerical analysis and calculation are in good agreement with the experimental results in terms of deformation mode and load–displacement curve, and the calculated specific energy absorption index has an error of less than 15% compared to the experimental results. According to the numerical analysis results, it can be concluded that increasing the relative density is an effective way to improve the bending modulus and specific energy absorption of biphasic lattice structures. With the increase in rod diameter, the improvement in bending modulus is more significant than that of specific energy absorption.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bai, L.; Gong, C.; Chen, X.; Sun, Y.; Xin, L.; Pu, H.; Peng, Y.; Luo, J. Mechanical properties and energy absorption capabilities of functionally graded lattice structures: Experiments and simulations. Int. J. Mech. Sci. 2020, 182, 105735. [Google Scholar] [CrossRef]
- Meza, L.R.; Das, S.; Greer, J.R. Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science 2014, 345, 1322–1326. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhang, J.; Wang, W.; Gao, L. Compression behaviors of the bio-inspired hierarchical lattice structure with improved mechanical properties and energy absorption capacity. J. Mater. Res. Technol. 2022, 17, 2755–2771. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved mechanical properties and energy absorption of BCC lattice structures with triply periodic minimal surfaces fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [PubMed]
- Nian, Y.; Wan, S.; Zhou, P.; Wang, X.; Santiago, R.; Li, M. Energy absorption characteristics of functionally graded polymer-based lattice structures filled aluminum tubes under transverse impact loading. Mater. Des. 2021, 209, 110011. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metama terials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Evans, A.G.; Hutchinson, J.W.; Fleck, N.A.; Ashby, M.F.; Wadley, H.N.G. The topological design of multifunctional cellular metals. Prog. Mater. Sci. 2001, 46, 309–327. [Google Scholar] [CrossRef]
- Zhang, J.; Chaisombat, K.; He, S.; Wang, C. Hybrid composite laminates reinforced with glass/carbon woven fabrics for lightweight load bearing structures. Mater. Des. 2012, 36, 75–80. [Google Scholar] [CrossRef]
- Mines, R.A.W.; Tsopanos, S.; Shen, Y.; Hasan, R.; McKown, S.T. Drop weight impact behaviour of sandwich panels with metallic micro lattice cores. Int. J. Impact Eng. 2013, 60, 120–132. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Fang, G.; Zhou, J. Additively manufactured scaffolds for bone tissue engineering and the prediction of their mechanical behavior: A review. Materials 2017, 10, 50. [Google Scholar] [CrossRef]
- Yan, D.; Chang, J.; Zhang, H.; Liu, J.; Song, H.; Xue, Z.; Zhang, F.; Zhang, Y. Soft three-dimensional network materials with rational bio-mimetic designs. Nat. Commun. 2020, 11, 1180–1191. [Google Scholar] [CrossRef] [PubMed]
- Meza, L.R.; Zelhofer, A.J.; Clarke, N.; Mateos, A.J.; Kochmann, D.M.; Greer, J.R. Resilient 3D hierarchical architected metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 11502–11507. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Qi, D.; Li, Y.; Xiao, D.; Wu, W. Impact energy absorption performances of ordinary and hierarchical chiral structures. Thin-Walled Struct. 2019, 140, 495–505. [Google Scholar] [CrossRef]
- Chung, H.; Das, S. Functionally graded Nylon-11/silica nanocomposites produced by selective laser sintering. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2008, 487, 251–257. [Google Scholar] [CrossRef]
- Li, S.; Zhao, S.; Hou, W.; Teng, C.; Hao, Y.; Li, Y.; Yang, R.; Misra, R.D.K. Functionally Graded Ti-6Al-4V Meshes with High Strength and Energy Absorption. Adv. Eng. Mater. 2016, 18, 34–38. [Google Scholar] [CrossRef]
- Liu, F.; Mao, Z.; Zhang, P.; Zhang, D.Z.; Jiang, J.; Ma, Z. Functionally graded porous scaffolds in multiple patterns: New design method, physical and mechanical properties. Mater. Des. 2018, 160, 849–860. [Google Scholar] [CrossRef]
- Choy, S.Y.; Sun, C.N.; Leong, K.F.; Wei, J. Compressive properties of functionally graded lattice structures manufactured by selective laser melting. Mater. Des. 2017, 131, 112–120. [Google Scholar] [CrossRef]
- Lakes, R. Materials with structural hierarchy. Nature 1993, 361, 511–515. [Google Scholar] [CrossRef]
- Moestopo, W.P.; Mateos, A.J.; Fuller, R.M.; Greer, J.R.; Portela, C.M. Pushing and Pulling on Ropes: Hierarchical Woven Materials. Adv. Sci. 2020, 7, 271–279. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Yang, F.; Ru, D.; Zheng, B.; Fan, H. Additive-manufactured hierarchical multi-circular lattice structures for energy absorption application. Mater. Des. 2021, 210, 110116. [Google Scholar] [CrossRef]
- Fratzl, P.; Weinkamer, R. Nature’s hierarchical materials. Prog. Mater. Sci. 2007, 52, 1263–1334. [Google Scholar] [CrossRef]
- Zheng, X.; Smith, W.; Jackson, J.; Moran, B.; Cui, H.; Chen, D.; Ye, J.; Fang, N.; Rodriguez, N.; Weisgraber, T.; et al. Multiscale metallic metamaterials. Nat. Mater. 2016, 15, 1100–1106. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, V.S.; Fleck, N.A. Collapse of truss core sandwich beams in 3-point bending. Int. J. Solids Struct. 2001, 38, 6275–6305. [Google Scholar] [CrossRef]
- Lai, C.Q.; Daraio, C. Highly porous microlattices as ultrathin and efficient impact absorbers. Int. J. Impact Eng. 2018, 120, 138–149. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and specific energy absorption of additively-manufactured metallic BCC metamaterials composed of tapered beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Andrew, J.J.; Schneider, J.; Ubaid, J.; Velmurugan, R.; Gupta, N.K.; Kumar, S. Energy absorption characteristics of additively manufactured plate-lattices under low- velocity impact loading. Int. J. Impact Eng. 2021, 149, 768–784. [Google Scholar] [CrossRef]
- Huang, Z.; Li, B.; Ma, L.; Li, Y. Mechanical properties and energy absorption performance of bio-inspired dual architecture phase lattice structures. Mech. Adv. Mater. Struct. 2023, 30, 1842–1852. [Google Scholar] [CrossRef]
- Santosa, S.; Banhart, J.; Wierzbicki, T. Experimental and numerical analyses of bending of foam-filled sections. Acta Mech. 2001, 148, 199–213. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Bhaskar, A. Flexural elasticity of woodpile lattice beams. Eur. J. Mech. A/Solids 2017, 67, 187–199. [Google Scholar] [CrossRef]




| Specimen | Design Mass (g) | Printing Mass (g) | Mean (g) | Error (%) | |
|---|---|---|---|---|---|
| SPL-SC | 24.14 | 24.48 | 24.28 | 24.38 | 1.0 |
| SPL-FCC | 96.43 | 85.68 | 91.65 | 88.67 | 8.0 |
| DPL-1 | 54.15 | 57.89 | 56.30 | 57.10 | 5.4 |
| DPL-2 | 54.15 | 55.21 | 55.22 | 55.22 | 2.0 |
| DPL-3 | 52.50 | 53.45 | 51.91 | 52.68 | 0.3 |
| DPL-4 | |||||
| DPL-5 | 49.16 | 48.75 | 47.78 | 48.27 | 1.8 |
| DPL-6 | |||||
| Specimen | Flexural Modulus (MPa) | Error (%) | |||
|---|---|---|---|---|---|
| FEA | EX-1 | EX-2 | Mean | ||
| SPL-SC | 13.45 | 15.34 | 15.98 | 15.67 | 14.17 |
| SPL-FCC | 174.10 | 173.22 | 174.66 | 173.94 | 0.09 |
| DPL-1 | 110.58 | 113.84 | 115.24 | 114.54 | 3.46 |
| DPL-2 | 108.23 | 112.17 | 110.76 | 111.47 | 2.91 |
| DPL-3 | 38.40 | 46.52 | 47.60 | 47.06 | 18.40 |
| DPL-4 | 134.12 | 144.18 | 120.54 | 132.36 | 1.33 |
| DPL-5 | 38.17 | 56.80 | 53.31 | 55.06 | 30.68 |
| DPL-6 | 102.50 | 86.14 | 89.68 | 87.91 | 16.60 |
| Specimen | EA (J) | SEA (mJ/g) | Error of SEA (%) | |||||
|---|---|---|---|---|---|---|---|---|
| FEA | EX-1 | EX-2 | FEA | EX-1 | EX-2 | Mean | ||
| SPL-SC | 0.46 | 0.53 | 0.54 | 19.06 | 21.74 | 22.15 | 21.94 | 13.13 |
| SPL-FCC | 5.04 | 5.16 | 5.20 | 52.27 | 58.19 | 58.64 | 58.42 | 10.53 |
| DPL-1 | 3.35 | 3.42 | 3.51 | 61.87 | 59.89 | 61.47 | 60.68 | 1.96 |
| DPL-2 | 3.33 | 3.37 | 3.28 | 61.50 | 61.03 | 59.40 | 60.21 | 2.14 |
| DPL-3 | 1.38 | 1.50 | 1.56 | 26.29 | 28.47 | 29.61 | 29.04 | 9.47 |
| DPL-4 | 3.85 | 4.18 | 3.76 | 73.33 | 79.35 | 71.37 | 75.36 | 2.69 |
| DPL-5 | 1.37 | 1.50 | 1.39 | 27.87 | 31.08 | 28.80 | 29.94 | 6.91 |
| DPL-6 | 2.89 | 2.67 | 2.81 | 58.79 | 55.31 | 58.21 | 56.76 | 3.58 |
| D (mm) | D/S*1000 | BM (MPa) | BM/YM | EA (J) | Mass (g) | SEA (mJ/g) |
|---|---|---|---|---|---|---|
| 0.9 | 5.00 | 29.55 | 0.05 | 0.95 | 21.56 | 44.25 |
| 1.2 | 6.68 | 63.71 | 0.10 | 1.96 | 36.49 | 53.59 |
| 1.5 | 8.36 | 110.58 | 0.18 | 3.35 | 54.15 | 61.87 |
| 1.8 | 10.00 | 175.67 | 0.29 | 5.27 | 73.84 | 71.43 |
| 2.1 | 11.68 | 262.70 | 0.44 | 7.92 | 94.87 | 83.45 |
| 2.4 | 13.36 | 376.81 | 0.63 | 11.16 | 116.56 | 95.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhu, Z.; Li, B.; Leng, K.; Yu, M.; Huang, Z.; Li, Y. Bending Collapse and Energy Absorption of Dual-Phase Lattice Structures. Materials 2024, 17, 3952. https://doi.org/10.3390/ma17163952
Chen Z, Zhu Z, Li B, Leng K, Yu M, Huang Z, Li Y. Bending Collapse and Energy Absorption of Dual-Phase Lattice Structures. Materials. 2024; 17(16):3952. https://doi.org/10.3390/ma17163952
Chicago/Turabian StyleChen, Zihao, Zijie Zhu, Bangzhen Li, Kehua Leng, Min Yu, Zhixin Huang, and Ying Li. 2024. "Bending Collapse and Energy Absorption of Dual-Phase Lattice Structures" Materials 17, no. 16: 3952. https://doi.org/10.3390/ma17163952






