An Internal-State-Variable-Based Continuous Dynamic Recrystallization Model for Thermally Deformed TC18 Alloy
Abstract
1. Introduction
2. Experiments
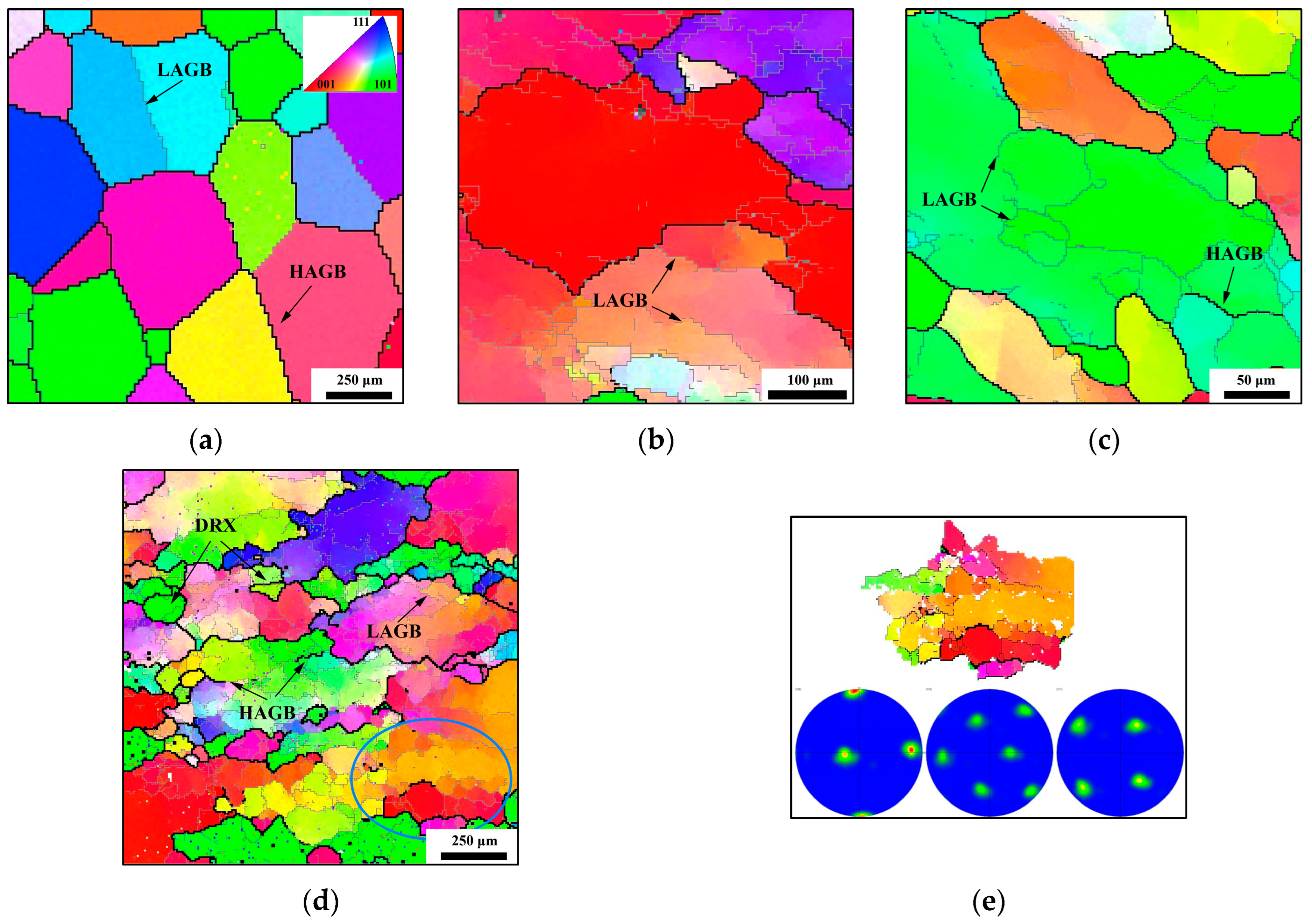
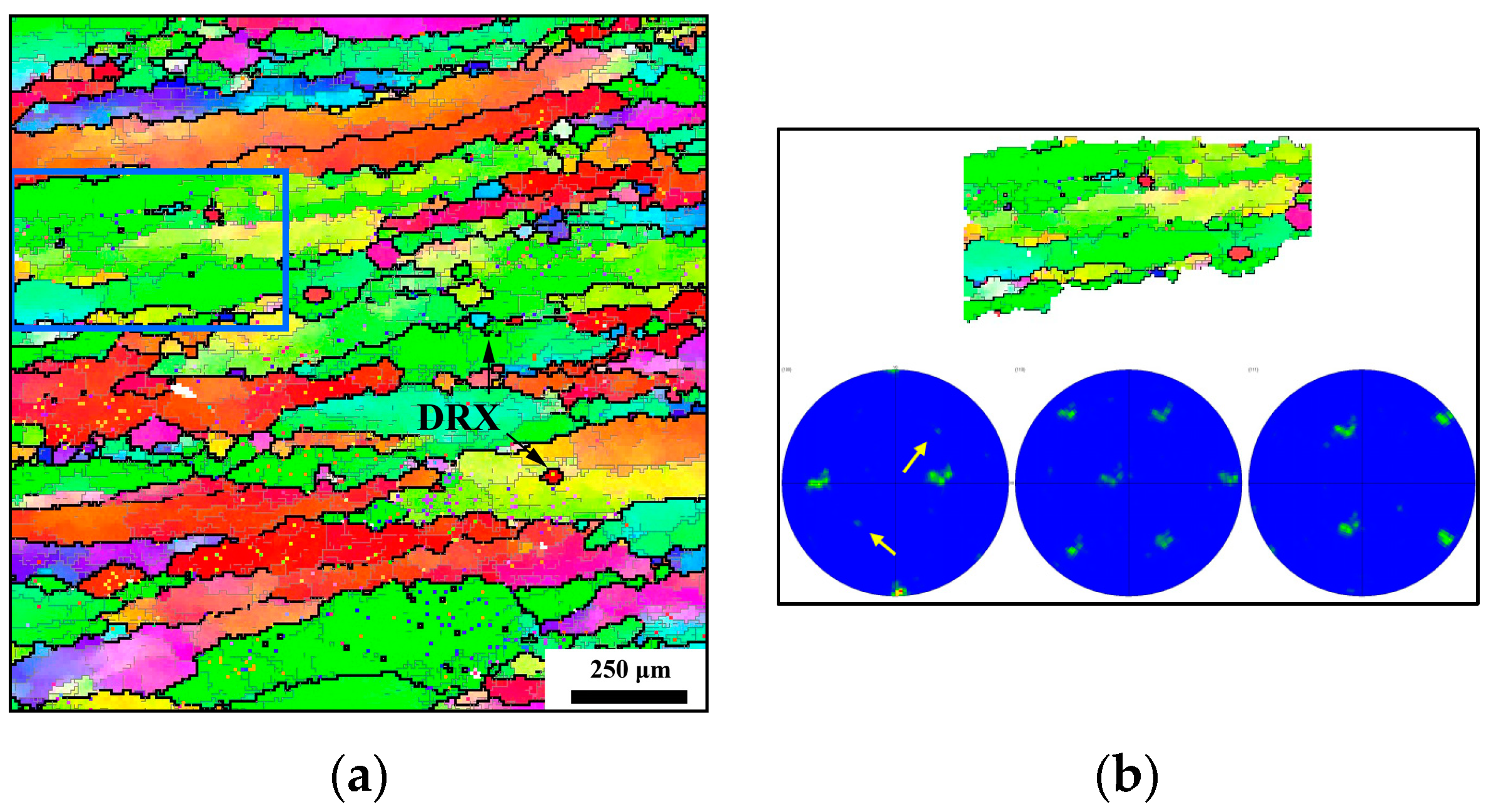
3. Continuous Dynamic Recrystallization Behavior of TC18 Alloy
4. Continuous Dynamic Recrystallization Model of TC18 Alloy
4.1. Modeling of Flow Behavior
4.2. Modeling of Microstructure Evolution
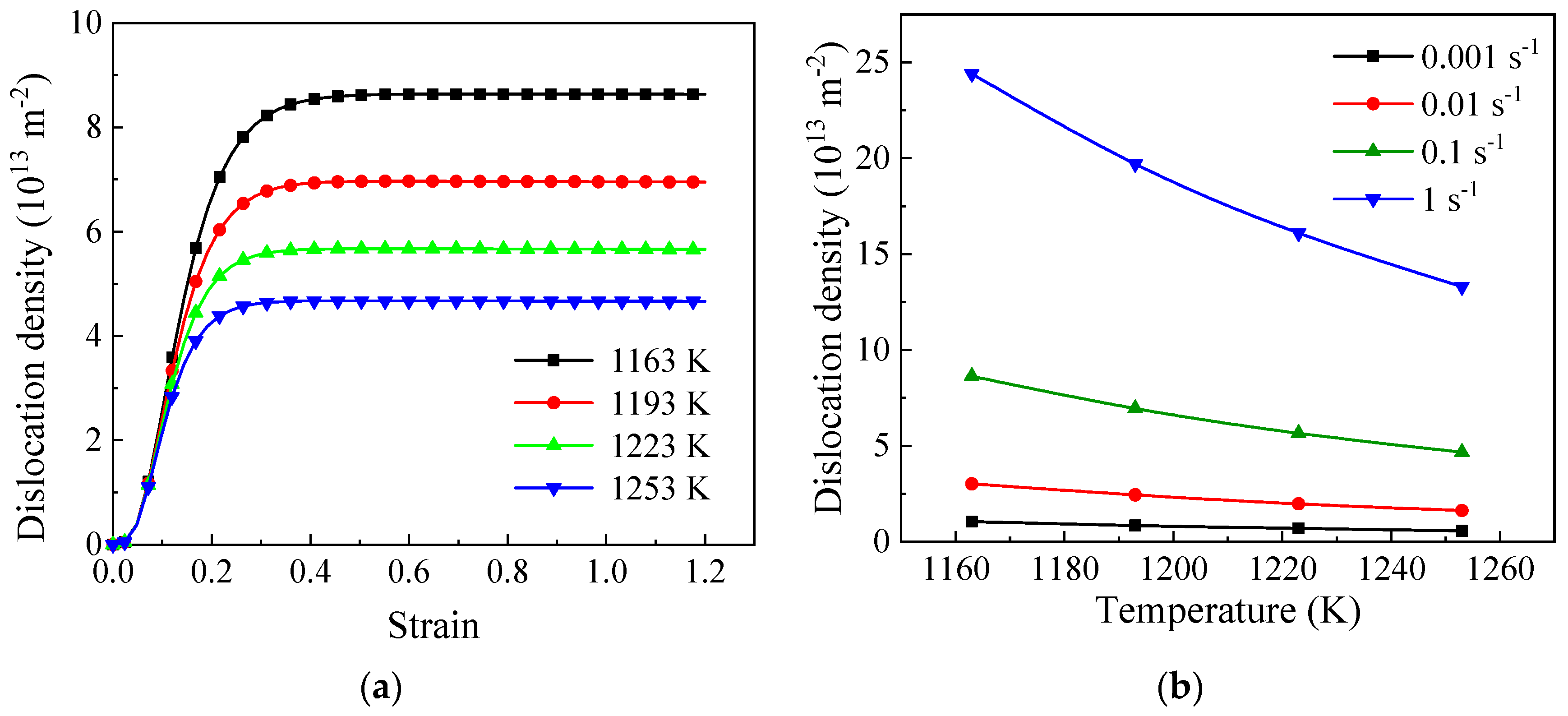
4.2.1. Dislocation Density Model
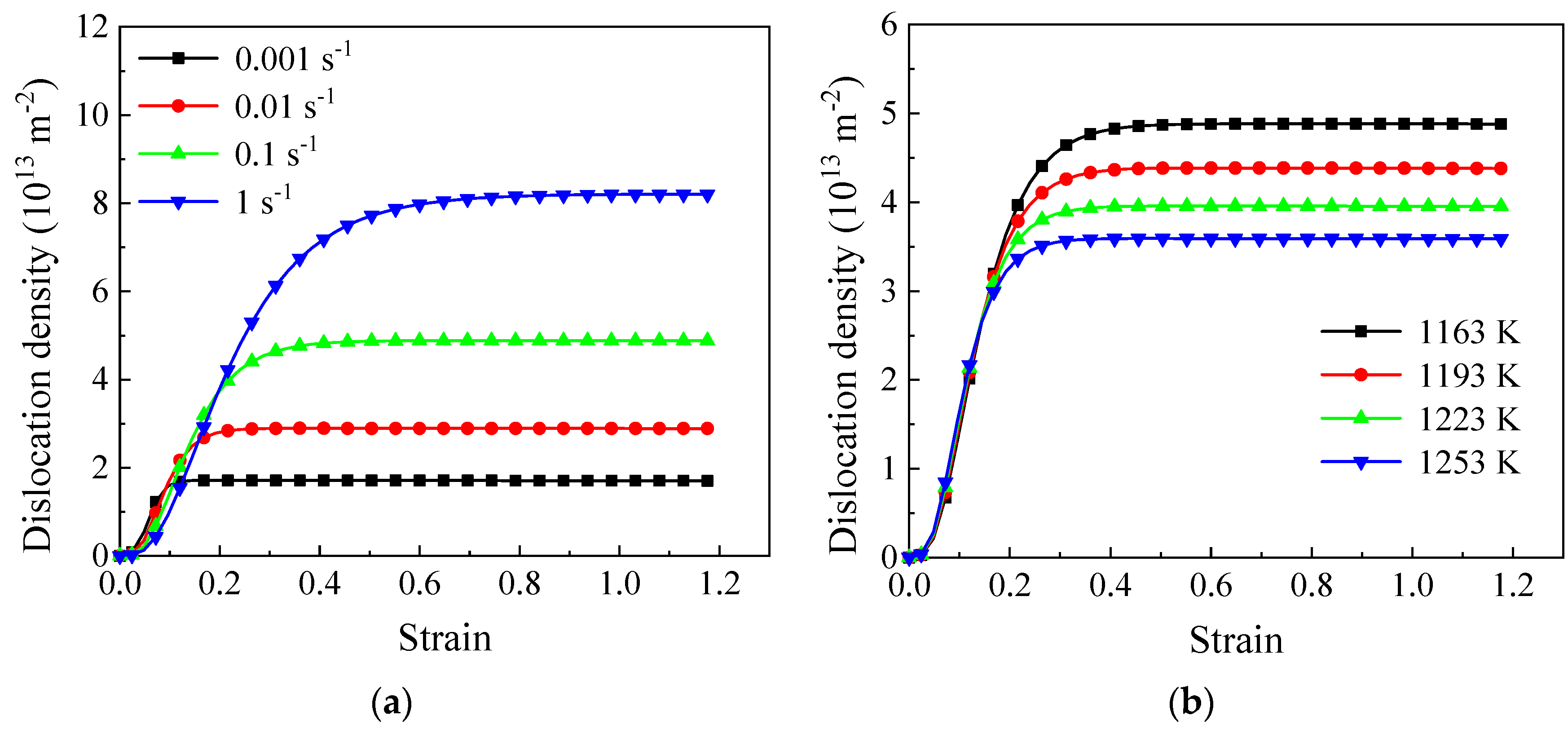
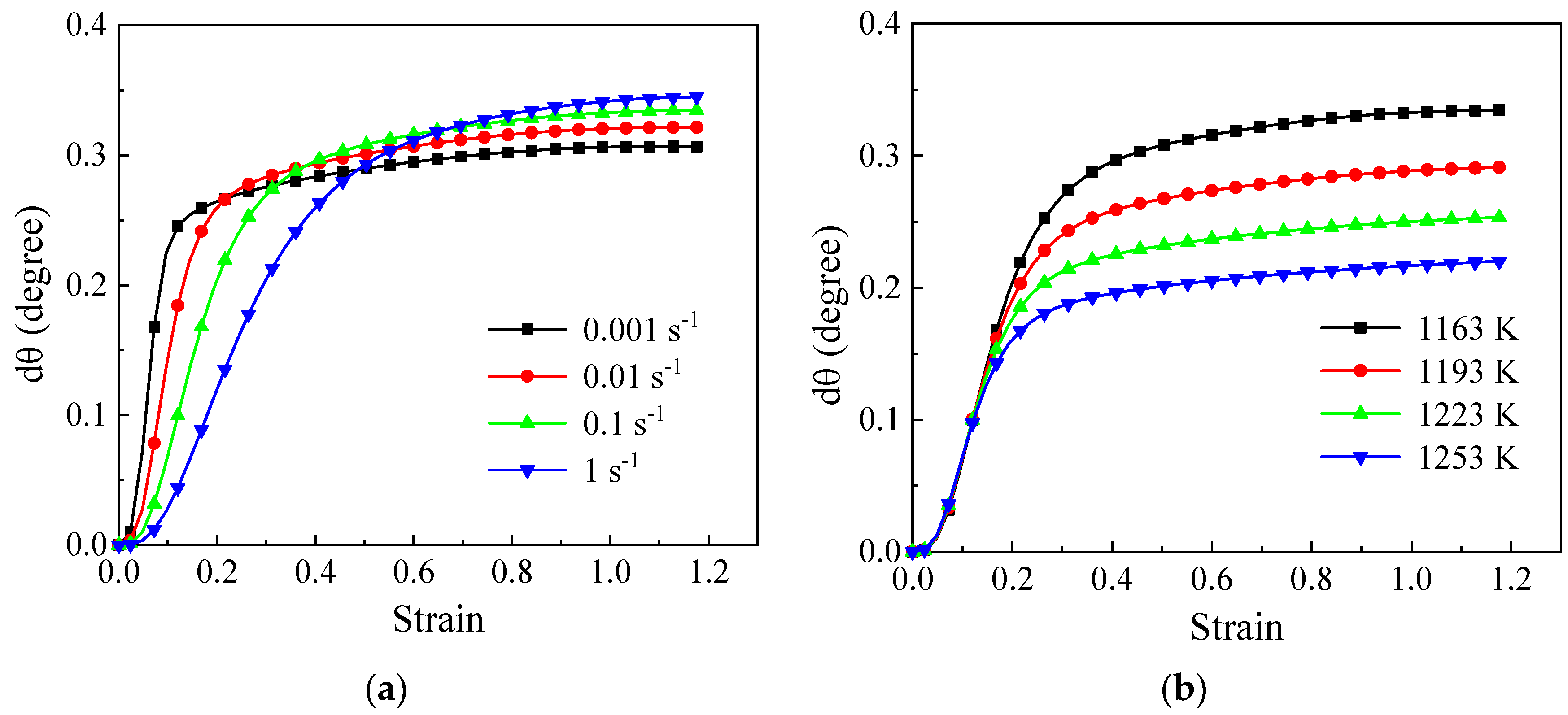
4.2.2. Subgrain Formation and Rotation Model
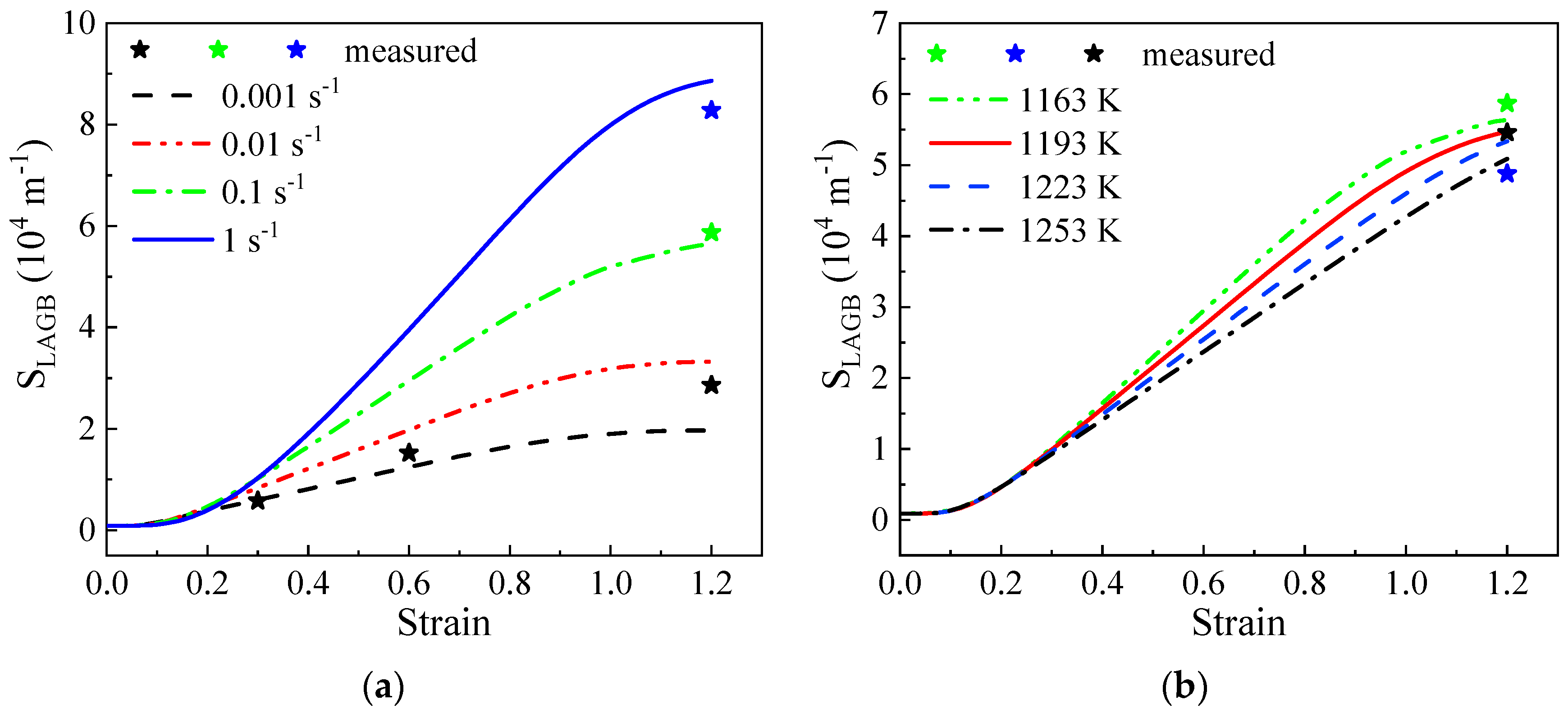
4.2.3. LAGB Area Evolution Model
4.2.4. HAGB Area Evolution Model
4.2.5. Grain Size Model
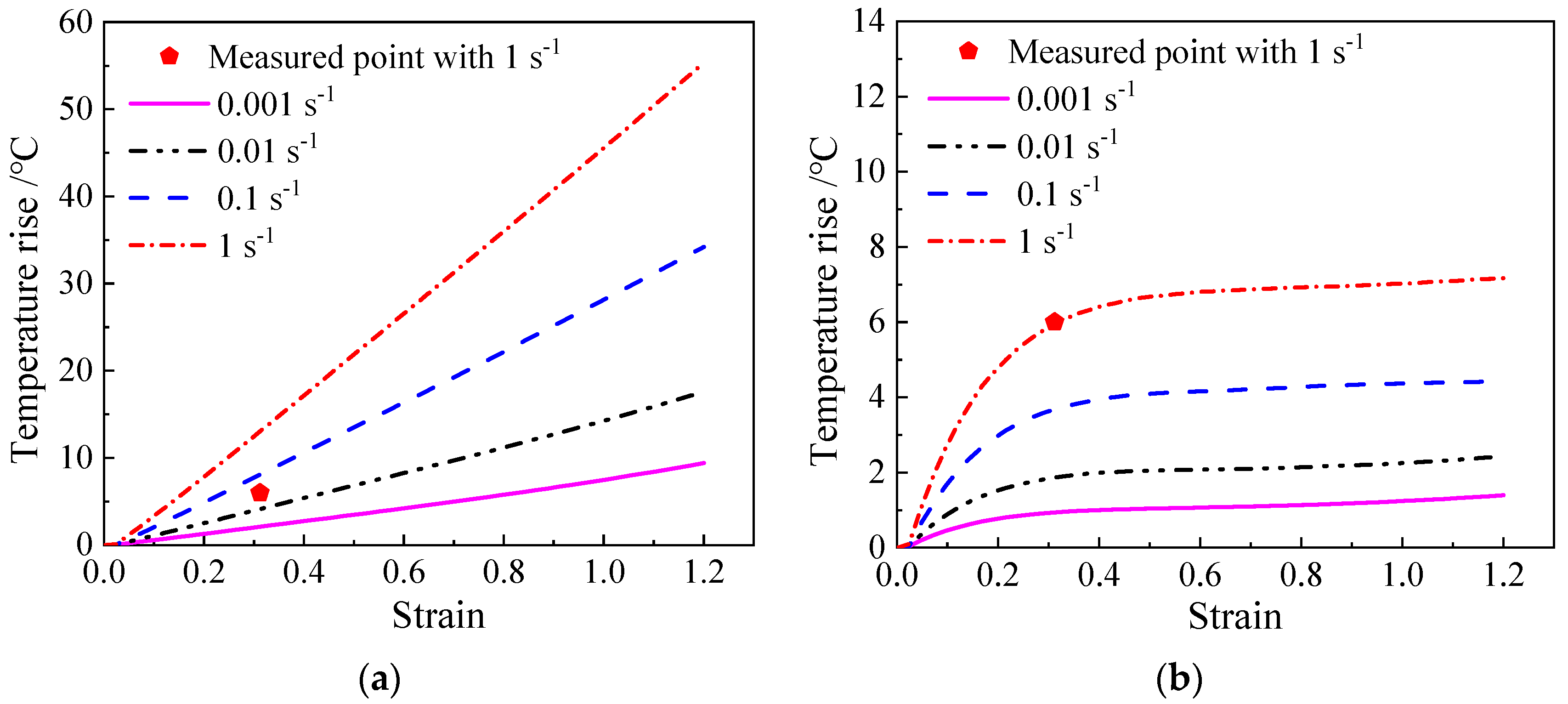
4.2.6. Temperature Rise Model
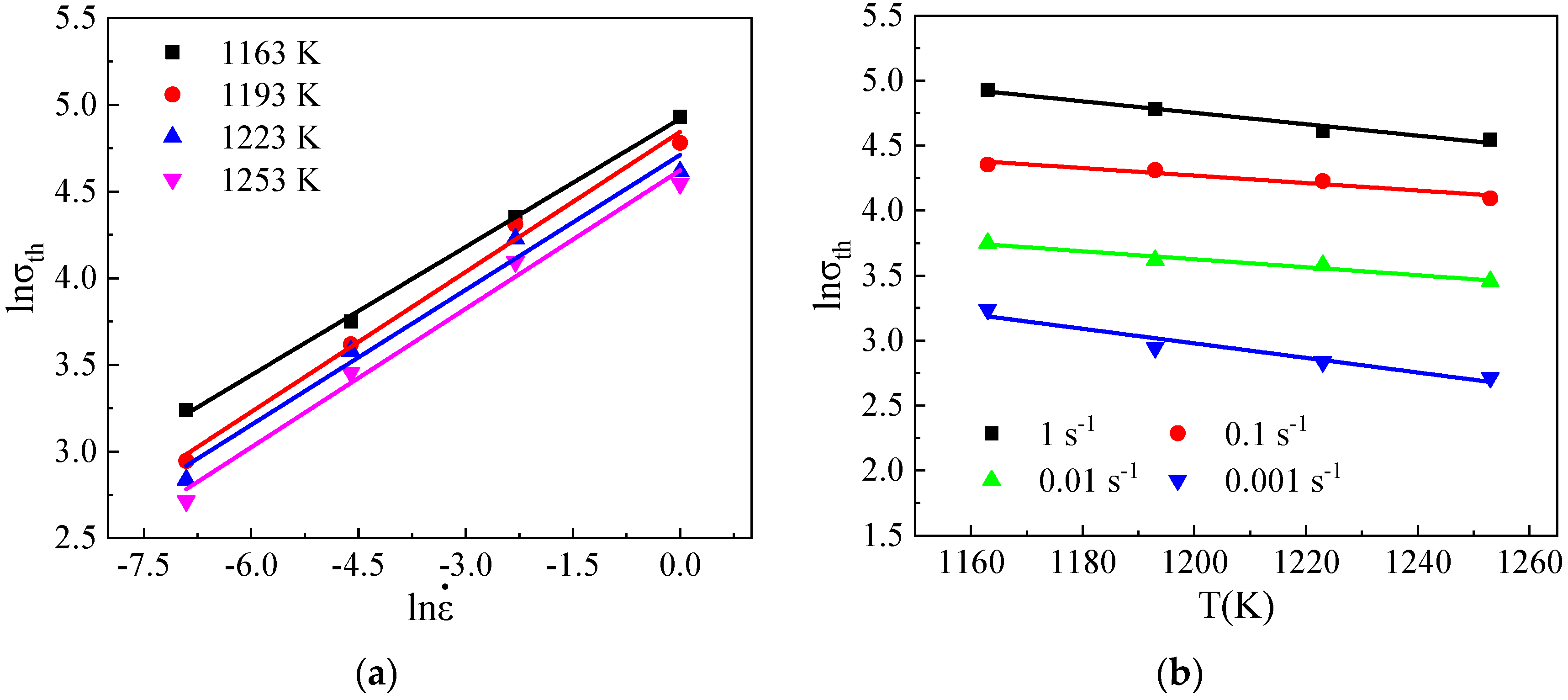
4.3. Identification of Material Constants
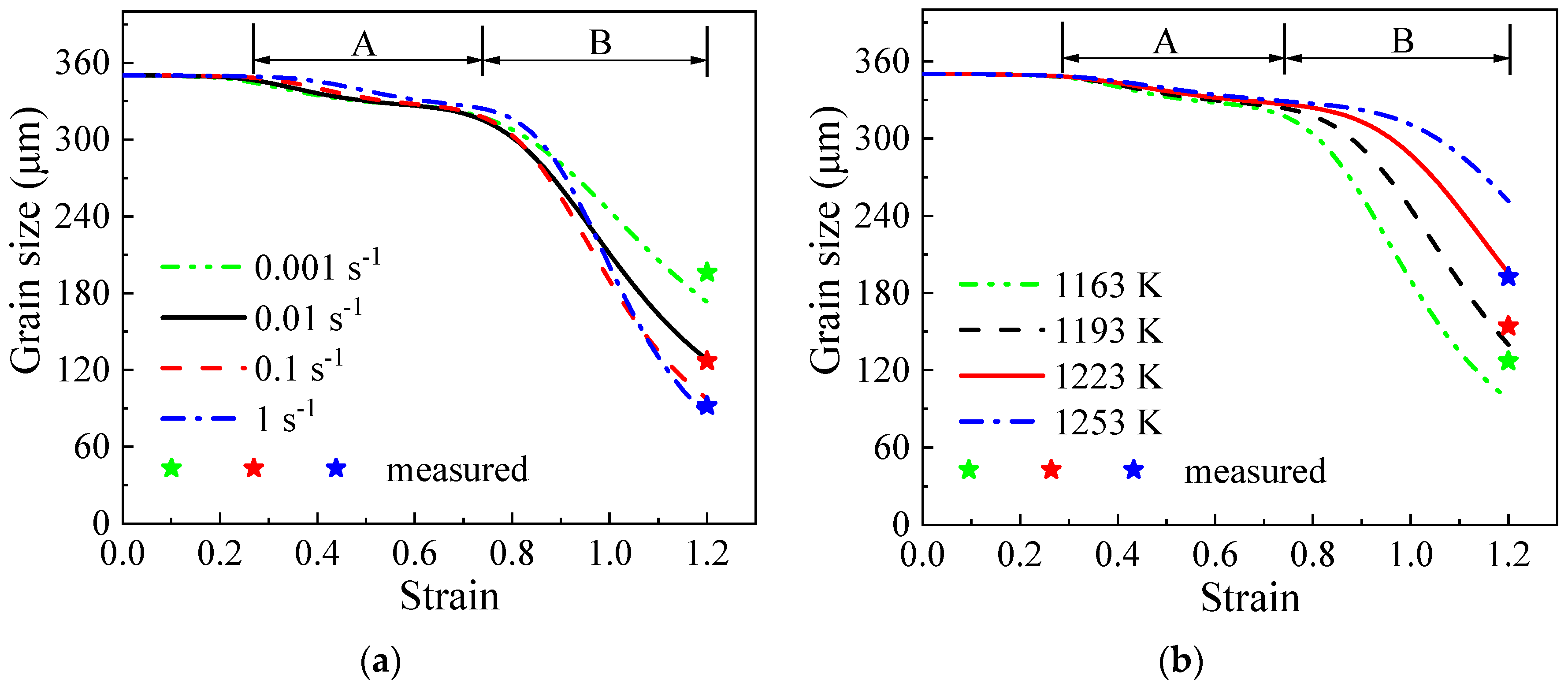
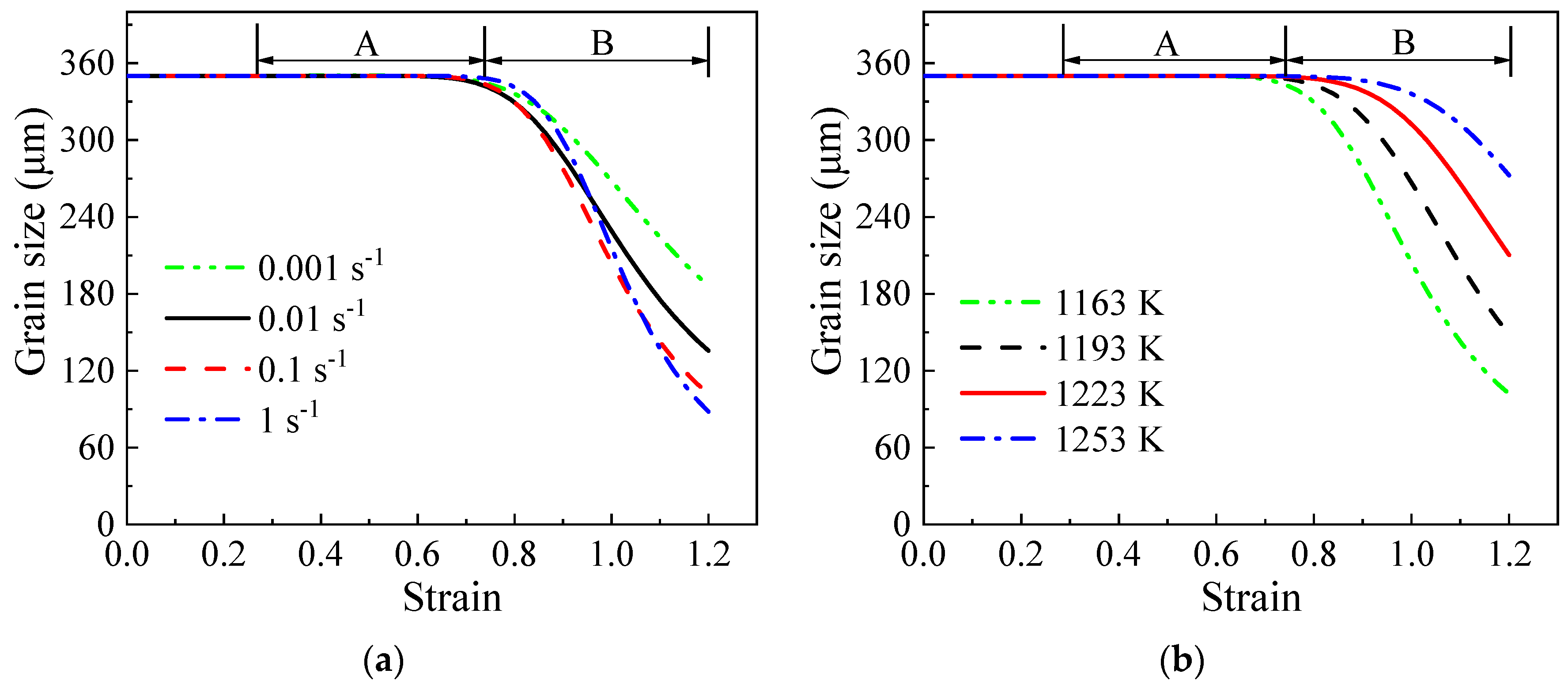
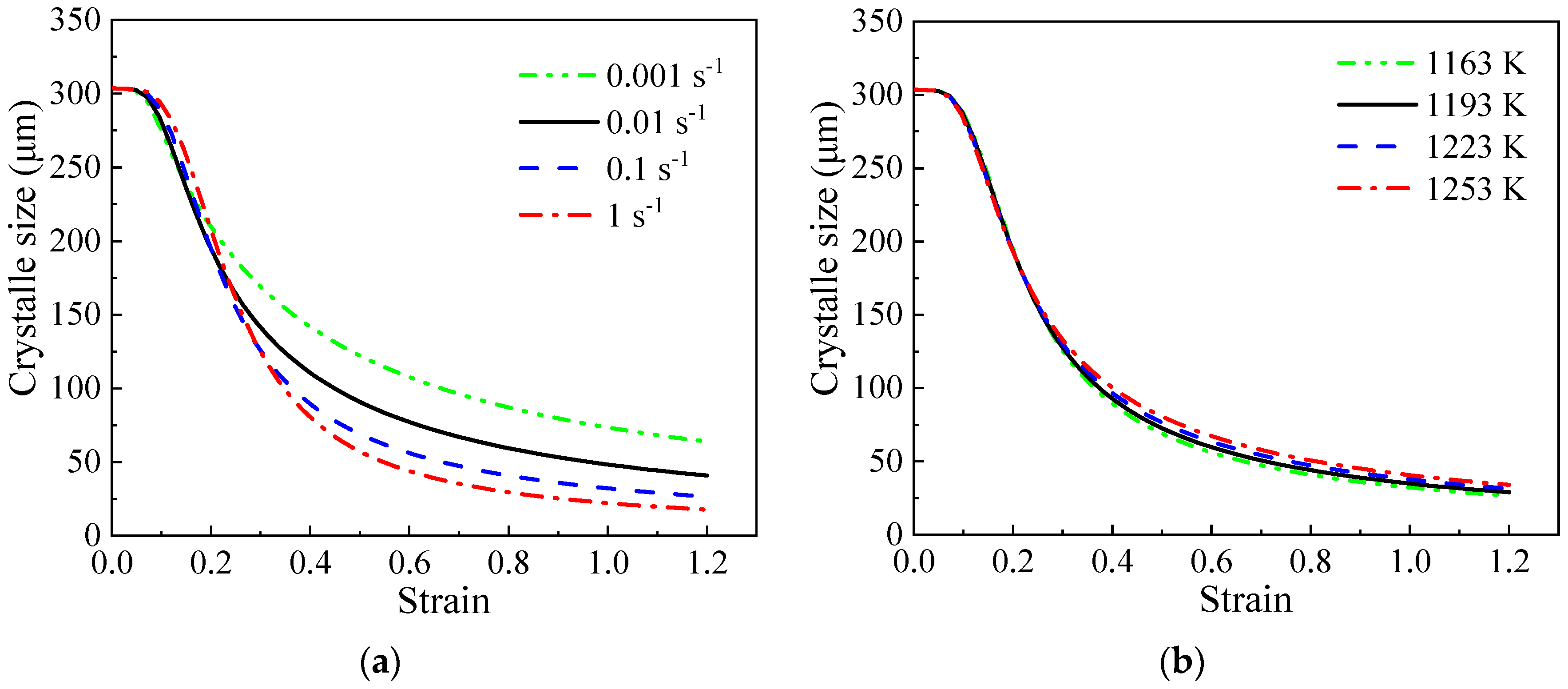
4.4. Model Validation
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| , , | flow stress, thermally independent stress, and thermal activation stress |
| , | strain and strain rate |
| , , , | Taylor coefficient, proportional coefficient, shear modulus, and Burgers vector |
| , , | unit volume grain boundary area, subgrain boundary area, and sum of grain boundary and subgrain boundary areas |
| dislocation density | |
| , | reference shear strain rate and strength coefficient |
| , | dislocation elimination coefficient and deformation activation energy |
| , , | grain boundary migration velocity, migration rate, and driving force |
| , , | characteristic grain boundary thickness, grain boundary self-diffusion coefficient, and Boltzmann constant |
| , | grain boundary self-diffusion activation energy and universal gas constant |
| , , | distance between two dislocations, misorientation angle of LAGBs, and initial angle of LAGBs |
| , | dislocation length per unit area and number of dislocation sets at grain boundary |
| , | initial and current average subgrain sizes |
| , , | LAGB energy storage, critical misorientation angle of LAGBs, and Poisson’s ratio |
| mean misorientation of LAGBs | |
| , | orientation distribution function and area fraction of LAGBs |
| , , | grain size, subgrain size, and crystallite size |
| , | LAGB migration rate and driving force |
| , , , | adiabatic heating temperature rise, efficiency of deformation energy conversion into thermal energy, specific heat capacity, and material density |
| , , , | temperature rise, initial temperature, current temperature, and equivalent heat dissipation rate |
| , , , | LAGB area with the initial misorientation, LAGB area transformed into HAGBs, LAGB area absorbed by HAGB migration, and LAGB area absorbed by LAGB migration |
| , , | HAGB area due to subgrain rotation, HAGB area absorbed by HAGB migration, and new HAGB area formed by HAGB migration |
| , , , , , , , , , , , , , , , , , , | material constants |
References
- Li, H.; Peng, L.F.; Meng, B.; Xu, Z.T.; Wang, L.L.; Ngaile, G.; Fu, M.W. Energy field assisted metal forming: Current status, challenges and prospects. Int. J. Mach. Tool Manufact. 2023, 192, 104075. [Google Scholar] [CrossRef]
- Momeni, A.; Abbasi, S.M.; Sadeghpour, S. A comparative study on the hot deformation behavior of Ti-5Al-5Mo-5Ve-3Cr and newly developed Ti-4Al-7Mo-3V-3Cr alloys. Vacuum 2019, 161, 410–418. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Abbasi, S.M.; Momeni, A.; Akhondzadeh, A.; Ghazi Mirsaed, S.M. Microstructure and mechanical behavior of hot compressed Ti-6V-6Mo-6Fe-3Al. Mater. Sci. Eng. A 2015, 639, 21–28. [Google Scholar] [CrossRef]
- Wu, G.C.; Li, S.Y.; Li, J.H.; Chen, J.; Li, R.; Guo, J.B.; Wang, X.X.; Wang, D.C.; Chen, Z.Q.; Lin, Y.C.; et al. Texture evolution during multi-pass cold rolling and annealing of Ti-2Al-1.5Mn alloy. J. Alloys Compd. 2024, 971, 172705. [Google Scholar] [CrossRef]
- Tiamiyu, A.A.; Pang, E.L.; Chen, X.; LeBeau, J.M.; Nelson, K.A.; Schuh, C.A. Nanotwinning-assisted dynamic recrystallization at high strains and strain rates. Nat. Mater. 2022, 21, 786–794. [Google Scholar] [CrossRef] [PubMed]
- Wahed, M.A.; Gupta, A.K.; Sharma, V.; Mahesh, K.; Singh, S.K.; Kotkunde, N. Material characterization, constitutive modelling, and processing map for superplastic deformation region in Ti-6Al-4V alloy. Int. J. Adv. Manuf. Technol. 2019, 104, 3419–3438. [Google Scholar] [CrossRef]
- Sun, Z.C.; Wu, H.L.; Cao, J.; Yin, Z.K. Modeling of continuous dynamic recrystallization of Al-Zn-Cu-Mg alloy during hot deformation based on the internal-state-variable (ISV) method. Int. J. Plast. 2018, 106, 73–87. [Google Scholar] [CrossRef]
- Sun, Y.W.; Pan, Q.L.; Huang, Z.Q.; Wang, W.Y.; Wang, X.D.; Li, M.J.; Lai, J.P. Evolutions of diffusion activation energy and Zener–Hollomon parameter of ultra-high strength Al-Zn-Mg-Cu-Zr alloy during hot compression. Prog. Nat. Sci. Mater. Int. 2018, 28, 635–646. [Google Scholar] [CrossRef]
- Sitdikov, O.S.; Kaybyshev, R.O.; Safarov, I.M.; Mazurina, I.A. Evolution of the microstructure and mechanisms of formation of new grains upon severe plastic deformation of the 2219 aluminum alloy. Phys. Met. Metallogr. 2001, 92, 270–280. [Google Scholar]
- Gourdet, S.; Montheillet, F. A model of continuous dynamic recrystallization. Acta Mater. 2003, 51, 2685–2699. [Google Scholar] [CrossRef]
- Ferraz, F.M.B.; Buzolin, R.H.; Ebenbauer, S.; Leitner, T.; Krumphals, A.; Poletti, M.C. A predictive mesoscale model for continuous dynamic recrystallization. Int. J. Plast. 2024, 179, 104022. [Google Scholar] [CrossRef]
- Poletti, C.; Germain, L.; Warchomicka, F.; Dikovits, M.; Mitsche, S. Unified description of the softening behavior of beta-metastable and alpha plus beta titanium alloys during hot deformation. Mater. Sci. Eng. A 2016, 651, 280–290. [Google Scholar] [CrossRef]
- Souza, P.M.; Hodgson, P.D.; Rolfe, B.; Singh, R.P.; Beladi, H. Effect of initial microstructure and beta phase evolution on dynamic recrystallization behaviour of Ti6Al4V alloy—An EBSD based investigation. J. Alloys Compd. 2019, 793, 467–479. [Google Scholar] [CrossRef]
- Chen, S.F.; Li, D.Y.; Zhang, S.H.; Han, H.N.; Lee, H.W.; Lee, M.G. Modelling continuous dynamic recrystallization of aluminum alloys based on the polycrystal plasticity approach. Int. J. Plast. 2020, 131, 102710. [Google Scholar] [CrossRef]
- Bobbili, R.; Ramudu, B.V.; Madhu, V. A physically-based constitutive model for hot deformation of Ti-10-2-3 alloy. J. Alloys Compd. 2017, 696, 295–303. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Y.X.; Ahmad, A.S. A novel simulation of continuous dynamic recrystallization process for 2219 aluminium alloy using cellular automata technique. Mater. Sci. Eng. A 2021, 815, 141256. [Google Scholar] [CrossRef]
- Li, Y.B.; Gu, B.; Jiang, S.; Liu, Y.Q.; Shi, Z.S.; Lin, J.G. A CDRX-based material model for hot deformation of aluminium alloys. Int. J. Plast. 2020, 134, 102844. [Google Scholar] [CrossRef]
- Tian, X.; Chen, F.; Jiang, J.N.; Wu, G.S.; Cui, Z.S.; Qian, D.S.; Han, X.H.; Wang, B.; Wang, H.Q.; Wang, H.; et al. Experimental analyses and numerical modeling of the microstructure evolution of aluminum alloy using an internal state variable plasticity-based approach coupled with the effects of second phase. Int. J. Plast. 2022, 158, 103416. [Google Scholar] [CrossRef]
- Maizza, G.; Pero, R.; Richetta, M.; Montanari, R. Continuous dynamic recrystallization (CDRX) model for aluminum alloys. J. Mater. Sci. 2017, 53, 4563–4573. [Google Scholar] [CrossRef]
- Buzolin, R.H.; Lasnik, M.; Krumphals, A.; Poletti, M.C. A dislocation-based model for the microstructure evolution and the flow stress of a Ti5553 alloy. Int. J. Plast. 2021, 136, 102862. [Google Scholar] [CrossRef]
- Buzolin, R.H.; Ferraz, F.M.B.; Lasnik, M.; Krumphals, A.; Poletti, M.C. Improved predictability of microstructure evolution during hot deformation of titanium alloys. Materials 2020, 13, 5678. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.Q.; Lin, Y.C.; Wang, G.Q.; Pang, G.D.; Huang, Z.C. Microstructure evolution and a unified constitutive model for a Ti-55511 alloy deformed in β region. J. Alloys Compd. 2021, 870, 159534. [Google Scholar] [CrossRef]
- Zhang, D.; Dong, X.J.; Xu, Y.; Lu, S.Q.; Wei, K.; Huang, L. Dynamic recrystallization mechanism of Ti-6554 alloy during high-temperature deformation. J. Alloys Compd. 2023, 959, 170534. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, Z.; Gao, P.; Yang, R.; Li, H.; Tang, B.; Kou, H.; Zhang, Y.; Esling, C.; Li, J. On the nature of a peculiar initial yield behavior in metastable β titanium alloy Ti-5Al-5Mo-5V-3Cr-0.5 Fe with different initial microstructures. J. Mater. Sci. Technol. 2020, 38, 135–147. [Google Scholar] [CrossRef]
- Zyguła, K.; Lypchanskyi, O.; Łukaszek-Sołek, A.; Korpała, G.; Stanik, R.; Kubiś, M.; Przybyszewski, B.; Wojtaszek, M.; Gude, M.; Prahl, U. Behavior of the metastable β titanium alloy prepared by blended elemental powder metallurgy approach. Metall. Mater. Trans. A 2024, 55, 933–954. [Google Scholar] [CrossRef]
- Mozumder, Y.H.; Arun Babu, K.; Saha, R.; Sarma, V.S.; Mandal, S. Dynamic microstructural evolution and recrystallization mechanism during hot deformation of intermetallic-hardened duplex lightweight steel. Mater. Sci. Eng. A 2020, 788, 139613. [Google Scholar] [CrossRef]
- Wu, G.C.; Lin, Y.C.; Chen, M.S.; Qiu, W.; Zeng, N.F.; Zhang, S.; Wan, M.; He, D.G.; Jiang, Y.Q.; Naseri, M. Continuous dynamic recrystallization behaviors in a single-phase deformed Ti-55511 alloy by cellular automata model. J. Alloys Compd. 2024, 1002, 175293. [Google Scholar] [CrossRef]
- Duan, X.; Sheppard, T. Simulation of substructural strengthening in hot flat rolling. J. Mater. Process. Technol. 2002, 125, 179–187. [Google Scholar] [CrossRef]
- Liu, G.X.; Zhang, D.H.; Yao, C.F. Investigation of the grain refinement mechanism in machining Ti-6Al-4V: Experiments and simulations. J. Manuf. Process. 2023, 94, 479–496. [Google Scholar] [CrossRef]
- Fan, X.G.; Yang, H. Internal-state-variable based self-consistent constitutive modeling for hot working of two-phase titanium alloys coupling microstructure evolution. Int. J. Plast. 2011, 27, 1833–1852. [Google Scholar] [CrossRef]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Wen, H.N.; Jin, J.S.; Tang, X.F.; Wang, X.Y.; Yang, H.Y.; Zhang, Y.D.; Zhang, M.; Deng, L.; Wei, Q.S.; Chen, J.Z.; et al. Machine learning-assisted constitutive modeling of a novel powder metallurgy superalloy. Int. J. Mech. Sci. 2023, 260, 108654. [Google Scholar] [CrossRef]
- Stüwe, H.P.; Ortner, B. Recrystallization in hot working and creep. Met. Sci. 1974, 8, 161–167. [Google Scholar] [CrossRef]
- OuYang, D.L.; Fu, M.W.; Lu, S.Q. Study on the dynamic recrystallization behavior of Ti-alloy Ti-10V-2Fe-3V in β processing via experiment and simulation. Mater. Sci. Eng. A 2014, 619, 26–34. [Google Scholar] [CrossRef]
- Kozlov, E.V.; Koneva, N.A.; Popova, N.A. Grain structure, geometrically necessary dislocations and second-phase particles in polycrystals of micro- and mesolevels. Phys. Mesomech. 2009, 12, 280–292. [Google Scholar] [CrossRef]
- Chen, F.; Tian, X.; Wu, G.S.; Zhu, H.J.; Ou, H.G.; Cui, Z.S. Coupled quantitative modeling of microstructural evolution and plastic flow during continuous dynamic recrystallization. Int. J. Plast. 2022, 156, 103372. [Google Scholar] [CrossRef]
- Mallick, A.; Vedantam, S. Phase field study of the effect of grain boundary energy anisotropy on grain growth. Comput. Mater. Sci. 2009, 46, 21–25. [Google Scholar] [CrossRef]
- Dillamore, I.; Smith, C.; Watson, T. Oriented nucleation in the formation of annealing textures in iron. Met. Sci. J. 1967, 1, 49–54. [Google Scholar] [CrossRef]
- Huang, Y.; Humphreys, F. Subgrain growth and low angle boundary mobility in aluminium crystals of orientation {110} <001>. Acta Mater. 2000, 48, 2017–2030. [Google Scholar]
- Zhang, M.X.; Zhang, B.J.; Jiao, X.Y.; Ding, H. Hot deformation behaviors and microstructure evolution of a supersaturated nickel-based superalloy. Mater. Charact. 2024, 211, 113915. [Google Scholar] [CrossRef]
- Semiatin, S.L.; Montheillet, F.; Shen, G.; Jonas, J.J. Self-consistent modeling of the flow behavior of wrought alpha/beta titanium alloys under isothermal and nonisothermal hot-working conditions. Metall. Mater. Trans. A 2002, 33, 2719–2727. [Google Scholar] [CrossRef]
- Liu, R.G.; Wang, B.Y.; Hu, S.S.; Zhang, H.B.; Feng, P.N. Unified modeling of the microstructure and densification of TC4 powder titanium alloy during hot deformation. J. Mater. Process. Technol. 2023, 24, 4904–4918. [Google Scholar] [CrossRef]
- Gao, Y.S.; Xue, X.Y.; Gao, H.X.; Luo, W.Z.; Wang, K.X.; Li, S.Q.; Liu, X.H.; Du, Y.X. Investigation of high-temperature constitutive behavior of Ti555211 titanium alloy subjected to plastic deformation in the different phase regions. Metals 2022, 12, 1562. [Google Scholar] [CrossRef]
- Souza, P.M.; Sivaswamy, G.; Hall, L.; Rahimi, S. An Analysis of the Forgeability of Ti-10V-2Fe-3Al β Titanium alloy using a combined Estrin Mecking and Avrami Material Constitutive Model. Int. J. Mech. Sci. 2022, 216, 106975. [Google Scholar] [CrossRef]
- Xu, J.W.; He, Q.W.; Jin, X.Z.; Bian, S.S.; Shan, D.B.; Wu, H.; Xu, W.C. A 3D cellular automaton with inhomogeneous nucleation for simulating dynamic recrystallization of low-alloy steel with mixed-grain microstructure. J. Mater. Process. Technol. 2023, 322, 118171. [Google Scholar] [CrossRef]
- Su, G.; Yun, Z.; Lin, Y.C.; He, D.G.; Zhang, S.; Cheng, Z.J. Microstructure evolution and a unified constitutive model of Ti-55511 alloy compressed at stepped strain rates. Materials 2021, 14, 6750. [Google Scholar] [CrossRef]
- Jiang, Y.Q.; Guo, Y.W.; Wang, M.B.; Han, J.J.; Huang, Z.C.; Huang, Z.F. Hot deformation and constitutive modeling of a Ti-Al-Sn-Zr-Mo-Cr-Nb alloy. Mater. Today Commun. 2024, 40, 110037. [Google Scholar] [CrossRef]
- Yang, Z.K.; Wu, J.J.; Wang, M.Y.; Zhang, Z.C.; Yan, J.; Wu, W.; Liu, L.; Wang, H.; Wang, W.Z. Tensile deformation behavior of high-strength TA18 titanium alloy tube under warm forming conditions and constitutive model based on dislocation density. Mater. Today Commun. 2023, 37, 107336. [Google Scholar] [CrossRef]




| (-) | (-) | (-) | (m−1) | (-) | (-) | (m−3) | (-) | (-) |
| 0.67 | 22.3 | 29.1 | 2.19 × 108 | 1.08 × 103 | 0.2307 | 7.16 × 107 | 0.46 | 1.09 × 108 |
| (-) | (-) | (-) | (-) | (-) | (-) | (-) | (MPa) | (K) |
| 2.6 × 107 | 1.45 × 106 | 1.54 × 1010 | 1.09 | 0.25 | 0.23 | 0.2604 | 3.41 × 103 | 70.255 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.-C.; Lin, Y.-C.; Wan, M.; Zeng, N.-F.; Zhang, S.; Zhang, H.-J.; Chen, M.-S.; Jiang, Y.-Q. An Internal-State-Variable-Based Continuous Dynamic Recrystallization Model for Thermally Deformed TC18 Alloy. Materials 2024, 17, 4026. https://doi.org/10.3390/ma17164026
Wu G-C, Lin Y-C, Wan M, Zeng N-F, Zhang S, Zhang H-J, Chen M-S, Jiang Y-Q. An Internal-State-Variable-Based Continuous Dynamic Recrystallization Model for Thermally Deformed TC18 Alloy. Materials. 2024; 17(16):4026. https://doi.org/10.3390/ma17164026
Chicago/Turabian StyleWu, Gui-Cheng, Yong-Cheng Lin, Miao Wan, Ning-Fu Zeng, Song Zhang, Hui-Jie Zhang, Ming-Song Chen, and Yu-Qiang Jiang. 2024. "An Internal-State-Variable-Based Continuous Dynamic Recrystallization Model for Thermally Deformed TC18 Alloy" Materials 17, no. 16: 4026. https://doi.org/10.3390/ma17164026
APA StyleWu, G.-C., Lin, Y.-C., Wan, M., Zeng, N.-F., Zhang, S., Zhang, H.-J., Chen, M.-S., & Jiang, Y.-Q. (2024). An Internal-State-Variable-Based Continuous Dynamic Recrystallization Model for Thermally Deformed TC18 Alloy. Materials, 17(16), 4026. https://doi.org/10.3390/ma17164026








