Research on the Mechanical Response and Constitutive Model of 18Ni300 Manufactured by SLM with Different Build Directions
Abstract
:1. Introduction
2. Materials and Methods
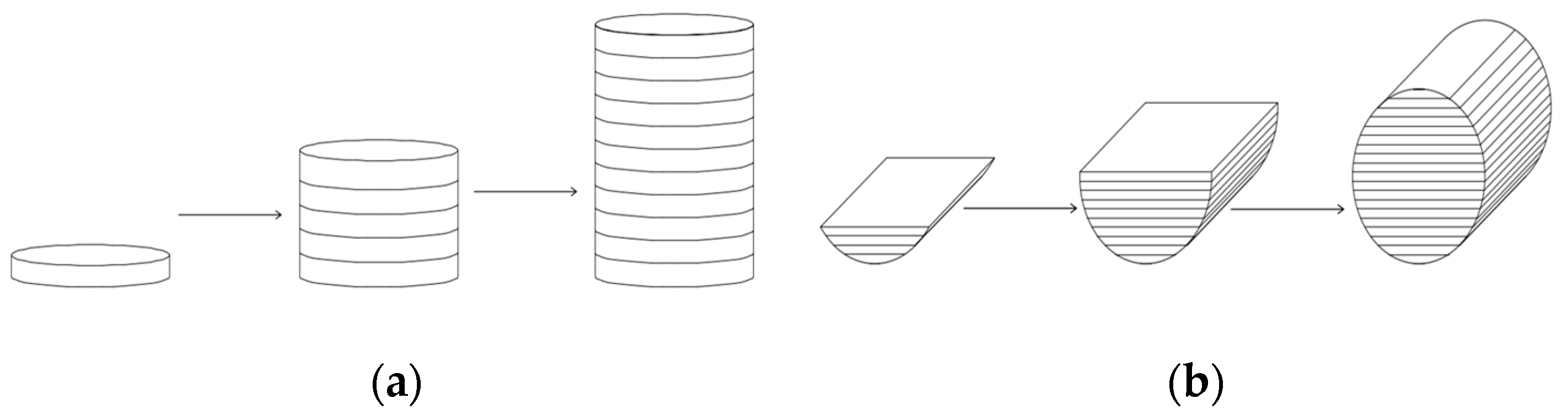
2.1. Specimen Manufacturing Method
2.2. Equivalent Static Compression
2.3. High-Temperature Compression Test
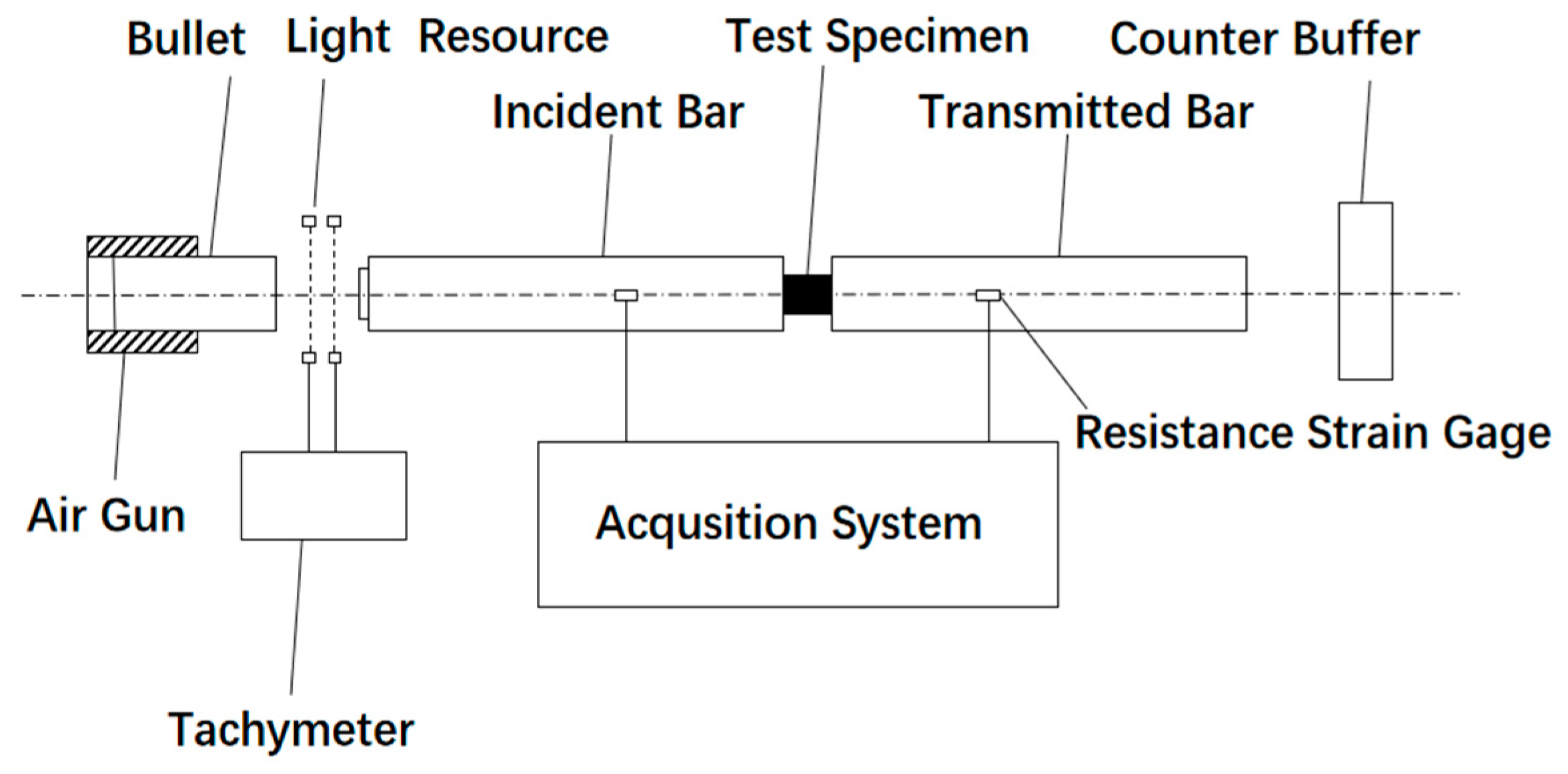
2.4. SHPB Test
2.5. Metallographic Test
3. Results and Discussion
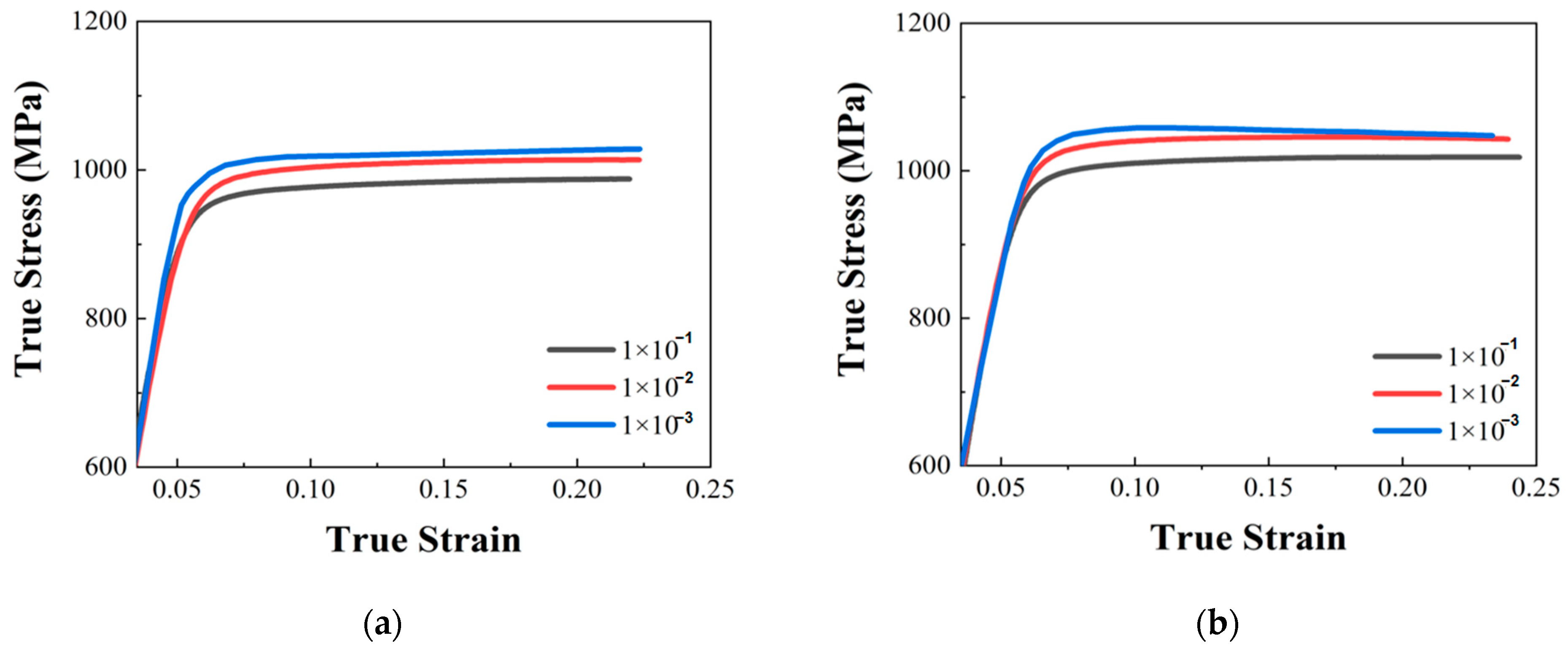
3.1. The Result of Quasi-Static Compression Test
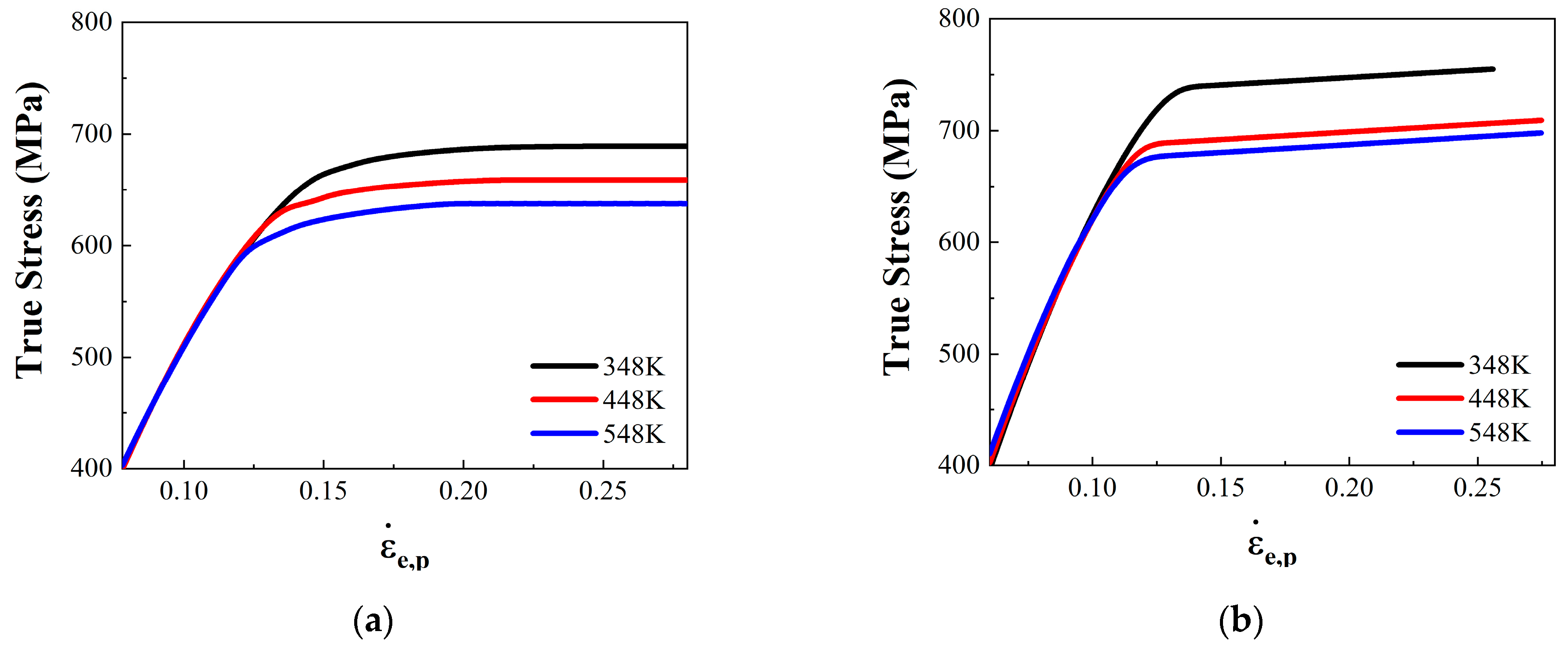
3.2. The Result of High-Temperature Compression Test
3.3. The Result of SHPB Test
3.4. The Result of Metallographic Test
4. Discussion
4.1. Strain Hardening Effect
4.2. Strain Rate Strengthening Effect
4.3. Thermal Softening Effect
4.4. Microstructure Characterization
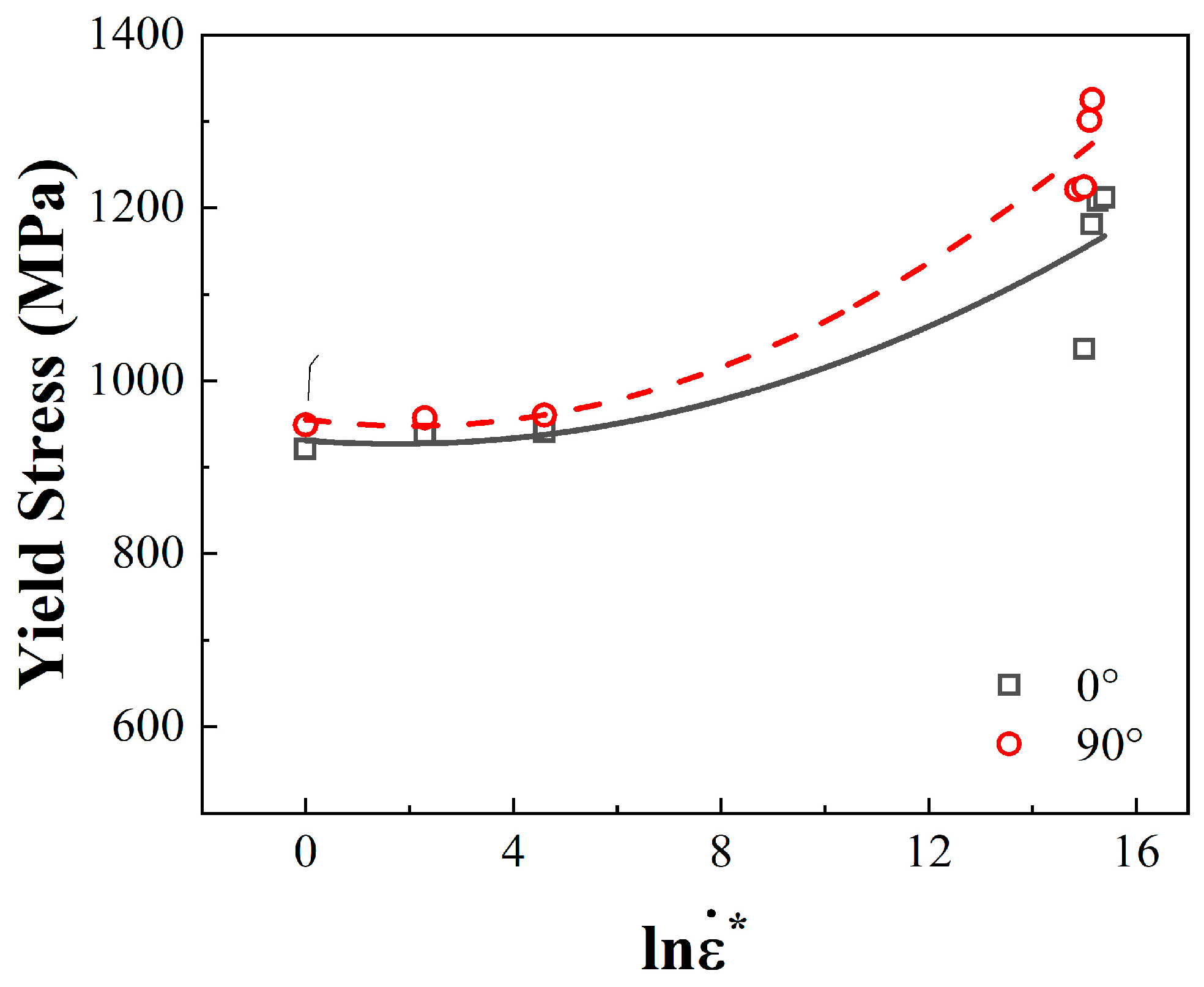
5. J-C Constitutive Model and Verification
5.1. J-C Constitutive Model
5.2. Result of Fitting Parameter
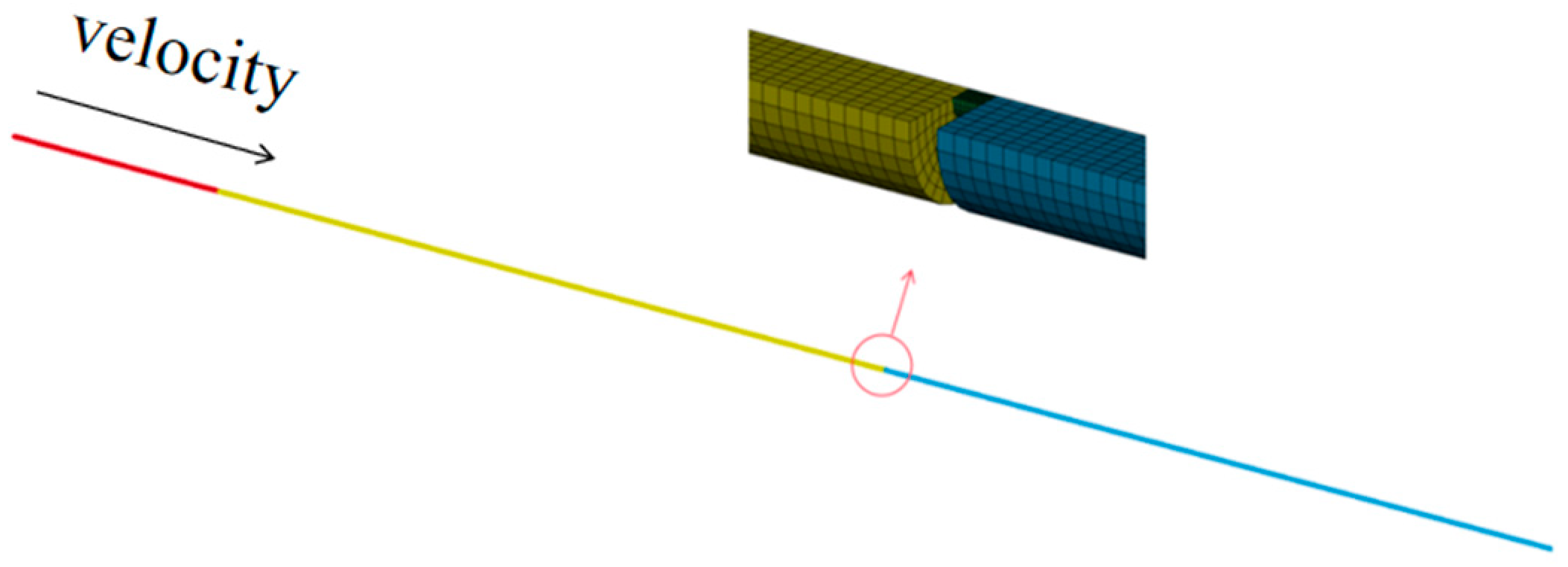
5.3. Finite Element Modelling
5.3.1. Numerical Modelling
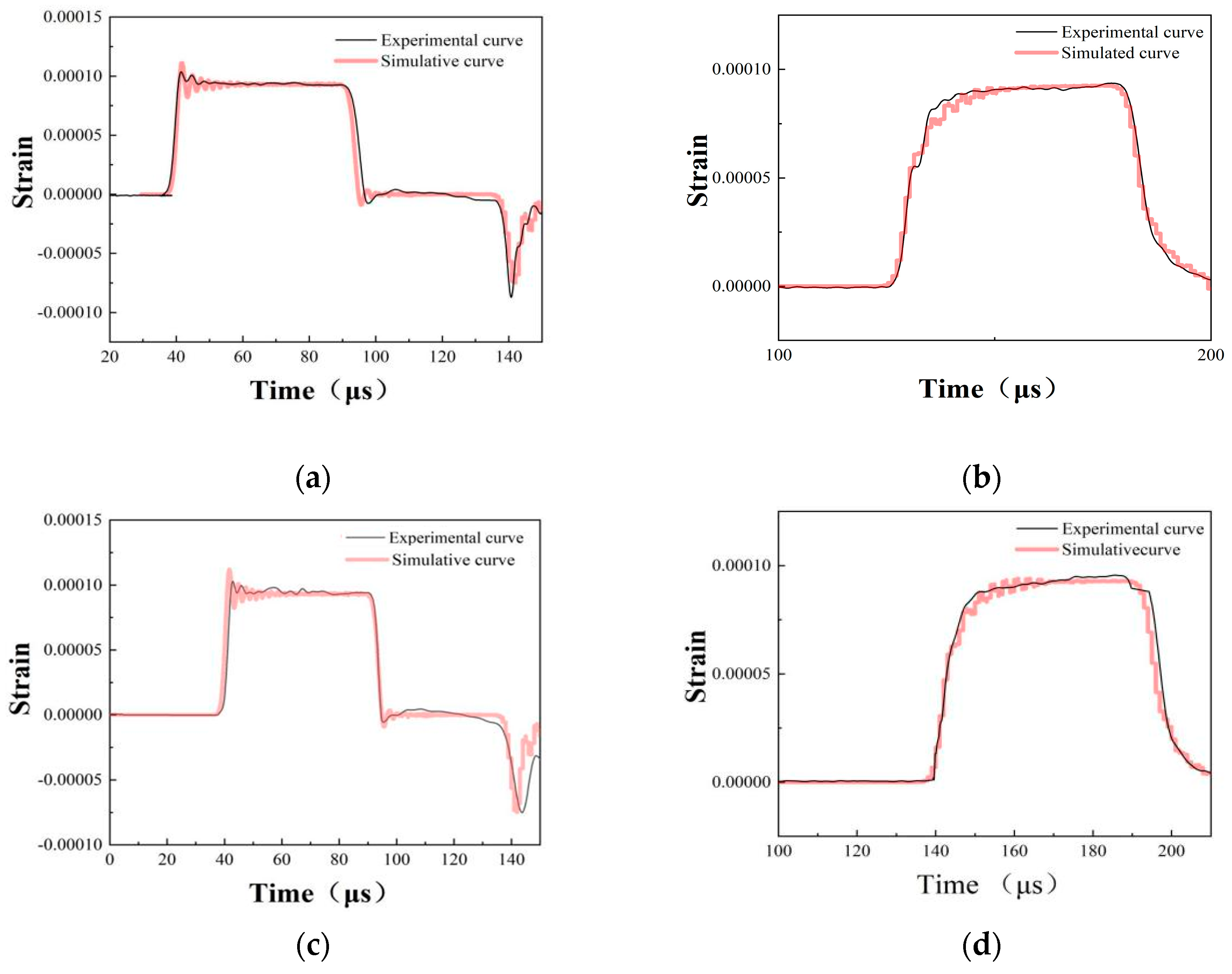
5.3.2. Analysis of the Numerical Simulation Results
6. Conclusions
- (1)
- By comparing the stress–strain curves at two construction directions in a static state, we found that 18Ni300 with the two build directions did not show yield points, and the 18Ni300 material with both build directions demonstrated a thermal softening effect. Moreover, 18Ni300 exhibited a strain rate strengthening effect for both build directions. However, the yield strength of 18Ni300 does not show significant differences in the two build directions. 18Ni300 exhibited strain hardening and strain rate strengthening effects for both build directions. However, the yield strength of 18Ni300 for the two build directions demonstrated certain differences under the four strain rates. Specifically, the yield strength of 18Ni300 for the 90° build direction was 9.6% higher than that of 18Ni300 for the 0° build direction. By comparing the micro-structures of 18Ni300 manufactured by SLM for the two build directions, we found that 18Ni300 for the 90° build direction contained more and bigger martensite phases than 18Ni300 for the 0° build direction, according to the microstructure. This was the reason for the difference in mechanical properties of the 18Ni300 material with the two build directions.
- (2)
- A J-C constitutive model of 18Ni300 with different construction directions was obtained, and the SHPB test was simulated according to the J-C parameters. The strain rate–time curve obtained from the SHPB simulation matches well with the experimental results. Comparing the numerical simulation results and the experimental results, the maximum error between the experimental and simulated results was around 8.9%. This proves the J-C model can precisely predict the mechanical properties of 18Ni300 under dynamic conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohammed, M.T. Mechanical Properities of SLM-Titanium Materials for Biomedical Applications: A Review. Mater. Today Proc. 2018, 5, 17903–17913. [Google Scholar]
- Ataee, A.; Li, Y.; Brandt, M.; Wen, C. Ultrahigh-strength titanium gyroid scaffolds manufactured by selective laser melting (SLM) for bone implant applications. Acta Mater. 2018, 158, 354–368. [Google Scholar] [CrossRef]
- Liu, R.; Wang, Z.; Sparks, T.; Liou, F.; Newkirk, J. 13-Aerospace applications of laser additive manufacturing. In Woodhead Publishing Series in Electronic and Optical Materials; Brandt, M., Ed.; Woodhead Publishing: Sawston, UK, 2017; pp. 351–371. [Google Scholar]
- Uriondo, A.; Esperon-Miguez, M.; Perinpanayagam, S. The present and future of additive manufacturing in the aerospace sector: A review of important aspects. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 2132–2147. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal additive manufacturing in aerospace: A Review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Krakhmalev, P.; Fredriksson, G.; Yadroitsava, I.; Kazantseva, N.; du Plessis, A.; Yadroitsev, I. Deformation Behavior and micro-structure of Ti6Al4V Manufactured by SLM. Phys. Procedia 2016, 83, 778–788. [Google Scholar] [CrossRef]
- Liverani, E.; Toschi, S.; Ceschini, L.; Fortunato, A. Effect of selective laser melting (SLM) process parameters on micro-structure and mechanical properties of 316L austenitic stainless steel. J. Mater. Process. Technol. 2017, 249, 255–263. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, Z.; Tse, Y.; Huang, C.; Zhang, W. Optimization of processing parameters and establishment of a relationship between micro-structure and mechanical properties of SLM titanium alloy. Opt. Laser Technol. 2019, 112, 159–167. [Google Scholar] [CrossRef]
- Iveković, A.; Montero-Sistiaga, M.L.; Vanmeensel, K.; Kruth, J.-P.; Vleugels, J. Effect of processing parameters on micro-structure and properties of tungsten heavy alloys fabricated by SLM. Int. J. Refract. Met. Hard Mater. 2019, 82, 23–30. [Google Scholar] [CrossRef]
- Yablokova, G.; Speirs, M.; Van Humbeeck, J.; Kruth, J.-P.; Schrooten, J.; Cloots, R.; Boschini, F.; Lumay, G.; Luyten, J. Rheological behavior of β-Ti and NiTi powders produced by atomization for SLM production of open porous orthopedic implants. Powder Technol. 2015, 283, 199–209. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Zhang, J.; Medvedev, A.; Sarker, A.; Ruan, D.; Lu, G.; Faruque, O.; Brandt, M. Effect of build orientation on the quasi-static and dynamic response of SLM AlSi10Mg. Mater. Sci. Eng. A 2020, 788, 139445. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, B.; Wu, S.; Liu, W. Anisotropic tension-compression asymmetry in SLM 316L stainless steel. Int. J. Mech. Sci. 2023, 246, 108139. [Google Scholar] [CrossRef]
- Brandl, E.; Heckenberger, U.; Holzinger, V.; Buchbinder, D. Additive manufactured AlSi10Mg samples using Selective Laser Melting (SLM): Micro-structure, high cycle fatigue, and fracture behavior. Mater. Des. 2012, 34, 159–169. [Google Scholar] [CrossRef]
- Li, Y. Mechanical Properties and Constitutive Model of Selective Laser Melting 316L Stainless Steel at Different Scanning Speeds. Adv. Mater. Sci. Eng. 2022, 1, 2905843. [Google Scholar] [CrossRef]
- Zheng, Z.; Jin, X.; Bai, Y.; Yang, Y.; Ni, C.; Lu, W.F.; Wang, H. Micro-structure and anisotropic mechanical properties of selective laser melted Ti6Al4V alloy under different scanning strategies. Mater. Sci. Eng. A 2022, 831, 142236. [Google Scholar] [CrossRef]
- Aktürk, M.; Boy, M.; Gupta, M.K.; Waqar, S.; Krolczyk, G.M.; Korkmaz, M.E. Numerical and experimental investigations of built orientation dependent Johnson–Cook model for selective laser melting manufactured AlSi10Mg. J. Mater. Res. Technol. 2021, 15, 6244–6259. [Google Scholar] [CrossRef]
- Alkhatib, S.E.; Xu, S.; Lu, G.; Karrech, A.; Sercombe, T.B. Dynamic constitutive behavior of LPBFed metal alloys. J. Mater. Res. Technol. 2023, 25, 581–592. [Google Scholar] [CrossRef]
- Li, P. Constitutive and failure behaviour in selective laser melted stainless steel for microlattice structures. Mater. Sci. Eng. A 2015, 622, 114–120. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, L.; Kong, D.; Liu, P.; He, X.; Ni, X.; Zhang, L.; Dong, C. Texture dependence on the mechanical properties of 18Ni300 maraging steel fabricated by laser powder bed fusion. Mater. Charact. 2022, 189, 111938. [Google Scholar] [CrossRef]
- Zerillli, F.J.; Armstrong, R.W. Dislocation-mechannics-based constitutive relations for meterial dynamics calculations. J. Appl. Phys. 1987, 5, 1816–1825. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rate and high temperatures. In Proceedings of the 7th International Symposiumon Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–548. [Google Scholar]
- Król, M.; Snopiński, P.; Hajnyš, J.; Pagáč, M.; Łukowiec, D. Selective Laser Melting of 18NI-300 Maraging Steel. Materials 2020, 13, 4268. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Zhou, K.; Tong, X.; Huang, Y.; Li, J.; Ma, W.; Li, F.; Kuang, T. Microstructure and Mechanical Properties of 18Ni-300 Maraging Steel Fabricated by Selective Laser Melting. In Advances in Engineering Research, Proceedings of the 2016 6th International Conference on Advanced Design and Manufacturing Engineering; Atlantis Press: Amsterdam, The Netherlands, 2017; p. 7. [Google Scholar]
- Song, J.; Tang, Q.; Feng, Q.; Han, Q.; Ma, S.; Chen, H.; Guo, F.; Setchi, R. Effect of remelting processes on the microstructure and mechanical behaviours of 18Ni-300 maraging steel manufactured by selective laser melting. Mater. Charact. 2022, 184, 111648. [Google Scholar] [CrossRef]
- GB/T 7314-2005; Metallic Materials—Compression Testing at Ambient Temperature. Standardization Administration of China (SAC): Beijing, China, 2005.
- Tan, C.; Zhou, K.; Ma, W.; Zhang, P.; Liu, M.; Kuang, T. Microstructural evolution, nanoprecipitation behavior and mechanical properties of selective laser melted high-performance grade 300 maraging steel. Mater. Des. 2017, 134, 23–34. [Google Scholar] [CrossRef]
- Bai, Y.; Zhao, C.; Wang, D.; Wang, H. Evolution mechanism of surface morphology and internal hole defect of 18Ni300 maraging steel fabricated by selective laser melting. J. Mater. Process. Technol. 2022, 299, 117328. [Google Scholar] [CrossRef]
- Zhao, Z.; Dong, C.; Kong, D.; Wang, L.; Ni, X.; Zhang, L.; Wu, W.; Zhu, L.; Li, X. Influence of pore defects on the mechanical property and corrosion behavior of SLM 18Ni300 maraging steel. Mater. Charact. 2021, 182, 111514. [Google Scholar] [CrossRef]
- Song, L.; Hu, S.-S. Two-wave and three-wave method in SHPB data processing. Explos. Shock. Waves 2005, 25, 368–373. [Google Scholar]
- Ferreira, D.; Miranda, G.; Oliveira, F.J.; Oliveira, J.M. Conventionally and SLM-manufactured 18Ni300 steel: Mechanical and tribological behavior in dry sliding against PP40 composite. Int. J. Adv. Manuf. Technol. 2022, 122, 1245–1258. [Google Scholar] [CrossRef]
- Huh, H.; Kang, W.J.; Han, S.S. A Tension Split Hokinson Bar for Investgating the Dynamic Behavior of sheet Metals. Acta Phys. Sin. 2016, 42, 8–17. [Google Scholar]
- Chen, G.; Ke, Z.; Ren, C.; Li, J. Constitutive modeling for Ti-6Al-4V alloy machining based on the SHPB tests and simulation. Adv. Manuf. Mach. Technol. 2016, 29, 962–970. [Google Scholar] [CrossRef]









| Ni | Ti | Co | Al | Mo | Si | Cr | Mn | C | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 17.70 | 0.72 | 9.05 | 0.077 | 4.79 | 0.025 | 0.031 | 0.022 | 0.007 | 67.578 |
| Material | Layer Thickness (mm) | Laser Power (W) | Scanning Speed (mm/s) | Heat Treatment Method |
|---|---|---|---|---|
| 18Ni300 | 0.05 | 200 | 1000 | Maintained at 900 °C for 2 h and cooled below 80 °C |
| Build Direction | Strain Rate (s−1) | Compression Yield Stress (MPa) |
|---|---|---|
| 0° | 1 × 10−3 | 921 |
| 1 × 10−2 | 939 | |
| 1 × 10−1 | 941 | |
| 90° | 1 × 10−3 | 949 |
| 1 × 10−2 | 957 | |
| 1 × 10−1 | 960 |
| Build Direction | Temperature (K) | Compression Yield Stress (MPa) |
|---|---|---|
| 0° | 348 | 573 |
| 448 | 560 | |
| 548 | 506 | |
| 90° | 348 | 620 |
| 448 | 565 | |
| 548 | 540 |
| Build Direction | Strain Rate (s−1) | Compression Yield Stress (MPa) |
|---|---|---|
| 0° | 2944 | 1037 |
| 3300 | 1181 | |
| 3500 | 1208 | |
| 3800 | 1212 | |
| 90° | 2850 | 1221 |
| 3330 | 1224 | |
| 3620 | 1301 | |
| 3880 | 1325 |
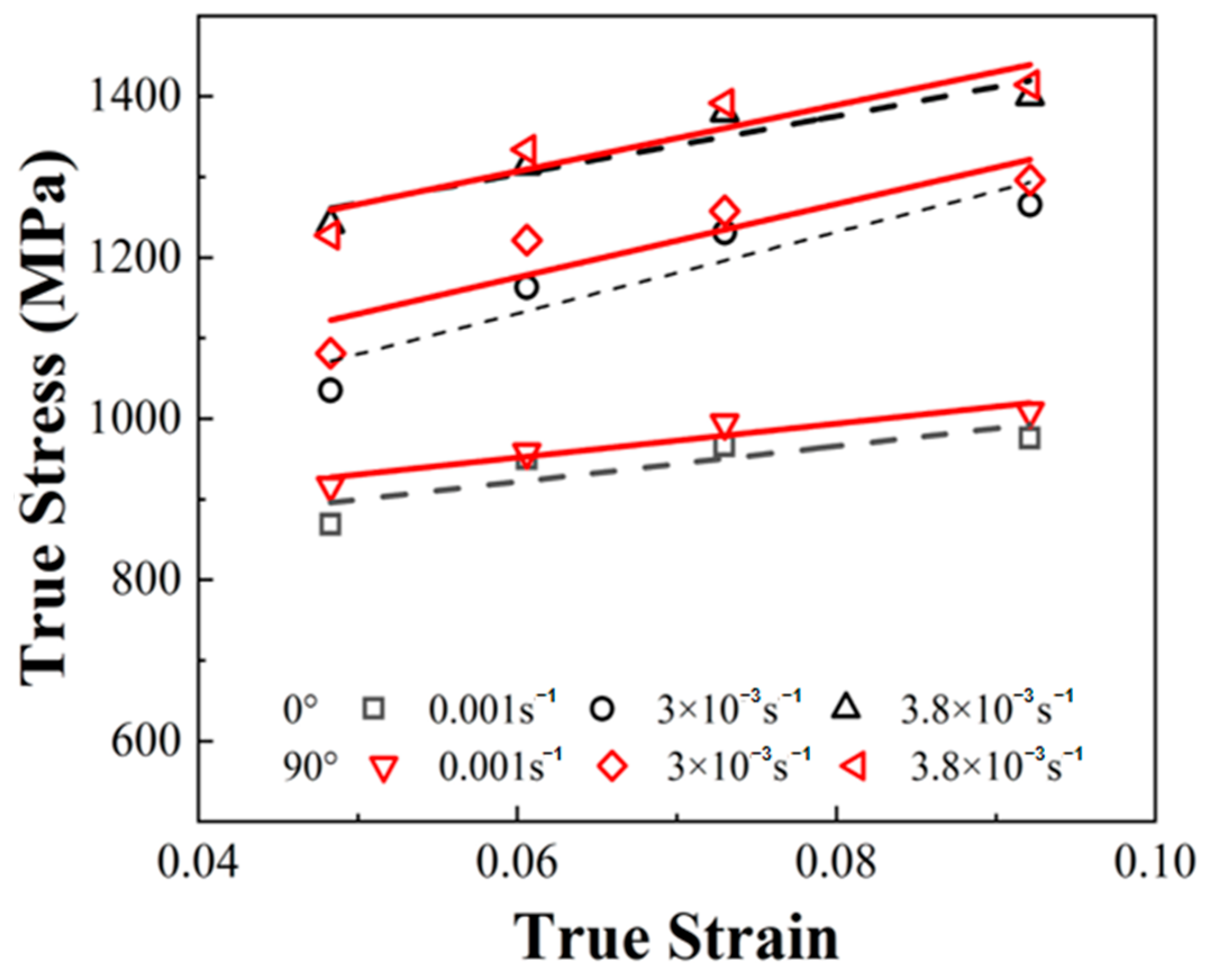
| Build Direction | Strain Rate (s−1) | Changes in Flow Stress (MPa) | Rate of Increase |
|---|---|---|---|
| 0° | 1 × 10−3 | 869–976 | 12.3% |
| 3 × 10−3 | 1035–1265 | 22.2% | |
| 3.8 × 10−3 | 1242–1400 | 12.7% | |
| 90° | 1 × 10−3 | 916–1009 | 9.2% |
| 3 × 10−3 | 1081–1296 | 19.8% | |
| 3.8 × 10−3 | 1227–1414 | 15.2% |
| ρ (g/cm3) | Elasticity Modulus E (GPa) | Yield Stress σS (MPa) | Poisson’s Ratio v |
|---|---|---|---|
| 8.2 | 210 | 1900 | 0.33 |
| Build Direction | A | B | n | C1 | C2 | mjc |
|---|---|---|---|---|---|---|
| 0° | 921 | 112 | 0.303 | 0.00117 | 0.00120 | 0.0928 |
| 90° | 949 | 100 | 0.209 | 0.00134 | 0.00259 | 0.1762 |
| Build Direction | Striking Velocity (m/s) | Strain Rate (s−1) |
|---|---|---|
| 0° | 6.36 | 2944 |
| 8.22 | 3300 | |
| 8.44 | 3500 | |
| 9.26 | 3800 | |
| 90° | 7.01 | 2850 |
| 8.26 | 3330 | |
| 9.31 | 3620 | |
| 10.01 | 3880 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Zhang, Q.; Li, W.; Li, W. Research on the Mechanical Response and Constitutive Model of 18Ni300 Manufactured by SLM with Different Build Directions. Materials 2024, 17, 4246. https://doi.org/10.3390/ma17174246
Liang Z, Zhang Q, Li W, Li W. Research on the Mechanical Response and Constitutive Model of 18Ni300 Manufactured by SLM with Different Build Directions. Materials. 2024; 17(17):4246. https://doi.org/10.3390/ma17174246
Chicago/Turabian StyleLiang, Zhenchao, Qing Zhang, Wenbin Li, and Weihang Li. 2024. "Research on the Mechanical Response and Constitutive Model of 18Ni300 Manufactured by SLM with Different Build Directions" Materials 17, no. 17: 4246. https://doi.org/10.3390/ma17174246
APA StyleLiang, Z., Zhang, Q., Li, W., & Li, W. (2024). Research on the Mechanical Response and Constitutive Model of 18Ni300 Manufactured by SLM with Different Build Directions. Materials, 17(17), 4246. https://doi.org/10.3390/ma17174246





