Energy Absorption Behavior of Carbon-Fiber-Reinforced Plastic Honeycombs under Low-Velocity Impact Considering Their Ply Characteristics
Abstract
:1. Introduction
2. Materials and Experiments
2.1. Material Introduction
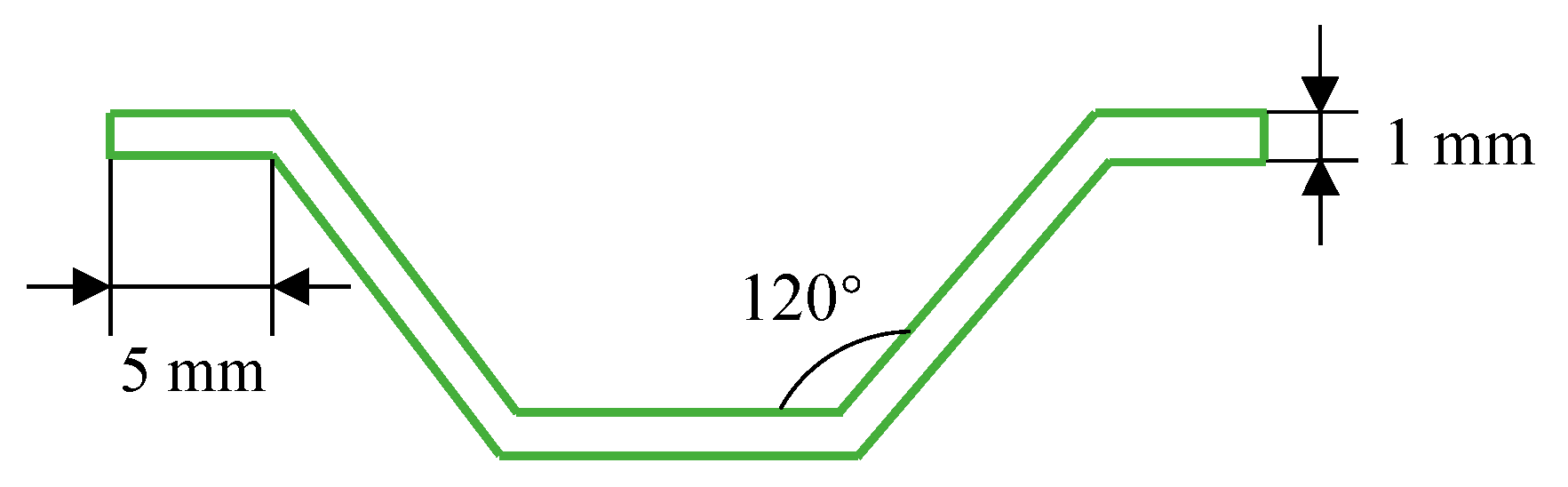
2.2. Fabrication Procedure
2.3. Quasi-Static Experiments
3. Finite Element Simulation of CFRP
3.1. Finite Element Model
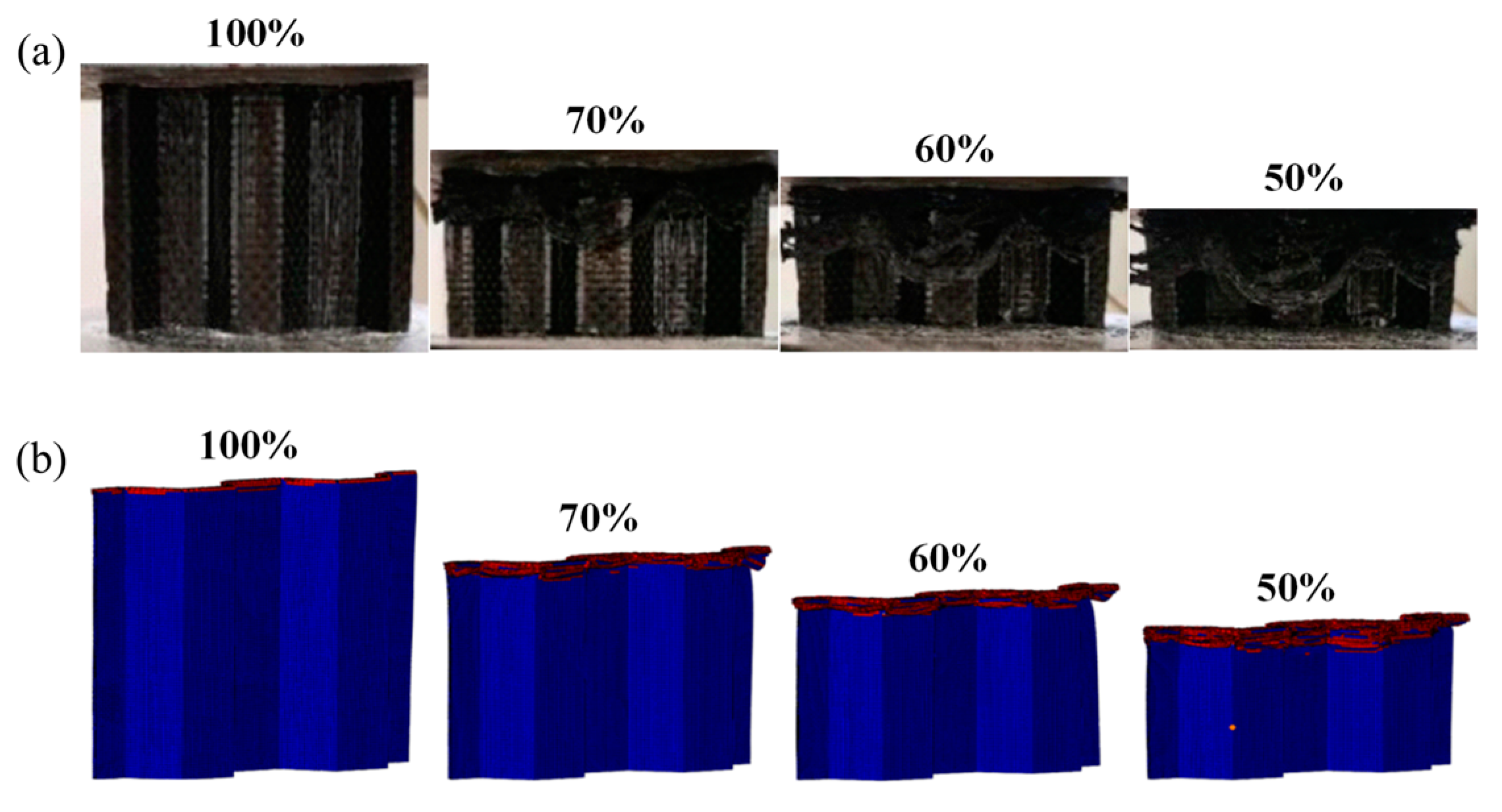
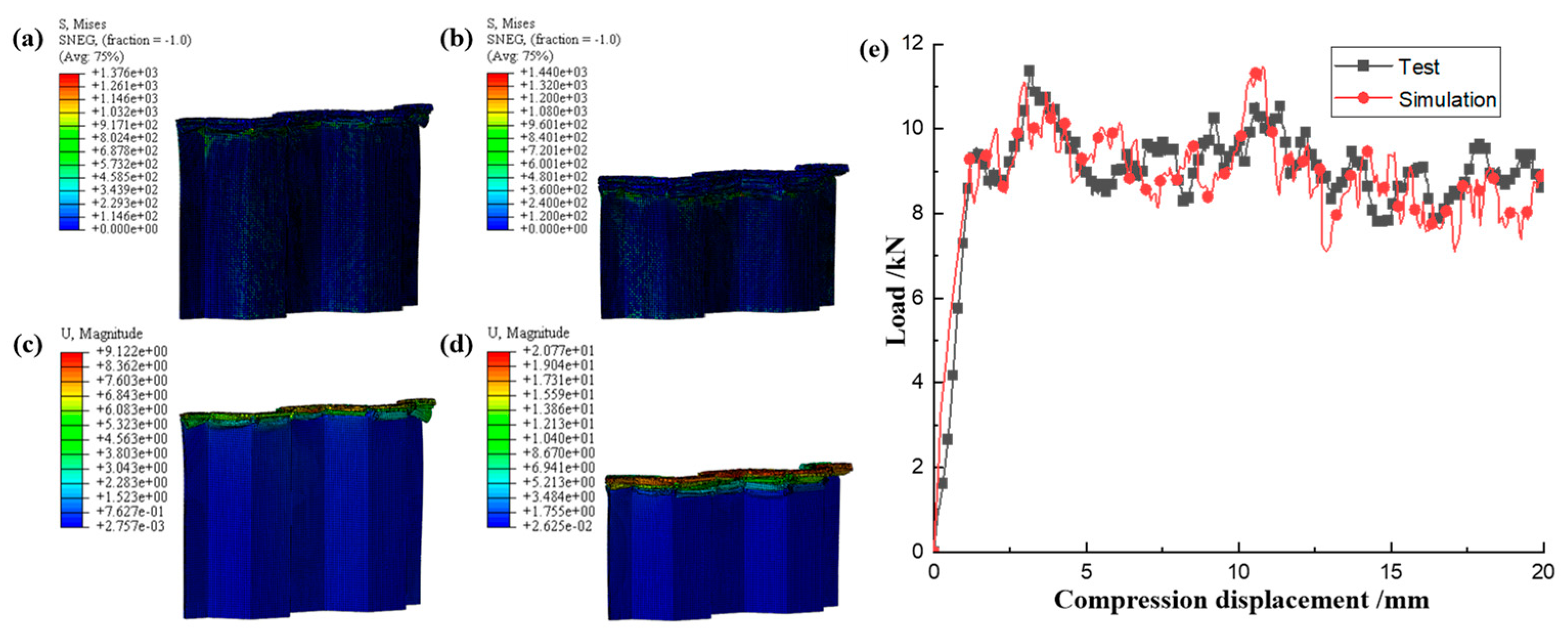
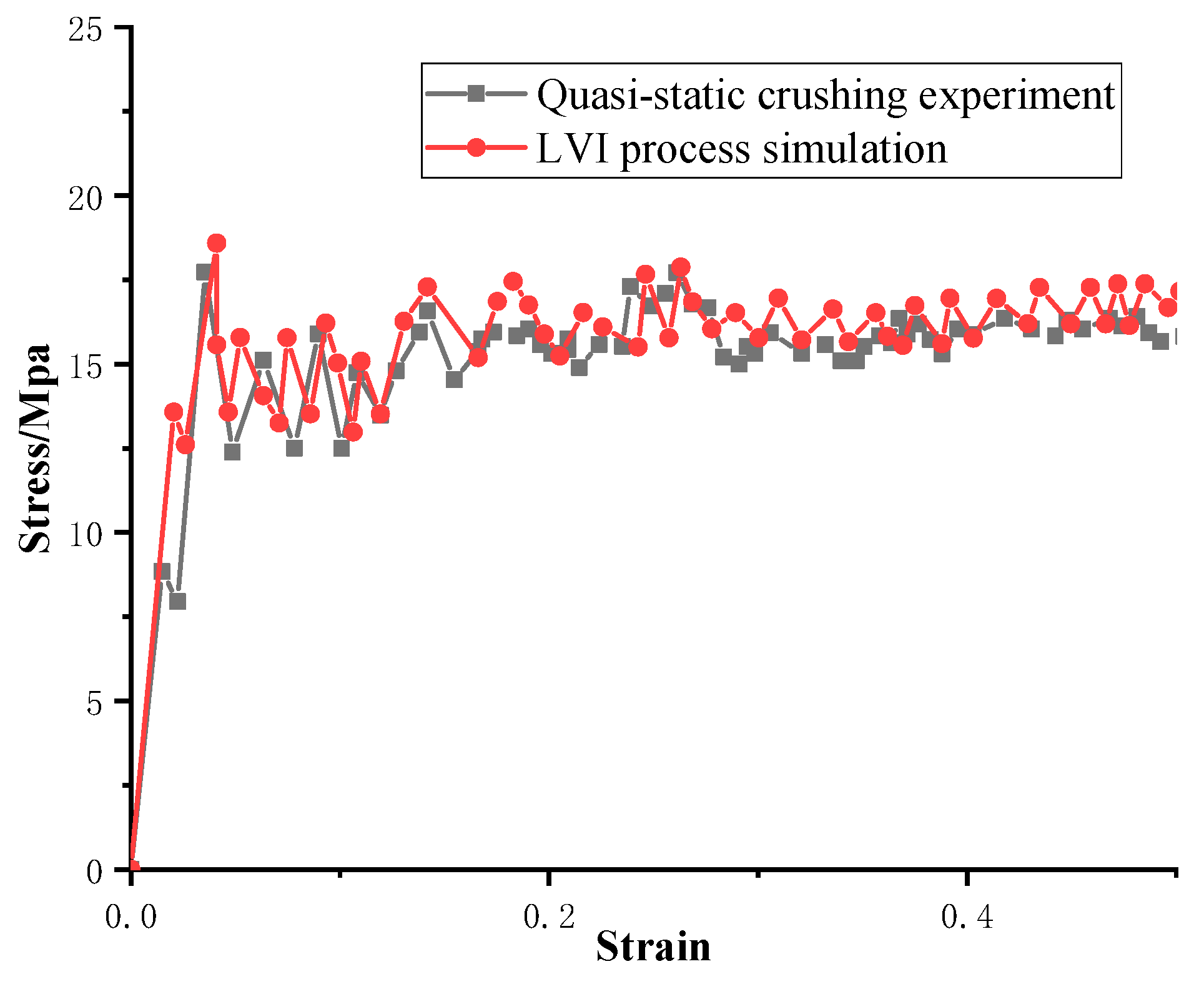
3.2. FEM Validation under Quasi-Static Compression
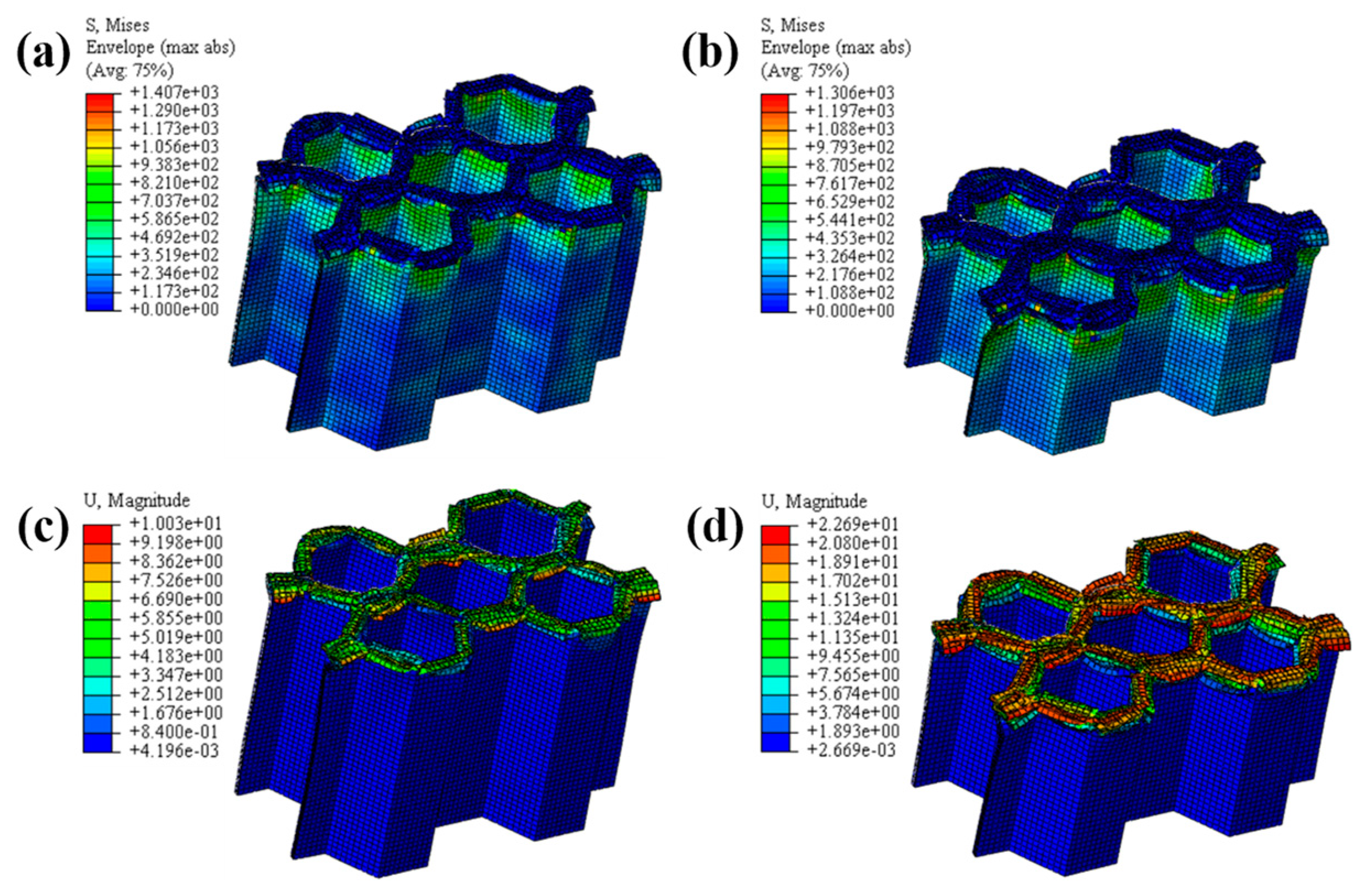
3.3. FEM Validation under LVI
4. Results and Discussion
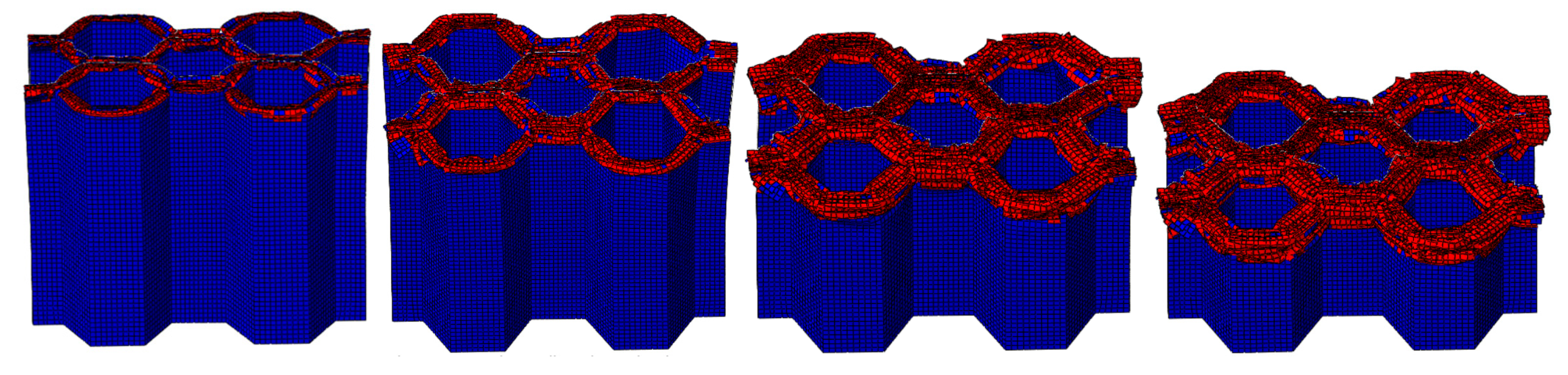
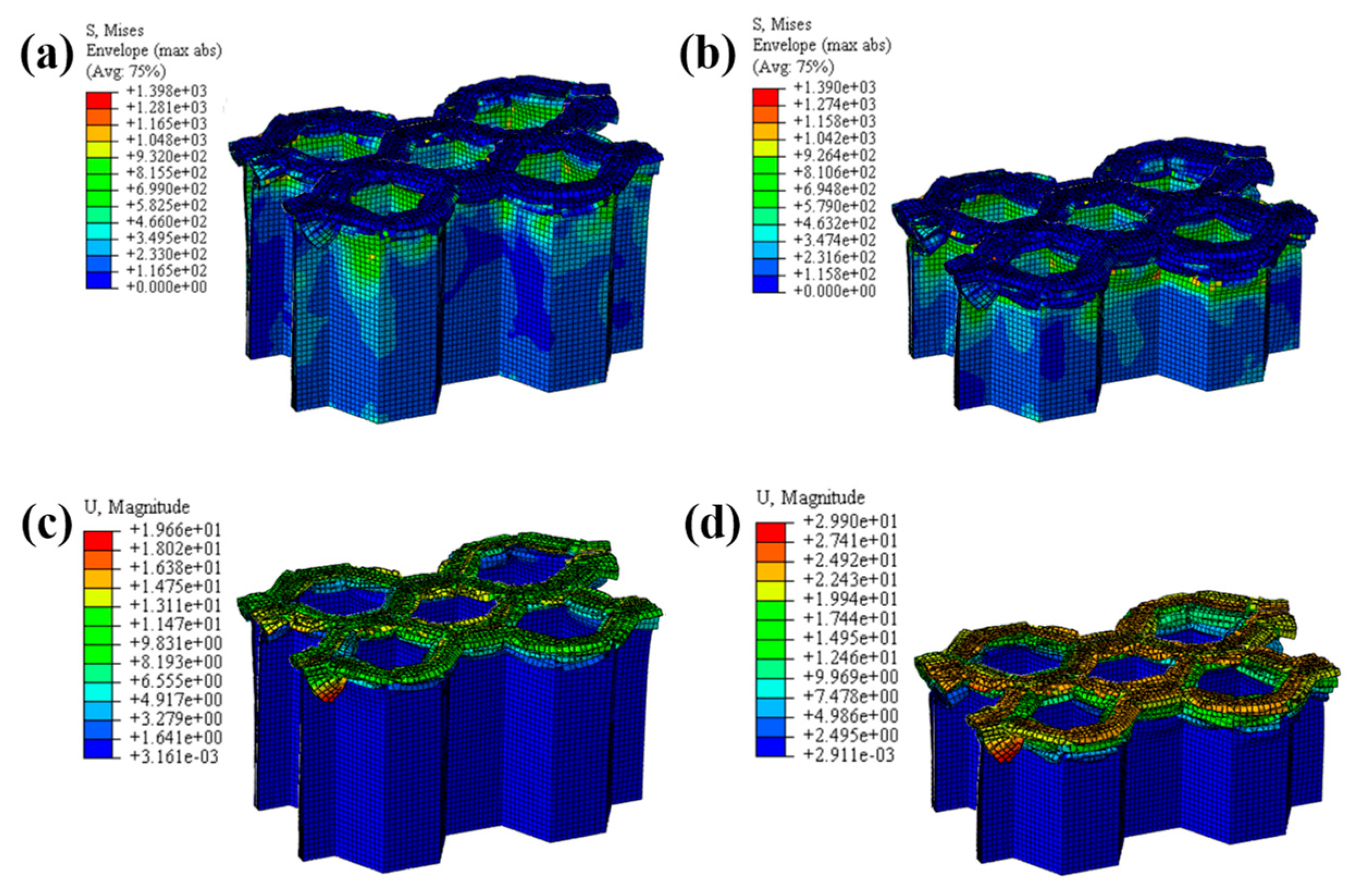
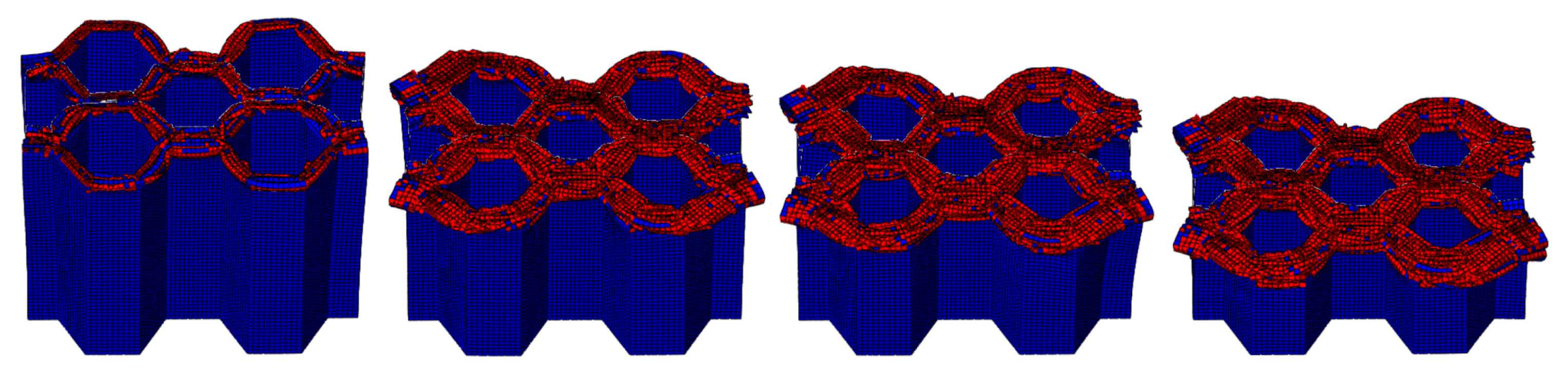
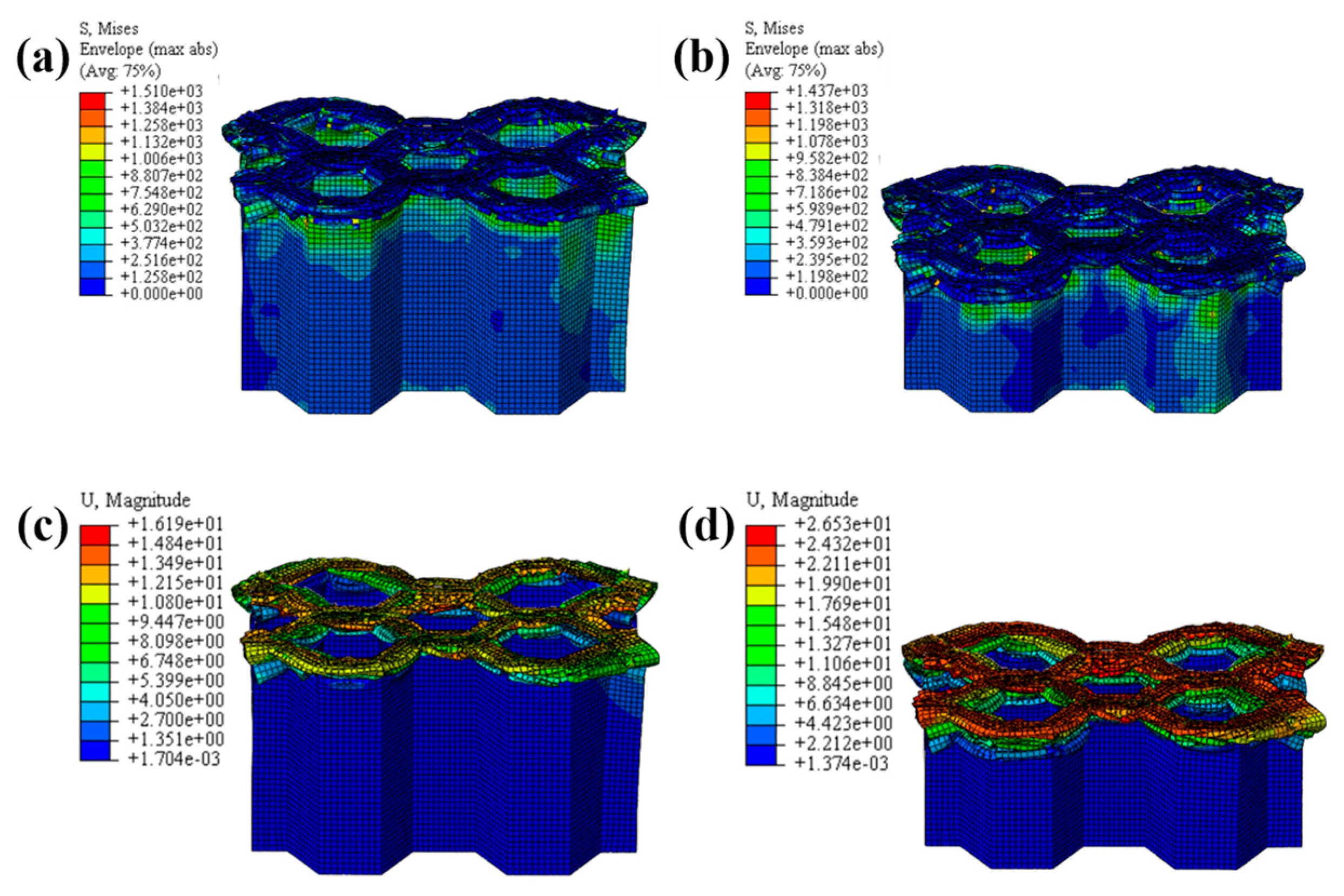
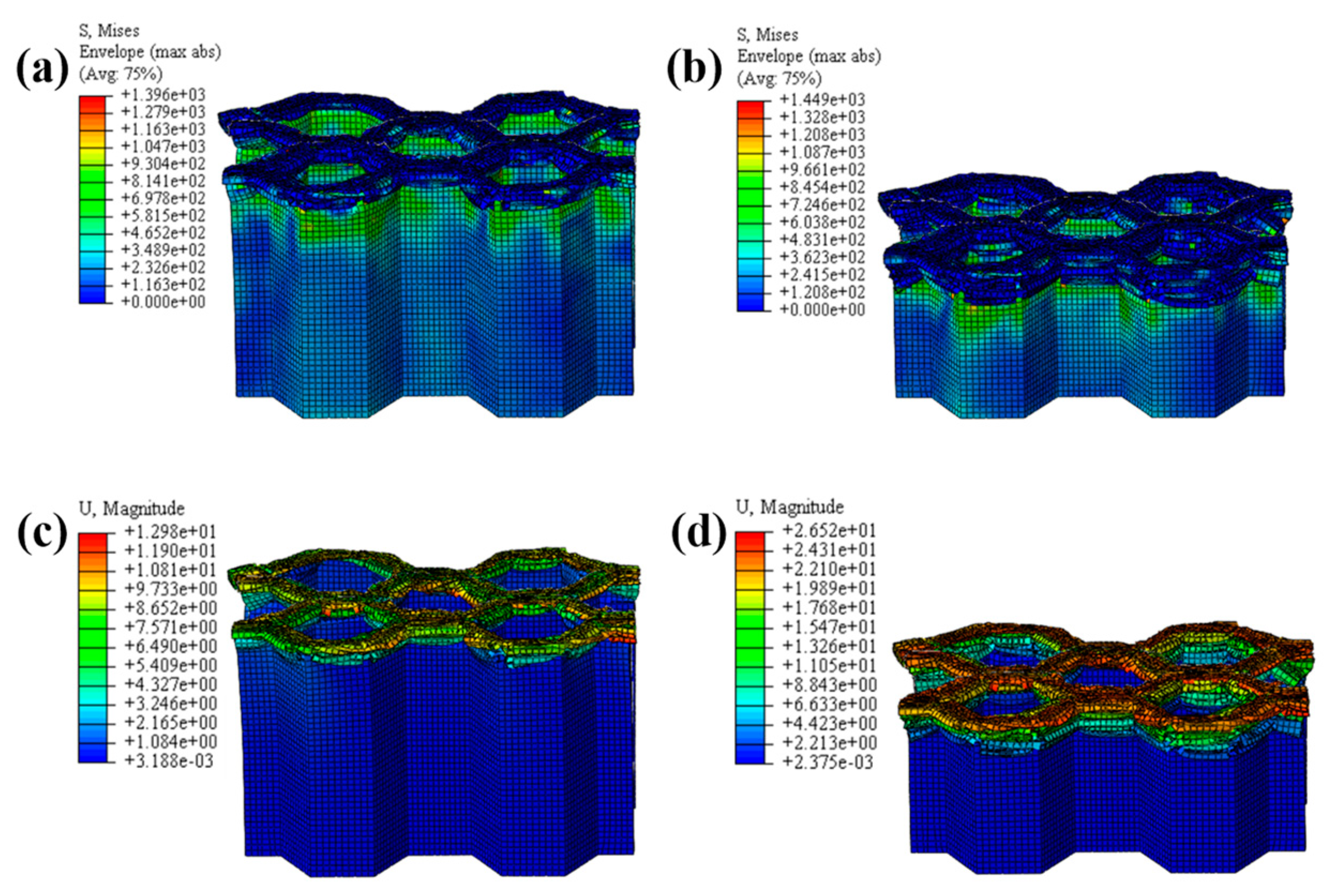
4.1. LVI Behavior of Honeycomb Structures
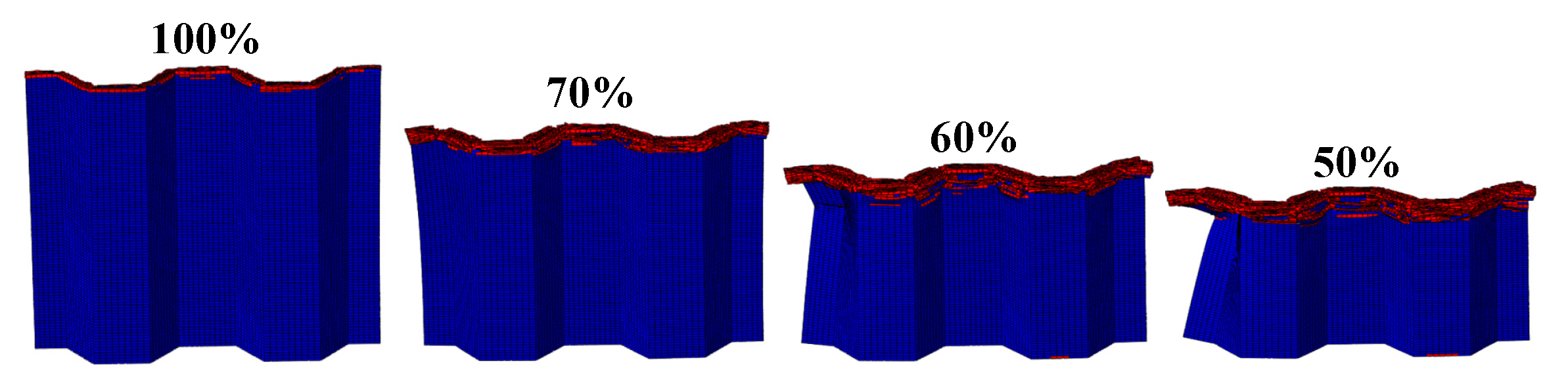
4.1.1. LVI Validation of Honeycomb Structures
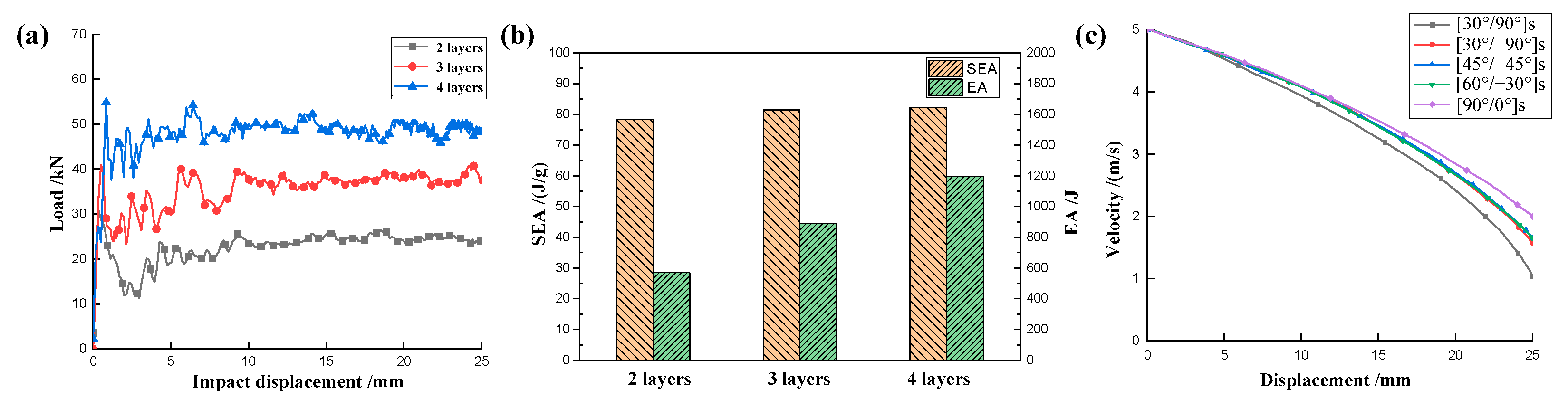
4.1.2. The Effect of the Number of Plies
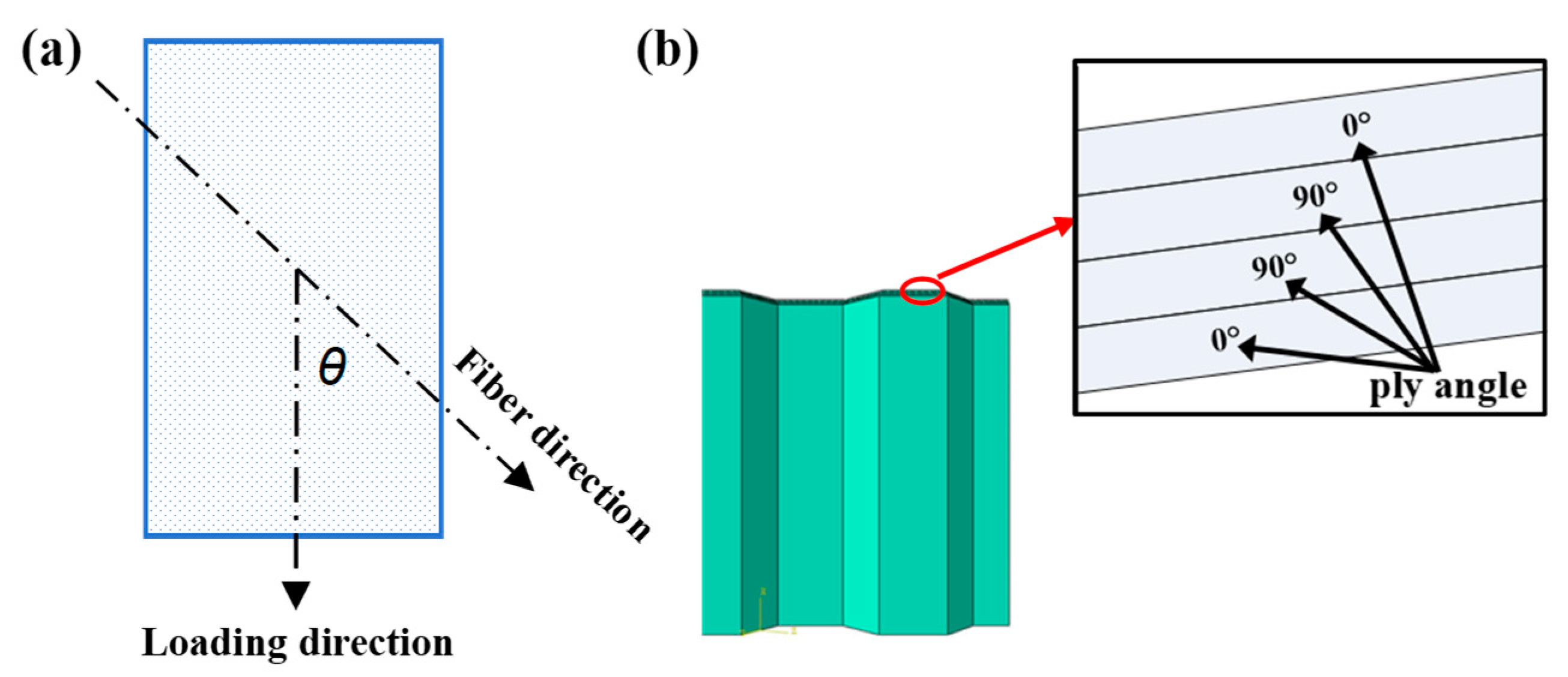
4.1.3. The Effect of Different Ply Angles
4.2. Comparison of Energy Absorption
4.2.1. Energy Absorption and Specific Energy Absorption
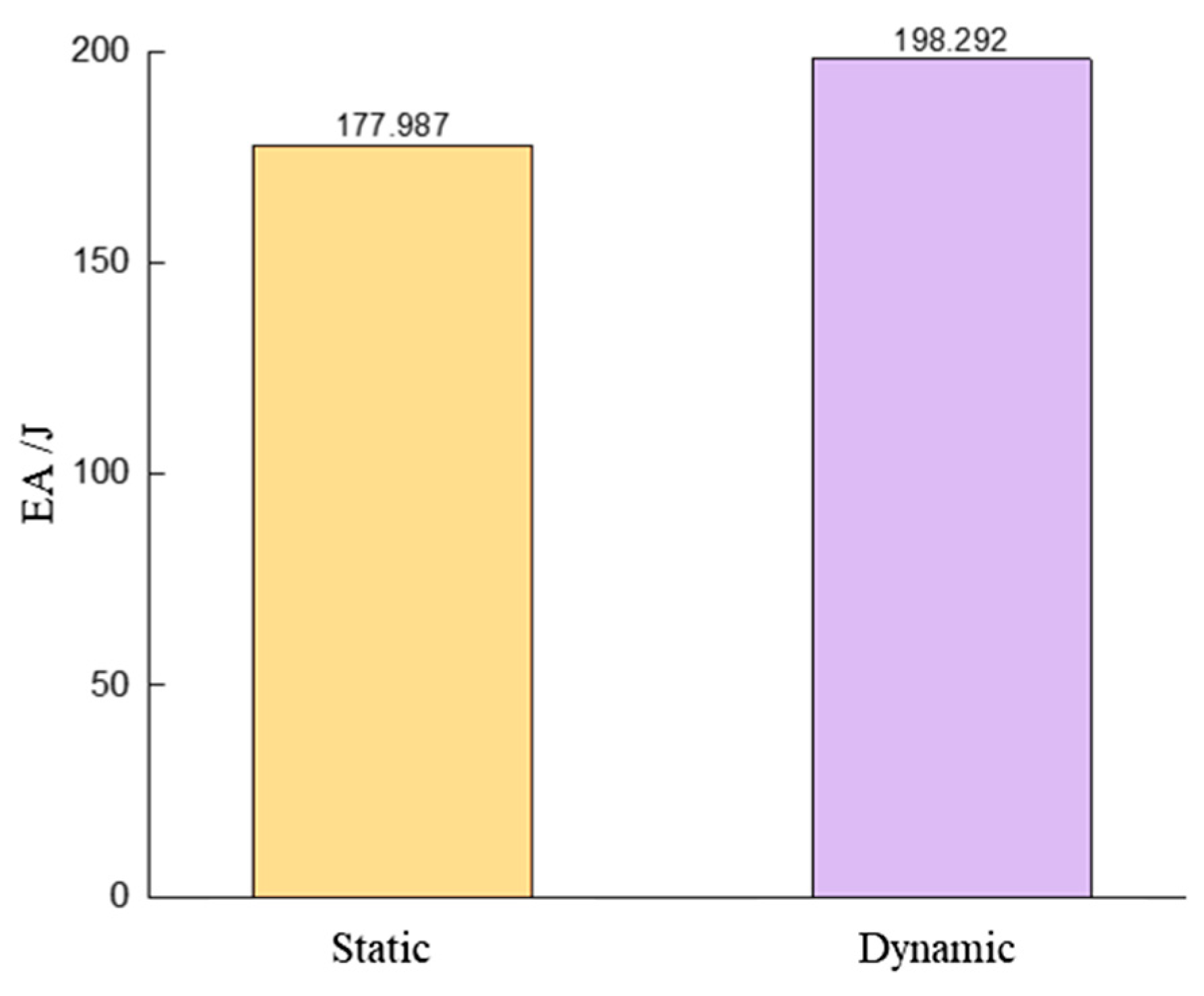
4.2.2. Energy Absorption Effect of Dynamic Shock and Quasi-Static Compression
5. Conclusions
- (1)
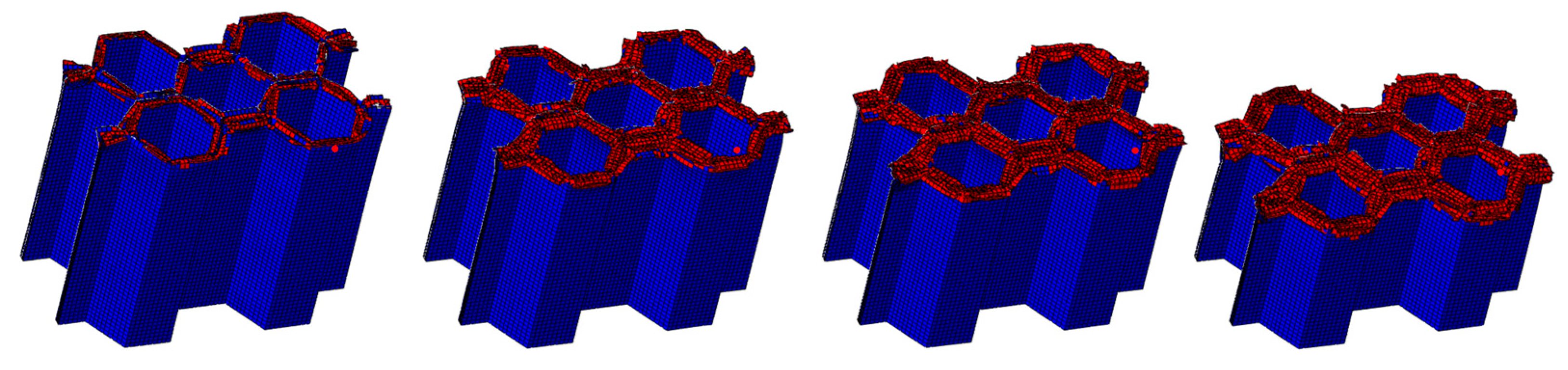
- During the crushing process, both the CFRP corrugated sheet and honeycomb are stably damaged, including matrix fracture, fiber fracture, matrix fragmentation, and layer failure. The crushed body flips from the center to the sides, while the crushed matrix and fiber flip to the outside and inside of the honeycomb holes, respectively.
- (2)
- The well-established FEM demonstrates remarkable accuracy in various simulations, including quasi-static compression of CFRP corrugated sheet, LVI of CFRP corrugated sheet, and LVI of CFRP honeycomb. The validated model can be applied to the structural design of spacecraft, significantly reducing the design cycle and R&D expenses.
- (3)
- A kind of index for evaluating the impact resistance was proposed: the velocity drop ratio. Under this evaluation index, the larger the value of the velocity drop ratio, the more effectively the CFRP honeycomb structure can slow down the velocity when subjected to impact, indicating that its impact resistance is better.
- (4)
- The best impact resistance performance of the honeycomb structure was determined by numerical simulations using a ply angle of [0°/90°]s. The energy absorption performance increases with the number of layers, and the relationship between the two is approximately linear.
- (5)
- A large amount of space inside the honeycomb structure can be used for enhancing mechanical properties. In subsequent research, there are some directions, such as the behavior of the CFRP honeycomb structure in high-speed impact, honeycomb filled with lightweight materials such as aluminum foam, polymer foam, and others, the optimal structure, and the mixture of materials and structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dou, H.; Ye, W.; Zhang, D.; Cheng, Y.; Huang, K.; Yang, F.; Rudykh, S. Research on drop-weight impact of continuous carbon fiber reinforced 3D printed honeycomb structure. Mater. Today Commun. 2021, 29, 102869. [Google Scholar] [CrossRef]
- Chandrasekar, M.; Ishak, M.R.; Jawaid, M.; Sapuan, S.M.; Leman, Z. Low velocity impact properties of natural fiber-reinforced composite materials for aeronautical applications. In Sustainable Composites for Aerospace Applications; Jawaid, M., Thariq, M., Eds.; Woodhead Publishing: Cambridge, UK, 2018; pp. 293–313. [Google Scholar]
- Deng, J.; Gong, X.; Xue, P.; Yin, Q.; Wang, X. A comprehensive analysis of damage behaviors of composite sandwich structures under localized impact. Mech. Adv. Mater. Struct. 2023, 30, 3231–3244. [Google Scholar] [CrossRef]
- Tang, E.; He, Z.; Chen, C.; Han, Y. Characterization of Dynamic Compressive Strength and Impact Release Energy of Al/PTFE Energetic Materials Reinforced by Aluminum Honeycomb Skeleton. Compos. Struct. 2020, 241, 112063. [Google Scholar] [CrossRef]
- Mohamadi, Y.; Ahmadi, H.; Razmkhah, O.; Liaghat, G. Axial crushing responses of aluminum honeycomb structures filled with elastomeric polyurethane foam. Thin-Walled Struct. 2021, 164, 107785. [Google Scholar] [CrossRef]
- Foo, C.C.; Chai, G.B.; Seah, L.K. Mechanical properties of Nomex material and Nomex honeycomb structure. Compos. Struct. 2007, 80, 588–594. [Google Scholar] [CrossRef]
- Liu, L.; Feng, H.; Tang, H.; Guan, Z. Impact resistance of Nomex honeycomb sandwich structures with thin fibre reinforced polymer facesheets. J. Sandw. Struct. Mater. 2018, 20, 531–552. [Google Scholar] [CrossRef]
- Fan, J.; Li, P.; Guo, W.; Zhao, X.; Su, C.; Xu, X. Experimental Investigation on the Low-Velocity Impact Response of Tandem Nomex Honeycomb Sandwich Panels. Polymers 2023, 15, 456. [Google Scholar] [CrossRef]
- Gilat, A.; Goldberg, R.K.; Roberts, G.D. Experimental study of strain-rate-dependent behavior of carbon/epoxy composite. Compos. Sci. Technol. 2002, 62, 1469–1476. [Google Scholar] [CrossRef]
- Pinho, S.T.; Robinson, P.; Iannucci, L. Fracture toughness of the tensile and compressive fibre failure modes in laminated composites. Compos. Sci. Technol. 2006, 66, 2069–2079. [Google Scholar] [CrossRef]
- Sokolinsky, V.S.; Indermuehle, K.C.; Hurtado, J.A. Numerical simulation of the compression collapse process of a corrugated composite plate. Compos. A Appl. Sci. Manuf. 2011, 42, 1119–1126. [Google Scholar] [CrossRef]
- Uddin, N.M.; Gandy, H.T.; Rahman, M.M.; Asmatulu, R. Adhesiveless honeycomb sandwich structures of prepreg carbon fiber composites for primary structural applications. Adv. Compos. Hybrid. Mater. 2019, 2, 339–350. [Google Scholar] [CrossRef]
- Zhong, J.; Zhao, C.; Liu, Y.; Ren, J.; Yang, C.; Zhang, Z. Meta-materials of Re-entrant Negative Poisson’s Ratio Structures Made from Fiber-Reinforced Plastics: A Short Review. Fibers Polym. 2024, 25, 395–406. [Google Scholar] [CrossRef]
- Zhao, C.; Zhong, J.; Wang, H.; Chen, C. Complete constitutive model of CFRP including continuous damage in low strain rate compression and temperature generation in high strain rate impact. Polym. Compos. 2024, 45, 3965–3989. [Google Scholar] [CrossRef]
- Caliskan, U.; Apalak, K.M. The response of pin-clamped carbon fibre-reinforced plastics composite sandwich beams with polyvinylchloride foam core under bending impact. J. Reinf. Plast. Compos. 2020, 39, 384–405. [Google Scholar] [CrossRef]
- Akar, D. Low-velocity impact, bending, and compression response of carbon fiber/epoxy-based sandwich composites with different types of core materials. J. Sandw. Struct. Mater. 2020, 23, 109963622090886. [Google Scholar]
- Zhao, C.F.; Ren, R.; Sun, C.B.; Ren, J.; Zhong, J.L.; Zhang, Z.D. Compression Mechanics for Carbon-Fiber reinforced Epoxy Resin Composites under Inplane and out-of-Plane Quasi-Static and Dynamic Loadings. Mech. Compos. Mater. 2023, 59, 507–520. [Google Scholar] [CrossRef]
- Zhao, C.; Pueh, L.H.; Lim, G.K.; Jianlin, Z.; Kebin, Z.; Zhendong, Z.; Jie, R.; Guigao, L. Preparation process and compression mechanics of carbon fiber reinforced plastics negative Poisson’s ratio structure (CFRP+NPRS). Compos. Struct. 2022, 292, 115667. [Google Scholar]
- Zhao, C.; Goh, K.L.; Lee, H.P.; Yin, C.; Zhang, K.; Zhong, J. Experimental study and finite element analysis on energy absorption of carbon fiber reinforced composite auxetic structures filled with aluminum foam. Compos. Struct. 2023, 303, 116319. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, Z.; Zhang, K.; Zhu, H.; Zhong, J.; Sun, C.; Ren, J.; Le, G. Experimental Study on Tensile Mechanics of Arrow Combination Structure with Carbon Fiber–Epoxy Resin Composite. Arab. J. Sci. Eng. 2021, 46, 2891–2900. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, Z.; Zhao, C.; Zhu, H.; Zhang, K.; Zhong, J.; Ren, J.; Le, G. Research on compression properties of unidirectional carbon fiber reinforced epoxy resin composite (UCFREP). J. Compos. Mater. 2021, 55, 1447–1458. [Google Scholar]
- Fedorenko, A.N.; Fedulov, B.N.; Lomakin, E.V. High rate damage of composite material for modelling of energy absorbing structures. Procedia Struct. Integr. 2020, 28, 804–810. [Google Scholar] [CrossRef]
- Ge, X.X.; Zhang, P.; Zhao, F.; Liu, M.; Liu, J.; Cheng, Y. Experimental and numerical investigations on the dynamic response of woven carbon fiber reinforced thick composite laminates under low-velocity impact. Compos. Struct. 2021, 279, 114792. [Google Scholar] [CrossRef]
- Seamone, A.; Davidson, P.; Waas, A.M.; Ranatunga, V. Low velocity impact and compressive response after impact of thin carbon fiber composite panels. Int. J. Solids Struct. 2022, 257, 111604. [Google Scholar] [CrossRef]
- Li, Y.; Meng, J.; Luo, J.; Wang, P.; Ma, J.; Zhao, Z.; Lei, H. Cryogenic mechanics and damage behaviors of carbon fiber reinforced polymer composites. Compos. Part A Appl. Sci. Manuf. 2023, 169, 107484. [Google Scholar] [CrossRef]
- Liu, B.; Wang, W.; Sutherland, L. Experimental and numerical response and failure of laterally impacted carbon/glass fibre-reinforced hybrid composite laminates. Int. J. Impact Eng. 2023, 179, 104654. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, Z.; Yu, G.; Wu, L. A new multifunctional carbon fiber honeycomb sandwich structure with excellent mechanical and thermal performances. Compos. Struct. 2021, 274, 114306. [Google Scholar] [CrossRef]
- Xue, D.; He, L.; Tan, S.; Li, Y.; Xue, P.; Yang, X. Study on compression characteristics of honeycomb sandwich structure with multistage carbon fiber reinforced composites. Polym. Compos. 2022, 43, 6252–6264. [Google Scholar] [CrossRef]
- Feng, J.; Yao, L.; Lyu, Z.; Wu, Z.; Zhang, G.; Zhao, H. Mechanical properties and damage failure of 3D-printed continuous carbon fiber-reinforced composite honeycomb sandwich structures with fiber-interleaved core. Polym. Compos. 2022, 44, 1980–1992. [Google Scholar] [CrossRef]
- Shunmugesh, K.; Raphel, A.; Unnikrishnan, T.G.; Akhil, K.T. Finite element modelling of carbon fiber reinforced with vespel and honey-comb structure. Mater. Today Proc. 2023, 72 Pt 4, 2163–2168. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, X.; Han, Y.; Tian, Y.; Zhang, D.; Yan, L. Failure mechanisms and process defects of 3D-printed continuous carbon fiber-reinforced composite circular honeycomb structures with different stacking directions. Aerosp. Sci. Technol. 2024, 148, 109075. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, K.; Zhao, C. Preparation of carbon fiber composite honeycomb structures and mechanical behavior of axial crush. Compos. Sci. Eng. 2024. Available online: https://link.cnki.net/urlid/10.1683.TU.20240308.1802.002 (accessed on 11 March 2024).
- Zhong, J.; Zhao, C.; Ren, J.; Liu, X.; Zhang, Z. A Constitutive Model for Carbon Fiber Reinforced Epoxy Resin Laminate under Compression Load: Considering the Initial Non-linearity. Appl. Compos. Mater. 2022, 29, 629–649. [Google Scholar] [CrossRef]
- Liu, Z.; Zhong, J.; Ren, R.; Tang, Z.; Zhao, C.; Liu, X.; Gao, Y.; Ren, J. Nonlinear Mechanical Behavior of Glass Fiber/Epoxy Resin Composite Under Medium and Low Strain Rates Loading. Appl. Compos. Mater. 2024, 31, 1369–1392. [Google Scholar] [CrossRef]













| Mechanical Properties | Symbol | Value |
|---|---|---|
| Longitudinal modulus (GPa) | E11 | 55.9 |
| Transverse modulus (GPa) | E22 = E33 | 54.4 |
| Shear modulus (GPa) | G12 = G23 = G31 | 4.2 |
| Principal Poisson’s ratio | ν12 | 0.042 |
| Longitudinal tensile strength (MPa) | XT | 911.3 |
| Longitudinal compressive strength (MPa) | XC | 704.0 |
| Transverse tensile strength (MPa) | YT | 770.1 |
| Transverse compressive strength (MPa) | YC | 698.2 |
| In-plane shear strength (MPa) | SL | 131.6 |
| Mechanical Properties | Symbol | Value |
|---|---|---|
| Fiber tensile fracture energy (kJ/m2) | Gft | 125 |
| Fiber compression fracture energy (kJ/m2) | Gfc | 250 |
| Matrix tensile fracture energy (kJ/m2) | Gmt | 95 |
| Matrix compression fracture energy(kJ/m2) | Gmc | 245 |
| Type I fracture toughness (kJ/m2) | GIc | 0.504 |
| Type II fracture toughness (kJ/m2) | GIIc | 1.566 |
| Normal nominal maximum stress (MPa) | N | 54 |
| Tangential nominal maximum stress (MPa) | S = T | 70 |
| Element Deletion Definition | Value |
|---|---|
| Maximum tensile strain in fiber direction | 0.1 |
| Maximum compression strain in fiber direction | 0.1 |
| Maximum tensile strain in the vertical fiber direction | 0.1 |
| Maximum compression strain in the vertical fiber direction | 0.1 |
| Maximum shear strain | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zou, K.; Zhang, Z. Energy Absorption Behavior of Carbon-Fiber-Reinforced Plastic Honeycombs under Low-Velocity Impact Considering Their Ply Characteristics. Materials 2024, 17, 4257. https://doi.org/10.3390/ma17174257
Liu Z, Zou K, Zhang Z. Energy Absorption Behavior of Carbon-Fiber-Reinforced Plastic Honeycombs under Low-Velocity Impact Considering Their Ply Characteristics. Materials. 2024; 17(17):4257. https://doi.org/10.3390/ma17174257
Chicago/Turabian StyleLiu, Zheng, Kai Zou, and Zhendong Zhang. 2024. "Energy Absorption Behavior of Carbon-Fiber-Reinforced Plastic Honeycombs under Low-Velocity Impact Considering Their Ply Characteristics" Materials 17, no. 17: 4257. https://doi.org/10.3390/ma17174257
APA StyleLiu, Z., Zou, K., & Zhang, Z. (2024). Energy Absorption Behavior of Carbon-Fiber-Reinforced Plastic Honeycombs under Low-Velocity Impact Considering Their Ply Characteristics. Materials, 17(17), 4257. https://doi.org/10.3390/ma17174257






