Natural and Artificial Aging Effects on the Deformation Behaviors of Al–Mg–Zn Alloy Sheets
Abstract
:1. Introduction
2. Materials and Methods
3. Results
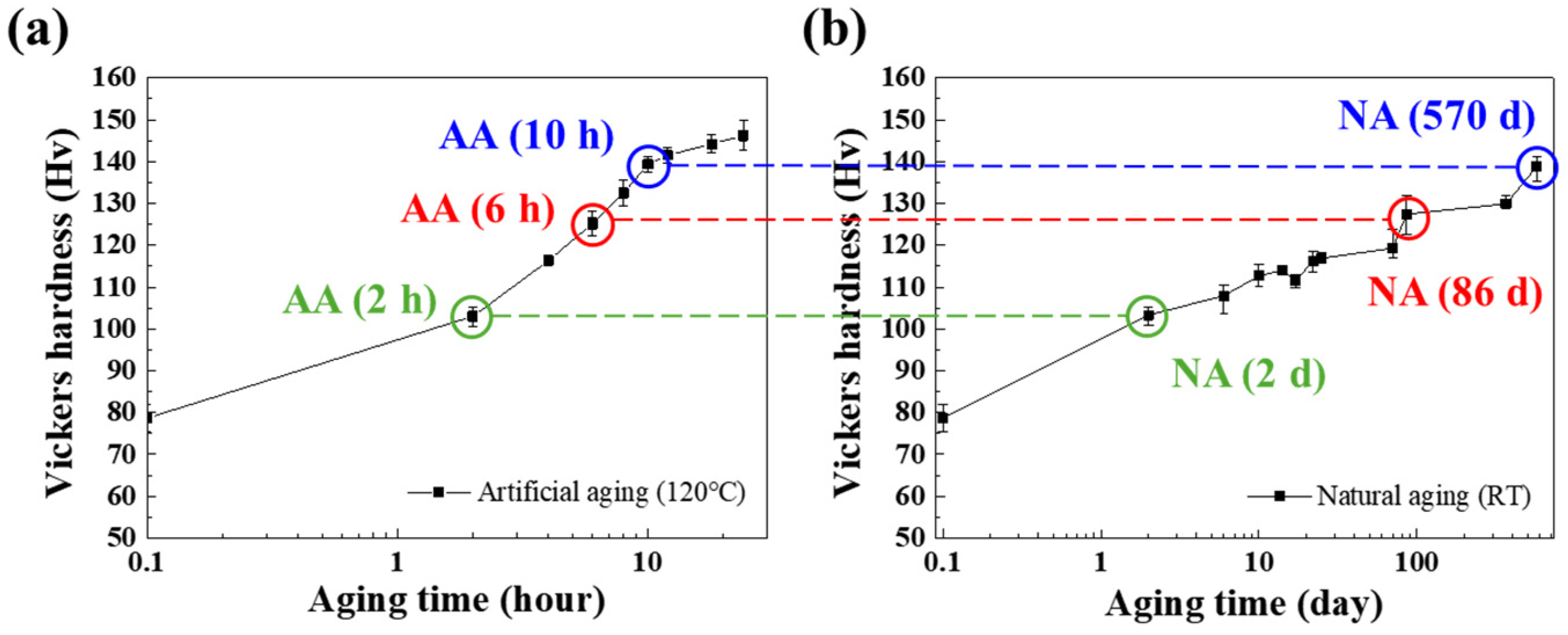
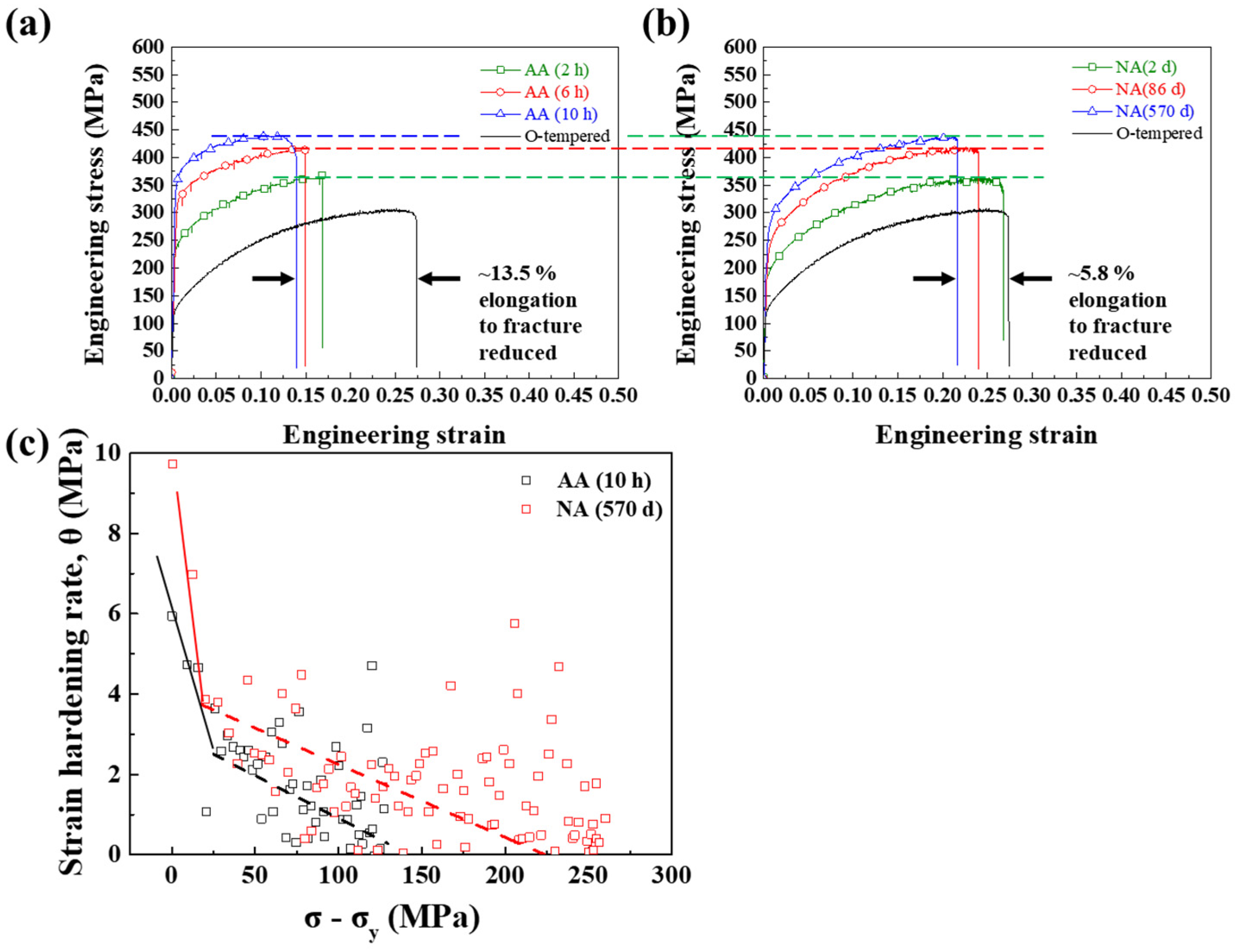
3.1. Mechanical Properties after AA and NA
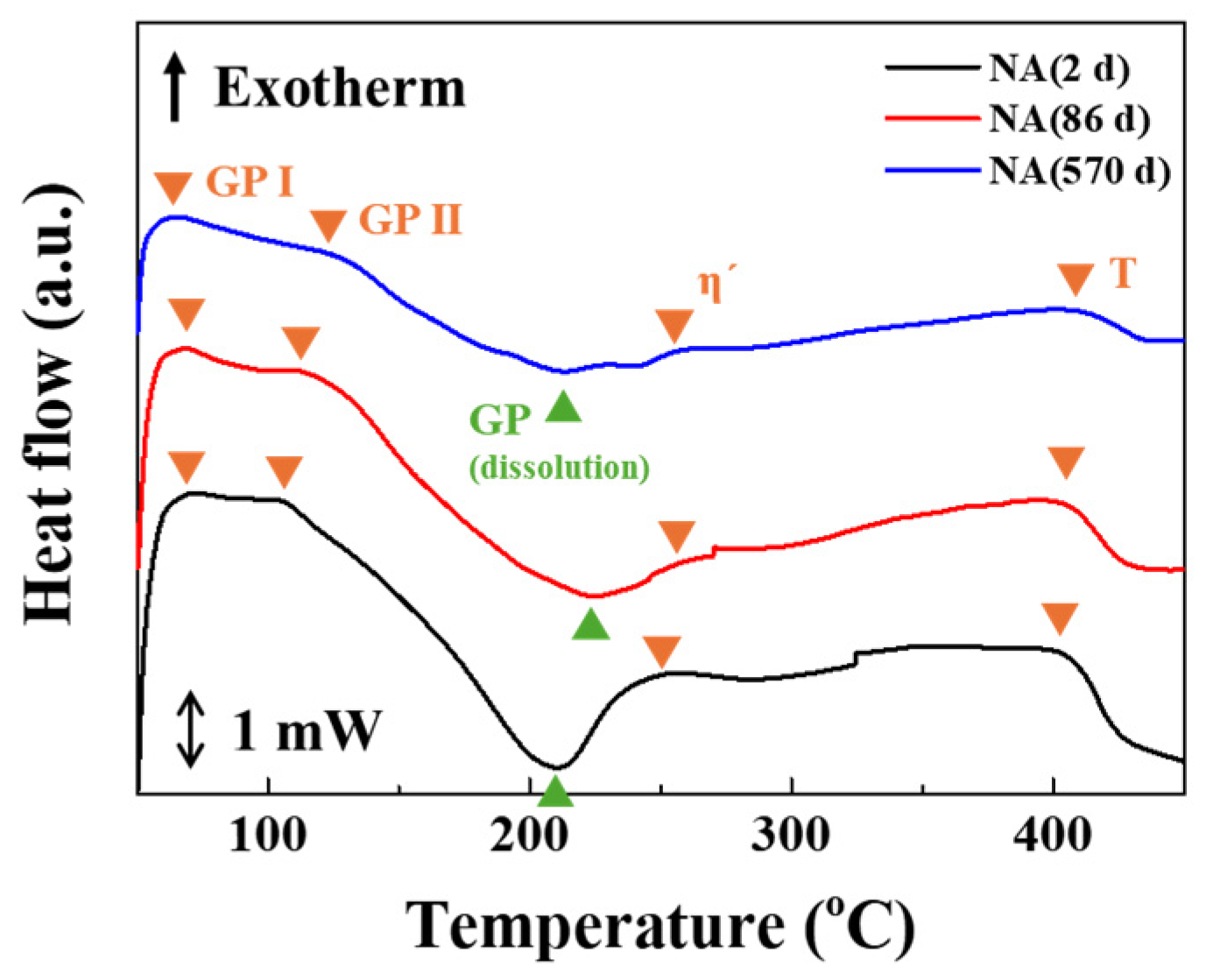
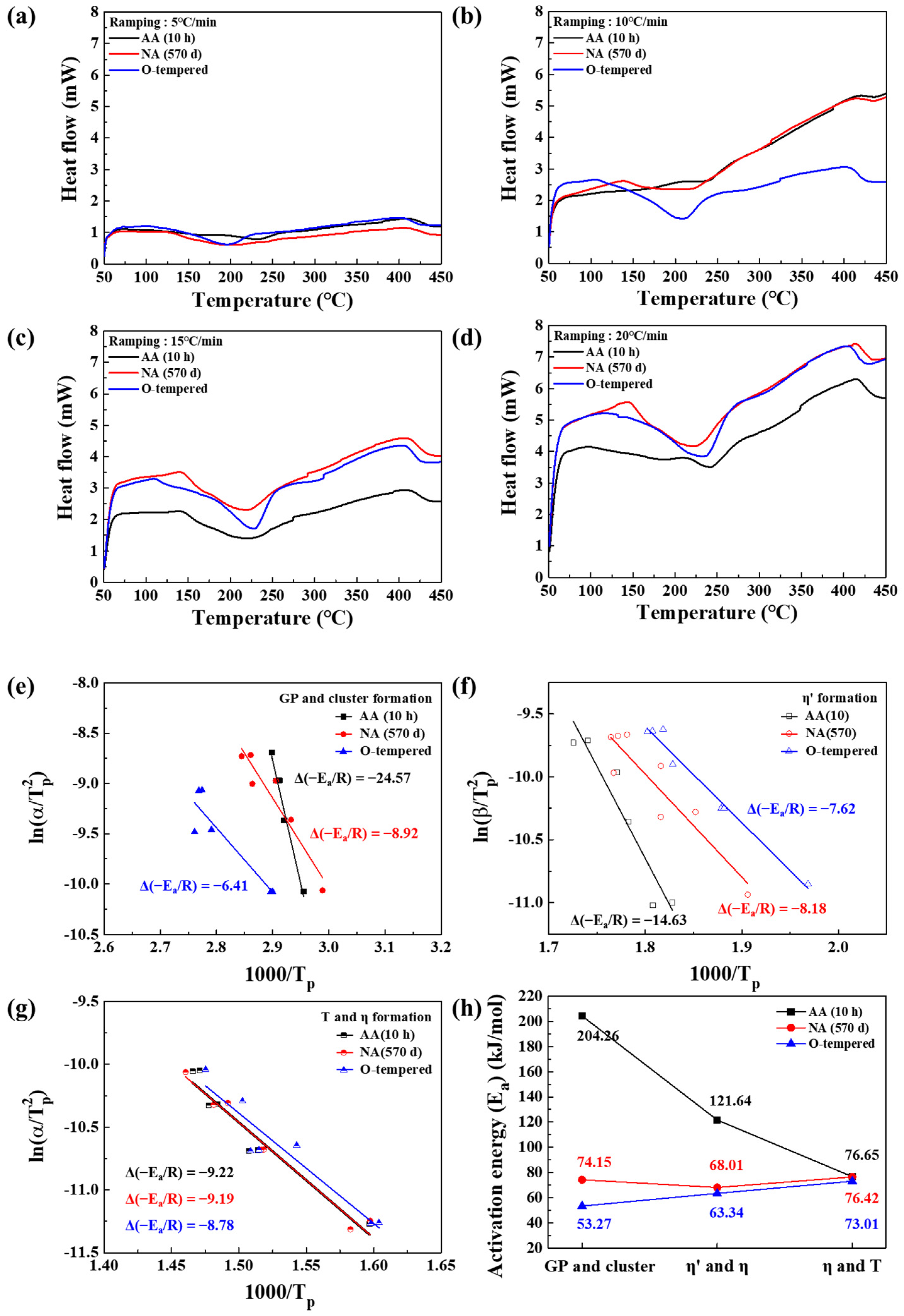
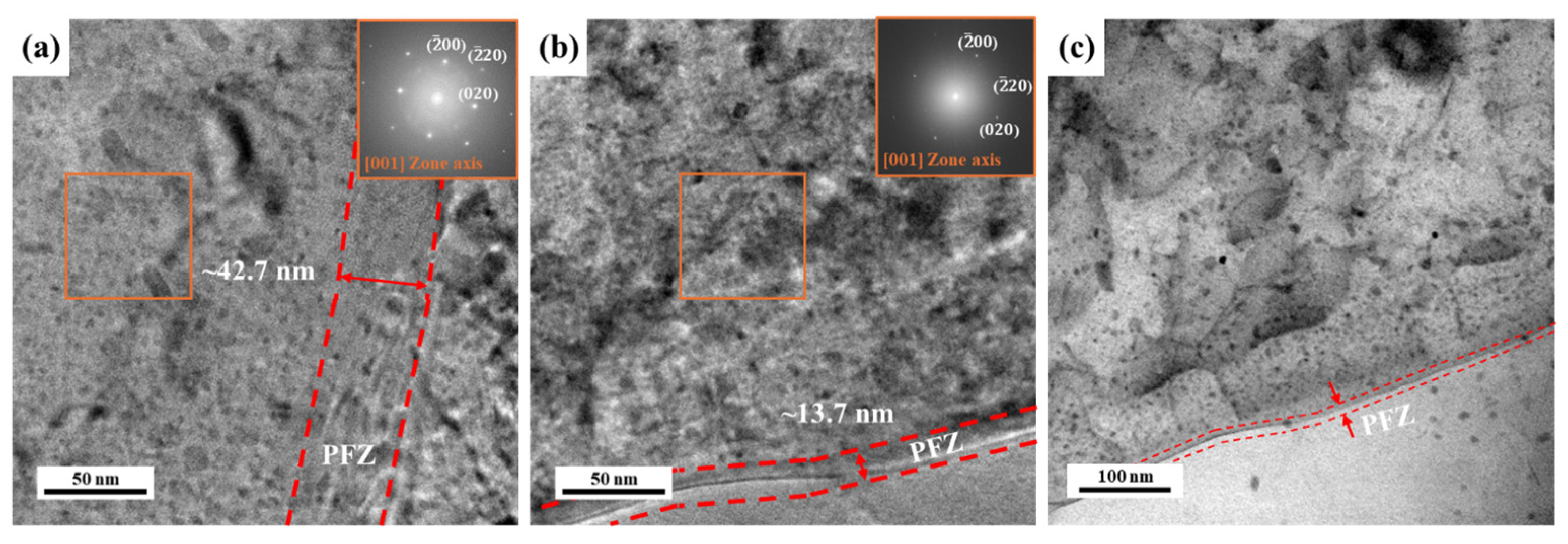
3.2. Precipitate Analysis and Microstructure of Al–Mg–Zn Alloy Sheet after AA and NA
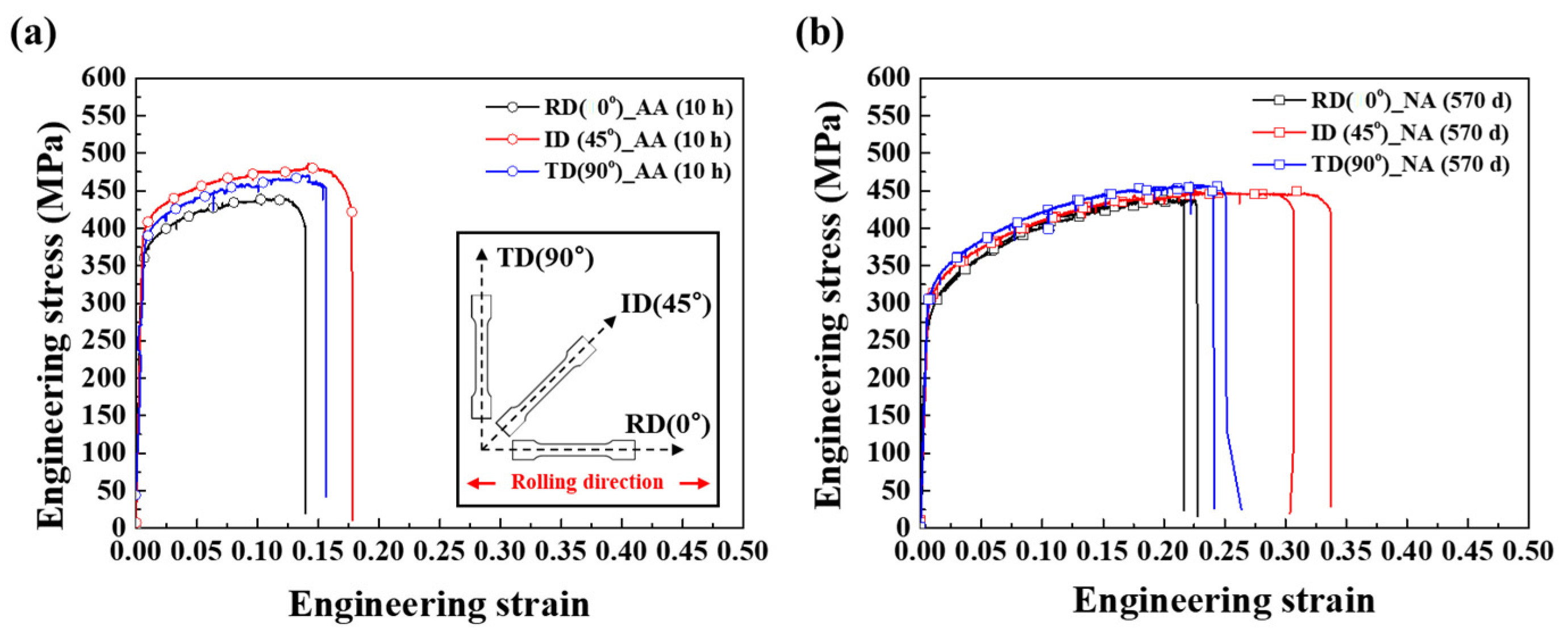
3.3. Anisotropy Analysis of Al–Mg–Zn Alloy Sheets after AA and NA
4. Conclusions
- (1)
- During the aging process, the Vickers hardness of Al–Mg–Zn alloy sheets was increased regardless of aging conditions. In the uniaxial tensile test, however, artificially aged sheets exhibited about 15% elongation to fracture, whereas naturally aged sheets showed about 25% elongation to fracture property.
- (2)
- The analysis of precipitates in AA (10 h) and NA (570 d) samples was performed using the DSC, and their activation energy to form the precipitates were calculated with the Kissinger method. The AA (10 h) sample dominantly had η′ and η-phases as strengthening precipitates; however, NA (570 d) samples had solute cluster, GP, and η′-phases.
- (3)
- TEM observation indicated that the densities of the GNDs in NA (570 d) were lower than AA (10 h); however, they were distributed more uniformly both internal and boundaries of grains. Furthermore, PFZ width varied depending on the aging conditions; hence, NA-treated alloy had a narrower PFZ width than AA-treated alloy.
- (4)
- The NA-treated sheets exhibited notable anisotropy in strength and plasticity with a higher average R-value than their AA-treated counterparts.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shin, J.; Kim, T.; Kim, D.; Kim, D.; Kim, K. Castability and mechanical properties of new 7xxx aluminum alloys for automotive chassis/body applications. J. Alloys Compd. 2017, 698, 577–590. [Google Scholar] [CrossRef]
- Kim, H.J.; McMillan, C.; Keoleian, G.A.; Skerlos, S.J. Greenhouse Gas emissions payback for lightweighted vehicles using aluminum and high-strength steel. J. Ind. Ecol. 2010, 14, 929–946. [Google Scholar] [CrossRef]
- Sharma, A.K.; Bhandari, R.; Aherwar, A.; Rimašauskienė, R.; Pinca-Bretotean, C. A study of advancement in application opportunities of aluminum metal matrix composites. Mater. Today 2020, 26, 2419–2424. [Google Scholar] [CrossRef]
- Azarniya, A.; Taheri, A.K.; Taheri, K.K. Recent advances in ageing of 7xxx series aluminum alloys: A physical metallurgy perspective. J. Alloys Compd. 2019, 781, 945–983. [Google Scholar] [CrossRef]
- Embury, J.; Nicholson, R. The nucleation of precipitates: The system Al-Zn-Mg. Acta Metall. 1965, 13, 403–417. [Google Scholar] [CrossRef]
- Sha, G.; Cerezo, A. Early-stage precipitation in Al–Zn–Mg–Cu alloy (7050). Acta Mater. 2004, 52, 4503–4516. [Google Scholar] [CrossRef]
- Zou, Y.; Wu, X.; Tang, S.; Zhu, Q.; Song, H.; Cao, L. Co-precipitation of T′ and η′ phase in Al-Zn-Mg-Cu alloys. Mater. Charact. 2020, 169, 110610. [Google Scholar] [CrossRef]
- Yang, Z.; Banhart, J. Natural and artificial ageing in aluminium alloys–the role of excess vacancies. Acta Mater. 2021, 215, 117014. [Google Scholar] [CrossRef]
- Yang, X.; Chen, J.; Liu, J.; Qin, F.; Xie, J.; Wu, C. A high-strength AlZnMg alloy hardened by the T-phase precipitates. J. Alloys Compd. 2014, 610, 69–73. [Google Scholar] [CrossRef]
- Stemper, L.; Tunes, M.A.; Tosone, R.; Uggowitzer, P.J.; Pogatscher, S. On the potential of aluminum crossover alloys. Prog. Mater. Sci. 2022, 124, 100873. [Google Scholar] [CrossRef]
- Zhao, L.; Yan, H.; Chen, J.; Xia, W.; Su, B.; Song, M.; Li, Z.; Li, X.; Liao, Y. High ductility and strong work-hardening behavior of Zn modified as-hot-rolled Al–Mg sheets. J. Alloys Compd. 2021, 854, 157079. [Google Scholar] [CrossRef]
- Smith, W.; Grant, N. Effects of chromium and copper additions on precipitation in Al− Zn− Mg alloys. Metall. Trans. 1971, 2, 1333–1340. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.; Zhang, D.; Zhang, J. The effect of Ag on the tensile strength and fracture toughness of novel Al-Mg-Zn alloys. J. Alloys Compd. 2022, 908, 164640. [Google Scholar] [CrossRef]
- Liu, J.; Hu, R.; Zheng, J.; Zhang, Y.; Ding, Z.; Liu, W.; Zhu, Y.; Sha, G. Formation of solute nanostructures in an Al–Zn–Mg alloy during long-term natural aging. J. Alloys Compd. 2020, 821, 153572. [Google Scholar] [CrossRef]
- Geng, Y.; Zhang, D.; Zhang, J.; Zhuang, L. Early-stage clustering and precipitation behavior in the age-hardened Al–Mg–Zn (-Cu) alloys. Mater. Sci. Eng. A 2022, 856, 144015. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Z.; Bai, S.; Zeng, D.; Luo, L.; Wang, J. Effects of natural aging on the formation and strengthening effect of GP zones in a retrogression and re-aged Al–Zn–Mg–Cu alloy. J. Alloys Compd. 2020, 829, 154469. [Google Scholar] [CrossRef]
- Ogura, T.; Otani, T.; Hirose, A.; Sato, T. Improvement of strength and ductility of an Al–Zn–Mg alloy by controlling grain size and precipitate microstructure with Mn and Ag addition. Mater. Sci. Eng. A 2013, 580, 288–293. [Google Scholar] [CrossRef]
- Tiryakioğlu, M.; Robinson, J.; Salazar-Guapuriche, M.; Zhao, Y.; Eason, P. Hardness–strength relationships in the aluminum alloy 7010. Mater. Sci. Eng. A 2015, 631, 196–200. [Google Scholar] [CrossRef]
- Du, J.; Zhang, Z.; Liu, Y.; Shao, Q.; Zhang, A.; Xiong, S.; Liu, F. Strength-ductility trade-off modulated by thermo-kinetic synergy of heat-treatable aluminum alloys. J. Mater. Sci. Technol. 2023, 24, 7876–7895. [Google Scholar] [CrossRef]
- Zhang, P.; Shi, K.; Bian, J.; Zhang, J.; Peng, Y.; Liu, G.; Deschamps, A.; Sun, J. Solute cluster evolution during deformation and high strain hardening capability in naturally aged Al–Zn–Mg alloy. Acta Mater. 2021, 207, 116682. [Google Scholar] [CrossRef]
- Wu, S.; Wang, G.; Wang, Q.; Jia, Y.; Yi, J.; Zhai, Q.; Liu, J.; Sun, B.; Chu, H.; Shen, J. Enhancement of strength-ductility trade-off in a high-entropy alloy through a heterogeneous structure. Acta Mater. 2019, 165, 444–458. [Google Scholar] [CrossRef]
- Kim, S.-H.; Kim, H.; Kim, N.J. Brittle intermetallic compound makes ultrastrong low-density steel with large ductility. Nature 2015, 518, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Noble, B.; Hansen, V.; Tafto, J. Influence of zirconium and copper on the early stages of aging in Al-Zn-Mg alloys. Metall. Mater. Trans. A 2001, 32, 1063–1073. [Google Scholar] [CrossRef]
- Kim, I.; Song, M.; Kim, J. Nanocluster formation and two-step aging behavior in Al–Mg–Si (-xCu: X= 0–4 mass%) alloys. J. Alloys Compd. 2021, 857, 157596. [Google Scholar] [CrossRef]
- Deng, Z.; He, H.; Liu, K.; Tao, X.; Shang, Z.; Gong, Z.; Wang, X. The influence of natural aging on the precipitation behavior of the low-alloy content Al-Zn-Mg aluminum alloys during subsequent artificial aging and related mechanisms. Mater. Sci. Eng. A 2024, 891, 145954. [Google Scholar] [CrossRef]
- Chen, M.; Liu, S.; He, K.; Zheng, X.; Jia, G. The effect of precipitate-free zone on mechanical properties in Al-Zn-Mg-Cu aluminum alloy: Strain-induced back stress strengthening. J. Alloys Compd. 2023, 969, 172426. [Google Scholar] [CrossRef]
- Kawabata, T.; Izumi, O. Ductile fracture in the interior of precipitate free zone in an Al-6.0% Zn-2.6% Mg alloy. Acta Metall. 1976, 24, 817–825. [Google Scholar] [CrossRef]
- Dowling, J.M.; Martin, J. The influence of MN additions on the deformation behaviour of an Al Mg Si alloy. Acta Metall. 1976, 24, 1147–1153. [Google Scholar] [CrossRef]
- Vasudevan, A.; Doherty, R. Grain boundary ductile fracture in precipitation hardened aluminum alloys. Acta Metall. 1987, 35, 1193–1219. [Google Scholar] [CrossRef]
- Itoh, G.; Kanno, M.; Hagiwara, T.; Sakamoto, T. Embrittlement in an age-hardened 2091 aluminum alloy by exposure at elevated temperatures below the aging temperature. Acta Mater. 1999, 47, 3799–3809. [Google Scholar] [CrossRef]
- Hirosawa, S.; Oguri, Y.; Ogura, T.; Sato, T. Formation mechanism of precipitate free zones in age-hardenable Al alloys. In Proceedings of the 9th International Conference on Aluminium Alloys, Brisbane, Australia, 2–5 August 2004; pp. 666–671. [Google Scholar]
- Khadyko, M.; Marioara, C.D.; Ringdalen, I.G.; Dumoulin, S.; Hopperstad, O.S. Deformation and strain localization in polycrystals with plastically heterogeneous grains. Int. J. Plast. 2016, 86, 128–150. [Google Scholar] [CrossRef]
- Arani, M.M.; Ramesh, N.S.; Wang, X.; Parson, N.; Li, M.; Poole, W. The localization of plastic deformation in the precipitate free zone of an Al-Mg-Si-Mn alloy. Acta Mater. 2022, 231, 117872. [Google Scholar] [CrossRef]
- Abe, M.; Asano, K.; Fujiwara, A. Influence of the precipitate-free zone width on the tensile properties of an Al-6 Wt pct Zn-1.2 Wt pct Mg alloy. Metall. Trans. 1973, 4, 1499–1505. [Google Scholar] [CrossRef]
- Nye, J.F. Some geometrical relations in dislocated crystals. Acta Metall. 1953, 1, 153–162. [Google Scholar] [CrossRef]
- Ashby, M. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Kuhlmann-Wilsdorf, D.; Hansen, N. Geometrically necessary, incidental and subgrain boundaries. Scr. Metall. Mater. 1991, 25, 1557–1562. [Google Scholar] [CrossRef]
- Konijnenberg, P.J.; Zaefferer, S.; Raabe, D. Assessment of geometrically necessary dislocation levels derived by 3D EBSD. Acta Mater. 2015, 99, 402–414. [Google Scholar] [CrossRef]
- Sun, S.; Tian, Y.; Lin, H.; Wang, Z.; Zhang, Z. Revisiting the role of prestrain history in the mechanical properties of ultrafine-grained CoCrFeMnNi high-entropy alloy. Mater. Sci. Eng. A 2021, 801, 140398. [Google Scholar] [CrossRef]
- Sidor, J.; Petrov, R.H.; Kestens, L.A. Deformation, recrystallization and plastic anisotropy of asymmetrically rolled aluminum sheets. Mater. Sci. Eng. A 2010, 528, 413–424. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Wang, Q.; Yang, Y.; Zhu, M.; Jia, P.; Duan, Y.; Zhang, Z. Study on anisotropic behavior of 7075 Al alloy after extrusion. Mater. Res. Express 2022, 9, 026508. [Google Scholar] [CrossRef]
- Hosford, W.F.; Caddell, R.M. Metal Forming: Mechanics and Metallurgy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]



| Mg | Zn | Mn | Fe | Al | |
|---|---|---|---|---|---|
| Desired composition | 5 | 4 | 0.3 | - | Bal. |
| Measured composition | 4.85 | 3.97 | 0.27 | 0.08 | Bal. |
| Aging Condition | Direction | Anisotropic Coefficient (R) |
|---|---|---|
| AA (10 h) | 0° | 0.602 |
| 45° | 0.672 | |
| 90° | 0.619 | |
| NA (570 d) | 0° | 0.778 |
| 45° | 0.828 | |
| 90° | 0.698 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, K.; Lee, S.; Bae, D. Natural and Artificial Aging Effects on the Deformation Behaviors of Al–Mg–Zn Alloy Sheets. Materials 2024, 17, 4478. https://doi.org/10.3390/ma17184478
Choi K, Lee S, Bae D. Natural and Artificial Aging Effects on the Deformation Behaviors of Al–Mg–Zn Alloy Sheets. Materials. 2024; 17(18):4478. https://doi.org/10.3390/ma17184478
Chicago/Turabian StyleChoi, Kwangmin, Sangjun Lee, and Donghyun Bae. 2024. "Natural and Artificial Aging Effects on the Deformation Behaviors of Al–Mg–Zn Alloy Sheets" Materials 17, no. 18: 4478. https://doi.org/10.3390/ma17184478
APA StyleChoi, K., Lee, S., & Bae, D. (2024). Natural and Artificial Aging Effects on the Deformation Behaviors of Al–Mg–Zn Alloy Sheets. Materials, 17(18), 4478. https://doi.org/10.3390/ma17184478





