Homogenization of Thermal Properties in Metaplates
Abstract
1. Introduction
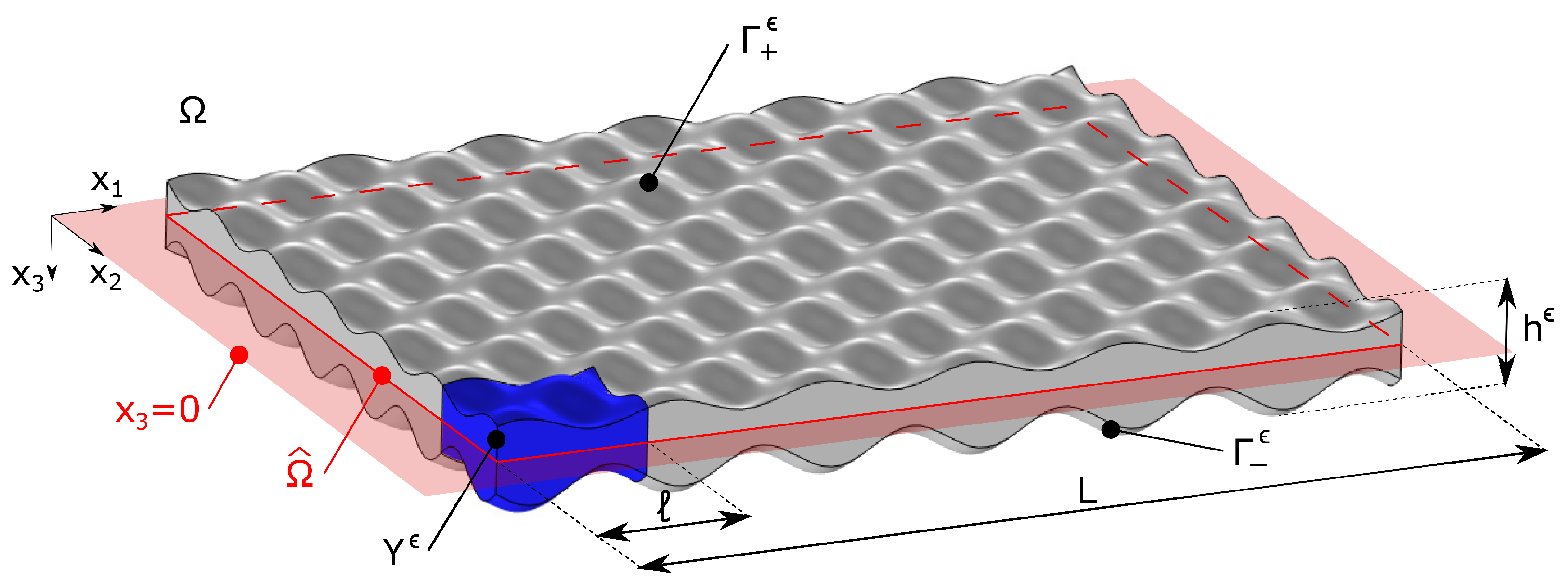
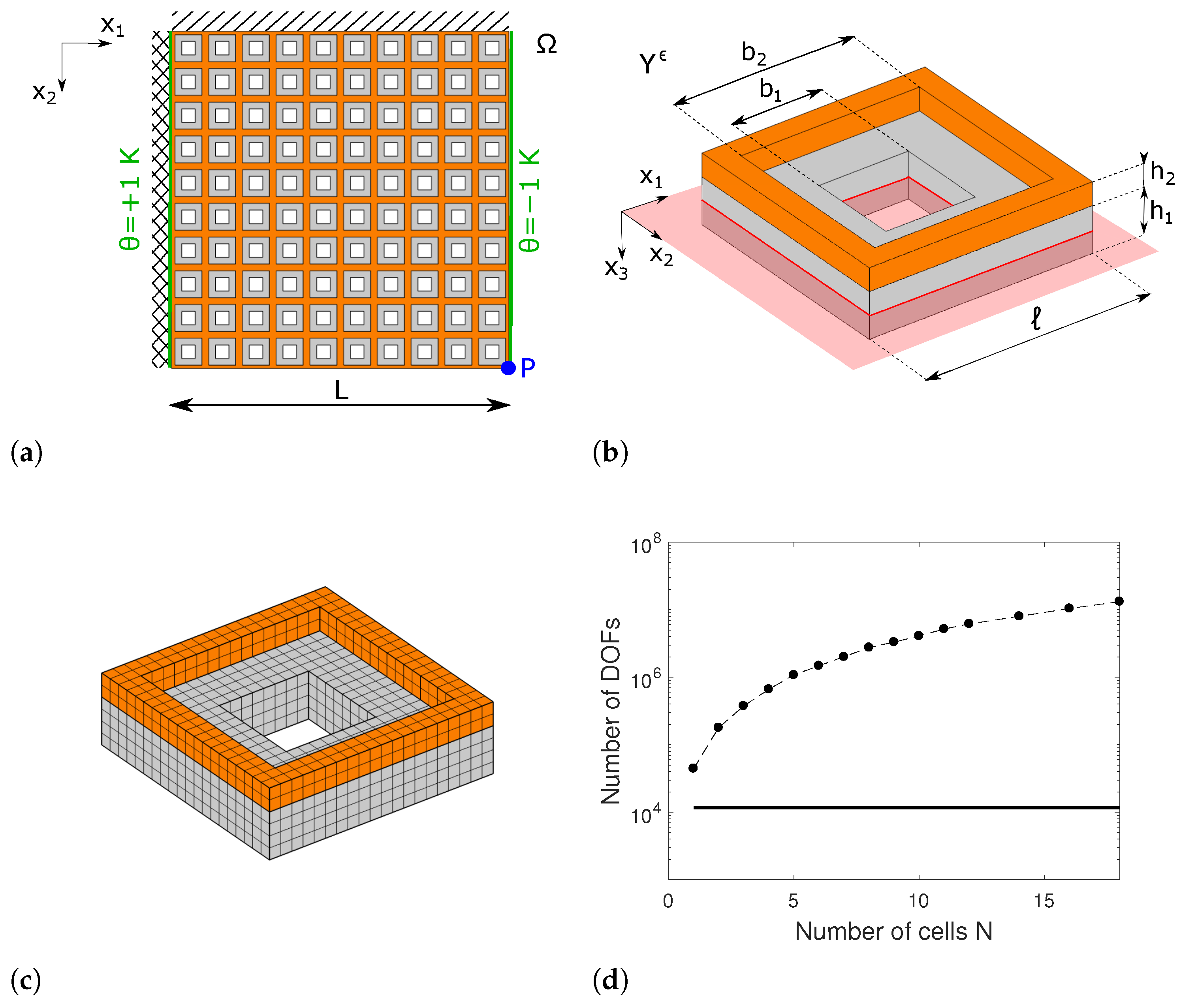
2. Problem Definition
- the characteristic in-plane dimension ℓ of the unit cell is much smaller than the characteristic in-plane dimension of the periodic media, i.e., ;
- the maximum transversal dimension of the body is much smaller than its characteristic in-plane dimension, i.e., ;
- external loadings and temperature variations are quasi-statically applied so that transient effects can be neglected;
- temperature variations are sufficiently small to assume that all material properties can be considered temperature independent.
3. Asymptotic Homogenization
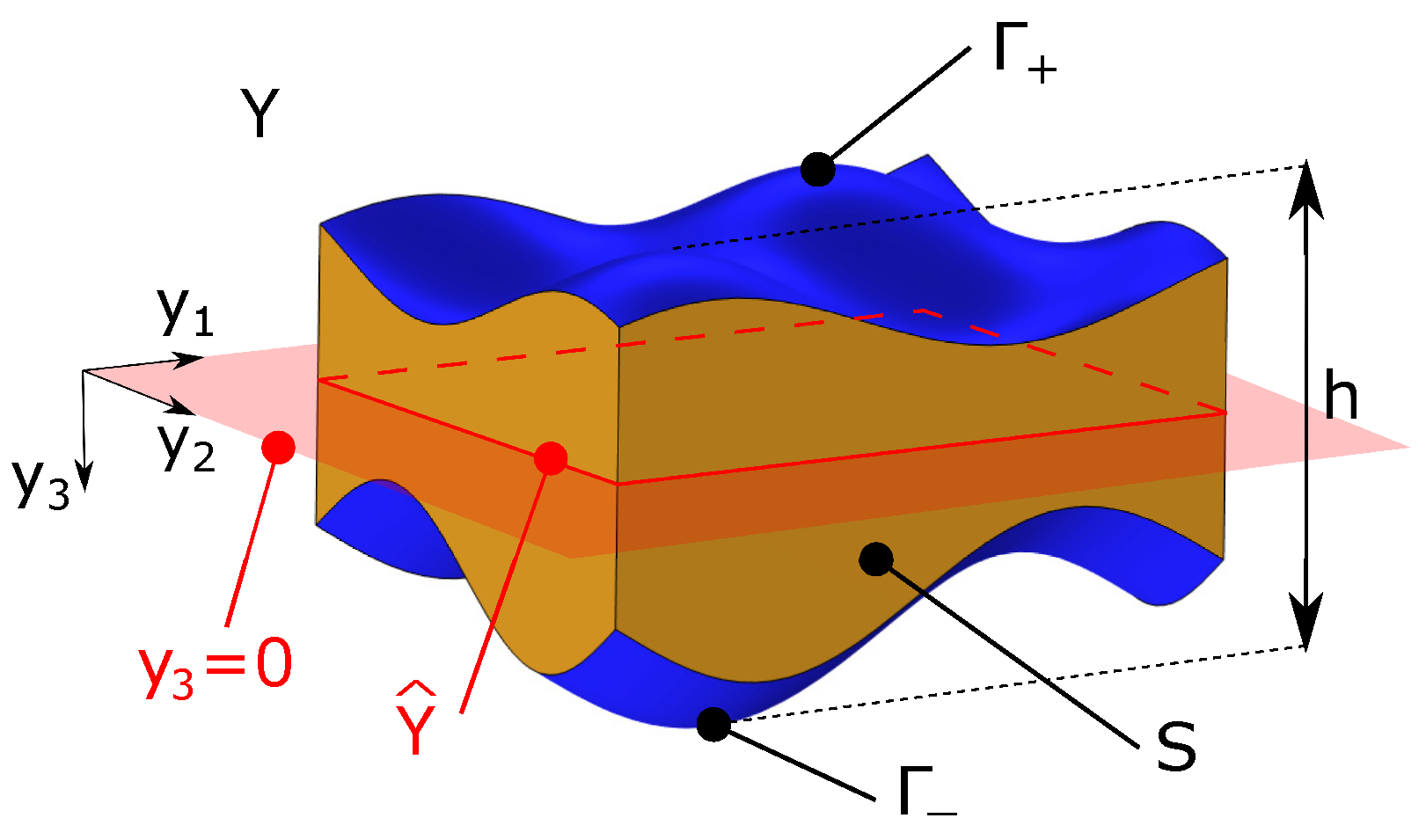
3.1. Scaling and Asymptotic Expansion
3.2. Thermal-Conductivity Problem
3.2.1. Problem
3.2.2. Problem
3.2.3. Problem
3.3. Mechanical Problem
3.3.1. Problem
3.3.2. Problem
3.3.3. Problems and
3.4. Effective Thermoelastic Properties
4. General Remarks
4.1. Back-Scaling of the Solution
4.2. Change of the Reference Mid-Plane
4.3. The Case of Symmetric Metaplates
4.4. The Case of Homogeneous Thermal Expansion Coefficient
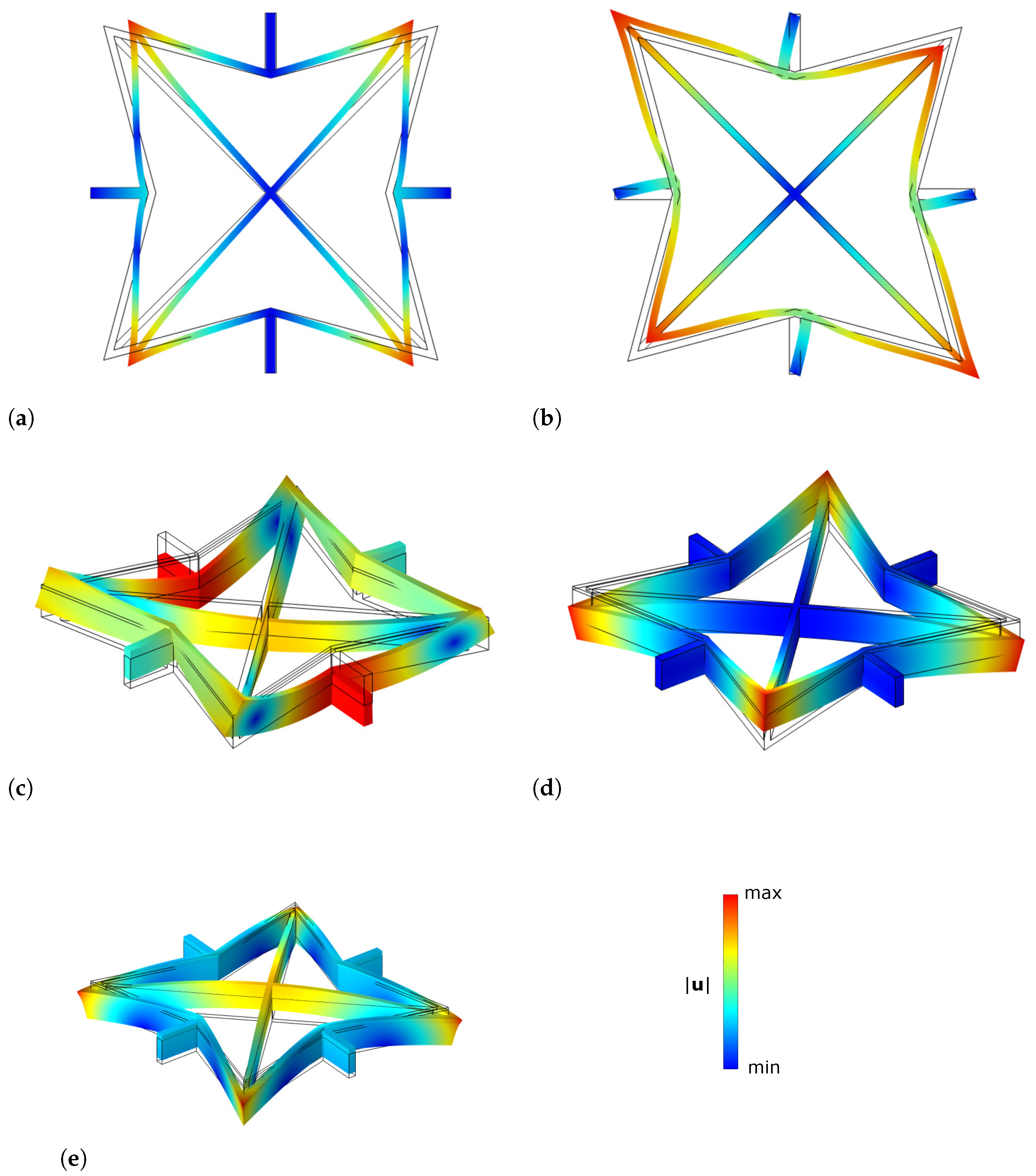
5. Numerical Examples
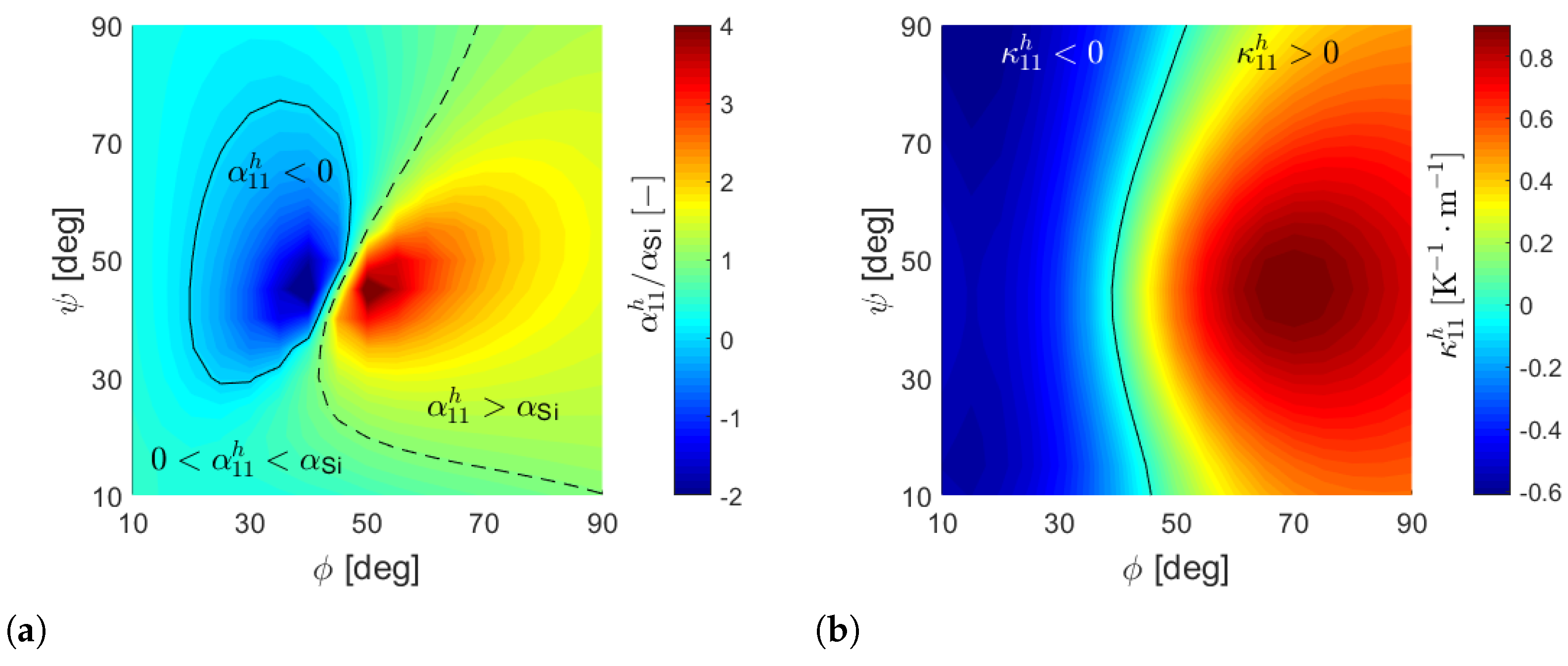
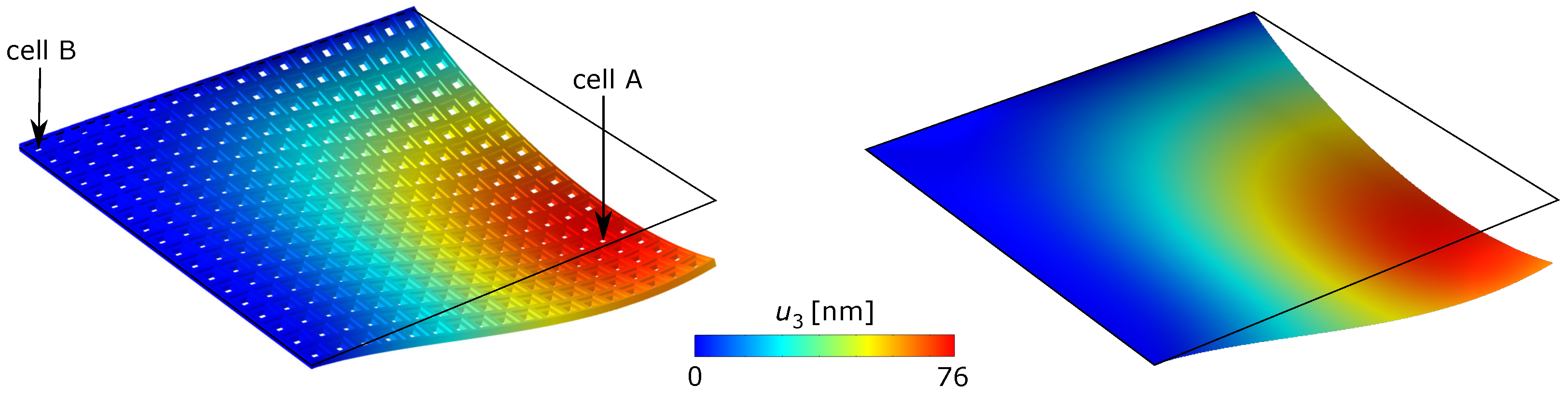
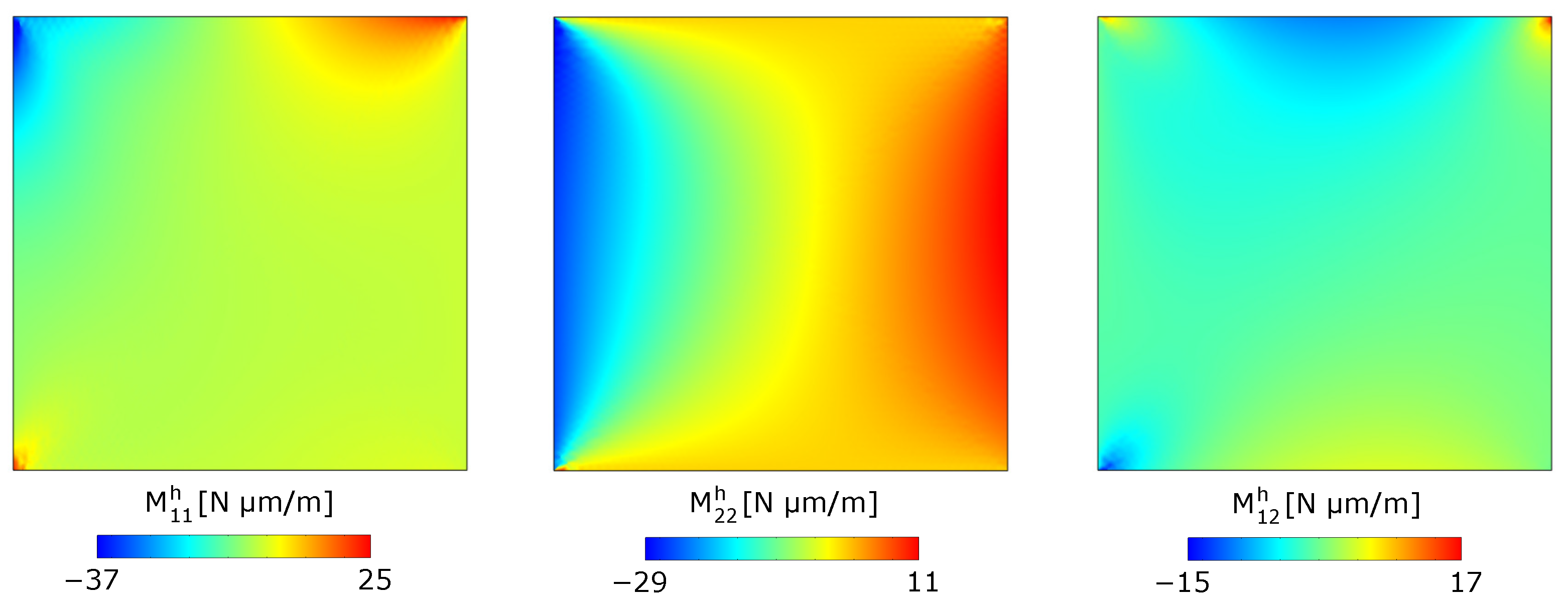
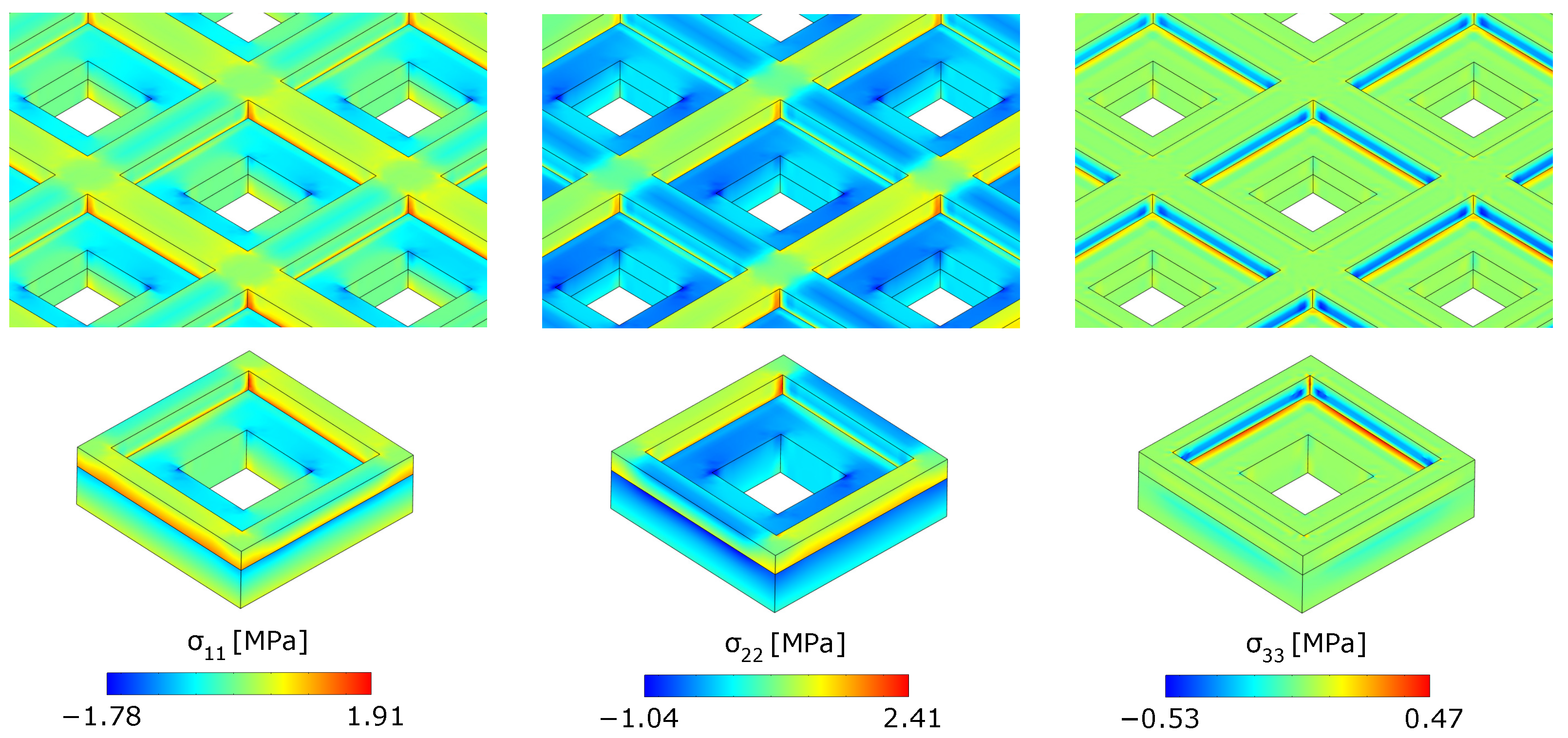
5.1. Parametric Studies
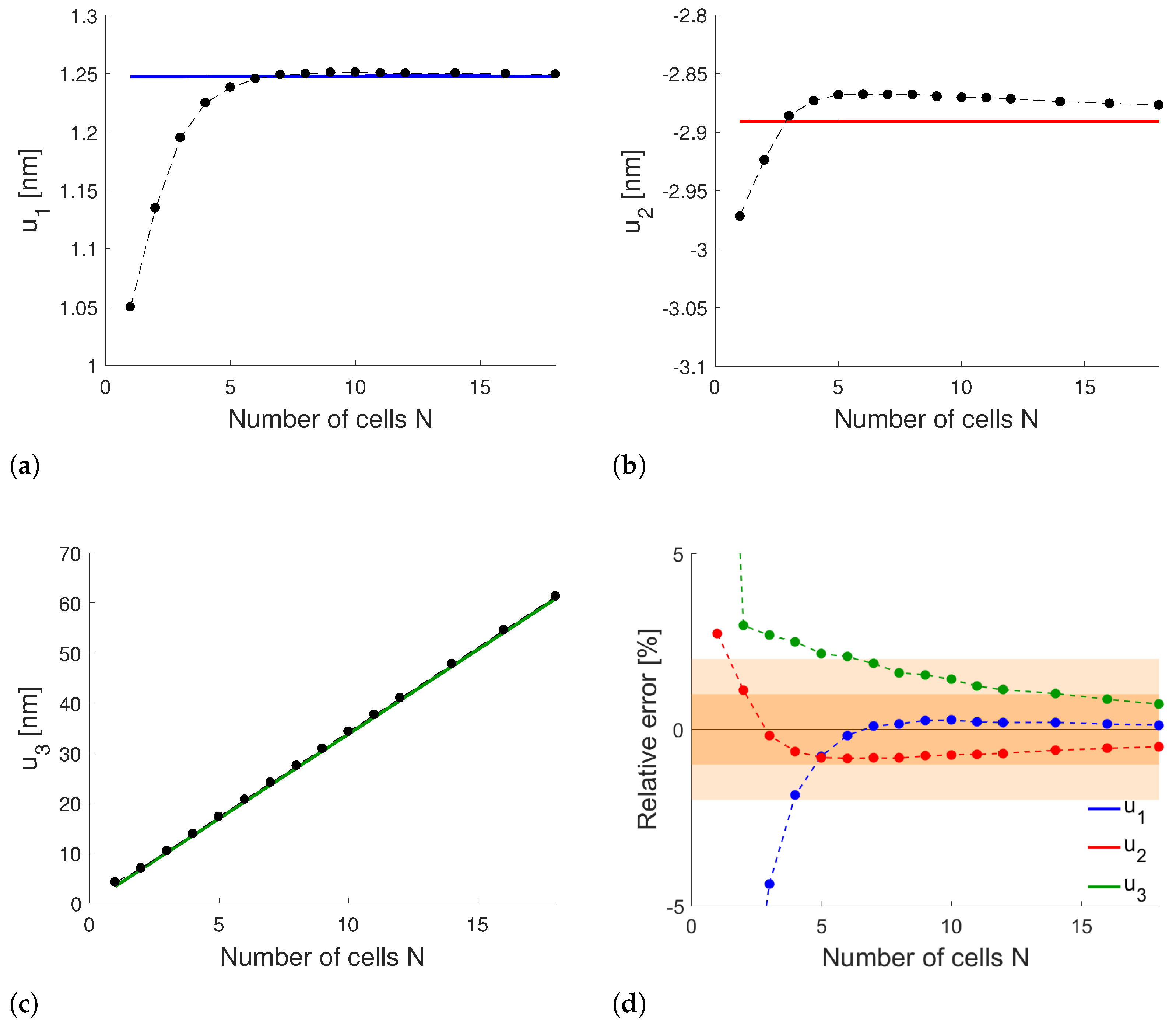
5.2. Convergence of the Homogenization Method
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mary, T.A.; Evans, J.S.O.; Vogt, T.; Sleight, A.W. Negative Thermal Expansion from 0.3 to 1050 Kelvin in ZrW2O8. Science 1996, 272, 90–92. [Google Scholar] [CrossRef]
- Khosrovani, N.; Sleight, A.; Vogt, T. Structure of ZrV2O7 from −263 to 470 °C. J. Solid State Chem. 1997, 132, 355–360. [Google Scholar] [CrossRef]
- Wang, K.; Chen, J.; Han, Z.; Wei, K.; Yang, X.; Wang, Z.; Fang, D. Synergistically program thermal expansional and mechanical performances in 3D metamaterials: Design-Architecture-Performance. J. Mech. Phys. Solids 2022, 169, 105064. [Google Scholar] [CrossRef]
- Dubey, D.; Mirhakimi, A.S.; Elbestawi, M.A. Negative Thermal Expansion Metamaterials: A Review of Design, Fabrication, and Applications. J. Manuf. Mater. Process. 2024, 8, 40. [Google Scholar] [CrossRef]
- Wu, L.; Li, B.; Zhou, J. Isotropic Negative Thermal Expansion Metamaterials. ACS Appl. Mater. Interfaces 2016, 8, 17721–17727. [Google Scholar] [CrossRef]
- Lim, T.C. Anisotropic and negative thermal expansion behavior in a cellular microstructure. J. Mater. Sci. 2005, 40, 3275–3277. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y. A series of auxetic metamaterials with negative thermal expansion based on L-shaped microstructures. Thin-Walled Struct. 2024, 197, 111596. [Google Scholar] [CrossRef]
- Vigna, B.; Ferrari, P.; Villa, F.F.; Lasalandra, E.; Zerbini, S. Silicon Sensors and Actuators; Springer: New York, NY, USA, 2022. [Google Scholar]
- Latella, M.; Faraci, D.; Comi, C. A new metamaterial plate with tunable thermal expansion. In Proceedings of the 9th European Congress on Computational Methods in Applied Sciences and Engineering, Lisbon, Portugal, 3–7 June 2024. [Google Scholar]
- Bensoussan, A.; Lions, J.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; American Mathematical Society: North-Holland, The Netherlands, 1978. [Google Scholar]
- Bakhvalov, N.; Panasenko, G. Homogenisation: Averaging Processes in Periodic Media; Kluwer Academic: London, UK, 1989. [Google Scholar]
- Auriault, J.L.; Bonnet, G.; Nous, I.; Nous, O. Dynamique des composites elastiques periodiques. Arch. Mech. 1985, 37, 269–284. [Google Scholar]
- Comi, C.; Marigo, J.J. Homogenization Approach and Bloch-Floquet Theory for Band-Gap Prediction in 2D Locally Resonant Metamaterials. J. Elast. 2020, 139, 61–90. [Google Scholar] [CrossRef]
- Craster, R.V.; Kaplunov, J.; Pichugin, A.V. High-frequency homogenization for periodic media. Proc. R. Soc. Math. Phys. Eng. Sci. 2010, 466, 2341–2362. [Google Scholar] [CrossRef]
- Francfort, G.A. Homogenization and Linear Thermoelasticity. SIAM J. Math. Anal. 1983, 14, 696–708. [Google Scholar] [CrossRef]
- Del Toro, R.; De Bellis, M.L.; Vasta, M.; Bacigalupo, A. Multifield asymptotic homogenization for periodic materials in non-standard thermoelasticity. Int. J. Mech. Sci. 2024, 265, 108835. [Google Scholar] [CrossRef]
- Auriault, J.; Boutin, C.; Geindreau, C. Homogenization of Coupled Phenomena in Heterogenous Media; ISTE Ltd. and John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Duvaut, G. Comportement macroscopique d’une plaque perforee periodiquement. In Singular Perturbations and Boundary Layer Theory. Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1977; pp. 131–145. [Google Scholar]
- Lewiński, T. Effective models of composite periodic plates-III. Two-dimensional approaches. Int. J. Solids Struct. 1991, 27, 1185–1203. [Google Scholar] [CrossRef]
- Faraci, D.; Comi, C.; Marigo, J.J. Band Gaps in Metamaterial Plates: Asymptotic Homogenization and Bloch-Floquet Approaches. J. Elast. 2022, 148, 55–79. [Google Scholar] [CrossRef]
- Duvaut, G. Homogeneisation des plaques a structure periodique en theorie non lineaire de von Karman. Lect. Notes Math. 1978, 665, 55–69. [Google Scholar]
- Faraci, D.; Comi, C. Nonlinear behaviour and homogenization of metaplates. In Proceedings of the X ECCOMAS Thematic Conference on Smart Structures and Materials, Patras, Greece, 3–5 July 2023. [Google Scholar]
- Caillerie, D. Plaques élastiques minces à structure périodique de période et d’épaisseur comparables. C. R. Acad. Sci. Paris 1982, 294, 159–162. [Google Scholar]
- Lewiński, T. Effective models of composite periodic plates-I. Asymptotic solution. Int. J. Solids Struct. 1991, 27, 1155–1172. [Google Scholar] [CrossRef]
- Caillerie, D.; Nedelec, J.C. Thin elastic and periodic plates. Math. Methods Appl. Sci. 1984, 6, 159–191. [Google Scholar] [CrossRef]
- Lewiński, T.; Telega, J.J. Plates, Laminates and Shells: Asymptotic Analysis and Homogenization; World Scientific Publishing: Singapore, 1999. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Holzapfel, G.A. Nonlinear Solid Mechanics; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Hernández-Acosta, M.; Martines-Arano, H.; Soto-Ruvalcaba, L.; Martínez-González, C.; Martínez-Gutiérrez, H.; Torres-Torres, C. Fractional thermal transport and twisted light induced by an optical two-wave mixing in single-wall carbon nanotubes. Int. J. Therm. Sci. 2020, 147, 106136. [Google Scholar] [CrossRef]
- Li, W.; Sigmund, O.; Zhang, X. Analytical realization of complex thermal meta-devices. Nat. Commun. 2024, 15, 5527. [Google Scholar] [CrossRef]
- Dumontet, H. Study of a boundary layer problem in elastic composite materials. Math. Model. Numer. Anal. 1986, 20, 265–286. [Google Scholar] [CrossRef]


| Material | E [GPa] | [−] | [ppm/K] |
|---|---|---|---|
| Silicon | 160 | 0.22 | 2.6 |
| Nickel | 200 | 0.29 | 12.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faraci, D.; Comi, C. Homogenization of Thermal Properties in Metaplates. Materials 2024, 17, 4557. https://doi.org/10.3390/ma17184557
Faraci D, Comi C. Homogenization of Thermal Properties in Metaplates. Materials. 2024; 17(18):4557. https://doi.org/10.3390/ma17184557
Chicago/Turabian StyleFaraci, David, and Claudia Comi. 2024. "Homogenization of Thermal Properties in Metaplates" Materials 17, no. 18: 4557. https://doi.org/10.3390/ma17184557
APA StyleFaraci, D., & Comi, C. (2024). Homogenization of Thermal Properties in Metaplates. Materials, 17(18), 4557. https://doi.org/10.3390/ma17184557







