Abstract
This work applied three machine learning (ML) models—linear regression (LR), random forest (RF), and support vector regression (SVR)—to predict the lattice parameters of the monoclinic B19′ phase in two distinct training datasets: previously published ZrO2-based shape-memory ceramics (SMCs) and NiTi-based high-entropy shape-memory alloys (HESMAs). Our findings showed that LR provided the most accurate predictions for ac, am, bm, and cm in NiTi-based HESMAs, while RF excelled in computing βm for both datasets. SVR disclosed the largest deviation between the predicted and actual values of lattice parameters for both training datasets. A combination approach of RF and LR models enhanced the accuracy of predicting lattice parameters of martensitic phases in various shape-memory materials for stable high-temperature applications.
1. Introduction
The most widely used NiTi-based shape-memory alloys (SMAs) are known for their good shape memory and superelastic characteristics, based on the transformation between austenite and martensite phases [1,2]. However, their low martensitic transformation temperatures (TTs) below 100 °C are the most common challenges for high-temperature applications [3]. A composition engineering strategy in adding more alloying elements of Pt, Pd, Co, Cu, Zr, and Hf is believed to significantly increase TTs in NiTi-based high-entropy SMAs (HESMAs) [4,5,6]. In addition to high TTs, small thermal hysteresis is expected for stable high-temperature applications of the NiTi-based HESMAs.
The application of machine learning (ML) techniques has garnered significant attention for their potential in predicting and designing alloy compositions with optimized structural and functional properties [7,8,9,10,11]. Xue et al. applied different ML models to predict the transformation temperatures in NiTi-based SMAs [12]. Several ML approaches such as linear regression (LR) [9,13], random forest (RF) [11,14], neural network (NN) [11,15], and support vector regression (SVR) [11,16], have been commonly employed for computational prediction of crystal structures. Li et al. employed the MLatticeABC algorithm, a random forest model, to predict the lattice constants of crystal materials [11]. Pang et al. have recently proposed a linear regression (LR) model to successfully compute the lattice parameters of monoclinic and tetragonal structures in ZrO2-based shape-memory ceramics (SMCs) [9]. Their approach has shed light on the composition design of new martensitic materials with desirable low thermal hysteresis and high TTs. Consequently, we are highly motivated to extend their promising strategy to our research field on the NiTi-based HESMAs.
The present study aimed to identify the most effective ML model for accurately predicting the lattice parameters of a monoclinic structure. We first followed previously published research to forecast the lattice parameters of monoclinic structures from a public training dataset of ZrO2-based SMCs [9] using two more nonlinear models of random forest (RF) and support vector regression (SVR), besides LR. We then applied these three various ML models to the training dataset of the NiTi-based HESMAs to evaluate the most effective ML approach in predicting all lattice parameters of monoclinic B19′ (am, bm, cm, and βm) and cubic B2 (ac) structures.
2. Materials and Methods
Three distinct ML models were applied to predict the lattice parameters in the two training datasets of ZrO2-based SMCs and NiTi-based HESMAs. LR, a fundamentally predictive method in statistics, is suitable for datasets with a roughly linear relationship between variables, and it can be either simple or multivariate. RF and SVR are considered for datasets with nonlinear relationships. RF is an ensemble learning method composed of numerous decision trees, with the final output being an aggregation of the individual trees’ predictions. This method is highly effective in evaluating feature importance, handling high-dimensional data, managing missing values, and demonstrating robust performance in diverse and unbalanced datasets. Therefore, RF enhances model diversity through random feature selection, effectively minimizing overfitting and increasing predictive accuracy. Conversely, SVR functions by mapping data to a high-dimensional space to identify the optimal fitting line or hyperplane. Employing kernel functions, SVR allows the construction of nonlinear relationships within the original feature space. A distinctive aspect of SVR is its ε-insensitivity band, tolerating minor prediction deviations without penalty, making it ideal for datasets with intricate or nonlinear associations. SVR’s regularization ensures strong generalization capabilities, effectively preventing overfitting. Both linear and nonlinear issues can be adeptly managed by selecting appropriate kernel functions. Like RF, SVR remains potent in scenarios where feature count surpasses sample size, ensuring reliable model predictions.
The feature for each data point was modeled as follows [9]:
where xave is the weighted average of all constituent elements, fi is the mole fraction of a specific element i, and xi is the feature value of element i.
Our training dataset of NiTi-based HESMAs included data points of 152 cubic and 176 monoclinic structures comprising constituent compositions of Ni, Ti, Hr, Hf, Cu, Fe, and Co in the Ni50-x-y-zTi50-h-kHfhZrkCuxFeyCoz, which was collected from previously published studies [4,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. A set of 14 input features were electronegativity, electron affinity, number of valence electrons, Pettifor chemical scale, ionic radius, slater atomic radius, Clementi atomic radius, size difference, Waber atomic radius, atomic number, atomic mass, temperature, mixing enthalpy, and mixing entropy. The test root mean square error (RMSE) during cross-validation of the best feature set was used to evaluate the accuracy of ML models. Figure 1 illustrates the procedure for the computational prediction of lattice constants in the NiTi-based HESMAs.
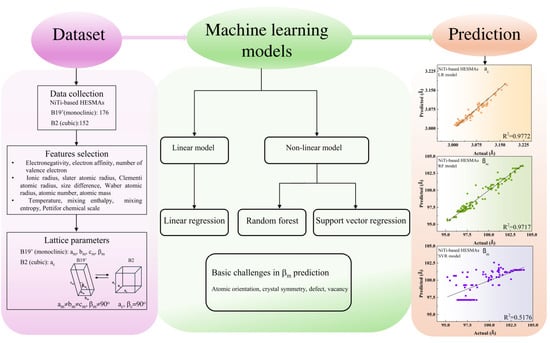
Figure 1.
Flowchart for the computational prediction of lattice constants in the NiTi-based HESMAs.
3. Results
In accompanying LR used in published research [9], we applied two more different nonlinear models of RF and SVR to the public training dataset of ZrO2-based SMCs to explore the most appropriate model in predicting the lattice parameters of monoclinic structure. Figure 2 shows the predicted versus actual lattice parameters fitted using three distinct models. A comparison of the test RMSE among the three ML models is presented in Table 1. Lower test RMSE values indicate higher accuracy between the predicted and actual values. The test RMSE values of am, bm, cm, and βm modeled by LR in the present work were in good accordance with those obtained in previously published work [9], seen in Table 1, demonstrating the reliability of our predictions in modeling the lattice parameters of the monoclinic phase.
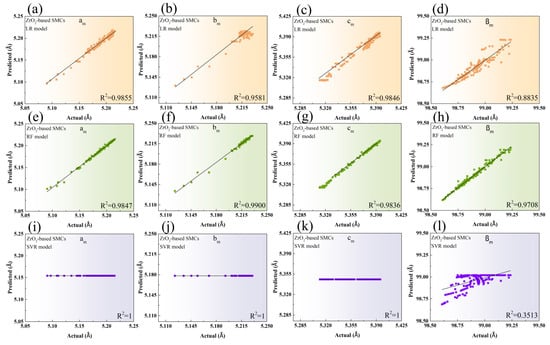
Figure 2.
The predicted versus actual lattice constants of am (a), bm (b), cm (c), and βm (d) modeled by LR. Those of am (e), bm (f), cm (g), and βm (h) modeled by RF. Those of am (i), bm (j), cm (k), and βm (l) modeled by SVR in the ZrO2-based SMCs. The solid black line depicts the perfect match between the predicted versus actual values of lattice constants.

Table 1.
A comparison of test RMSE values among three ML models in predicting the lattice parameters of the ZrO2-based SMCs and NiTi-based HESMAs.
The LR in Figure 2a–d revealed a closer fit between the predicted and actual values for am and cm, in agreement with R2 values. The RF in Figure 2e–h showed a better match for bm and βm, as also seen in the test RMSE and R2. It is noted that a lower accuracy of bm and βm than am and cm by LR was found to be modeled more accurately by RF. The predicted values of am, bm, and cm could not be distinguished from their actual corresponding values, and a very high value of the test RMSE in predicting βm was obtained by SVR, suggesting that SVR was not suited to compute the lattice parameters of monoclinic structures, shown in Figure 2i–l and Table 1.
Both LR and RF were found to be more suitable ML models for forecasting all lattice parameters of ZrO2-based SMCs, as there was a negligible discrepancy in the test RMSE between them. However, RF demonstrated higher accuracy in predicting bm and βm compared to LR, as evidenced by its lower test RMSE and higher R² values.
To verify the potential of LR and RF ML models, we employed them to forecast the lattice parameters of monoclinic structures in the NiTi-based HESMAs in Figure 3. The predicted values of am, bm, cm, and ac exhibited the best match with the actual values when using LR, as illustrated in Figure 3a–e. βm demonstrated the highest accuracy between the predicted and actual values using RF, as shown in Figure 3f–j and corroborated by the test RMSE values in Table 1. The remarkable accuracy of RF in predicting βm in the NiTi-based HESMAs was also observed in the ZrO2-based SMCs. Conversely, SVR exhibited the poorest accuracy in modeling all lattice parameters of the monoclinic phase, as shown in Figure 3k–n. Moreover, no distinguishable prediction of ac was computed by SVR in Figure 3o, which was similar to the predicted values of am, bm, and cm by SVR in the ZrO2-based SMCs (Figure 2i–k). A trivial discrepancy of experimental lattice parameters between data points was ascribed to the predicted values indistinguishable from the actual values in SVR.
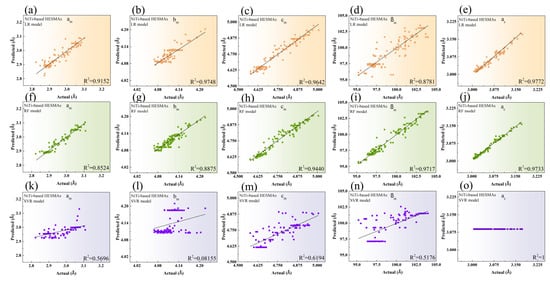
Figure 3.
The predicted versus actual lattice constants of am (a), bm (b), cm (c), βm (d), and ac (e) modeled by LR. Those of am (f), bm (g), cm (h), βm (i), and ac (j) modeled by RF. Those of am (k), bm (l), cm (m), βm (n), and ac (o) modeled by SVR in the NiTi-based HESMAs. The solid black line depicts the perfect match between the predicted versus actual values of lattice constants.
As shown in Figure 4, the lowest test RMSE values for βm were achieved in both datasets, indicating that RF is the most effective approach for predicting βm. Superior prediction of lattice angles using RF model has also been reported [11]. The test RMSE values of am, bm, cm, and ac in LR were slightly lower than those in RF, especially in the training dataset of the NiTi-based HESMAs, suggesting the superiority of the LR model in computing am, bm, cm, and ac.
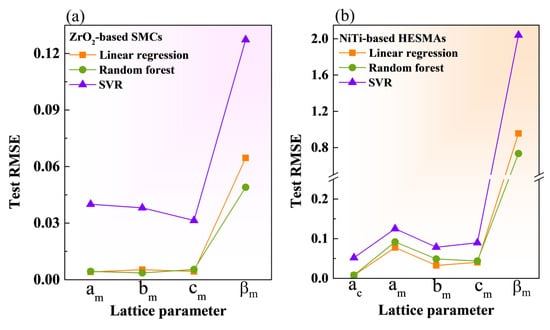
Figure 4.
The test RMSE values among three ML models in computing the predicted lattice parameters of am, bm, cm, and βm in the ZrO2-based SMCs (a). Those of ac, am, bm, cm, and βm in the NiTi-based HESMAs (b).
4. Conclusions
Among the three various ML approaches, the LR and RF models achieved lower test RMSE values and better prediction performance of the lattice constants for both monoclinic and cubic phases in the NiTi-based HESMAs. There was a better match between the predicted and actual values of am, bm, cm, and ac using LR in the NiTi-based HESMAs, which was also demonstrated in the published dataset of ZrO2-based SMCs. Meanwhile, greater accuracy of the βm was found using the RF model in both the ZrO2-based SMCs and NiTi-based HESMAs. The concurrent combination of LR and RF models is expected to attain the highest accuracy in predicting all the unit-cell edge lengths and the inclination angles of the crystal structures. These initial predictive results are very crucial to the compositional design of new NiTi-based HESMAs with large recoverable strain and low density for their stable and cost-effective high-temperature applications in biomedicine, actuators, and the aerospace industry.
Author Contributions
Conceptualization, E.-W.H.; methodology, E.-W.H.; formal analysis, J.J., M.-C.H., S.-R.T., M.-Y.L., and S.-T.H.; investigation, J.J., M.-C.H., and S.-R.T.; resources, W.-J.L. and C.-H.C.; supervision, E.-W.H.; writing—original draft preparation, T.-N.L.; writing—review and editing, T.-N.L., J.J., M.-C.H., S.-R.T., M.-Y.L., S.-T.H., W.-J.L., C.-H.C., and E.-W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Council (NSTC) under grants NSTC 113-2221-E-A49-003-, 113-2221-E-492-013-, and 113-2811-E-A49-525-. This work was financially supported by the “High Entropy Materials Center” from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) and from the project MOST 111-2634-F-007-008- by NSTC in Taiwan. The present work was supported by the Higher Education Sprout Project of the National Yang Ming Chiao Tung University and MOE, Taiwan. This work was financially supported by the “Center for Advanced Semiconductor Technology Research” from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the MOE in Taiwan. The present work is supported by the “Overseas Project for Post Graduate Research” from the National Science and Technology Council (NSTC) in Taiwan.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Bhaumik, S.K. Progress in the understanding of NiTi shape memory alloys. Trans. Indian Inst. Met. 2008, 61, 435–445. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti–Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Ma, J.; Karaman, I.; Noebe, R.D. High temperature shape memory alloys. Int. Mater. Rev. 2013, 55, 257–315. [Google Scholar] [CrossRef]
- Chang, S.H.; Lin, P.T.; Tsai, C.W. High-temperature martensitic transformation of CuNiHfTiZr high- entropy alloys. Sci. Rep. 2019, 9, 19598. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.-H.; Kao, W.-P.; Hsiao, K.-Y.; Yeh, J.-W.; Lu, M.-Y.; Tsai, C.-W. High-temperature shape memory properties of Cu15Ni35Ti25Hf12.5Zr12.5 high-entropy alloy. J. Mater. Res. Technol. 2021, 14, 1235–1242. [Google Scholar] [CrossRef]
- Frenzel, J.; Wieczorek, A.; Opahle, I.; Maaß, B.; Drautz, R.; Eggeler, G. On the effect of alloy composition on martensite start temperatures and latent heats in Ni–Ti-based shape memory alloys. Acta Mater. 2015, 90, 213–231. [Google Scholar] [CrossRef]
- Chang, Y.-J.; Jui, C.-Y.; Lee, W.-J.; Yeh, A.-C. Prediction of the Composition and Hardness of High-Entropy Alloys by Machine Learning. JOM 2019, 71, 3433–3442. [Google Scholar] [CrossRef]
- Huang, E.W.; Lee, W.-J.; Singh, S.S.; Kumar, P.; Lee, C.-Y.; Lam, T.-N.; Chin, H.-H.; Lin, B.-H.; Liaw, P.K. Machine-learning and high-throughput studies for high-entropy materials. Mater. Sci. Eng. R Rep. 2022, 147, 100645. [Google Scholar] [CrossRef]
- Pang, E.L.; Olson, G.B.; Schuh, C.A. Low-hysteresis shape-memory ceramics designed by multimode modelling. Nature 2022, 610, 491–495. [Google Scholar] [CrossRef]
- Thapa, S.; Lomholt, M.A.; Krog, J.; Cherstvy, A.G.; Metzler, R. Bayesian analysis of single-particle tracking data using the nested-sampling algorithm: Maximum-likelihood model selection applied to stochastic-diffusivity data. Phys. Chem. Chem. Phys. 2018, 20, 29018–29037. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yang, W.; Dong, R.; Hu, J. Mlatticeabc: Generic Lattice Constant Prediction of Crystal Materials Using Machine Learning. ACS Omega 2021, 6, 11585–11594. [Google Scholar] [CrossRef] [PubMed]
- Xue, D.; Xue, D.; Yuan, R.; Zhou, Y.; Balachandran, P.V.; Ding, X.; Sun, J.; Lookman, T. An informatics approach to transformation temperatures of NiTi-based shape memory alloys. Acta Mater. 2017, 125, 532–541. [Google Scholar] [CrossRef]
- Jiang, L.Q.; Guo, J.K.; Liu, H.B.; Zhu, M.; Zhou, X.; Wu, P.; Li, C.H. Prediction of lattice constant in cubic perovskites. J. Phys. Chem. Solids 2006, 67, 1531–1536. [Google Scholar] [CrossRef]
- Majid, A.; Khan, A.; Choi, T.-S. Predicting lattice constant of complex cubic perovskites using computational intelligence. Comput. Mater. Sci. 2011, 50, 1879–1888. [Google Scholar] [CrossRef]
- Cao, Z.; Dan, Y.; Xiong, Z.; Niu, C.; Li, X.; Qian, S.; Hu, J. Convolutional Neural Networks for Crystal Material Property Prediction Using Hybrid Orbital-Field Matrix and Magpie Descriptors. Crystals 2019, 9, 191. [Google Scholar] [CrossRef]
- Takahashi, K.; Takahashi, L.; Baran, J.D.; Tanaka, Y. Descriptors for predicting the lattice constant of body centered cubic crystal. J. Chem. Phys. 2017, 146, 204104. [Google Scholar] [CrossRef]
- Azeem, M.A. Diffraction Investigations of High Temperature Shape Memory Alloys. Ph.D. Thesis, Imperial College London, London, UK, 2013. [Google Scholar]
- Benafan, O.; Bigelow, G.S.; Garg, A.; Noebe, R.D.; Gaydosh, D.J.; Rogers, R.B. Processing and Scalability of NiTiHf High-Temperature Shape Memory Alloys. Shape Mem. Superelasticity 2021, 7, 109–165. [Google Scholar] [CrossRef]
- Bertheville, B. Powder metallurgical processing of ternary Ni50Ti50−xZrx (x = 5, 10at.%) alloys. J. Alloys Compd. 2005, 398, 94–99. [Google Scholar] [CrossRef]
- Bricknell, R.H.; Melton, K.N.; Mercier, O. The Structure of NiTiCu Shape Memory Alloys. Metall. Trans. A 1979, 10, 693–697. [Google Scholar] [CrossRef]
- Dalle, F.; Perrin, E.; Vermaut, P.; Masse, M.; Portier, R. Interface mobility in Ni49.8Ti42.2Hf8 shape memory alloy. Acta Mater. 2002, 50, 3557–3565. [Google Scholar] [CrossRef]
- Evirgen, A.; Karaman, I.; Santamarta, R.; Pons, J.; Hayrettin, C.; Noebe, R.D. Relationship between crystallographic compatibility and thermal hysteresis in Ni-rich NiTiHf and NiTiZr high temperature shape memory alloys. Acta Mater. 2016, 121, 374–383. [Google Scholar] [CrossRef]
- Goryczka, T.; Pisarski, W.A.; Morawiec, H.; Humbeeck, J.V. Structure and transformation sequence of NiTiCu shape memory alloys obtained by powder technology. In Applied Crystallography; World Scientific: Singapore, 2001; pp. 200–205. [Google Scholar]
- Han, X.D.; Zou, W.H.; Wang, R.; Zhang, Z.; Yang, D.Z. Structure and substructure of martensite in a Ti36.5Ni48.5Hf15 high temperature shape memory alloy. Acta Mater. 1996, 44, 3711–3721. [Google Scholar] [CrossRef]
- Hsieh, S.F.; Wu, S.K. A study on lattice parameters of martensite in Ti50.5−xNi49.5Zrx shape memory alloys. J. Alloys Compd. 1998, 270, 237–241. [Google Scholar] [CrossRef]
- Khalil-Allafi, J.; Schmahl, W.W.; Wagner, M.; Sitepu, H.; Toebbens, D.M.; Eggeler, G. The influence of temperature on lattice parameters of coexisting phases in NiTi shape memory alloys—A neutron diffraction study. Mater. Sci. Eng. A 2004, 378, 161–164. [Google Scholar] [CrossRef]
- Kim, W.C.; Kim, Y.J.; Kim, J.S.; Kim, Y.S.; Na, M.Y.; Kim, W.T.; Kim, D.H. Correlation between the thermal and superelastic behavior of Ni50−xTi35Zr15Cux shape memory alloys. Intermetallics 2019, 107, 24–33. [Google Scholar] [CrossRef]
- Lee, J.; Ikeda, Y.; Tanaka, I. Solution effect on improved structural compatibility of NiTi-based alloys by systematic first-principles calculations. J. Appl. Phys. 2019, 125, 055106. [Google Scholar] [CrossRef]
- Li, S.; Cong, D.; Chen, Z.; Li, S.; Song, C.; Cao, Y.; Nie, Z.; Wang, Y. A high-entropy high-temperature shape memory alloy with large and complete superelastic recovery. Mater. Res. Lett. 2021, 9, 263–269. [Google Scholar] [CrossRef]
- Liu, Y. Some factors affecting the transformation hysteresis in shape memory alloys. Shape Mem. Alloys 2010, 369, 361–369. [Google Scholar]
- Malvasio, B.F.; Isola, L.M.; Giordana, M.F.; Malarria, J.A. Shape memory behavior of sputter-deposited Ni46.2Ti51.1Co2.7 (at.%) thin films. J. Alloys Compd. 2022, 918, 165671. [Google Scholar] [CrossRef]
- Mironov, Y.P. Motion picture x-ray diffraction investigation of the martensitic transformation in nickel-titanium alloy. Russ. Phys. J. 1994, 37, 741–745. [Google Scholar] [CrossRef]
- Miyazaki, S.; Hashinaga, T.; Ishida, A. Martensitic transformations in sputter-deposited Ti−Ni−Cu shape memory alloy thin films. Thin Solid. Film. 1996, 281–282, 364–367. [Google Scholar] [CrossRef]
- Patriarca, L.; Sehitoglu, H.; Panchenko, E.Y.; Chumlyakov, Y.I. High-temperature functional behavior of single crystal Ni51.2Ti23.4Hf25.4 shape memory alloy. Acta Mater. 2016, 106, 333–343. [Google Scholar] [CrossRef]
- Peltier, L.; Lohmuller, P.; Meraghni, F.; Berveiller, S.; Patoor, E.; Laheurte, P. Investigation and Composition Characterization of a “NiTi-like” Alloy Combining High Temperature Shape Memory and High Entropy. Shape Mem. Superelasticity 2020, 6, 273–283. [Google Scholar] [CrossRef]
- Potapov, P.L.; Shelyakov, A.V.; Gulyaev, A.A.; Svistunov, E.L.; Matveeva, N.M.; Hodgson, D. Effect of Hf on the structure of Ni-Ti martensitic alloys. Mater. Lett. 1997, 32, 247–250. [Google Scholar] [CrossRef]
- Prasher, M.; Sen, D.; Tewari, R.; Krishna, P.S.R.; Babu, P.D.; Krishnan, M. Effect of Hf solute addition on the phase transformation behavior and hardness of a Ni-rich NiTi alloy. Mater. Chem. Phys. 2020, 247, 122890. [Google Scholar] [CrossRef]
- Prokoshkin, S.D.; Korotitskiy, A.V.; Gundyrev, V.M.; Zeldovich, V.I. Low-temperature X-ray diffraction study of martensite lattice parameters in binary Ti–Ni alloys. Mater. Sci. Eng. A 2008, 481–482, 489–493. [Google Scholar] [CrossRef]
- Pushin, V.; Kuranova, N.; Marchenkova, E.; Pushin, A. Design and Development of Ti-Ni, Ni-Mn-Ga and Cu-Al-Ni-based Alloys with High and Low Temperature Shape Memory Effects. Materials 2019, 12, 2616. [Google Scholar] [CrossRef] [PubMed]
- Ren, G.; Sehitoglu, H. Interatomic potential for the NiTi alloy and its application. Comput. Mater. Sci. 2016, 123, 19–25. [Google Scholar] [CrossRef]
- Sanjabi, S.; Cao, Y.Z.; Sadrnezhaad, S.K.; Barber, Z.H. Binary and ternary NiTi-based shape memory films deposited by simultaneous sputter deposition from elemental targets. J. Vac. Sci. Technol. A 2005, 23, 1425–1429. [Google Scholar] [CrossRef]
- Tong, Y.; Chen, F.; Tian, B.; Li, L.; Zheng, Y. Microstructure and martensitic transformation of Ti49Ni51−xHfx high temperature shape memory alloys. Mater. Lett. 2009, 63, 1869–1871. [Google Scholar] [CrossRef]
- Tong, Y.; Shuitcev, A.; Zheng, Y. Recent Development of TiNi-Based Shape Memory Alloys with High Cycle Stability and High Transformation Temperature. Adv. Eng. Mater. 2020, 22, 1900496. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Ma, Z.; Ren, Y.; Jiang, D.; Cui, L.; Yu, K. Small stress-hysteresis in a nanocrystalline TiNiCuFe alloy for elastocaloric applications over wide temperature window. J. Alloys Compd. 2022, 928, 167195. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).