Temperature Effect Separation of Structure Responses from Monitoring Data Using an Adaptive Bandwidth Filter Algorithm
Abstract
1. Introduction
2. Algorithm of the Adaptive Bandwidth Filter
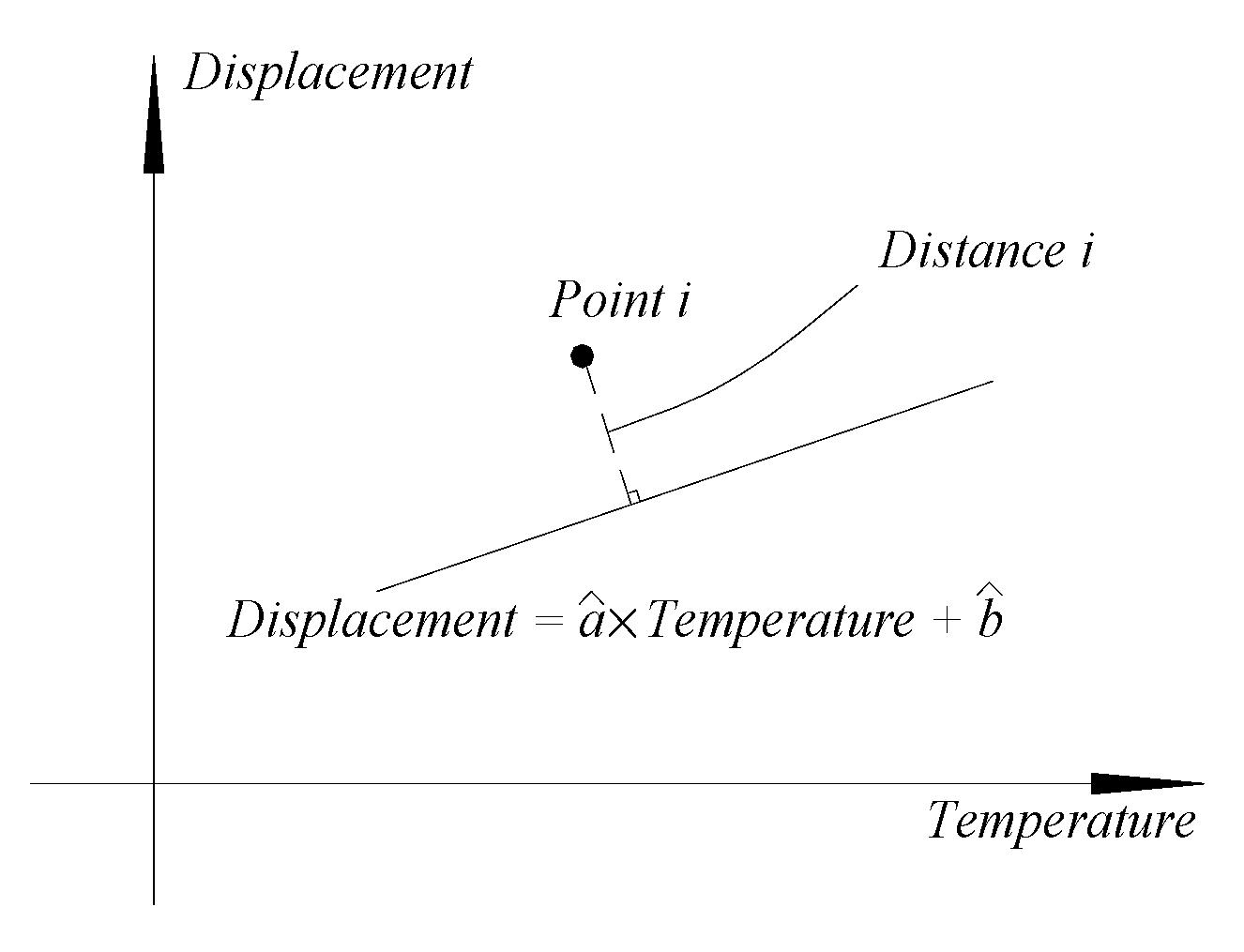
2.1. Model and Algorithm
- Obtain the same time span signal of temperature and structure response.
- Set the center frequencies of DTE and YTE.
- Set the iteration index t = 0 and filter updating parameters and (i = d and y, corresponding to DTE and YTE, respectively) randomly.
- Compute the cost function according to Equation (3). Update the particle velocities, position fi, and local and global memories according to Formula (5).
- Limited new particle positions to lie within a logical bound according to Formula (4) so that the band-pass filter can work.
- If t < tmax (the maximum cycle time), then t = t +1 and go to step 4; otherwise stop iteration.
- Use the best fi obtained from PSO to filter the signals of temperature and structure response so that two different time scale signals corresponding to DTE and YTE are acquired.
- Regress linear factor of DTE and YTE to day temperature (DT) and year temperature (YT), respectively.
- Calculate day and year temperature effects by summation of linear factor multiplied by DT and YT, respectively.
2.2. Performance Measures
3. Simulation Analysis
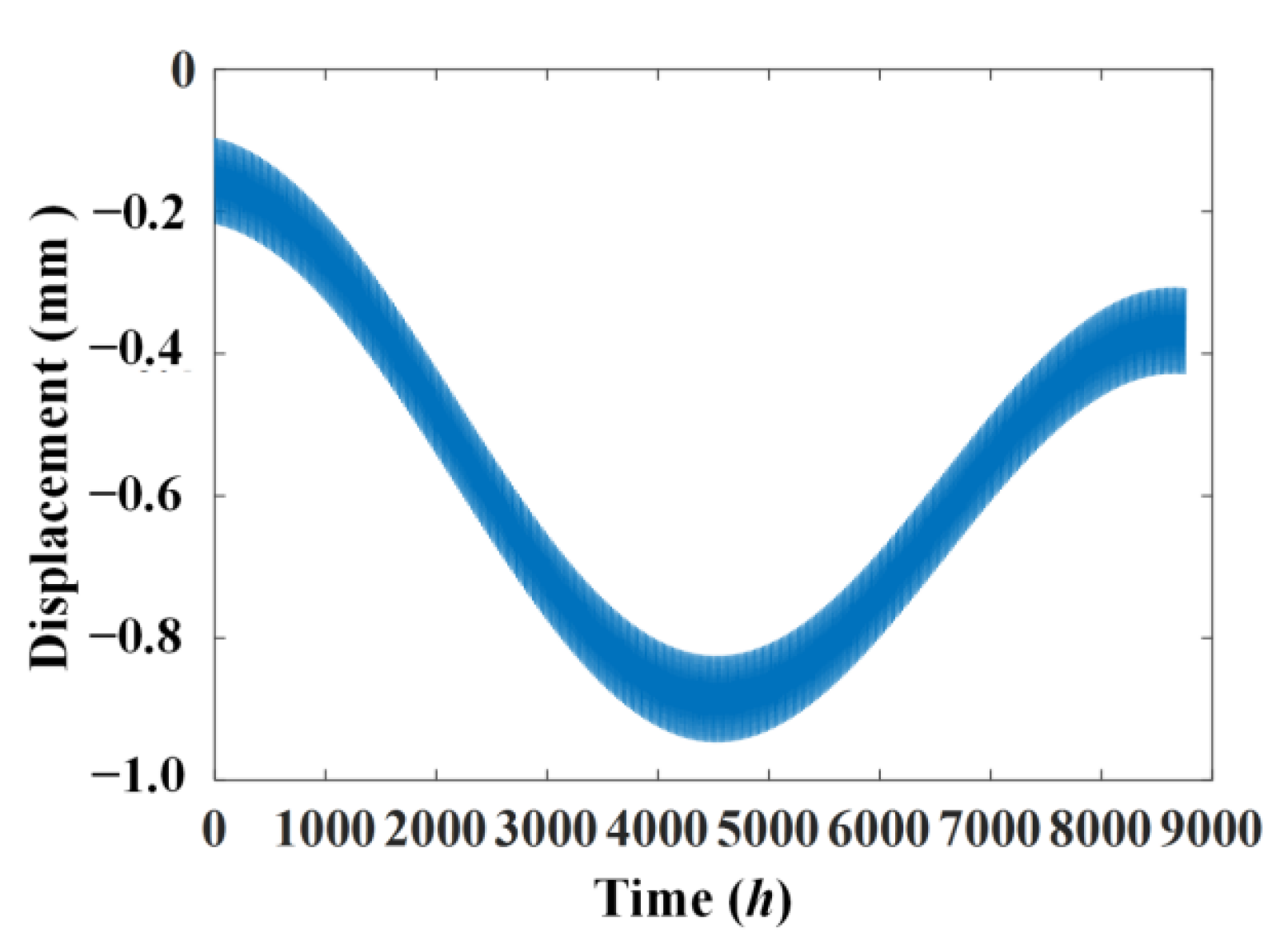
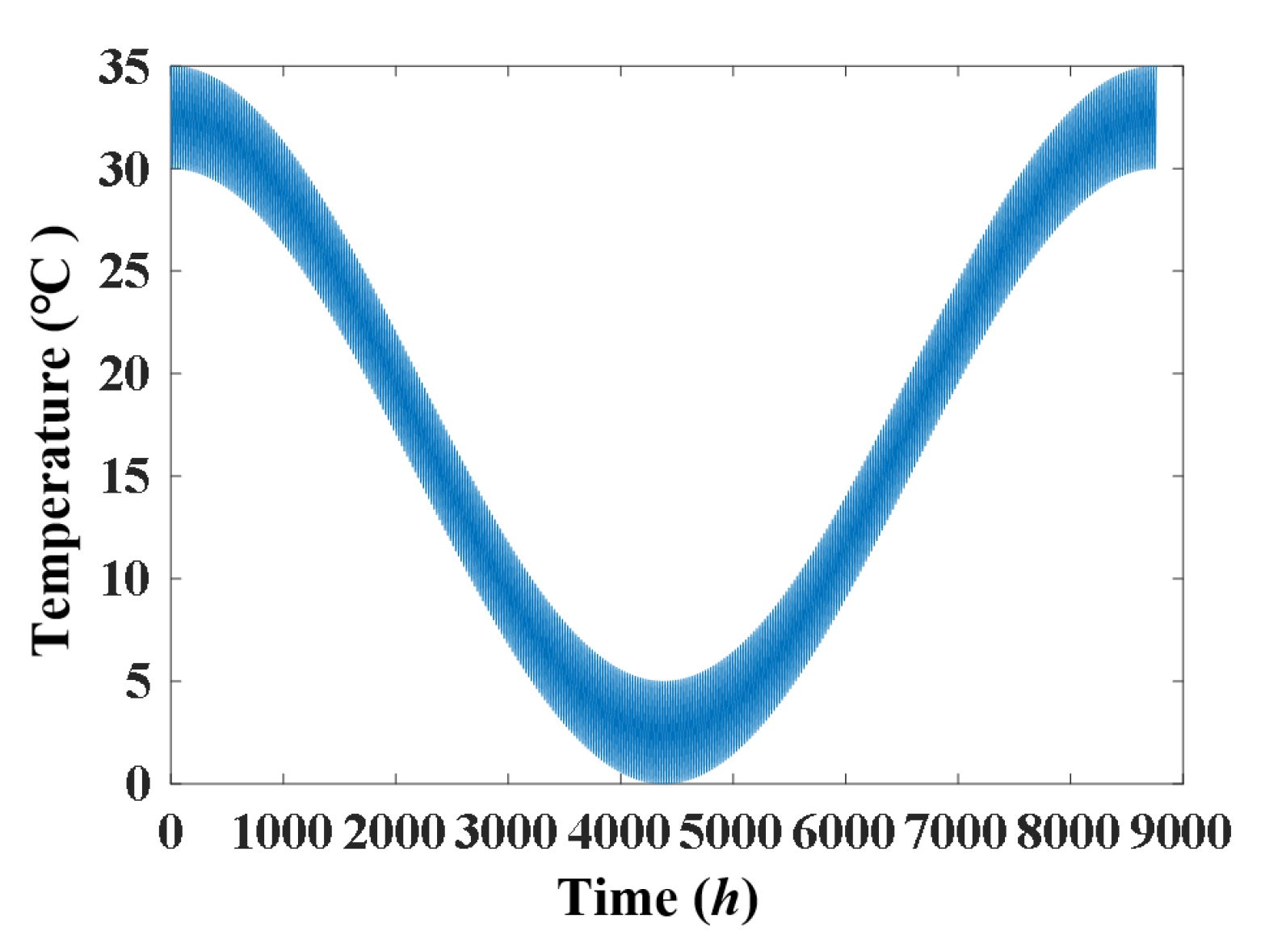
3.1. The Simulated Temperature and Displacement Signals
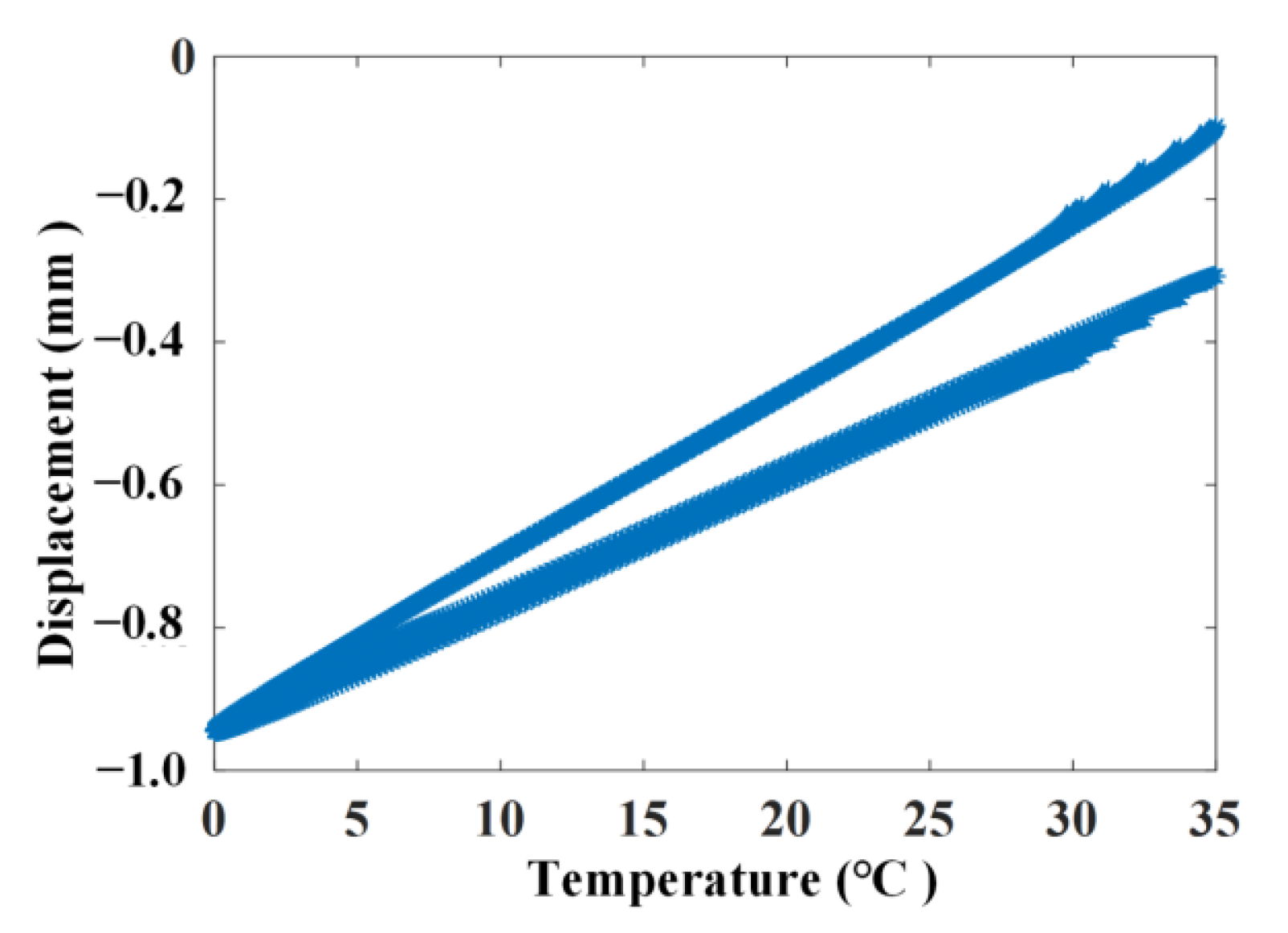
3.2. Relationship between Linear Correlation Using the ABFA
3.3. Relationship between Linear Correlation Using the Long Short-Term Memory Network (LSTM) Method
3.4. Relationship between IAI and Different Time Spans of Signals Using the ABFA
- The computation time can be cut down greatly.
- A reliable health assessment on the bridge can be advanced. Actually, in order to meet the requirement of frequency resolution for the year temperature filter, several year reference periods are needed at least. But for most bridges, especially for deteriorated bridges, this period is so long that collapse accidents may not be prevented timely.
3.5. Damage Detection Using the ABFA
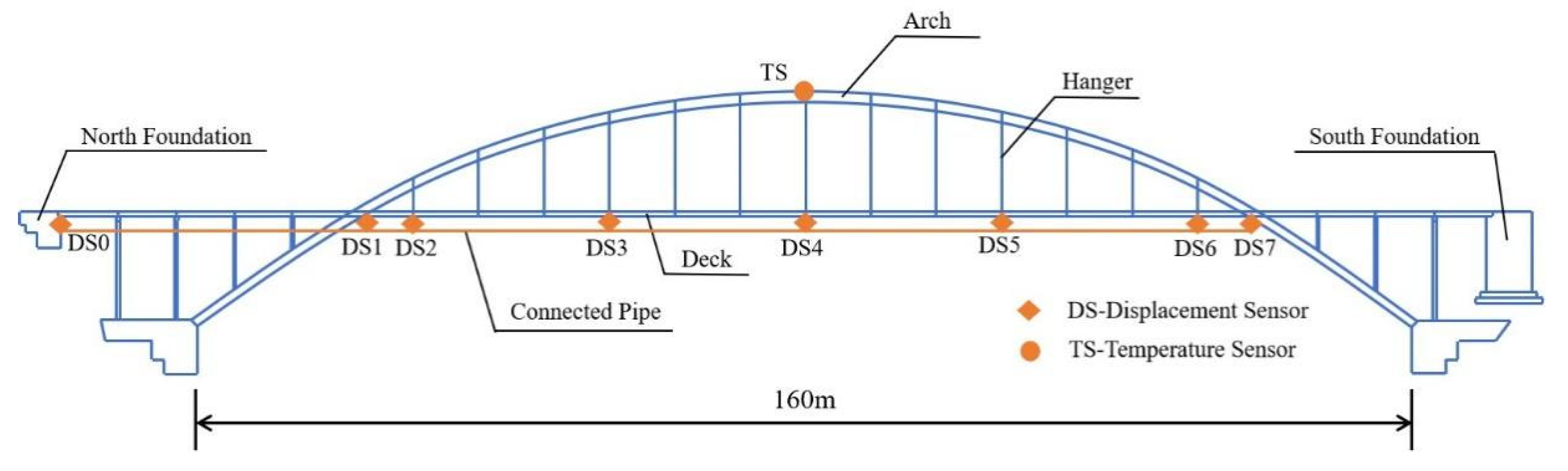
4. Applications
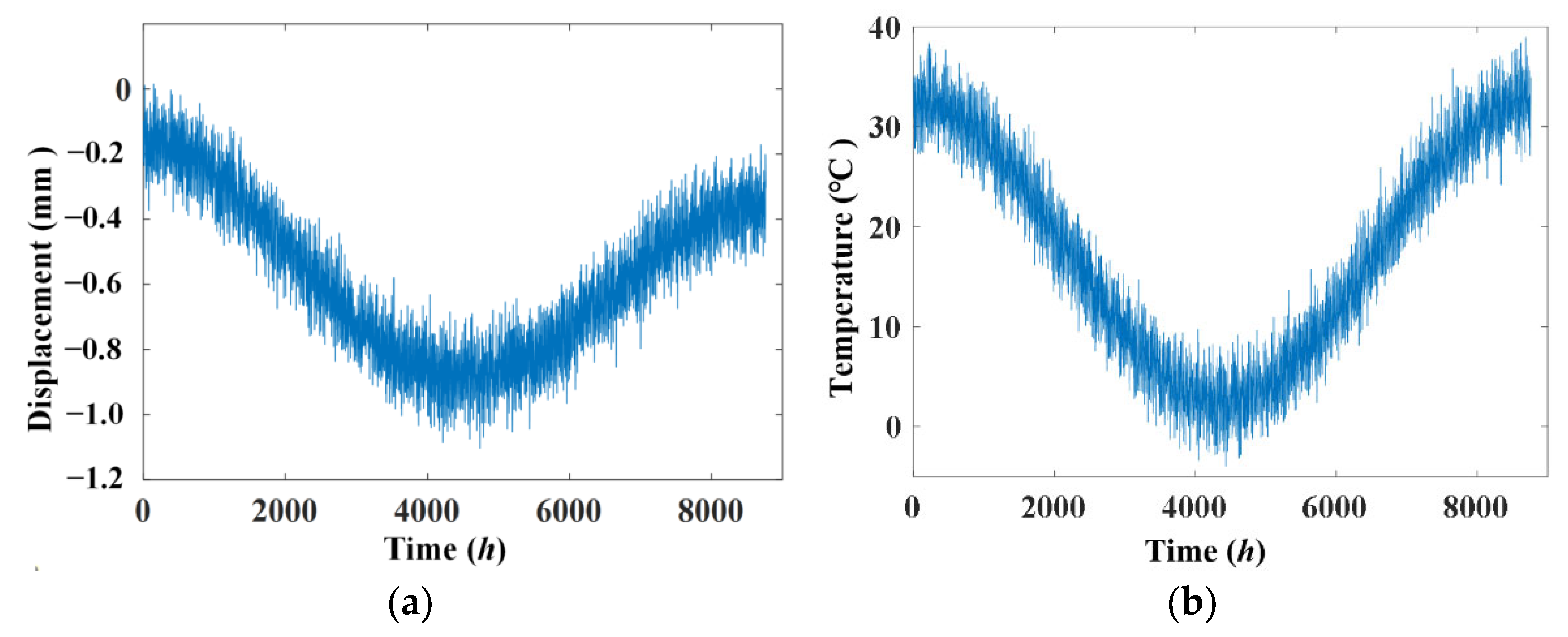
4.1. The Measured Temperature and Displacement Signals
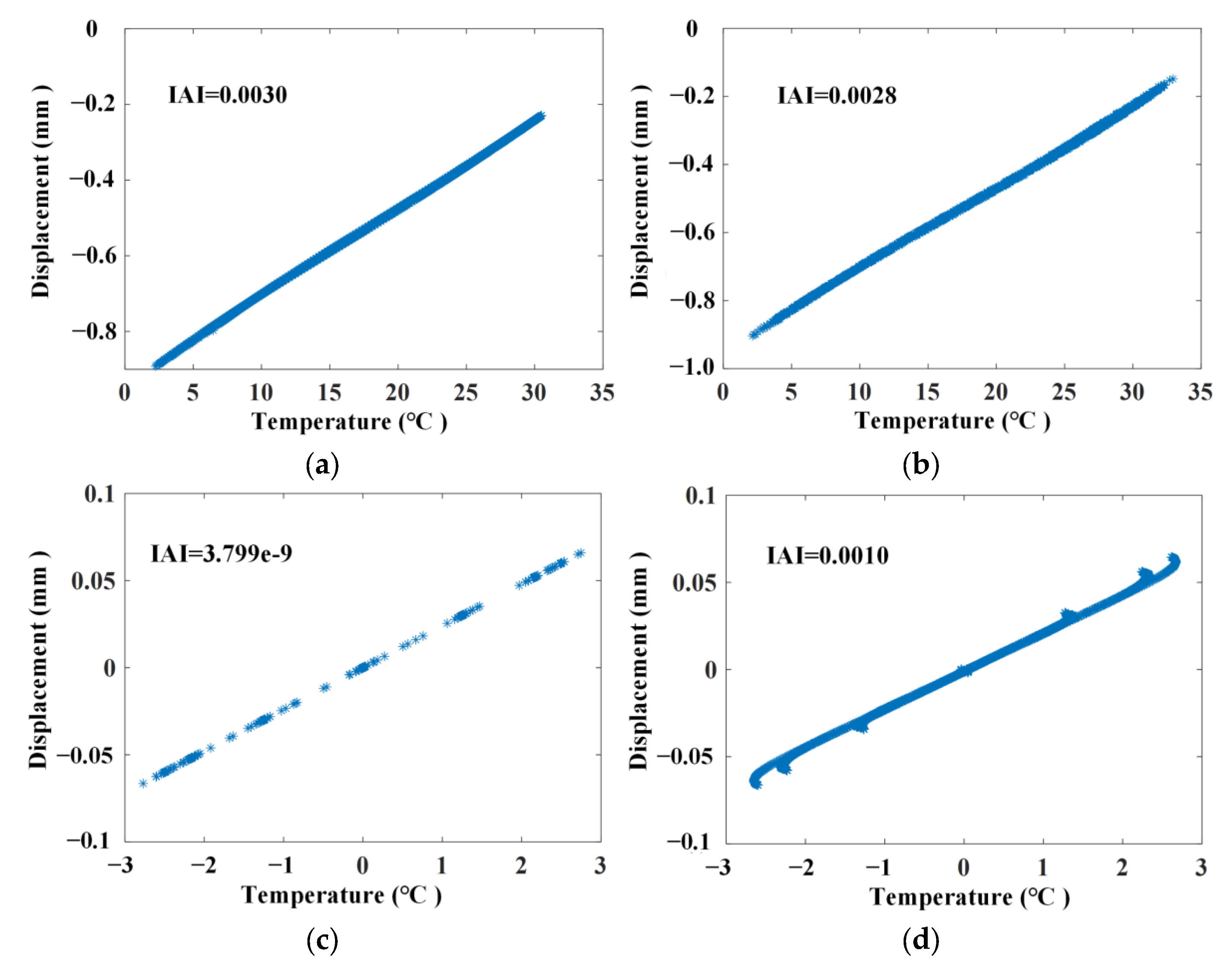
4.2. Relationship between Linear Correlation Using the ABFA
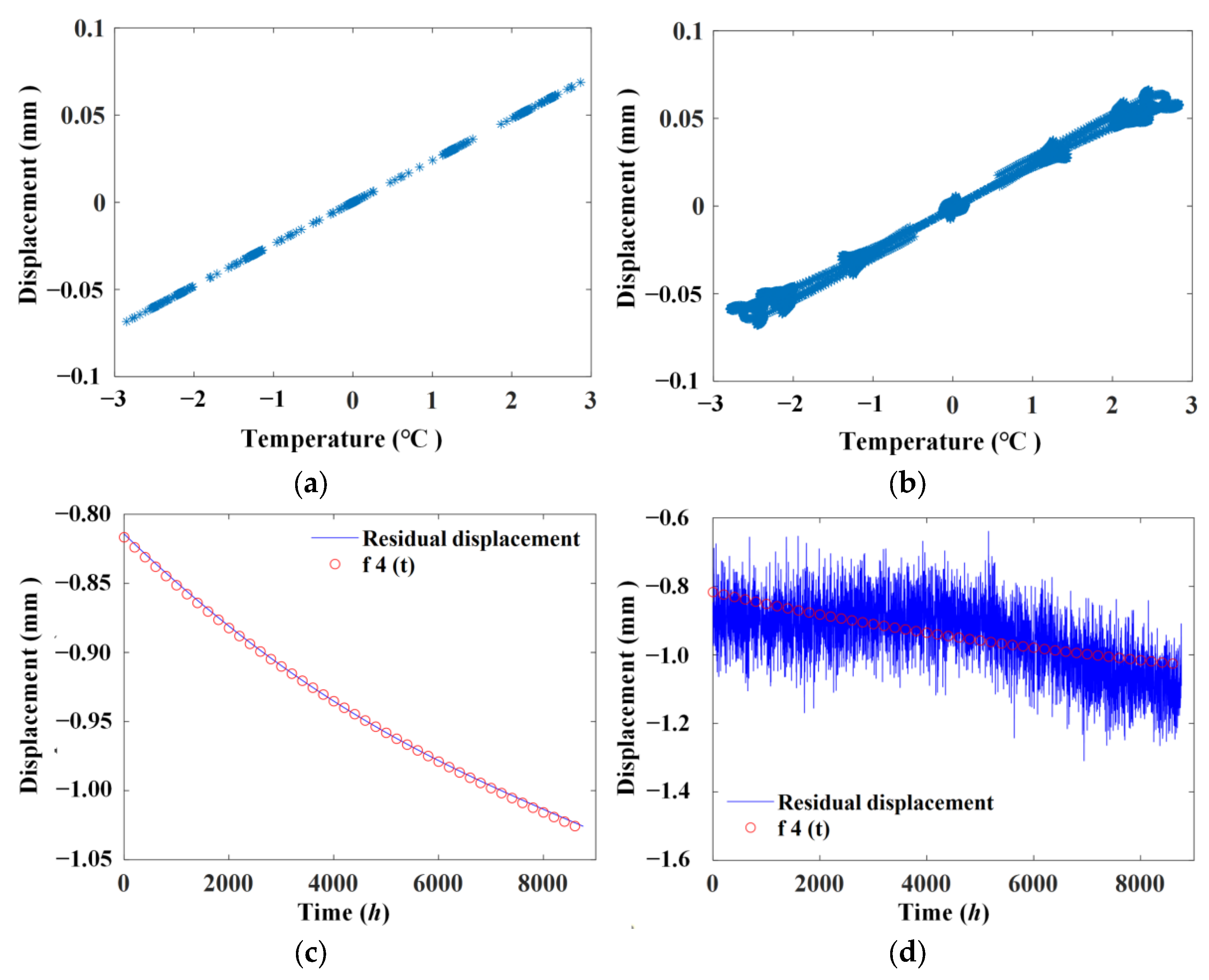
4.3. The Temperature Separation Results Using ABFA
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wah, W.S.L. Damage detection of structures under changing environmental and operational conditions using the COVRATIO statistic. Eng. Struct. 2023, 281, 1–10. [Google Scholar]
- Luo, J.; Liu, G.; Huang, Z.; Law, S. Mode shape identification based on Gabor transform and singular value decomposition under uncorrelated colored noise excitation. Mech. Syst. Signal Process. 2019, 128, 446–462. [Google Scholar] [CrossRef]
- Lei, Z.; Liu, G.; Cong, Y.; Tang, W. Research on fatigue damage mitigation of offshore wind turbines by a bi-directional PSTMD under stochastic wind-wave actions. Eng. Struct. 2024, 301, 117275. [Google Scholar] [CrossRef]
- Liu, G.; Li, M.; Mao, Z. Dynamic monitoring of structure in civil engineering for phase motion estimation via Hilbert transform. Mech. Syst. Signal Process. 2020, 166, 108418. [Google Scholar]
- Gaebler, K.O.; Hedegaard, B.D.; Shield, C.K.; Linderman, L.E. Signal selection and analysis methodology of long-term vibration data from the i-35w st. anthony falls bridge. Struct. Control. Health Monit. 2018, 25, e2182. [Google Scholar] [CrossRef]
- Farrar, C.R.; Baker, W.E.; Bell, T.M.; Cone, K.M.; Darling, T.W.; Duffey, T.A.; Eklund, A.; Migliori, A. Dynamic Characterization and Damage Detection in the I-40 Bridge over the Rio Grande; LA-12767-MS; Los Alamos National Laboratory Report: Washington, DC, USA, 1994.
- Standoli, G.; Clementi, F.; Gentile, C.; Lenci, S. Post-earthquake continuous dynamic monitoring of the twin belfries of the Cathedral of Santa Maria Annunziata of Camerino, Italy. Procedia Struct. Integr. 2023, 44, 2066–2073. [Google Scholar]
- Maes, K.; Meerbeeck, L.V.; Reynders, E.P.B.; Lombaert, G. Validation of vibration-based structural health monitoring on retrofitted railway bridge KW51. Mech. Syst. Signal Process. 2022, 165, 108380. [Google Scholar] [CrossRef]
- Sohn, H.; Dzwonczyk, M.; Straser, E.G.; Kiremidjian, A.S.; Law, K.H.; Meng, T. An experimental study of temperature effect on modal parameters of the Alamosa Canyon Bridge. Earthq. Eng. Struct. Dyn. 1999, 28, 879–897. [Google Scholar]
- Zimin, V.D.; Zimmerman, D.C. Structural Damage Detection Using Time Domain Periodogram Analysis. Struct. Health Monit. 2009, 8, 125–135. [Google Scholar] [CrossRef]
- Datteo, A.; Luca, F.; Busca, G. Statistical pattern recognition approach for long-time monitoring of the g.meazza stadium by means of AR models and PCA. Eng. Struct. 2017, 153, 317–333. [Google Scholar] [CrossRef]
- Wang, J.; Tong, X.; Yue, C.; Liu, W.; Zhang, Q.; Zeng, L.; Huang, G. Real-time temperature distribution reconstruction via linear parameter-varying state-space model and Kalman filter in rack-based cooling data centers. Build. Environ. 2023, 242, 110601. [Google Scholar]
- Shah, S.A.A.; Bais, A.; Alashaikh, A.; Alanazi, E. Discrete wavelet transform based branched deep hybrid network for environmental noise classification. Comput. Intell. 2023, 39, 478–498. [Google Scholar]
- Eltotongy, A.; Awad, M.I.; Maged, S.A.; Onsy, A. Fault Detection and Classification of Machinery Bearing Under Variable Operating Conditions Based on Wavelet Transform and CNN. In Proceedings of the 2021 International Mobile, Intelligent, and Ubiquitous Computing Conference: International Mobile, Intelligent, and Ubiquitous Computing Conference (MIUCC), Cairo, Egypt, 26–27 May 2021; pp. 117–123. [Google Scholar]
- Yu, X.; Liang, Z.; Wang, Y.; Yin, H.; Liu, X.; Yu, W.; Huang, Y. A wavelet packet transform-based deep feature transfer learning method for bearing fault diagnosis under different working conditions. Measurement 2022, 201, 111597. [Google Scholar]
- Fritzen, C.R.; Mengelkamp, G.; Guemes, A. Elimination of temperature effects on damage detection within a smart structure concept. Struct. Health Monit. 2003, 15, 17. [Google Scholar]
- Manson, G. Identifying Damage Sensitive, Environmental Insensitive Features for Damage Detection. In Proceedings of the Third International Conference Identification in Engineering Systems, University of Wales Swansea, Wales, UK, 15–17 April 2002. [Google Scholar]
- Yang, C.; Liu, Y. Detecting the damage of bridges under changing environmental conditions using the characteristics of the nonlinear narrow dimension of damage features. Mech. Syst. Signal Process. 2021, 159, 107842. [Google Scholar]
- Soo Lon Wah, W.; Xia, Y. Elimination of outlier measurements for damage detection of structures under changing environmental conditions. Struct. Health Monit. 2022, 21, 320–338. [Google Scholar] [CrossRef]
- Diao, Y.; Sui, Z.; Guo, K. Structural damage identification under variable environmental/operational conditions based on singular spectrum analysis and statistical control chart. Struct. Control. Health Monit. 2021, 28, e2721. [Google Scholar] [CrossRef]
- García-Macías, E.; Hernández-González, I.A.; Puertas, E.; Gallego, R.; Castro-Triguero, R.; Ubertini, F. Meta-Model Assisted Continuous Vibration-Based Damage Identification of a Historical Rammed Earth Tower in the Alhambra Complex. Int. J. Archit. Herit. 2022, 4, 1–27. [Google Scholar]
- Jabid, Q.; Luis, M.; Rodolfo, V.; Magda, R.; Johanatan, C. PCA based stress monitoring of cylindrical specimens using pzts and guided waves. Sensors 2017, 17, 2788. [Google Scholar] [CrossRef]
- Tenelema, F.J.; Delgadillo, R.M.; Casas, J.R. Bridge Damage Detection and Quantification under Environmental Effects by Principal Component Analysis; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Khanesar, M.A.; Yan, M.; Isa, M.A.; Piano, S.; Branson, D.T. Precision Denavit–Hartenberg Parameter Calibration for Industrial Robots Using a Laser Tracker System and Intelligent Optimization Approaches. Sensors 2023, 23, 5368. [Google Scholar] [CrossRef] [PubMed]
- Chafi, M.R.S.; Narm, H.G.; Kalat, A.A. Calibration of fluxgate sensor using Least Square Method and Particle Swarm Optimization Algorithm. J. Magn. Magn. Mater. 2023, 570, 170364. [Google Scholar] [CrossRef]
- Mhaya, A.M.; Baghban, M.H.; Faridmehr, I.; Huseien, G.F.; Abidin, A.R.Z.; Ismail, M. Performance Evaluation of Modified Rubberized Concrete Exposed to Aggressive Environments. Materials 2021, 14, 1900. [Google Scholar] [CrossRef] [PubMed]








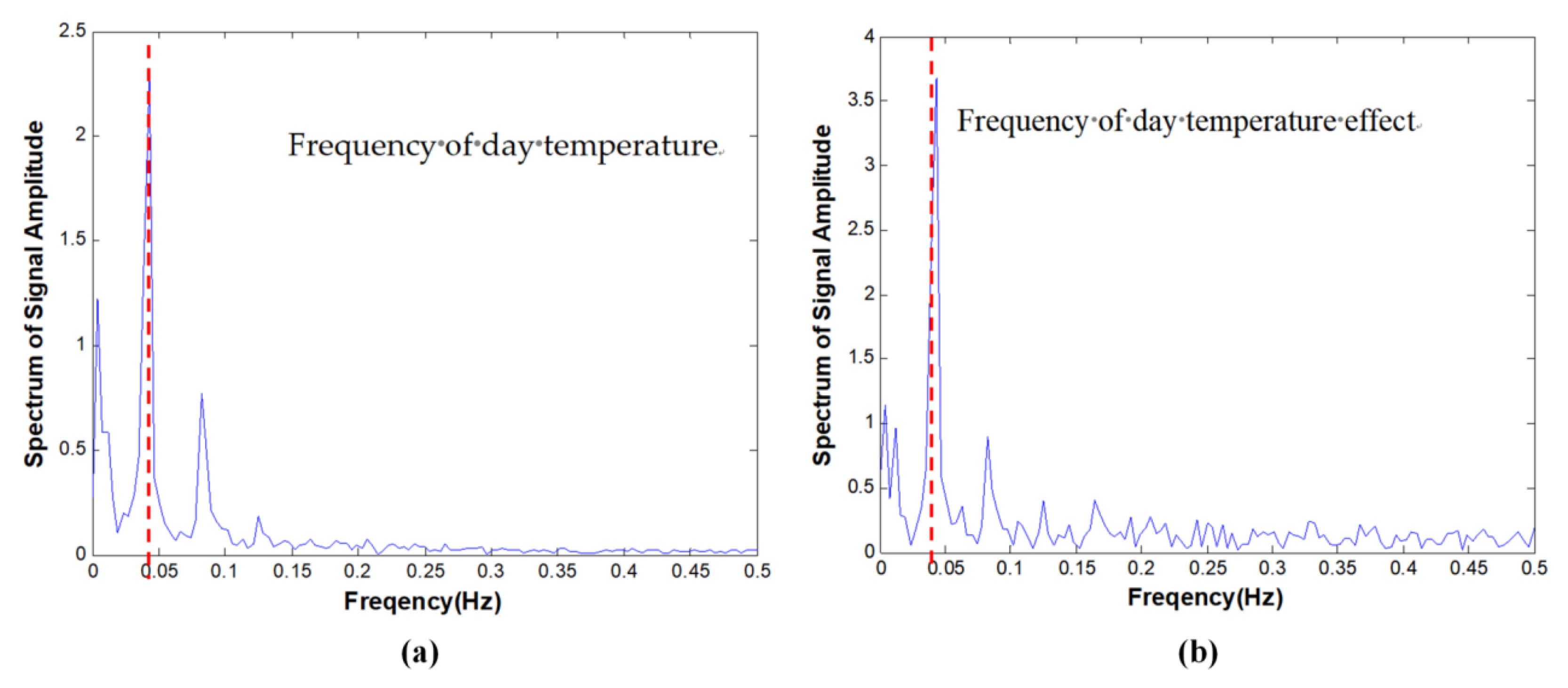

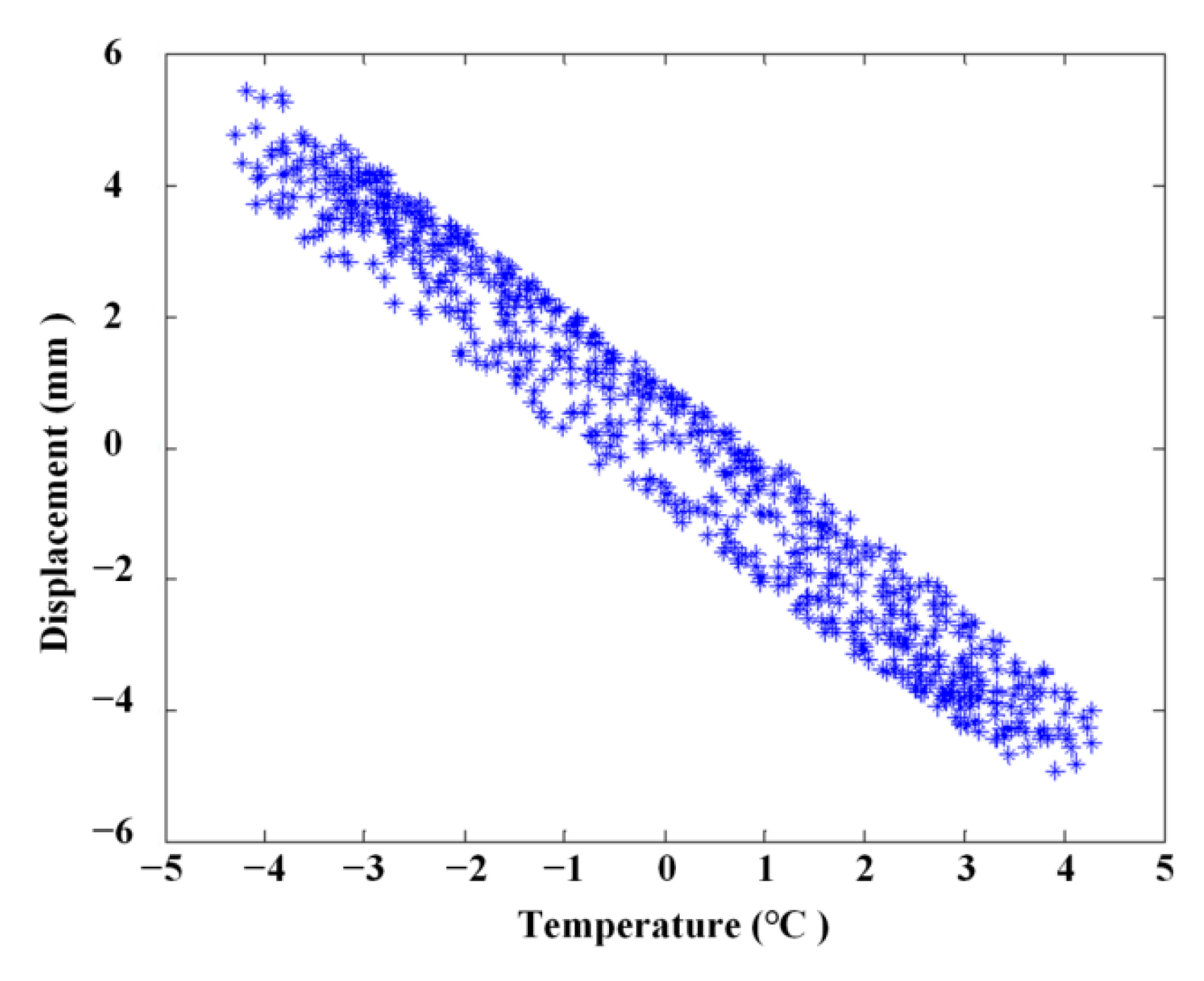
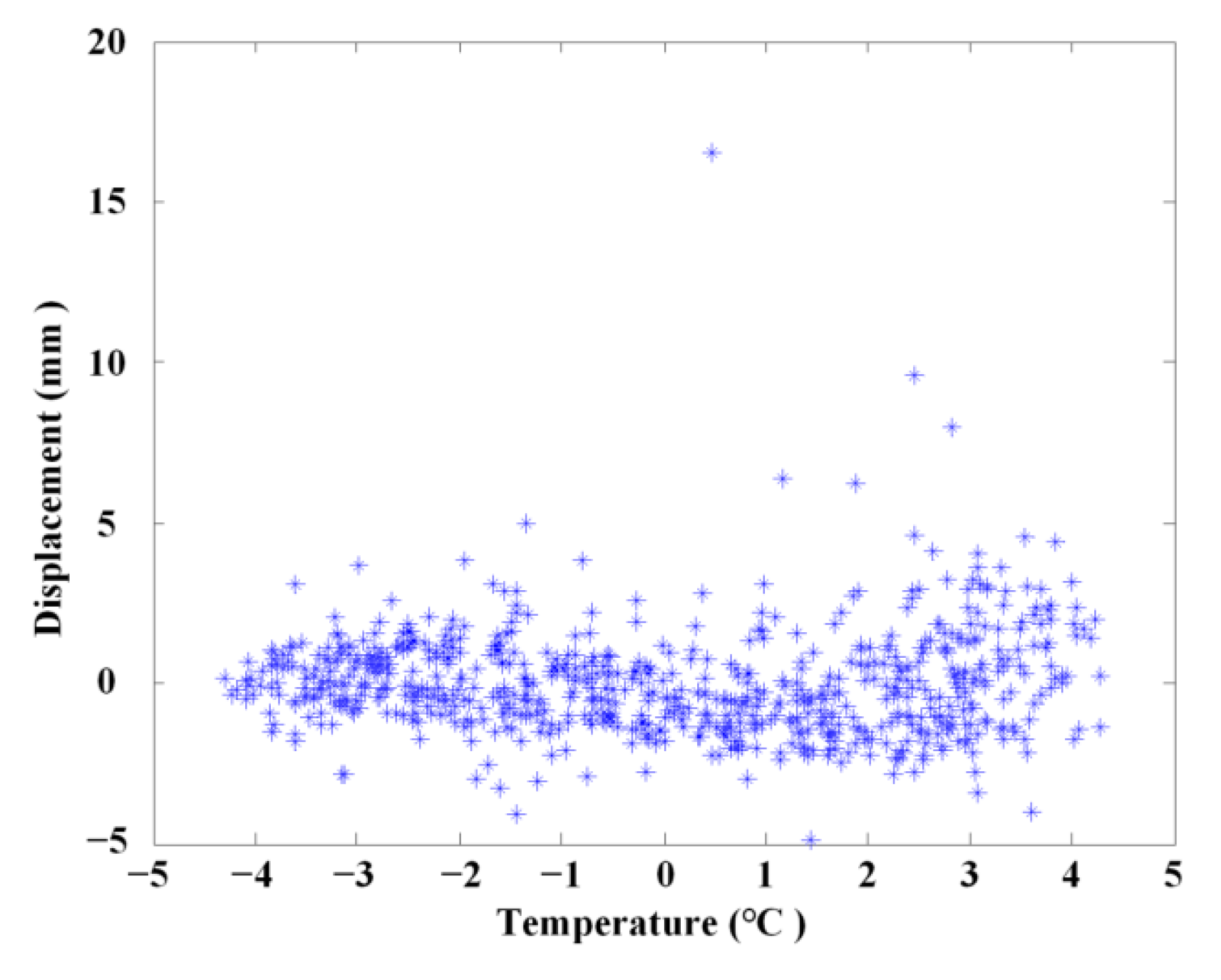
| Six Months | One Year | Two Years | Three Years | |
|---|---|---|---|---|
| No noise | 2.09 × 10−5 | 1.60 × 10−7 | 6.06 × 10−8 | 3.07 × 10−8 |
| With noise | 0.0050 | 0.0043 | 0.0026 | 0.0014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, A.; Liu, G.; Deng, C.; Luo, J. Temperature Effect Separation of Structure Responses from Monitoring Data Using an Adaptive Bandwidth Filter Algorithm. Materials 2024, 17, 465. https://doi.org/10.3390/ma17020465
Hu A, Liu G, Deng C, Luo J. Temperature Effect Separation of Structure Responses from Monitoring Data Using an Adaptive Bandwidth Filter Algorithm. Materials. 2024; 17(2):465. https://doi.org/10.3390/ma17020465
Chicago/Turabian StyleHu, Anqing, Gang Liu, Changjun Deng, and Jun Luo. 2024. "Temperature Effect Separation of Structure Responses from Monitoring Data Using an Adaptive Bandwidth Filter Algorithm" Materials 17, no. 2: 465. https://doi.org/10.3390/ma17020465
APA StyleHu, A., Liu, G., Deng, C., & Luo, J. (2024). Temperature Effect Separation of Structure Responses from Monitoring Data Using an Adaptive Bandwidth Filter Algorithm. Materials, 17(2), 465. https://doi.org/10.3390/ma17020465






