Dynamic Behavior and Energy Absorption of Typical Porous Materials under Impacts
Abstract
:1. Introduction
- (1)
- Investigating the influence of the shape and size of the openings on the deformation form and mechanical response of porous materials;
- (2)
- Explaining the connection between the deformation forms and energy absorption capacity of different porous materials;
- (3)
- Exploring the application value of the characteristics of porous materials (quasi-zero rigidity phenomenon in this study) in the field of energy absorption.
2. Materials and Methods
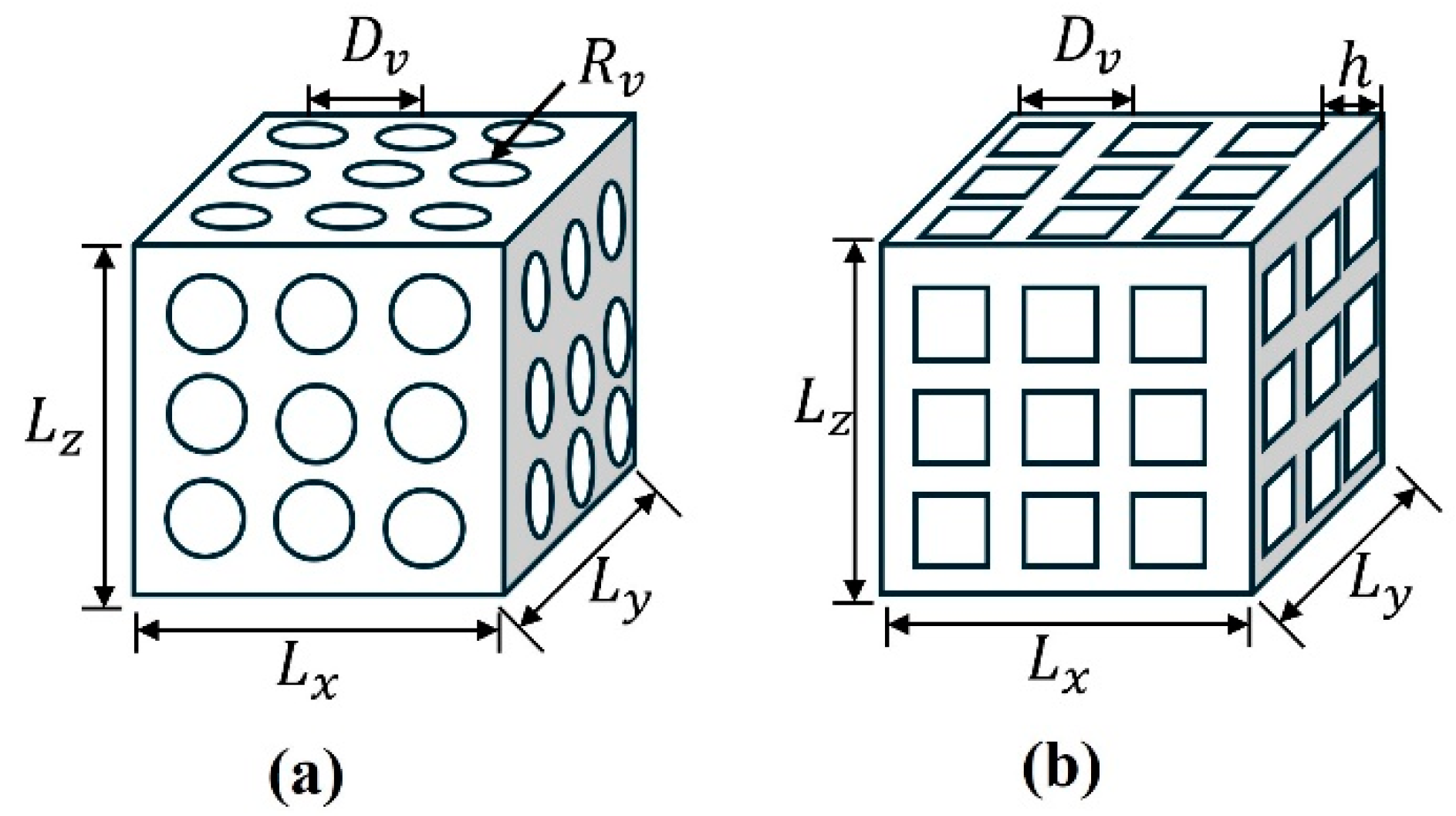
2.1. The Parameters of the Ti-6Al-4V Specimen
2.2. Simulation Calculation Method
3. Results and Discussion
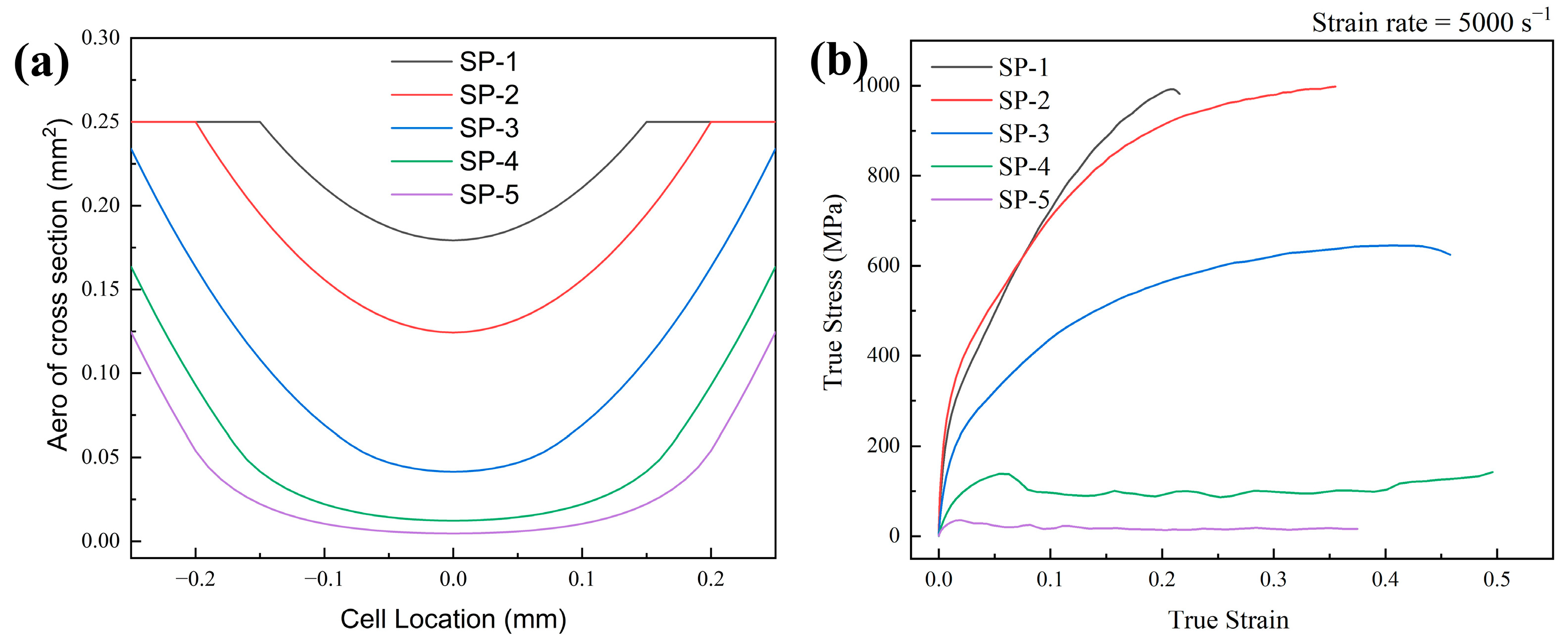
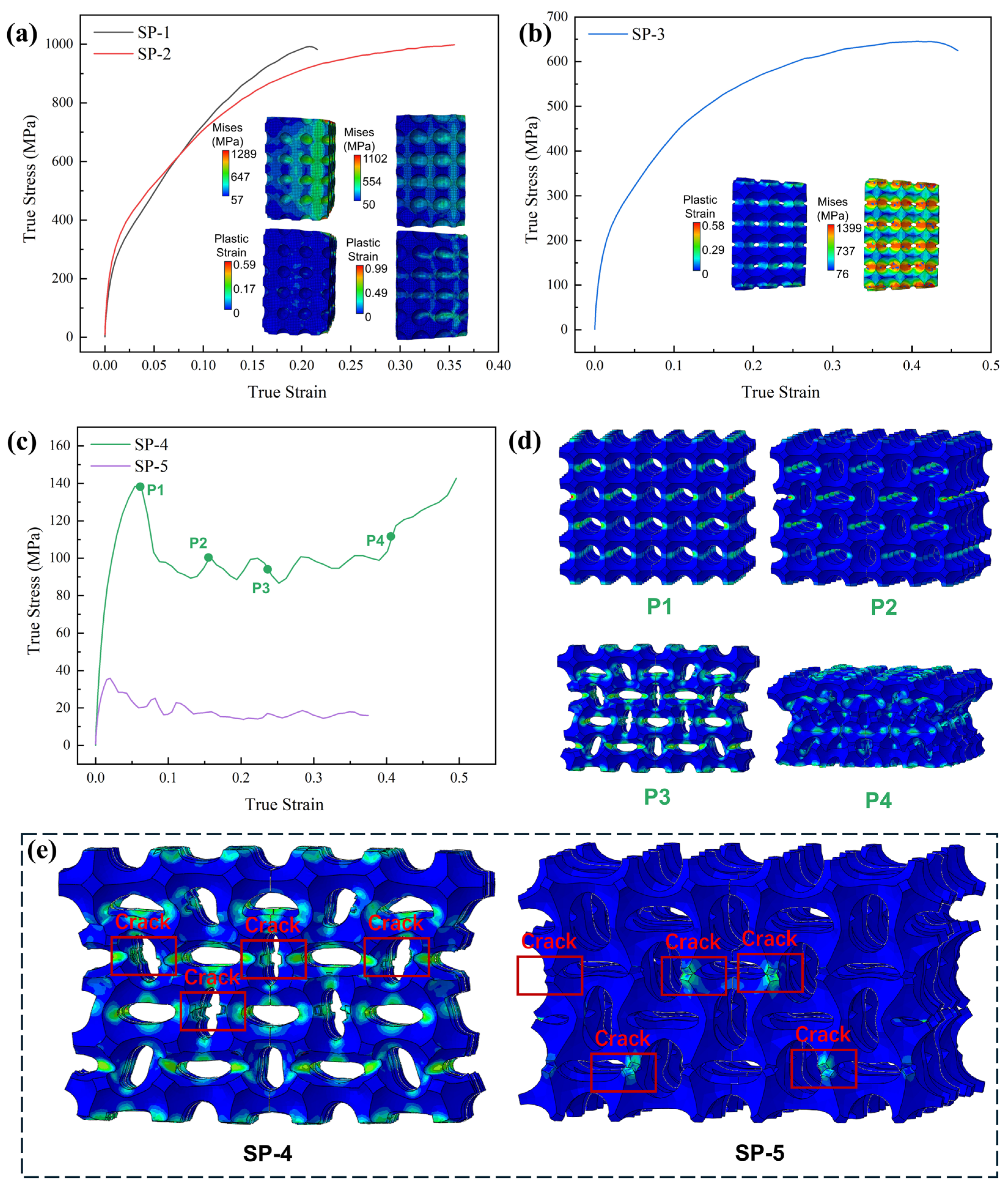
3.1. Dynamic Response of Array Spherical Hole Models
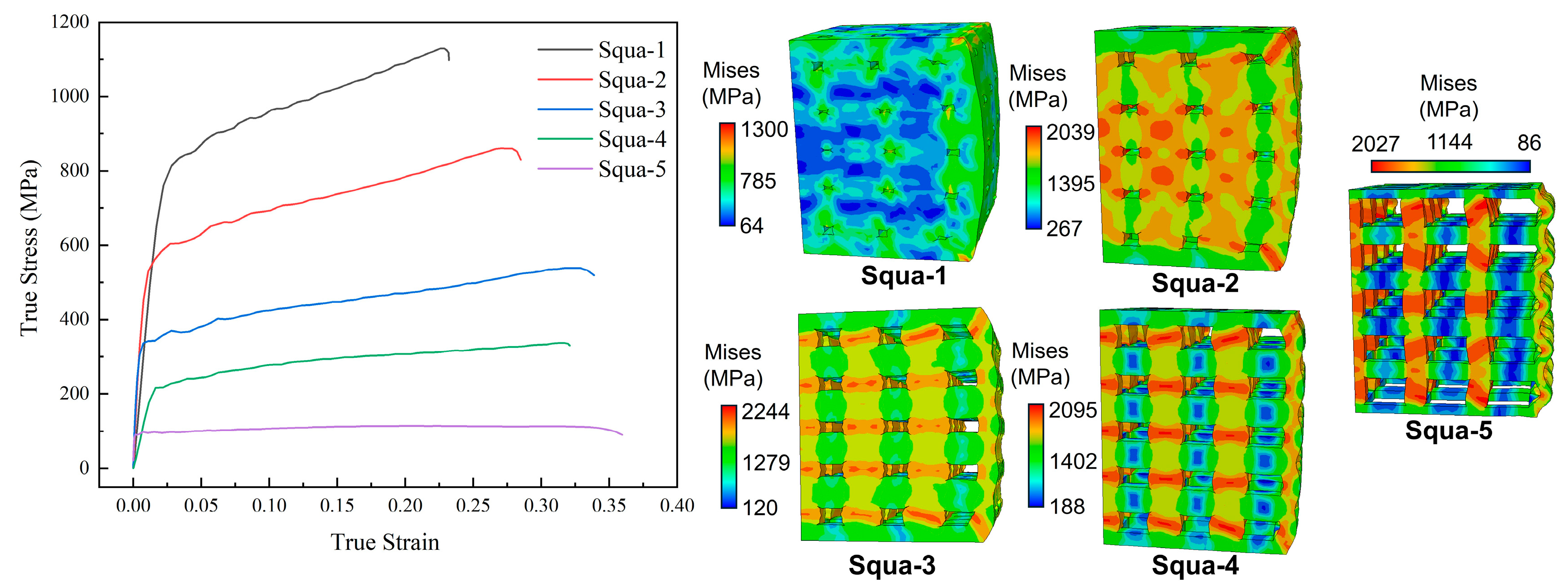
3.2. Dynamic Response of Square Hole Model
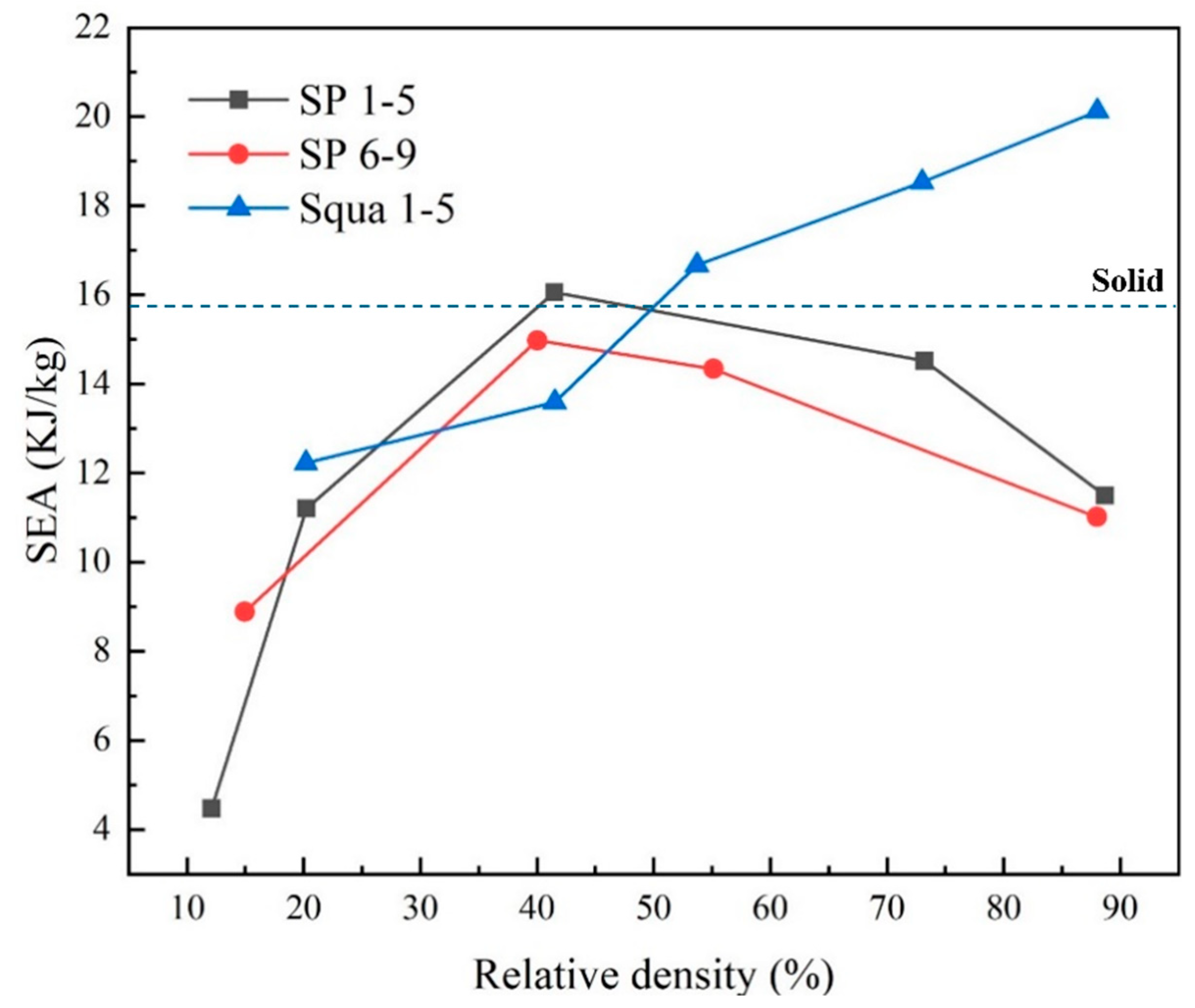
3.3. Energy Absorption Capacity with Relative Density
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Mei, Y.; Peng, J.; Sun, Y. Strength-Induced Peridynamic Model for the Dynamic Failure of Porous Materials. Thin-Walled Struct. 2024, 202, 112064. [Google Scholar] [CrossRef]
- Li, S.; Zhang, H.; Li, S.; Wang, J.; Wang, Q.; Cheng, Z. Advances in Hierarchically Porous Materials: Fundamentals, Preparation and Applications. Renew. Sustain. Energy Rev. 2024, 202, 114641. [Google Scholar] [CrossRef]
- Sun, W.; Ren, S.; Wang, Q.; Che, F.; Lei, Y.; Wang, H.; Zhang, X.; Hou, H.; Zeng, X. Underwater Sound Absorption Characteristics of Water-Saturated Porous Materials. Eur. J. Mech.-A/Solids 2024, 107, 105387. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, X.; Li, Y.; Xie, X.; Hu, J.; Wu, S.; Song, K.; Chu, Q. Full Utilization of Poplar Sawdust with Chemical-Mechanical Pretreatment for Coproduction of Xylooligosaccharides, Fermentable Sugars and Porous Carbon Materials. Ind. Crops Prod. 2024, 214, 118538. [Google Scholar] [CrossRef]
- Costanza, G.; Solaiyappan, D.; Tata, M.E. Properties, Applications and Recent Developments of Cellular Solid Materials: A Review. Materials 2023, 16, 7076. [Google Scholar] [CrossRef]
- Wang, S.; Ding, Y.; Wang, C.; Zheng, Z.; Yu, J. Dynamic Material Parameters of Closed-Cell Foams under High-Velocity Impact. Int. J. Impact Eng. 2017, 99, 111–121. [Google Scholar] [CrossRef]
- Yao, B.; Zhang, Z.; Li, Z.; Liu, M.; Li, H.; Zhu, J.; Wen, T.; Qi, Y. Compressive Properties and Energy Absorption of Selective Laser Melting Formed Ti-6Al-4V Porous Radial Gradient Scaffold. Powder Technol. 2024, 442, 119856. [Google Scholar] [CrossRef]
- Tang, M.; Wang, L.; Xin, Z.; Luo, Z. High Energy Absorption Design of Porous Metals Using Deep Learning. Int. J. Mech. Sci. 2024, 282, 109593. [Google Scholar] [CrossRef]
- Luo, X.; Xu, J.; Bai, E.; Li, W. Study on the Effect of Basalt Fiber on the Energy Absorption Characteristics of Porous Material. Constr. Build. Mater. 2014, 68, 384–390. [Google Scholar] [CrossRef]
- Zhang, X.W.; Zhang, Q.M.; Ren, X.J. Theoretical Study on the Dynamic Compression and Energy Absorption of Porous Materials Filled with Magneto-Rheological Fluid. Int. J. Impact Eng. 2022, 161, 104105. [Google Scholar] [CrossRef]
- Meng, L.; Zhai, X.; Wang, Y. Investigation on Lateral Impact Resistant Performance of Aluminum Foam-Filled 6082-T6 Aluminum Alloy Circular Tubes: Experimental and Numerical Study. Thin-Walled Struct. 2023, 188, 110816. [Google Scholar] [CrossRef]
- Saleem, F.; Li, S.; Cui, S.; Liu, X.; Xu, T.; Mei, L.; Bian, Y.; Miao, C.; Luo, T. The Strain Rate and Density Dependence of the Mechanical Properties of Closed-Cell Aluminum Foam. Mater. Sci. Eng. A 2023, 884, 145568. [Google Scholar] [CrossRef]
- Ejeh, C.J.; Barsoum, I.; Abu Al-Rub, R.K. Impact Behavior of Periodic, Stochastic, and Anisotropic Minimal Surface-Lattice Sandwich Structures. Int. J. Mech. Sci. 2024, 276, 109359. [Google Scholar] [CrossRef]
- Zhang, J.; Kikuchi, N.; Li, V.; Yee, A.; Nusholtz, G. Constitutive Modeling of Polymeric Foam Material Subjected to Dynamic Crash Loading. Int. J. Impact Eng. 1998, 21, 369–386. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A. Isotropic Constitutive Models for Metallic Foams. J. Mech. Phys. Solids 2000, 48, 1253–1283. [Google Scholar] [CrossRef]
- Wang, W.-J.; Zhang, W.-M.; Guo, M.-F.; Yang, H.; Ma, L. Impact Resistance of Assembled Plate-Lattice Auxetic Structures. Compos. Struct. 2024, 338, 118132. [Google Scholar] [CrossRef]
- Song, W.; Feng, G.; Yu, G.; Shi, G.; Xiao, L. Dynamic Mechanical Behavior of Additively Manufactured Bio-Inspired Metallic Lattice Structure Subjected to High Strain Rate Impact Loading. Int. J. Impact Eng. 2023, 181, 104752. [Google Scholar] [CrossRef]
- Zou, S.; Gong, H.; Gao, J. Study on Design and Impact Energy Absorption of Voronoi Porous Structure with Tunable Poisson’s Ratio. Thin-Walled Struct. 2024, 197, 111552. [Google Scholar] [CrossRef]
- Siddique, S.H.; Hazell, P.J.; Wang, H.; Escobedo, J.P.; Ameri, A.A.H. Lessons from Nature: 3D Printed Bio-Inspired Porous Structures for Impact Energy Absorption—A Review. Addit. Manuf. 2022, 58, 103051. [Google Scholar] [CrossRef]
- Yue, L.; Liu, H.; Cheng, Z.; Kan, Q.; Kang, G. Dynamic Crushing Behavior of a Novel Bi-Directional Gradient Lattice Structure under Axial and Oblique Impact Loadings. Thin-Walled Struct. 2024, 198, 111697. [Google Scholar] [CrossRef]
- Kappe, K.; Hoschke, K.; Riedel, W.; Hiermaier, S. Multi-Objective Optimization of Additive Manufactured Functionally Graded Lattice Structures under Impact. Int. J. Impact Eng. 2024, 183, 104789. [Google Scholar] [CrossRef]
- Liu, X.; Qu, J.; Mao, J.; Yao, H. Mechanical Responses and Damage Characteristics of the High-Velocity Impact of Ice Projectiles on Foam Sandwich Structure. Int. J. Impact Eng. 2024, 191, 104994. [Google Scholar] [CrossRef]
- Long, C.; Liu, S.; Sun, R.; Lu, J. Impact of Structural Characteristics on Thermal Conductivity of Foam Structures Revealed with Machine Learning. Comput. Mater. Sci. 2024, 237, 112898. [Google Scholar] [CrossRef]
- Rambabu, S.; Parthasarathy, P.; Ratna Kishore, V. A Numerical Investigation to Determine Longitudinal Dispersion Coefficient in Ideal and Randomized Reticulated Porous Structures Using Transient Direct Pore Level Simulation. Chem. Eng. Sci. 2023, 274, 118664. [Google Scholar] [CrossRef]
- McDonnell, B.; O’Hara, E.M.; Harrison, N.M. Simulation-Driven-Design of Metal Lattice Structures for a Target Stress–Strain Curve. Mater. Des. 2024, 237, 112543. [Google Scholar] [CrossRef]
- Watanabe, T.; Ishikawa, S.; Kawashima, M.; Shimoyama, K.; Onodera, N.; Hasegawa, Y.; Inagaki, A. Structure of Drifting Snow Simulated by Lagrangian Particle Dispersion Model Coupled with Large-Eddy Simulation Using the Lattice Boltzmann Method. J. Wind Eng. Ind. Aerodyn. 2024, 250, 105783. [Google Scholar] [CrossRef]
- Hu, H.; Wang, W.; Ning, H.; Liu, B. Numerical Simulation and Experimental Study on the Compression Performance of a Double Layer Cross-Lattice-Core Sandwich Structure. Structures 2024, 64, 106531. [Google Scholar] [CrossRef]
- Yuan, L.; Xu, S.; Chen, M.; Xie, Y.; Lu, J.; Wang, P. Stress Wave in the Mesoscopic Discontinuous Medium by Fractional Approach. Int. J. Mech. Sci. 2024, 272, 109197. [Google Scholar] [CrossRef]
- Caputo, M.; Mainardi, F. Linear Models of Dissipation in Anelastic Solids. Riv. Nuovo Cimento 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Rezasefat, M.; Giglio, M.; Manes, A. Numerical Investigation of the Effect of Open Holes on the Impact Response of CFRP Laminates. Appl. Compos. Mater. 2022, 29, 1555–1578. [Google Scholar] [CrossRef]
- Li, L.; Tang, H.; Hu, Y. Size-Dependent Nonlinear Vibration of Beam-Type Porous Materials with an Initial Geometrical Curvature. Compos. Struct. 2018, 184, 1177–1188. [Google Scholar] [CrossRef]
- Chen, X.; Chen, L.; Lu, Y. Imperfection Sensitivity of Nonlinear Primary Resonance Behavior in Bi-Directional Functionally Graded Porous Material Beam. Compos. Struct. 2021, 271, 114142. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Y.; Cao, X.; Xu, J.; Yao, L. A Slice Model for Thermoelastic Analysis of Porous Functionally Graded Material Sandwich Beams with Temperature-Dependent Material Properties. Thin-Walled Struct. 2024, 198, 111700. [Google Scholar] [CrossRef]
- Xu, C.; Gu, X.; Mao, Y.; Wang, C. Experimental Studies on Simultaneously Reducing Flow Drag and Noise of a Circular Cylinder with a Downstream Porous Material Plate. Exp. Therm. Fluid Sci. 2024, 155, 111209. [Google Scholar] [CrossRef]
- Shou, H.; Hoang, V.N.V.; Shi, P. Thermal Vibration Analysis of Bi-Directionally Stepped Porous Functionally Graded Plates with Segment-Specific Material Property Variation Supported by Kerr Foundation. Thin-Walled Struct. 2024, 204, 112239. [Google Scholar] [CrossRef]
- Liu, X. Dynamic Constitutive Relationship of TC4 Titanium Alloy; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2010. [Google Scholar]
- Xiang, X.; Xiao, C.; Lu, G.; Xie, Y.M.; Yang, H.; Zhang, J.; Ha, N.S. Novel Interaction Effects Enhance Specific Energy Absorption in Foam-Filled CFRP Tapered Tubes. Compos. Struct. 2024, 343, 118288. [Google Scholar] [CrossRef]
- Lv, H.; Shi, S.; Chen, B.; Liu, Z. Low-Velocity Impact Performance of Orthogonal Grid Reinforced CFRP-Foam Sandwich Structure. Thin-Walled Struct. 2023, 193, 111236. [Google Scholar] [CrossRef]
- Wan, L.; Hu, D.; Zhang, H.; Yang, Z. Energy Absorption of Foam-Filled TPMS-Based Tubular Lattice Structures Subjected to Quasi-Static Lateral Crushing. Eng. Struct. 2024, 316, 118581. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, B.; Xian, G.; Xin, M.; Huang, S.; Shen, H. Quasi-Static and Low-Velocity Impact Behaviors of Steel-Aluminum Foam Sandwich Beams. Structures 2024, 64, 106549. [Google Scholar] [CrossRef]




| A (MPa) | B (MPa) | n | C | m | D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|---|---|---|---|---|
| 1077 | 845 | 0.58 | 0.025 | 0.7538 | 0.0395 | 1.0072 | 1.9234 | 0.014 | 3.87 |
(GPa) | Poisson’s Ratio | |
|---|---|---|
| 4500 | 110 | 0.3 |
| Case | (mm) | (mm) | (mm) | Volume | Relative Density (%) |
|---|---|---|---|---|---|
| SP-1 | 3, 3, 2.5 | 0.5 | 0.150 | 20.0 | 88.70 |
| SP-2 | 3, 3, 2.5 | 0.5 | 0.200 | 16.5 | 73.21 |
| SP-3 | 3, 3, 2.5 | 0.5 | 0.260 | 9.34 | 41.51 |
| SP-4 | 3, 3, 2.5 | 0.5 | 0.300 | 4.55 | 20.22 |
| SP-5 | 3, 3, 2.5 | 0.5 | 0.320 | 2.72 | 12.11 |
| SP-6 | 3, 3, 2.5 | 0.4 | 0.150 | 19.8 | 88.00 |
| SP-7 | 3, 3, 2.5 | 0.4 | 0.190 | 12.4 | 55.14 |
| SP-8 | 3, 3, 2.5 | 0.4 | 0.210 | 9.01 | 40.03 |
| SP-9 | 3, 3, 2.5 | 0.4 | 0.250 | 3.36 | 14.95 |
| Squa-1 | 3, 3, 2.5 | 0.5 | 0.196 | 19.8 | 88.02 |
| Squa-2 | 3, 3, 2.5 | 0.5 | 0.165 | 16.4 | 73.02 |
| Squa-3 | 3, 3, 2.5 | 0.5 | 0.131 | 12.1 | 53.72 |
| Squa-4 | 3, 3, 2.5 | 0.5 | 0.111 | 9.34 | 41.52 |
| Squa-5 | 3, 3, 2.5 | 0.5 | 0.072 | 4.55 | 20.20 |
| Mesh Size (mm) | Maximum Stress (MPa) | Relative Error (%) |
|---|---|---|
| 0.03 | 2095.08 | 0 |
| 0.04 | 2139.73 | 2.13 |
| 0.05 | 2189.29 | 4.50 |
| 0.07 | 1304.19 | 9.98 |
| 0.10 | 2526.74 | 20.6 |
| Case | Solid | SP | Squa |
|---|---|---|---|
| 6.14 | 13.79 | 9.56 |
| Case | Material | SEA (kJ/kg) | Comparison |
|---|---|---|---|
| This Work | Ti-6Al-4V | 19.8 | |
| Hangyu Lv 2023 | CFRP | 0.72 | low-velocity impact |
| Liang Wan 2024 | 316L | 17.8 | quasi-static lateral crushing |
| Zhen Wang 2024 | aluminum foam | 0.43 | quasi-static |
| Lei Yue 2024 | Nylon | 5.3 | low-velocity axial impact |
| Konstantin Kappe 2024 | Al-Sc-Mg alloy | 9.4 | Multi-objective optimization; low-velocity axial impact |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, K.; Li, M.; Shen, J. Dynamic Behavior and Energy Absorption of Typical Porous Materials under Impacts. Materials 2024, 17, 5035. https://doi.org/10.3390/ma17205035
Xie K, Li M, Shen J. Dynamic Behavior and Energy Absorption of Typical Porous Materials under Impacts. Materials. 2024; 17(20):5035. https://doi.org/10.3390/ma17205035
Chicago/Turabian StyleXie, Kui, Menglong Li, and Jianghua Shen. 2024. "Dynamic Behavior and Energy Absorption of Typical Porous Materials under Impacts" Materials 17, no. 20: 5035. https://doi.org/10.3390/ma17205035
APA StyleXie, K., Li, M., & Shen, J. (2024). Dynamic Behavior and Energy Absorption of Typical Porous Materials under Impacts. Materials, 17(20), 5035. https://doi.org/10.3390/ma17205035







