Research on Safety of Aero-Engine Oil Pipe Under Heating Conditions Based on Fluid–Solid Thermal Coupling
Abstract
:1. Introduction
2. Computational Models, Methods, and Mesh
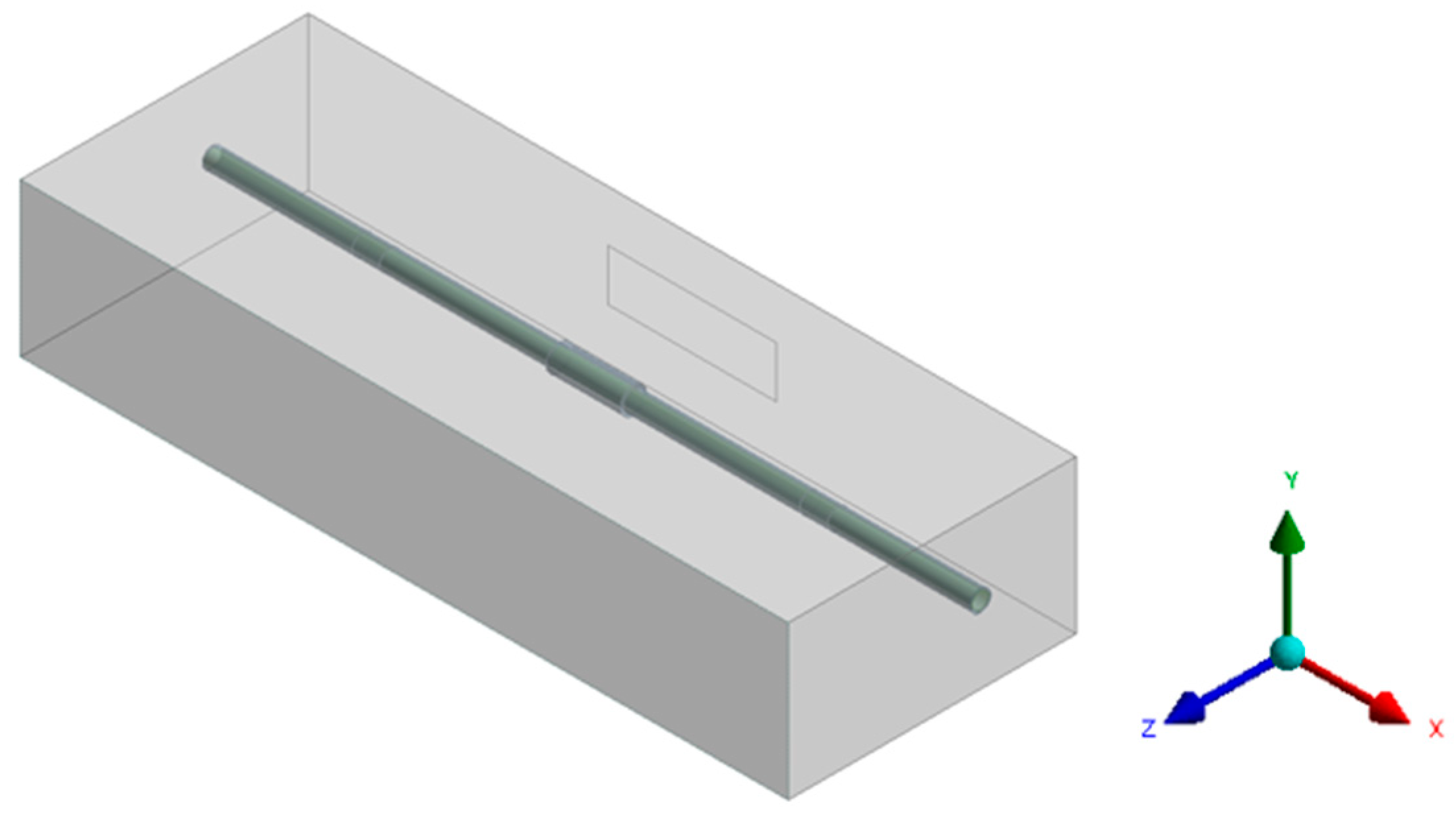
2.1. Computational Domain Models
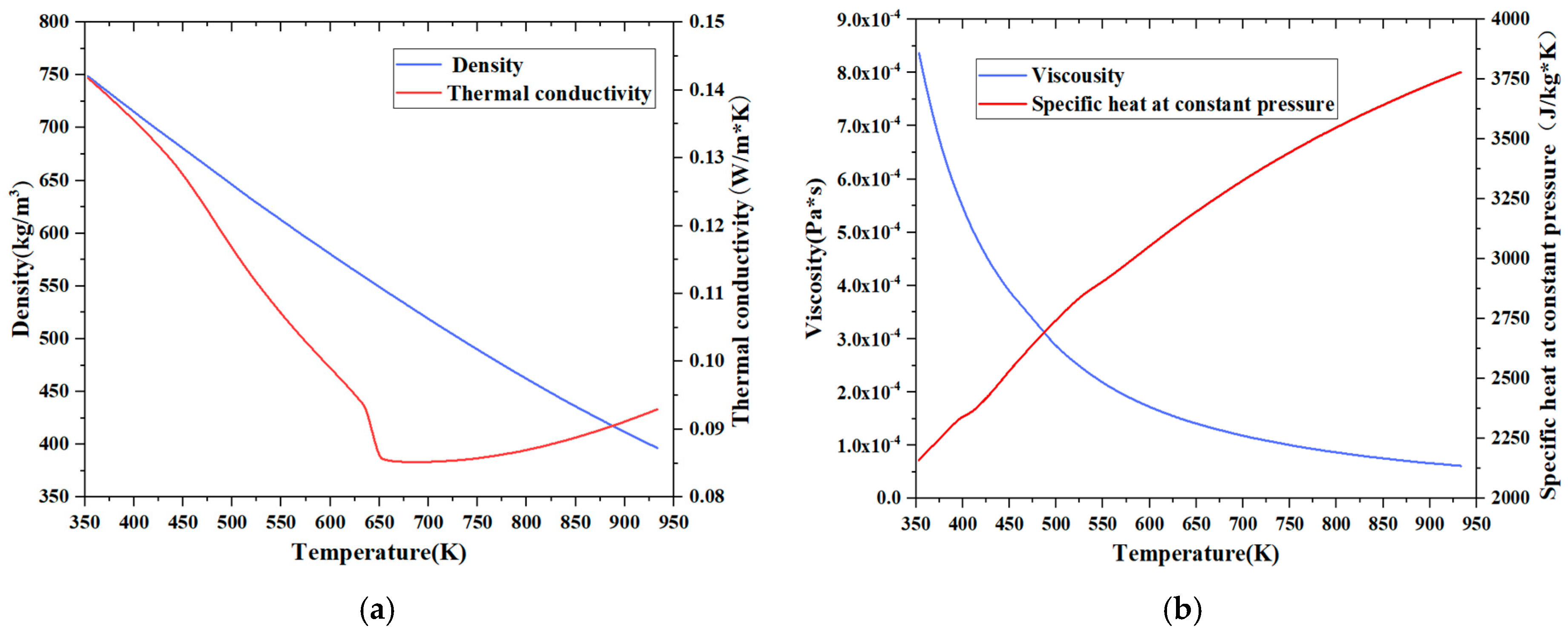
2.2. Pipe Materials and Fluid
2.3. Computational Methods
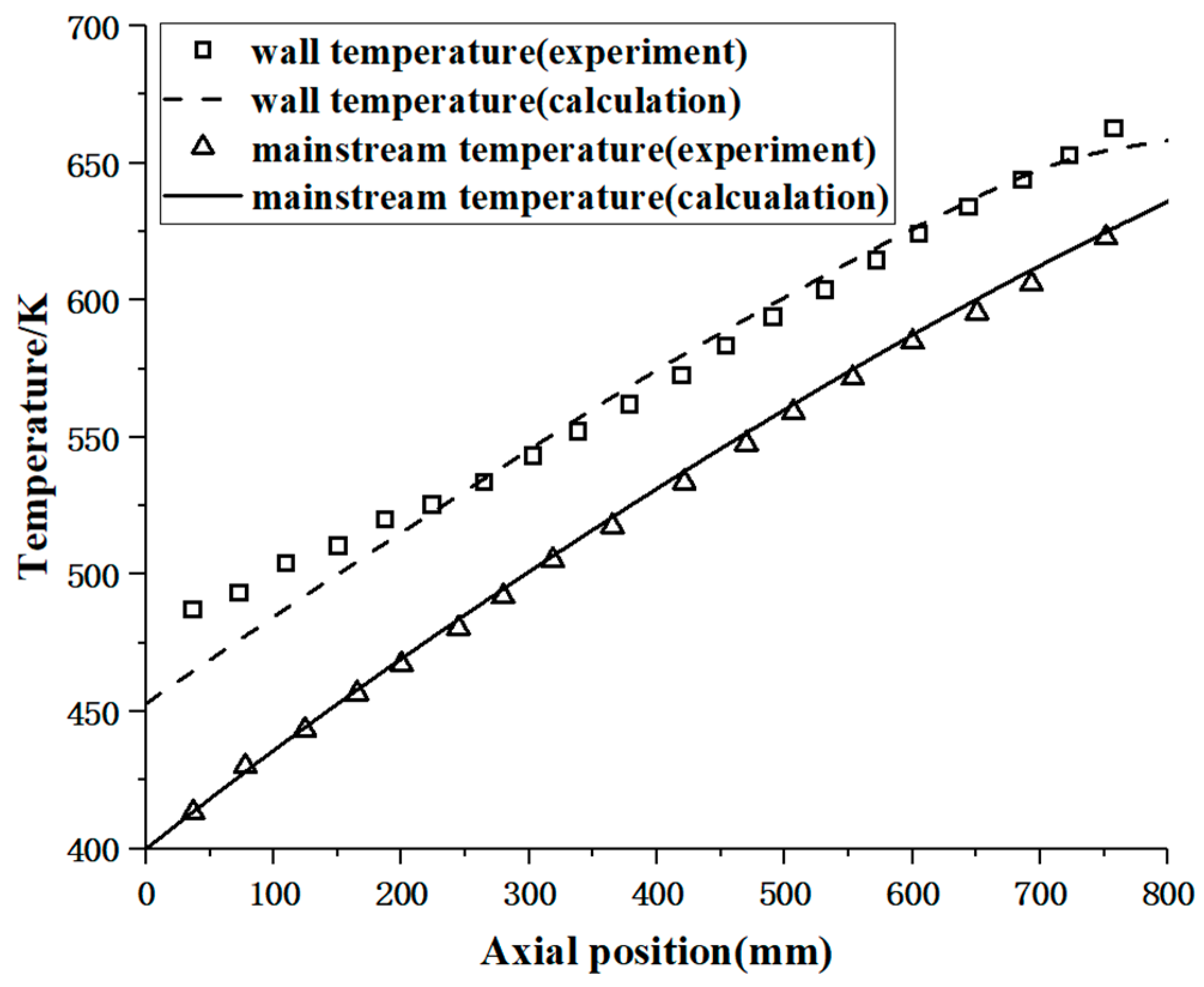
2.4. Validation of the Computational Method
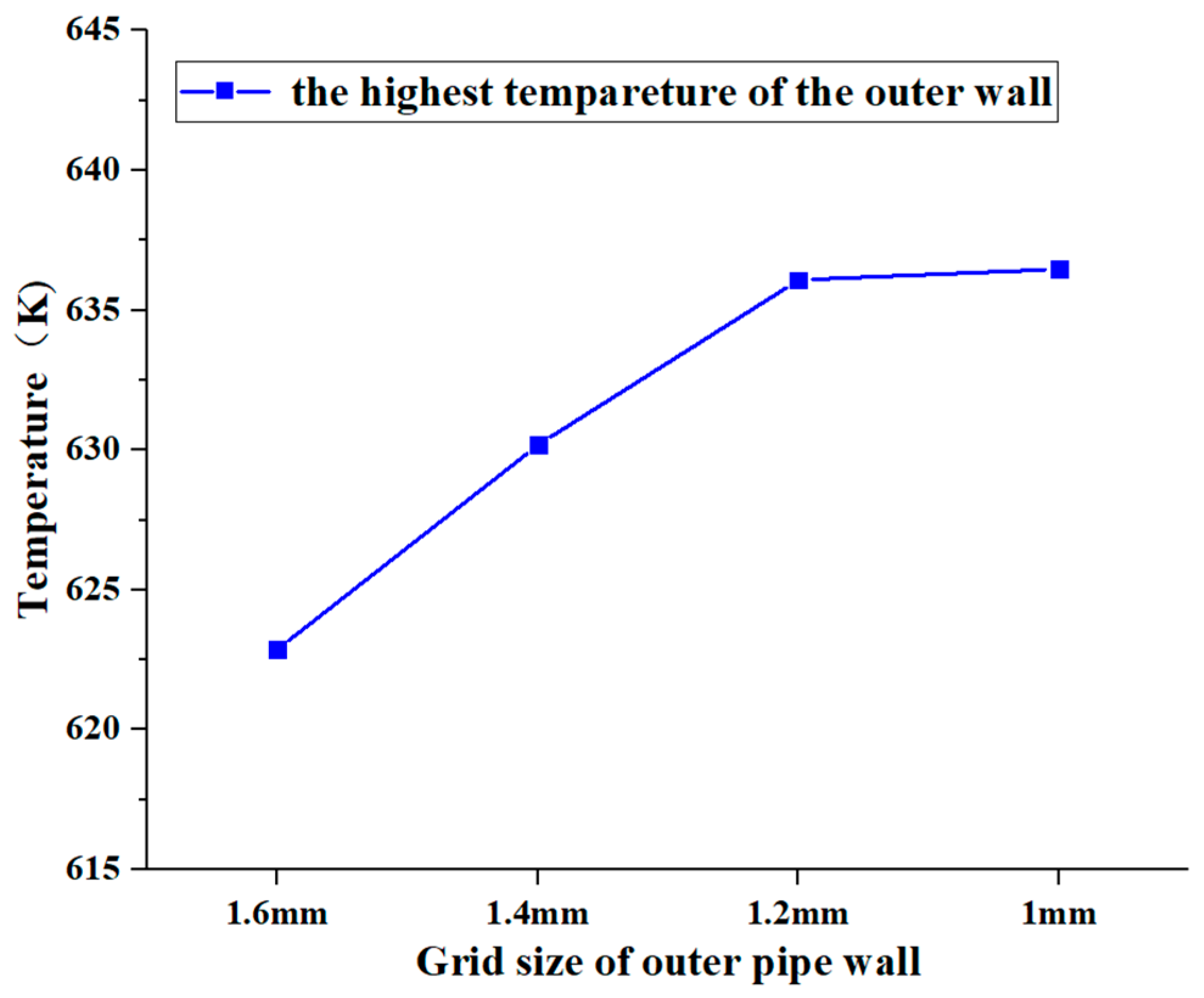
2.5. Mesh
3. Fluid–Solid Thermal Coupling Calculations
3.1. Boundary and Working Conditions
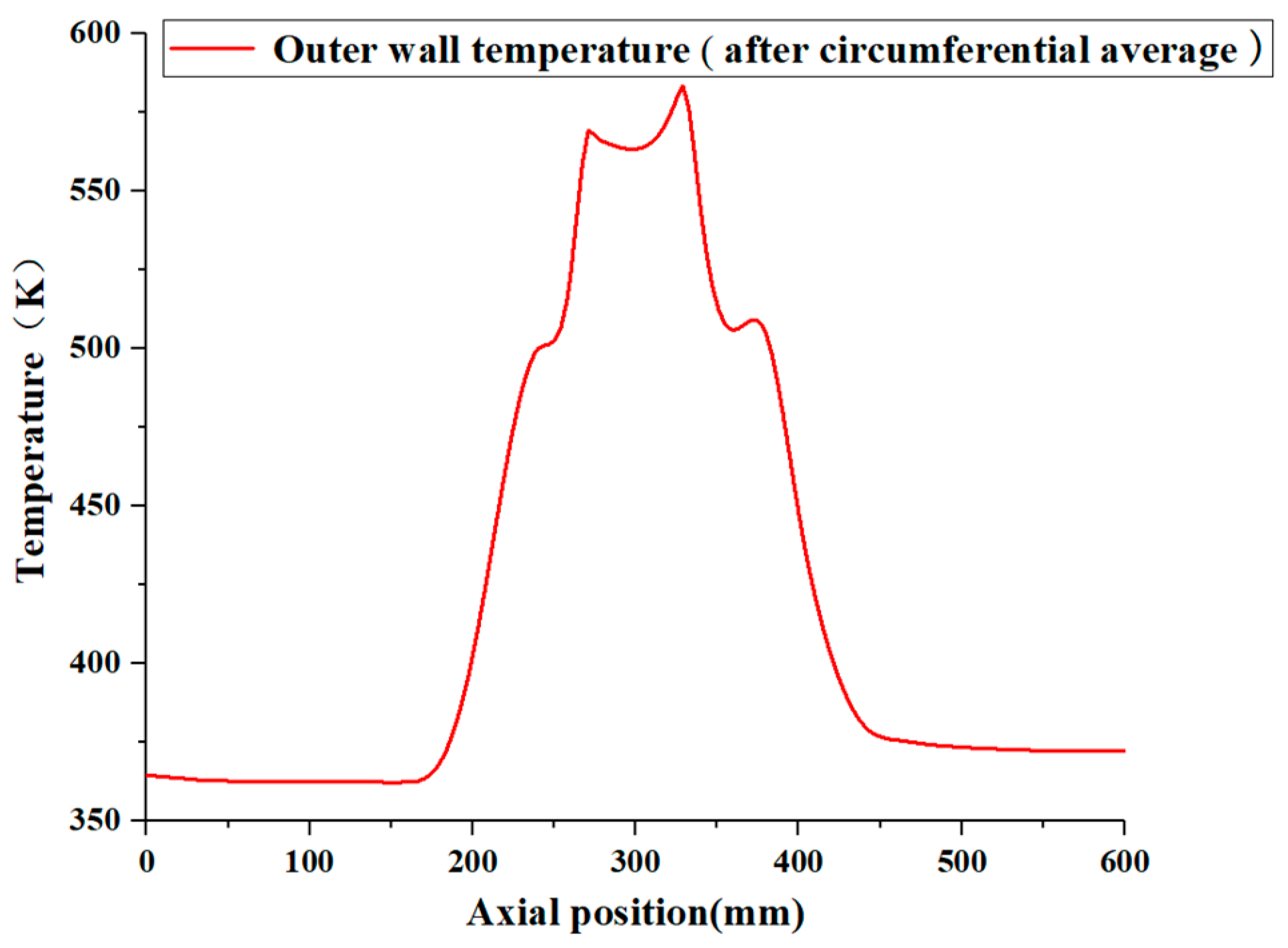
3.2. Analysis of Calculation Results under 5.07 L/Min Flow Condition
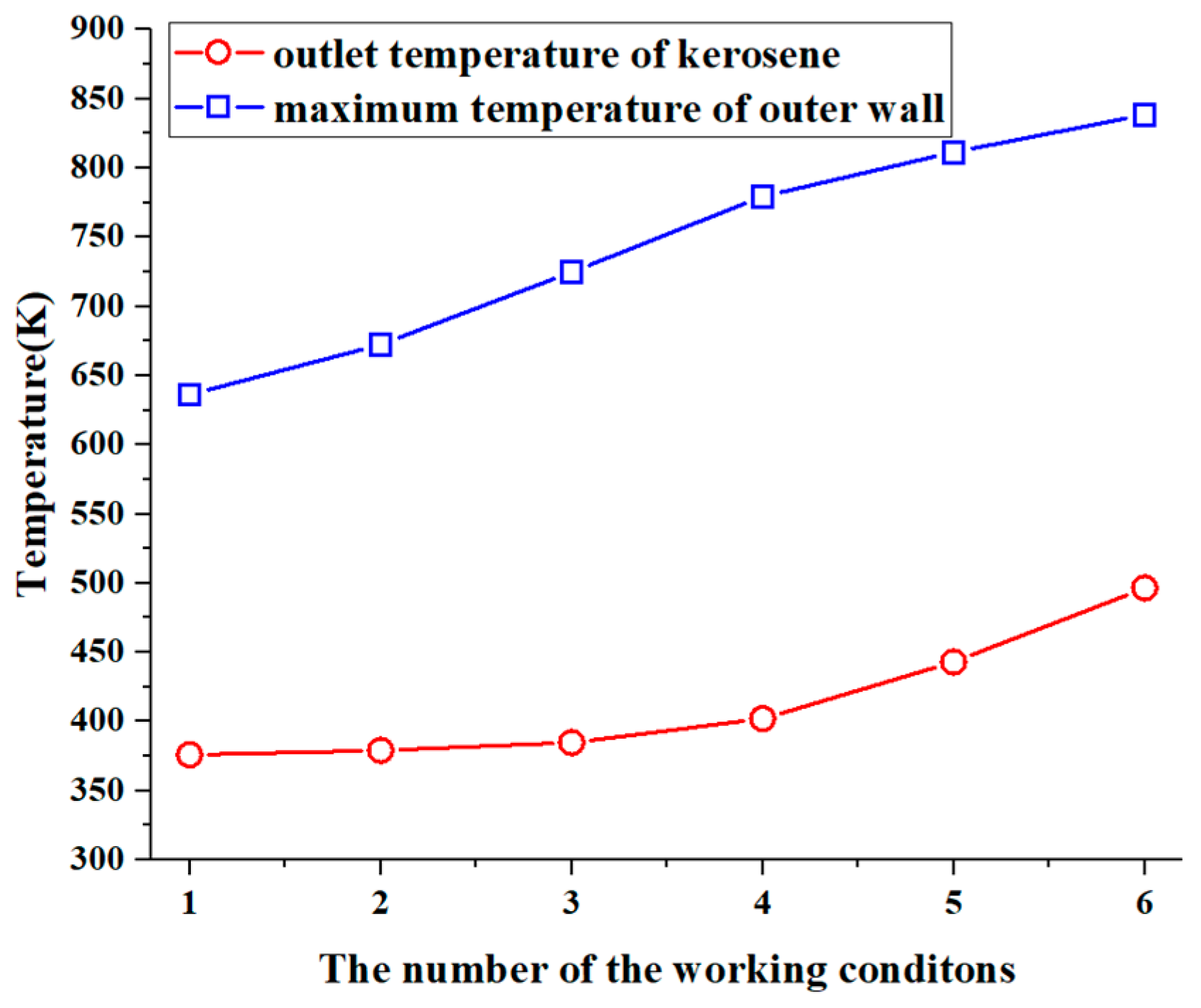
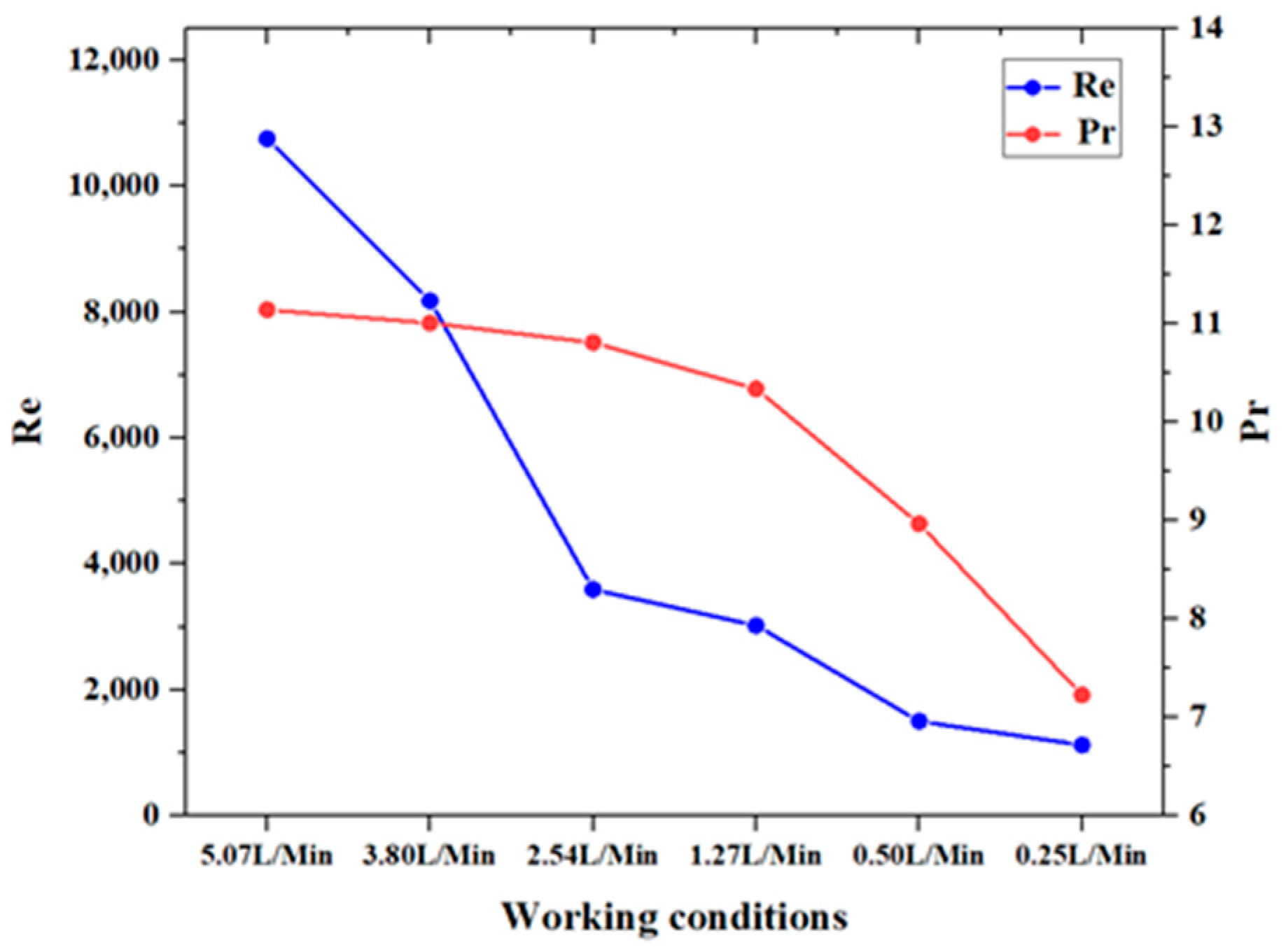
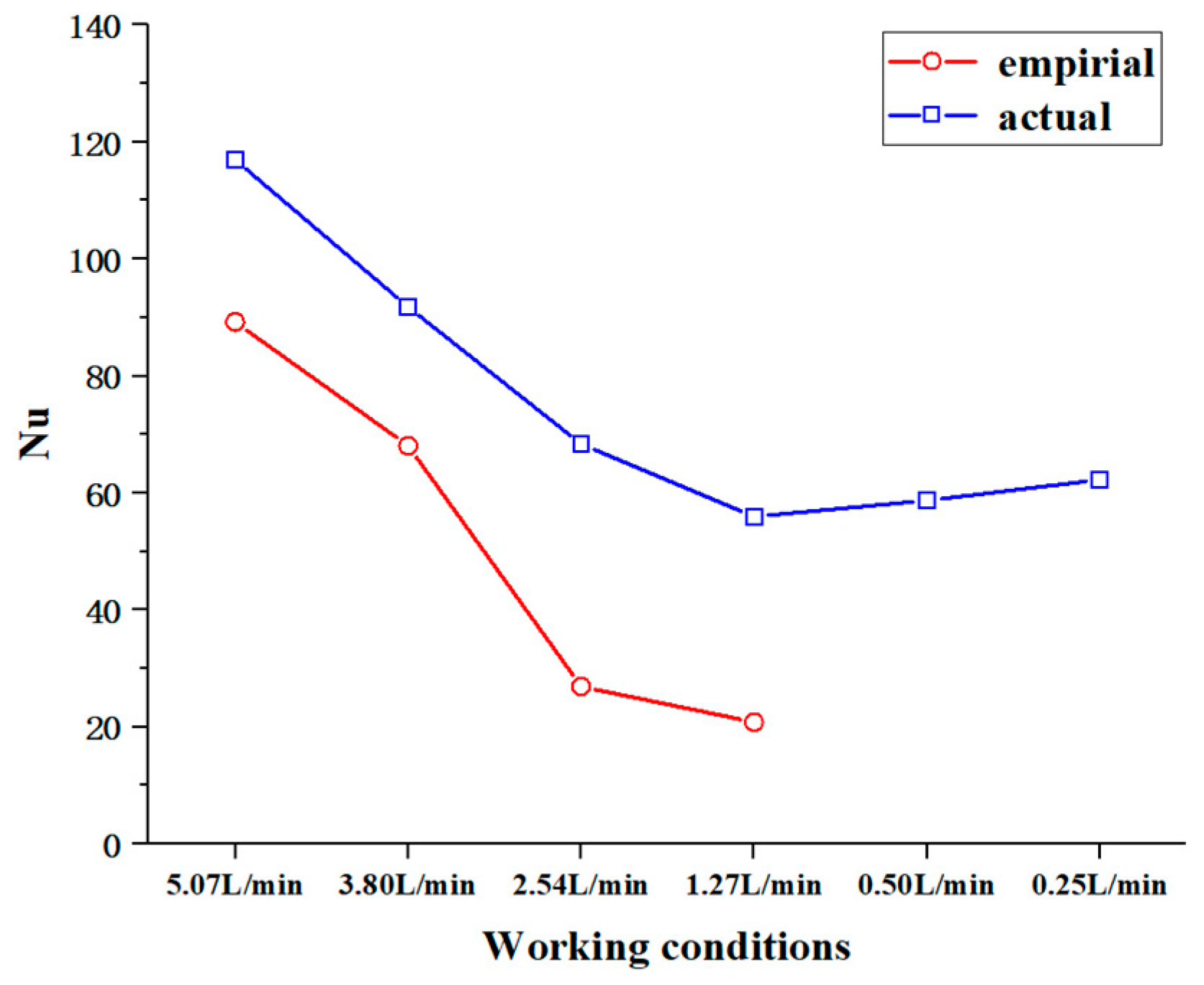
3.3. Effect of Kerosene Inlet Flow on Convective Heat Transfer
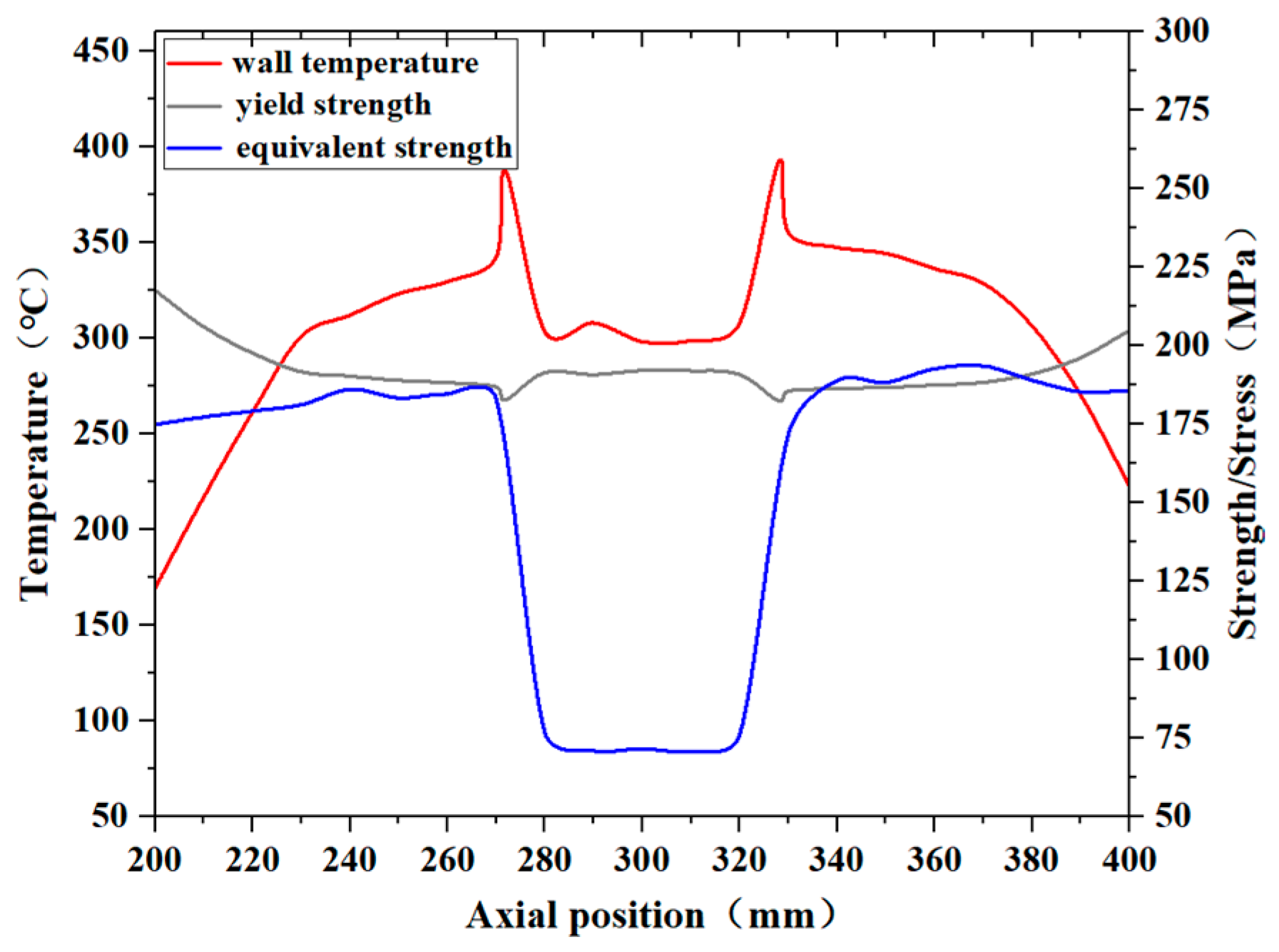
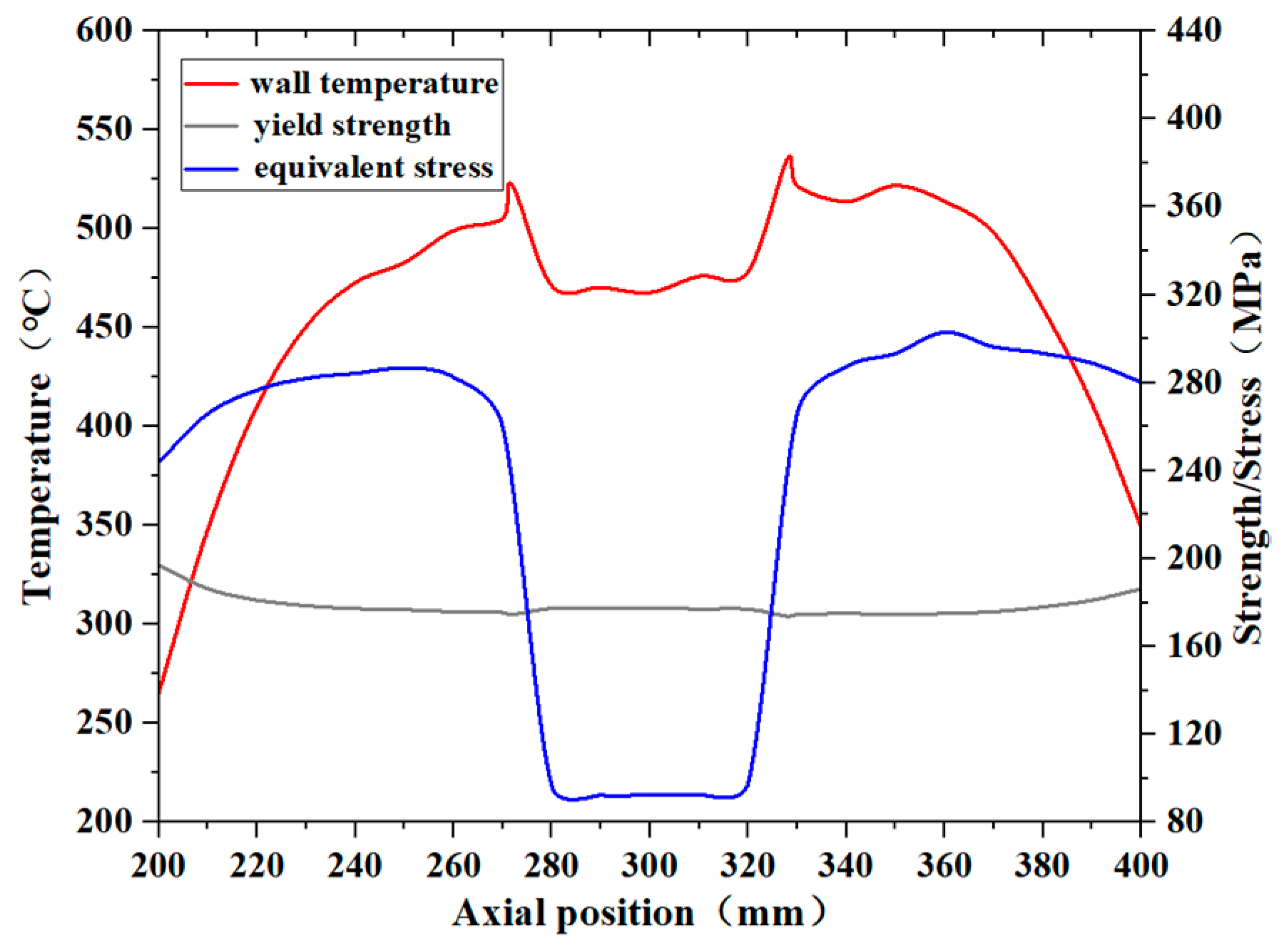
4. Pipe Stress Calculation and Safety Analysis
5. Conclusions
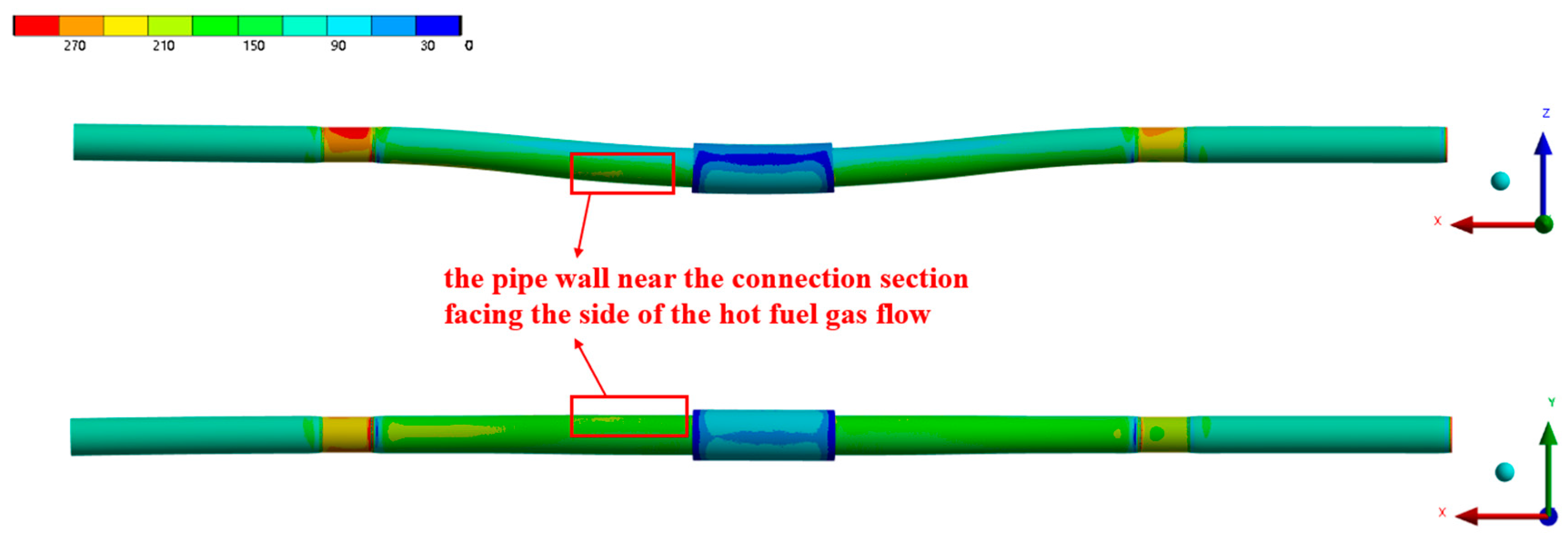
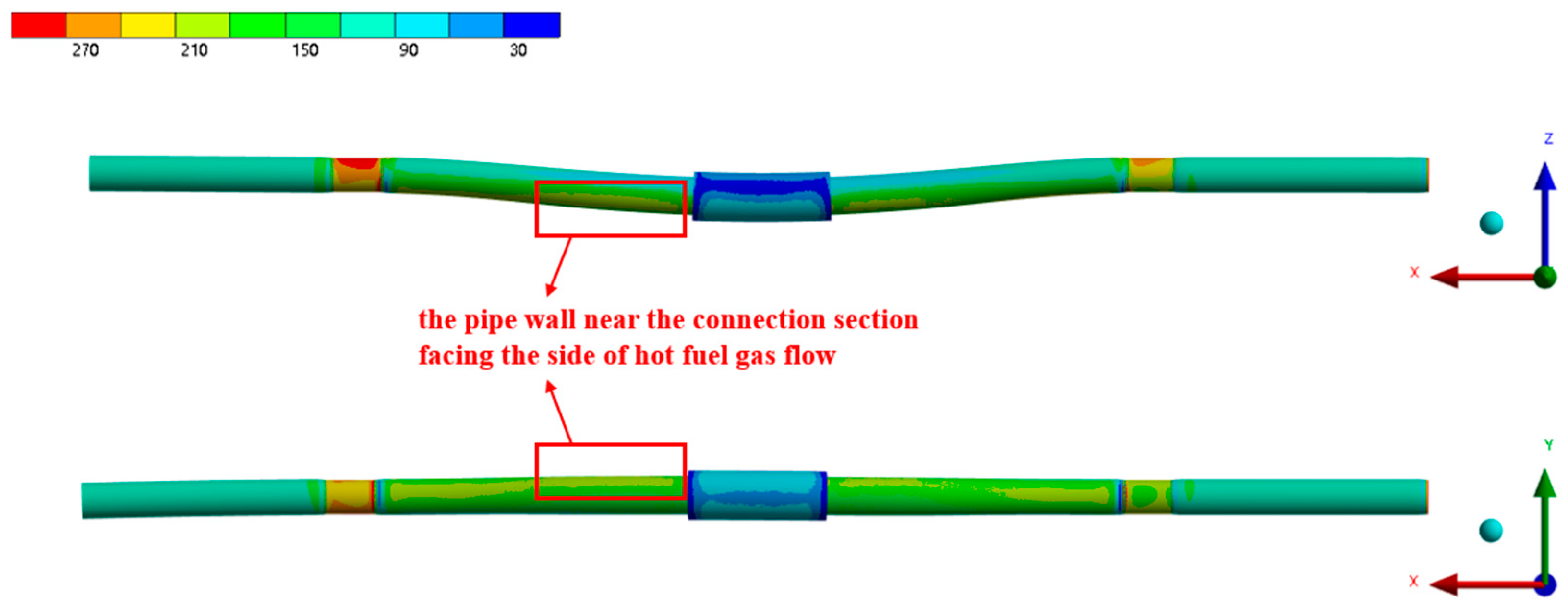
- Under the heating conditions specified in the fire test standard, the pipe wall temperature exhibited a three-layer stepped distribution along the axial direction, with higher temperatures in the middle and lower temperatures on both sides. The temperature rise between the first and second layers was primarily influenced by the lateral sweep of the hot flue gas, while the increase between the second and third layers was mainly due to the expansion of the heating surface area. The temperature distribution of the outer wall in the circumferential direction was also uneven, which generated thermal stress and, consequently, raised the risk of pipe wall rupture.
- As the kerosene flow rate decreased, both the pipe wall temperature and the kerosene outlet temperature increased, while the heat transfer coefficient between the kerosene and the pipe wall exhibited an overall decline. This suggests a deterioration in the heat transfer efficiency. However, when the flow rate was decreased further, the effect of the changes in the thermophysical properties of the kerosene due to the temperature rise became significant. At this point, the heat transfer coefficient between the kerosene and the pipe wall no longer decreased significantly with the flow rate. The Reynolds and Prandtl numbers for the middle section of the pipe indicated significant changes in the flow characteristics and thermophysical properties of the kerosene, while the Nusselt number indicated that the calculated actual Nusselt number was greater than that obtained from the empirical formula. This suggests that the changes in the thermophysical properties of the supercritical kerosene significantly influenced its heat transfer behavior.
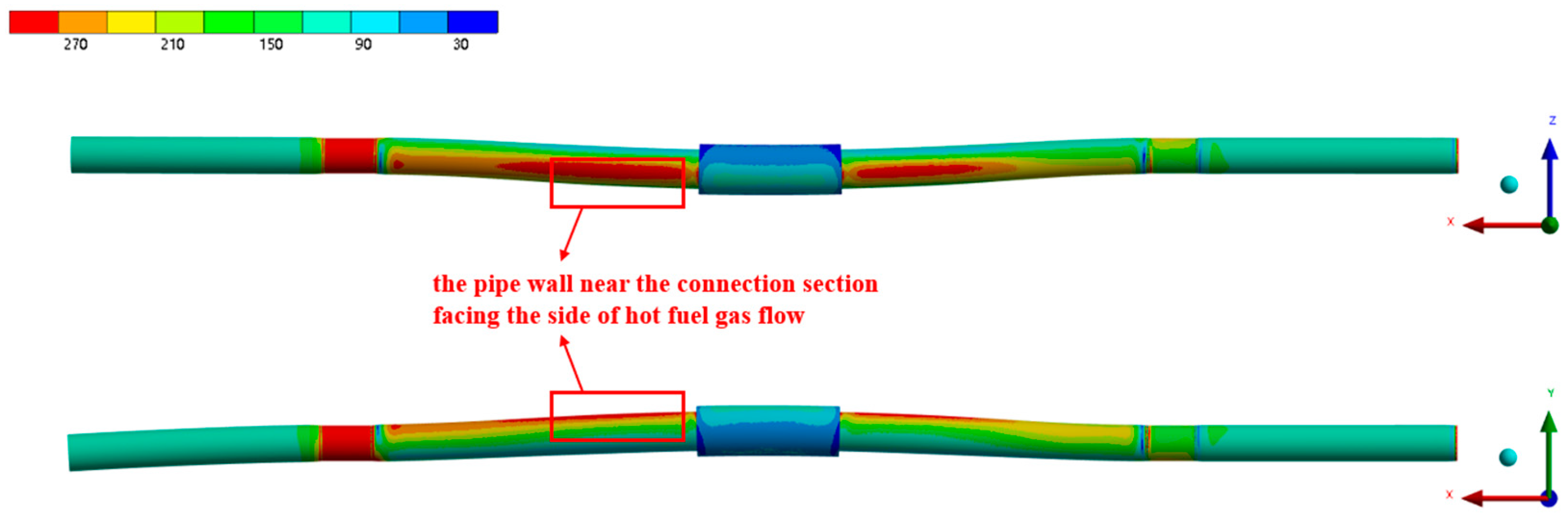
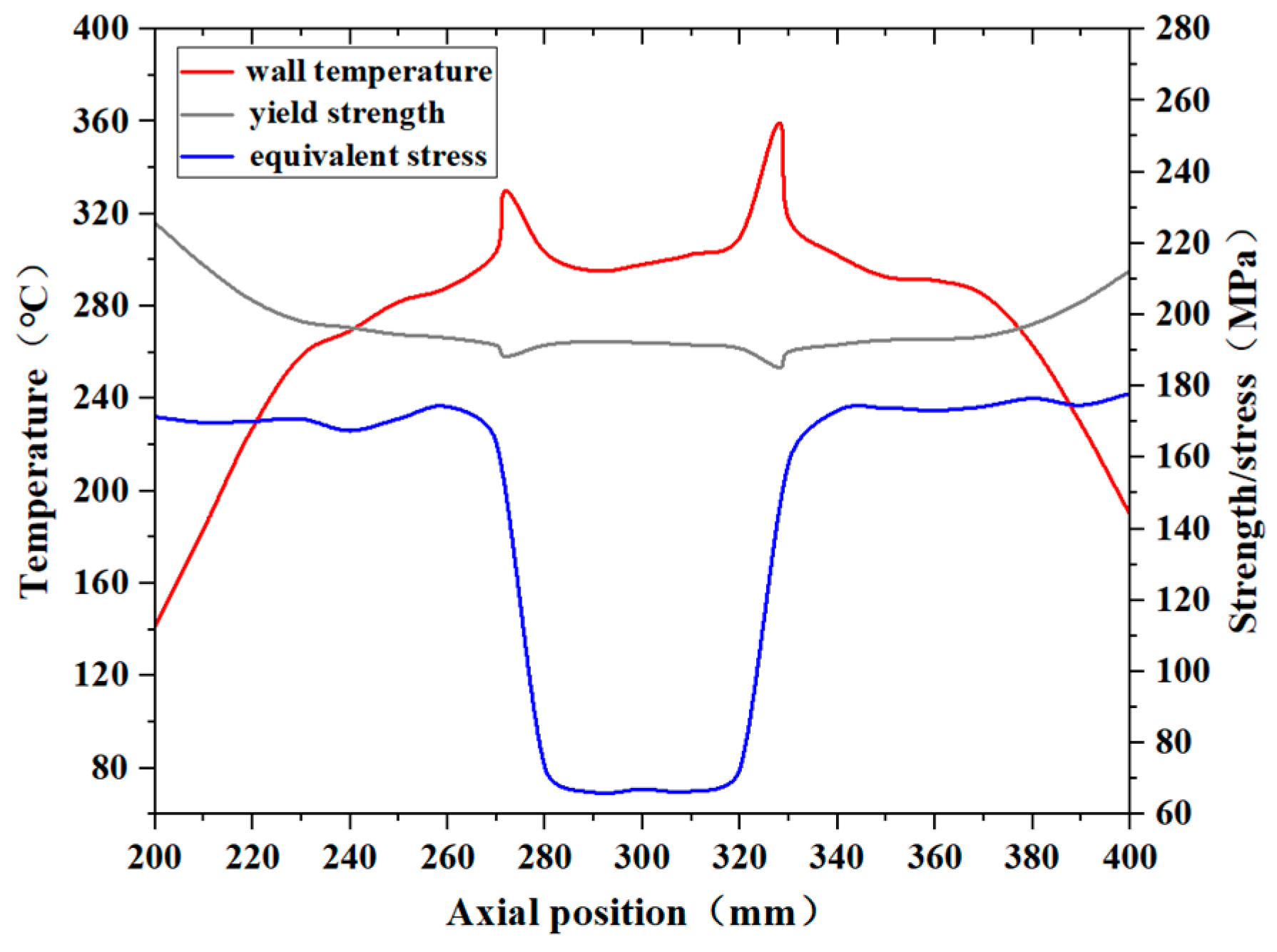
- An increase in the temperature amplified the temperature gradient across the pipe wall, which led to a higher thermal stress and a reduction in the material’s yield strength, thereby raising the risk of a pipe wall rupture. Under the fire test conditions, when the kerosene inlet flow rate decreased to 75% of the standard flow rate, the local equivalent stress of the pipe wall exceeded the material’s yield strength at the corresponding temperature. When the flow rate further decreased to 10% of the standard, the equivalent stress at most locations on the pipe wall surpassed the yield strength. Given that the engine pipe was also subjected to additional loads, such as vibration, and that a pipe wall deformation can alter the flow and heat transfer conditions, the actual working environment of the pipeline was likely even more severe, with an elevated risk of rupture.
- In this study, the pipe wall located approximately 70 mm downstream from the center of the connection along the flow direction was found to have a higher risk of rupture under the fire test conditions. Therefore, it is crucial to enhance the fire resistance of this area in the design of aero-engine fuel and lubricating oil systems.
Author Contributions
Funding
Institution Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, J.; Sun, Y.; Wang, F. Analysis of airworthiness requirements for powerplant fire protection of transport category. In Proceedings of the 2010 Airworthiness and Air Traffic Management Academic Annual Meeting, Beijing, China, 12 October 2010. [Google Scholar]
- Ministry of Transport of the People’s Repiblic of China. Aviation Engine Airworthiness Regulations; Ministry of Transport of the People’s Repiblic of China: Beijing, China, 2016; pp. 7–8.
- US Department of Transportation, Federal Aviation Administration. Airworthiness Standards: Aircraft engines. In Federal Aviation Regulations; US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2013; Part 33; pp. 40–45+86–88. [Google Scholar]
- European Union Aviation Safety Agency. Certification Specification for Engine CS-E; European Union Aviation Safety Agency: Cologne, Germany, 2009.
- Wang, W.; Lv, K.; Ye, Z. Convection and Radiation Heat Transfer Calculation of Aero-engine Fire Test. In Proceedings of the CSAA Symposium on Aircraft Fire Protection System (2nd SAFPS 2015), Hefei, China, 19 November 2015. [Google Scholar]
- Robert, I.O. Development of a Nex-Generation Burner for Use in Testing Thermal Acoistic Insulation Burn through Resistance; DOT/FAA/AR-TN09/23; US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2009.
- Kao, Y. Experimental Investigation of NexGen and Gas Burner for FAA Fire Test. Master’s Thesis, University of Cincinnati, Cincinnati, OH, USA, 2012. [Google Scholar]
- Liu, S. Simulation Research on Heat Flux Distribution of Aero-Engine Fire Protection Test. Master’s Thesis, Civil Aviation University of China, Tianjin, China, 2016. [Google Scholar]
- Xia, Y. Standard for fire test methods for aircraft hose and hard tube assemblies. Aeronaut. Stand. Qual. 1995, 2, 6–10. [Google Scholar]
- Ding, F.; Li, S.; Cui, Z.; Wang, K. Fire Simulation Analysis Method of Fuel and Lubricating Oil Pipeline. CN 114528722 A, 24 May 2022. [Google Scholar]
- Wu, J.; Song, J. Investigation of fire protection certification for aircraft engine components. Int. J. Energy Power Eng. 2019, 8, 73–78. [Google Scholar]
- Jiang, Y.; Li, S.; Cui, Z. The effects of nacelle pipe design patameters on resistance to fire. In Proceedings of the 14th International Conference on Mechanical and Areospace Engineering, Porto, Portugal, 18–21 July 2023. [Google Scholar]
- Wang, X.; Li, S. Method for auxiliary judging pipeline fireproof capability by estimating pipeline wall temperatures. Ordance Ind. Autom. 2023, 42, 91–96. [Google Scholar]
- Wang, W.; Shi, J. Research on fire test technology of external pipeline of aeroengine. Eng. Test 2024, 64, 66–69. [Google Scholar]
- Wang, X. Cause analysis on airworthiness fireproof test failure of an aero-engine lubricating oil pipeline. Aviat. Maint. Eng. 2022, 9, 92–96. [Google Scholar]
- HB 7044-2014; Requirement for Fire Testing of Flexible Hose and Tube Assemblies of Commercial Aircraft. Ministry of Industry and Information Technology of the People’s Republic of China: Beijing, China, 2014.
- HB 7842-2008; Tube Assembles for Flareless Connection, Swager Type, 28MPa. Ministry of Industry and Information Technology of the People’s Republic of China: Beijing, China, 2008.
- Wang, S.; Wang, Z.; Cui, Z.; Wang, K. China Aviation Materials Handbook, 1st ed.; Standards Press of China: Beijing, China, 1988; pp. 817–818. [Google Scholar]
- Zhong, F.; Fan, X.; Yu, G. Heat Transfer of aviation kerosene at supercritical conditions. J. Thermophys. Heat Transf. 2009, 23, 543–550. [Google Scholar] [CrossRef]
- Pei, X.; Hou, L. Effect of different species on physical properties for the surrogate of aviation fuel. J. Tsinghua Univ. (Sci. Technol.) 2017, 57, 774–779. [Google Scholar]
- Sun, Q.; Mi, Z.; Zhang, X. Determination of critical properties (te, pe) of endothermic dydrocarbon fuels RP-3 and simulated JP-7. J. Fuel Chem. Technol. 2006, 34, 466–470. [Google Scholar]
- Pu, H.; Chang, H.; Wang, J. Experimental investigation and analysis of convective heat transfer to supercritical pressure aviation kerosene RP-3 in vertical miniature tubes based on the pseudo-boiling theory. Appl.-Therm. Eng. 2023, 219, 119651. [Google Scholar] [CrossRef]
- Fu, Y.; Huang, H.; Wen, J. Experimental investigation on convectivr heat transfer of supercritical RP-3 in vertical miniature tubes with various diameters. Int. J. Heat Mass Transf. 2017, 112, 814–824. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, J.; Lin, J.; Huang, D. Numerical study of heat transfer characteristics of downward supercritical kerosene flow inside circular tube. J. Zhejiang Univ. 2018, 19, 158–170. [Google Scholar] [CrossRef]
- Dang, G.; Zhong, F.; Zhang, Y. Numerical study of heat transfer deterioration of turbulent supercritical kerosene flow in heated circular tube. Int. J. Heat Mass Transf. 2015, 85, 1003–1011. [Google Scholar] [CrossRef]
- Su, W.; Huang, S. Forst heaving damage mechanism of a buried natural gas pipeline in a river and creek region. Materials 2022, 15, 5795. [Google Scholar] [CrossRef] [PubMed]
- Pu, H. Characteristics and Mechanism of Convective Heat Transfer t Spercritical Pressure RP-3 in Mini-Channels. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Gnielinski, V. On hear transfer in tubes. Int. J. Heat Mass Transf. 2015, 63, 134–140. [Google Scholar] [CrossRef]





| Element | C | Mn | Si | Cr | Ni | S | P | Ti |
|---|---|---|---|---|---|---|---|---|
| Content, % | ≤0.12 | ≤2.0 | ≤0.80 | 17.00~19.00 | 8.00~11.00 | ≤0.025 | ≤0.035 | 5 × (C% − 0.02%)~0.80% |
| Temperature, °C | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
|---|---|---|---|---|---|---|---|---|---|
| λ, W/(m·K) | 16.3 | 17.6 | 18.8 | 20.5 | 21.8 | 23.5 | 24.7 | 26.4 | 28.5 |
| Operating Condition Number | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Pressure (MPa) | 28 | 28 | 28 | 28 | 28 | 28 |
| Temperature (K) | 366.15 | 366.15 | 366.15 | 366.15 | 366.15 | 366.15 |
| Flow rate (L/min) | 5.07 | 3.80 | 2.54 | 1.27 | 0.50 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Wang, F.; Wen, F.; Jin, J. Research on Safety of Aero-Engine Oil Pipe Under Heating Conditions Based on Fluid–Solid Thermal Coupling. Materials 2024, 17, 5137. https://doi.org/10.3390/ma17215137
Yang Y, Wang F, Wen F, Jin J. Research on Safety of Aero-Engine Oil Pipe Under Heating Conditions Based on Fluid–Solid Thermal Coupling. Materials. 2024; 17(21):5137. https://doi.org/10.3390/ma17215137
Chicago/Turabian StyleYang, Yuepeng, Fang Wang, Fang Wen, and Jie Jin. 2024. "Research on Safety of Aero-Engine Oil Pipe Under Heating Conditions Based on Fluid–Solid Thermal Coupling" Materials 17, no. 21: 5137. https://doi.org/10.3390/ma17215137
APA StyleYang, Y., Wang, F., Wen, F., & Jin, J. (2024). Research on Safety of Aero-Engine Oil Pipe Under Heating Conditions Based on Fluid–Solid Thermal Coupling. Materials, 17(21), 5137. https://doi.org/10.3390/ma17215137






