Strengthening Effect Evaluation of Developed Stiff-Type Polyurea Sprayed on Masonry Beam Surface Under Static Loading in Experimental and Numerical Tests
Abstract
1. Introduction
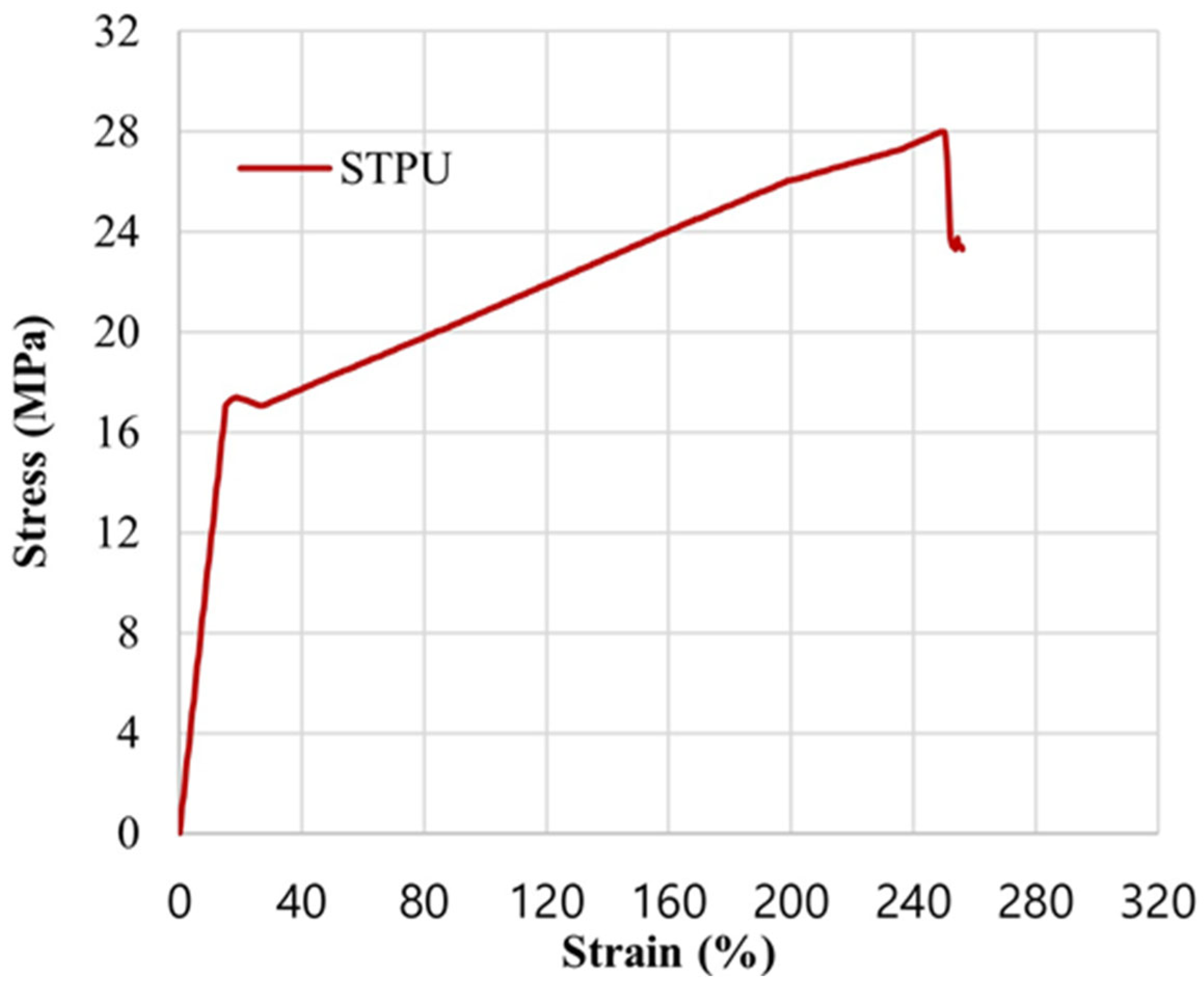
2. Flexural Strength Test for STPU Surface-Sprayed Masonry Beam
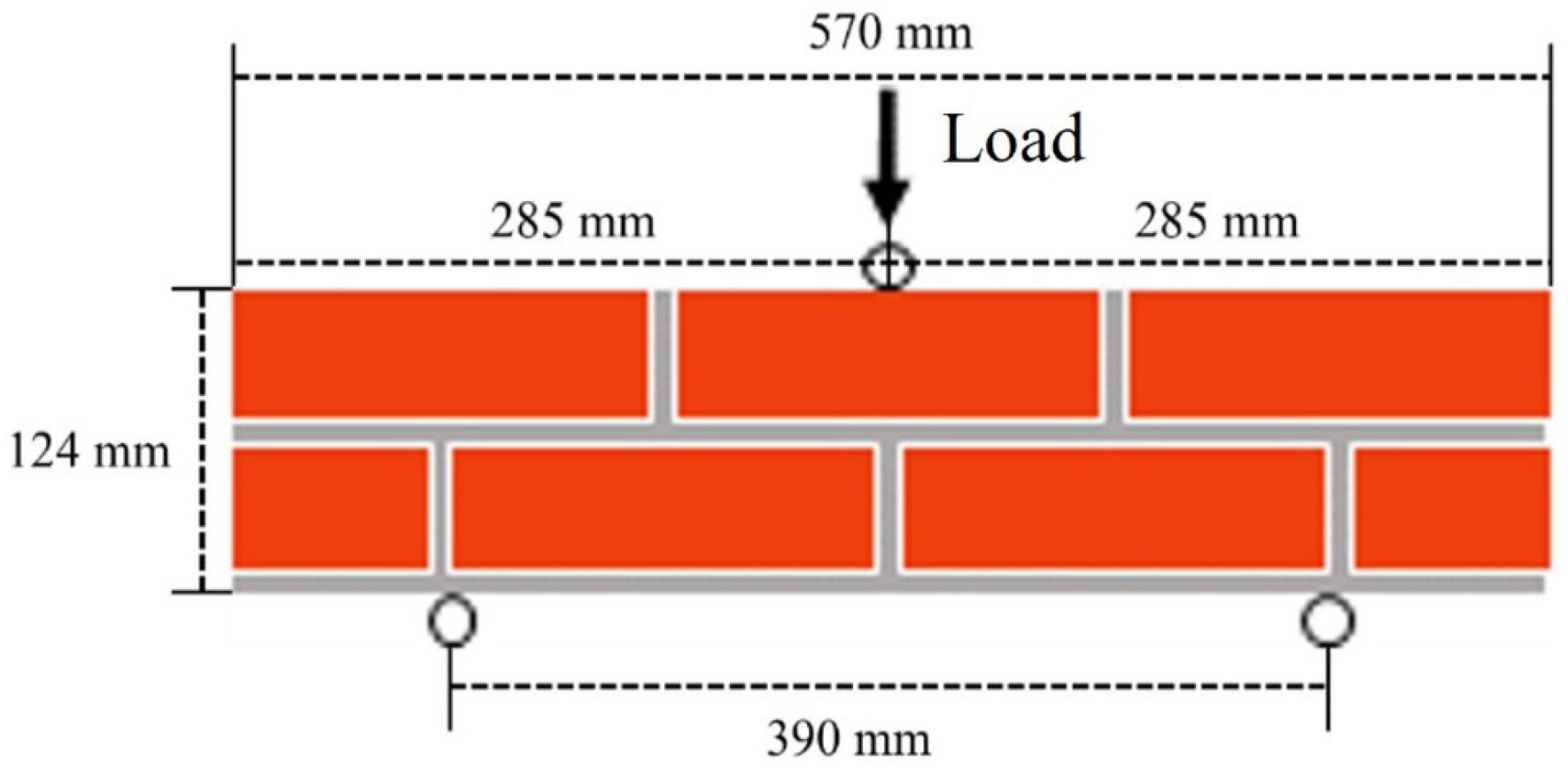
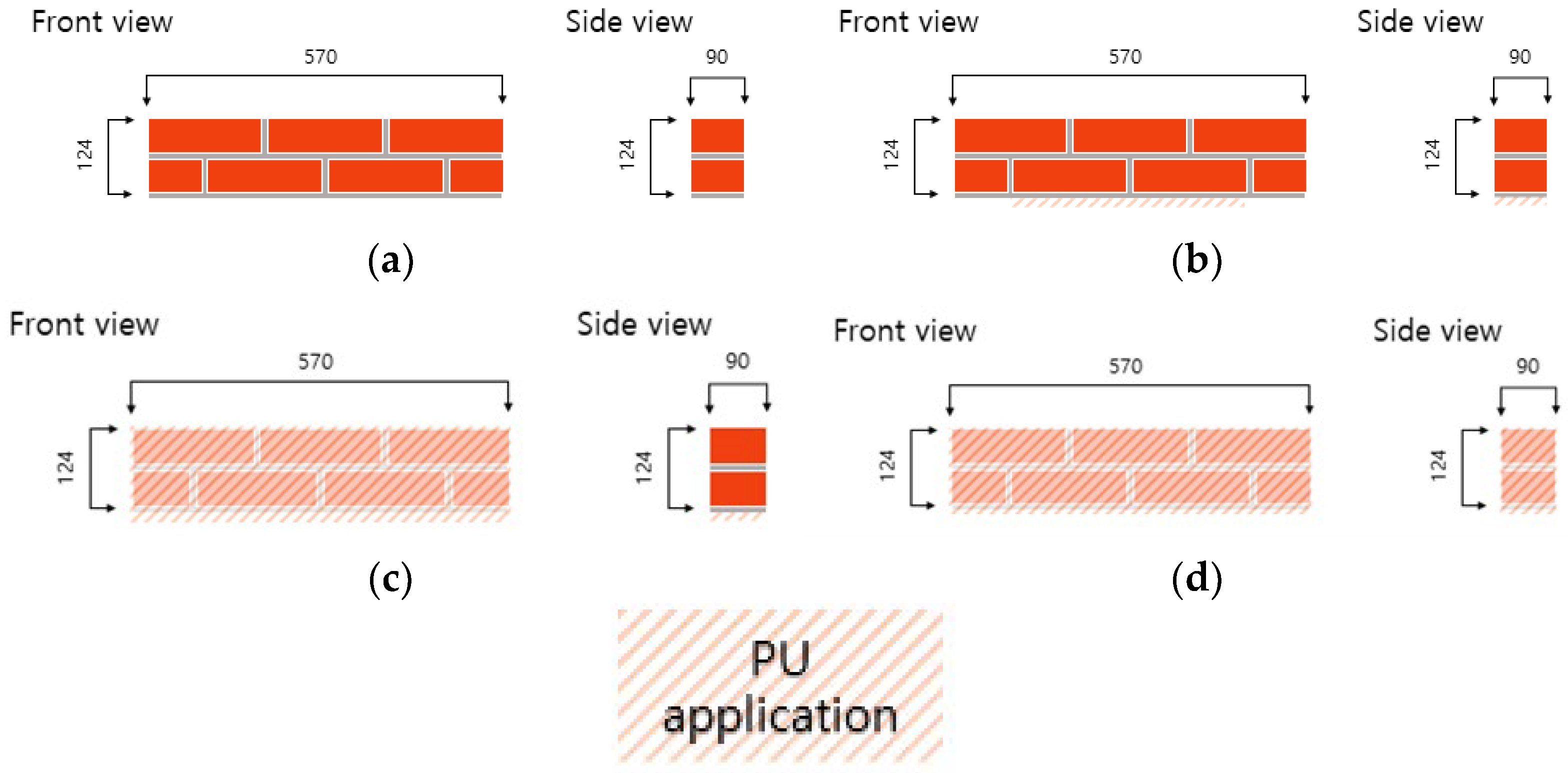
2.1. Specimen Details

2.2. Flexural Strength Test Result
3. Numerical Evaluation for STPU Surface-Sprayed Masonry Beam
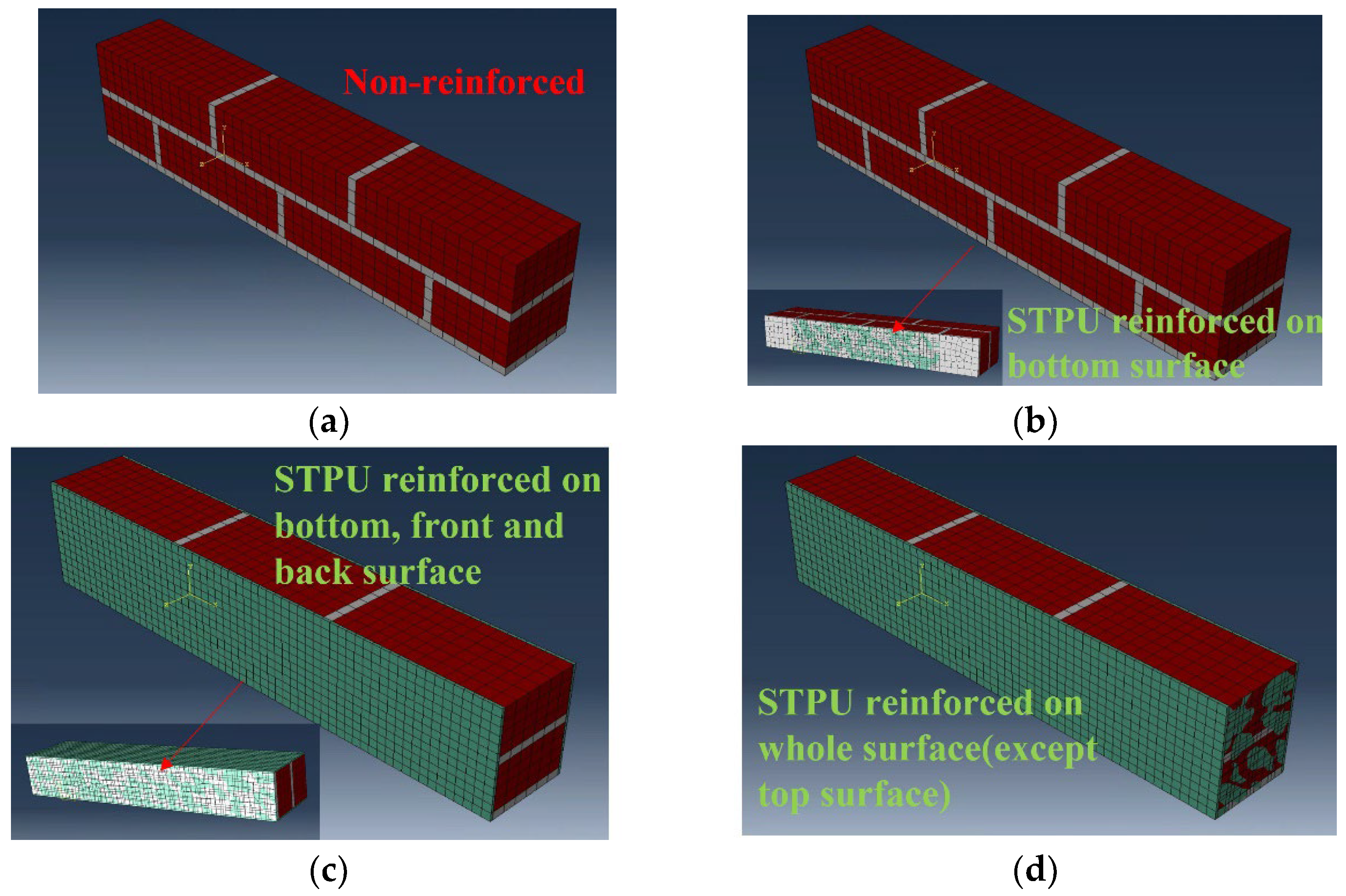
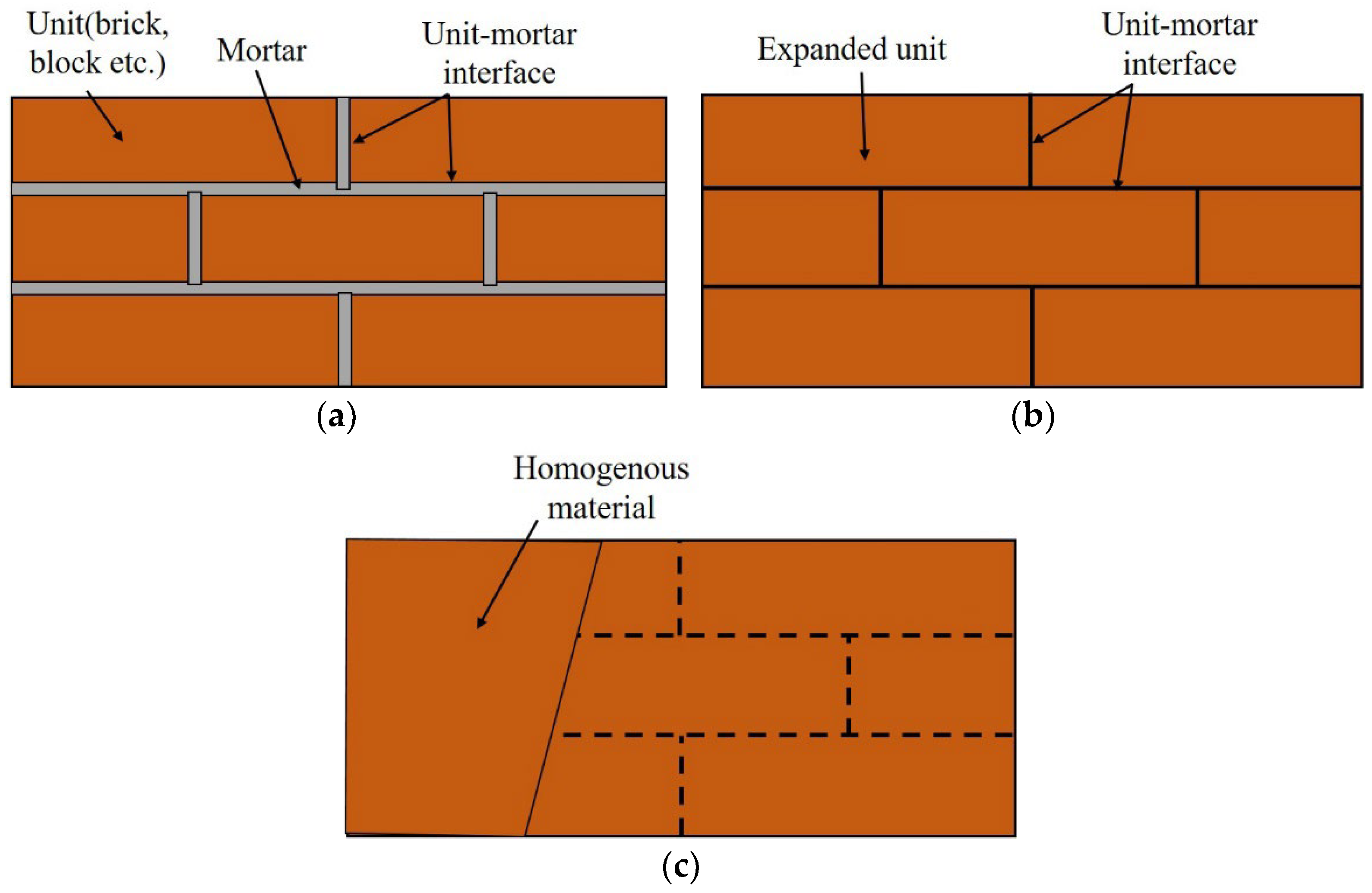
3.1. Numerical Modeling Method of Masonry Beam
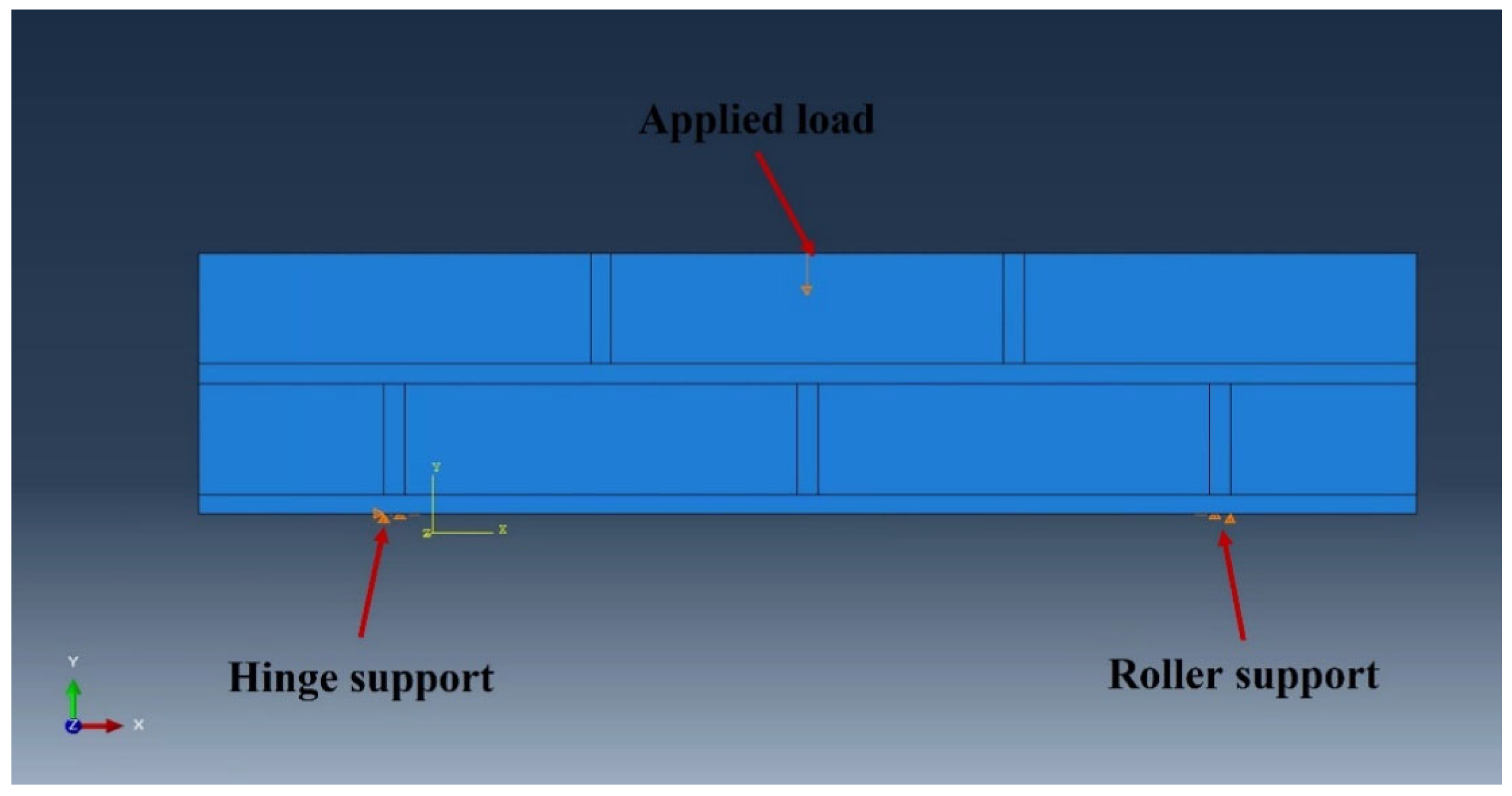
3.2. Modeling and Variables of the Flexural Strength Test
| Density (kg/m3) | Elastic Modulus (MPa) | ν | ψ | ϵ | σb0/σc0 | Kc | μ | |
|---|---|---|---|---|---|---|---|---|
| Brick | 2100 | 5730 | 0.15 | 28 | 0.1 | 1.16 | 0.667 | 0 |
| Mortar | 2400 | 14,000 | 0.2 | 40 | 0.1 | 1.16 | 0.667 | 0 |
3.3. Numerical Analysis of Flexural Strength Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chanter, B.; Swallow, P. Building Maintenance Management; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Park, S.; Ahn, Y.; Lee, S. Analyzing the finishing works service life pattern of public housing in South Korea by probabilistic approach. Sustainability 2018, 10, 4469. [Google Scholar] [CrossRef]
- Park, M.; Kwon, N.; Lee, J.; Lee, S.; Ahn, Y. Probabilistic maintenance cost analysis for aged multi-family housing. Sustainability 2019, 11, 1843. [Google Scholar] [CrossRef]
- Cavalcante, C.A.V.; Alencar, M.H.; Lopes, R.S. Multicriteria model to support maintenance planning in residential complexes under warranty. J. Constr. Eng. Manag. 2017, 143, 04016110. [Google Scholar] [CrossRef]
- Silva, A.; De Brito, J. Do we need a buildings’ inspection, diagnosis and service life prediction software? J. Build. Eng. 2019, 22, 335–348. [Google Scholar] [CrossRef]
- Chan, D.W. Sustainable building maintenance for safer and healthier cities: Effective strategies for implementing the Mandatory Building Inspection Scheme (MBIS) in Hong Kong. J. Build. Eng. 2019, 24, 100737. [Google Scholar] [CrossRef]
- Seoul Institute of Technology (SIT). Spotlight. Available online: https://www.sit.re.kr (accessed on 29 September 2024).
- Zhang, P.; Wang, S.; Tao, X.; Li, Z.; Liu, Y.; Peng, E.; Lv, J. Experimental study on the flexural behaviors of ECC-reinforced masonry beams with GFRP mesh. Eng. Struct. 2024, 315, 118479. [Google Scholar] [CrossRef]
- Tralli, A.; Alessandri, C.; Milani, G. Computational methods for masonry vaults: A review of recent results. Open Civ. Eng. J. 2014, 8, 272–287. [Google Scholar] [CrossRef]
- Atamturktur, S.; Li, T.; Ramage, M.H.; Farajpour, I. Load carrying capacity assessment of a scaled masonry dome: Simulations validated with non-destructive and destructive measurements. Constr. Build. Mater. 2012, 34, 418–429. [Google Scholar] [CrossRef]
- Mahini, S.S.; Eslami, A.; Ronagh, H.R. Lateral performance and load carrying capacity of an unreinforced, CFRP-retrofitted historical masonry vault—A case study. Constr. Build. Mater. 2012, 28, 146–156. [Google Scholar] [CrossRef]
- Al-Jaberi, Z.; Myers, J.J.; ElGawady, M.A. Experimental and analytical approach for prediction of out-of-plane capacity of reinforced masonry walls strengthened with externally bonded FRP laminate. J. Compos. Constr. 2019, 23, 04019026. [Google Scholar] [CrossRef]
- Dizhur, D.; Griffith, M.; Ingham, J. Out-of-plane strengthening of unreinforced masonry walls using near surface mounted fibre reinforced polymer strips. Eng. Struct. 2014, 59, 330–343. [Google Scholar] [CrossRef]
- Syiemiong, H.; Marthong, C. Flexural behavior of low strength masonry wallettes strengthened with welded wire mesh. Mater. Today Proc. 2021, 43, 1774–1779. [Google Scholar] [CrossRef]
- Syiemiong, H.; Marthong, C. The effect of mortar grade on the out-of-plane behaviour of low-strength masonry wall strengthened with welded wire mesh. Constr. Build. Mater. 2021, 279, 122393. [Google Scholar] [CrossRef]
- Ma, G.; Hou, C.; Hwang, H.J.; Wang, Z. Axial Compressive Behavior of Predamaged Concrete Cylinders Retrofitted with CFRP Grid-Reinforced ECC. J. Compos. Constr. 2023, 27, 04023060. [Google Scholar] [CrossRef]
- Flora, F.; Pinto, F.; Meo, M. Manufacturing and characterisation of a new thermal pre-stressed carbon fibre-reinforced lattice core for sandwich panels. J. Compos. Mater. 2022, 56, 1233–1254. [Google Scholar] [CrossRef]
- Lim, C.; Jeong, Y.; Kim, J.; Kwon, M. Experimental study of reinforced concrete beam-column joint retrofitted by CFRP grid with ECC and high strength mortar. Constr. Build. Mater. 2022, 340, 127694. [Google Scholar] [CrossRef]
- Al-Lami, A.; Hilmer, P.; Sinapius, M. Eco-efficiency assessment of manufacturing carbon fiber reinforced polymers (CFRP) in aerospace industry. Aerosp. Sci. Technol. 2018, 79, 669–678. [Google Scholar] [CrossRef]
- Dehghani, A.; Nateghi, E.F. Experimental results and conclusions obtained on the masonry-infilled concrete frames strengthened by CFRP. In Proceedings of the 14th European Conference on Earthquake Engineering, Ohrid, North Macedonia, 30 August–3 September 2010; Volume 7, pp. 5592–5599. [Google Scholar]
- Grujicic, M.; Pandurangan, B.; He, T.; Cheeseman, B.A.; Yen, C.F.; Randow, C.L. Computational investigation of impact energy absorption capability of polyurea coatings via deformation-induced glass transition. Mater. Sci. Eng. A 2010, 527, 7741–7751. [Google Scholar] [CrossRef]
- Toader, G.; Rusen, E.; Teodorescu, M.; Diacon, A.; Stanescu, P.O.; Rotariu, T.; Rotariu, A. Novel polyurea polymers with enhanced mechanical properties. J. Appl. Polym. Sci. 2016, 133, 43967. [Google Scholar] [CrossRef]
- Mott, P.H.; Giller, C.B.; Fragiadakis, D.; Rosenberg, D.A.; Roland, C.M. Deformation of polyurea: Where does the energy go? Polymer 2016, 105, 227–233. [Google Scholar] [CrossRef]
- Broekaert, M. Polyurea Spray Coatings; Huntsman Polyurethanes: The Woodlands, TX, USA, 2002. [Google Scholar]
- Komurlu, E.; Kesimal, A. Improved performance of rock bolts using sprayed polyurea coating. Rock Mech. Rock Eng. 2015, 48, 2179–2182. [Google Scholar] [CrossRef]
- Iqbal, N.; Tripathi, M.; Parthasarathy, S.; Kumar, D.; Roy, P.K. Polyurea coatings for enhanced blast-mitigation: A review. RSC Adv. 2016, 6, 109706–109717. [Google Scholar] [CrossRef]
- Cho, C.M.; Choi, J.H.; Rhee, S.H.; Kim, T.K.; Kim, J.H.J. Material performance evaluation of polyurea for structural seismic retrofitting. J. Korea Concr. Inst. 2017, 29, 131–139. [Google Scholar] [CrossRef]
- Lee, T.H.; Park, J.H.; Yang, D.H.; Kim, J.H.J.; Noor, N.B.M. Material enhancements of newly developed stiff type polyurea for retrofitting of concrete structures. Case Stud. Constr. Mater. 2022, 17, e01431. [Google Scholar] [CrossRef]
- Shojaei, B.; Najafi, M.; Yazdanbakhsh, A.; Abtahi, M.; Zhang, C. A review on the applications of polyurea in the construction industry. Polym. Adv. Technol. 2021, 32, 2797–2812. [Google Scholar] [CrossRef]
- KSF 2408; Standard Test Method for Flexural Strength of Concrete. Korea Standards Association: Seoul, Republic of Korea, 2016.
- Abdulla, K.F.; Cunningham, L.S.; Gillie, M. Simulating masonry wall behaviour using a simplified micro-model approach. Eng. Struct. 2017, 151, 349–365. [Google Scholar] [CrossRef]
- Milani, G.; Valente, M. Failure analysis of seven masonry churches severely damaged during the 2012 Emilia-Romagna (Italy) earthquake: Non-linear dynamic analyses vs conventional static approaches. Eng. Fail. Anal. 2015, 54, 13–56. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Non-linear dynamic and static analyses on eight historical masonry towers in the North-East of Italy. Eng. Struct. 2016, 114, 241–270. [Google Scholar] [CrossRef]
- Rull, N.; Basnayake, A.; Heitzmann, M.; Frontini, P.M. Constitutive modelling of the mechanical response of a polycaprolactone based polyurethane elastomer: Finite element analysis and experimental validation through a bulge test. J. Strain Anal. Eng. Des. 2021, 56, 206–215. [Google Scholar] [CrossRef]
- Chen, D.; Wu, H.; Wei, J.S.; Xu, S.L.; Fang, Q. Nonlinear visco-hyperelastic tensile constitutive model of spray polyurea within wide strain-rate range. Int. J. Impact Eng. 2022, 163, 104184. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Bhosale, S.D.; Desai, A.K. Simulation of masonry wall using concrete damage plasticity model. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 1241–1244. [Google Scholar]
- Borah, B.; Kaushik, H.B.; Singhal, V. Finite element modelling of confined masonry wall under in-plane cyclic load. IOP Conf. Ser. Mater. Sci. Eng. 2020, 936, 012020. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, B. Modeling of masonry structures using a new 3D cohesive interface material model considering dilatancy softening. Eng. Struct. 2023, 277, 115466. [Google Scholar] [CrossRef]
- Gattesco, N.; Amadio, C.; Bedon, C. Experimental and numerical study on the shear behavior of stone masonry walls strengthened with GFRP reinforced mortar coating and steel-cord reinforced repointing. Eng. Struct. 2015, 90, 143–157. [Google Scholar] [CrossRef]
- Griffith, M.C.; Kashyap, J.; Ali, M.M. Flexural displacement response of NSM FRP retrofitted masonry walls. Constr. Build. Mater. 2013, 49, 1032–1040. [Google Scholar] [CrossRef]

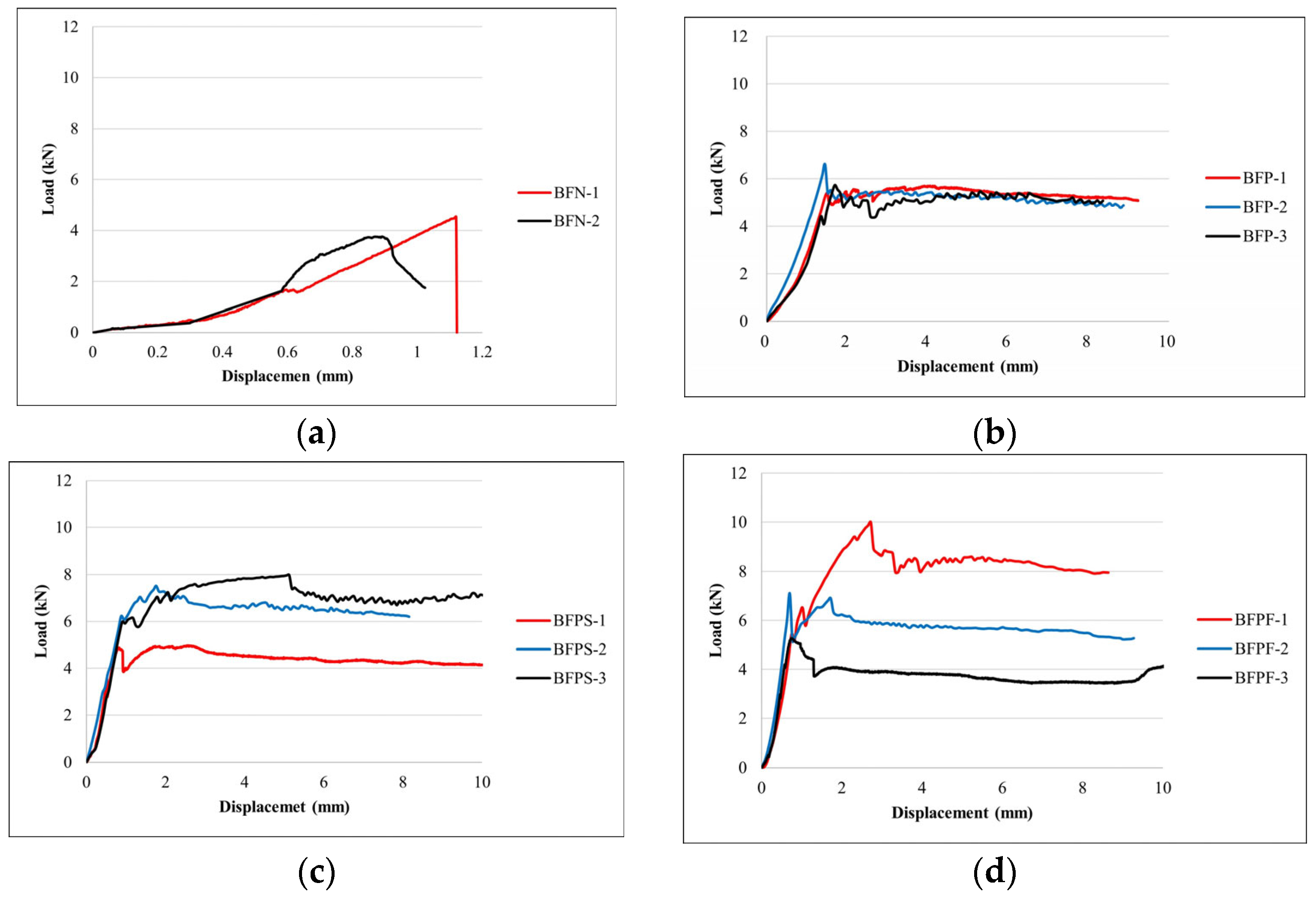


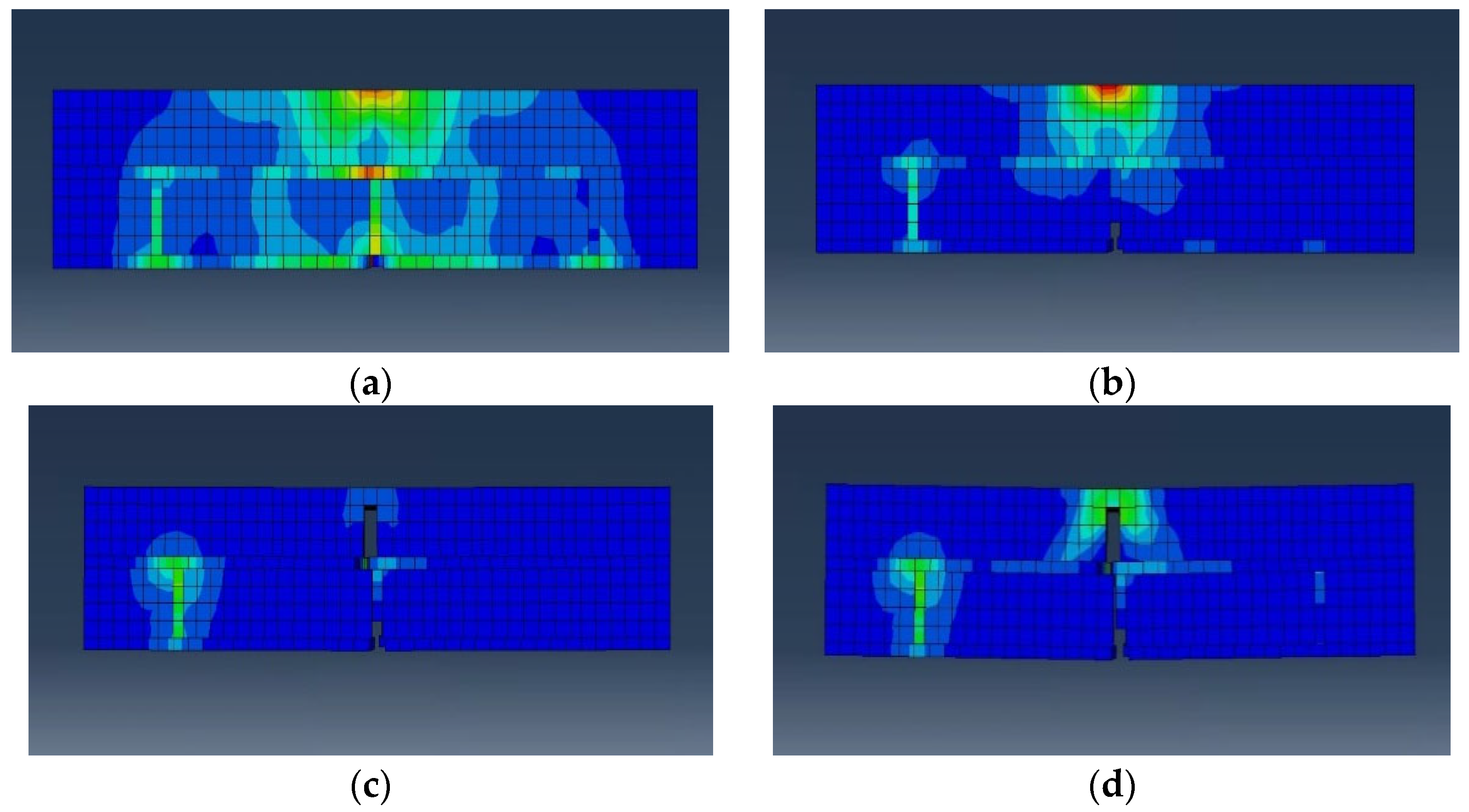
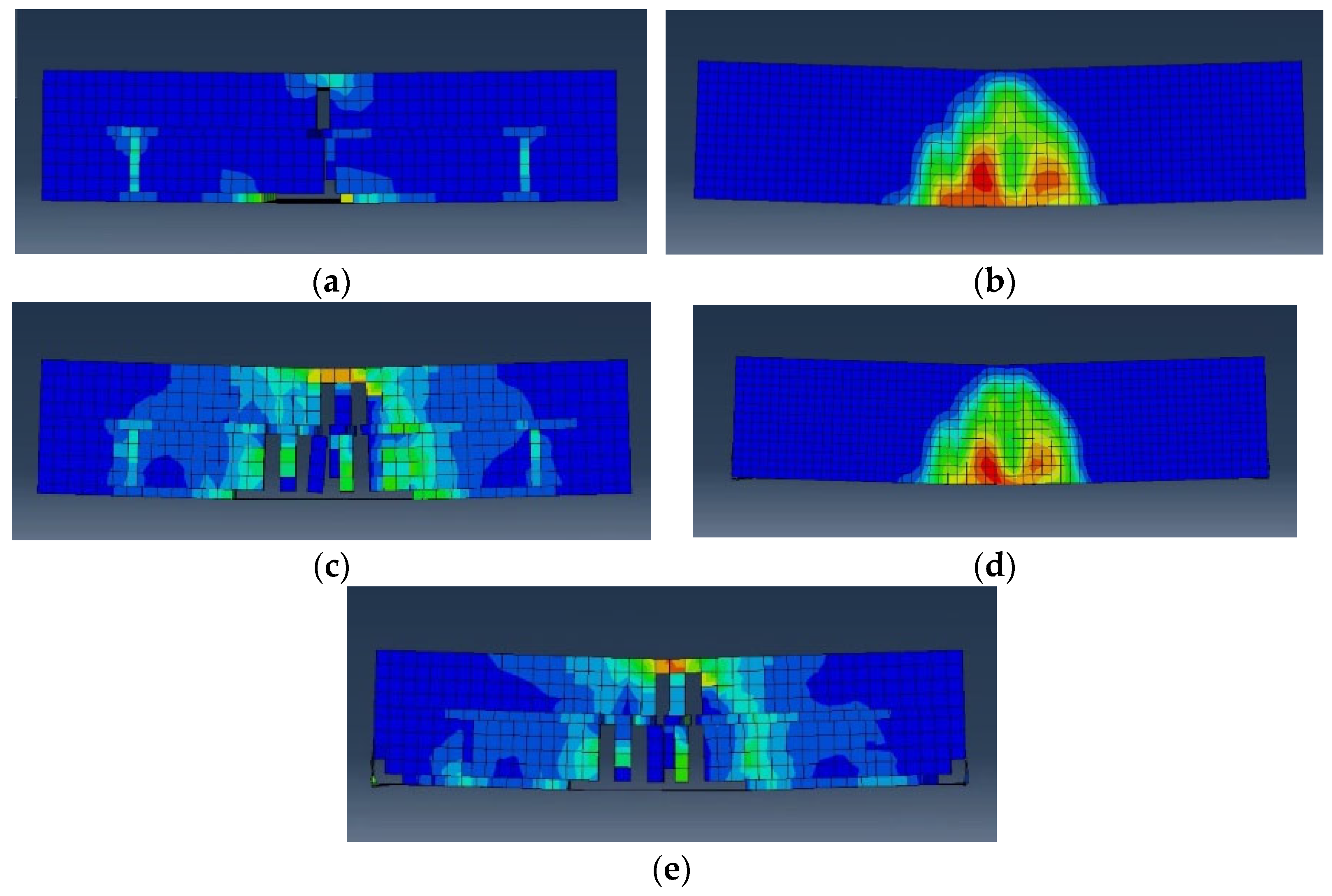
| Test Specimen Number | Ultimate Load (kN) | Maximum Displacement (mm) | Flexural Strength (MPa) | |
|---|---|---|---|---|
| BFN | 1 | - | - | - |
| 2 | 3.75 | 1.02 | 1.59 | |
| 3 | 4.54 | 1.12 | 1.92 | |
| Average | 4.15 | 1.07 | 1.75 | |
| BFP | 1 | 5.70 | 9.23 | 2.41 |
| 2 | 6.94 | 8.87 | 2.93 | |
| 3 | 5.74 | 8.36 | 2.43 | |
| Average | 6.13 | 8.82 | 2.59 | |
| BFPS | 1 | 4.88 | 12.70 | 2.06 |
| 2 | 7.61 | 8.16 | 3.22 | |
| 3 | 8.24 | 11.74 | 3.48 | |
| Average | 6.91 | 10.87 | 2.92 | |
| BFPF | 1 | 10.03 | 8.68 | 4.24 |
| 2 | 6.93 | 9.29 | 2.93 | |
| 3 | 8.24 | 10.26 | 3.48 | |
| Average | 8.40 | 9.41 | 3.55 |
| Tangential Behavior | Cohesive Behavior | |||
|---|---|---|---|---|
| Friction Coefficient | Stiffness of Joint in the Normal Direction Knn (N/mm2) | Stiffness of Joint in the First Shear Direction Kss (N/mm2) | Stiffness of Joint in the Second Shear Direction Ktt (N/mm2) | |
| Brick and Mortar | 0.75 | 35 | 14.42 | 41.42 |
| Brick and STPU | 0.06 | 41.6 | 17.5 | 17.5 |
| Specimen | Data Type | Ultimate Load (kN) | Maximum Displacement (mm) | Flexural Strength (MPa) |
|---|---|---|---|---|
| BFN | Numerical | 3.86 | 0.80 | 1.63 |
| Experimental | 4.15 | 1.07 | 1.75 | |
| Ratio | 0.93 | 0.75 | 0.93 | |
| BFP | Numerical | 5.52 | 8.40 | 2.34 |
| Experimental | 6.13 | 8.82 | 2.59 | |
| Ratio | 0.90 | 0.95 | 0.90 | |
| BFPS | Numerical | 7.18 | - | 3.04 |
| Experimental | 6.91 | 10.87 | 2.92 | |
| Ratio | 1.04 | - | 1.04 | |
| BFPF | Numerical | 7.03 | - | 2.97 |
| Experimental | 8.40 | 9.41 | 3.55 | |
| Ratio | 0.84 | - | 0.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, T.-H.; Kim, J.-H.J. Strengthening Effect Evaluation of Developed Stiff-Type Polyurea Sprayed on Masonry Beam Surface Under Static Loading in Experimental and Numerical Tests. Materials 2024, 17, 5243. https://doi.org/10.3390/ma17215243
Lee T-H, Kim J-HJ. Strengthening Effect Evaluation of Developed Stiff-Type Polyurea Sprayed on Masonry Beam Surface Under Static Loading in Experimental and Numerical Tests. Materials. 2024; 17(21):5243. https://doi.org/10.3390/ma17215243
Chicago/Turabian StyleLee, Tae-Hee, and Jang-Ho Jay Kim. 2024. "Strengthening Effect Evaluation of Developed Stiff-Type Polyurea Sprayed on Masonry Beam Surface Under Static Loading in Experimental and Numerical Tests" Materials 17, no. 21: 5243. https://doi.org/10.3390/ma17215243
APA StyleLee, T.-H., & Kim, J.-H. J. (2024). Strengthening Effect Evaluation of Developed Stiff-Type Polyurea Sprayed on Masonry Beam Surface Under Static Loading in Experimental and Numerical Tests. Materials, 17(21), 5243. https://doi.org/10.3390/ma17215243






