Thermoelectric Properties of Cu2S Doped with P, As, Sb and Bi—Theoretical and Experimental Studies
Abstract
1. Introduction
2. Materials and Methods
2.1. Computational Details
2.2. Experimental Details
3. Results and Discussion
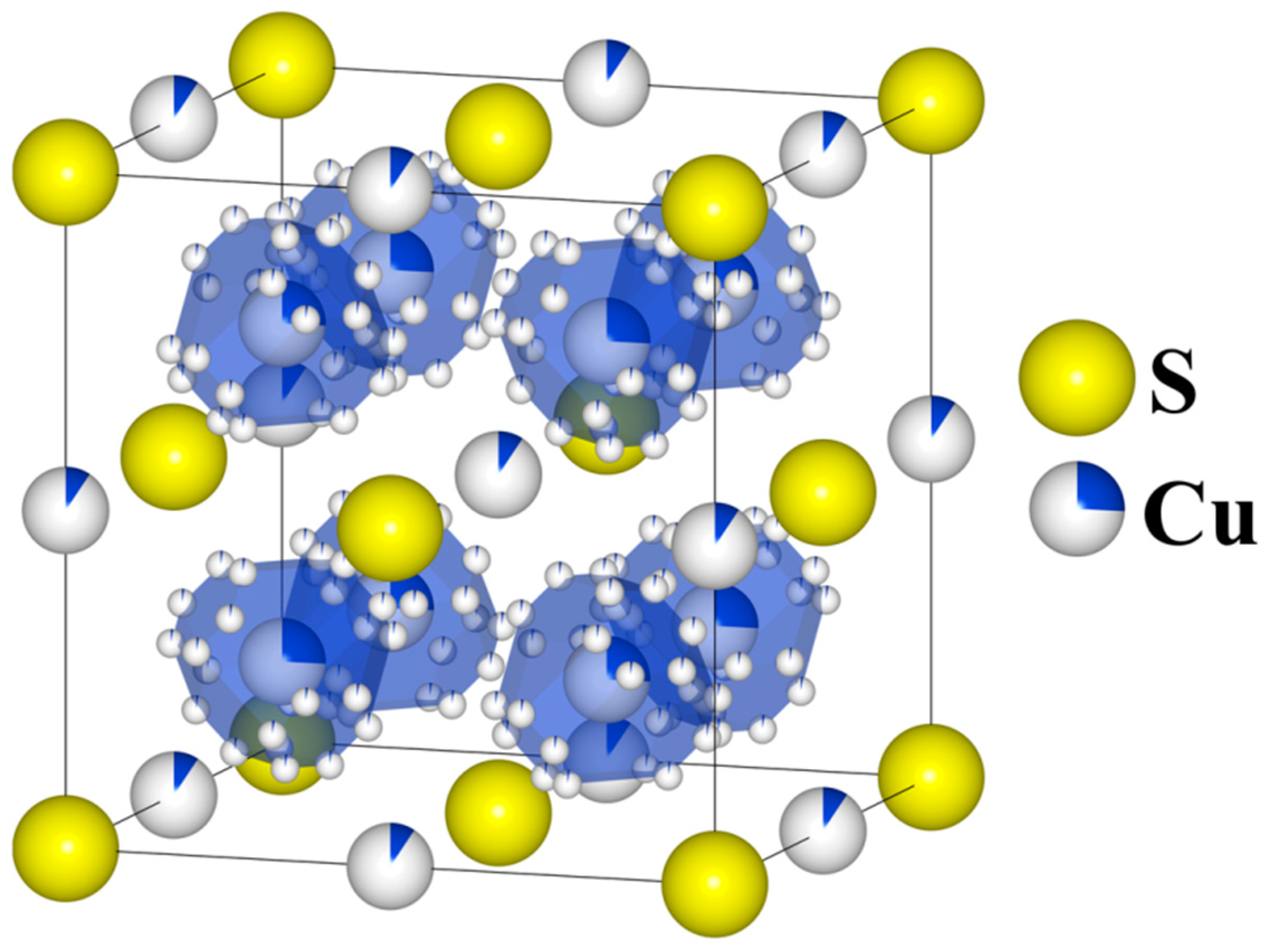
3.1. Electronic Structure and Enthalpy of Doping
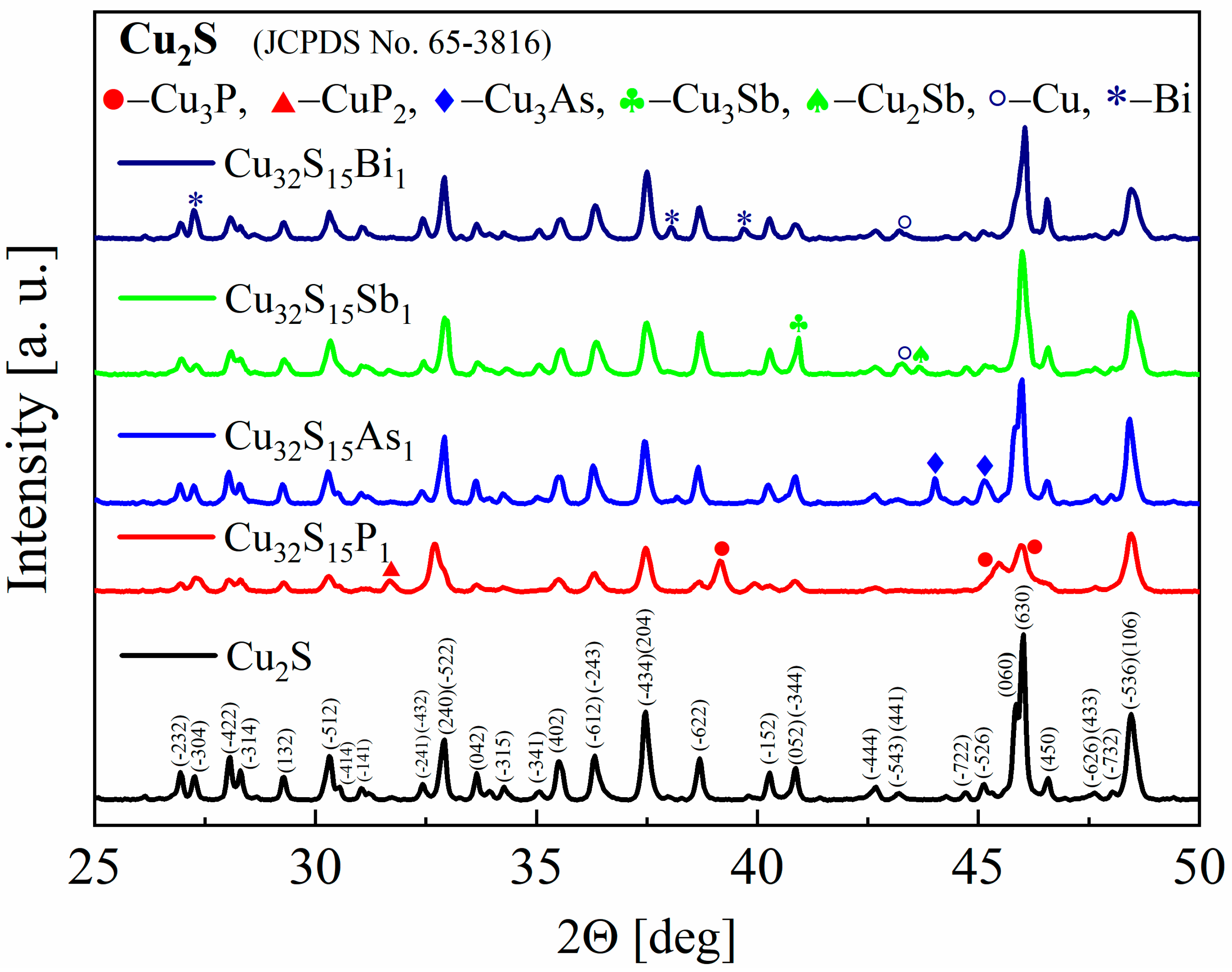
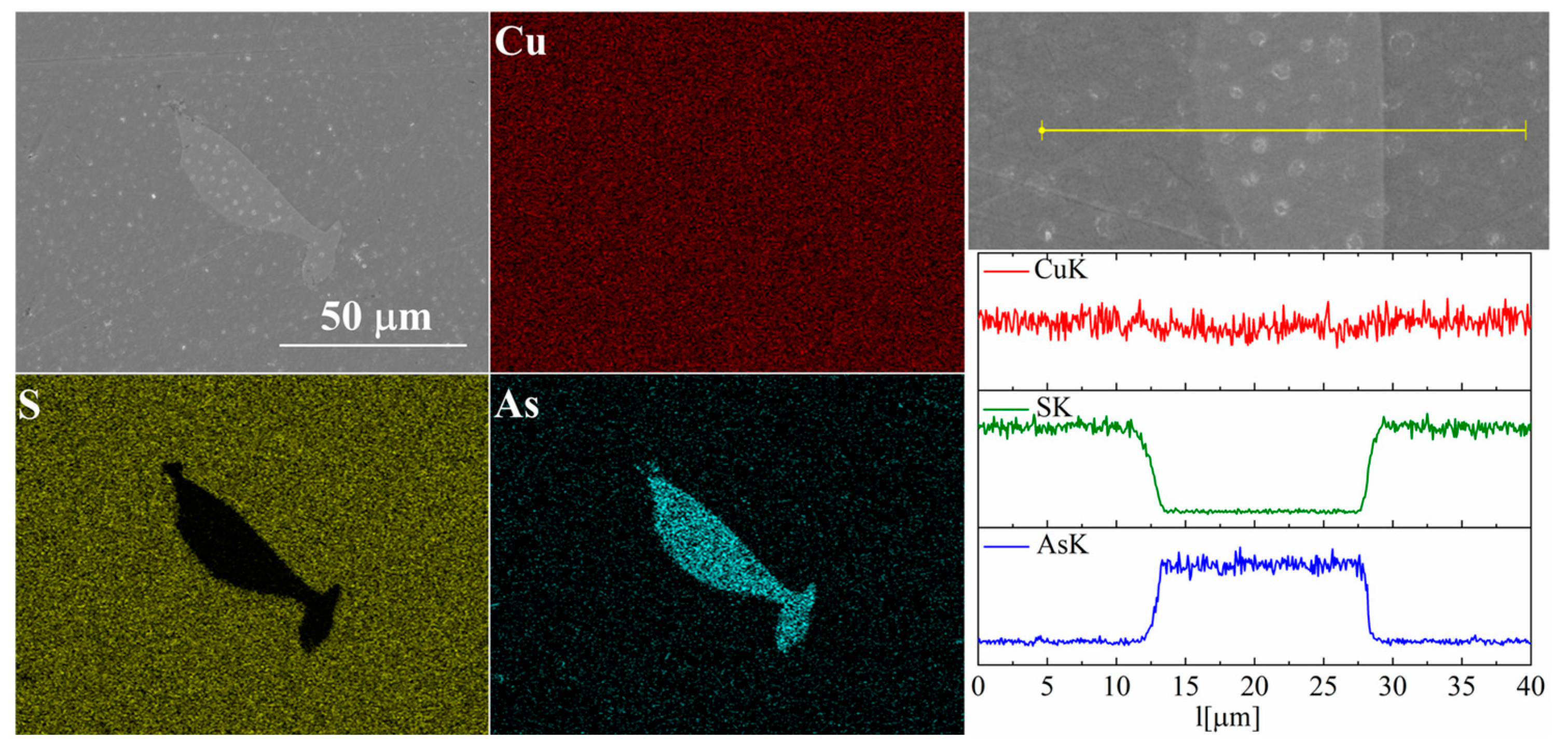
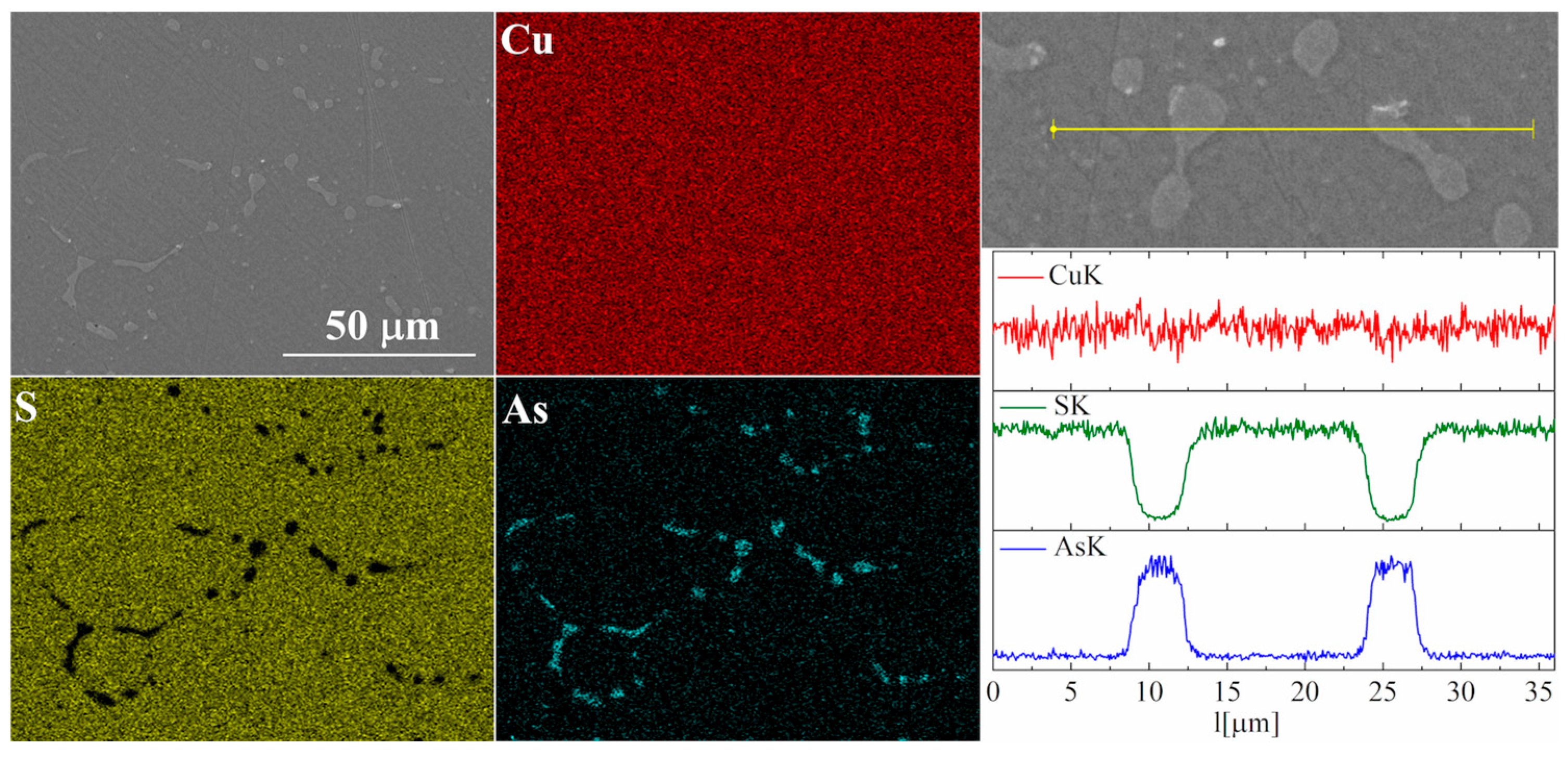
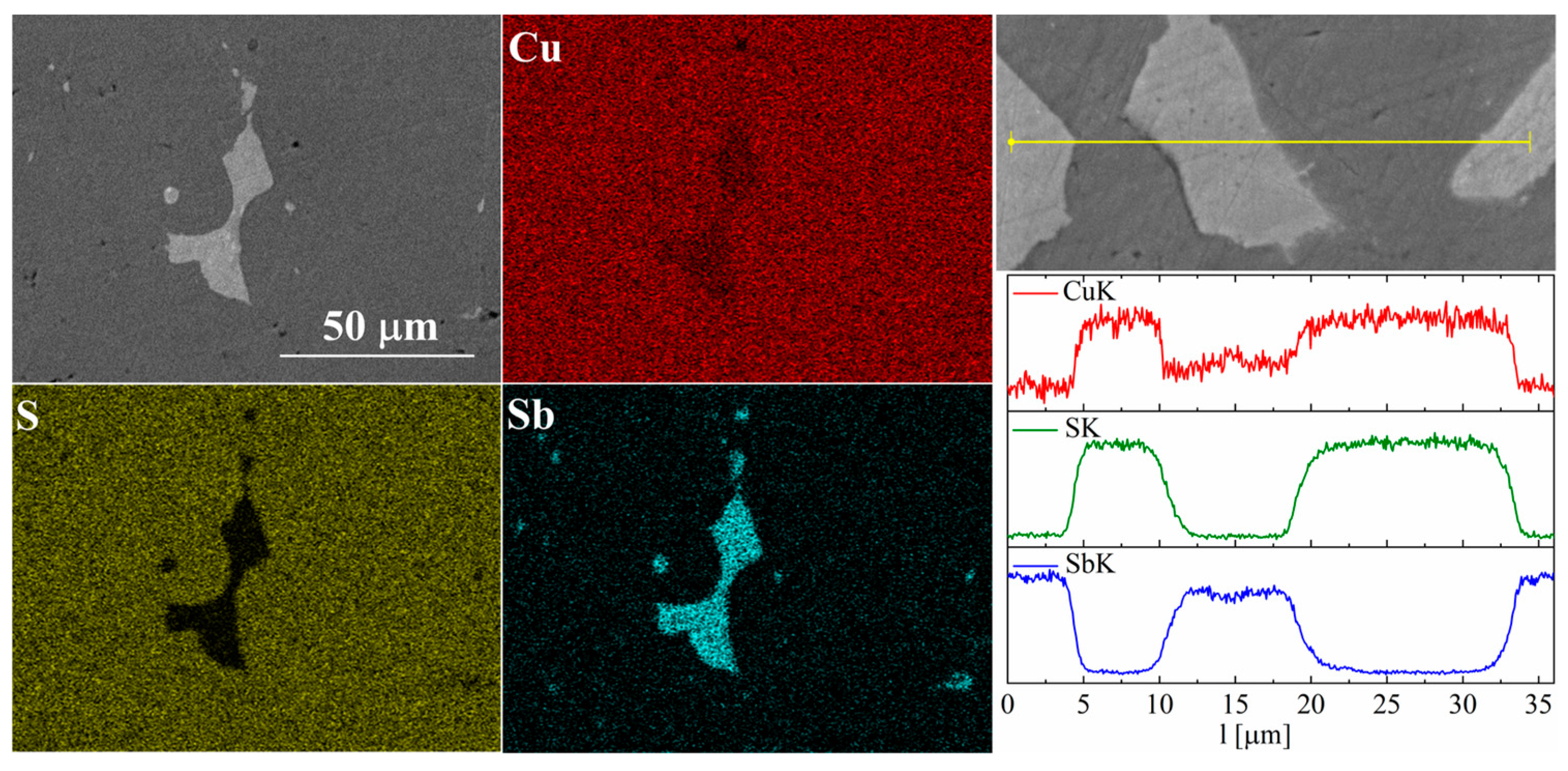
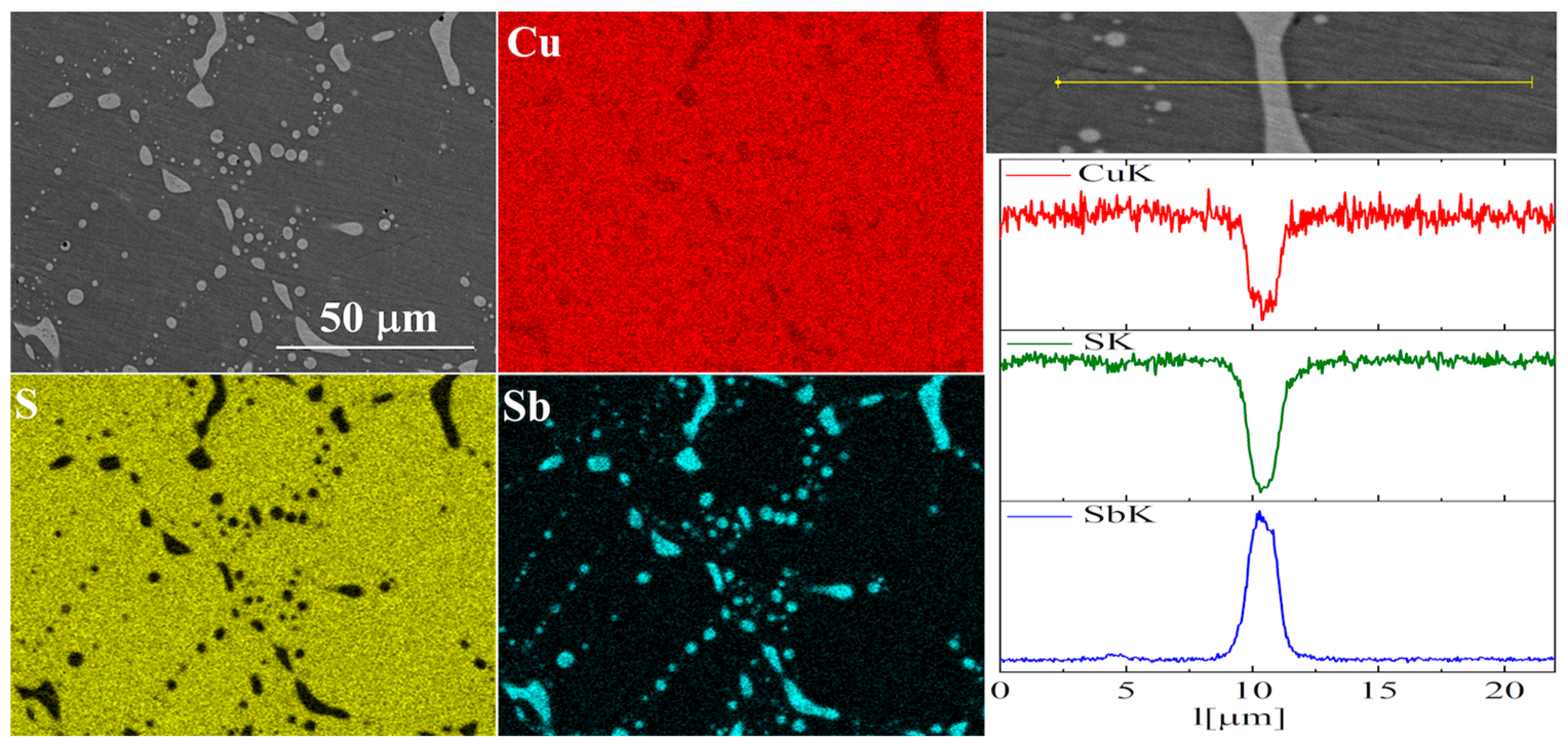
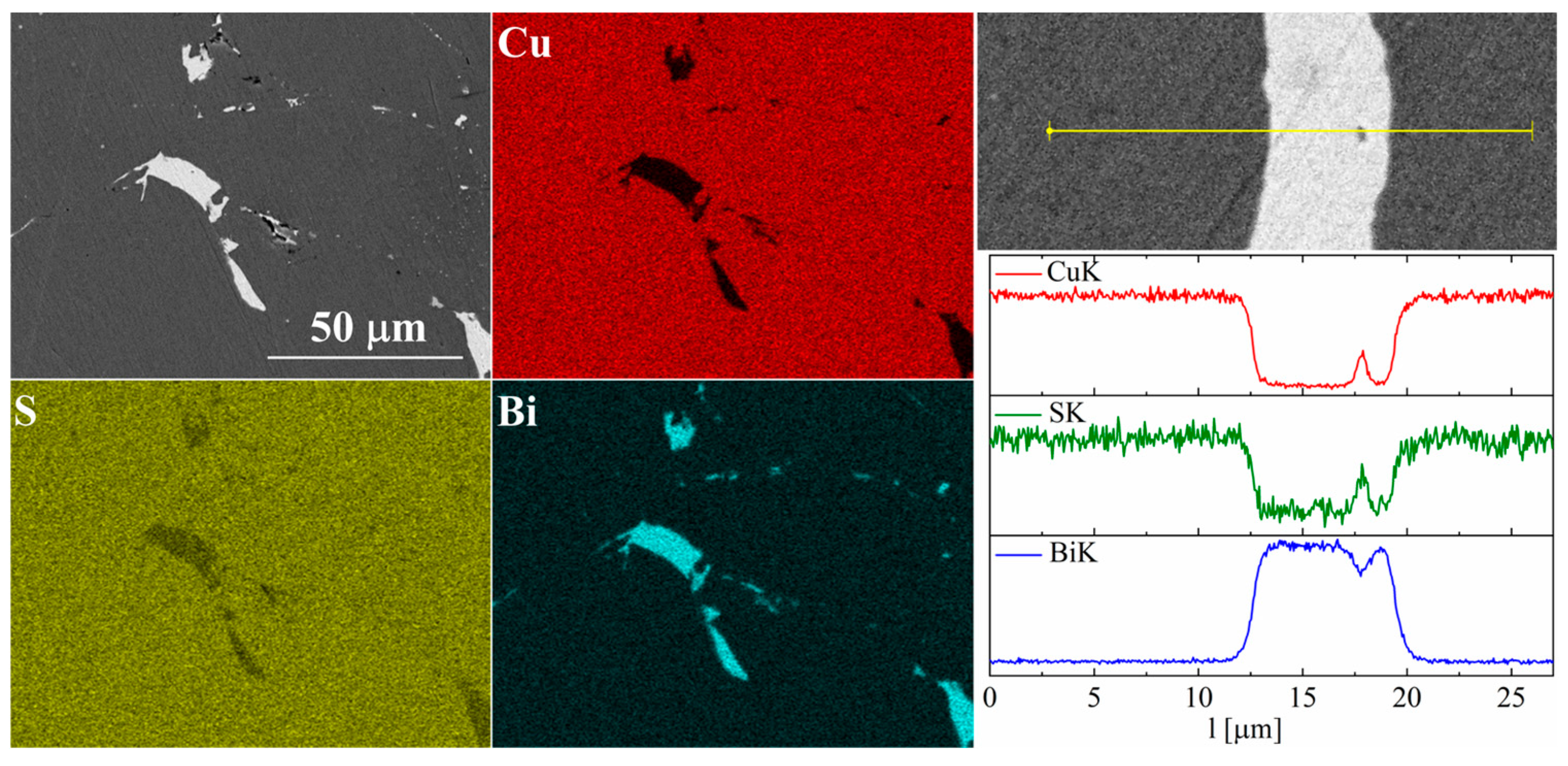
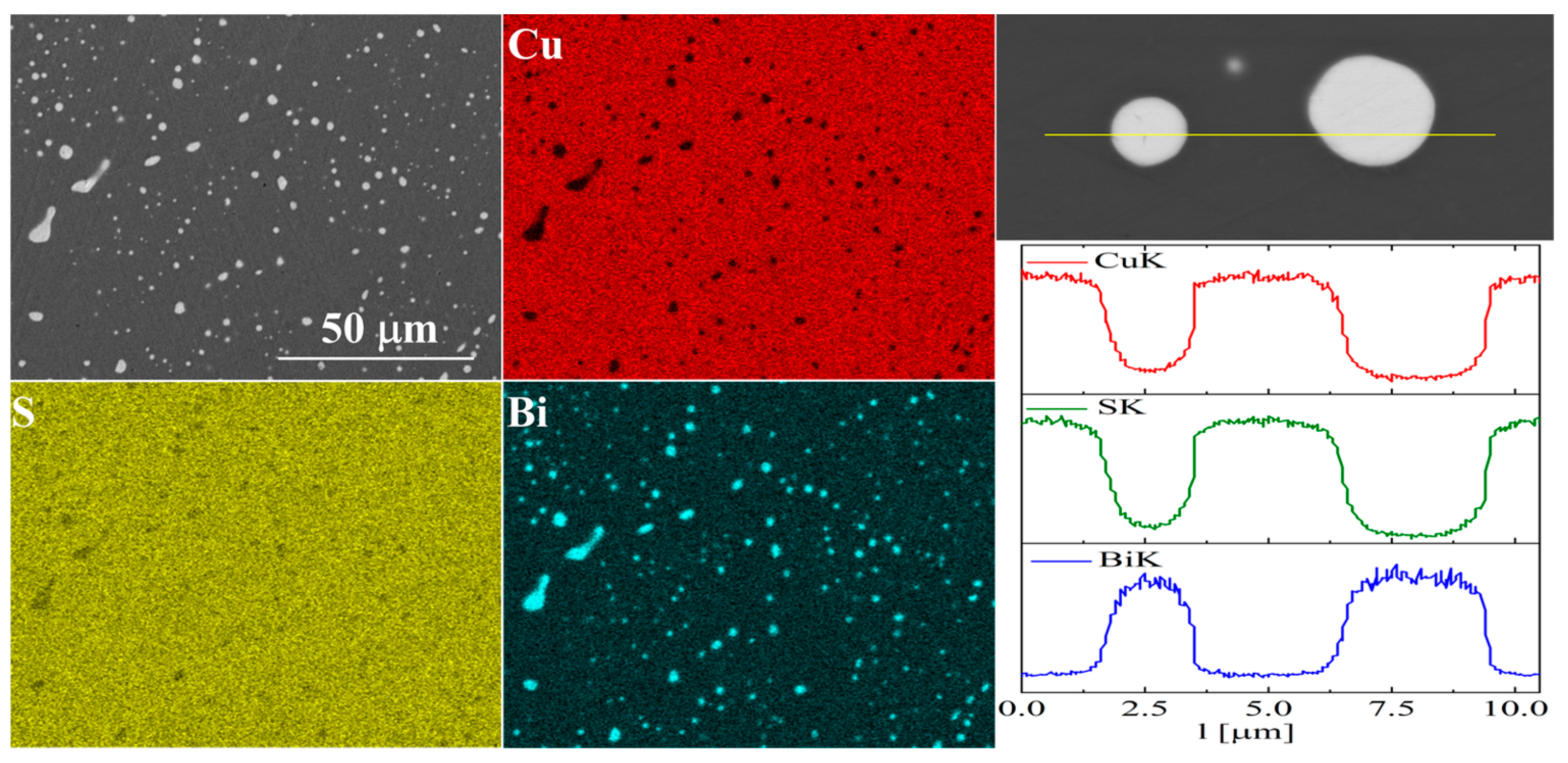
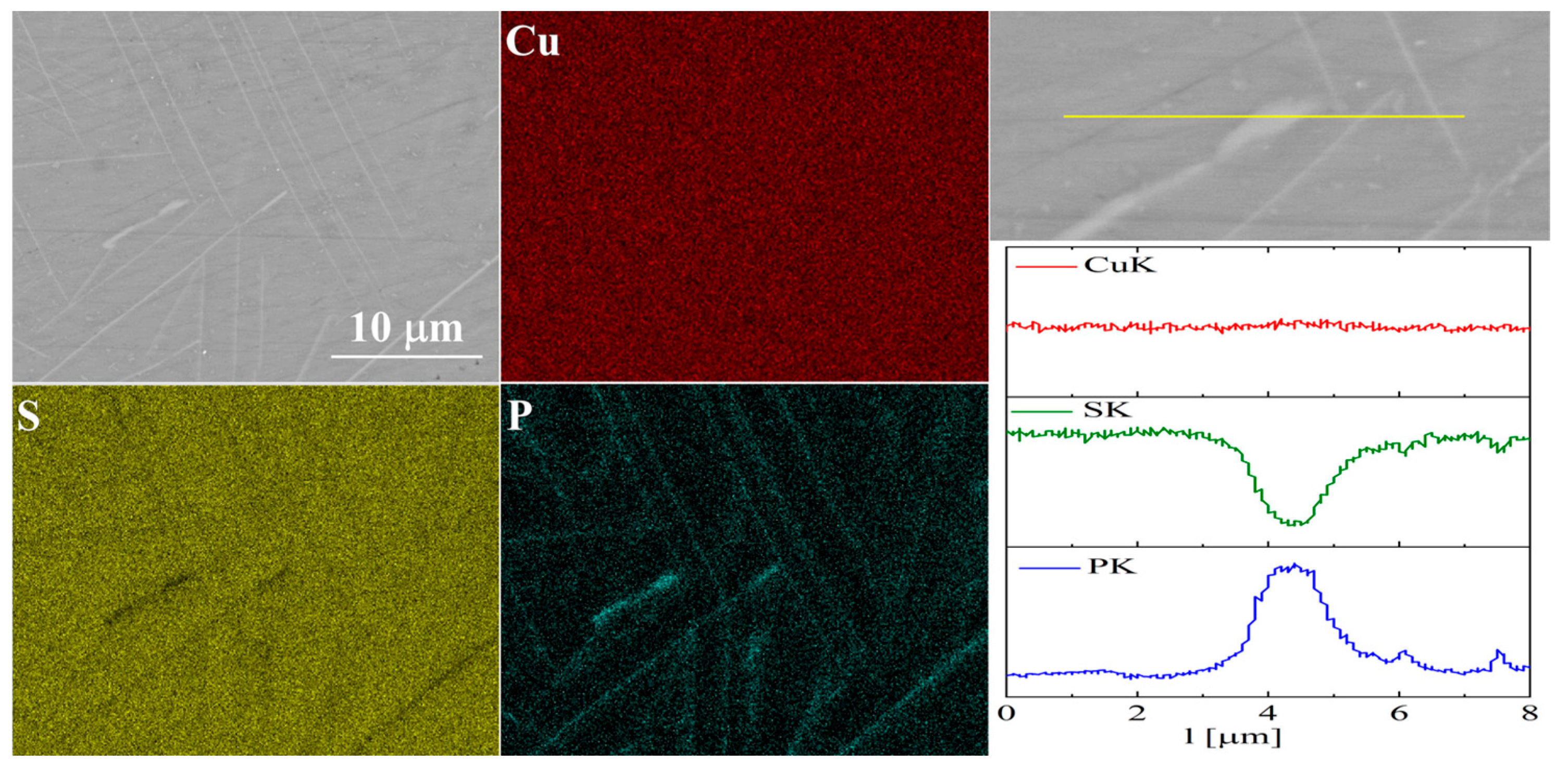
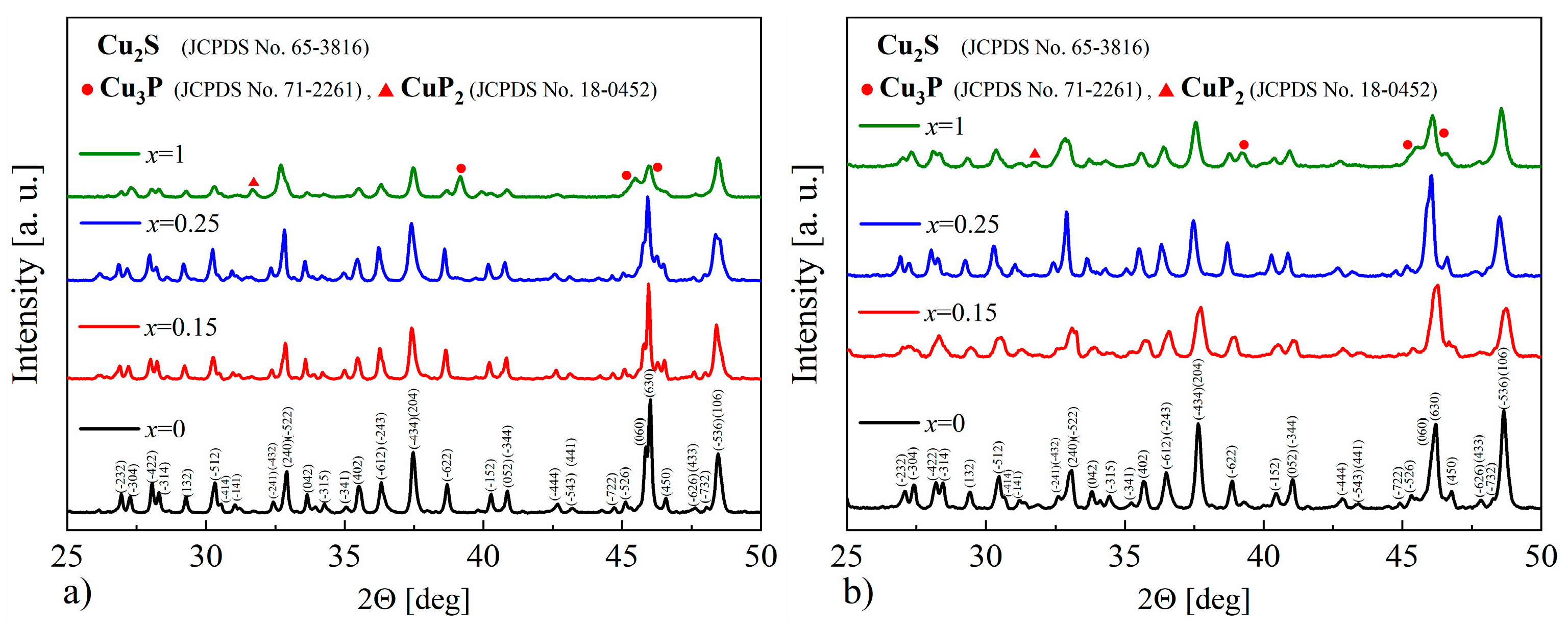
3.2. Structural and Microstructural Analysis
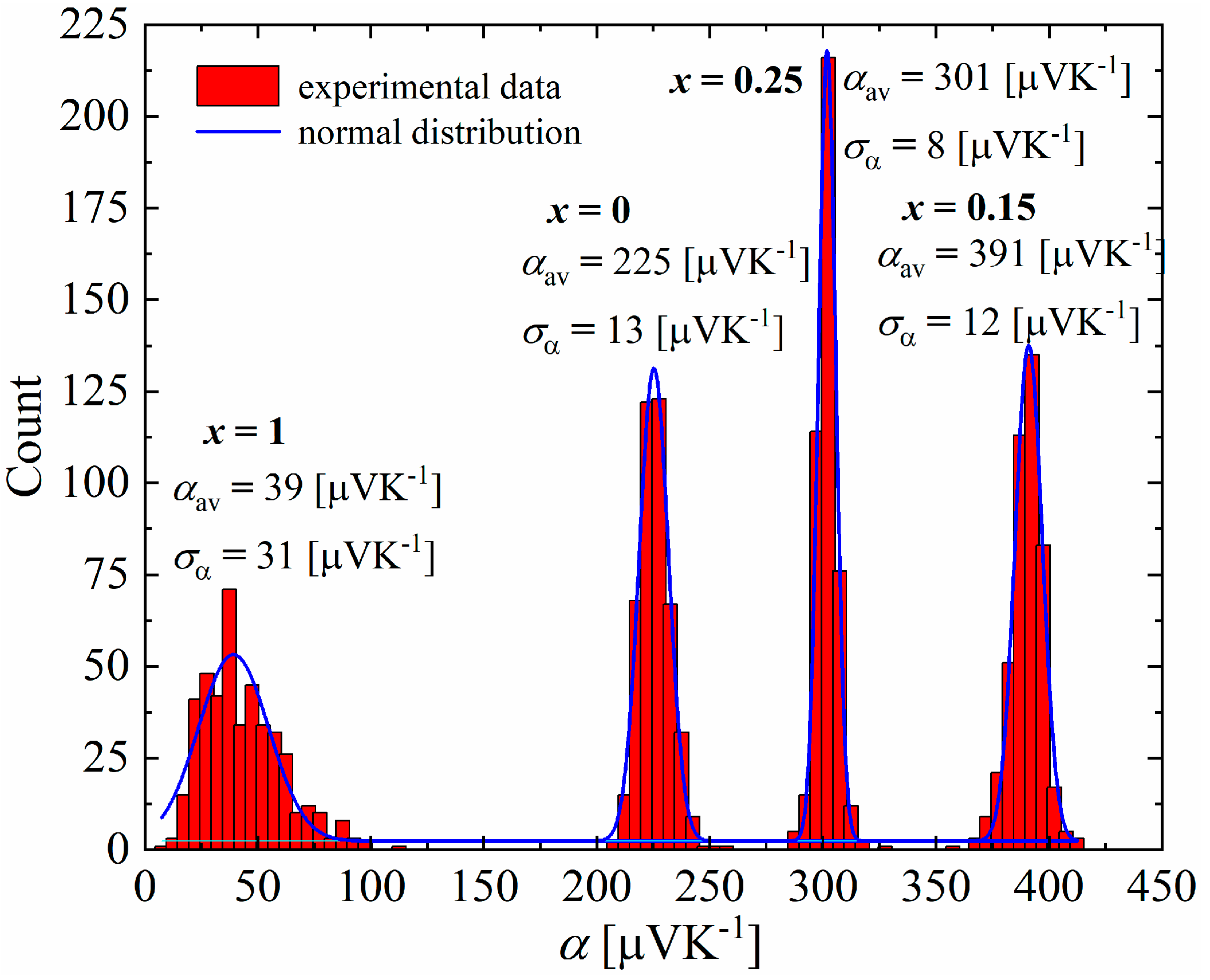
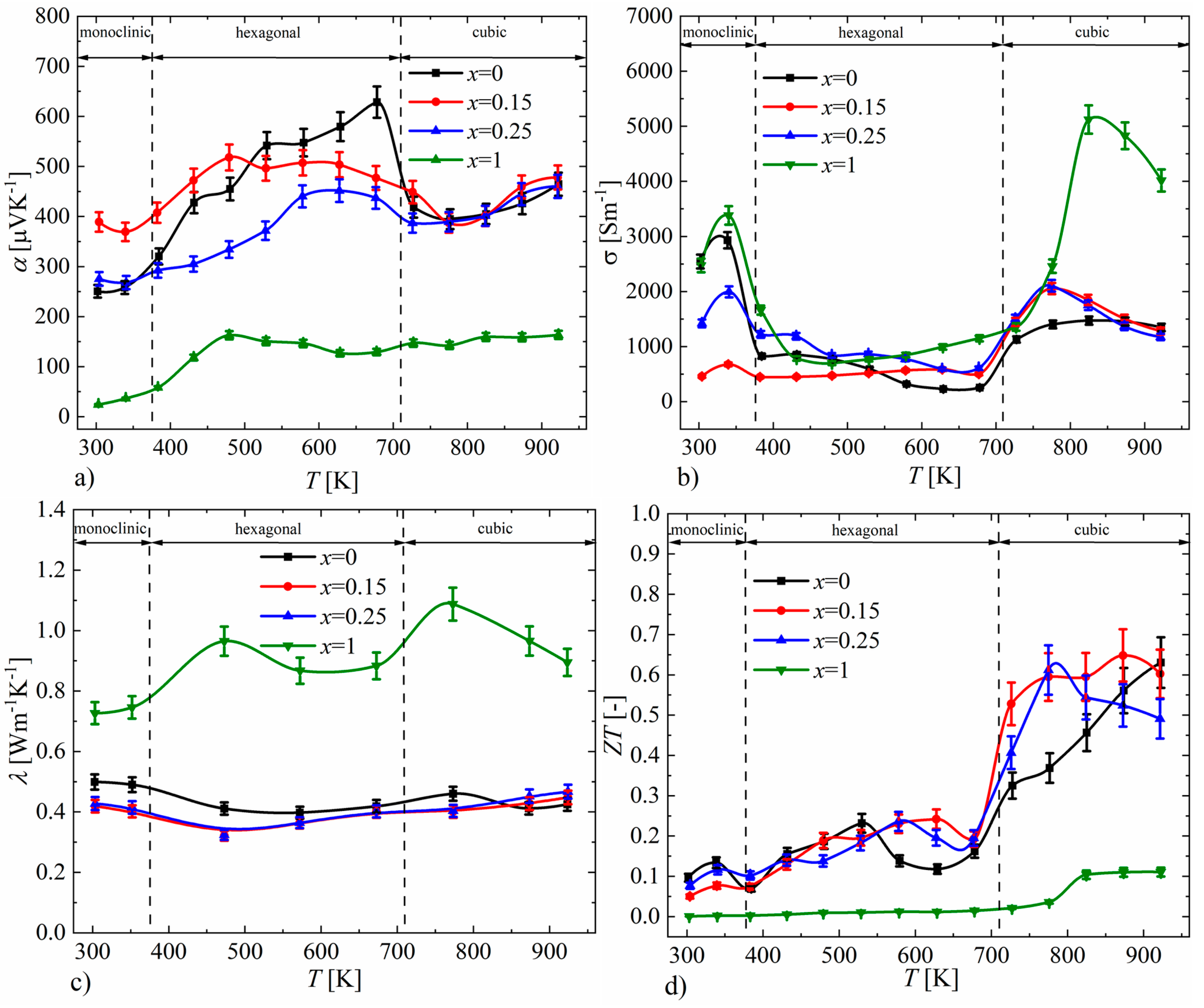
3.3. Thermoelectric Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, W.-D.; Yang, L.; Chen, Z.-G.; Zou, J. Promising and eco-friendly Cu2X-based thermoelectric materials: Progress and applications. Adv. Mater. 2020, 32, 1905703. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Qiu, P.; Shi, X.; Chen, L. Recent Advances in Liquid-Like Thermoelectric Materials. Adv. Funct. Mater. 2020, 30, 1903867. [Google Scholar] [CrossRef]
- Qiu, P.; Shi, X.; Chen, L. Cu-based thermoelectric materials. Energy Storage Mater. 2016, 3, 85–97. [Google Scholar] [CrossRef]
- Liu, H.; Shi, X.; Xu, F.; Zhang, L.; Zhang, W.; Chen, L.; Li, Q.; Uher, C.; Day, T.; Snyder, J. Copper ion liquid-like thermoelectrics. Nat. Mater. 2012, 11, 422–425. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, D.J.; Laughlin, D.E. The Cu-S (Copper-Sulfur) system. Bull. Alloy Phase Diagr. 1983, 4, 255–271. [Google Scholar] [CrossRef]
- Will, G.; Hinze, E.; Rahman, A.; Abdelrahman, M. Crystal structure analysis and refinement of digenite, Cu1.8S, in the temperature range 20 to 500 °C under controlled sulfur partial pressure. Eur. J. Miner. 2002, 14, 591–598. [Google Scholar] [CrossRef]
- Uher, C. Materials Aspect of Thermoelectricity; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Nieroda, P.; Leszczyński, J.; Mikuła, A.; Mars, K.; Kruszewski, M.J.; Koleżyński, A. Thermoelectric properties of Cu2S obtained by high temperature synthesis and sintered by IHP method. Ceram. Int. 2020, 46, 25460–25466. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B.-P.; Pei, J.; Liu, Y.-C.; Li, J.-F. Thermoelectric performance enhancement of Cu2S by Se doping leading to a simultaneous power factor increase and thermal conductivity reduction. J. Mater. Chem. C 2017, 5, 7845–7852. [Google Scholar] [CrossRef]
- He, Y.; Lu, P.; Shi, X.; Xu, F.; Zhang, T.; Snyder, J.; Uher, C.; Chen, L. Ultrahigh thermoelectric performance in mosaic crystals. Adv. Mater. 2015, 27, 3639–3644. [Google Scholar] [CrossRef]
- He, Y.; Day, T.; Zhang, T.; Liu, H.; Shi, X.; Chen, L.; Snyder, J.G. High thermoelectric performance in non-toxic earth abundant copper sulfide. Adv. Mater. 2014, 26, 3974–3978. [Google Scholar] [CrossRef]
- Zhao, L.; Xiaolin, W.; Fei, F.Y.; Wang, J.; Cheng, Z.; Dou, S.; Wang, J.; Snyder, G.J. High thermoelectric and mechanical performance in highly dense Cu2−xS bulks prepared by a meltsolidification technique. J. Mater. Chem. A 2015, 3, 9432–9437. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B.-P.; Pei, J.; Sun, Q.; Nie, G.; Zhang, W.-Z.; Zhuo, Z.-T.; Zhou, W. High Thermoelectric Figure of Merit Achieved in Cu2S1−xTex Alloys Synthesized by Mechanical Alloying and Spark Plasma Sintering. ACS Appl. Mater. Interfaces 2018, 10, 32201–32211. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Zhu, C.; Qiu, P.; Blichfeld, A.B.; Eikeland, E.; Ren, D.; Iversen, B.B.; Xu, F.; Shi, X.; Chen, L. High thermoelectric performance and low thermal conductivity in Cu2−yS1/3Se1/3Te1/3 liquid-like materials with nanoscale mosaic structures. Nano Energy 2017, 42, 43–50. [Google Scholar] [CrossRef]
- Guan, M.-J.; Qiu, P.-F.; Song, Q.-F.; Yang, J.; Ren, D.-D.; Shi, X.; Chen, L.-D. Improved electrical transport properties and optimized thermoelectric figure of merit in lithium-doped copper sulfides. Rare Met. 2018, 37, 282–289. [Google Scholar] [CrossRef]
- Liang, X.; Jin, D.; Dai, F. Phase Transition Engineering of Cu2S to Widen the Temperature Window of Improved Thermoelectric Performance. Adv. Electron. Mater. 2019, 5, 1900486. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef]
- Nieroda, P.; Kruszewski, M.J.; Leszczyński, J.; Mars, K.; Koleżyński, A. Influence of DC and AC current in the SPS sintering process on homogeneity of thermoelectric properties of Cu2S and Cu2Se. Ceram. Int. 2023, 49, 9681–9690. [Google Scholar] [CrossRef]
- Honig, R.E. Vapor Pressure Data For The More Common Elements. RCA Rev. 1957, 18, 195–204. [Google Scholar]
- Nieroda, P.; Kutorasinski, K.; Tobola, J.; Wojciechowski, K.T. Search for resonant-like impurity in Ag-doped CoSb3 skutterudite: Theoretical and experimental study. J. Electron. Mater. 2014, 43, 1681–1688. [Google Scholar] [CrossRef]
- Platzek, D.; Karpinski, G.; Stiewe, C.; Ziolkowski, P.; Drasar, C.; Müller, E. Potential Seebeck-microprobe (PSM): Measuring the spatial resolution of the Seebeck coefficient and the electric potential. In Proceedings of the ICT 2005 24th International Conference on Thermoelectrics, Clemson, SC, USA, 19–23 June 2005; pp. 13–16. [Google Scholar]
- Min, S.; Blumm, J.; Lindemann, A. A new laser flash system for measurement of the thermophysical properties. Thermochim. Acta 2007, 455, 46–49. [Google Scholar] [CrossRef]
- Shinzato, K.; Baba, T. A Laser Flash Apparatus for Thermal Diffusivity and Specific Heat Capacity Measurements. J. Therm. Anal. Calorim. 2001, 64, 413–422. [Google Scholar] [CrossRef]
- Snyder, J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Giri, K.; Wang, Y.-L.; Chen, T.-H.; Chen, C.-H. Challenges and strategies to optimize the figure of merit: Keeping eyes on thermoelectric metamaterials. Mater. Sci. Semicond. Process. 2022, 150, 106944. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, R. Thermoelectricity and Advanced Thermoelectric Materials; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Predel, B. Cu-P (Copper-Phosphorus). In Landolt-Börnstein—Group IV Physical Chemistry; Madelung, O., Ed.; Springer Materials; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Subramanian, P.R.; Laughlin, D.E. The As-Cu (Arsenic-Copper) System. Bull. Alloy Phase Diagr. 1988, 9, 605–618. [Google Scholar] [CrossRef]
- Crovetto, A.; Unold, T.; Zakutayev, A. Is Cu3−xP a Semiconductor, a Metal, or a Semimetal? Chem. Mater. 2023, 35, 1259–1272. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, K.; Garrity, K.F.; Tavazza, F. Data-driven discovery of 3D and 2D thermoelectric materials. J. Phys. Condens. Matter 2020, 32, 475501. [Google Scholar] [CrossRef]
- Liang, X. Mobile copper ions as heat carriers in polymorphous copper sulfide superionic conductors. Appl. Phys. Lett. 2017, 111, 133902. [Google Scholar]





| Model Structure | Enthalpy of Doping ∆H [eV/atom] |
|---|---|
| Cu32S15P1 | −0.00682 |
| Cu32S15As1 | 0.00722 |
| Cu32S15Sb1 | 0.02018 |
| Cu32S15Bi1 | −0.21230 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nieroda, P.; Leszczyński, J.; Kapera, K.; Rutkowski, P.; Ziewiec, K.; Szymańska, A.; Kruszewski, M.J.; Rudnik, M.; Koleżyński, A. Thermoelectric Properties of Cu2S Doped with P, As, Sb and Bi—Theoretical and Experimental Studies. Materials 2024, 17, 5440. https://doi.org/10.3390/ma17225440
Nieroda P, Leszczyński J, Kapera K, Rutkowski P, Ziewiec K, Szymańska A, Kruszewski MJ, Rudnik M, Koleżyński A. Thermoelectric Properties of Cu2S Doped with P, As, Sb and Bi—Theoretical and Experimental Studies. Materials. 2024; 17(22):5440. https://doi.org/10.3390/ma17225440
Chicago/Turabian StyleNieroda, Paweł, Juliusz Leszczyński, Krzysztof Kapera, Paweł Rutkowski, Krzysztof Ziewiec, Aleksandra Szymańska, Mirosław J. Kruszewski, Małgorzata Rudnik, and Andrzej Koleżyński. 2024. "Thermoelectric Properties of Cu2S Doped with P, As, Sb and Bi—Theoretical and Experimental Studies" Materials 17, no. 22: 5440. https://doi.org/10.3390/ma17225440
APA StyleNieroda, P., Leszczyński, J., Kapera, K., Rutkowski, P., Ziewiec, K., Szymańska, A., Kruszewski, M. J., Rudnik, M., & Koleżyński, A. (2024). Thermoelectric Properties of Cu2S Doped with P, As, Sb and Bi—Theoretical and Experimental Studies. Materials, 17(22), 5440. https://doi.org/10.3390/ma17225440






