Scott Blair Fractional-Type Viscoelastic Behavior of Clear Spruce Wood: Influence of Compression Wood on Power-Law Stiffness Parameters
Abstract
:1. Introduction
- (i)
- One may pose the question how the density influences the observed stiffness of compression wood (as compared to the well-described density-based material functions for regular wood)?
- (ii)
- In the case the data are normalized, i.e., when comparing regular wood and compression wood with the same density (but both sample batches are cut from a unique macro-sample, e.g., board), what is the difference in behavior?
- (iii)
- On a more theoretical note, we address the question of which viscoelastic material model may represent the experimental data best, with special emphasis on the medium-term (order of several days) prediction of material behavior.
2. Methodology
2.1. Preparation and Handling of Specimens
2.2. Setup of Creep Experiments
- Application of the target load with a loading ramp characterized by a constant rate of applied force within a duration of 10 s.
- Sustaining the target load for a duration of the dwelling phase of 1800 s at a constant temperature level of 20 °C and a sample mass equilibrium associated to an enclosing humidity of 65%, resulting in a moisture content of approximately 12%.
- Unloading the specimens and subsequently reloading until bending failure within s [24,25]. Note that, as the bending strength was determined on specimens which have been exposed to (however, only moderate) loading for the duration of the creep test, the failure strength as reported in this paper does not comply with the prevalent standards for the conduction of strength experiments and needs to be taken with a grain of salt.
2.3. Evaluation of the Uniaxial Compliance Function from Three-Point Bending Experiments
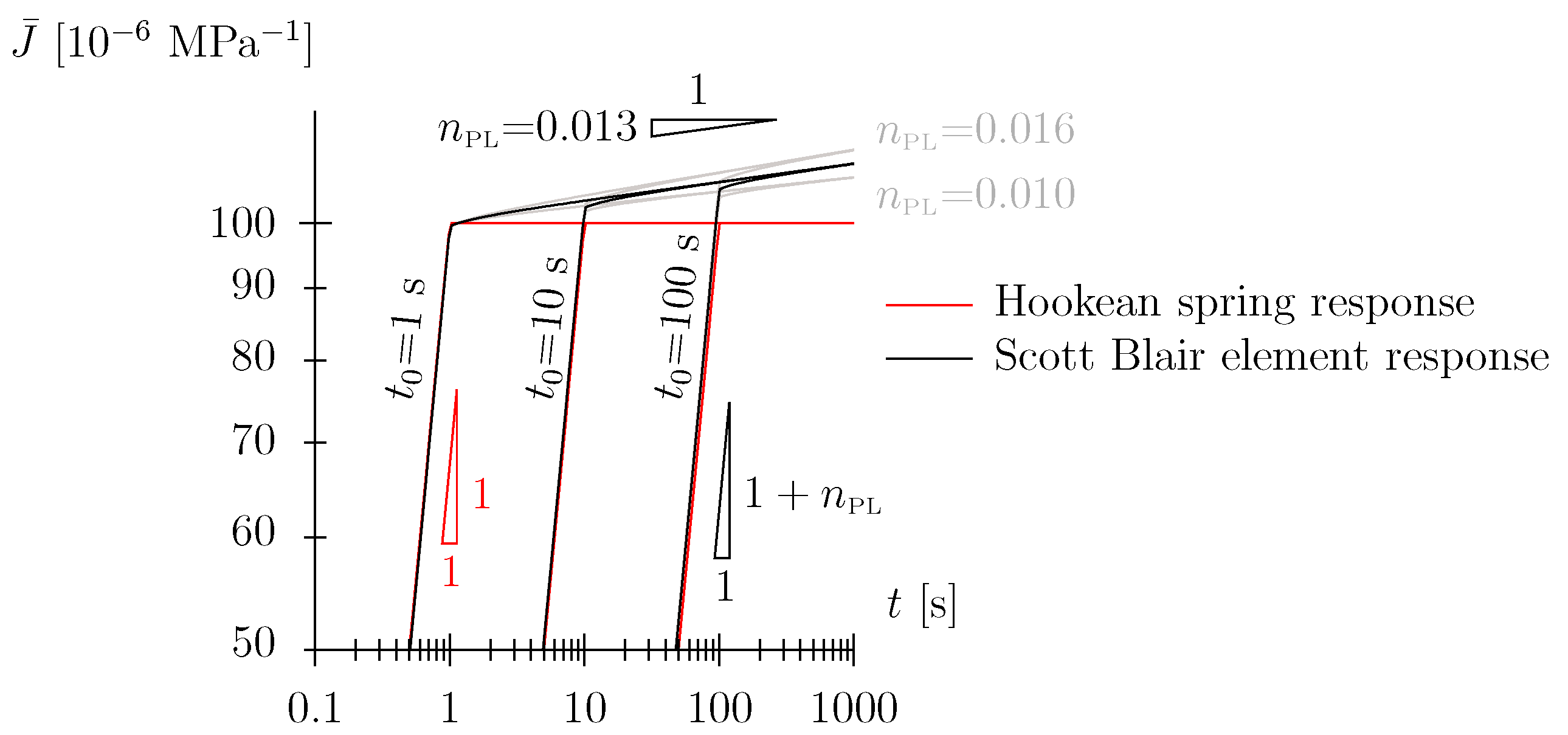
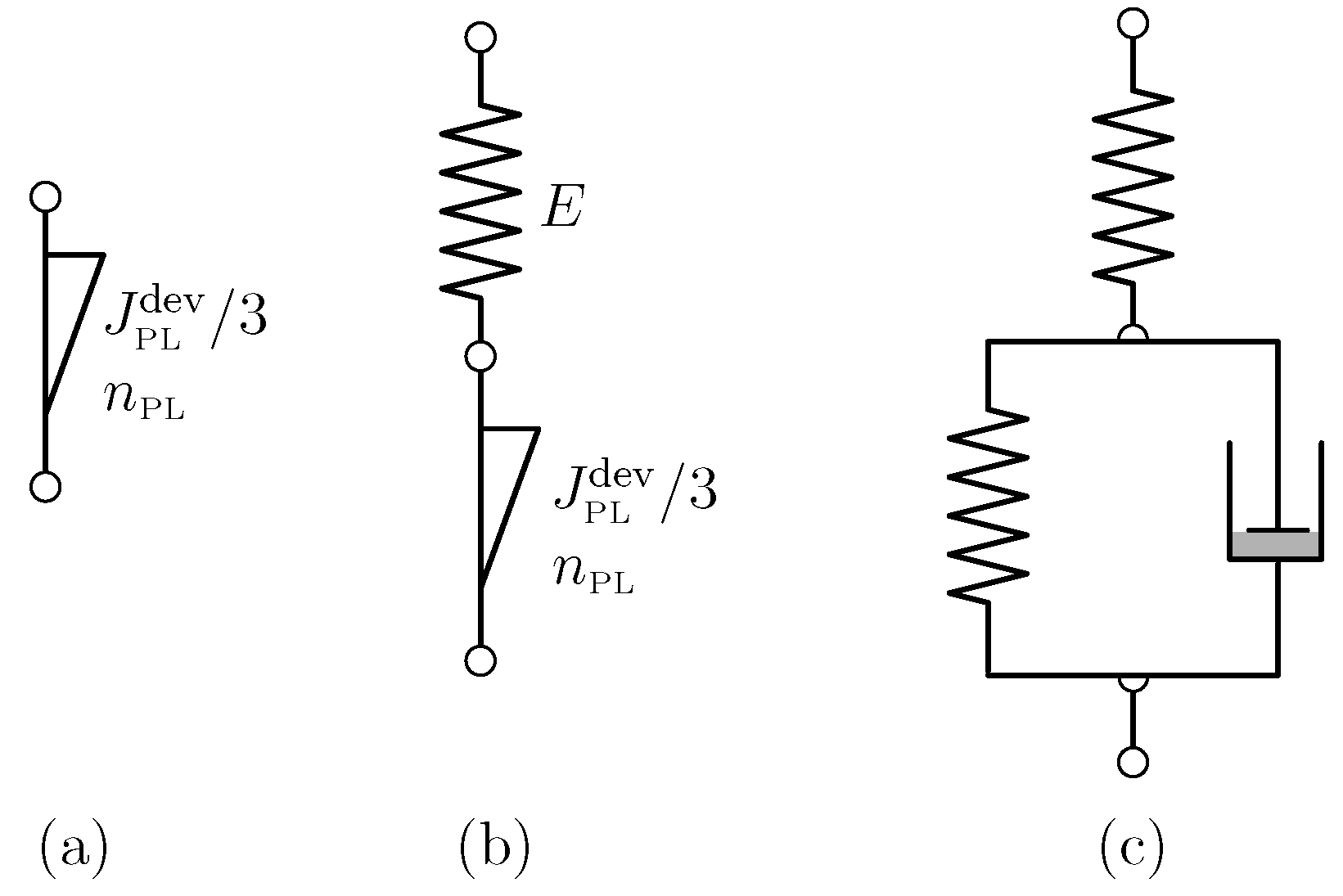
2.4. Constitutive Modeling of Viscoelastic Behavior of Wood with Scott Blair Element
2.5. What Is Our Motivation to Abstain from Employing a Hookean Spring in the Viscoelastic Model?
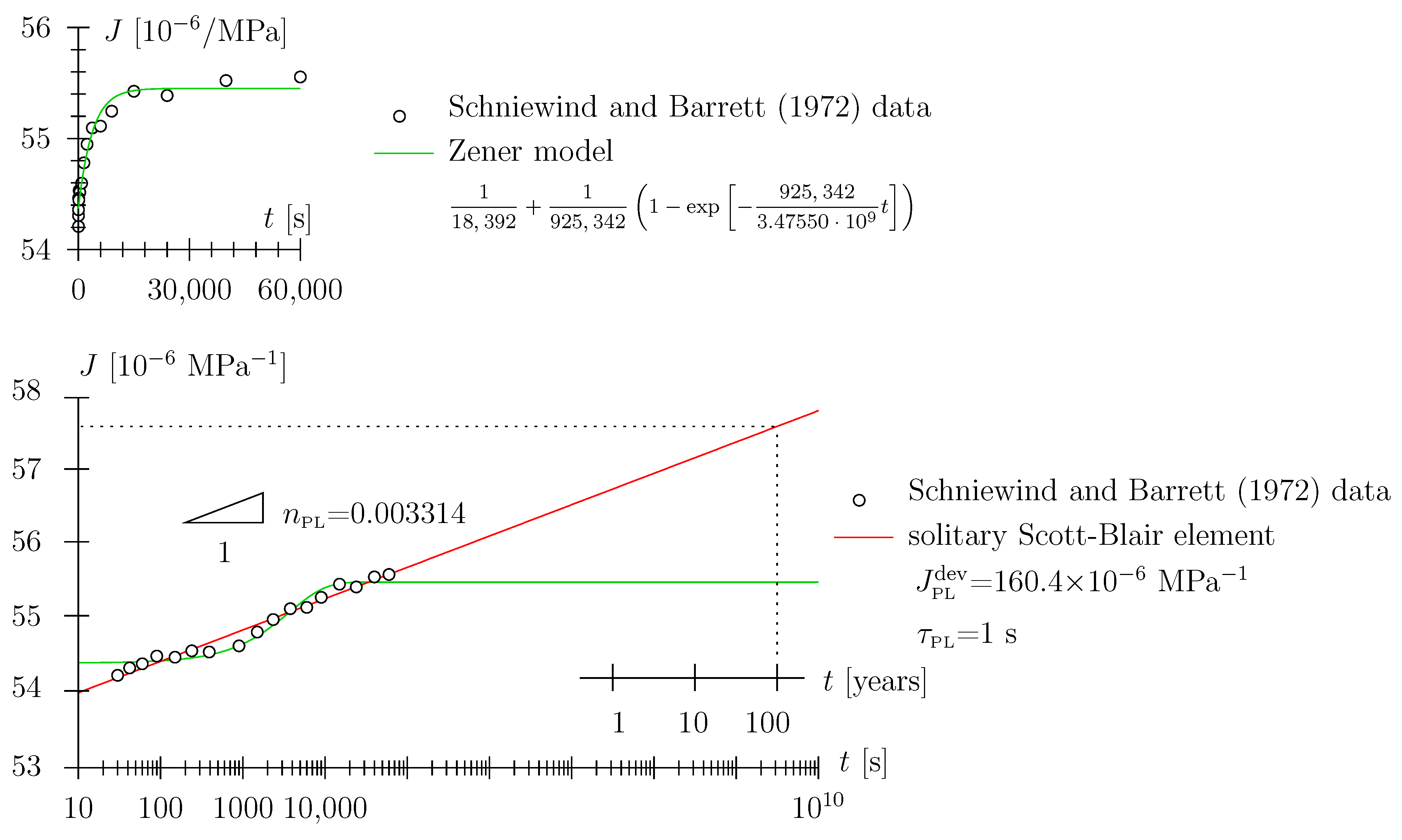
- We have already addressed the nonlinear Maxwell model employed by [9] to some extent. An additional point to mention is that the introduction of the Hookean spring leads to a seemingly ever-increasing slope in the log-log diagram; the prescribed power-law exponent of the Scott Blair element = 0.0608 is reached only after a ridiculously long time span (see small inlay in Figure 4). The allowance of this quasi-ever-increasing slope (in the log-log diagram in terms of engineering application of the model), with the associated implication on the long-term behavior of the order of days or weeks (or even months), i.e., prediction of material behavior, seems, in our estimation, to be too bold a statement to be made based upon the underlying data.
- We might argue that back-calculation of the [9] data with a solitary Scott Blair element (see red graph in Figure 5) may seem appropriate and the prediction of the medium- or long-term behavior quite plausible; however, in fairness, one has to state that, based on data quality, one cannot decide which model depicts reality better. Playing devil’s advocate, this statement may also be tested against other viscoelastic models, e.g., the Zener model: a Hookean spring connected in series with a Kelvin–Voigt element, with the latter constituted by a Hookean spring connected in parallel with a Newtonian damper (see green graph in Figure 5; for a schematic of the Zener model, see Figure 3c). Considering the least-square residual (from the employed nonlinear parameter identification algorithm) as the only measure for model fitness, the Zener model may even be victorious among the models considered. When depicting the data in a linear diagram (see small inlay in Figure 5) one may even trick an unalert reader to think this model is superior to the ones previously discussed. However, considering the (non-existent) long-term predictive capability may constitute a strong motivation for model dismissal.
2.6. Supposition That Three-Parameter Models Are Overdetermined with Respect to the Number of Free Parameters and Lead to Non-Uniqueness of the Back-Calculated Material Parameters
3. Results
- The loading direction with respect to the growth ring plane (either perpendicular or parallel to) does not significantly influence the material parameters (see circle and square symbols in Figure 8). This should come as no surprise as the observed deformation in a slender beam is primarily caused by the normal stress in the longitudinal direction. Geometrical considerations make shear stresses (in the radial or tangential direction, depending on the sample orientation during testing) negligible as regards the observed deformation.
- There is no significant influence of the dry density on the power-law exponent ; the latter is back-calculated in a narrow range from approximately 0.010 to 0.015 (see Figure 8b). Some of our unpublished work, however, hints at the possibility that is a function of the moisture content. As the moisture content has not been varied in the present study (approximately 11 to 12% throughout the experimental campaign), this possible dependency is left to future discussions.
4. Discussion
4.1. In Reply to Engineering Questions (i) and (ii), Respectively
4.2. In Reply to Engineering Question (iii)
5. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Ramp Compliance of a Scott Blair Element
Appendix B. Mechano-Sorptive Coupling Effects Relevant in Creep Experiments
Appendix C. Statistical Analysis of Data
| # | [ ] | nPL [–] | Q [–] |
|---|---|---|---|
| 1 | 335.50 ± 0.48 | 0.014308 ± 0.000200 | 1.0000000000000000 |
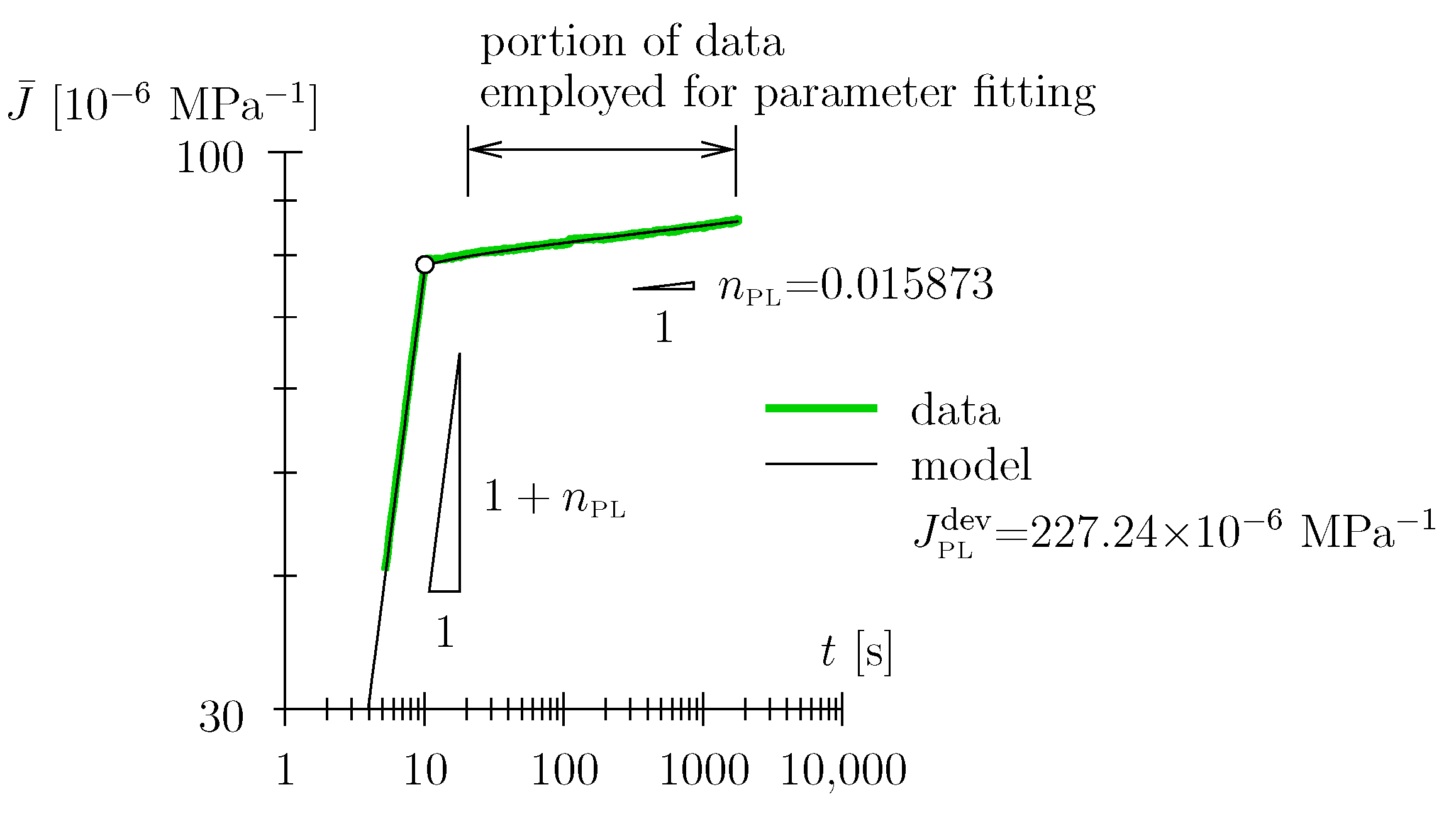
| 2 | 227.24 ± 0.48 | 0.015873 ± 0.000293 | 1.0000000000000000 |
| 3 | 265.79 ± 0.49 | 0.012124 ± 0.000256 | 1.0000000000000000 |
| 4 | 299.66 ± 0.47 | 0.017845 ± 0.000220 | 1.0000000000000000 |
| 5 | 289.66 ± 0.47 | 0.016017 ± 0.000230 | 1.0000000000000000 |
| 6 | 277.87 ± 0.47 | 0.017777 ± 0.000237 | 1.0000000000000000 |
| 7 | 307.68 ± 0.49 | 0.010005 ± 0.000224 | 1.0000000000000000 |
| 8 | 228.33 ± 0.49 | 0.010350 ± 0.000301 | 1.0000000000000000 |
| 9 | 249.03 ± 0.49 | 0.011992 ± 0.000274 | 1.0000000000000000 |
| 10 | 294.67 ± 0.48 | 0.014686 ± 0.000228 | 1.0000000000000000 |
| 11 | 248.15 ± 0.49 | 0.010785 ± 0.000276 | 1.0000000000000000 |
| 16 | 272.09 ± 0.49 | 0.010174 ± 0.000253 | 1.0000000000000000 |
| 17 | 311.15 ± 0.49 | 0.011241 ± 0.000220 | 1.0000000000000000 |
| 23 | 249.09 ± 0.49 | 0.008761 ± 0.000278 | 1.0000000000000000 |
| 24 | 275.92 ± 0.48 | 0.013655 ± 0.000244 | 1.0000000000000000 |
| 26 | 292.81 ± 0.48 | 0.013320 ± 0.000231 | 1.0000000000000000 |
| 14 | 313.33 ± 0.48 | 0.013558 ± 0.000215 | 1.0000000000000000 |
| 15 | 314.16 ± 0.48 | 0.013437 ± 0.000215 | 1.0000000000000000 |
| 19 | 304.51 ± 0.49 | 0.011739 ± 0.000224 | 1.0000000000000000 |
| 20 | 301.99 ± 0.50 | 0.006894 ± 0.000232 | 1.0000000000000000 |
| 21 | 318.49 ± 0.48 | 0.014725 ± 0.000210 | 1.0000000000000000 |
| 22 | 318.10 ± 0.48 | 0.013254 ± 0.000213 | 1.0000000000000000 |
| 25 | 319.54 ± 0.49 | 0.011012 ± 0.000215 | 1.0000000000000000 |
| 28 | 314.16 ± 0.48 | 0.013934 ± 0.000215 | 1.0000000000000000 |
| 29 | 338.20 ± 0.48 | 0.014405 ± 0.000199 | 1.0000000000000000 |
| 30 | 305.03 ± 0.48 | 0.012485 ± 0.000223 | 1.0000000000000000 |
| 31 | 328.15 ± 0.49 | 0.011616 ± 0.000208 | 1.0000000000000000 |
| 12 | 285.35 ± 0.48 | 0.013207 ± 0.000237 | 1.0000000000000000 |
Appendix D

References
- Niemz, P.; Teischinger, A.; Sandberg, D. Springer Handbook of Wood Science and Technology; Springer Handbooks; Springer International Publishing: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Rosenthal, M.; Bäucker, E. Druckholz–Reaktionsholz der Nadelhölzer: Ausgewählte Eigenschaften und wesentliche Unterschiede zum normalen Holzgewebe. Holz-Zentralblatt 2012, 138, 1104–1107. [Google Scholar]
- Gindl, W.; Teischinger, A. Axial compression strength of Norway spruce related to structural variability and lignin content. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1623–1628. [Google Scholar] [CrossRef]
- Burgert, I.; Gierlinger, N.; Eder, M.; Fratzl, P. The mechanical design of wood cell walls. J. Biomech. 2006, 39, S351. [Google Scholar] [CrossRef]
- Kollmann, F. Technologie des Holzes und der Holzwerkstoffe; Springer: Berlin/Heidelberg, Germany, 1951. [Google Scholar]
- Clair, B.; Thibaut, B. Physical and Mechanical Properties of Reaction Wood. In The Biology of Reaction Wood; Gardiner, B., Barnett, J., Saranpää, P., Gril, J., Eds.; Springer Series in Wood Science; Springer: Berlin/Heidelberg, Germany, 2014; pp. 171–200. [Google Scholar]
- Ross, R.J. Wood Handbook: Wood as an Engineering Material; Technical report; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010. [Google Scholar]
- DIN4074. DIN 4074-1:2012-06; Sortierung von Holz nach der Tragfähigkeit-Teil 1: Nadelschnittholz. Technical report; Beuth Verlag GmbH: Berlin/Heidelberg, Germany, 2012.
- Schniewind, A.P.; Barrett, J.D. Wood as a linear orthotropic viscoelastic material. Wood Sci. Technol. 1972, 6, 43–57. [Google Scholar] [CrossRef]
- Pech, S.; Lukacevic, M.; Füssl, J. A robust multisurface return-mapping algorithm and its implementation in Abaqus. Finite Elem. Anal. Des. 2021, 190, 103531. [Google Scholar] [CrossRef]
- Pichler, C.; Oberparleiter, S.; Lackner, R. Scott Blair fractional-type viscoelastic behavior of thermoplastic polyurethane. Polymers 2023, 15, 3770. [Google Scholar] [CrossRef]
- Tissaoui, J. Effects of Long-Term Creep on the Integrity of Modern Wood Structures. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 1996. [Google Scholar]
- Ozyhar, T.; Hering, S.; Niemz, P. Viscoelastic characterization of wood: Time dependence of the orthotropic compliance in tension and compression. J. Rheol. 2013, 57, 699–717. [Google Scholar] [CrossRef]
- Liu, T. Creep of wood under a large span of loads in constant and varying environments: Part 1: Experimental observations and analysis. Holz Roh- Werkst. 1993, 51, 400–405. [Google Scholar] [CrossRef]
- Tong, D.; Brown, S.A.; Corr, D.; Cusatis, G. Wood creep data collection and unbiased parameter identification of compliance functions. Holzforschung 2020, 74, 1011–1020. [Google Scholar] [CrossRef]
- Schwaighofer, M.; Königsberger, M.; Zelaya-Lainez, L.; Lukacevic, M.; Serna-Loaiza, S.; Harasek, M.; Zikeli, F.; Friedl, A.; Füssl, J. The viscoelastic behavior of lignin: Quantification through nanoindentation relaxation testing on hot-pressed technical lignin samples from various origins. Mech. Mater. 2024, 188, 104864. [Google Scholar] [CrossRef]
- Lotfy, M.; El-Osta, M.; Wellwood, R.W. Short-Term Creep as Related To Microfibril Angle. Wood Fiber Sci. 1972, 4, 26–32. [Google Scholar]
- Peng, H.; Salmen, L.; Jiang, J.; Lu, J. Creep properties of compression wood fibers. Wood Sci. Technol. 2020, 54, 1497–1510. [Google Scholar] [CrossRef]
- Haque, M.N.; Langrish, T.A.G.; Keep, L.B.; Keey, R.B. Model fitting for visco-elastic creep of Pinus radiata during kiln drying. Wood Sci. Technol. 2000, 34, 447–457. [Google Scholar] [CrossRef]
- Hunt, D.G. The prediction of long-time viscoelastic creep from short-time data. Wood Sci. Technol. 2004, 38, 479–492. [Google Scholar] [CrossRef]
- Hoyle, R.J.; Griffith, M.C.; Itani, R.Y. Primary Creep in Douglas-Fir Beams of Commercial Size and Quality. Wood Fiber Sci. 1985, 17, 300–314. [Google Scholar]
- Bach, L. Nonlinear Mechanical Behavior of Wood in Longitudinal Tension. Ph.D. Thesis, State University of New York College of Environmental Science and Forestry, New York, NY, USA, 1966. [Google Scholar]
- Hofer, U.; Pichler, C.; Maderebner, R.; Lackner, R. Lomnitz-type viscoelastic behavior of clear spruce wood as identified by creep and relaxation experiments: Influence of moisture content and elevated temperatures up to 80 degrees Celcius. Wood Sci. Technol. 2019, 53, 765–783. [Google Scholar] [CrossRef]
- ISO 13061-3:2014; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 3: Determination of Ultimate Strength in Static Bending. Technical Report; International Organization for Standardization: Geneva, Switzerland, 2014.
- DIN 52186:1978-06; Prüfung von Holz. Biegeversuch. Technical Report; Beuth Verlag GmbH: Berlin/Heidelberg, Germany, 1978.
- Eitelberger, J.; Bader, T.K.; de Borst, K.; Jäger, A. Multiscale prediction of viscoelastic properties of softwood under constant climatic conditions. Comput. Mater. Sci. 2012, 55, 303–312. [Google Scholar] [CrossRef]
- Pichler, C.; Maier, M.; Lackner, R. Viscoelastic response of closed-cell polyurethane foams from half hour-long creep tests: Identification of Lomnitz behavior. ASME J. Eng. Mater. Technol. 2019, 141, 021001. [Google Scholar] [CrossRef]
- Pandey, V.; Holm, S. Linking the fractional derivative and the Lomnitz creep law to non-Newtonian time-varying viscosity. Phys. Rev. E 2016, 94, 032606. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Press, H.P.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Yang, J.L.; Evans, R. Prediction of MOE of eucalypt wood from microfibril angle and density. Holz Roh Werkst. 2003, 61, 449–452. [Google Scholar] [CrossRef]
- Acker, P.; Ulm, F.J. Creep and shrinkage of concrete: Physical origins and practical measurements. Nucl. Eng. Des. 2001, 203, 148–158. [Google Scholar] [CrossRef]
- Bazant, Z.P. Constitutive equation of wood at variable humidity and temperature. Wood Sci. Technol. 1985, 19, 159–177. [Google Scholar] [CrossRef]
- Pichler, C.; Lackner, R. Post-peak decelerating reaction of Portland cement: Monitoring by heat flow calorimetry, modelling by Elovich-Landsberg model and reaction-order model. Constr. Build. Mater. 2019, 231, 117107. [Google Scholar] [CrossRef]


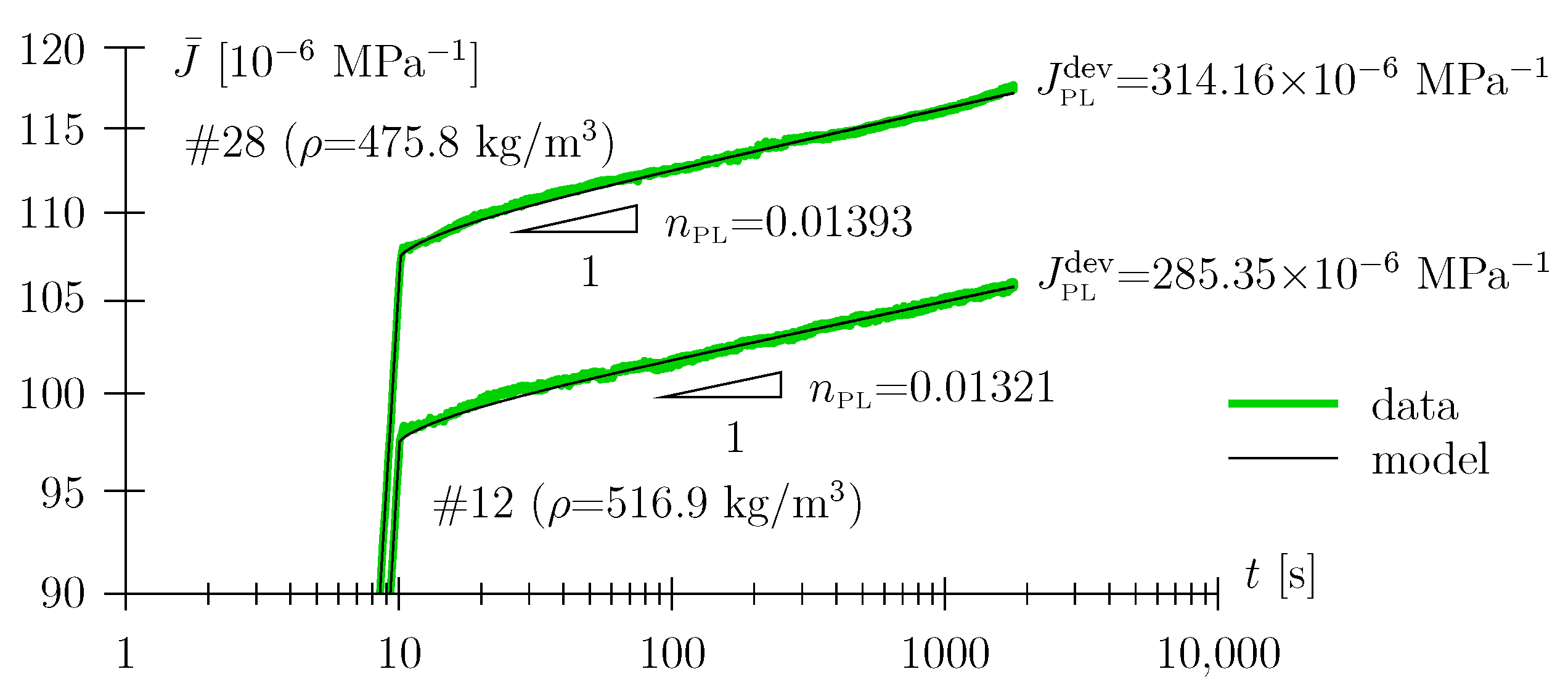

| # | Loading Direction | Midspan Load [N] | Moisture Content [%] | Dry Density [kg/m3] | Compression Wood Content [%] | [10−6 MPa−1] | nPL [–] | Bending Strength [MPa] |
|---|---|---|---|---|---|---|---|---|
| 1 | ⊥ | 225 | 11.23 | 341.1 | 0 | 335.5 | 0.01430 | 72.5 |
| 2 | ‖ | 225 | 11.62 | 438.5 | 0 | 227.2 | 0.01587 | 111.2 |
| 3 | ⊥ | 225 | 11.31 | 353.9 | 0 | 265.8 | 0.01212 | 85.3 |
| 4 | ‖ | 225 | 11.62 | 346.8 | 0 | 299.7 | 0.01785 | 68.1 |
| 5 | ⊥ | 225 | 11.54 | 358.9 | 0 | 289.7 | 0.01602 | 82.7 |
| 6 | ‖ | 225 | 11.19 | 356.8 | 0 | 277.9 | 0.01778 | 76.0 |
| 7 | ⊥ | 225 | 11.31 | 349.5 | 0 | 307.7 | 0.01000 | 76.5 |
| 8 | ‖ | 225 | 11.24 | 440.8 | 0 | 228.3 | 0.01035 | 110.8 |
| 9 | ⊥ | 225 | 11.54 | 383.5 | 0 | 249.0 | 0.01199 | 93.8 |
| 10 | ‖ | 225 | 11.25 | 346.9 | 0 | 294.7 | 0.01468 | 73.7 |
| 11 | ⊥ | 225 | 11.36 | 431.1 | 0 | 248.1 | 0.01078 | 95.2 |
| 16 | ‖ | 225 | 11.93 | 437.0 | 35.00 | 272.1 | 0.01017 | 96.4 |
| 17 | ⊥ | 225 | 11.62 | 398.1 | 32.33 | 311.2 | 0.01124 | 83.1 |
| 23 | ⊥ | 225 | 11.84 | 458.3 | 30.47 | 249.1 | 0.00876 | 89.3 |
| 24 | ‖ | 225 | 11.72 | 439.0 | 30.78 | 275.9 | 0.01366 | 90.9 |
| 26 | ‖ | 225 | 11.79 | 384.7 | 25.11 | 292.8 | 0.01332 | 80.4 |
| 14 | ‖ | 225 | 11.91 | 466.3 | 41.99 | 313.3 | 0.01356 | 96.8 |
| 15 | ⊥ | 225 | 12.04 | 447.7 | 41.24 | 314.2 | 0.01344 | 86.3 |
| 19 | ⊥ | 225 | 11.81 | 468.7 | 48.94 | 304.5 | 0.01174 | 94.6 |
| 20 | ‖ | 225 | 12.10 | 480.2 | 47.49 | 302.0 | 0.00689 | 97.0 |
| 21 | ⊥ | 225 | 11.95 | 455.9 | 44.24 | 318.5 | 0.01472 | 88.9 |
| 22 | ‖ | 225 | 11.97 | 458.5 | 45.54 | 318.1 | 0.01325 | 91.1 |
| 25 | ⊥ | 225 | 11.65 | 462.2 | 42.11 | 319.5 | 0.01101 | 87.9 |
| 28 | ‖ | 225 | 11.91 | 475.8 | 44.18 | 314.2 | 0.01393 | 89.6 |
| 29 | ⊥ | 325 | 12.00 | 444.6 | 44.82 | 338.2 | 0.01440 | 86.7 |
| 30 | ‖ | 325 | 11.85 | 455.7 | 46.63 | 305.0 | 0.01248 | 90.9 |
| 31 | ⊥ | 325 | 11.79 | 461.4 | 47.57 | 328.1 | 0.01162 | 93.3 |
| 12 | ‖ | 225 | 11.70 | 516.9 | 53.27 | 285.3 | 0.01321 | 94.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pichler, C.; Maderebner, R.; Dummer, A.; Stieb, T.; Lackner, R. Scott Blair Fractional-Type Viscoelastic Behavior of Clear Spruce Wood: Influence of Compression Wood on Power-Law Stiffness Parameters. Materials 2024, 17, 5477. https://doi.org/10.3390/ma17225477
Pichler C, Maderebner R, Dummer A, Stieb T, Lackner R. Scott Blair Fractional-Type Viscoelastic Behavior of Clear Spruce Wood: Influence of Compression Wood on Power-Law Stiffness Parameters. Materials. 2024; 17(22):5477. https://doi.org/10.3390/ma17225477
Chicago/Turabian StylePichler, Christian, Roland Maderebner, Alexander Dummer, Thomas Stieb, and Roman Lackner. 2024. "Scott Blair Fractional-Type Viscoelastic Behavior of Clear Spruce Wood: Influence of Compression Wood on Power-Law Stiffness Parameters" Materials 17, no. 22: 5477. https://doi.org/10.3390/ma17225477
APA StylePichler, C., Maderebner, R., Dummer, A., Stieb, T., & Lackner, R. (2024). Scott Blair Fractional-Type Viscoelastic Behavior of Clear Spruce Wood: Influence of Compression Wood on Power-Law Stiffness Parameters. Materials, 17(22), 5477. https://doi.org/10.3390/ma17225477






