Enhanced Mechanical Properties of Mn- and Fe-Doped Na0.5Bi0.5TiO3 Ceramics
Abstract
1. Introduction
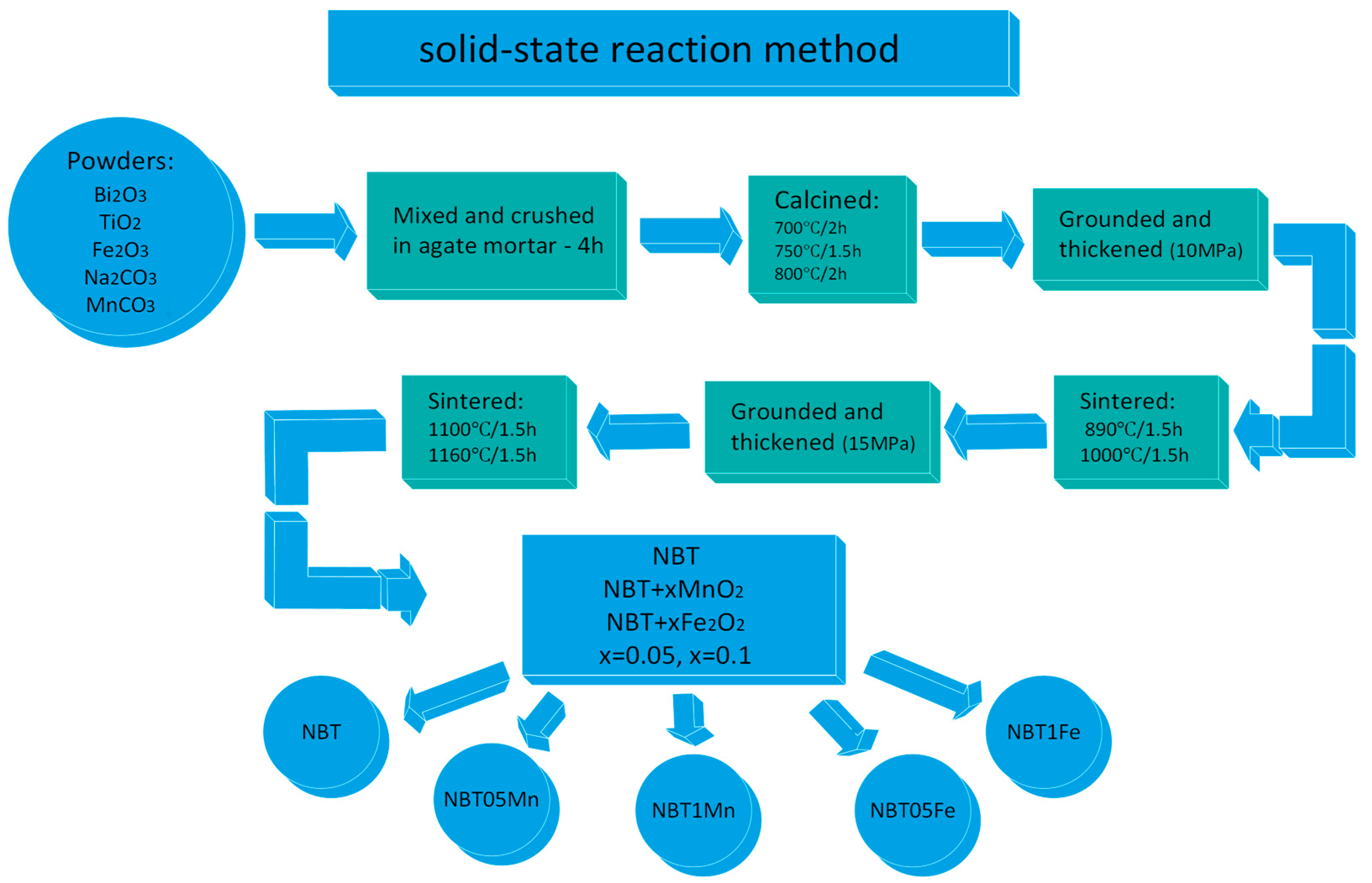
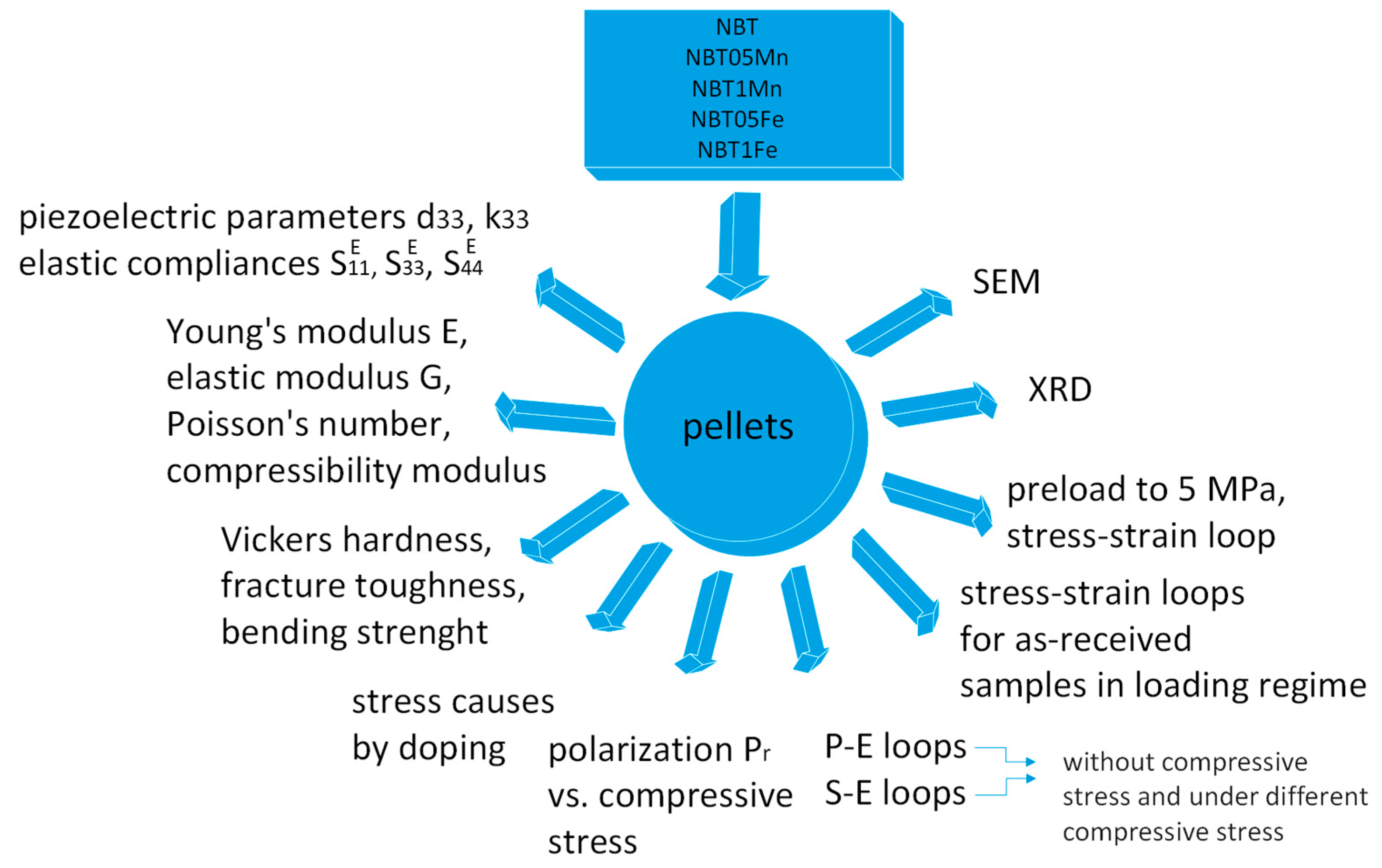
2. Experimental Procedure
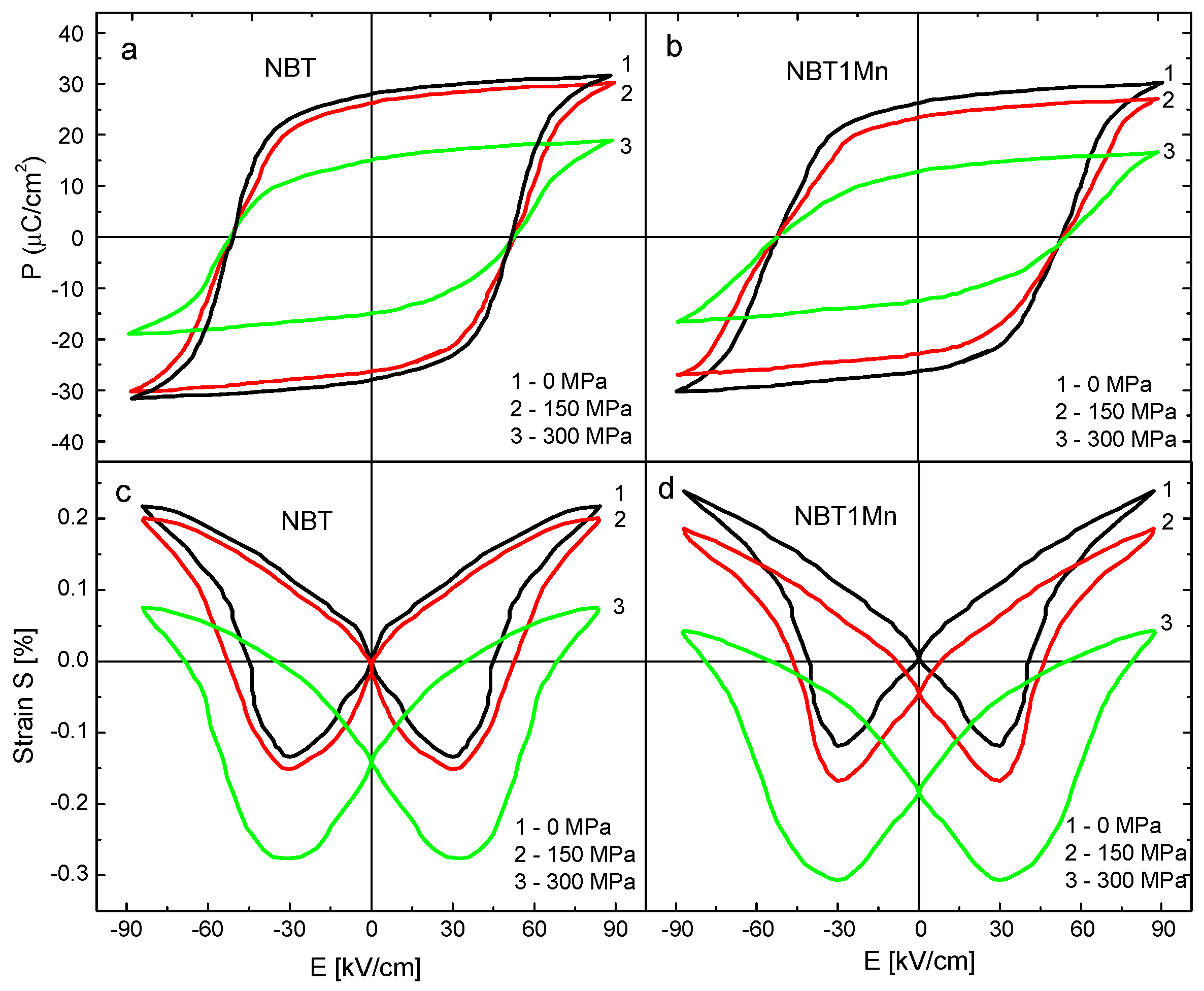
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shuvalov, L.A. Segnetoelastyki. Izv. Akad. Nauk SSSR, Ser. Fiz. Evisa 1979, 43, 1554–1560. (In Russian) [Google Scholar]
- Jaita, P.; Jarupoom, P.; Sweatman, D.R.; Rujijanagul, G. Energy harvesting, electrical and magnetic properties of potassium bismuth titanate-based lead-free ceramics. J. Asian Ceram. Soc. 2021, 9, 947–963. [Google Scholar] [CrossRef]
- Webber, K.G.; Vögler, M.; Khansur, N.H.; Kaeswurn, B.; Daniels, J.E.; Schader, F.H. Review of the mechanical and fracture behavior of perovskite lead-free ferroelectrics for actuator applications. Smart Mater. Struct. 2017, 26, 063001. [Google Scholar] [CrossRef]
- Seo, Y.H.; Vögler, M.; Isaia, D.; Aulbach, E.; Rödel, J.; Webber, K.G. Temperature-dependent R curve behavior of Pb(Zr1−xTix)O3. Acta Mater. 2013, 61, 6418–6427. [Google Scholar] [CrossRef]
- Bermejo, R.; Grünbichler, H.; Kreith, J.; Auer, C. Fracture resistance of a doped PZT ceramic for multilayer piezoelectric actuators: Effect of mechanical load and temperature. J. Eur. Ceram. Soc. 2010, 30, 705–712. [Google Scholar] [CrossRef]
- Dos Santos e Lucato, S.L.; Lupascu, D.C.; Rödel, J. Effect of poling direction on R-Curve behavior in lead zirconate titanate. J. Am. Ceram. Soc. 2000, 83, 424–426. [Google Scholar] [CrossRef]
- Vögler, M.; Daniels, J.E.; Webber, K.G.; Rödel, J. Absence of toughening behavior in 0.94(Na0.5Bi0.5)TiO3-0.06BaTiO3 relaxor ceramic. Scr. Mater. 2017, 136, 115–119. [Google Scholar] [CrossRef]
- Meschke, F.; Kolleck, A.; Schneider, G.A. R-curve behaviour of BaTiO3 due to stress-induced ferroelastic domain switching. J. Eur. Ceram. Soc. 1997, 17, 1143–1149. [Google Scholar] [CrossRef]
- Mgbemere, H.E.; Jellito, H.; Schneider, G.A. Investigation of the fracture toughness and electrical properties of (K, Na, Li) (Nb, Ta, Sb)O3 ceramics. Ceram. Int. 2016, 42, 17711–17716. [Google Scholar] [CrossRef]
- Vögler, M.; Acosta, M.; Brandt, D.R.J.; Molina-Luna, L.; Webber, K.G. Temperature-dependent R-curve behavior of the lead-free ferroelectric 0.615Ba(Zr0.2Ti0.8)O3 0.385(Ba0.7Ca0.3)TiO3 ceramic. Eng. Fract. Mech. 2015, 144, 68–77. [Google Scholar] [CrossRef]
- Cho, J.H.; Jeong, Y.H.; Nam, J.H.; Yun, J.S.; Park, Y.J. Fracture Toughness and Electrical Properties of 0.975Bi(Na0.78K0.22)TiO3–0.025BiAlO3 Ceramics. Jpn. J. Appl. Phys. 2013, 52, 101501. [Google Scholar] [CrossRef]
- Okada, K.; Takagi, Y.; Nam, H.; Nagata, H. Dipole pinning and quenching effects on depolarization temperature of ZnO and (Bi0.5Na0.5)TiO3 ceramics composites. J. Cer. Soc. Jpn. 2024, 132, 330–338. [Google Scholar] [CrossRef]
- Zhuo, F.; Wang, B.; Cheng, L.; Zatterin, E.; Jiang, T.; Ni, F.; Breckner, P.; Li, Y.; Guiblin, N.; Isaia, D.; et al. Unlocking electrostrain in plasticity deformed barium titanate. Adv. Mater. 2024, 20, 2413713. [Google Scholar] [CrossRef]
- Ge, W.; Li, J.; Viehland, D.; Luo, H. Influence of Mn doping on the structure and properties of Na0.5Bi0.5TiO3 single crystals. J. Am. Cer. Soc. 2010, 93, 1372–1377. [Google Scholar] [CrossRef]
- Aksel, E.; Erdem, E.; Jakes, P.; Jones, J.L.; Eichel, R.A. Defect structure and materials hardening in Fe2O3-doped Na0.5Bi0.5TiO3 ferroelectrics. Appl. Phys. Lett. 2010, 97, 012903. [Google Scholar] [CrossRef]
- Davies, M.; Aksel, E.; Jones, J.L. Enhanced high-temperature piezoelectric coefficients and thermal stability of Fe- and Mn-substituted Na0.5Bi0.5TiO3 ceramics. J. Am. Cer. Soc. 2011, 94, 1314–1316. [Google Scholar] [CrossRef]
- Ruth, D.E.J.; Rahman, R.A.U.; Dhamodarn, M.; Lakshmanan, V.; Balasubramanian, S.; Schmid- Beurmann, P.; Zhou, P.; Srinivasan, G.; Ramaswamy, M. Room temperature magnetoelectric coupling in Fe-doped sodium bismuth titanate ceramics. J. Alloys Comp. 2020, 830, 154679. [Google Scholar] [CrossRef]
- Aksel, E.; Forrester, J.S.; Kowalski, B.; Deluca, M.; Damjanovic, D.; Jones, L.J. Structure and properties of Fe-modified Na0.5Bi0.5TiO3 at ambient and elevated temperature. Phys. Rev. 2012, B85, 024121. [Google Scholar] [CrossRef]
- Suchanicz, J.; Wąs, M.; Nowakowska-Malczyk, M.; Sitko, D.; Kluczewska-Chmielarz, K.; Konieczny, K.; Jagło, G.; Czaja, P.; Handke, B.; Kucia, Z.; et al. Properties of Na0.5Bi0.5TiO3 ceramics modified with Fe and Mn. Materials 2022, 15, 6204. [Google Scholar] [CrossRef]
- Piekarczyk, J.; Hennicke, H.W.; Pampuch, R. On determining the elastic constants of porous zinc ferrite materials. cfi/Ber. Dtsch. Keram. Ges. 1982, 59, 227–232. [Google Scholar]
- Piekarczyk, J. Optymalne wymiary próbek do badań ultradźwiękowych. Inżynieria Materiałowa 1992, 13, 72–73. (In Polish) [Google Scholar]
- Cao, H.; Evans, A.G. Nonlinear Deformation of Ferroelectric Ceramics. J. Amer. Cer. Soc. 1993, 76, 890–896. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Zhao, J.; Uchino, K.; Zheng, J. Change of the weak-field properties of Pb(ZrTi)O3 piezoceramics with compressive uniaxial stresses and its links to the effect of dopants on the stability of the polarizations in the materials. J. Mater. Res. 1997, 12, 226–234. [Google Scholar] [CrossRef]
- Lynch, C.S. The effect of uniaxial stress on the electro-mechanical response of 8/65/35 PLZT. Acta Mater. 1996, 44, 4137–4148. [Google Scholar] [CrossRef]
- Wu, J.; Xiao, D.; Zhu, J. Potassium-sodium niobate lead-free piezoelectric materials: Past, present, and future of phase boundaries. Chem. Rev. 2015, 115, 2559–2595. [Google Scholar] [CrossRef]
- Sharma, N.; Das, A.; Prajapat, C.I.; Meena, S.S. Spin reorientation behavior in YMn1-xMxO3 (M=Ti, Fe, Ga; x=0, 0.1). J. Magn. Magn. Mater. 2013, 348, 120–127. [Google Scholar] [CrossRef]
- Suchanicz, J.; Kwapulinski, J. X-ray diffraction study of the phase transitions in Na0.5Bi0.5TiO3. Ferroelectrics 1995, 165, 249–253. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction; John Wiley& Sons Inc.: New York, NY, USA, 2003. [Google Scholar]
- Ghorbal, G.B.; Tricoteaux, A.; Thuault, A.; Louis, G.; Chicot, D. Comparison of conventional Knopp and Vickers hardness of ceramic materials. J. Am. Ceram. Soc. 2017, 37, 2531–2535. [Google Scholar] [CrossRef]
- Suchanicz, J.; Wąs, M.; Nowakowska-Malczyk, M.; Konieczny, K.; Czaja, P.; Kluczewska-Chmielarz, K.; Sitko, D.; Kruzina, T.V.; Trubitsyn, M.P.; Sokolowski, M. Effect of Nb-doping and E-poling on dielectric and electric properties of NBT ceramic. Phase Transit. 2021, 94, 210–218. [Google Scholar] [CrossRef]
- Domingues, N.B.; Galvão, B.R.; Ribeiro, S.; Alves de Almeida Junior, A.; Longhini, D.; Luís Adabo, G. Comparison of the indentation strength and single-edge-v-notched beam methods for dental ceramic fracture toughness testing. Braz. J. Oral Sci. 2016, 15, 109–112. [Google Scholar] [CrossRef]
- Yilmaz, E.D.; Mgbemere, H.E.; Öscoban, H.; Fernandes, R.P.; Schneider, G.A. Investigation of fracture toughness of modified (KxNa1-x)NbO3 lead-free piezoelectric ceramics. J. Europ. Ceram. Soc. 2012, 32, 3339–3344. [Google Scholar] [CrossRef]
- Schreiber, D. Elastic Constants and Their Measurement; Mc Graw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Kovácik, J. Correlation between elastic modulus, shear modulus, Poisson’s ratio and porosity in porous materials. Adv. Eng. Mater. 2008, 10, 250–252. [Google Scholar] [CrossRef]
- Rohrbeck, A.; de la Flor, G.; Aroyo, M.I.; Gospodinov, M.; Bismayer, U.; Mihailova, B. The effect of chemical variations on the structural polarity of relaxor ferroelectrics studied by resonance Raman spectroscopy. J. Phys. Condens. Matter. 2016, 28, 475902. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Lin, D.; Chen, Z.; Cheng, Z.; Wang, J.; Li, C.; Xu, Z.; Huang, Q.; Liao, X.; Chen, L.-Q.; et al. Ultrahigh Piezoelectricity in Ferroelectric Ceramics by Design. Nat. Mater. 2018, 17, 349–354. [Google Scholar] [CrossRef] [PubMed]
- Vorobiev, A.; Gevorgian, S. Intrinsically switchable thin film bulk acoustic wave resonators. Appl. Phys. Lett. 2014, 104, 222905. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, J.; Zhang, S.; Shen, J.; Tian, J.; Chen, W.; Zhang, Q. Direct measurement of electric field-induced strains of a single lead zirconate titanate piezoelectric ceramic fibre under various conditions. Ceram. Int. 2015, 4, 1657–1662. [Google Scholar] [CrossRef]


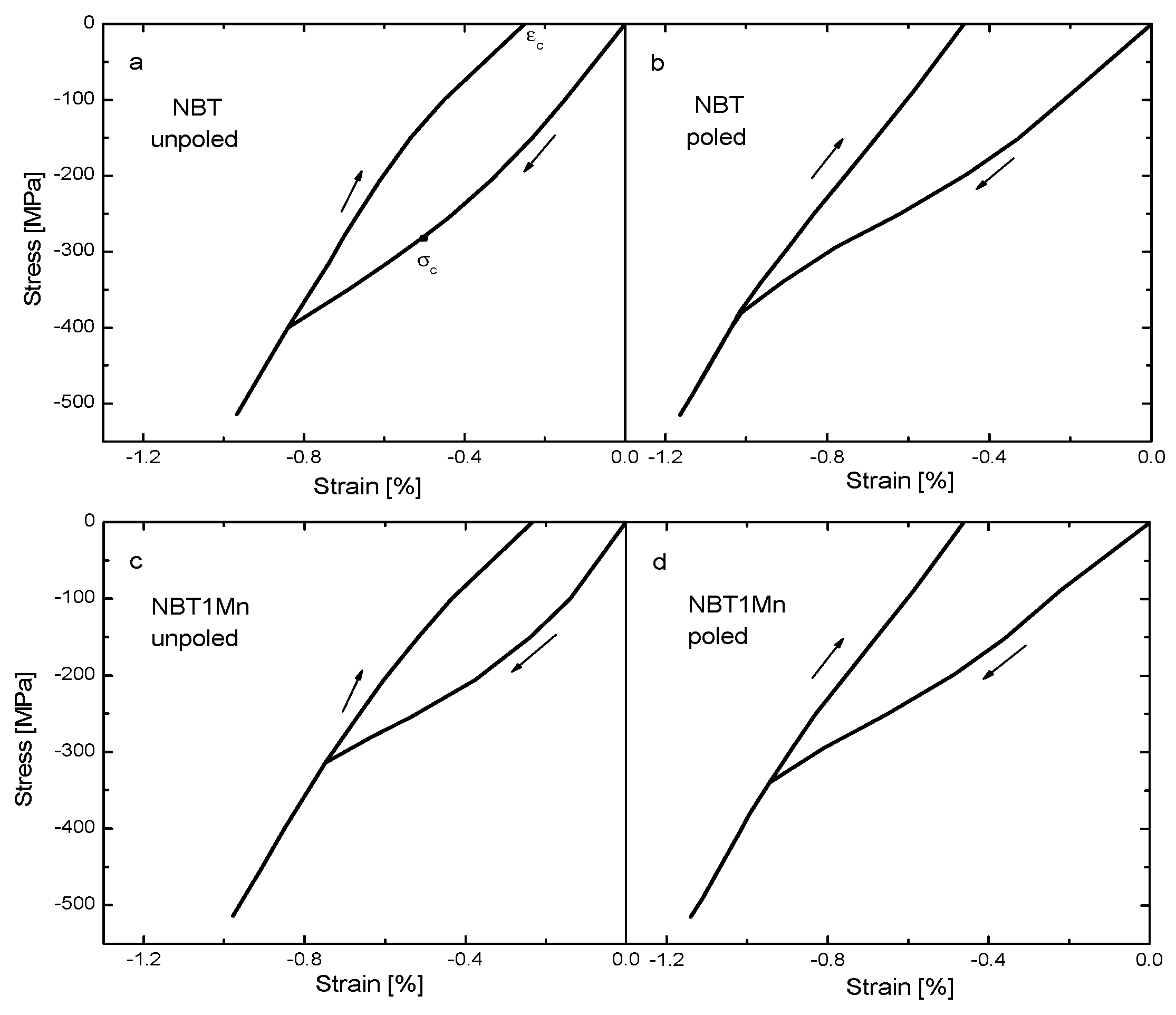

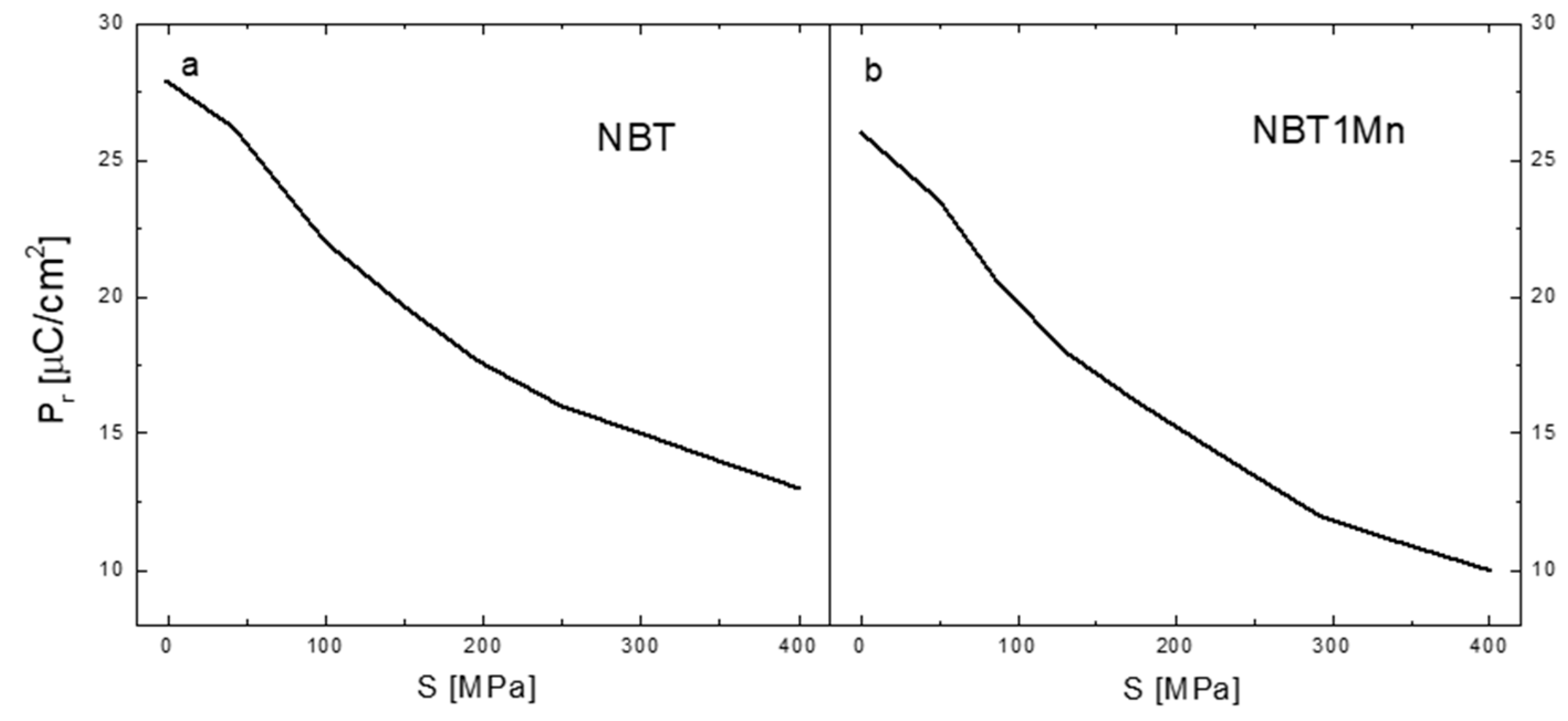
| Material | εr [%] (Unpoled/Poled) | σc [MPa] (Unpoled/Poled) |
|---|---|---|
| NBT | −0.27/−0.48 | −325/−255 |
| NBT05Mn | −0.28/−0.36 | −287/−208 |
| NBT1Mn | −0.29/−0.38 | −286/−206 |
| NBT05Fe | −0.28/−0.37 | −285/−205 |
| NBT1Fe | −0.28/−0.38 | −283/−205 |
| E [GPa] | ηd*10−4 | s [GPa] | |
|---|---|---|---|
| Material | |||
| NBTMn | 138 | ||
| Mn2+ | 0.8 | 0.011 | |
| Mn3+ | 0.1 | 0.001 | |
| Mn4+ | 0.3 | 0.004 | |
| NBTFe | 137 | ||
| Fe2+ | 0.6 | 0.008 | |
| Fe3+ | 0.1 | 0.001 | |
| Fe4+ | 0.1 | 0.001 |
| Hardness HV [GPa] | Critical Stress Intensity Factor | |
|---|---|---|
| Material | (Unpoled/Poled) | KIc [MPam0.5] (Unpoled/Poled) |
| NBT | 520/525 | 1.15/1.16 |
| NBT05Mn | 535/539 | 1.17/1.18 |
| NBT1Mn | 533/537 | 1.17/1.16 |
| NBT05Fe | 530/532 | 1.19/1.20 |
| NBT1Fe | 528/529 | 1.18/1.18 |
| E [GPa] | G [GPa] | μ | K [GPa] | G/K [GPa] | |
|---|---|---|---|---|---|
| Material | (Unpoled/Poled) | (Unpoled/Poled) | (Unpoled/Poled) | (Unpoled/Poled) | (Unpoled/Poled) |
| NBT | 136.95/137.57 | 52.87/53.03 | 0.295/0.297 | 92.91/92.15 | 0.569/0.575 |
| NBT05Mn | 138.02/138.08 | 52.09/51.85 | 0.347/0.352 | 92.94/92.96 | 0.561/0.558 |
| NBT1Mn | 137.93/137.99 | 50.71/50.64 | 0.324/0.331 | 92.84/92.97 | 0.546/0.545 |
| NBT05Fe | 137.52/137.54 | 50.65/50.54 | 0.382/0.389 | 92.93/92.61 | 0.545/0.546 |
| NBT1Fe | 137.16/137/53 | 51.23/51.87 | 0.354/0.361 | 92.52/92.61 | 0.554/0.560 |
| Bending Strength σm (MPa) | |
|---|---|
| Material | (Unpoled/Poled) |
| NBT | 200/205 |
| NBT05Mn | 203/205 |
| NBT1Mn | 204/207 |
| NBT05Fe | 202/204 |
| NBT1Fe | 203/205 |
| Material | |||||
|---|---|---|---|---|---|
| NBT | 73 | 21 | 8.0 | 8.9 | 19.9 |
| NBT05Mn | 89 | 24 | 7.9 | 8.7 | 19.7 |
| NBT1Mn | 97 | 27 | 7.8 | 8.6 | 19.6 |
| NBT05Fe | 74 | 21 | 7.8 | 8.7 | 19.6 |
| NBT1Fe | 71 | 20 | 7.7 | 8.7 | 19.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suchanicz, J.; Wąs, M.; Kluczewska-Chmielarz, K.; Jagło, G.; Brzezińska, D.; Rosiek, R.; Stachowski, G.; Sokolowski, M. Enhanced Mechanical Properties of Mn- and Fe-Doped Na0.5Bi0.5TiO3 Ceramics. Materials 2024, 17, 5645. https://doi.org/10.3390/ma17225645
Suchanicz J, Wąs M, Kluczewska-Chmielarz K, Jagło G, Brzezińska D, Rosiek R, Stachowski G, Sokolowski M. Enhanced Mechanical Properties of Mn- and Fe-Doped Na0.5Bi0.5TiO3 Ceramics. Materials. 2024; 17(22):5645. https://doi.org/10.3390/ma17225645
Chicago/Turabian StyleSuchanicz, Jan, Marcin Wąs, Kamila Kluczewska-Chmielarz, Grzegorz Jagło, Dagmara Brzezińska, Roman Rosiek, Grzegorz Stachowski, and Mariusz Sokolowski. 2024. "Enhanced Mechanical Properties of Mn- and Fe-Doped Na0.5Bi0.5TiO3 Ceramics" Materials 17, no. 22: 5645. https://doi.org/10.3390/ma17225645
APA StyleSuchanicz, J., Wąs, M., Kluczewska-Chmielarz, K., Jagło, G., Brzezińska, D., Rosiek, R., Stachowski, G., & Sokolowski, M. (2024). Enhanced Mechanical Properties of Mn- and Fe-Doped Na0.5Bi0.5TiO3 Ceramics. Materials, 17(22), 5645. https://doi.org/10.3390/ma17225645






