Hydrogen Trapping at Fe/Cu Interfaces
Highlights
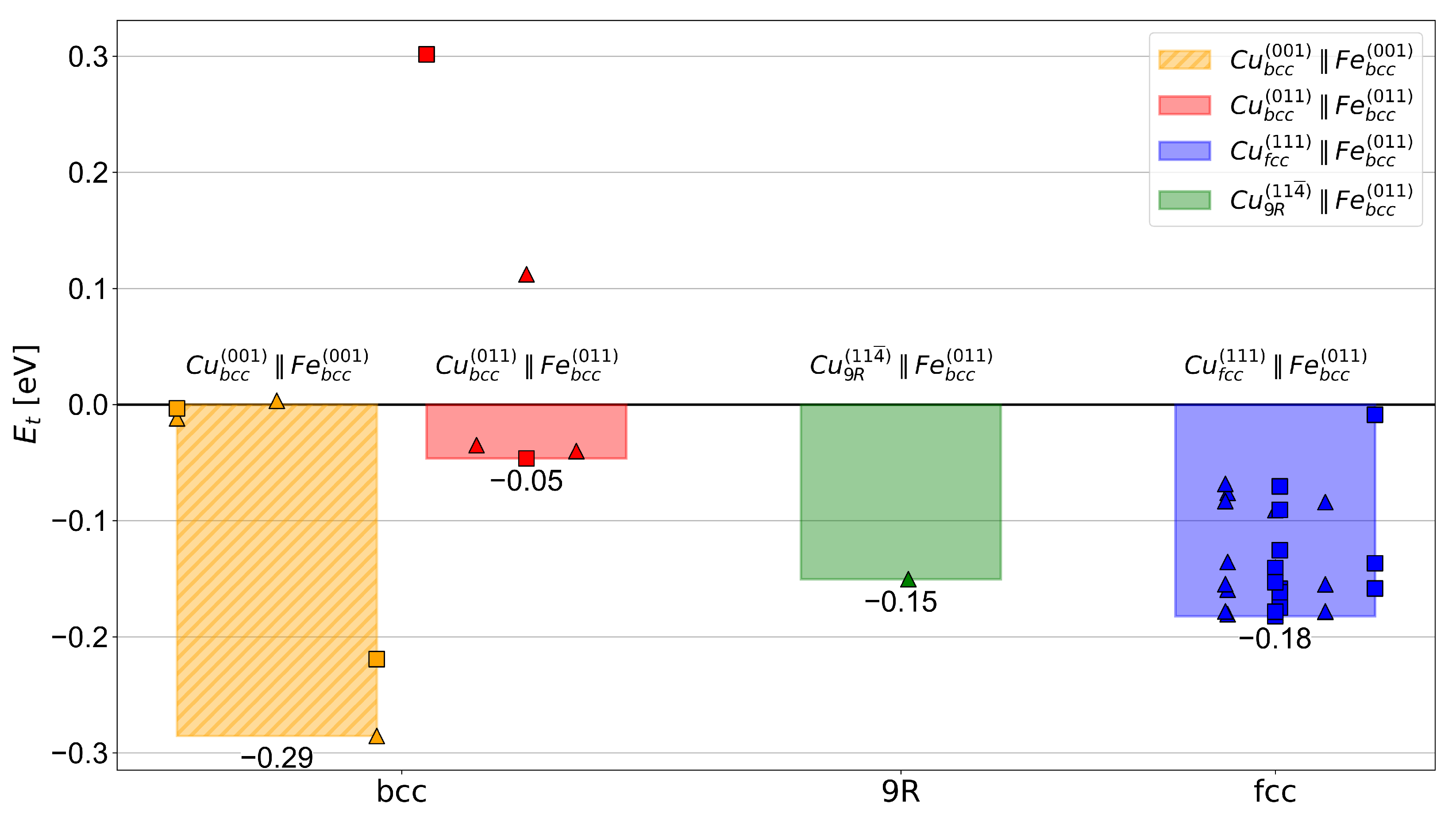
- DFT predicts H trapping energies spanning from −0.05 to −0.20 eV for Cu precipitates.
- Thermodynamic calculations indicate that fcc Cu precipitates can reduce H at dislocations.
- Tailored alloying and precipitation of Cu has the potential to reduce HELP.
Abstract
1. Introduction
2. Computational Details
2.1. DFT Calculations
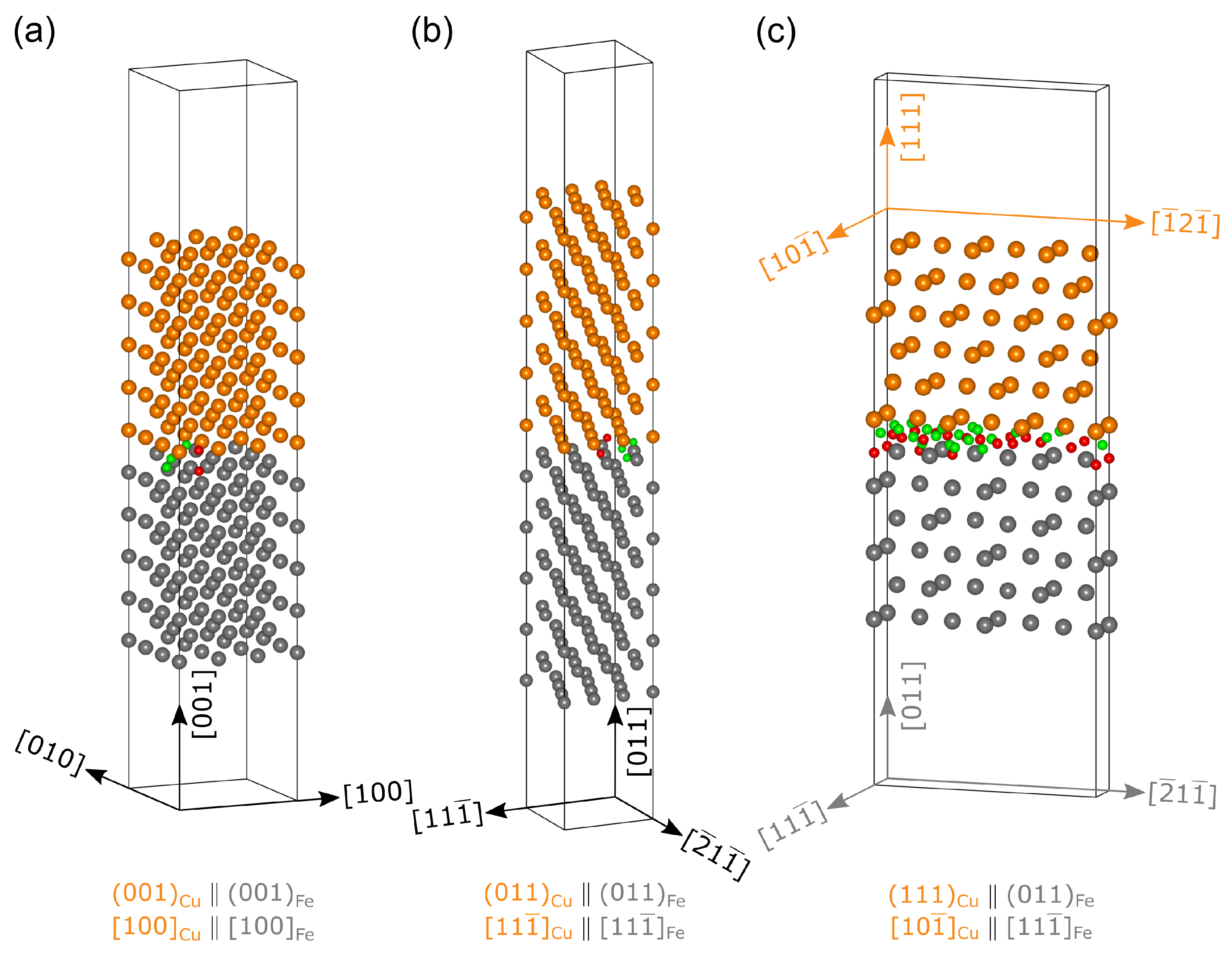
2.2. Interface Models
2.2.1. Interface
2.2.2. Interface
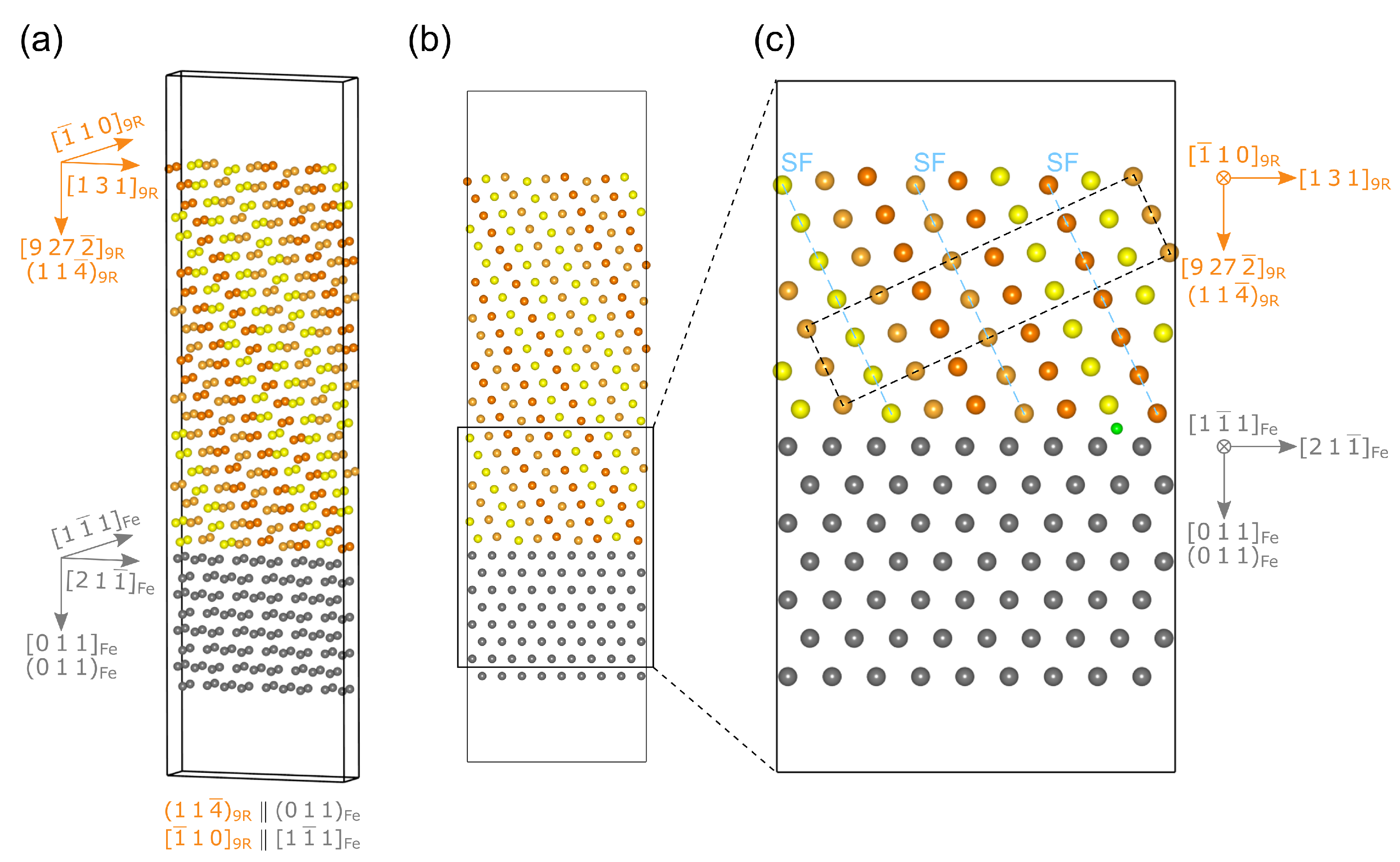
2.2.3. Interface
2.3. Hydrogen-Trapping Energy
2.4. Thermodynamic Model
3. Results
3.1. Hydrogen Trapping at Cu/Fe Interfaces from DFT
3.2. Thermodynamic Modeling of Hydrogen Trapping at Cu/Fe Interfaces
4. Discussion
5. Conclusions
- The H-trapping energy obtained by the DFT calculations follows the experimentally observed evolution of the Cu precipitate structure [4,5,22,74], with trapping energies of −0.05 eV, −0.15 eV, and −0.18 eV for the model interfaces of , , and precipitates with Fe, respectively. These results are found to agree well with the experimental findings of Refs. [36,37,38,41].
- The strongest trapping energy of 0.18 eV obtained for the /Fe interface is found to be in the range of dislocations, and thus, is considered rather moderate compared with GBs, vacancies, and interfaces with coherent carbides, which all have significantly lower trapping energies (i.e., are stronger traps) for H atoms in [25,60].
- Although the precipitates provide a substantially increased trap density compared with the precipitates due to their smaller size, the precipitates could still trap a higher concentration of H owing to them offering slightly deeper traps. This emphasizes the importance of trapping energy differences even as small as 3 kJ/mol on the trapped concentration of H for weak-to-moderate H traps.
- While precipitates with a large interface area introduced through intentional Cu alloying might significantly contribute to the H redistribution in a steel microstructure, Cu residuals from the steelmaking process are expected to only have a minor effect on overall H trapping.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Urtsev, V.N.; Mirzaev, D.A.; Yakovleva, I.L.; Tereshchenko, N.A.; Okishev, K.Y. On the mechanism of nucleation of copper precipitates upon aging of Fe-Cu alloys. Phys. Met. Metallogr. 2010, 110, 346–355. [Google Scholar] [CrossRef]
- Gorbatov, O.I.; Razumov, I.K.; Gornostyrev, Y.N.; Razumovskiy, V.I.; Korzhavyi, P.A.; Ruban, A.V. Role of magnetism in Cu precipitation in α-Fe. Phys. Rev. Condens. Matter Mater. Phys. 2013, 88, 174113. [Google Scholar] [CrossRef]
- Vaynman, S.; Guico, R.S.; Fine, M.E.; Manganello, S.J. Estimation of atmospheric corrosion of high-strength, low-alloy steels. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 1997, 28, 1274–1276. [Google Scholar] [CrossRef]
- Deschamps, A.; Militzer, M.; Poole, W.J. Precipitation kinetics and strengthening of a Fe-0.8wt%Cu alloy. ISIJ Int. 2001, 41, 196–205. [Google Scholar] [CrossRef]
- Deschamps, A.; Militzer, M.; Poole, W.J. Comparison of precipitation kinetics and strengthening in an Fe-0.8%Cu alloy and a 0.8% Cu-containing low-carbon steel. ISIJ Int. 2003, 43, 1826–1832. [Google Scholar] [CrossRef][Green Version]
- Stechauner, G.; Kozeschnik, E. Thermo-kinetic modeling of Cu precipitation in α-Fe. Acta Mater. 2015, 100, 135–146. [Google Scholar] [CrossRef]
- Wei, X.; Cao, X.; Luan, J.H.; Jiao, Z.B.; Liu, C.T.; Zhang, Z.W. Synergy of strengthening and toughening of a Cu-rich precipitate-strengthened steel. Mater. Sci. Eng. A 2022, 832, 142487. [Google Scholar] [CrossRef]
- Kan, L.; Ye, Q.; Wang, Z.; Zhao, T. Improvement of strength and toughness of 1 GPa Cu-bearing HSLA steel by direct quenching. Mater. Sci. Eng. A 2022, 855, 143875. [Google Scholar] [CrossRef]
- Daigo, I.; Goto, Y. Comparison of tramp element contents of steel bars from Japan and China. ISIJ Int. 2015, 55, 2027–2032. [Google Scholar] [CrossRef]
- Imai, N.; Komatsubara, N.; Kunishige, K. Effect of Cu and Ni on hot workability of hot-rolled mild steel. ISIJ Int. 1997, 37, 224–231. [Google Scholar] [CrossRef]
- Yin, L.; Balaji, S.; Sridhar, S. Effects of nickel on the oxide/metal interface morphology and oxidation rate during high-temperature oxidation of Fe-Cu-Ni alloys. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2010, 41, 598–611. [Google Scholar] [CrossRef]
- United Nations Department of Economic and Social Affairs. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015. Available online: https://sdgs.un.org/2030agenda (accessed on 7 March 2023).
- Fetting, C. The European Green Deal. 2020. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52019DC0640&from=EN (accessed on 7 March 2023).
- Towards Competitive and Clean European Steel. 2021. Available online: https://commission.europa.eu/system/files/2021-05/swd-competitive-clean-european-steel_en.pdf (accessed on 7 March 2023).
- Barrera, O.; Bombac, D.; Chen, Y.; Daff, T.D.; Galindo-Nava, E.; Gong, P.; Haley, D.; Horton, R.; Katzarov, I.; Kermode, J.R.; et al. Understanding and mitigating hydrogen embrittlement of steels: A review of experimental, modelling and design progress from atomistic to continuum. J. Mater. Sci. 2018, 53, 6251–6290. [Google Scholar] [CrossRef] [PubMed]
- Bhadeshia, H. Prevention of Hydrogen Embrittlement in Steels. ISIJ Int. 2016, 56, 24–36. [Google Scholar] [CrossRef]
- Robertson, I.M.; Sofronis, P.; Nagao, A.; Martin, M.L.; Wang, S.; Gross, D.W.; Nygren, K.E. Hydrogen Embrittlement Understood. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2015, 46, 1085–1103. [Google Scholar] [CrossRef]
- Nikolaidis, P.; Poullikkas, A. A comparative overview of hydrogen production processes. Renew. Sustain. Energy Rev. 2017, 67, 597–611. [Google Scholar] [CrossRef]
- Fekete, J.R.; Sowards, J.W.; Amaro, R.L. Economic impact of applying high strength steels in hydrogen gas pipelines. Int. J. Hydrogen Energy 2015, 40, 10547–10558. [Google Scholar] [CrossRef]
- Othen, P.J.; Jenkins, M.L.; Smith, G.D. High-resolution electron microscopy studies of the structure of Cu precipitates in α-Fe. Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop. 1994, 70, 1–24. [Google Scholar] [CrossRef]
- Monzen, R.; Jenkins, M.L.; Sutton, A.R. The bcc-to-9R martensitic transformation of Cu precipitates and the relaxation process of elastic strains in an Fe-Cu alloy. Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop. 2000, 80, 711–723. [Google Scholar] [CrossRef]
- Han, G.; Xie, Z.J.; Li, Z.Y.; Lei, B.; Shang, C.J.; Misra, R.D. Evolution of crystal structure of Cu precipitates in a low carbon steel. Mater. Des. 2017, 135, 92–101. [Google Scholar] [CrossRef]
- Wasim, M.; Djukic, M.B.; Ngo, T.D. Influence of hydrogen-enhanced plasticity and decohesion mechanisms of hydrogen embrittlement on the fracture resistance of steel. Eng. Fail. Anal. 2021, 123, 105312. [Google Scholar] [CrossRef]
- Djukic, M.B.; Bakic, G.M.; Sijacki Zeravcic, V.; Sedmak, A.; Rajicic, B. The synergistic action and interplay of hydrogen embrittlement mechanisms in steels and iron: Localized plasticity and decohesion. Eng. Fract. Mech. 2019, 216, 106528. [Google Scholar] [CrossRef]
- Hammer, P.; Razumovskiy, V.I.; Scheiber, D.; Leitner, S.; Ecker, W. Chapter 11—High-strength alloys with reduced hydrogen embrittlement susceptibility. In Innovative Lightweight and High-Strength Alloys; Zikry, M.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 335–364. [Google Scholar] [CrossRef]
- Hammer, P.; Romaner, L.; Razumovskiy, V.I. Hydrogen trapping in mixed carbonitrides. Acta Mater. 2024, 268, 119754. [Google Scholar] [CrossRef]
- Di Stefano, D.; Nazarov, R.; Hickel, T.; Neugebauer, J.; Mrovec, M.; Elsässer, C. First-principles investigation of hydrogen interaction with TiC precipitates in α-Fe. Phys. Rev. B 2016, 93, 184108. [Google Scholar] [CrossRef]
- Vandewalle, L.; Depover, T.; Verbeken, K. Current state-of-the-art of hydrogen trapping by carbides: From theory to experiment. Int. J. Hydrogen Energy 2024, in press. [Google Scholar] [CrossRef]
- Zheng, Y.; Huili, S.; Yan, L.; Pang, X.; Volinsky, A.A.; Gao, K. Review of metal carbide nanoprecipitate effects on hydrogen embrittlement of high strength martensitic steel. Anti-Corros. Methods Mater. 2022, 69, 409–416. [Google Scholar] [CrossRef]
- Chen, Y.S.; Huang, C.; Liu, P.Y.; Yen, H.W.; Niu, R.; Burr, P.; Moore, K.L.; Martínez-Pañeda, E.; Atrens, A.; Cairney, J.M. Hydrogen trapping and embrittlement in metals—A review. Int. J. Hydrogen Energy 2024, in press. [Google Scholar] [CrossRef]
- Eškinja, M.; Winter, G.; Schnideritsch, H.; Klarner, J.; Razumovskiy, V.; Moshtaghi, M.; Mori, G. Influence of Mo carbides and two-stage tempering methodology on the susceptibility of medium carbon martensitic steel to hydrogen embrittlement. Eng. Fail. Anal. 2024, 163, 108562. [Google Scholar] [CrossRef]
- Takano, N.; Yokka, Y.; Terasaki, F. The effect of copper precipitation on hydrogen embrittlement in iron. Mater. Sci. Eng. A 2004, 387–389, 428–432. [Google Scholar] [CrossRef]
- Song, H.; Jo, M.; Kim, D.W. Vanadium or copper alloyed duplex lightweight steel with enhanced hydrogen embrittlement resistance at room temperature. Mater. Sci. Eng. A 2021, 817, 141347. [Google Scholar] [CrossRef]
- Yoo, J.; Jo, M.C.; Kim, D.W.; Song, H.; Koo, M.; Sohn, S.S.; Lee, S. Effects of Cu addition on resistance to hydrogen embrittlement in 1 GPa-grade duplex lightweight steels. Acta Mater. 2020, 196, 370–383. [Google Scholar] [CrossRef]
- Wang, J.; Xu, N.; Wu, T.; Xi, X.; Wang, G.; Chen, L. Response of hydrogen diffusion and hydrogen embrittlement to Cu addition in low carbon low alloy steel. Mater. Charact. 2023, 195, 112478. [Google Scholar] [CrossRef]
- Komazaki, S.I.; Koyama, A.; Misawa, T. Effect of morphology of copper precipitation particles on hydrogen embrittlement behavior in Cu-added ultra low carbon steel. Mater. Trans. 2002, 43, 2213–2218. [Google Scholar] [CrossRef]
- McCarroll, I.E.; Lin, Y.C.; Rosenthal, A.; Yen, H.W.; Cairney, J.M. Hydrogen trapping at dislocations, carbides, copper precipitates and grain boundaries in a dual precipitating low-carbon martensitic steel. Scr. Mater. 2022, 221, 114934. [Google Scholar] [CrossRef]
- Lin, Y.C.; McCarroll, I.E.; Lin, Y.T.; Chung, W.C.; Cairney, J.M.; Yen, H.W. Hydrogen trapping and desorption of dual precipitates in tempered low-carbon martensitic steel. Acta Mater. 2020, 196, 516–527. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, D.; Chiang, M.H.; Cheng, G.J.; Lin, H.C.; Yen, H.W. Response of Hydrogen Desorption and Hydrogen Embrittlement to Precipitation of Nanometer-Sized Copper in Tempered Martensitic Low-Carbon Steel. Jom 2019, 71, 1349–1356. [Google Scholar] [CrossRef]
- Sun, H.; Lv, W.; Yang, Y.; Li, D.; Yan, L.; Pang, X.; He, Y.; Gao, K. Optimizing the hydrogen embrittlement resistance by tuning the structures of Cu-rich nanoprecipitates in high strength martensite stainless steels. Acta Mater. 2023, 246, 118722. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Hu, J.; Tian, Y.; Xi, X.; Chen, L. Optimizing the hydrogen embrittlement resistance by Cu addition in a low carbon high strength steel. Eng. Fail. Anal. 2024, 158, 108004. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, H.; Xu, S.S.; Mao, M.J.; Chen, L.; Gokhman, O.; Zhang, Z.W. Effects of Solid Solution Treatments on the Microstructure and Mechanical Properties of a Nanoscale Precipitate-Strengthened Ferritic Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2018, 49, 3383–3393. [Google Scholar] [CrossRef]
- Zhao, X.L.; Zhang, C.X.; Zhang, Y.J.; Hui, W.J.; Zhao, X.M. Hydrogen-induced delayed fracture of Cu-containing high-strength bolt steel. J. Iron Steel Res. Int. 2023, 30, 375–383. [Google Scholar] [CrossRef]
- Tanabe, T.; Sawada, K.; Imoto, S. Hydrogen Diffusion and Permeation Through Duplex Membrane of Cu-Ni and Cu-Fe. Trans. Jpn. Inst. Met. 1986, 27, 321–327. [Google Scholar] [CrossRef][Green Version]
- Koyama, M.; Rohwerder, M.; Tasan, C.C.; Bashir, A.; Akiyama, E.; Takai, K.; Raabe, D.; Tsuzaki, K. Recent progress in microstructural hydrogen mapping in steels: Quantification, kinetic analysis, and multi-scale characterisation. Mater. Sci. Technol. 2017, 33, 1481–1496. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillonin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The materials project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Gao, H.; Wang, J.; Sun, B. First-Principles Study on the Cu/Fe Interface Properties of Ternary Cu-Fe-X Alloys. Materials 2020, 13, 3112. [Google Scholar] [CrossRef]
- Korzhavyi, P.A.; Sandström, R. Monovacancy in copper: Trapping efficiency for hydrogen and oxygen impurities. Comput. Mater. Sci. 2014, 84, 122–128. [Google Scholar] [CrossRef]
- Gao, X.; Wang, H.; Ma, C.; Xing, L.; Ren, H. Study on the Partitioning of Alloying Elements Between bcc-Fe Matrix and bcc-Cu Precipitates and the Corresponding Effects on the Precipitation Interface. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2020, 51, 5444–5452. [Google Scholar] [CrossRef]
- Kholtobina, A.S.; Pippan, R.; Romaner, L.; Scheiber, D.; Ecker, W.; Razumovskiy, V.I. Hydrogen trapping in bcc iron. Materials 2020, 13, 2288. [Google Scholar] [CrossRef]
- Echeverri Restrepo, S.; Di Stefano, D.; Mrovec, M.; Paxton, A.T. Density functional theory calculations of iron—Vanadium carbide interfaces and the effect of hydrogen. Int. J. Hydrogen Energy 2020, 45, 2382–2389. [Google Scholar] [CrossRef]
- Ma, Y.; Shi, Y.; Wang, H.; Mi, Z.; Liu, Z.; Gao, L.; Yan, Y.; Su, Y.; Qiao, L. A first-principles study on the hydrogen trap characteristics of coherent nano-precipitates in α-Fe. Int. J. Hydrogen Energy 2020, 45, 27941–27949. [Google Scholar] [CrossRef]
- Wampler, W.; Schober, T.; Lengeler, B. Precipitation and trapping of hydrogen in copper. Philos. Mag. 1976, 34, 129–141. [Google Scholar] [CrossRef]
- Catto, I.; Le Bris, C.; Lions, P.L. Recent mathematical results on the quantum modeling of crystals. In Mathematical Models and Methods for Ab Initio Quantum Chemistry, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 74, Chapter 5; pp. 95–119. [Google Scholar] [CrossRef]
- Han, L.; Liu, Q.; Gu, J. High-resolution Transmission Electron Microscopy Characterization of the Structure of Cu Precipitate in a Thermal-aged Multicomponent Steel. Chin. J. Mech. Eng. 2019, 32, 81. [Google Scholar] [CrossRef]
- Garrett, A.M.; Race, C.P. Cu nanoprecipitate morphologies and interfacial energy densities in bcc Fe from density functional theory (DFT). Comput. Mater. Sci. 2021, 188, 110149. [Google Scholar] [CrossRef]
- Garrett, A.M.; Race, C.P. Ab-initio calculations of substitutional co-segregation interactions at coherent bcc Fe-Cu interfaces. J. Nucl. Mater. 2022, 569, 153923. [Google Scholar] [CrossRef]
- Hjorth Larsen, A.; Jørgen Mortensen, J.; Blomqvist, J.; Castelli, I.E.; Christensen, R.; Dułak, M.; Friis, J.; Groves, M.N.; Hammer, B.; Hargus, C.; et al. The atomic simulation environment—A Python library for working with atoms. J. Phys. Condens. Matter 2017, 29, 273002. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Heo, Y.U.; Kim, Y.K.; Kim, J.S.K.; Kim, J.S.K. Phase transformation of Cu precipitates from bcc to fcc in Fe-3Si-2Cu alloy. Acta Mater. 2013, 61, 519–528. [Google Scholar] [CrossRef]
- Sun, H.; Li, D.; Diao, Y.; He, Y.; Yan, L.; Pang, X.; Gao, K. Nanoscale Cu particle evolution and its impact on the mechanical properties and strengthening mechanism in precipitation-hardening stainless steel. Mater. Charact. 2022, 188, 111885. [Google Scholar] [CrossRef]
- Gao, X.; Wang, H.; Xing, L.; Ma, C.; Li, Y.; Sha, G.; Ren, H. The synergistic effects of ultrafine grains and nano-size Cu-rich precipitates on the mechanical properties of DP steels. Mater. Sci. Eng. A 2021, 805, 140547. [Google Scholar] [CrossRef]
- Koumatos, K.; Muehlemann, A. A theoretical investigation of orientation relationships and transformation strains in steels. Acta Crystallogr. Sect. A Found. Adv. 2017, 73, 115–123. [Google Scholar] [CrossRef]
- Jung, J.G.; Jung, M.; Lee, S.M.; Shin, E.; Shin, H.C.; Lee, Y.K. Cu precipitation kinetics during martensite tempering in a medium C steel. J. Alloys Compd. 2013, 553, 299–307. [Google Scholar] [CrossRef]
- Erhart, P.; Marian, J.; Sadigh, B. Thermodynamic and mechanical properties of copper precipitates in α-iron from atomistic simulations. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88, 024116. [Google Scholar] [CrossRef]
- Lee, T.H.; Kim, Y.O.; Kim, S.J. Crystallographic model for bcc-to-9R martensitic transformation of Cu precipitates in ferritic steel. Philos. Mag. 2007, 87, 209–224. [Google Scholar] [CrossRef]
- Kajiwara, S. Theoretical Analysis of the Crystallography of the Martensitic Transformation of BCC to 9R Close-Packed Structure. Trans. Jpn. Inst. Met. 1976, 17, 435–446. [Google Scholar] [CrossRef][Green Version]
- Othen, P.J.; Jenkins, M.L.; Smith, G.D.; Phythianj, W.J. Transmission electron microscope investigations of the structure of copper precipitates in thermally-aged fe-cu and fe-cu-ni. Philos. Mag. Lett. 1991, 64, 383–391. [Google Scholar] [CrossRef]
- Monzen, R.; Iguchi, M.; Jenkins, M.L. Structural changes of 9R copper precipitates in an aged Fe-Cu alloy. Philos. Mag. Lett. 2000, 80, 137–148. [Google Scholar] [CrossRef]
- Oriani, R.A. The diffusion and trapping of hydrogen in steel. Acta Metall. 1970, 18, 147–157. [Google Scholar] [CrossRef]
- Fischer, F.D.; Svoboda, J.; Kozeschnik, E. Interstitial diffusion in systems with multiple sorts of traps. Model. Simul. Mater. Sci. Eng. 2013, 21, 025008. [Google Scholar] [CrossRef]
- Drexler, A.; Depover, T.; Leitner, S.; Verbeken, K.; Ecker, W. Microstructural based hydrogen diffusion and trapping models applied to Fe-C-X alloys. J. Alloys Compd. 2020, 826, 154057. [Google Scholar] [CrossRef]
- Leitner, S.; Ecker, W.; Fischer, F.D.; Svoboda, J. Thermodynamic trapping and diffusion model for multiple species in systems with multiple sorts of traps. Acta Mater. 2022, 233, 117940. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Turk, A.; Joshi, G.R.; Gintalas, M.; Callisti, M.; Rivera-Díaz-del Castillo, P.E.; Galindo-Nava, E.I. Quantification of hydrogen trapping in multiphase steels: Part I—Point traps in martensite. Acta Mater. 2020, 194, 118–133. [Google Scholar] [CrossRef]
- Pötz, M. Design of Hydrogen Resistant High-Strength Steel Fasteners. Master’s Thesis, Montanuniversität Leoben, Leoben, Austria, 2021. [Google Scholar]
- Sato, R.; Takai, K. Quantitative hydrogen trap states on high-angle grain boundaries and at dislocations in iron. Scr. Mater. 2023, 228, 115339. [Google Scholar] [CrossRef]
- Drexler, A.; Vandewalle, L.; Depover, T.; Verbeken, K.; Domitner, J. Critical verification of the Kissinger theory to evaluate thermal desorption spectra. Int. J. Hydrogen Energy 2021, 46, 39590–39606. [Google Scholar] [CrossRef]
- Kirchheim, R. Bulk Diffusion-Controlled Thermal Desorption Spectroscopy with Examples for Hydrogen in Iron. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2016, 47, 672–696. [Google Scholar] [CrossRef]
- Counts, W.A.; Wolverton, C.; Gibala, R. First-principles energetics of hydrogen traps in α-Fe: Point defects. Acta Mater. 2010, 58, 4730–4741. [Google Scholar] [CrossRef]



| Parameter | Value | Reference | Comment |
|---|---|---|---|
| 1 wt.ppm | - | Model assumption | |
| T | 293.15 K | - | Room temperature (20 °C) |
| −19.9 kJ/mol | [87] | 8.68 kJ/mol migration barrier [25,26,27,90] | |
| −35.0 kJ/mol | [87] | 8.68 kJ/mol migration barrier [25,26,27,90] | |
| −17.4 kJ/mol | Table 2 | −0.18 eV converted to kJ/mol | |
| [7] | Martensite tempered at 525 °C for 25 h | ||
| 14.8 m | [7] | Martensite tempered at 525 °C for 25 h | |
| 10 nm | [7] | Martensite tempered at 525 °C for 25 h | |
| 1.6 vol.-% | [7] | Martensite tempered at 525 °C for 25 h | |
| mol/ | [81,85] | Lattice trap density for ferrite | |
| mol/ | Equation (11) | Dislocation trap density | |
| mol/ | Equation (12) | Grain boundary trap density | |
| mol/ | Equation (14) | Trap density of precipitates |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammer, P.; Militzer, M.; Razumovskiy, V.I. Hydrogen Trapping at Fe/Cu Interfaces. Materials 2024, 17, 5671. https://doi.org/10.3390/ma17225671
Hammer P, Militzer M, Razumovskiy VI. Hydrogen Trapping at Fe/Cu Interfaces. Materials. 2024; 17(22):5671. https://doi.org/10.3390/ma17225671
Chicago/Turabian StyleHammer, Philipp, Matthias Militzer, and Vsevolod I. Razumovskiy. 2024. "Hydrogen Trapping at Fe/Cu Interfaces" Materials 17, no. 22: 5671. https://doi.org/10.3390/ma17225671
APA StyleHammer, P., Militzer, M., & Razumovskiy, V. I. (2024). Hydrogen Trapping at Fe/Cu Interfaces. Materials, 17(22), 5671. https://doi.org/10.3390/ma17225671








