Determining Thermophysical Parameters of Cryopreserved Articular Cartilage Using Evolutionary Algorithms and Experimental Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Direct Problem
2.1.1. Heat Transfer Model
2.1.2. Mass Transfer Model
2.2. Numerical Model
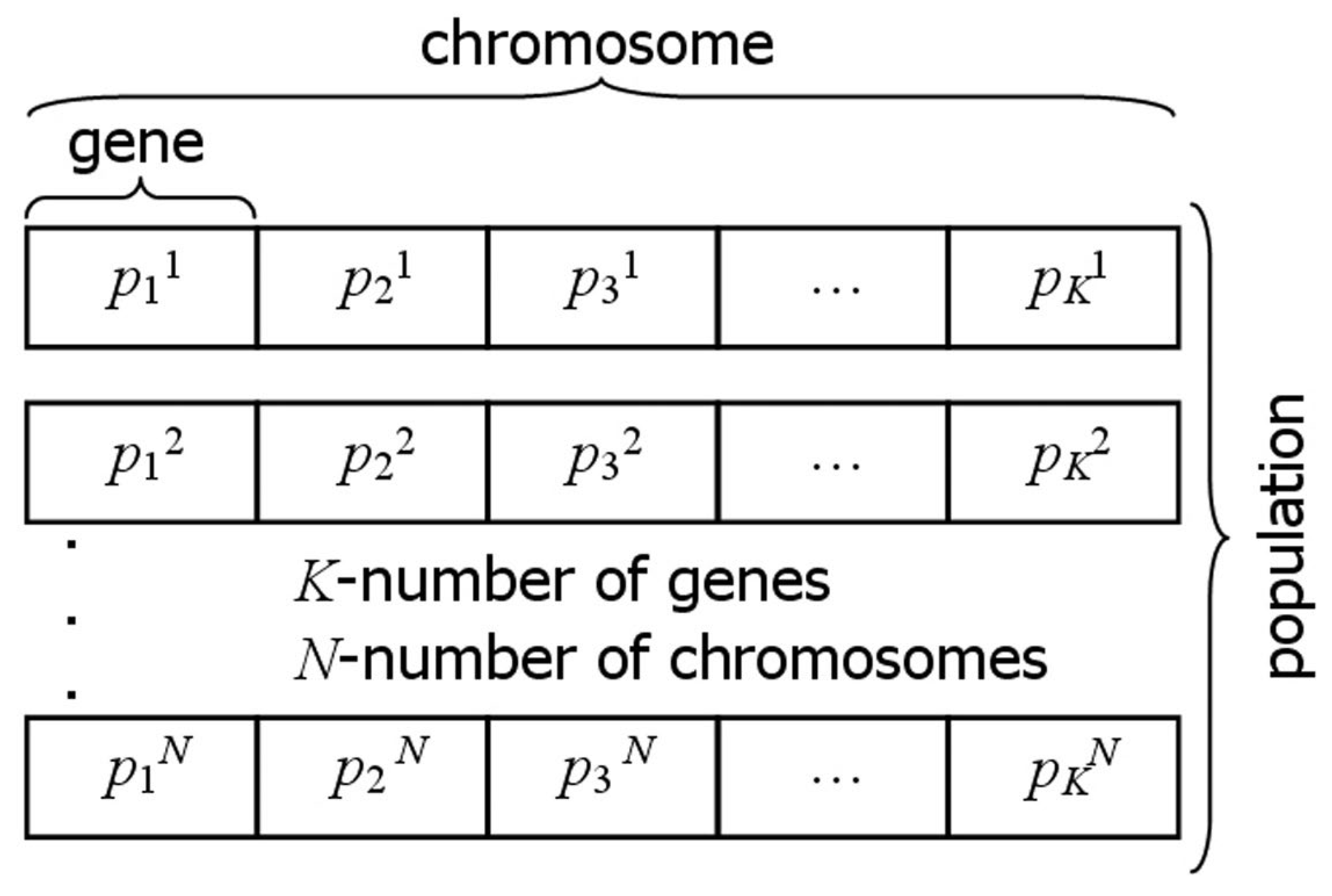
2.3. Inverse Problem and Evolutionary Algorithm
- The fitness function value is zero.
- Once the predefined number of generations is reached.
- Insufficient improvement in the fitness function value across successive iterations.
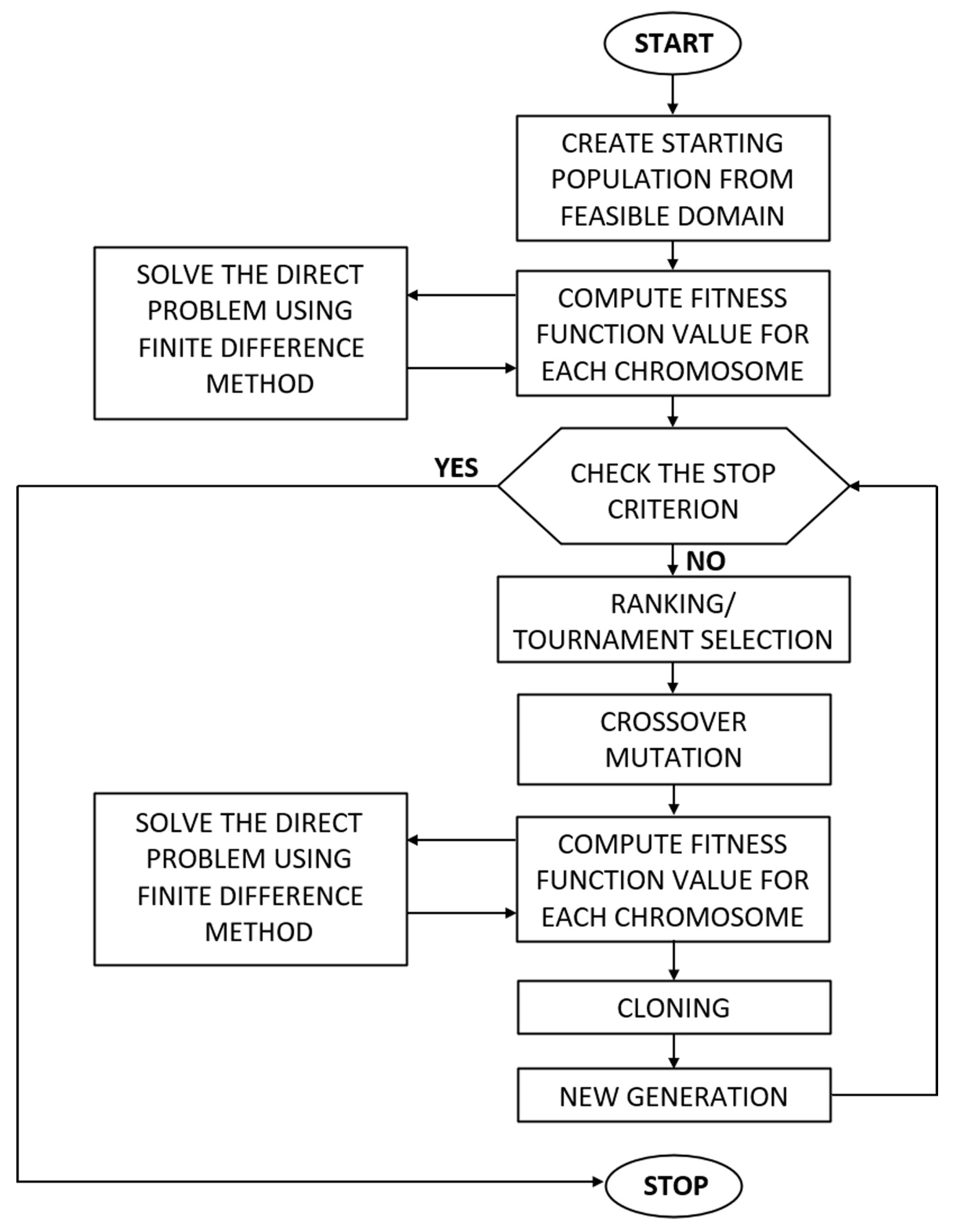
- A uniform mutation operator that modifies the gene values in a chromosome by randomly selecting new ones.
- A non-uniform mutation operator that uses a Gaussian distribution to change the gene values in a chromosome. The amplitude of such mutation in each generation is equal to , where pop is the number of generations.
- An arithmetic crossover operator that creates a new chromosome by forming a linear combination of genes from two randomly selected chromosomes, a cloning that enables the best chromosome to be carried over to the next population.
3. Results and Discussion
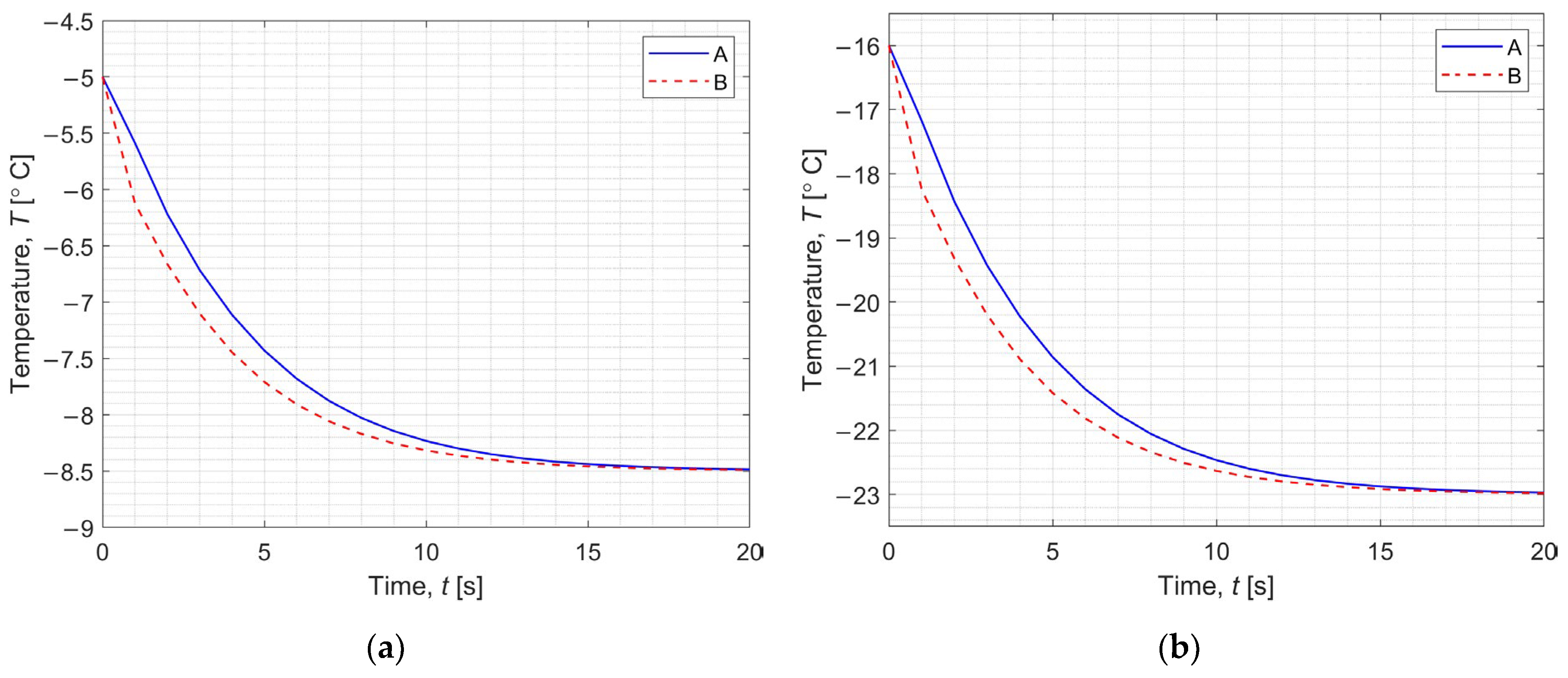
3.1. Direct Problem
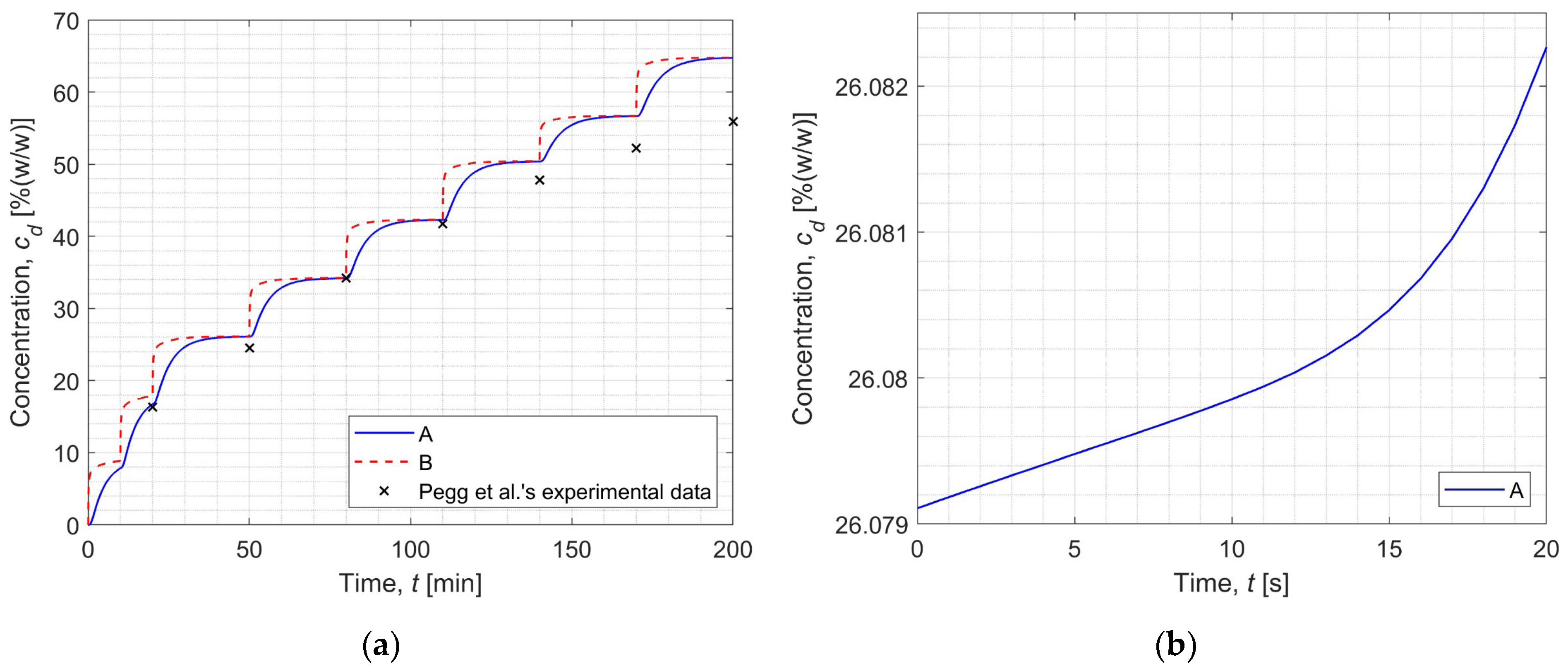
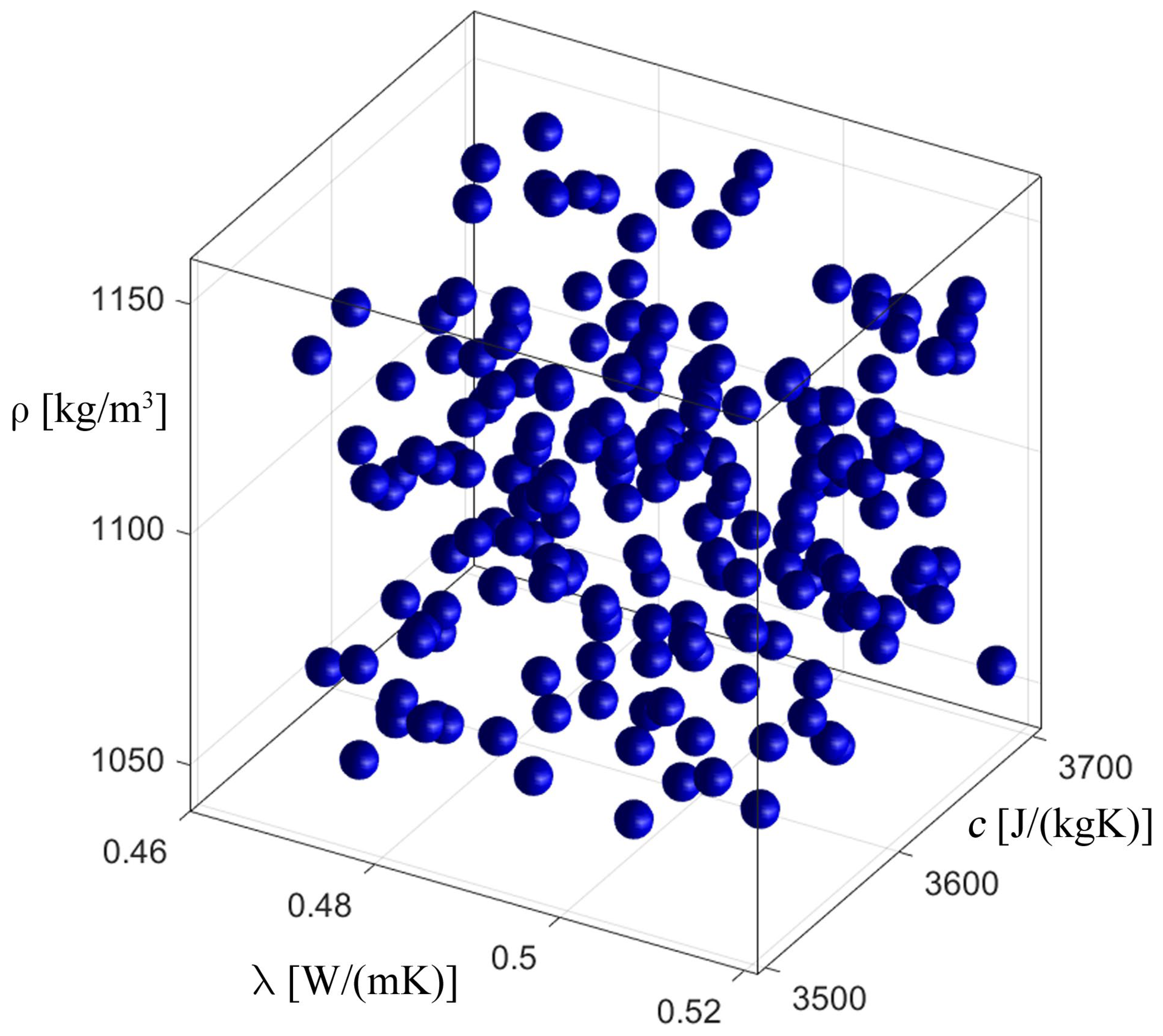
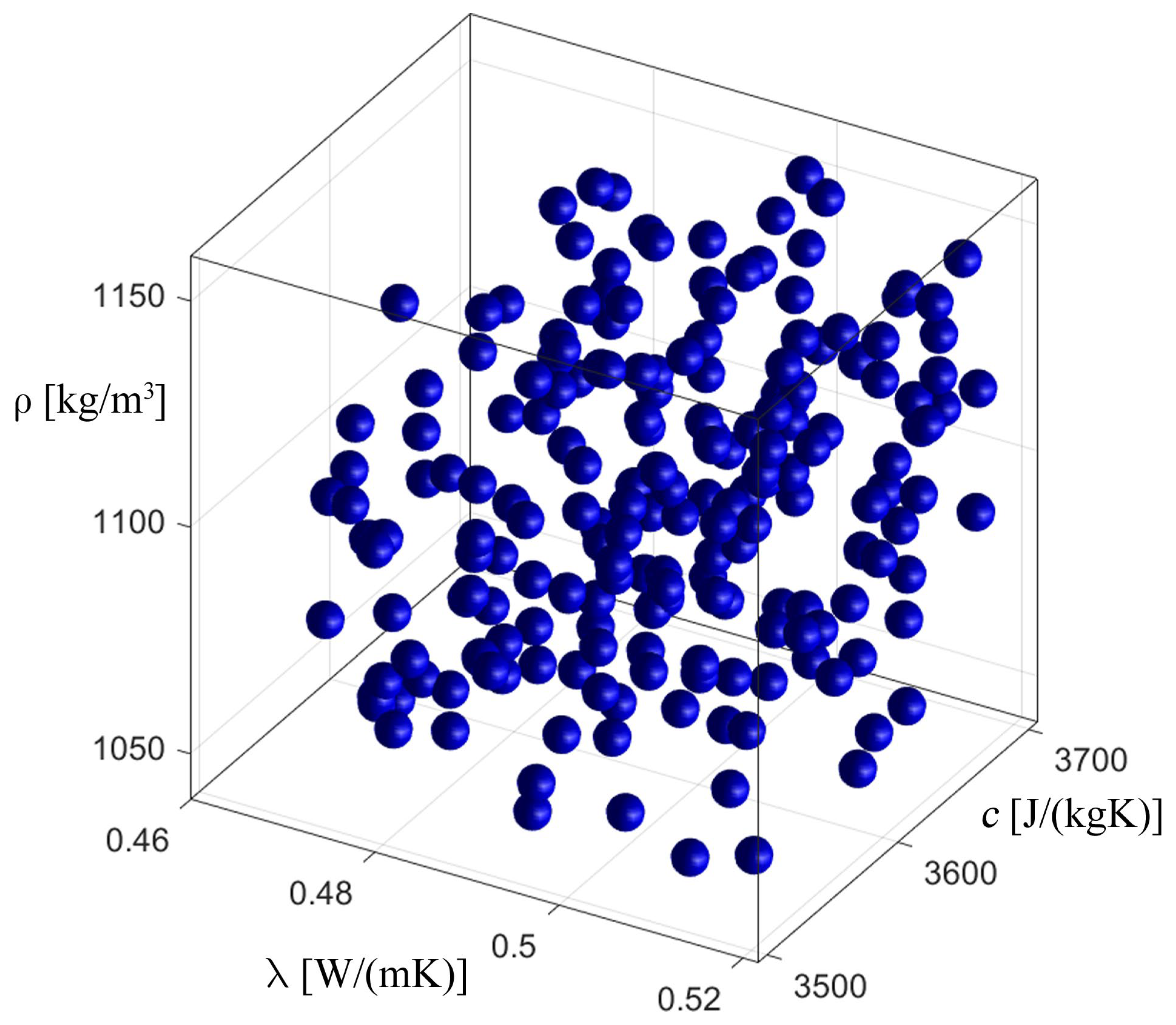
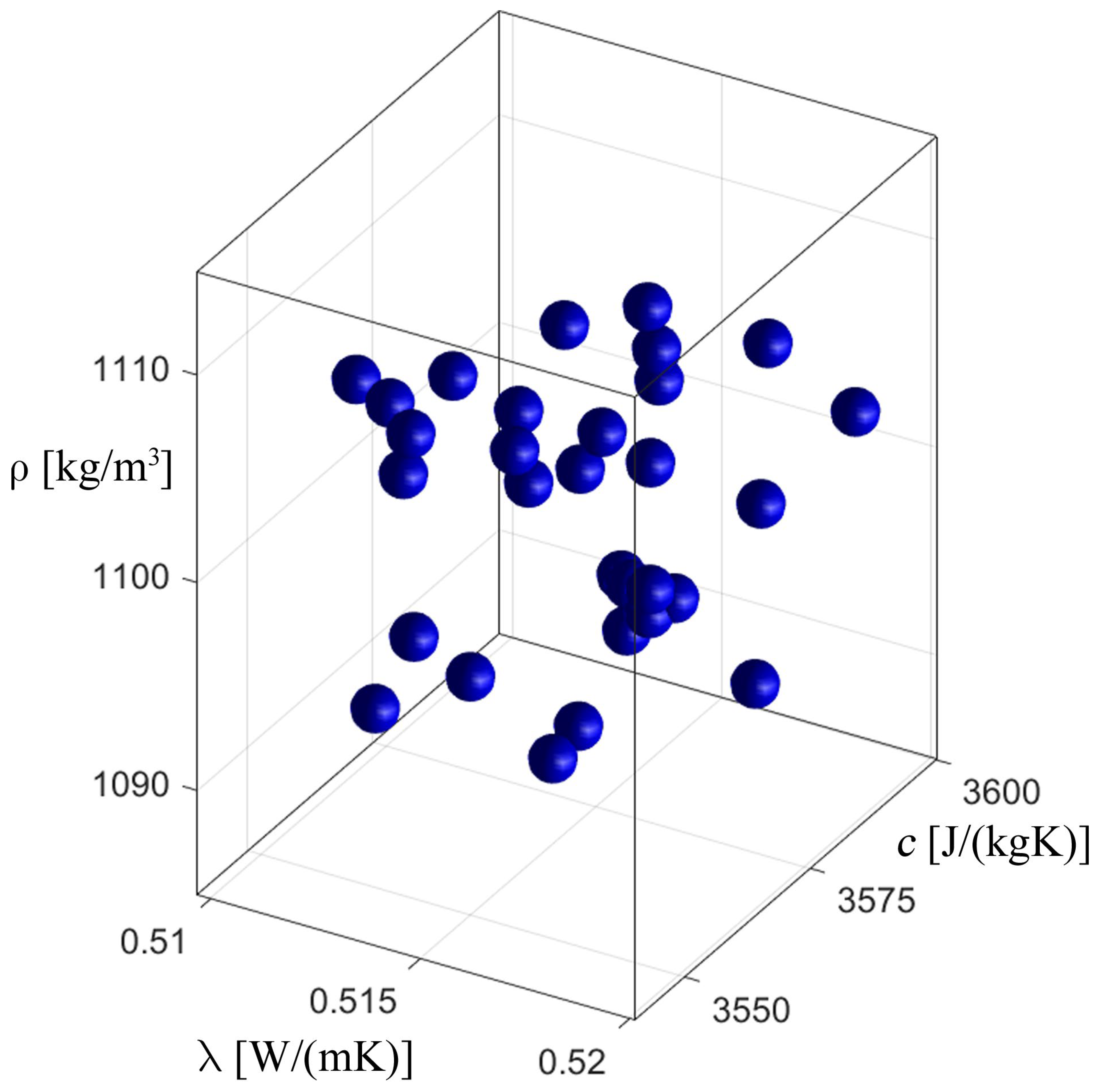
3.2. Inverse Problem
- Thermal conductivity λ = 0.47 ÷ 0.52 W·m−1·K−1.
- Specific heat capacity c = 3500 ÷ 3664 J·kg−1·K−1.
- Density ρ = 1099 ÷ 1100 kg·m−3.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jang, T.H.; Park, S.C.; Yang, J.H.; Kim, J.Y.; Seok, J.H.; Park, U.S.; Choi, C.W.; Lee, S.R.; Han, J. Cryopreservation and Its Clinical Applications. Integr. Med. Res. 2017, 6, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Moon, S.; Zhang, X.; Shao, L.; Song, Y.S.; Demirci, U. Multi-Scale Heat and Mass Transfer Modelling of Cell and Tissue Cryopreservation. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 561–583. [Google Scholar] [CrossRef] [PubMed]
- Jungare, K.A.; Radha, R.; Sreekanth, D. Cryopreservation of Biological Samples—A Short Review. Mater. Today Proc. 2022, 51, 1637–1641. [Google Scholar] [CrossRef]
- Kulkarni, P.G.; Paudel, N.; Magar, S.; Santilli, M.F.; Kashyap, S.; Baranwal, A.K.; Zamboni, P.; Vasavada, P.; Katiyar, A.; Singh, A.V. Overcoming Challenges and Innovations in Orthopedic Prosthesis Design: An Interdisciplinary Perspective. Biomed. Mater. Devices 2024, 2, 58–69. [Google Scholar] [CrossRef] [PubMed]
- Trzcińska, M.; Bryła, M. Kierunki i Możliwości Modyfikacji Metod Kriokonserwacji Oraz Oceny Jakości Nasienia Knura; Instytut Zootechniki PIB: Kraków, Poland, 2020; ISBN 978-83-7607-337-8. (In Polish) [Google Scholar]
- Mazur, P. Kinetics of Water Loss from Cells at Subzero Temperatures and the Likelihood of Intracellular Freezing. J. Gen. Physiol. 1963, 47, 347–369. [Google Scholar] [CrossRef]
- Kay, A.G.; Hoyland, J.A.; Rooney, P.; Kearney, J.N.; Pegg, D.E. A Liquidus Tracking Approach to the Cryopreservation of Human Cartilage Allografts. Cryobiology 2015, 71, 77–84. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, S. Freezing of Biological Tissues During Cryosurgery Using Hyperbolic Heat Conduction Model. Math. Model. Anal. 2015, 20, 443–456. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, G.; Wang, T.; Yu, Q.; Su, M.; He, X. Three-Dimensional Numerical Simulation of the Effects of Fractal Vascular Trees on Tissue Temperature and Intracelluar Ice Formation during Combined Cancer Therapy of Cryosurgery and Hyperthermia. Appl. Therm. Eng. 2015, 90, 296–304. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, S. Numerical Study on Biological Tissue Freezing Using Dual Phase Lag Bio-Heat Equation. In Trends in Biomathematics: Modeling, Optimization and Computational Problems: Selected Works from the BIOMAT Consortium Lectures, Moscow 2017; Mondaini, R.P., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 283–300. ISBN 978-3-319-91092-5. [Google Scholar]
- Yu, X.; Zhang, S.; Chen, G. Modeling the Addition/Removal of Dimethyl Sulfoxide into/from Articular Cartilage Treated with the Liquidus-Tracking Method. Int. J. Heat Mass Transf. 2019, 141, 719–730. [Google Scholar] [CrossRef]
- Zhou, X.; Jiang, Z.; Liang, X.M.; Liu, J.; Fang, P.; Liu, Z.; Gao, D. Microfiltration-Based Sequential Perfusion: A New Approach for Improved Loading/Unloading of Cryoprotectants. Sens. Actuators B Chem. 2020, 312, 127957. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, G.; Shu, Z.; Wang, T.; Zhu, K.; Gao, D. High-Precision Approach Based on Microfluidic Perfusion Chamber for Quantitative Analysis of Biophysical Properties of Cell Membrane. Int. J. Heat Mass Transf. 2015, 86, 869–879. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, X.; Chen, G. Permeation of Dimethyl Sulfoxide into Articular Cartilage at Subzero Temperatures. J. Zhejiang Univ. Sci. B 2012, 13, 213–220. [Google Scholar] [CrossRef] [PubMed]
- Elmoazzen, H.Y.; Elliott, J.A.W.; McGann, L.E. Osmotic Transport across Cell Membranes in Nondilute Solutions: A New Nondilute Solute Transport Equation. Biophys. J. 2009, 96, 2559–2571. [Google Scholar] [CrossRef] [PubMed]
- Skorupa, A.; Piasecka-Belkhayat, A. Numerical Modeling of Heat and Mass Transfer during Cryopreservation Using Interval Analysis. Appl. Sci. 2020, 11, 302. [Google Scholar] [CrossRef]
- Skorupa, A. Multi-Scale Modelling of Heat and Mass Transfer in Tissues and Cells During Cryopreservation Including Interval Methods. Ph.D. Thesis, Politechnika Śląska, Gliwice, Poland, 2023. [Google Scholar]
- Pegg, D.E.; Wang, L.; Vaughan, D. Cryopreservation of Articular Cartilage. Part 3: The Liquidus-Tracking Method. Cryobiology 2006, 52, 360–368. [Google Scholar] [CrossRef]
- Paruch, M. Identification of the Degree of Tumor Destruction on the Basis of the Arrhenius Integral Using the Evolutionary Algorithm. Int. J. Therm. Sci. 2018, 130, 507–517. [Google Scholar] [CrossRef]
- Mochnacki, B.; Majchrzak, E.; Paruch, M. Soft Tissue Freezing Process. Identification of the Dual-Phase Lag Model Parameters Using the Evolutionary Algorithm. AIP Conf. Proc. 2018, 1922, 060001. [Google Scholar] [CrossRef]
- Paruch, M.; Piasecka-Belkhayat, A.; Korczak, A. Identification of the Ultra-Short Laser Parameters during Irradiation of Thin Metal Films Using the Interval Lattice Boltzmann Method and Evolutionary Algorithm. Adv. Eng. Softw. 2023, 180, 103456. [Google Scholar] [CrossRef]
- Fourier, J.B.J. Théorie Analytique de La Chaleur; Firmin Didot: Paris, France, 1882. [Google Scholar]
- Piasecka-Belkhayat, A.; Skorupa, A. Application of Interval Arithmetic in Numerical Modeling of Cryopreservation Process during Cryoprotectant Loading to Microchamber. Numer. Heat Transf. Part A Appl. 2022, 84, 83–101. [Google Scholar] [CrossRef]
- Majchrzak, E.; Mochnacki, B. Numerical Methods. Theoretical Base, Practical Aspects, Algorithms; Publication of the Silesian University of Technology: Gliwice, Poland, 2004. (In Polish) [Google Scholar]
- Mochnacki, B.; Suchy, J. Numerical Methods in Computations of Foundry Processes; PFTA: Kraków, Poland, 1995. [Google Scholar]
- Singh, A.V.; Chandrasekar, V.; Prabhu, V.M.; Bhadra, J.; Laux, P.; Bhardwaj, P.; Al-Ansari, A.A.; Aboumarzouk, O.M.; Luch, A.; Dakua, S.P. Sustainable Bioinspired Materials for Regenerative Medicine: Balancing Toxicology, Environmental Impact, and Ethical Considerations. Biomed. Mater. 2024, 19, 060501. [Google Scholar] [CrossRef]
- Arabas, J. Lectures of Evolutionary Algorithms; WNT: Warsaw, Poland, 2001. [Google Scholar]
- Paruch, M.; Majchrzak, E. Identification of Tumor Region Parameters Using Evolutionary Algorithm and Multiple Reciprocity Boundary Element Method. Eng. Appl. Artif. Intell. 2007, 20, 647–655. [Google Scholar] [CrossRef]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin, Germany, 1996. [Google Scholar]
- Schulze, B.M.; Watkins, D.L.; Zhang, J.; Ghiviriga, I.; Castellano, R.K. Estimating the Shape and Size of Supramolecular Assemblies by Variable Temperature Diffusion Ordered Spectroscopy. Org. Biomol. Chem. 2014, 12, 7932–7936. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.trimen.pl/witek/ciecze/old_index.html (accessed on 10 July 2024). (In Polish).
- Youn, J.-I.; Telenkov, S.A.; Kim, E.; Bhavaraju, N.C.; Wong, B.J.F.; Valvano, J.W.; Milner, T.E. Optical and Thermal Properties of Nasal Septal Cartilage. Lasers Surg. Med. 2000, 27, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://itis.swiss/virtual-population/tissue-properties/database/ (accessed on 10 July 2024).
- Mochnacki, B.; Piasecka-Belkhayat, A. Numerical Modeling of Skin Tissue Heating Using the Interval Finite Difference Method. Mol. Cell. Biomech. 2013, 10, 233–244. [Google Scholar] [CrossRef]
- Piasecka-Belkhayat, A.; Skorupa, A. Cryopreservation Analysis Considering Degree of Crystallisation Using Fuzzy Arithmetic. J. Theor. Appl. Mech. 2024, 62, 207–218. [Google Scholar] [CrossRef]
- Skorupa, A.; Piasecka-Belkhayat, A. Comparison of Heat Transfer Phenomena for Two Different Cryopreservation Methods: Slow Freezing and Vitrification. J. Appl. Math. Comput. Mech. 2023, 22, 53–65. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Number of generations | 300 |
| Number of chromosomes | 200 |
| Probability of uniform mutation | 5% |
| Probability of non-uniform mutation | 5% |
| Probability of arithmetic crossover | 40% |
| Probability of cloning | 100% |
| Step | Time Duration | Temperature of Bath Solution | Concentration of Bath Solution |
|---|---|---|---|
| t [min] | Tbath [°C] | cbath [%(w/w)] | |
| 1 | 10 | 22 | 10 |
| 2 | 10 | 22 | 20 |
| 3 | 30 | −5 | 29 |
| 4 | 30 | −8.5 | 38 |
| 5 | 30 | −16 | 47 |
| 6 | 30 | −23 | 56 |
| 7 | 30 | −35 | 63 |
| 8 | 30 | −48.5 | 72 |
| Step | DMSO Concentration | Experimental Data | Relative Error |
|---|---|---|---|
| cd [%(w/w)] | cd [%(w/w)] | δ [%] | |
| 1 | 7.8411 | - | - |
| 2 | 16.7257 | 16.3 ± 1.3 | 2.6118 |
| 3 | 26.0791 | 24.5 ± 1.1 | 6.4453 |
| 4 | 34.1795 | 34.2 ± 0.9 | 0.0600 |
| 5 | 42.2754 | 41.7 ± 3.3 | 1.3799 |
| 6 | 50.3709 | 47.8 ± 2.8 | 5.3784 |
| 7 | 56.6698 | 52.2 ± 1.3 | 8.5628 |
| 8 | 64.7463 | 55.9 ± 2.9 | 15.8253 |
| Parameter | Value from [32,33] | Found Value | Fitness Function |
|---|---|---|---|
| Thermal conductivity, λ [W·m−1·K−1] | 0.518 | 0.522 | 107.852194 |
| Specific heat capacity, c [J·kg−1·K−1] | 3567.5 | 3571.2 | |
| Density, ρ [kg·m−3] | 1100 | 1089.3 |
| Step | DMSO Concentration | Experimental Data |
|---|---|---|
| cd [%(w/w)] | cd [%(w/w)] | |
| 1 | 7.8411 | - |
| 2 | 16.7257 | 16.3 ± 1.3 |
| 3 | 26.0791 | 24.5 ± 1.1 |
| 4 | 34.1794 | 34.2 ± 0.9 |
| 5 | 42.2754 | 41.7 ± 3.3 |
| 6 | 50.3708 | 47.8 ± 2.8 |
| 7 | 56.6697 | 52.2 ± 1.3 |
| 8 | 64.7463 | 55.9 ± 2.9 |
| Parameter | Value from [32,33] | Found Value | Fitness Function |
|---|---|---|---|
| Thermal conductivity, λ [W·m−1·K−1] | 0.518 | 0.519 | 29.594674 |
| Specific heat capacity, c [J·kg−1·K−1] | 3567.5 | 3565.9 | |
| Density, ρ [kg·m−3] | 1100 | 1100 |
| Step | DMSO Concentration | Experimental Data |
|---|---|---|
| cd [%(w/w)] | cd [%(w/w)] | |
| 1 | 7.8411 | - |
| 2 | 16.7257 | 16.3 ± 1.3 |
| 3 | 26.0791 | 24.5 ± 1.1 |
| 4 | 34.1794 | 34.2 ± 0.9 |
| 5 | 42.2754 | 41.7 ± 3.3 |
| 6 | 50.3708 | 47.8 ± 2.8 |
| 7 | 56.6697 | 52.2 ± 1.3 |
| 8 | 64.7463 | 55.9 ± 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piasecka-Belkhayat, A.; Skorupa, A.; Paruch, M. Determining Thermophysical Parameters of Cryopreserved Articular Cartilage Using Evolutionary Algorithms and Experimental Data. Materials 2024, 17, 5703. https://doi.org/10.3390/ma17235703
Piasecka-Belkhayat A, Skorupa A, Paruch M. Determining Thermophysical Parameters of Cryopreserved Articular Cartilage Using Evolutionary Algorithms and Experimental Data. Materials. 2024; 17(23):5703. https://doi.org/10.3390/ma17235703
Chicago/Turabian StylePiasecka-Belkhayat, Alicja, Anna Skorupa, and Marek Paruch. 2024. "Determining Thermophysical Parameters of Cryopreserved Articular Cartilage Using Evolutionary Algorithms and Experimental Data" Materials 17, no. 23: 5703. https://doi.org/10.3390/ma17235703
APA StylePiasecka-Belkhayat, A., Skorupa, A., & Paruch, M. (2024). Determining Thermophysical Parameters of Cryopreserved Articular Cartilage Using Evolutionary Algorithms and Experimental Data. Materials, 17(23), 5703. https://doi.org/10.3390/ma17235703






