Residual Stress Measurement Using EMAT for X80 Pipeline Steel: Effects of Coating Thickness and Surface Roughness Under Low Surface Preparation Requirements
Abstract
1. Introduction
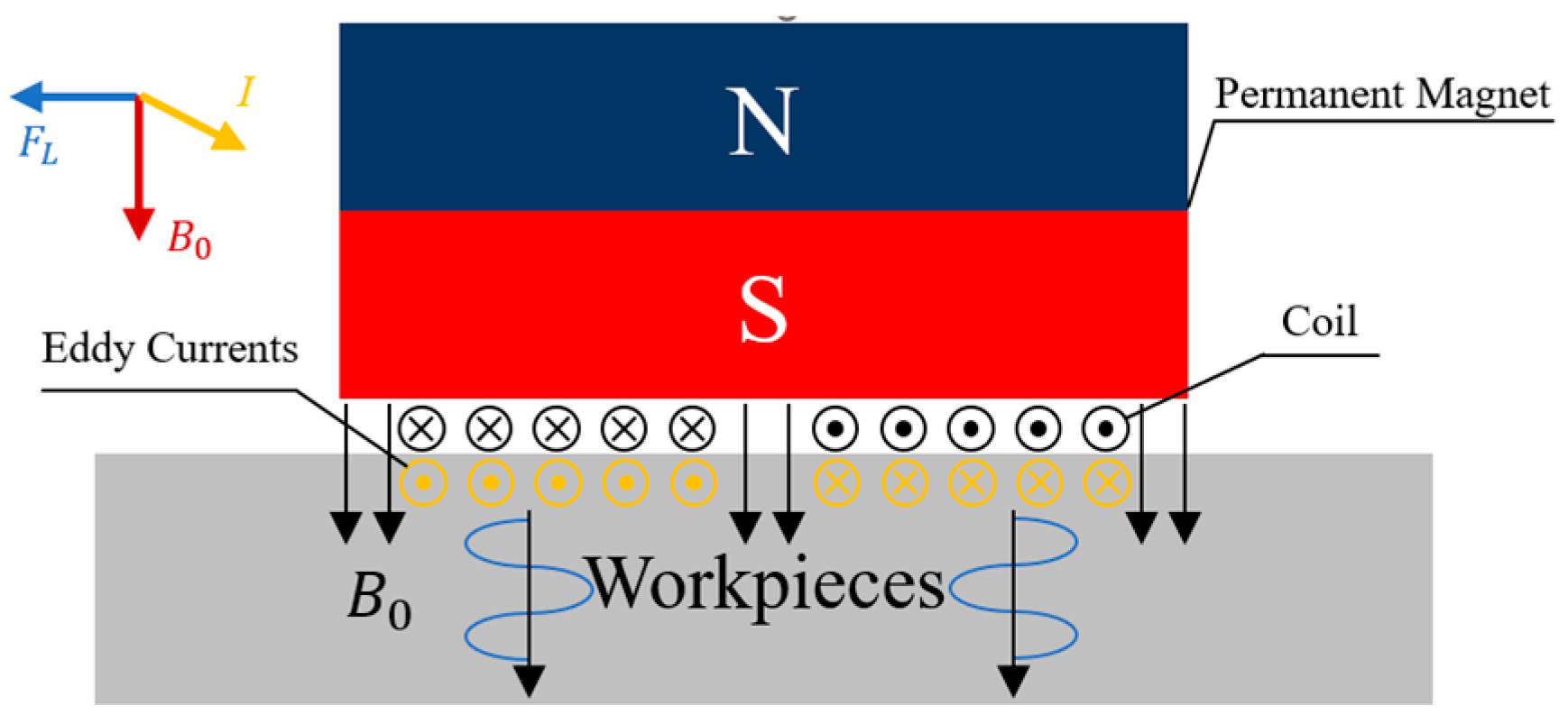
2. Stress Detection Theory of EMAT
3. Experimental Contents
3.1. Experimental Equipment
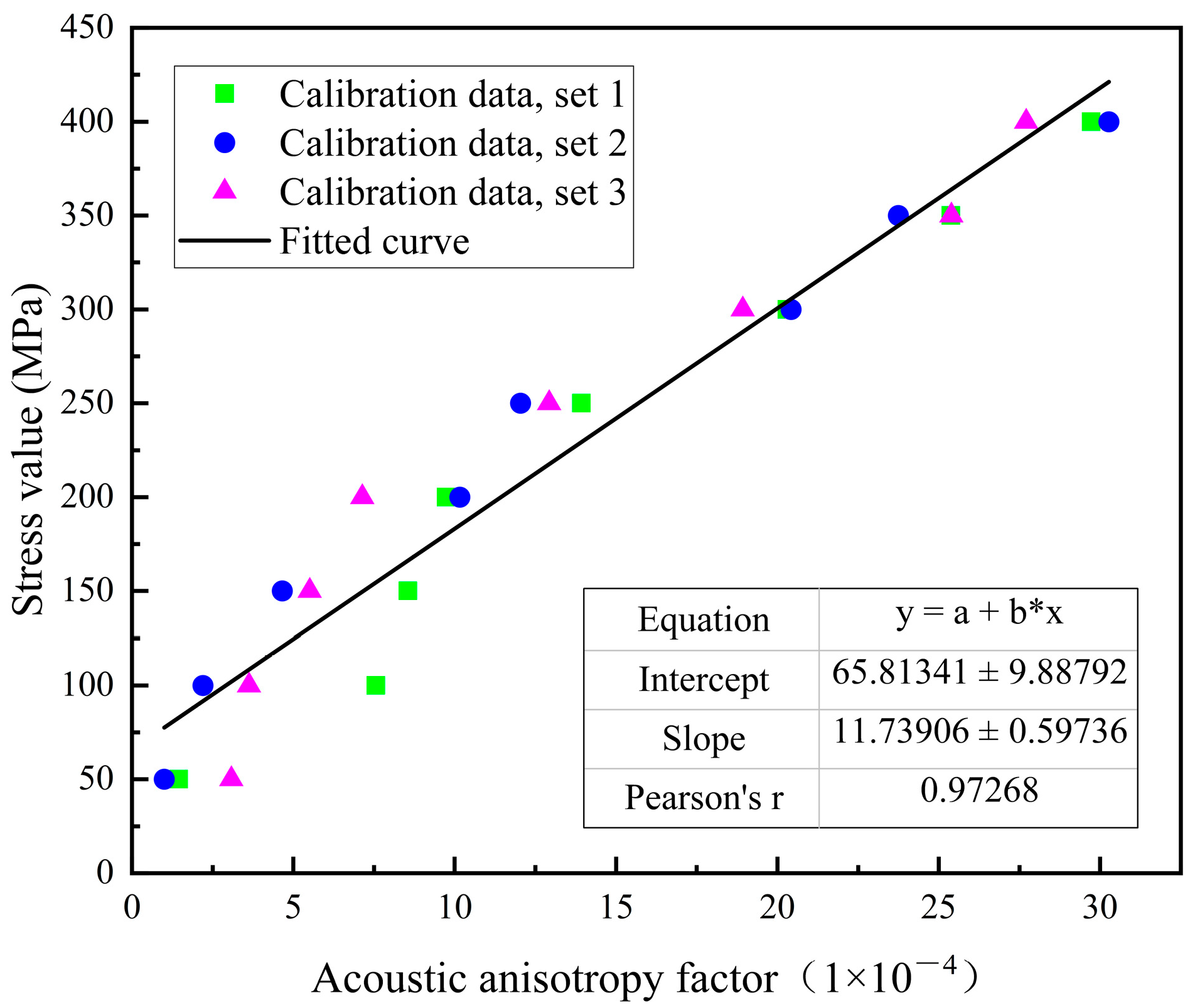
3.2. Calibration Process
3.3. Coating Specimen Preparation
3.4. Roughness Specimen Preparation
4. Results and Discussion
4.1. Calibration Results
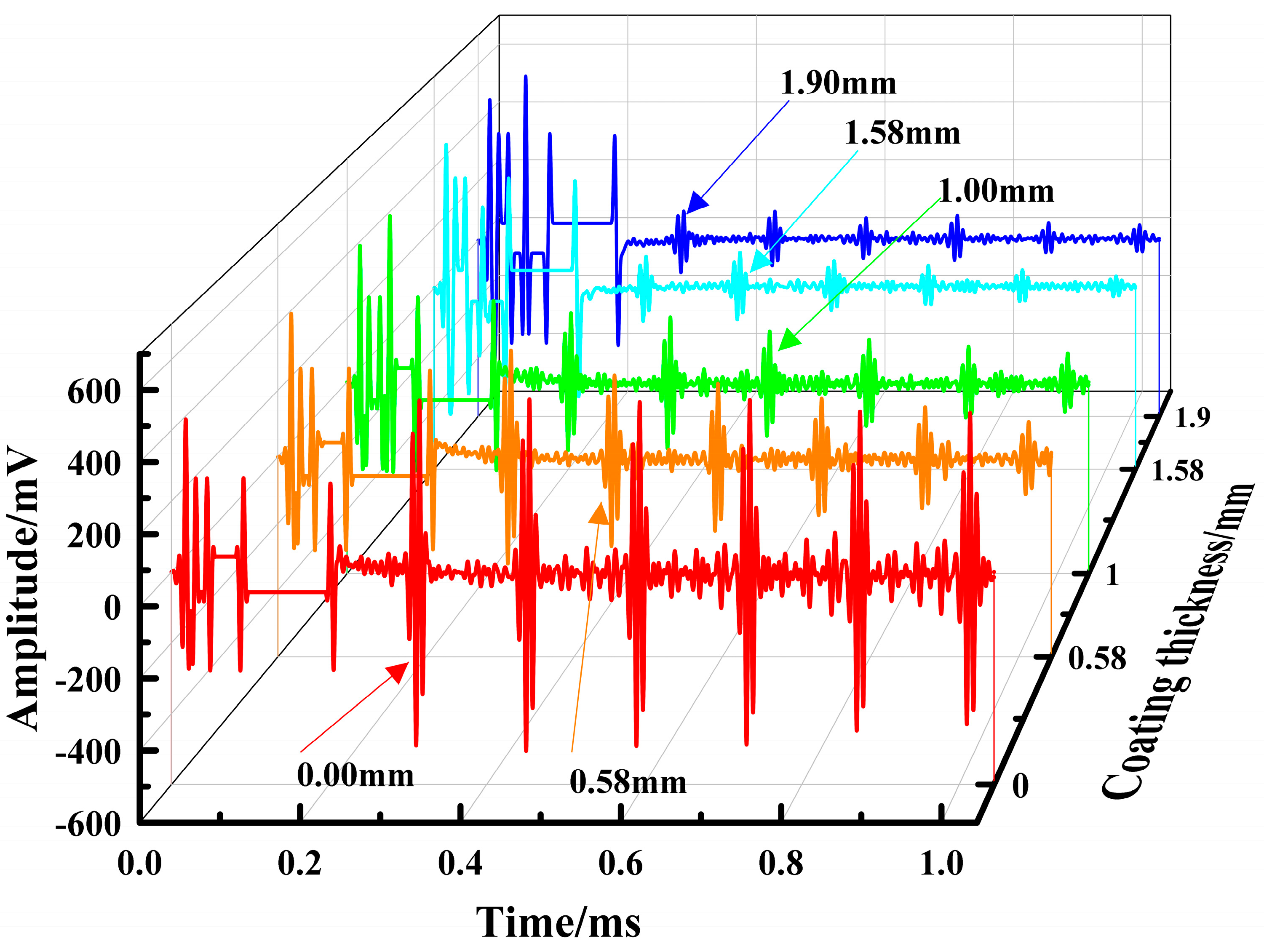
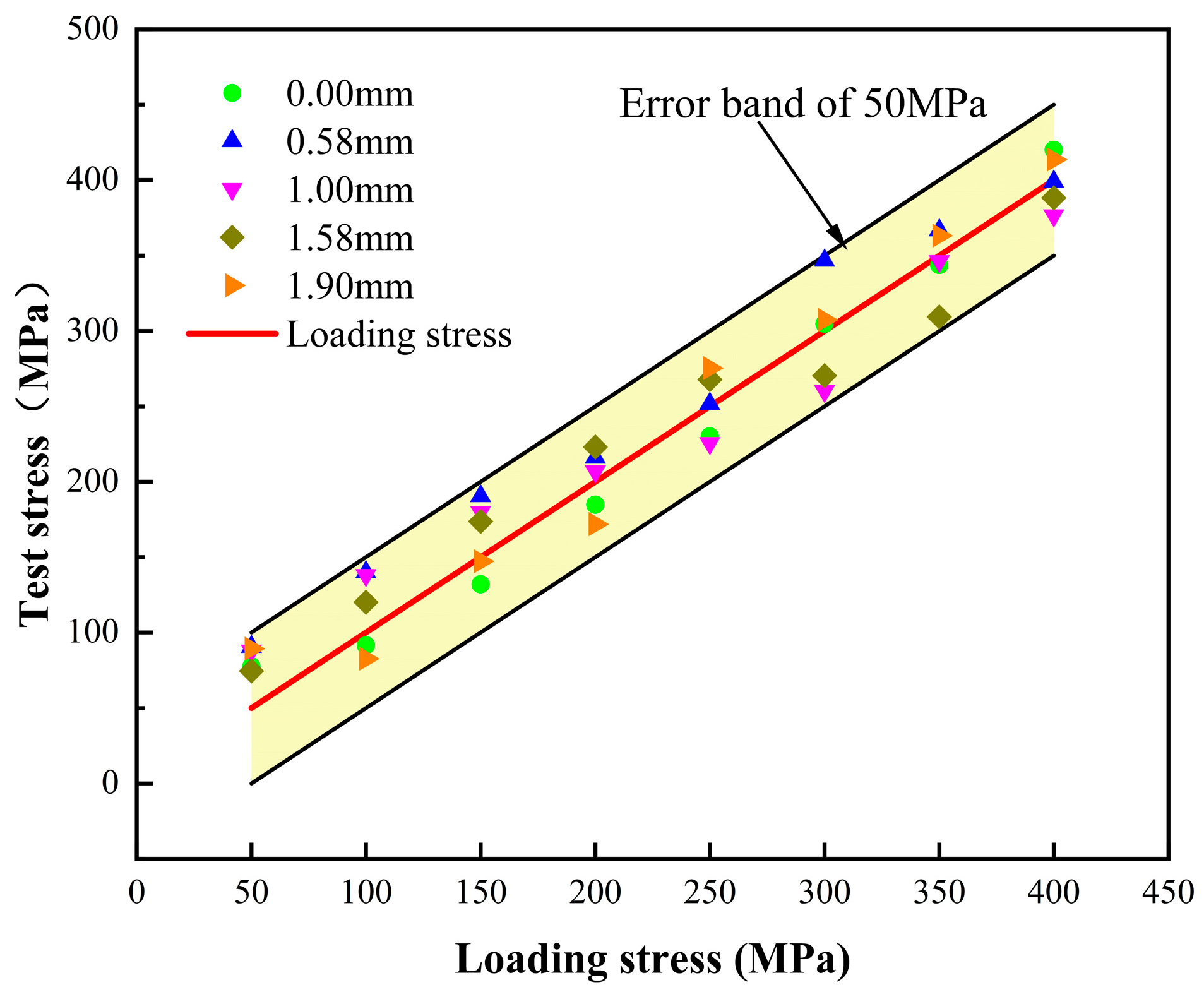
4.2. Influence of Coating Thickness
4.3. Influence of Surface Roughness
5. Conclusions
- (1)
- For specimens with coating thicknesses of 0.58 mm, 1 mm, 1.58 mm, and 1.9 mm, the stress measurement error compared to applied stress values remains in the range of 50 MPa. These indicate that the influence of the coating thickness on the measurement accuracy is negligible.
- (2)
- The comparison of the stress measurements of roughness samples to unpolished samples revealed that the variation is less than 30 MPa, indicating that EMAT maintains good measurement stability across different surface roughness levels.
- (3)
- Stress measurements of roughness specimens using LCR waves revealed that as surface roughness increased, the variation in stress measurement values significantly increased, highlighting the significant impact of surface roughness on the measurement accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arumugam, T.; Kumar, S.D.V.; Karuppanan, S.; Ovinis, M. The Influence of Axial Compressive Stress and Internal Pressure on a Pipeline Network: A Review. Appl. Sci. 2023, 13, 3799. [Google Scholar] [CrossRef]
- Liu, C.; Bhole, S.D. Challenges and developments in pipeline weldability and mechanical properties. Sci. Technol. Weld. Join. 2013, 18, 169–181. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, W.; Zhang, H.; Han, B.; Jin, H.; Gao, Q. 3D finite element analysis and optimization of welding residual stress in the girth joints of X80 steel pipeline. J. Manuf. Process. 2021, 66, 166–178. [Google Scholar] [CrossRef]
- Biezma, M.V.; Andres, M.A.; Agudo, D.; Briz, E. Most fatal oil & gas pipeline accidents through history: A lessons learned approach. Eng. Fail. Anal. 2020, 110, 104446. [Google Scholar] [CrossRef]
- Guo, J.; Fu, H.; Pan, B.; Kang, R. Recent progress of residual stress measurement methods: A review. Chin. J. Aeronaut. 2021, 34, 54–78. [Google Scholar] [CrossRef]
- Carvalho, A.A.; Rebello, J.M.A.; Souza, W.V.; Sagrilo, L.V.S.; Soares, S.D. Reliability of non-destructive test techniques in the inspection of pipelines used in the oil industry. Int. J. Press. Vessel. Pip. 2008, 85, 745–751. [Google Scholar] [CrossRef]
- Acevedo, R.; Sedlak, P.; Kolman, R.; Fredel, M. Residual stress analysis of additive manufacturing of metallic parts using ultrasonic waves: State of the art review. J. Mater. Res. Technol. 2020, 9, 9457–9477. [Google Scholar] [CrossRef]
- Parlak, B.O.; Yavasoglu, H.A. A Comprehensive Analysis of In-Line Inspection Tools and Technologies for Steel Oil and Gas Pipelines. Sustainability 2023, 15, 2783. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Li, T.; Zhang, X.; Liu, Y.; Liu, K.; Wang, Y. Influence factors analysis and accuracy improvement for stress measurement using ultrasonic longitudinal critically refracted (LCR) wave. Appl. Acoust. 2018, 141, 178–187. [Google Scholar] [CrossRef]
- Shujuan, W.; Lei, K.; Zaixin, Z.; Guofu, Z. Overview of Research Advances in Electromagnetic Acoustic Transducer. Intstrument Tech. Sens. 2006, 5, 47–50. [Google Scholar]
- Nakamura, N.; Ashida, K.; Takishita, T.; Ogi, H.; Hirao, M. Inspection of stress corrosion cracking in welded stainless steel pipe using point-focusing electromagnetic-acoustic transducer. NDT E Int. 2016, 83, 88–93. [Google Scholar] [CrossRef]
- Thon, A.; Painchaud-April, G.; Le Duff, A.; Belanger, P. Optimization of a Lorentz forces EMAT for the reconstruction of the circumferential thickness profile of a steel pipe using high order shear horizontal modes. NDT E Int. 2022, 128, 102631. [Google Scholar] [CrossRef]
- Trushkevych, O.; Edwards, R.S. Characterisation of small defects using miniaturised EMAT system. NDT E Int. 2019, 107, 102140. [Google Scholar] [CrossRef]
- Thon, A.; Painchaud-April, G.; Le Duff, A.; Belanger, P. On the use of a linear array EMAT for remote thickness gauging using the reflected modes on a steel pipe. NDT E Int. 2023, 139, 102917. [Google Scholar] [CrossRef]
- Song, H.; Xiao, Q.; Wang, G.; Zhang, J.; Hu, W. A Composite Approach of Electromagnetic Acoustic Transducer and Eddy Current for Inner and Outer Corrosion Defects Detection. IEEE Trans. Instrum. Meas. 2023, 72, 6001211. [Google Scholar] [CrossRef]
- Murav’ev, V.V.; Volkova, L.V.; Platunov, A.V.; Kulikov, V.A. An electromagnetic-acoustic method for studying stress-strain states of rails. Russ. J. Nondestruct. Test. 2016, 52, 370–376. [Google Scholar] [CrossRef]
- Wang, H.; Feng, J.; Shi, S.; Ouyang, L.; Xu, F.; Chen, Z.; He, Y.; Li, G. Electromagnetic ultrasonic measurement for welding residual stress detection-comparison between experiment with numerical simulation. J. Phys. Conf. Ser. 2019, 1303, 012011. [Google Scholar] [CrossRef]
- Dang, G.; Pei, C.; Yang, Z.; Zhou, H. Residual strain measurement based on longitudinal to shear wave velocity ratio with a dual-mode EMAT. Front. Mater. 2023, 10, 1273190. [Google Scholar] [CrossRef]
- Ogi, H. Erratum: Field dependence of coupling efficiency between electromagnetic field and ultrasonic bulk waves [J. Appl. Phys. 82, 3940 (1997)]. J. Appl. Phys. 2012, 112, 059901. [Google Scholar] [CrossRef]
- HIRAOM, O. Electromagnetic Acoustic Transducers: Noncontacting Ultrasonic Measurements Using EMATs; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Hughes, D.S.; Kelly, J.L. Second-order elastic deformation of solids. Phys. Rev. 1953, 92, 1145. [Google Scholar] [CrossRef]
- Zhang, K.; Yi, P.; Li, Y.; Hui, B.; Zhang, X. A New Method to Evaluate Surface Defects with an Electromagnetic Acoustic Transducer. Sensors 2015, 15, 17420–17432. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, Y. Orthogonal Optimal Design Method for Spiral Coil EMAT Considering Lift-off Effect: A Case Study. IEEE Access 2021, 9, 22062–22070. [Google Scholar] [CrossRef]
- Wang, Z.; Cui, X.; Pu, H.; Kang, Y. Influence of surface roughness on energy change of excitation process in EMAT thickness measurement. Int. J. Appl. Electromagn. Mech. 2019, 59, 1479–1486. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, Z.C.; Chen, X.D.; Cheng, J.W.; Wang, H.B.; Bu, Y.G. Modeling and experimental analysis of electromagnetic ultrasonic testing considering effect of rough surface. In Proceedings of the ASME Pressure Vessels and Piping Conference (PVP) on Re-Energizing the Pressure Vessels and Piping Community, Atlanta, GA, USA, 16–21 July 2023. [Google Scholar]
- Xiang, L.; Dixon, S.; Thring, C.B.; Li, Z.; Edwards, R.S. Lift-off performance of electromagnetic acoustic transducers (EMATs) for surface acoustic wave generation. NDT E Int. 2022, 126, 102576. [Google Scholar] [CrossRef]
- Huang, S.; Zhao, W.; Zhang, Y.; Wang, S. Study on the lift-off effect of EMAT. Sens. Actuators A-Phys. 2009, 153, 218–221. [Google Scholar] [CrossRef]





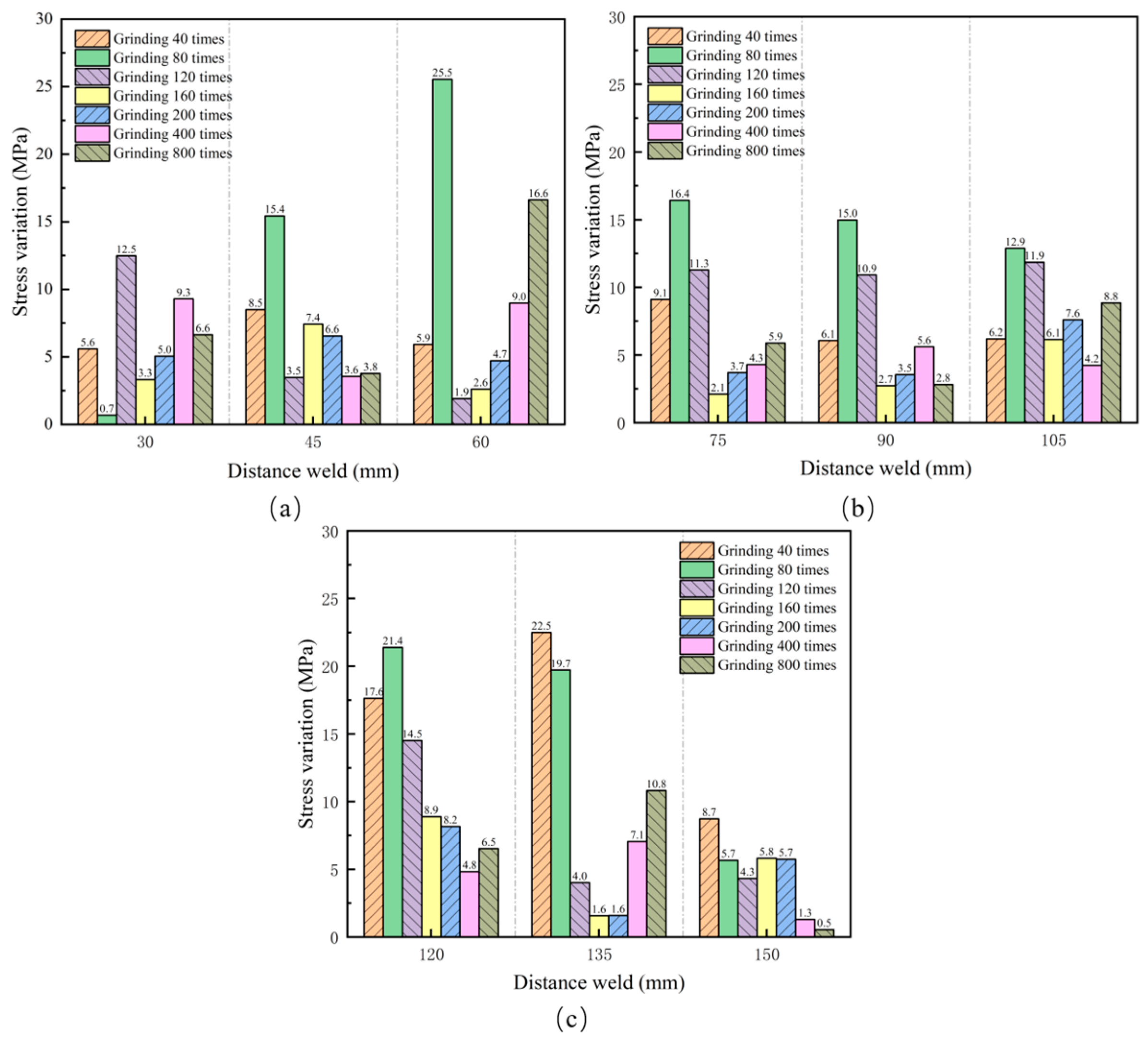
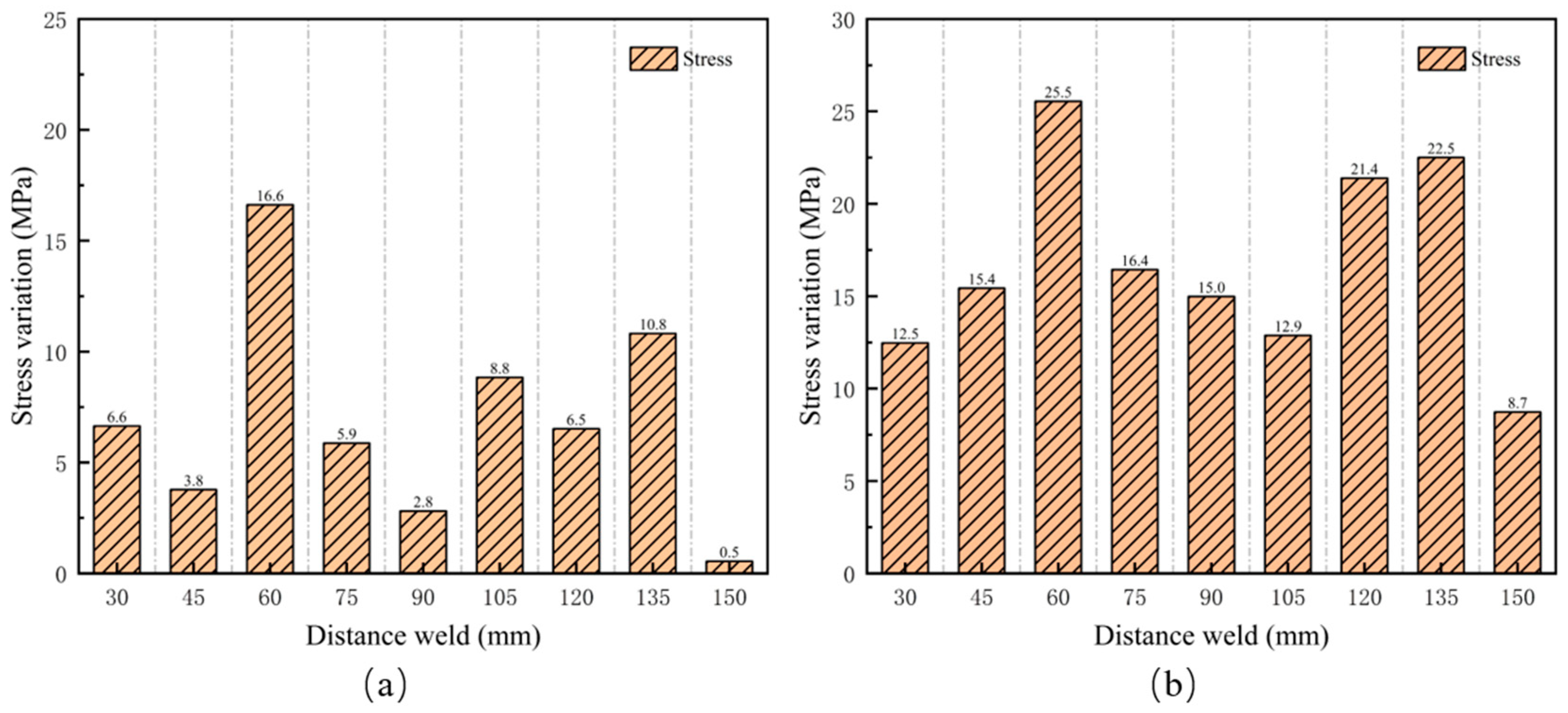
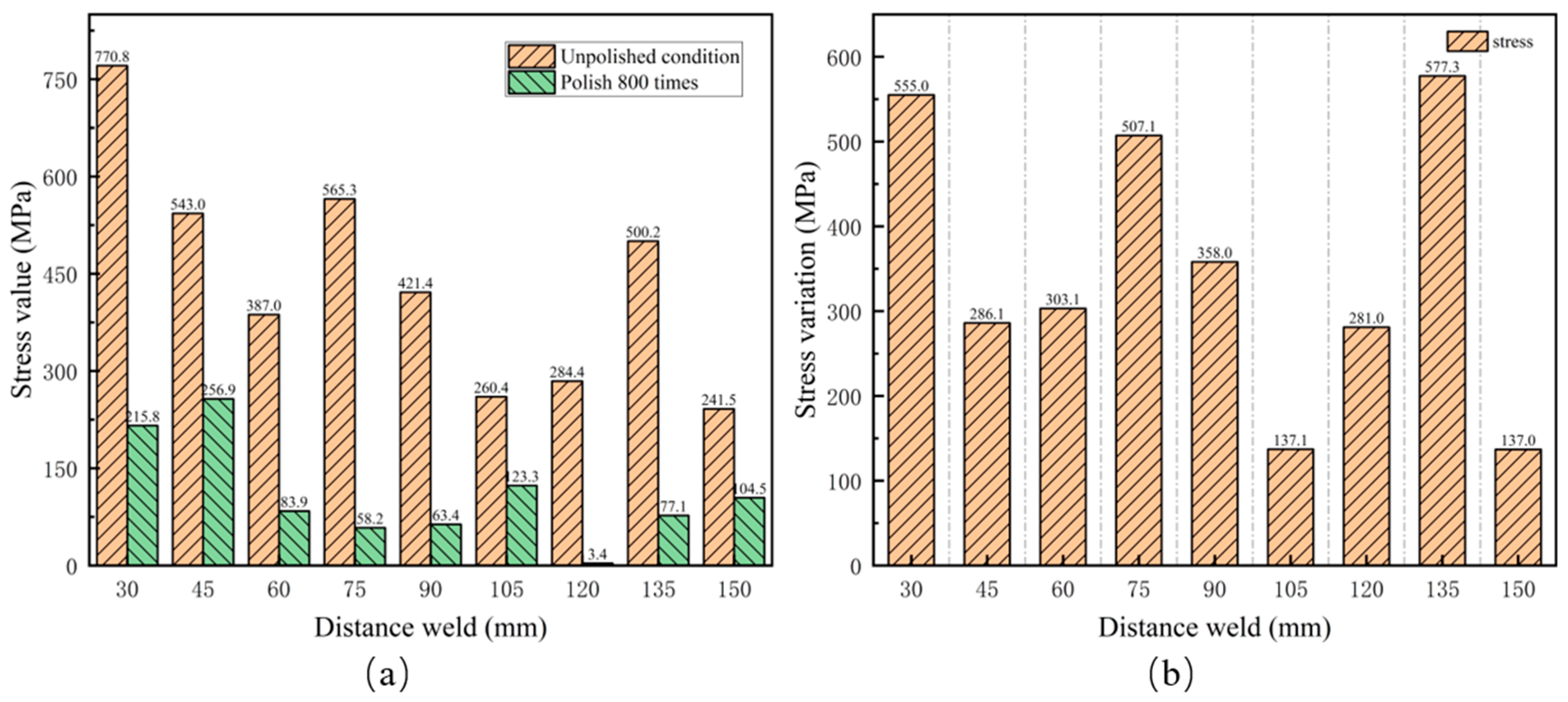

| Coating thickness/times | 0 | 40 | 80 | 120 | 160 | 200 | 400 | 800 |
| /μm | 180.3 | 165.7 | 125.6 | 114.6 | 81.8 | 69.2 | 46.7 | 18.2 |
| Coating thickness/mm | 0 | 0.58 | 1 | 1.58 | 1.9 |
| Echo amplitude/mV | 481.1 | 320.2 | 215.1 | 109.4 | 98.7 |
| Coating thickness/mm | 0 | 0.58 | 1 | 1.58 | 1.9 |
| Load stress/MPa | Test stresses/MPa | ||||
| 50 | 77.5 | 90.6 | 87.9 | 74. 6 | 89.3 |
| 100 | 91.5 | 140.1 | 138.1 | 120.1 | 82.6 |
| 150 | 132.0 | 190.5 | 179.9 | 173.7 | 147.3 |
| 200 | 184.7 | 216.1 | 206.8 | 223.1 | 171.8 |
| 250 | 230.1 | 251.7 | 225.6 | 267.8 | 275.3 |
| 300 | 304.7 | 346.6 | 260.1 | 270.4 | 307.2 |
| 350 | 343.7 | 366.8 | 346.2 | 309.3 | 363.1 |
| 400 | 420.0 | 398.9 | 376.6 | 388.3 | 413.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Chen, B.; Xia, L.; Xu, L.; Liu, X.; Zou, S.; Peng, D.; Gou, G. Residual Stress Measurement Using EMAT for X80 Pipeline Steel: Effects of Coating Thickness and Surface Roughness Under Low Surface Preparation Requirements. Materials 2024, 17, 5799. https://doi.org/10.3390/ma17235799
Luo C, Chen B, Xia L, Xu L, Liu X, Zou S, Peng D, Gou G. Residual Stress Measurement Using EMAT for X80 Pipeline Steel: Effects of Coating Thickness and Surface Roughness Under Low Surface Preparation Requirements. Materials. 2024; 17(23):5799. https://doi.org/10.3390/ma17235799
Chicago/Turabian StyleLuo, Chunlang, Bing Chen, Li Xia, Lintao Xu, Xuan Liu, Sunmin Zou, Dongchuan Peng, and Guoqing Gou. 2024. "Residual Stress Measurement Using EMAT for X80 Pipeline Steel: Effects of Coating Thickness and Surface Roughness Under Low Surface Preparation Requirements" Materials 17, no. 23: 5799. https://doi.org/10.3390/ma17235799
APA StyleLuo, C., Chen, B., Xia, L., Xu, L., Liu, X., Zou, S., Peng, D., & Gou, G. (2024). Residual Stress Measurement Using EMAT for X80 Pipeline Steel: Effects of Coating Thickness and Surface Roughness Under Low Surface Preparation Requirements. Materials, 17(23), 5799. https://doi.org/10.3390/ma17235799







