Improved Method for the Calculation of the Air Film Thickness of an Air Cushion Belt Conveyor
Abstract
1. Introduction
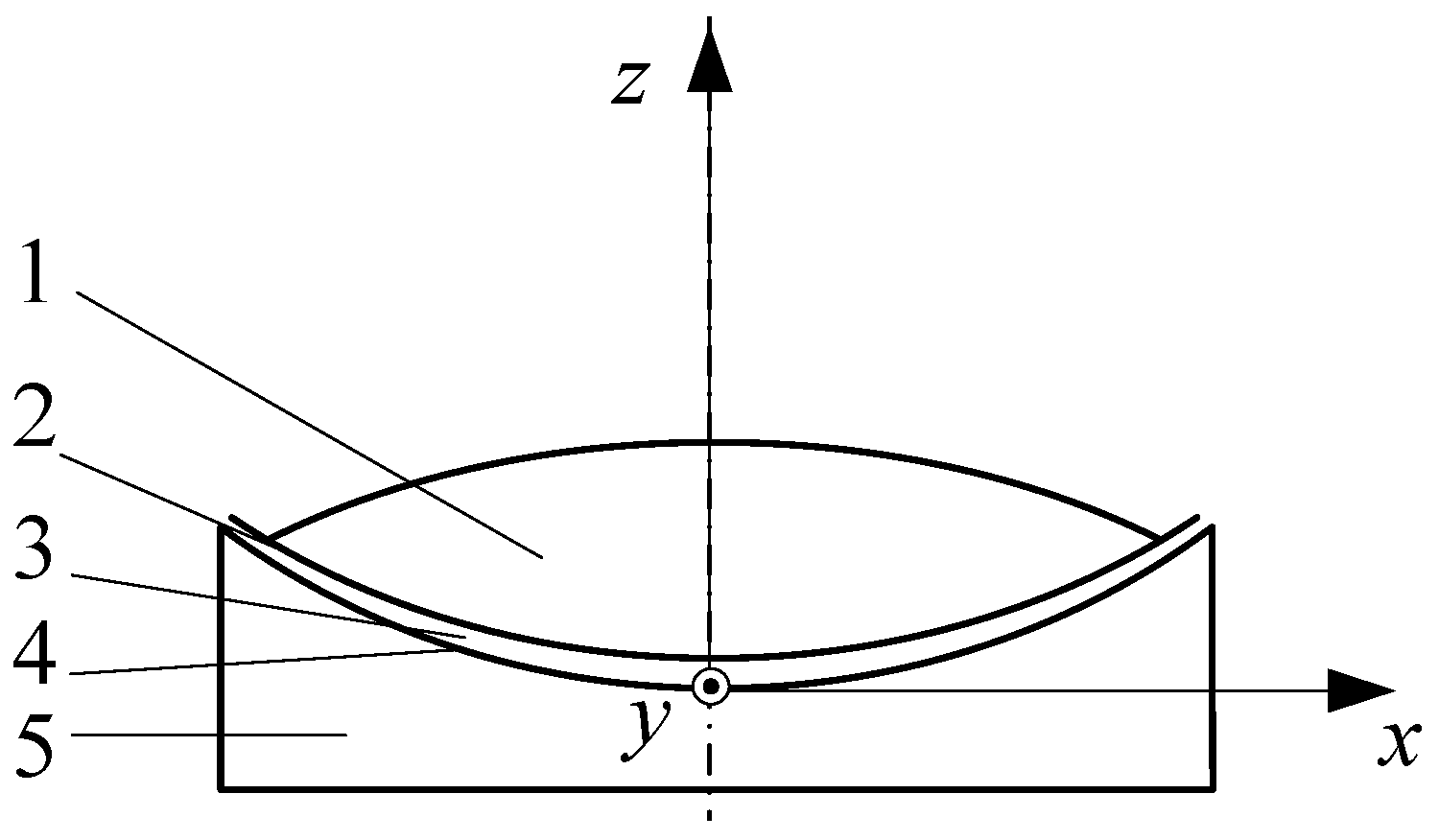
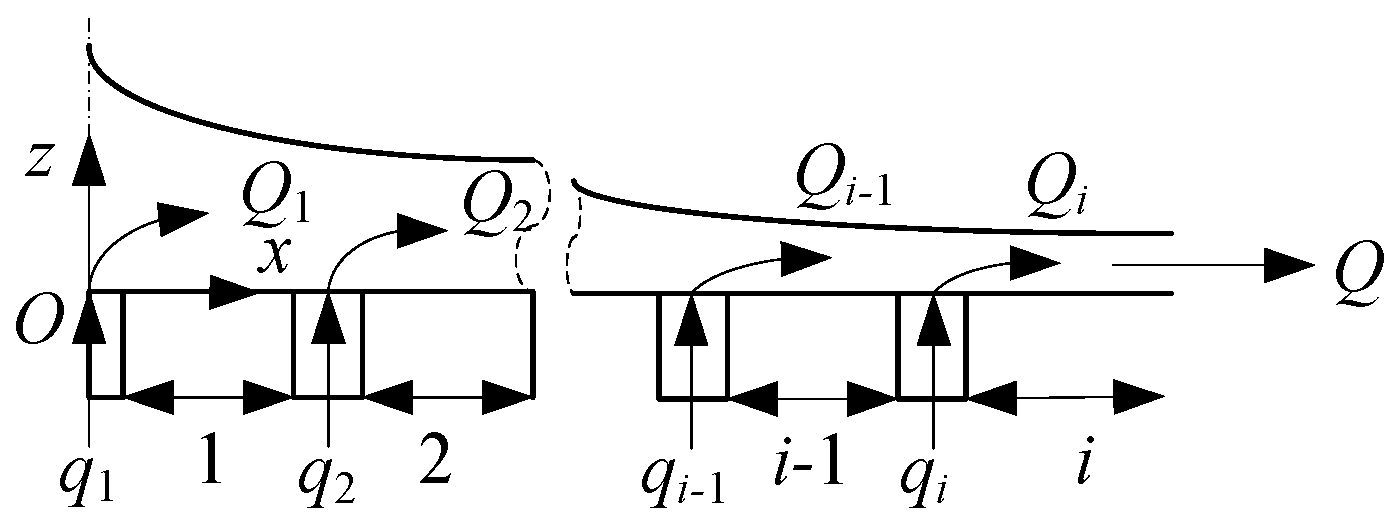
2. Calculation Method of Air Cushion Thickness
2.1. Mathematical Model of Air Cushion Flow Field
2.2. Calculation of Air Cushion Thickness
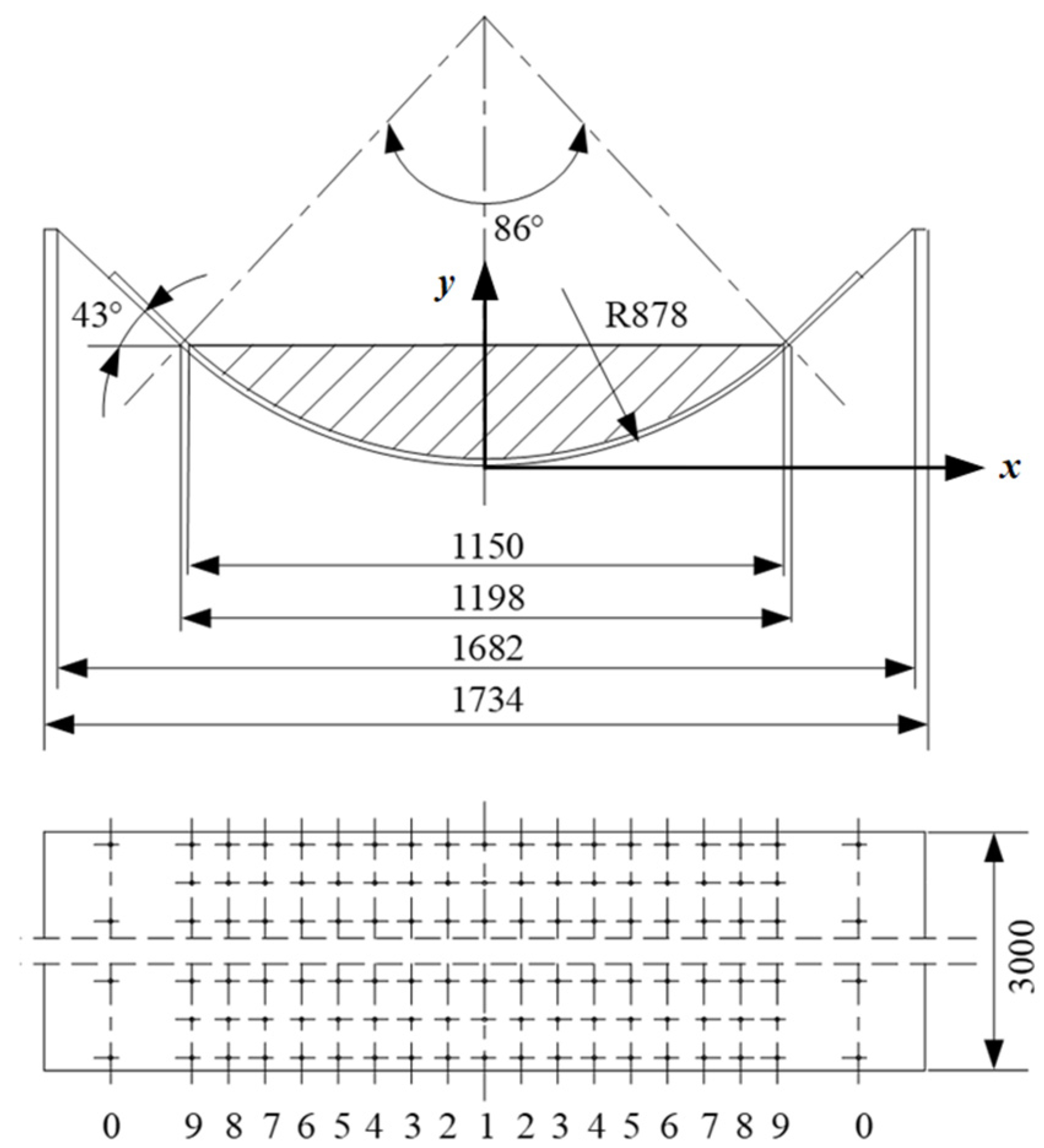
3. Verification of Air Cushion Thickness Calculation Method
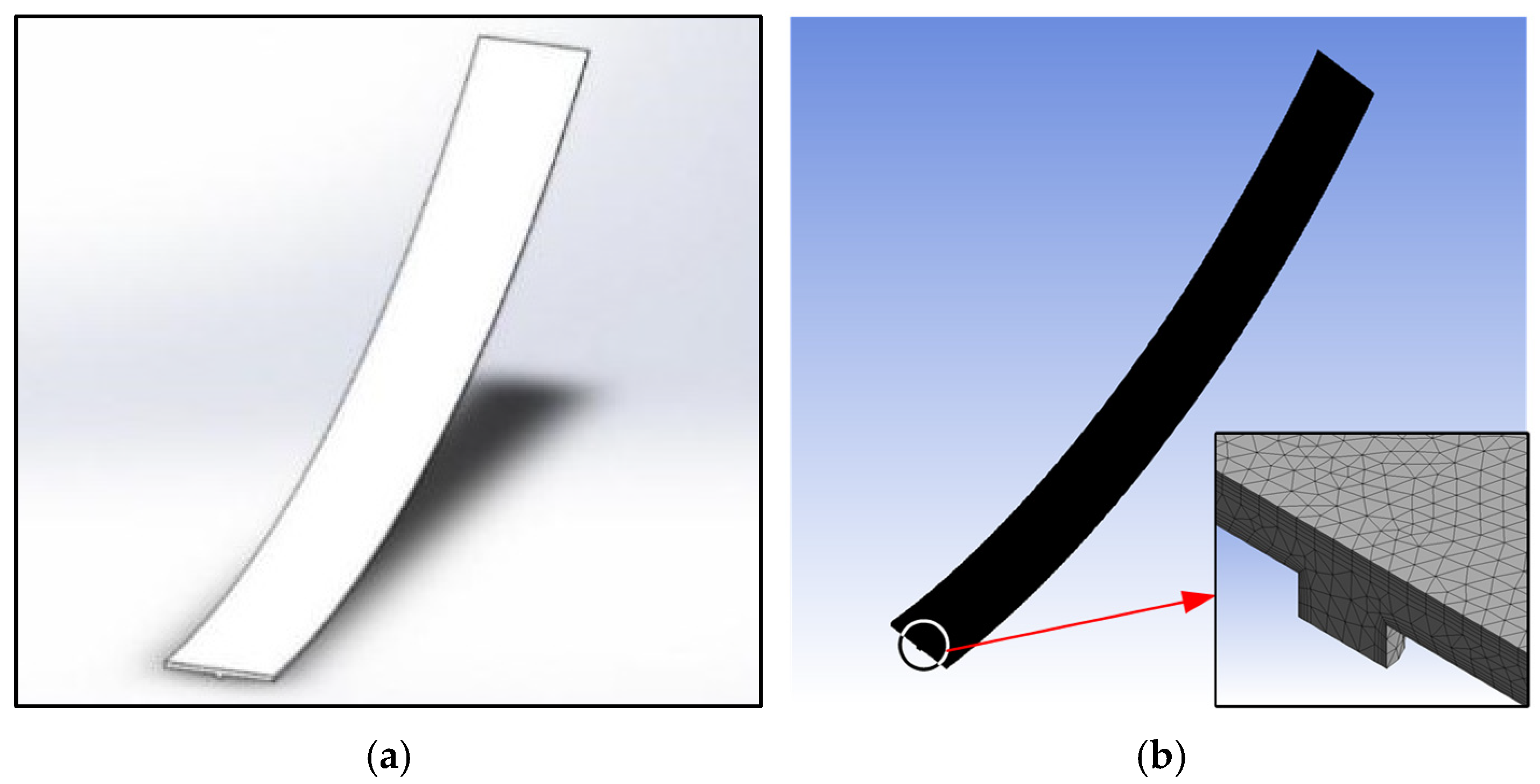
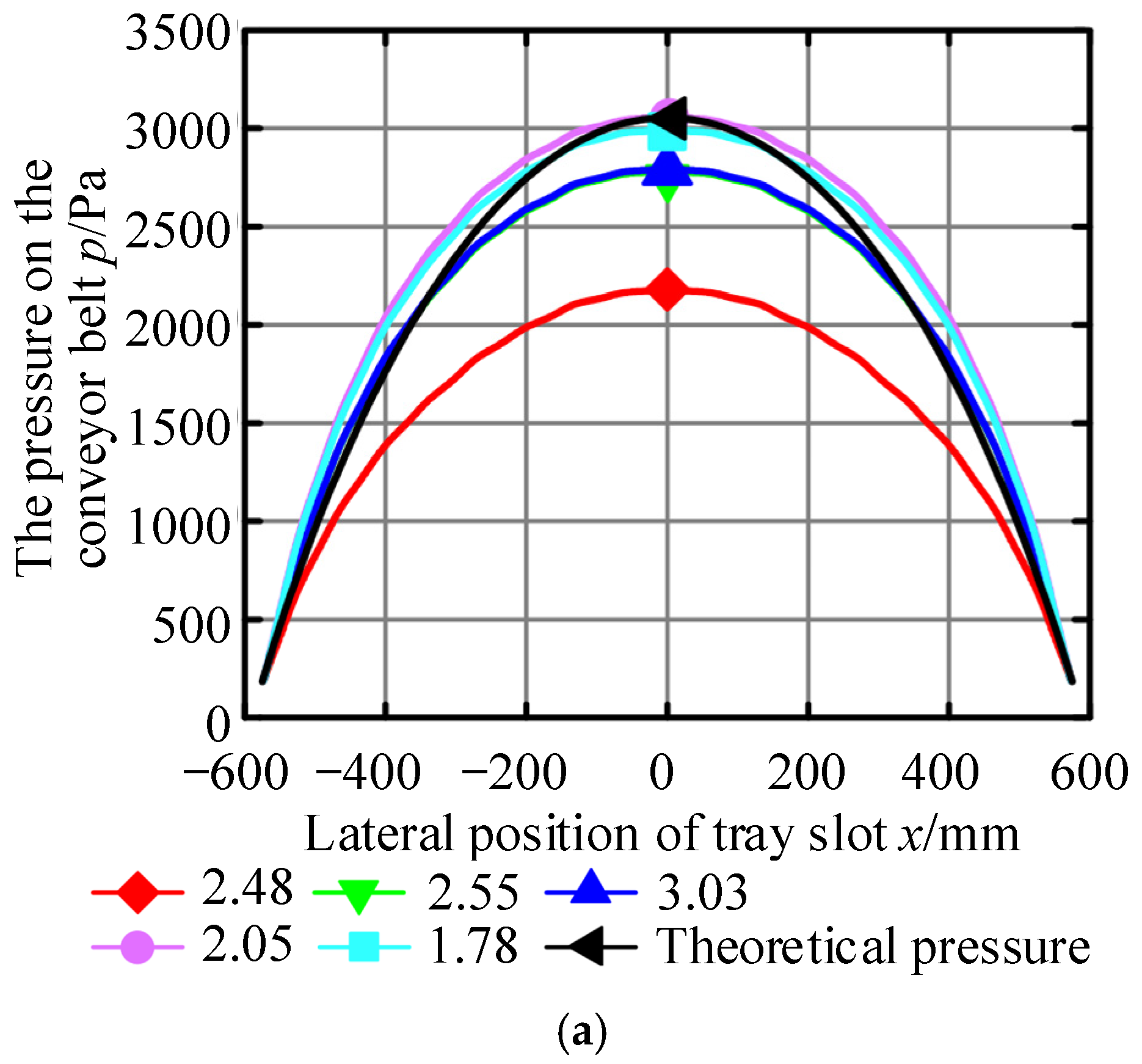
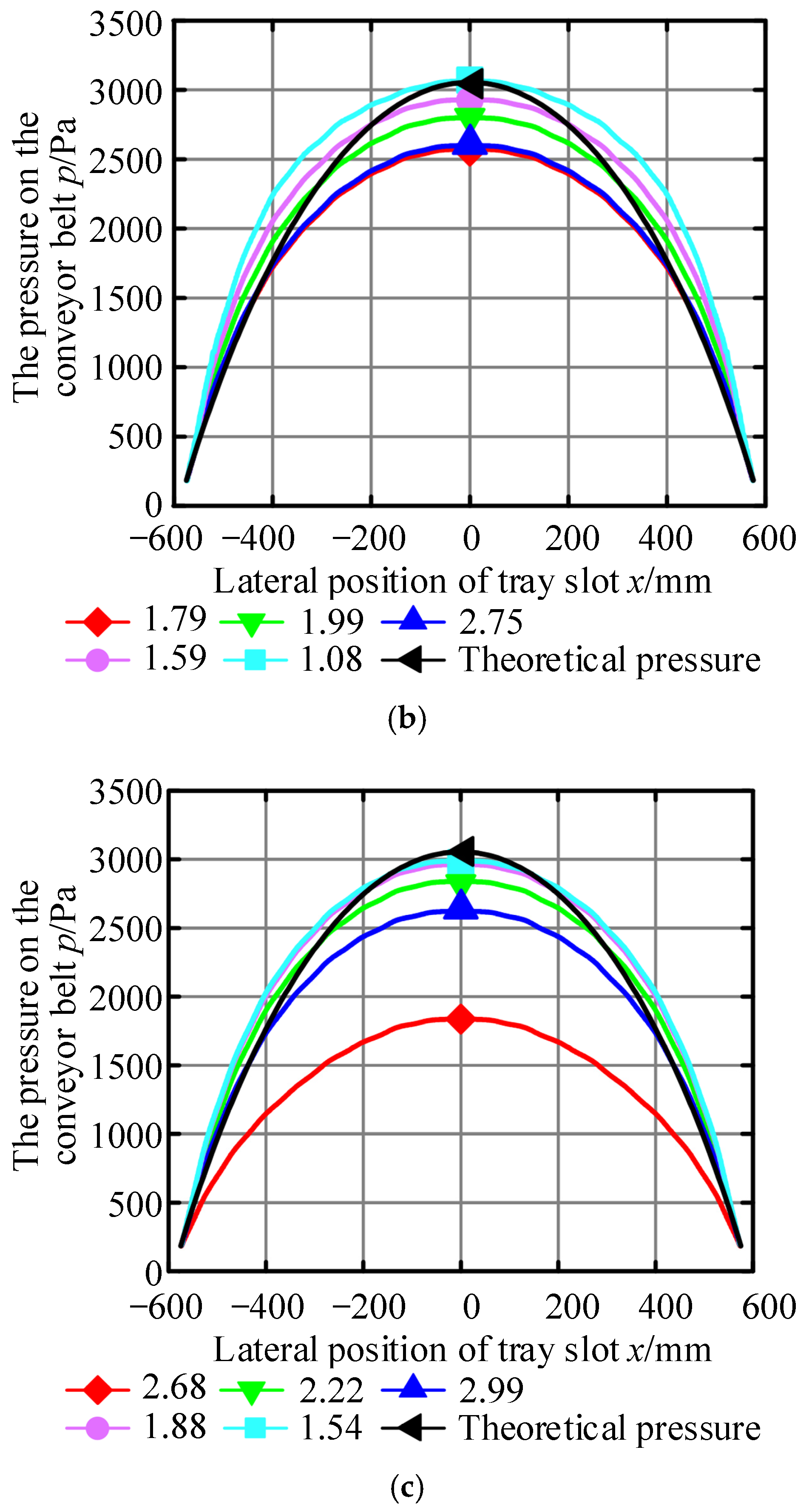
3.1. Numerical Validation
3.2. Test Verification
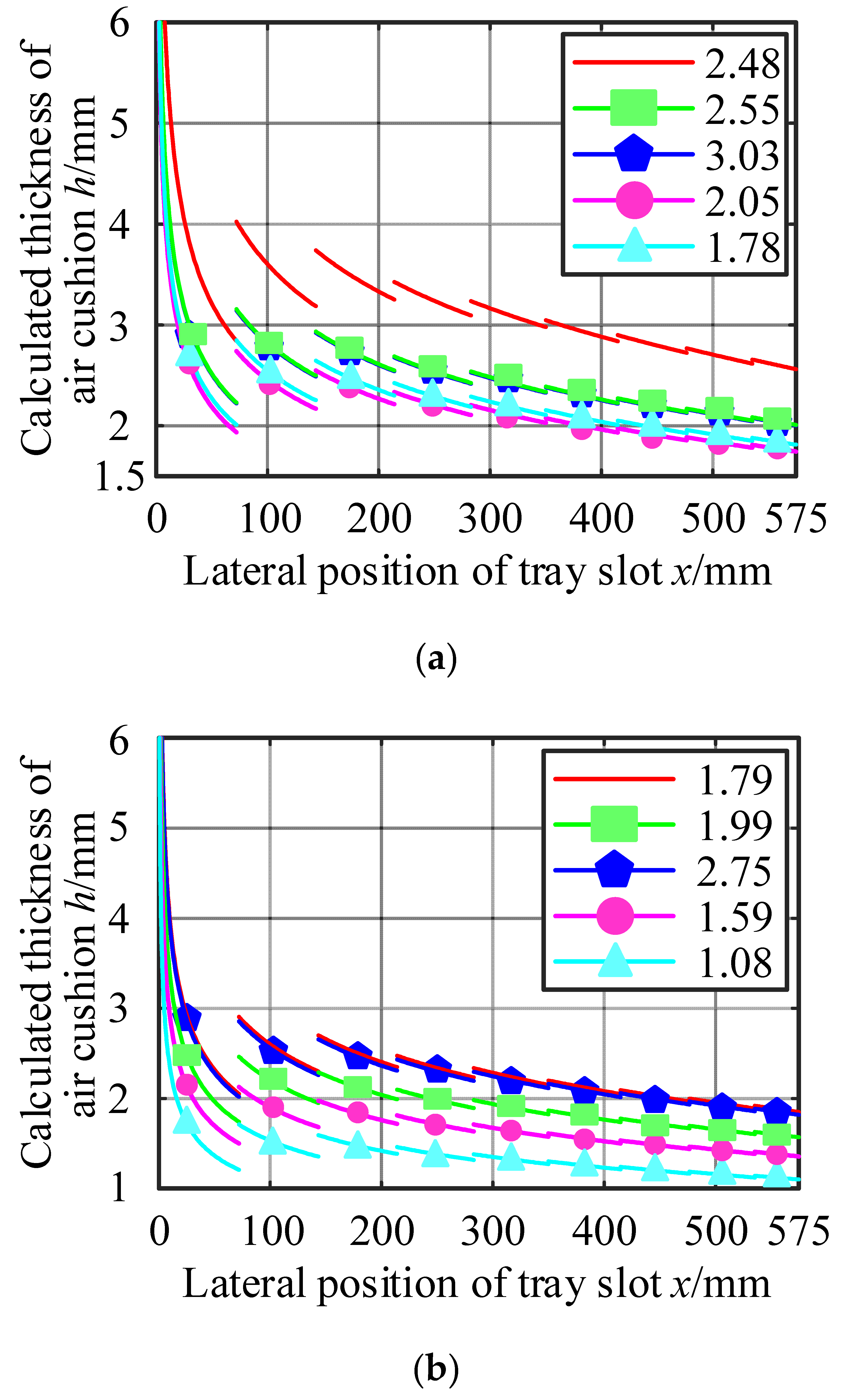
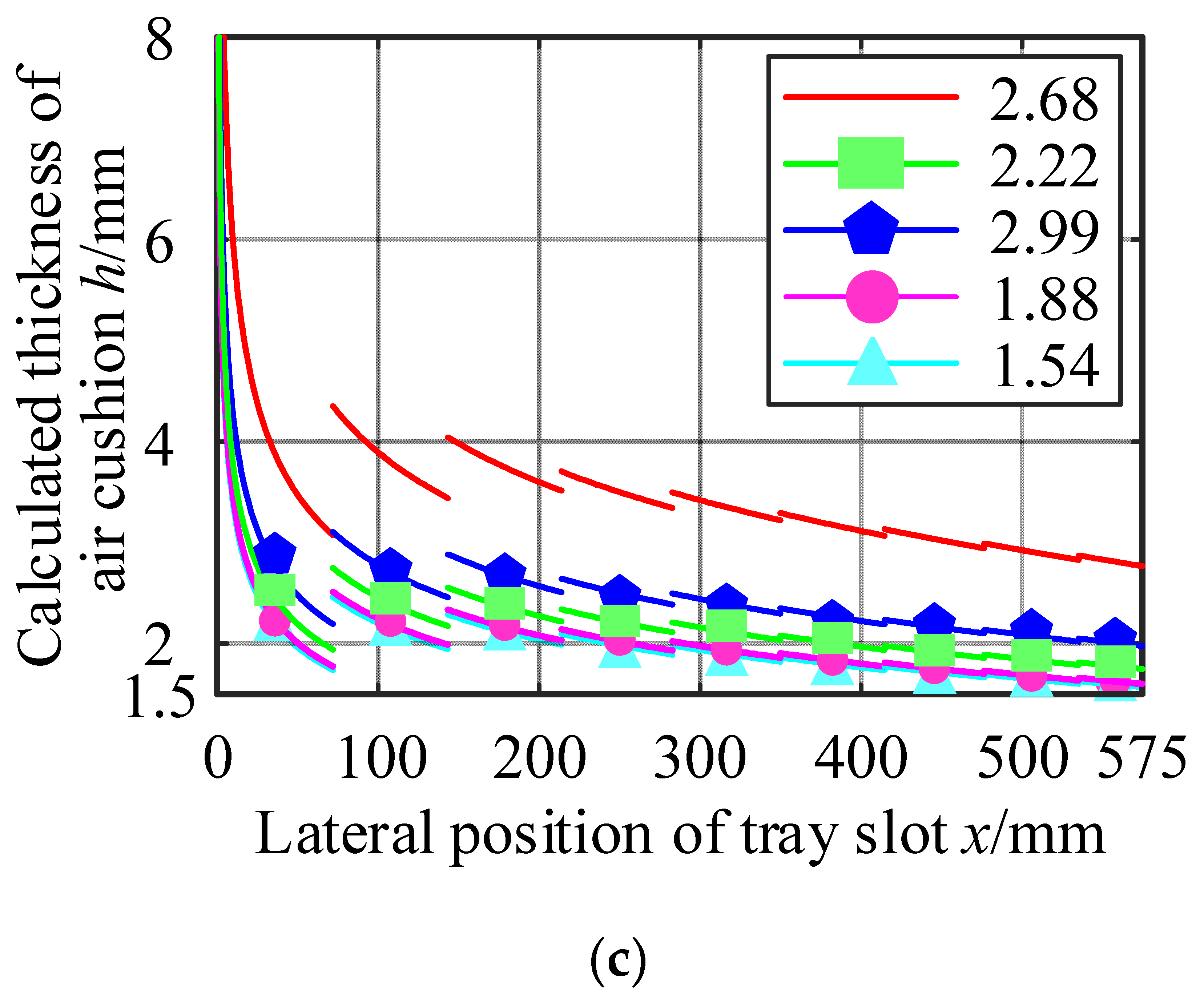
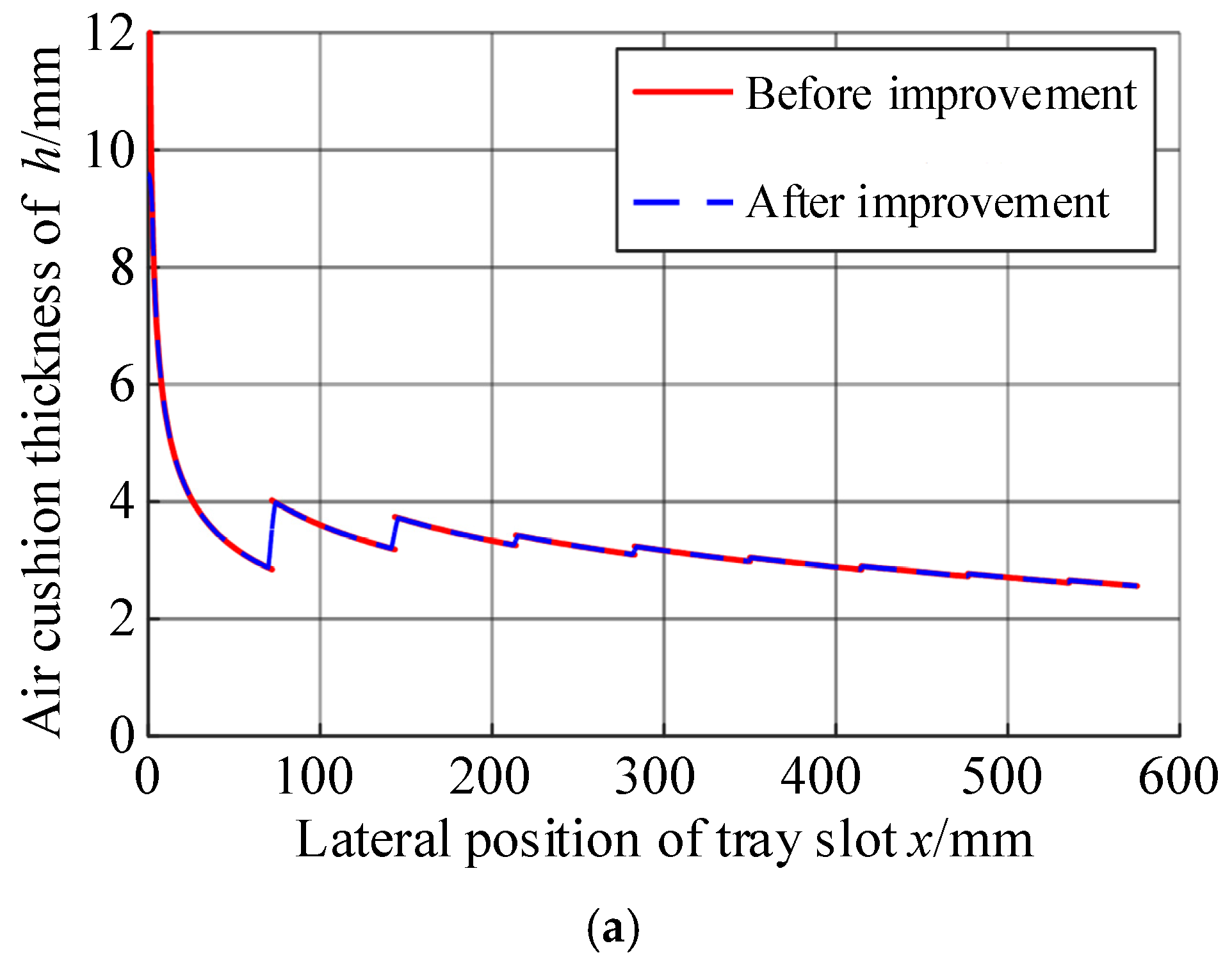
4. Improvement of Calculation Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, W.; Meng, F.; Zhang, X.; Gong, X.; Gao, Y. Research progress on design and calculation methods of belt conveyor products in China. Lift. Transp. Mach. 2020, 20, 73–84. [Google Scholar]
- Li, M.; Zhang, M.; Wang, C.; Li, X. Research and development of high-strength air cushion belt conveyor and conveyor belt in coal conveying system. Surf. Min. Technol. 2020, 35, 64–68. [Google Scholar]
- Lan, X. Discussion on technical issues of large-flow air cushion belt conveyor. Mod. Food 2021, 18, 10–13. [Google Scholar]
- Li, J.F.; Zhang, S. Optimization of groove-hole distribution with equidistant and unequal diameter on air-cushion belt conveyor. Adv. Mater. Res. 2008, 44–46, 635–642. [Google Scholar] [CrossRef]
- Ding, Z. Application analysis of air cushion belt conveyor in coal conveying system of coal mine (coal preparation plant). China Coal 2017, 43, 89–92. [Google Scholar]
- Li, Y. Finite element analysis of air film bearing capacity of belt air cushion belt conveyor. Lubr. Seal. 2000, 5, 14–16. [Google Scholar]
- Tian, L.; Kou, Z.; Wu, J.; Wang, F. Study on air cushion flow field characteristics of air cushion belt conveyor. Mech. Electr. Eng. 2022, 39, 1004–1009+1016. [Google Scholar]
- Zhang, S.; Zhao, P.; Li, J.; Jing, X. Discussion on key technology design of air cushion belt conveyor. Min. Mach. 2008, 36, 56–58. [Google Scholar]
- Peng, B.; Yan, J.; Cao, S. Design & Calculation of Air Chamber of Air Cushion Belt Conveyor. App. Mec. Mat. 2013, 473, 3–6. [Google Scholar]
- Guo, S.; Liu, J.; Li, Z.; Zhang, D.; Huang, W. Experimental research on air film formation behavior of air cushion belt conveyor with stable load. Sci. China Technol. Sci. 2013, 56, 1424–1434. [Google Scholar] [CrossRef]
- Fang, Y. Formation of air film in air cushion belt conveyor and its influencing factors. J. Zhejiang Wanli Univ. 1999, 1, 1–6. [Google Scholar]
- Yu, F.; Jia, Z.; Wang, Y. Calculation of air film thickness of air cushion belt conveyor. J. Taiyuan Inst. Heavy Mach. 2001, 1, 85–87. [Google Scholar]
- Pang, M. Calculation of air film thickness of air cushion belt conveyor. Coal Mine Electromech. 2006, 2, 46–49. [Google Scholar]
- Zhu, X.; Rui, Y.; Zhu, H. Research on air film thickness of air cushion belt conveyor. Mech. Strength 2017, 39, 723–726. [Google Scholar]
- Zhang, B.; Meng, W.; Zhang, H. Research on the pressure field and loading characteristics of air film of air cushion belt conveyor. AIP Adv. 2022, 12, 095123. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L.; Kou, Z.; Tian, L. Research on air cushion flow field and bearing characteristics of single row hole air cushion belt conveyor. Actuators 2024, 13, 424. [Google Scholar] [CrossRef]
- Zhang, B.; Meng, W.; Yuan, Y.; Yin, X.; Liang, W. Numerical simulation and experimental study of the influence of disk groove structure optimization on the air film flow field signature of an air-cushion sandwich belt conveyor. Case Stud. Therm. Eng. 2024, 63, 105239. [Google Scholar] [CrossRef]
- Qing, H.; Meng, W. Improvement and simulation of air chamber structure of air cushion belt conveyor. Crane Transp. Mach. 2020, 21, 44–49. [Google Scholar]




| Row Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| Aperture/mm | 4.8 | 4.6 | 4.5 | 3 | 3 | 2.2 | 2.2 | 2 | 2 | 2 |
| Solver Type | Pressure-Based Method |
|---|---|
| Time type | Steady state |
| Velocity equation | Absolute velocity |
| Turbulence model | Standard k − ε |
| Pressure inlet boundary/Pa | 3943/3467/3686 |
| Pressure outlet boundary/Pa | 185.1452 |
| Symmetric boundary | Each section of the cut-off section |
| Solid wall boundary | Tray slot, air hole surface, and interface between air cushion and conveyor belt |
| Solution method | SIMPLE |
| Test No. | Air Chamber Pressure/Pa | Air Cushion Thickness at Each Position h/mm | ||||
|---|---|---|---|---|---|---|
| x = −0.509 m | x = −0.215 m | x = 0.025 m | x = 0.263 m | x = 0.492 m | ||
| 1 | 3943 | 2.48 | 2.55 | 3.03 | 2.05 | 1.78 |
| 2 | 3467 | 1.79 | 1.99 | 2.75 | 1.59 | 1.08 |
| 3 | 3686 | 2.68 | 2.22 | 2.99 | 1.88 | 1.54 |
| Parameter Name | Numerical Value |
|---|---|
| Conveyor belt unit length gravity GBM (N/m) | 441.45 |
| Bandwidth B (m) | 1.8 |
| Tray slot radius R (m) | 0.878 |
| Material density γ (kg/m3) | 1307.2 |
| Gravitational acceleration g (m/s2) | 9.81 |
| Tray slot angle λ (rad) | 0.714 |
| Material accumulation angle β (rad) | 0 |
| Test No. | Measured Thickness he/mm | Calculated Value of Air Cushion Thickness at Each Position h/mm | Mean Error/% [he − (h1 + h2 + h3 + h4 + h5)/5]/he | ||||
|---|---|---|---|---|---|---|---|
| h1 (x =−0.503 m) | h2 (x =−0.215 m) | h3 (x =0.025 m) | h4 (x =0.263 m) | h5 (x =0.492 m) | |||
| 1 | 2.48 | 2.48 | 3.25 | 3.88 | 3.01 | 2.52 | −22.10 |
| 2.55 | 1.95 | 2.55 | 3.04 | 2.36 | 1.97 | 6.90 | |
| 3.03 | 1.91 | 2.54 | 3.03 | 2.35 | 1.94 | 22.31 | |
| 2.05 | 1.66 | 2.22 | 2.64 | 2.05 | 1.69 | −0.10 | |
| 1.78 | 1.76 | 2.3 | 2.74 | 2.13 | 1.78 | −20.34 | |
| 2 | 1.79 | 1.79 | 2.35 | 2.8 | 2.17 | 1.82 | −22.12 |
| 1.99 | 1.52 | 1.99 | 2.37 | 1.84 | 1.54 | 6.93 | |
| 2.75 | 1.76 | 2.31 | 2.75 | 2.14 | 1.79 | 21.82 | |
| 1.59 | 1.31 | 1.72 | 2.05 | 1.59 | 1.33 | −0.63 | |
| 1.08 | 1.06 | 1.38 | 1.63 | 1.28 | 1.08 | −19.07 | |
| 3 | 2.68 | 2.68 | 3.51 | 4.19 | 3.25 | 2.72 | −22.01 |
| 2.22 | 1.69 | 2.22 | 2.65 | 2.05 | 1.72 | 6.94 | |
| 2.99 | 1.88 | 2.51 | 2.99 | 2.32 | 1.91 | 22.34 | |
| 1.88 | 1.53 | 2.03 | 2.42 | 1.88 | 1.55 | −0.11 | |
| 1.54 | 1.52 | 1.99 | 2.37 | 1.84 | 1.54 | −20.26 | |
| No. | Air Cushion Thickness Substitution Value/mm | Simulation Inlet/Test Chamber Pressure/Pa | Simulation–Theoretical Pressure Distribution Mean Error/Pa | Simulated Bearing Capacity/N | Absolute Error of Bearing Capacity/% |
|---|---|---|---|---|---|
| 1 | 2.48 | 3943 | 530.751 | 68.745 | −25.155 |
| 2 | 2.55 | 125.629 | 89.262 | −4.638 | |
| 3 | 3.03 | 122.140 | 89.591 | −4.309 | |
| 4 | 2.05 | 142.763 | 98.781 | 4.881 | |
| 5 | 1.78 | 113.993 | 96.558 | 2.658 | |
| 6 | 1.79 | 3467 | 221.200 | 83.278 | −10.622 |
| 7 | 1.99 | 139.613 | 91.411 | −2.489 | |
| 8 | 2.75 | 208.376 | 84.066 | −9.834 | |
| 9 | 1.59 | 155.875 | 96.897 | 2.997 | |
| 10 | 1.08 | 241.840 | 102.92 | 9.02 | |
| 11 | 2.68 | 3686 | 780.831 | 57.685 | −36.215 |
| 12 | 2.22 | 116.524 | 91.973 | −1.927 | |
| 13 | 2.99 | 195.716 | 84.484 | −9.416 | |
| 14 | 1.88 | 124.464 | 96.537 | 2.637 | |
| 15 | 1.54 | 131.936 | 97.495 | 3.595 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, B.; Chen, H.; Sun, L.; Xu, K.; Ren, X. Improved Method for the Calculation of the Air Film Thickness of an Air Cushion Belt Conveyor. Materials 2024, 17, 6020. https://doi.org/10.3390/ma17236020
Song B, Chen H, Sun L, Xu K, Ren X. Improved Method for the Calculation of the Air Film Thickness of an Air Cushion Belt Conveyor. Materials. 2024; 17(23):6020. https://doi.org/10.3390/ma17236020
Chicago/Turabian StyleSong, Bo, Hongliang Chen, Long Sun, Kunpeng Xu, and Xiaoyong Ren. 2024. "Improved Method for the Calculation of the Air Film Thickness of an Air Cushion Belt Conveyor" Materials 17, no. 23: 6020. https://doi.org/10.3390/ma17236020
APA StyleSong, B., Chen, H., Sun, L., Xu, K., & Ren, X. (2024). Improved Method for the Calculation of the Air Film Thickness of an Air Cushion Belt Conveyor. Materials, 17(23), 6020. https://doi.org/10.3390/ma17236020






