Establishment and Application of an Elastic–Plastic Damage Constitutive Model for Ceramic Fiber Insulation Tiles
Abstract
:1. Introduction
2. Materials and Parameter Tests
2.1. Materials
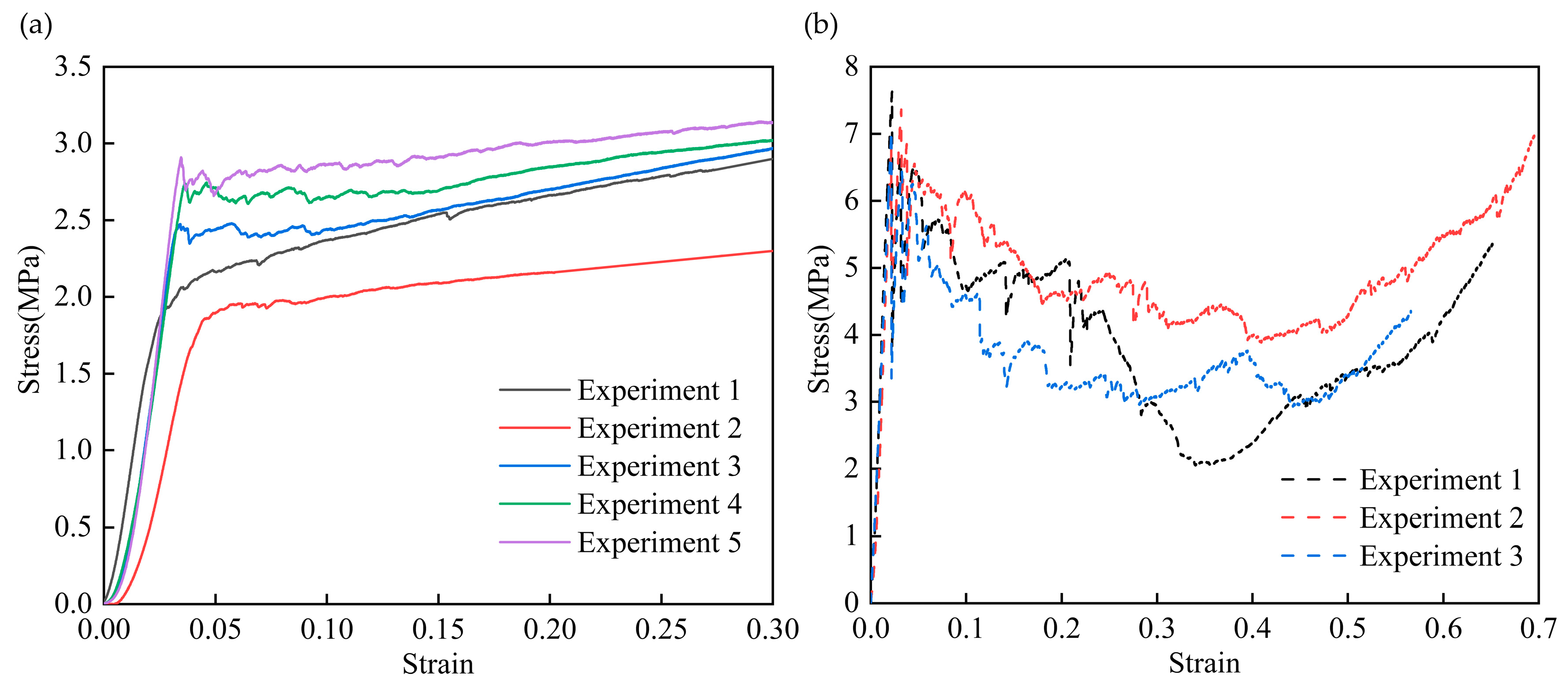
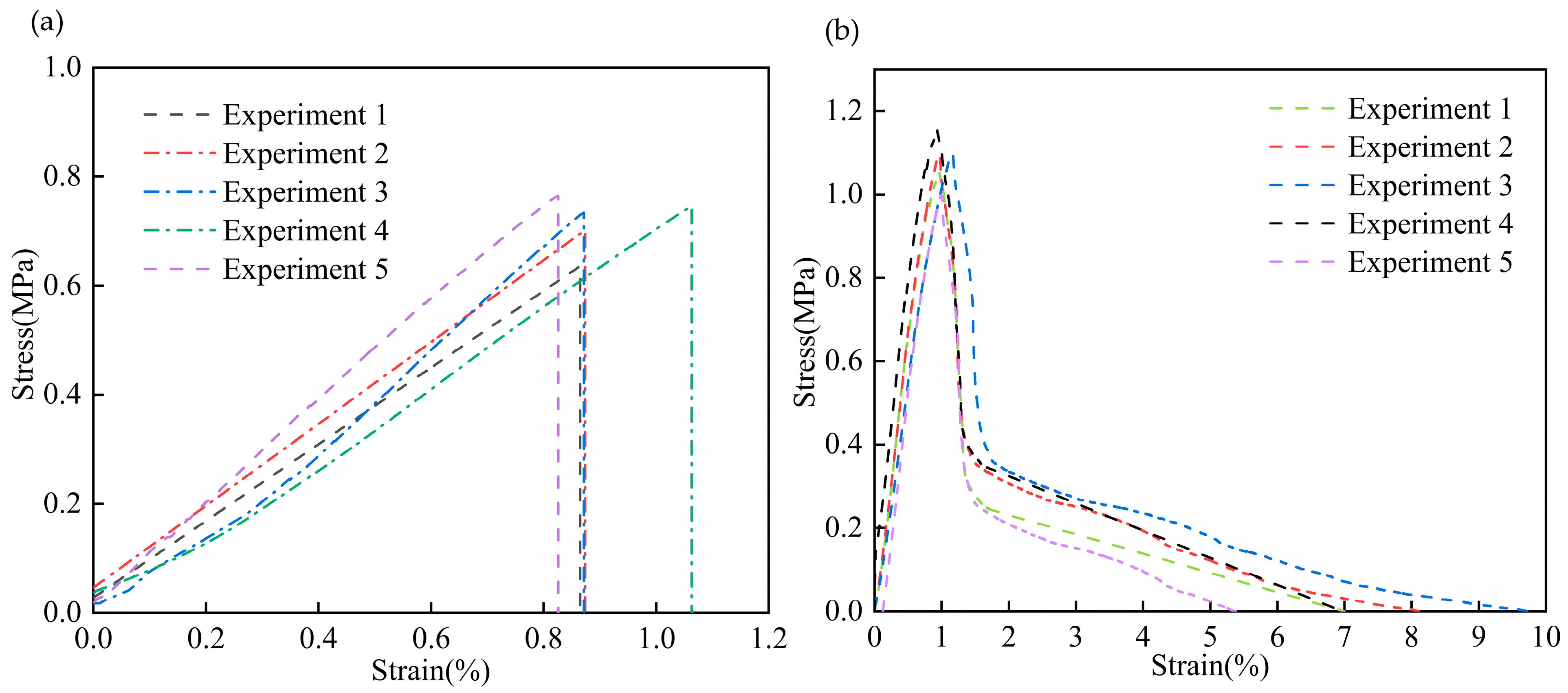
2.2. Parameter Tests
3. Elastic–Plastic Damage Constitutive Model
3.1. Fundamental Assumptions
- (1)
- In the elastic stage, the CFIT is an ideal transversely isotropic material;
- (2)
- The yield rule of the material complies with simplified Hashin criteria;
- (3)
- The CFIT behaves as an ideal linear elastic material before tensile and shear failure, and brittle fracture occurs after tensile and shear failure;
- (4)
- During compression, the CFIT behaves as an ideal linear elastic material before yielding; it enters a hardening stage after yielding and it experiences an entirely plastic flow after reaching the final yield surface.
3.2. Elastic Property
3.3. Yield Rule
3.4. Damage Reinforcement Rule
3.5. Plastic Flow Rule
4. Finite Element Model and Calculation Parameters
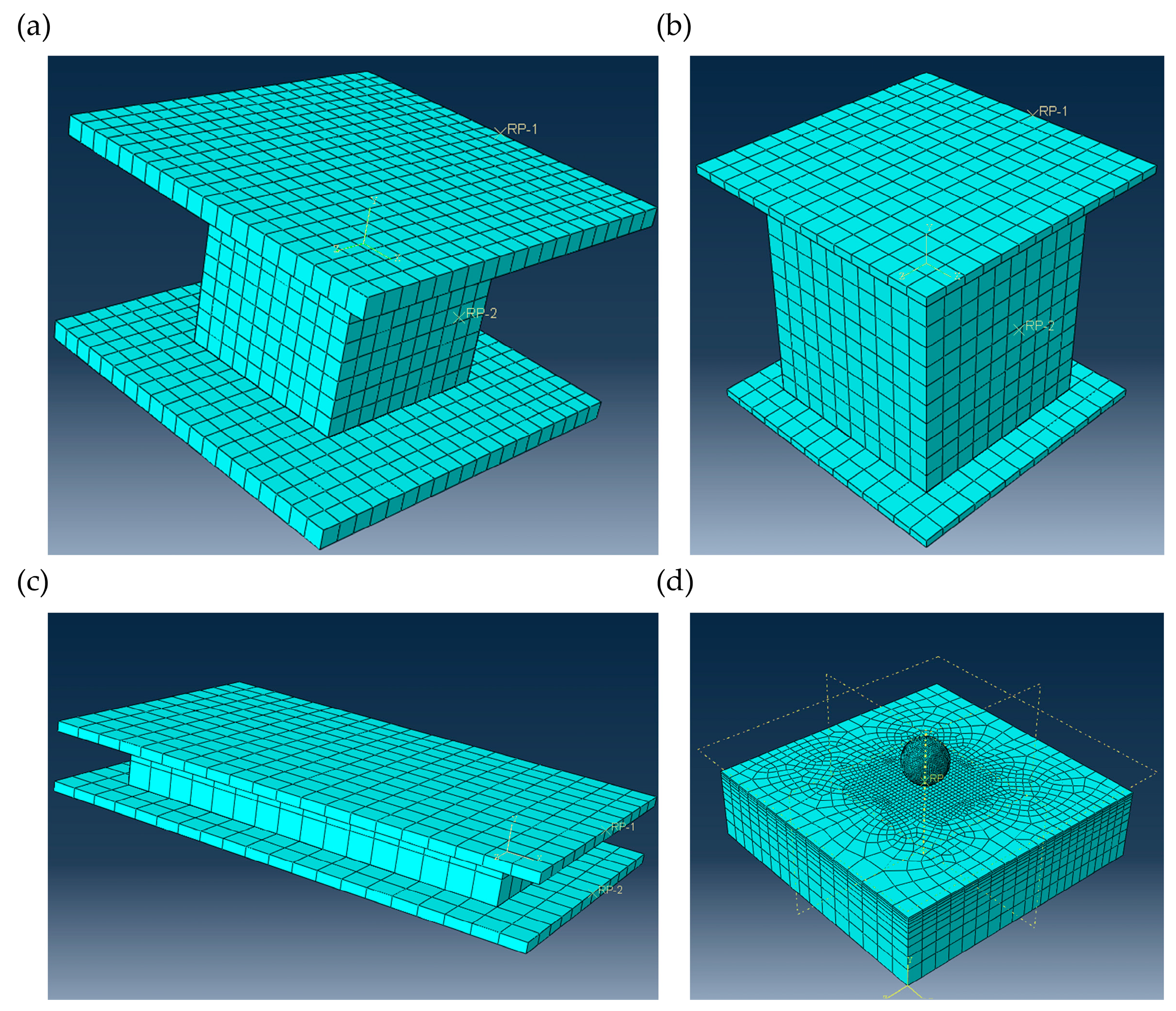
4.1. Finite Element Model
4.2. Calculation Parameters
5. Simulation Results and Experimental Verification
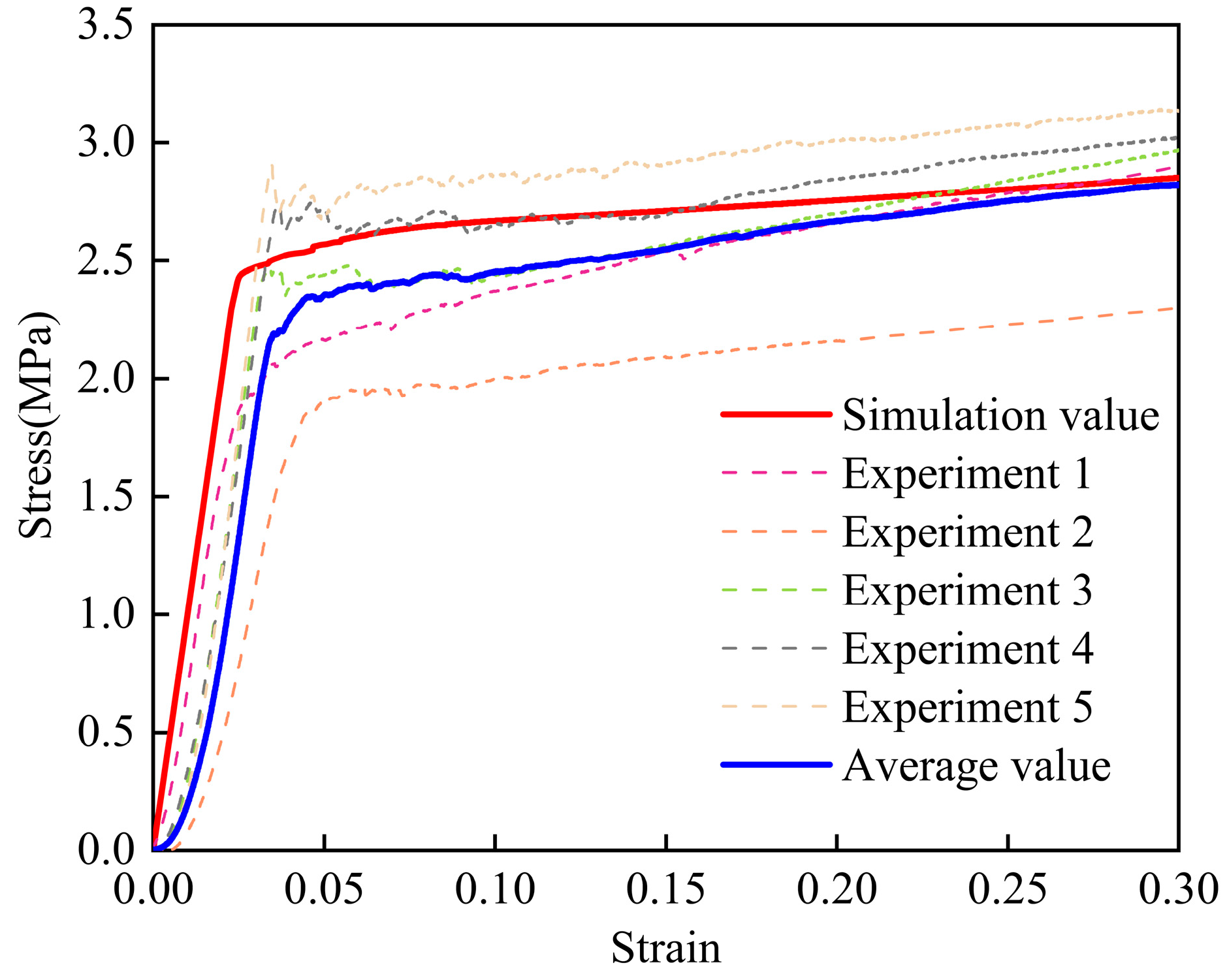
5.1. Simulation and Verification of Compressive Properties
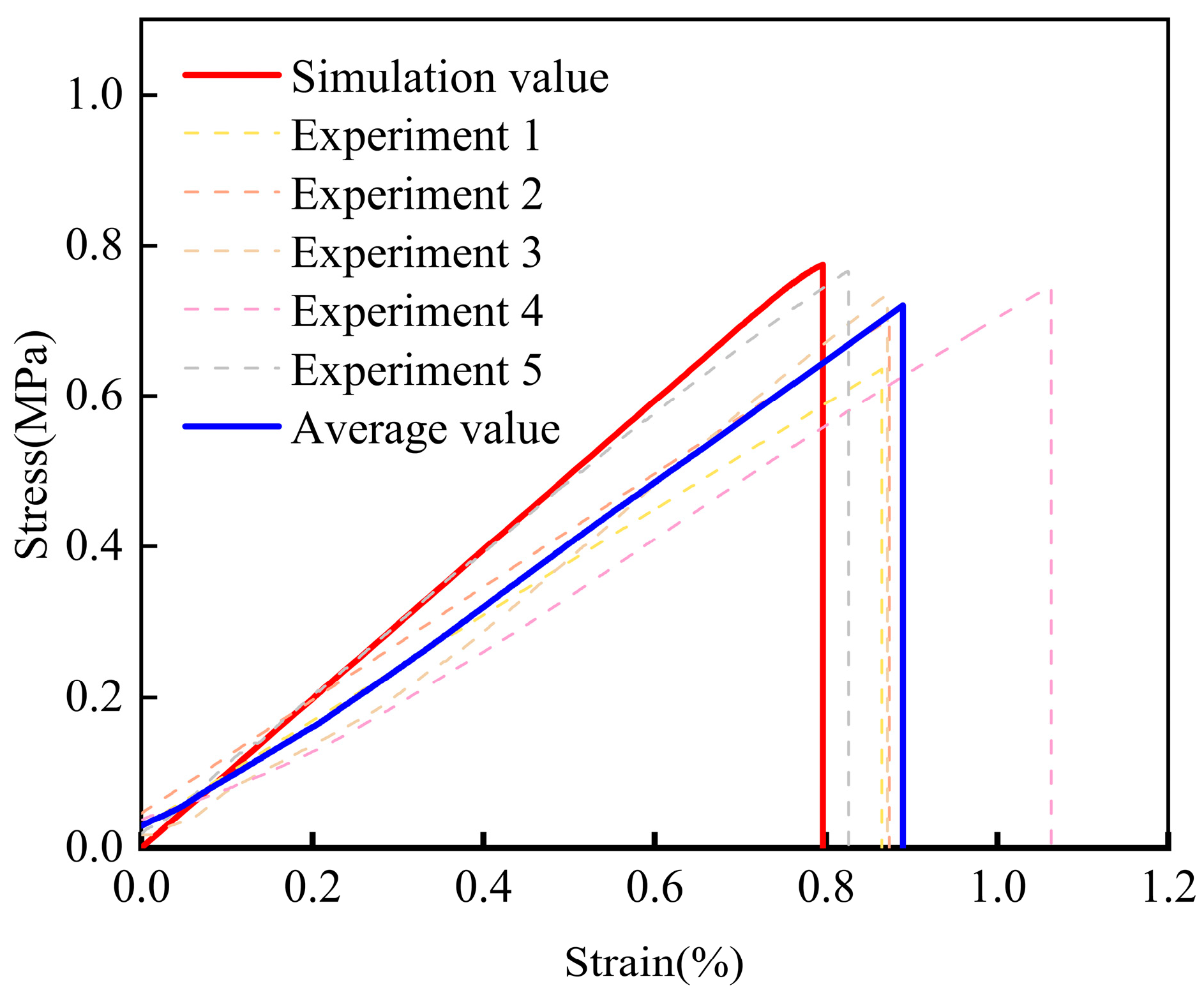
5.2. Simulation and Verification of Tensile Properties
5.3. Simulation and Verification of Shear Properties
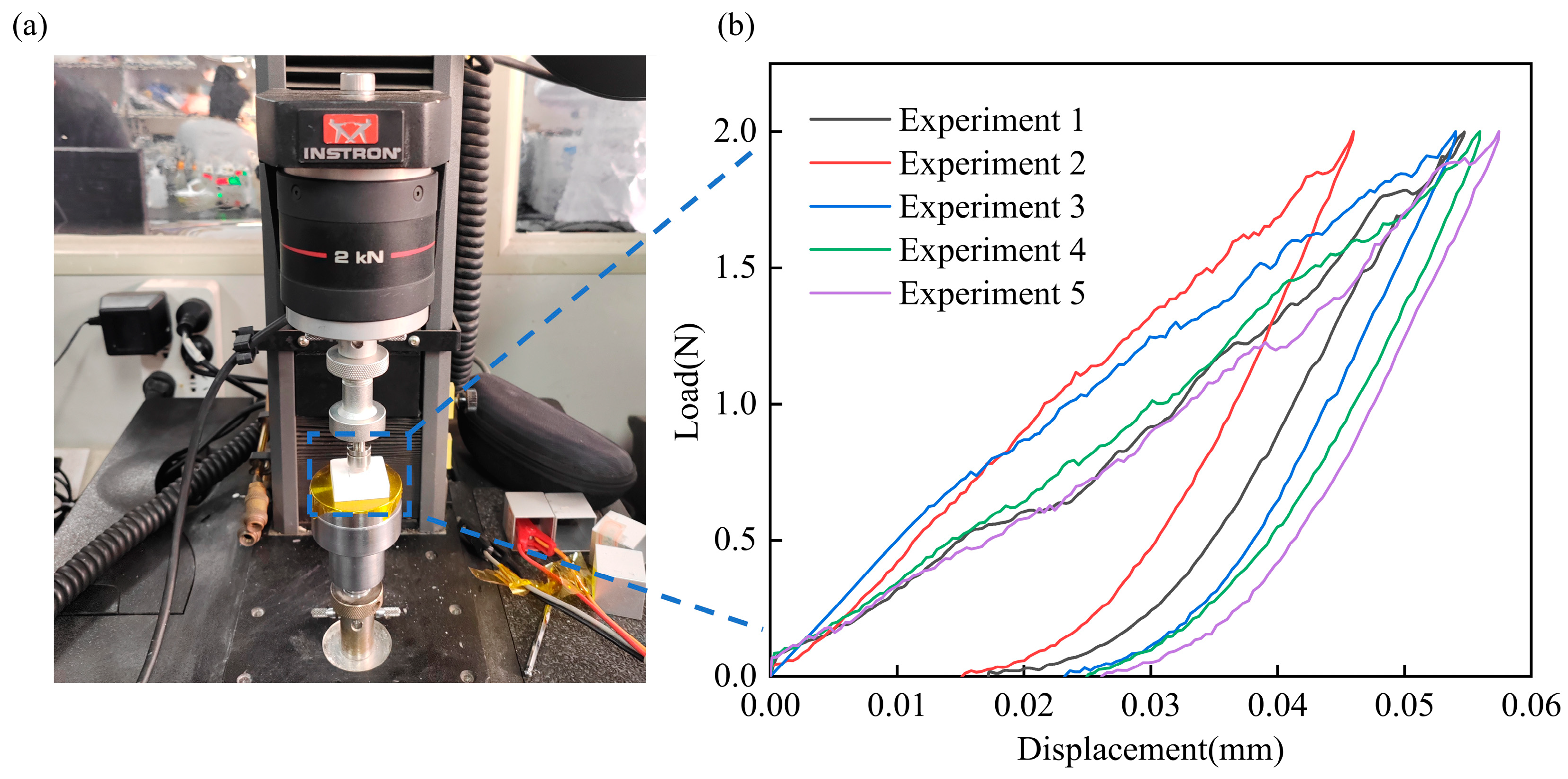
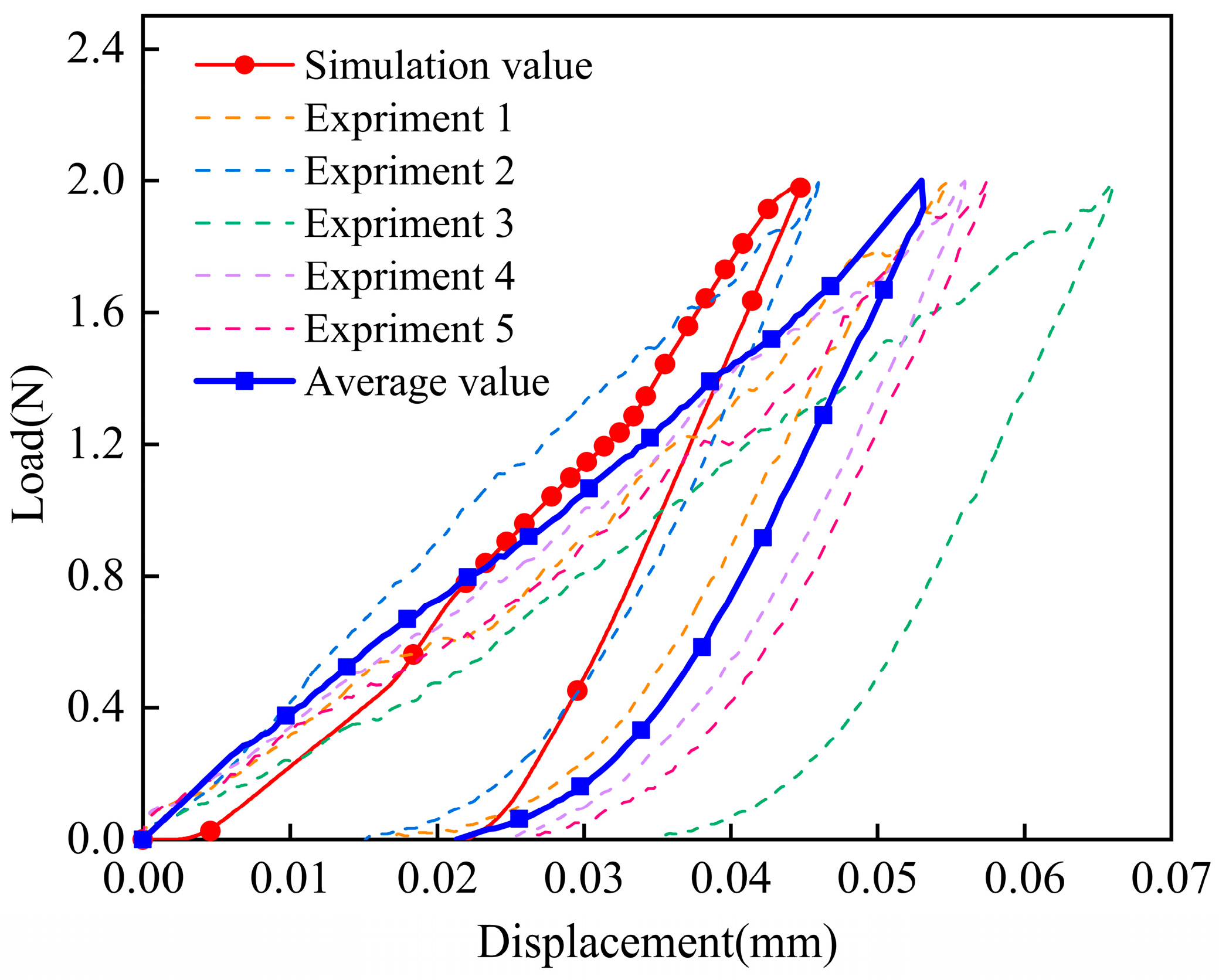
5.4. Simulation and Verification of Indentation Properties
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uyanna, O.; Najafi, H. Thermal protection systems for space vehicles: A review on technology development, current challenges and future prospects. Acta Astronaut. 2020, 176, 341–356. [Google Scholar] [CrossRef]
- Wang, Z.; Meng, X.; Lv, H. Thermodynamic Analysis of Damaged Thermal Protection System Tiles. Adv. Mater. Res. 2011, 211–212, 352–356. [Google Scholar] [CrossRef]
- Lee, D.G.; Kim, S.; Kim, S.; Yu, J.H.; Cho, S.W. Prediction of Material Properties of Ceramic Composite Material by Porous Structure and Porosity Using the Finite Element Method. Int. J. Precis. Eng. Manuf. 2019, 20, 805–814. [Google Scholar] [CrossRef]
- Koo, J.H.; Ho, D.W.H. A Review of Numerical and Experimental Characterization of Thermal Protection Materials–Part II. Properties Characterization. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Rambaldi, E.; Prete, F.; Bignozzi, M.C. Acoustic and thermal performances of ceramic tiles and tiling systems. Ceram. Int. 2015, 41, 7252–7260. [Google Scholar] [CrossRef]
- Lopez-Calle, I.; Franco, A.I. Comparison of cubesat and microsat catastrophic failures in function of radiation and debris impact risk. Sci. Rep. 2023, 13, 385. [Google Scholar] [CrossRef]
- Wang, W.; Qian, W.; Bai, Y.; Wang, K. Numerical studies on the thermal-fluid-structure coupling analysis method of hypersonic flight vehicle. Therm. Sci. Eng. Prog. 2023, 40, 101792. [Google Scholar] [CrossRef]
- Marwege, A.; Kirchheck, D.; Klevanski, J.; Gülhan, A. Hypersonic retro propulsion for reusable launch vehicles tested in the H2K wind tunnel. CEAS Space J. 2022, 14, 473–499. [Google Scholar] [CrossRef]
- Constantinescu, D.M.; Sandu, M.; Volceanov, E.; Gavan, M.; Sorohan, S. Experimental and Numerical Analysis of the Behaviour of Ceramic Tiles Under Impact. Adv. Strength Mater. 2009, 399, 161–168. [Google Scholar] [CrossRef]
- Sun, C.C.; Hu, Z.J.; Li, T.Q.; Zhang, H.B.; Sun, Z.J.; Zhang, Z.G. Preparation and Properties of Ceramic Tiles for Heat Insulation. Mater. Sci. Forum 2007, 546–549, 2157–2162. [Google Scholar] [CrossRef]
- Luo, G.; Zhu, Y.; Zhang, R.; Cao, P.; Liu, Q.; Zhang, J.; Sun, Y.; Yuan, H.; Guo, W.; Shen, Q.; et al. A Review on Mechanical Models for Cellular Media: Investigation on Material Characterization and Numerical Simulation. Polymers 2021, 13, 3283. [Google Scholar] [CrossRef] [PubMed]
- Ni, Y.; Liu, K.; Wang, J.; Sun, H.; Du, Y.; Liu, W. Establishment of constitutive models and numerical simulation of dry pressing and solid state sintering processes of MgTiO3 ceramic. Ceram. Int. 2021, 47, 8769–8780. [Google Scholar] [CrossRef]
- Chen, D.; Zheng, Z.; Wang, J. Three-dimensional simulation of sintering crunodes of metal powders or fibers by level set method. J. Cent. S. Univ. 2015, 22, 2446–2455. [Google Scholar] [CrossRef]
- Fernández-Fdz, D.; Zaera, R.; Fernández-Sáez, J. A constitutive equation for ceramic materials used in lightweight armors. Comput. Struct. 2011, 89, 2316–2324. [Google Scholar] [CrossRef]
- Li, D.; Xia, W.; Yu, W.; Fang, Q.; Shen, S. Investigations on the compressive behavior of 3D random fibrous materials at elevated temperatures. Ceram. Int. 2017, 43, 5195–5203. [Google Scholar] [CrossRef]
- Li, D.; Gao, Y.; Wei, X.; Jiang, J.; Xia, W.; Wang, B. Cryogenic fracture toughness of 3D random fibrous materials. Mater. Today Commun. 2023, 35, 105911. [Google Scholar] [CrossRef]
- Shi, L.; Long, K.; Zhong, Y. Compressive and shear performance of three-dimensional rigid stochastic fibrous networks: Experiment, finite element simulation, and factor analysis. J. Eur. Ceram. Soc. 2020, 40, 115–126. [Google Scholar] [CrossRef]
- Long, K.; Zhong, Y.; Li, M. Three-dimensional sintering morphology simulation of silica fibrous insulator and its quantitative description. Ceram. Int. 2022, 48, 19557–19566. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y.; Chiang, F. Modeling the Large Deformation and Microstructure Evolution of Nonwoven Polymer Fiber Networks. J. Appl. Mech. 2019, 86, 011010. [Google Scholar] [CrossRef]
- Son, K.J.; Fahrenthold, E.P. Simulation of Orbital Debris Impact on Porous Ceramic Tiles. J. Spacecr. Rocket. 2014, 51, 1349–1359. [Google Scholar] [CrossRef]
- Xie, J.; Fang, G.; Chen, Z.; Liang, J. An anisotropic elastoplastic damage constitutive model for 3D needled C/C-SiC composites. Compos. Struct. 2017, 176, 164–177. [Google Scholar] [CrossRef]
- Qi, S.; Tan, X.; Li, X.; Meng, Z.; Xu, Y. Numerical simulation and experimental verification studies on a unified strength theory-based elastoplastic damage constitutive model of shale. Nat. Gas Ind. B 2021, 8, 267–277. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, Q.; Zhang, B. Three-dimensional elastic-plastic damage constitutive model of wood. Holzforschung 2021, 75, 526–544. [Google Scholar] [CrossRef]
- Benvenuti, E.; Orlando, N.; Gebhardt, C.; Kaliske, M. An orthotropic multi-surface damage-plasticity FE-formulation for wood: Part I–Constitutive model. Comput. Struct. 2020, 240, 106350. [Google Scholar] [CrossRef]
- Park, J.; Yoon, J.W. A general FRC (fiber reinforced composite) constitutive model considering transverse isotropy and accumulated damage. J. Mech. Sci. Technol. 2022, 36, 6147–6156. [Google Scholar] [CrossRef]
- Boyina, G.R.T.; Rayavarapu, V.K.; VV, S.R. Continuum damage mechanics based failure prediction and damage assessment in laminated composite structures. Mech. Based Des. Struct. Mech. 2023, 52, 2255–2283. [Google Scholar] [CrossRef]
- Danielsson, H.; Gustafsson, P.J. A three dimensional plasticity model for perpendicular to grain cohesive fracture in wood. Eng. Fract. Mech. 2013, 98, 137–152. [Google Scholar] [CrossRef]
- Valipour, H.; Khorsandnia, N.; Crews, K.; Foster, S. A simple strategy for constitutive modelling of timber. Constr. Build. Mater. 2014, 53, 138–148. [Google Scholar] [CrossRef]
- Iraola, B.; Cabrero, J.M. An algorithm to model wood accounting for different tension and compression elastic and failure behaviors. Eng. Struct. 2016, 117, 332–343. [Google Scholar] [CrossRef]
- Tagarielli, V.L.; Deshpande, V.S.; Fleck, N.A.; Chen, C. A constitutive model for transversely isotropic foams, and its application to the indentation of balsa wood. Int. J. Mech. Sci. 2005, 47, 666–686. [Google Scholar] [CrossRef]
- GB/T 1964-2023; Porous Ceramics-Test Method for Compressive Strength at Room Temperature. Shandong Industrial Ceramics Research and Design Institute Co., Ltd.: Zibo, China, 2023.
- GB/T 1452-2018; Test Method for Flatwise Tension Strength of Sandwich Constructions. Shanghai Fiberglass Re-search Institute Co., Ltd: Shanghai, China, 2018.
- GB/T 10007-2008; Rigid Cellular Plastics-Determination of Shear Strength. Beijing Technology and Business University: Beijing, China, 2008.
- Zhang, L.; Yang, N. Evaluation of a modified Iosipescu shear test method for determining the shear properties of clear wood. Wood Sci. Technol. 2017, 51, 323–343. [Google Scholar] [CrossRef]
- Dai, L.; Yang, N.; Zhang, L.; Yang, Q.; Law, S. Monitoring crowd load effect on typical ancient Tibetan building. Struct. Control Health Monit. 2016, 23, 998–1014. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, L. Investigation of elastic constants and ultimate strengths of Korean pine from compression and tension tests. J. Wood Sci. 2018, 64, 85–96. [Google Scholar] [CrossRef]



| Number | Diameter | Length | Raw Materials | Temperature Gradient |
|---|---|---|---|---|
| 1 | 1–2 μm | 5–6.5 mm | 20–30% Alumina fiber | 120–170 °C Dry 1200–1300 °C Sintering |
| 2 | 1–2 μm | 5–6.5 mm | 40–60% Quartz ceramic fiber | |
| 3 | 5–8 μm | 5–6.5 mm | 10–20% Aluminum borosilicate fiber |
| Performance Index | Value |
|---|---|
| Density | 0.34 g/cm3 |
| Compressive strength (in the TTT direction) | 2.50 ± 0.51 MPa |
| Compressive modulus (in the TTT direction) | 115.54 ± 16.74 MPa |
| Compressive strength (in the IP direction) | 7.4 ± 0.32 MPa |
| Compressive modulus (in the IP direction) | 380 ± 2.48 MPa |
| Tensile strength (in the TTT direction) | 0.78 ± 0.25 MPa |
| Tensile modulus (in the TTT direction) | 62.46 ± 15.28 MPa |
| Shear strength (in the TTT direction) | 1.12 ± 0.09 MPa |
| Shear modulus (in the TTT direction) | 126.18 ± 15.39 MPa |
| Input | Parameter | Value | Physical Meaning |
|---|---|---|---|
| PROPS(1) | E11 | 380 MPa | Elastic modulus in the IP direction |
| PROPS(2) | E22 | 98.8 MPa | Elastic modulus in the TTT direction |
| PROPS(3) | MU12 | 0.1 | Poisson’s ratio IP in the IP direction |
| PROPS(4) | MU23 | 0.1 | Poisson’s ratio IP in the TTT direction |
| PROPS(5) | G12 | 101 MPa | Shear modulus in the IP direction |
| PROPS(6) | G23 | 131 MPa | Shear modulus in the TTT direction |
| PROPS(7) | XT | 1.3 MPa | Shear strength in the IP direction |
| PROPS(8) | XC | 7.6 MPa | Compressive strength in the IP direction |
| PROPS(9) | XS | 1.1 MPa | Shear strength in the TTT direction |
| PROPS(10) | YT | 0.8 MPa | Tensile strength in the TTT direction |
| PROPS(11) | YC | 2.7 MPa | Compressive strength in the TTT direction |
| PROPS(12) | YS | 1.7 MPa | Tensile strength in the IP direction |
| PROPS(13) | NL | 0.1 | Coefficient of transfer degree from initial compressive yield surface to final compressive yield surface in the TTT direction |
| PROPS(14) | NT | 0.1 | Coefficient of transfer degree from initial compressive yield surface to final compressive yield surface in the IP direction |
| PROPS(15) | CL | 3 | Intensity coefficient factor in the TTT direction |
| PROPS(16) | CT | 3 | Intensity coefficient factor in the IP direction |
| PROPS(17) | GHARD | 0.1 | Hardening factor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhong, Y.; Huang, Y.; Ma, X.; Shi, L.; He, X. Establishment and Application of an Elastic–Plastic Damage Constitutive Model for Ceramic Fiber Insulation Tiles. Materials 2024, 17, 6094. https://doi.org/10.3390/ma17246094
Wang Y, Zhong Y, Huang Y, Ma X, Shi L, He X. Establishment and Application of an Elastic–Plastic Damage Constitutive Model for Ceramic Fiber Insulation Tiles. Materials. 2024; 17(24):6094. https://doi.org/10.3390/ma17246094
Chicago/Turabian StyleWang, Yiming, Yesheng Zhong, Yining Huang, Xiaoliang Ma, Liping Shi, and Xiaodong He. 2024. "Establishment and Application of an Elastic–Plastic Damage Constitutive Model for Ceramic Fiber Insulation Tiles" Materials 17, no. 24: 6094. https://doi.org/10.3390/ma17246094
APA StyleWang, Y., Zhong, Y., Huang, Y., Ma, X., Shi, L., & He, X. (2024). Establishment and Application of an Elastic–Plastic Damage Constitutive Model for Ceramic Fiber Insulation Tiles. Materials, 17(24), 6094. https://doi.org/10.3390/ma17246094




