Capacitance Determination for the Evaluation of Electrochemically Active Surface Area in a Catalyst Layer of NiFe-Layered Double Hydroxides for Anion Exchange Membrane Water Electrolyser
Abstract
1. Introduction
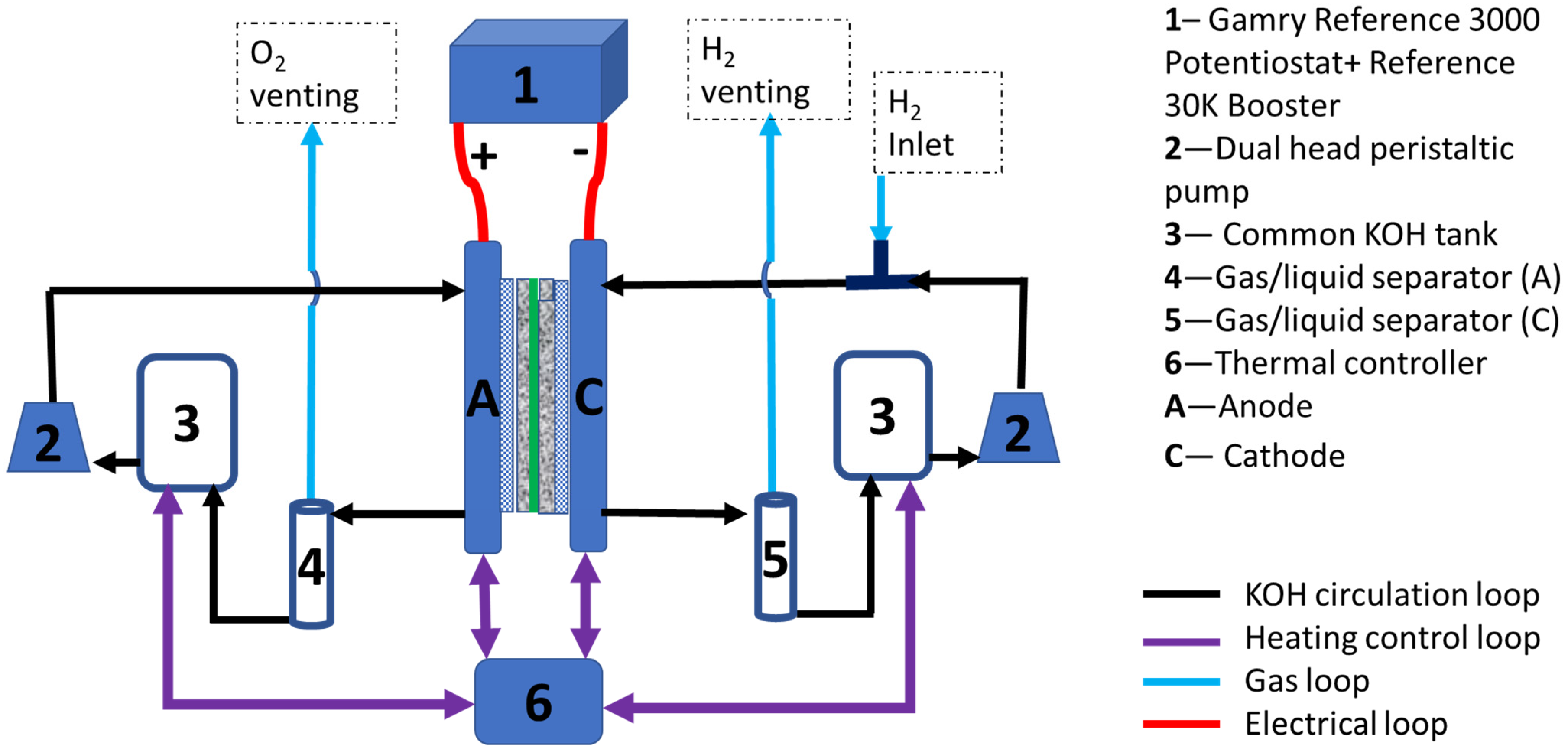
2. Experimental Setup and Procedure
3. Theoretical Considerations
3.1. Capacitance and ECSA
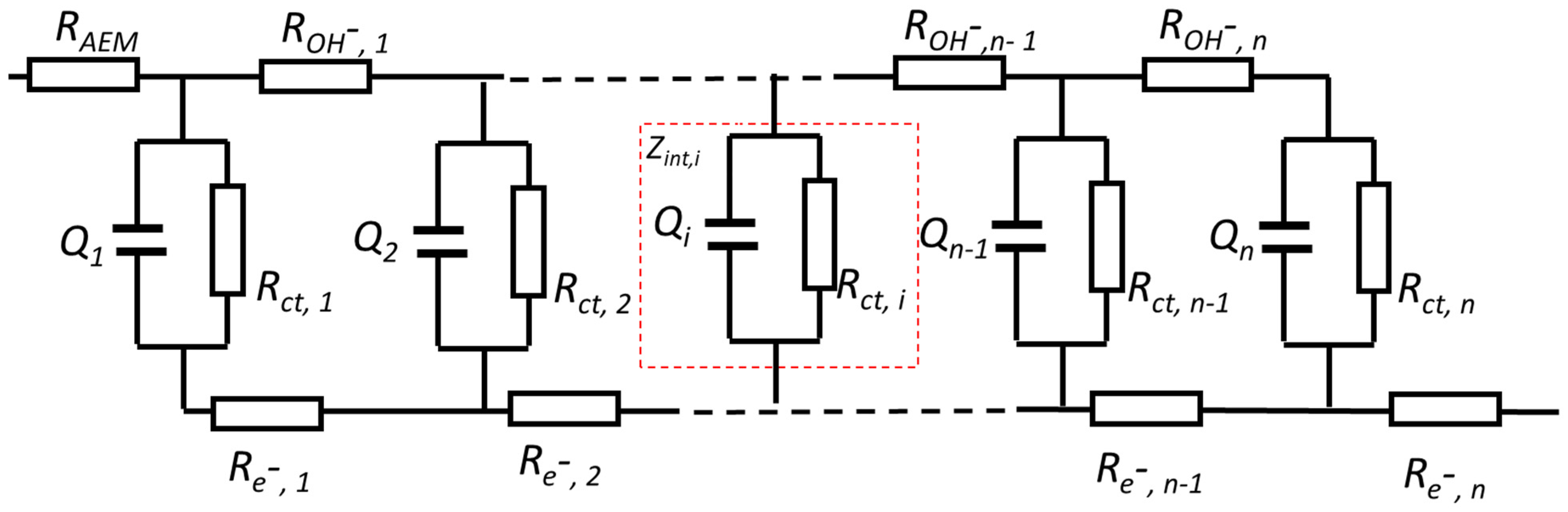
3.2. Determination of Capacitance for a Porous Electrode
3.2.1. Determination of the Capacitance of a Porous Electrode by CV
3.2.2. Determination of the Capacitance of a Porous Electrode by EIS
4. Experimental Results and Discussion
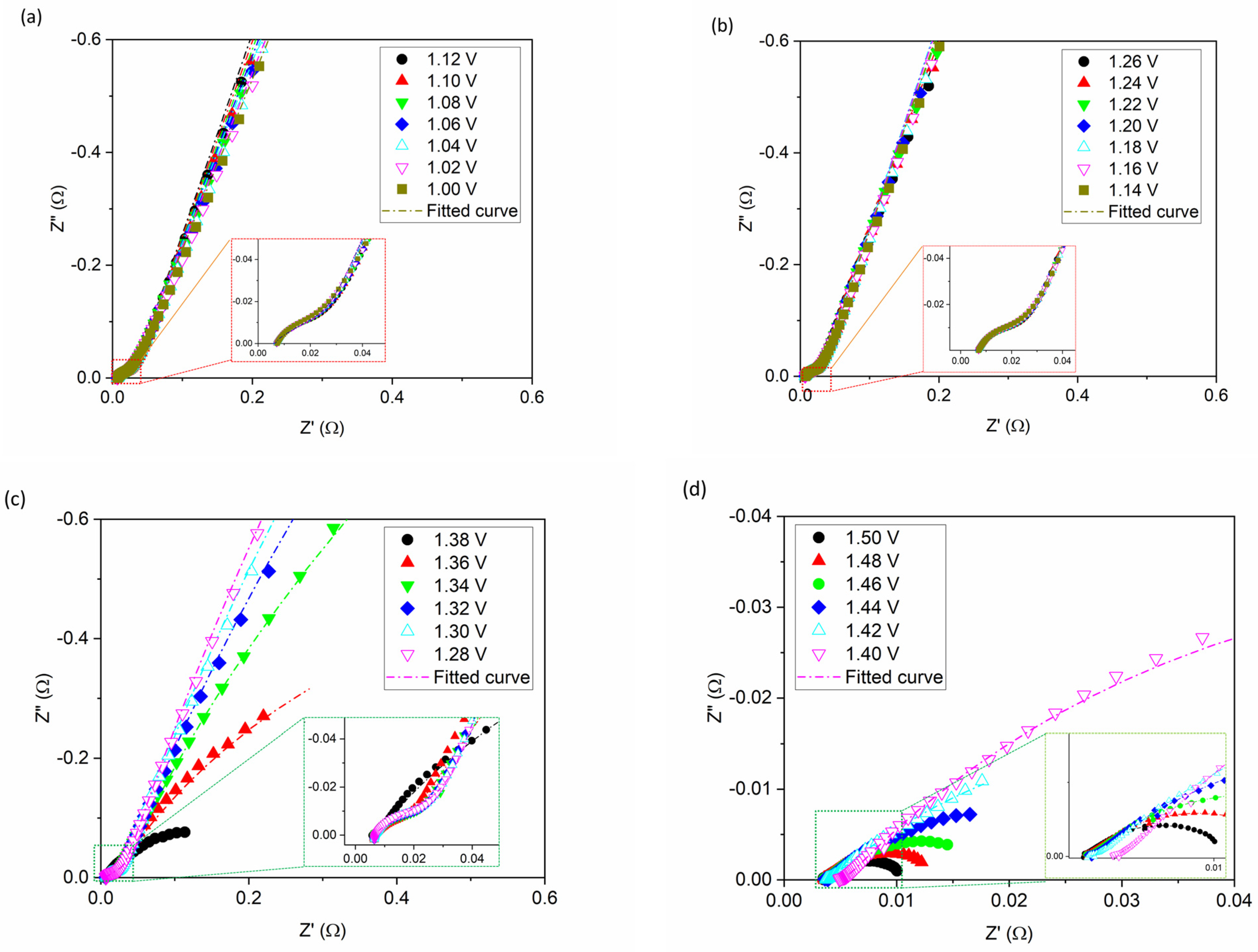
4.1. Capacitance (Q) Determination Using EIS
4.1.1. Non-Faradic Region
4.1.2. Faradic Region
4.2. CL Degradation Evaluation with QF
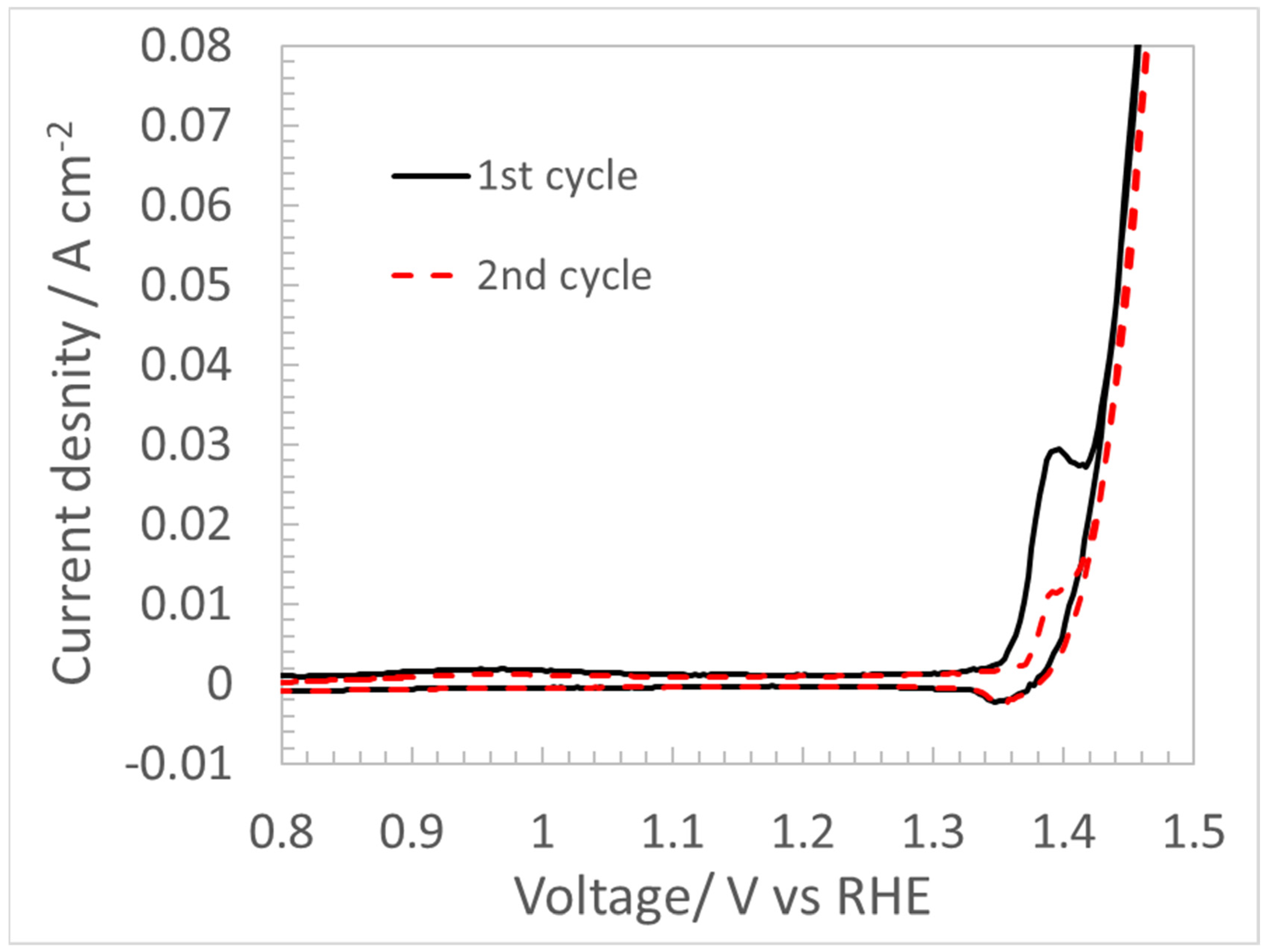
4.3. CV for Double Layer Capacitance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AC | alternating current |
| AEM | anion exchange membrane |
| BET | Brunauer–Emmett–Teller |
| C | general definition of capacitance |
| Cdl | double layer capacitance determined by CV method |
| CL | catalyst layer |
| CPE | constant phase element |
| Cs | specific area capacitance |
| CV | cyclic voltammetry |
| ECSA | electrochemically active surface area |
| EIS | electrochemical impedance spectroscopy |
| H-UPD | hydrogen under potential deposition |
| c | charging current density |
| i+ | positive charge current density |
| i− | negative discharge current density |
| j | imaginary unit |
| KOH | potassium hydroxide |
| LDH | layered double hydroxide |
| MEA | membrane-electrode-assembly |
| OCV | open circuit voltage |
| OER | oxygen evolution reaction |
| PEM | proton exchange membrane |
| PTL | porous transport layer |
| Q | capacitance determined by EIS |
| Qi | double layer capacitance distributed within the porous CL |
| Qt | Total capacitance determined by EIS |
| Qdl | double layer capacitance determined by the EIS method in the non-Faradic region |
| QF | Faradic capacitance determined by the EIS method in the Faradic region |
| Rct,i | interfacial charge transfer distributed within the porous CL |
| Rct | charge transfer resistance |
| Re,i | interfacial electron resistance distributed within the porous CL |
| RHE | reversible hydrogen electrode |
| RMS | root mean square |
| ROH− | ionic resistance in the pore within the CL |
| TOF | turnover frequency |
| TML | transmission line |
| ν | scanning rate |
| WE | water electrolysers |
| Ws | Warburg diffusion element |
| ZCL | impedance of the CL |
| Zint,i | interfacial impedance for the unit length pore |
| Zint | total interfacial impedance in the pores within the CL |
| Zcpe | impedance of the CPE |
| α | impedance phase angle |
| ω | angular frequency |
References
- Pham, C.V.; Escalera-López, D.; Mayrhofer, K.; Cherevko, S.; Thiele, S. Essentials of high performance water electrolyzers –from catalyst layer materials to electrode engineering. Adv. Energy Mater. 2021, 11, 2101998. [Google Scholar] [CrossRef]
- Miller, H.A.; Bouzek, K.; Hnat, J.; Loos, S.; Bernäcker, C.I.; Weißgärber, T.; Röntzsch, L.; Meier-Haack, J. Green hydrogen from anion exchange membrane water electrolysis: A review of recent developments in critical materials and operating conditions. Sustain. Energy Fuels 2020, 4, 2114. [Google Scholar] [CrossRef]
- Cho, M.K.; Lim, A.; Lee, S.Y.; Kim, H.-J.; Yoo, S.J.; Sung, Y.-E.; Park, H.S.; Jang, J.H. A review on membranes and catalysts for anion exchange membrane water electrolysis single cells. J. Electrochem. Sci. Tech. 2017, 8, 183. [Google Scholar] [CrossRef]
- Wan, X.; Song, Y.; Zhou, H.; Shao, M. Layered double hydroxides for oxygen evolution reaction towards efficient hydrogen generation. Energy Mater. Adv. 2022, 2022, 9842610. [Google Scholar] [CrossRef]
- Zhou, D.; Li, P.; Lin, X.; McKinley, A.; Kuang, Y.; Liu, W.; Lin, W.; Sun, X.; Duan, X. Layered double hydroxide-based electrocatalysts for the oxygen evolution reaction: Identification and tailoring of active sites, and superaerophobic nanoarray electrode assembly. Chem. Soc. Rev. 2021, 50, 87. [Google Scholar] [CrossRef] [PubMed]
- Suen, N.; Hung, S.; Quan, Q.; Zhang, N.; Xu, Y.; Chen, H.M. Electrocatalysis for the oxygen evolution reaction: Recent development and future perspectives. Chem. Soc. Rev. 2017, 46, 337. [Google Scholar] [CrossRef]
- Xu, D.; Stevens, M.B.; Cosby, M.R.; Oener, S.Z.; Smith, A.M.; Enman, L.J.; Ayers, K.E.; Capuano, C.B.; Renner, J.N.; Danilovic, N.; et al. Earth-abundant oxygen electrocatalysts for alkaline anion exchange-membrane water electrolysis: Effects of catalyst conductivity and comparison with performance in three-electrode cells. ACS Catal. 2019, 9, 7. [Google Scholar] [CrossRef]
- Park, Y.S.; Jeong, J.-Y.; Jang, M.J.; Kwon, C.-Y.; Kim, G.H.; Jeong, J.; Lee, J.-H.; Lee, J.; Choi, S.M. Ternary layered double hydroxide oxygen evolution reaction electrocatalyst for anion exchange membrane alkaline seawater electrolysis. J. Energy Chem. 2022, 75, 127. [Google Scholar] [CrossRef]
- Koshikawa, H.; Murase, H.; Hayashi, T.; Nakajima, K.; Mashiko, H.; Shiraishi, S.; Tsuji, Y. Single nanometer-sized NiFe-layered double hydroxides as anode catalyst in anion exchange membrane water electrolysis cell with energy conversion efficiency of 74.7% at 1.0 A cm−2. ACS Catal. 2020, 10, 1886. [Google Scholar] [CrossRef]
- Krivina, R.A.; Lindquist, G.A.; Beaudoin, S.R.; Stovall, T.N.; Thompson, W.L.; Twight, L.P.; Marsh, D.; Grzyb, J.; Fabrizio, K.; Hutchison, J.E. Anode catalysts in anion-exchange-membrane electrolysis without supporting electrolyte: Conductivity, dynamics, and ionomer degradation. Adv. Mater. 2022, 34, 2203033. [Google Scholar] [CrossRef]
- Stevens, M.B.; Enman, L.J.; Batchellor, A.S.; Cosby, M.R.; Vise, A.E.; Trang, C.D.M.; Boettcher, S.W. Measurement techniques for the study of thin film heterogeneous water oxidation electrocatalysts. Chem. Mater. 2017, 29, 120. [Google Scholar] [CrossRef]
- Schalenbach, M.; Durmus, Y.E.; Tempel, H.; Kungl, H.; Eichel, R.A. Double layer capacitances analysed with impedance spectroscopy and cyclic voltammetry: Validity and limits of the constant phase element parameterization. Phys. Chem. Chem. Phys. 2021, 23, 21097. [Google Scholar] [CrossRef] [PubMed]
- Sinha, P.; Datar, A.; Jeong, C.; Deng, X.; Chung, Y.G.; Lin, L. Surface area determination of porous materials using the Brunauer–Emmett–Teller (BET) method: Limitations and improvements. J. Phys. Chem. C 2019, 33, 20195. [Google Scholar] [CrossRef]
- Aufa, M.H.; Watzele, S.A.; Hou, S.; Haid, R.W.; Kluge, R.M.; Bandarenka, A.S.; Garlyyev, B. Fast and accurate determination of the electroactive surface area of MnOx. Electrochimi. Acta 2021, 389, 138692. [Google Scholar] [CrossRef]
- Qian, H.; Wei, J.; Yu, C.; Tang, F.; Jiang, W.; Xia, D.; Gan, L. In situ quantification of the active sites, turnover frequency, and stability of Ni−Fe (Oxy)hydroxides for the oxygen evolution reaction. ACS Catal. 2022, 12, 14280. [Google Scholar] [CrossRef]
- Maillard, F.; Pronkin, S.; Savinova, E.R. Handbook of Fuel Cells: Fundamentals, Technology and Applications; Vielstich, W., Gasteiger, H.A., Lamm, A., Yokokawa, H., Eds.; WILEY: Hoboken, NJ, USA, 2009. [Google Scholar]
- Garrick, T.R.; Moylan, T.E.; Carpenter, M.K.; Kongkanand, A. Editors’ choice—Electrochemically active surface area measurement of aged Pt alloy catalysts in PEM fuel cells by CO stripping. J. Electrochem. Soc. 2017, 164, F55. [Google Scholar] [CrossRef]
- Wei, C.; Sun, S.; Mandler, D.; Wang, X.; Qiao, S.Z.; Xu, Z.J. Approaches for measuring the surface areas of metal oxide electrocatalysts for determining their intrinsic electrocatalytic activity. Chem. Soc. Rev. 2019, 48, 2518. [Google Scholar] [CrossRef]
- Dionigi, F.; Zeng, Z.; Sinev, I.; Deshpande, T.M.S.; Lopez, M.B.; Kunze, S.; Zegkinoglou, I.; Sarodnik, H.; Fan, D.; Bergmann, A.; et al. In-situ structure and catalytic mechanism of NiFe and CoFe layered double hydroxides during oxygen evolution. Nat. Commun. 2020, 11, 2522. [Google Scholar] [CrossRef]
- McCrory, C.C.L.; Jung, S.; Peters, J.C.; Jaramillo, T.F. Benchmarking heterogeneous electrocatalysts for the oxygen evolution reaction. J. Am. Chem. Soc. 2013, 135, 16977. [Google Scholar] [CrossRef]
- Trasatti, S.; Petrii, O.A. Real surface area measurements in electrochemistry. Pure Appl. Chem. 1991, 63, 711. [Google Scholar] [CrossRef]
- Watzele, S.; Bandarenk, A.S. Quick determination of electroactive surface area of some oxide electrode materials. Electroanalysis 2016, 28, 2394. [Google Scholar] [CrossRef]
- Watzele, S.; Hauenstein, P.; Liang, Y.; Xue, S.; Fichtner, J.; Garlyyev, B.; Scieszka, D.; Claudel, F.; Maillard, F.; Bandarenka, A.S. Determination of electroactive surface area of Ni-, Co-, Fe-, and Ir-based oxide electrocatalysts. ACS Catal. 2019, 9, 9222. [Google Scholar] [CrossRef]
- Singh, C.; Liberman, I.; Shimoni, R.; Ifraemov, R.; Hod, I. Pristine versus pyrolyzed metal−organic framework-based oxygen evolution electrocatalysts: Evaluation of intrinsic activity using electrochemical impedance spectroscopy. J. Phys. Chem. Lett. 2019, 10, 3630. [Google Scholar] [CrossRef]
- Connor, P.; Schuch, J.; Kaiser, B.; Jaegermann, W. The determination of electrochemical active surface area and specific capacity revisited for the system MnOx as an oxygen evolution catalyst. Z. Phys. Chem. 2020, 234, 979. [Google Scholar] [CrossRef]
- Jeon, S.S.; Kang, P.W.; Klingenhof, M.; Lee, H.; Dionigi, F.; Strasser, P. Active Surface Area and Intrinsic Catalytic Oxygen Evolution Reactivity of NiFe LDH at Reactive Electrode Potentials Using Capacitances. ACS Catal. 2023, 13, 1186–1196. [Google Scholar] [CrossRef]
- Oswald, S.; Pritzl, D.; Wetjen, M.; Gasteiger, H.A. Novel method for monitoring the electrochemical capacitance by in situ impedance spectroscopy as indicator for particle cracking of nickel-rich NCMs: Part I. theory and validation. J. Electrochem. Soc. 2020, 167, 100511. [Google Scholar] [CrossRef]
- Dionigi, F.; Zhu, J.; Zeng, Z.; Merzdorf, T.; Sarodnik, H.; Gliech, M.; Pan, L.; Li, W.; Greeley, J.; Strasser, P. Intrinsic electrocatalytic activity for oxygen evolution of crystalline 3d transition metal layered double hydroxides. Angew. Chem. Int. Ed. 2021, 60, 14446. [Google Scholar] [CrossRef]
- Anantharaj, S.; Kundu, S. Do the Evaluation Parameters Reflect Intrinsic Activity of Electrocatalysts in Electrochemical Water Splitting? ACS Energy Lett. 2019, 4, 1260. [Google Scholar] [CrossRef]
- Huang, J.; Gao, Y.; Luo, J.; Wang, S.; Li, C.; Chen, S.; Zhang, J. Editors’ choice—Review—Impedance response of porous electrodes: Theoretical framework, physical models and applications. J. Electrochem. Soc. 2020, 167, 166503. [Google Scholar] [CrossRef]
- Kosakian, A.; Secanell, M. Estimating charge-transport properties of fuel-cell and electrolyzer catalyst layers via electrochemical impedance spectroscopy. Electrochimi. Acta 2021, 367, 137521. [Google Scholar] [CrossRef]
- Eikerling, M.; Kornyshev, A. Electrochemical impedance of the cathode catalyst layer in polymer electrolyte fuel cells. J. Electroanal. Chem. 1999, 475, 107. [Google Scholar] [CrossRef]
- Obermaier, M.; Bandarenka, A.S.; Tymozhynsky, C.L. A comprehensive physical impedance model of polymer electrolyte fuel cell cathodes in oxygen-free atmosphere. Sci. Rep. 2018, 8, 4933. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Liu, J.; Sabarirajan, D.C.; Huang, Y.; Perego, A.; Haug, A.T.; Zenyuk, I.V. Interpreting ionic conductivity for polymer electrolyte fuel cell catalyst layers with electrochemical impedance spectroscopy and transmission line modeling. J. Electrochem. Soc. 2021, 168, 054502. [Google Scholar] [CrossRef]
- Hilario, F.; Junior, V.R.A.M.J.; Nogueira, R.P. Application of the transmission line model for porous electrodes to analyse the impedance response of TiO2 nanotubes in physiological environment. Electrochimi. Acta 2017, 253, 599. [Google Scholar] [CrossRef]
- De Levie, R. On porous electrodes in electrolyte solutions-IV. Electrochimi. Acta 1964, 9, 1231. [Google Scholar] [CrossRef]
- Makharia, R.; Mathias, M.; Baker, D. Measurement of catalyst layer electrolyte resistance in PEFCs using electrochemical impedance spectroscopy. J. Electrochem. Soc. 2005, 152, A970. [Google Scholar] [CrossRef]
- Reid, O.; Saleh, F.S.; Easton, E.B. Determining electrochemically active surface area in PEM fuel cell electrodes with electrochemical impedance spectroscopy and its application to catalyst durability. Electrochimi. Acta 2013, 114, 278. [Google Scholar] [CrossRef]
- Liu, J.; Kang, Z.; Li, D.; Pak, M.; Alia, S.M.; Fujimoto, C.; Bender, G.; Kim, Y.S.; Weber, A.Z. Elucidating the role of hydroxide electrolyte on anion-exchange-membrane water electrolyzer performance. J. Electrochem. Soc. 2021, 168, 054522. [Google Scholar] [CrossRef]

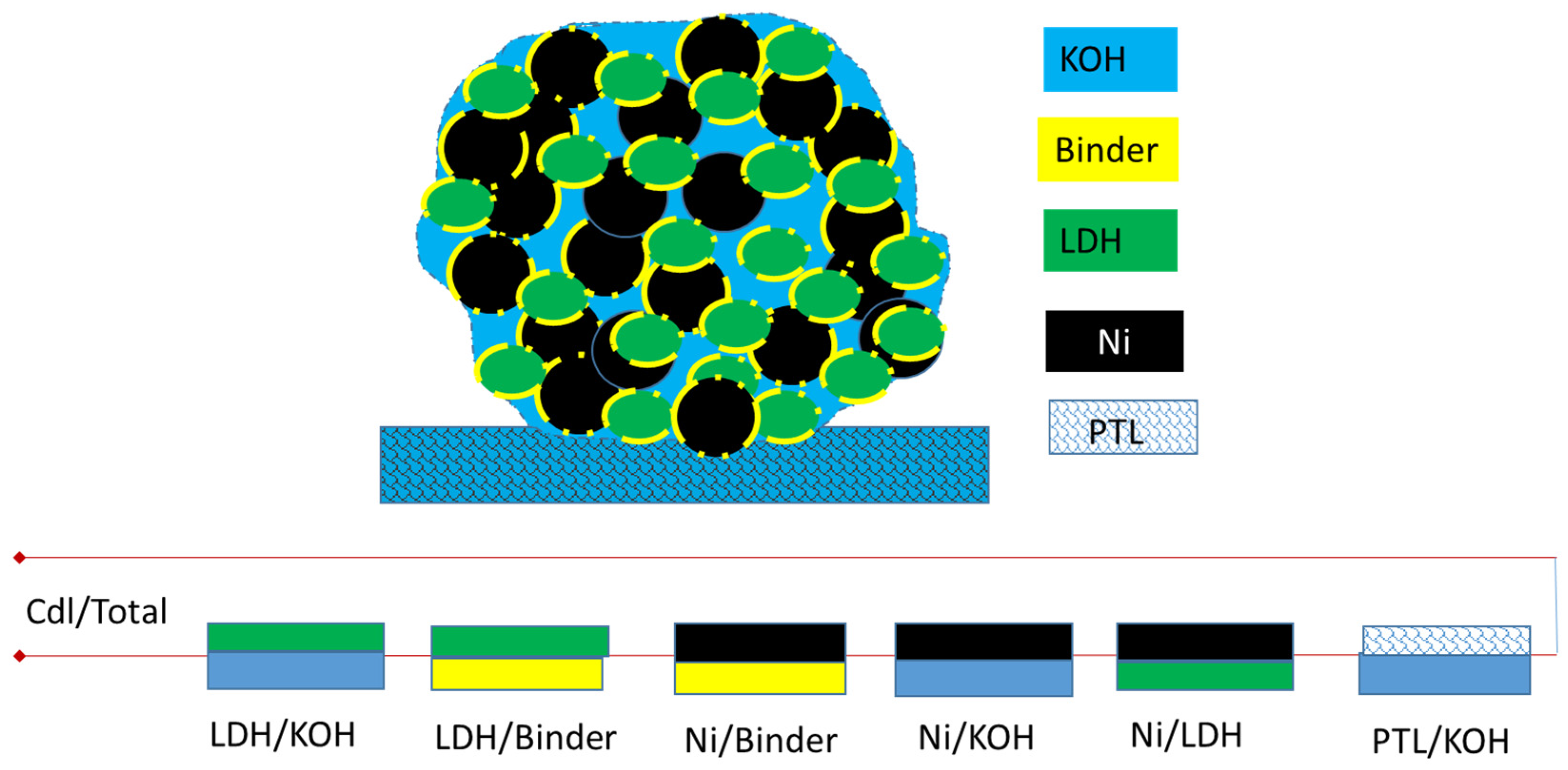

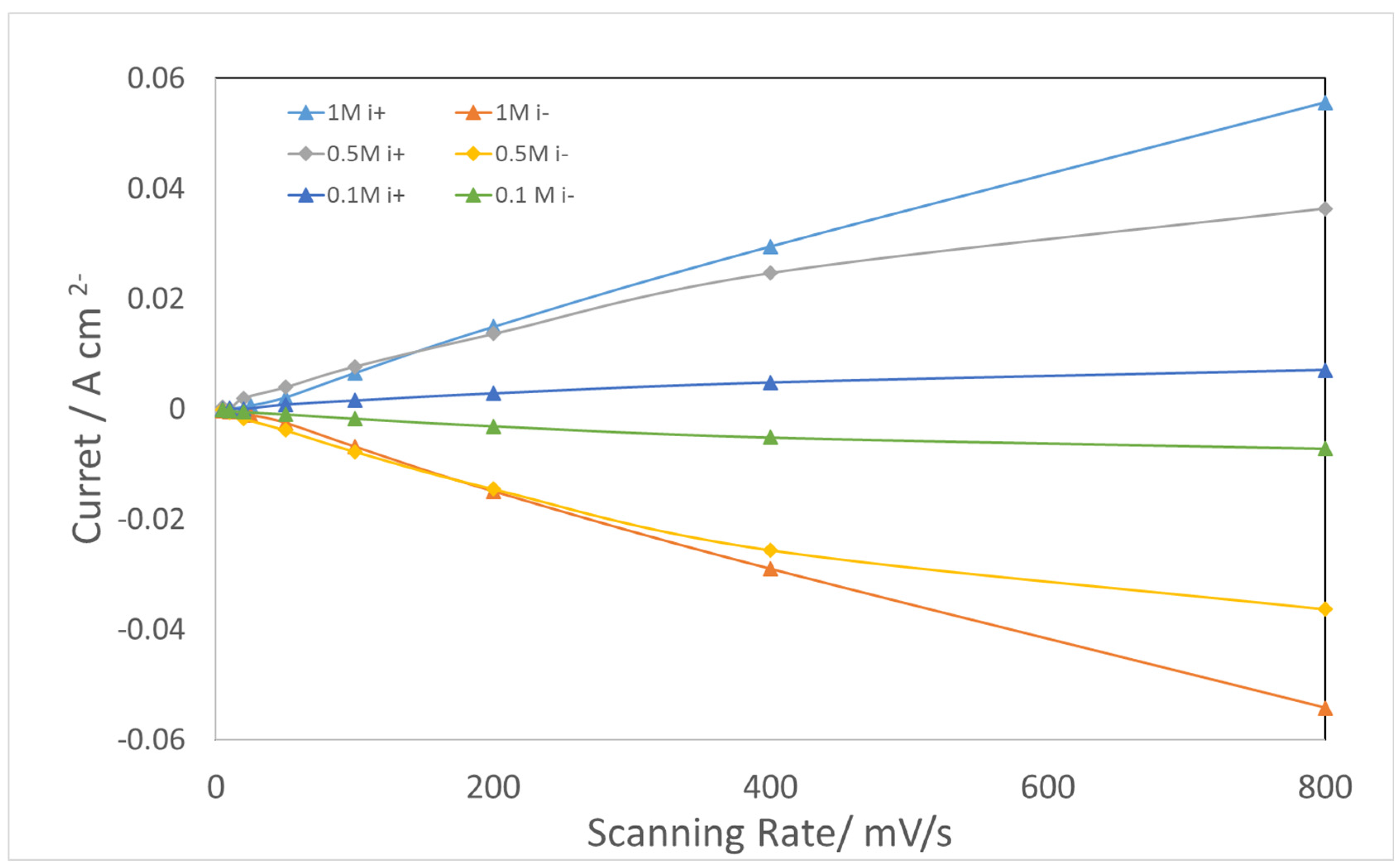
| KOH Concentration/M | 1 | 0.5 | 0.1 |
| Cdl Charge/F | 1.9 | 1.5 | 0.3 |
| Cdl discharge/F | 1.9 | 1.6 | 0.3 |
| Qdl/F/s 1−α from EIS @1.0 V | 1.89 | 1.73 | 1.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Qu, W.; Fisher, E.A.; Fahlman, J.; Asazawa, K.; Hayashi, T.; Shirataki, H.; Murase, H. Capacitance Determination for the Evaluation of Electrochemically Active Surface Area in a Catalyst Layer of NiFe-Layered Double Hydroxides for Anion Exchange Membrane Water Electrolyser. Materials 2024, 17, 556. https://doi.org/10.3390/ma17030556
Xie Z, Qu W, Fisher EA, Fahlman J, Asazawa K, Hayashi T, Shirataki H, Murase H. Capacitance Determination for the Evaluation of Electrochemically Active Surface Area in a Catalyst Layer of NiFe-Layered Double Hydroxides for Anion Exchange Membrane Water Electrolyser. Materials. 2024; 17(3):556. https://doi.org/10.3390/ma17030556
Chicago/Turabian StyleXie, Zhong, Wei Qu, Elizabeth A. Fisher, Jason Fahlman, Koichiro Asazawa, Takao Hayashi, Hiroshi Shirataki, and Hideaki Murase. 2024. "Capacitance Determination for the Evaluation of Electrochemically Active Surface Area in a Catalyst Layer of NiFe-Layered Double Hydroxides for Anion Exchange Membrane Water Electrolyser" Materials 17, no. 3: 556. https://doi.org/10.3390/ma17030556
APA StyleXie, Z., Qu, W., Fisher, E. A., Fahlman, J., Asazawa, K., Hayashi, T., Shirataki, H., & Murase, H. (2024). Capacitance Determination for the Evaluation of Electrochemically Active Surface Area in a Catalyst Layer of NiFe-Layered Double Hydroxides for Anion Exchange Membrane Water Electrolyser. Materials, 17(3), 556. https://doi.org/10.3390/ma17030556





