Effect of Nb-Ti Microalloyed Steel Precipitation Behavior on Hot Rolling Strip Shape and FEM Simulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Materials
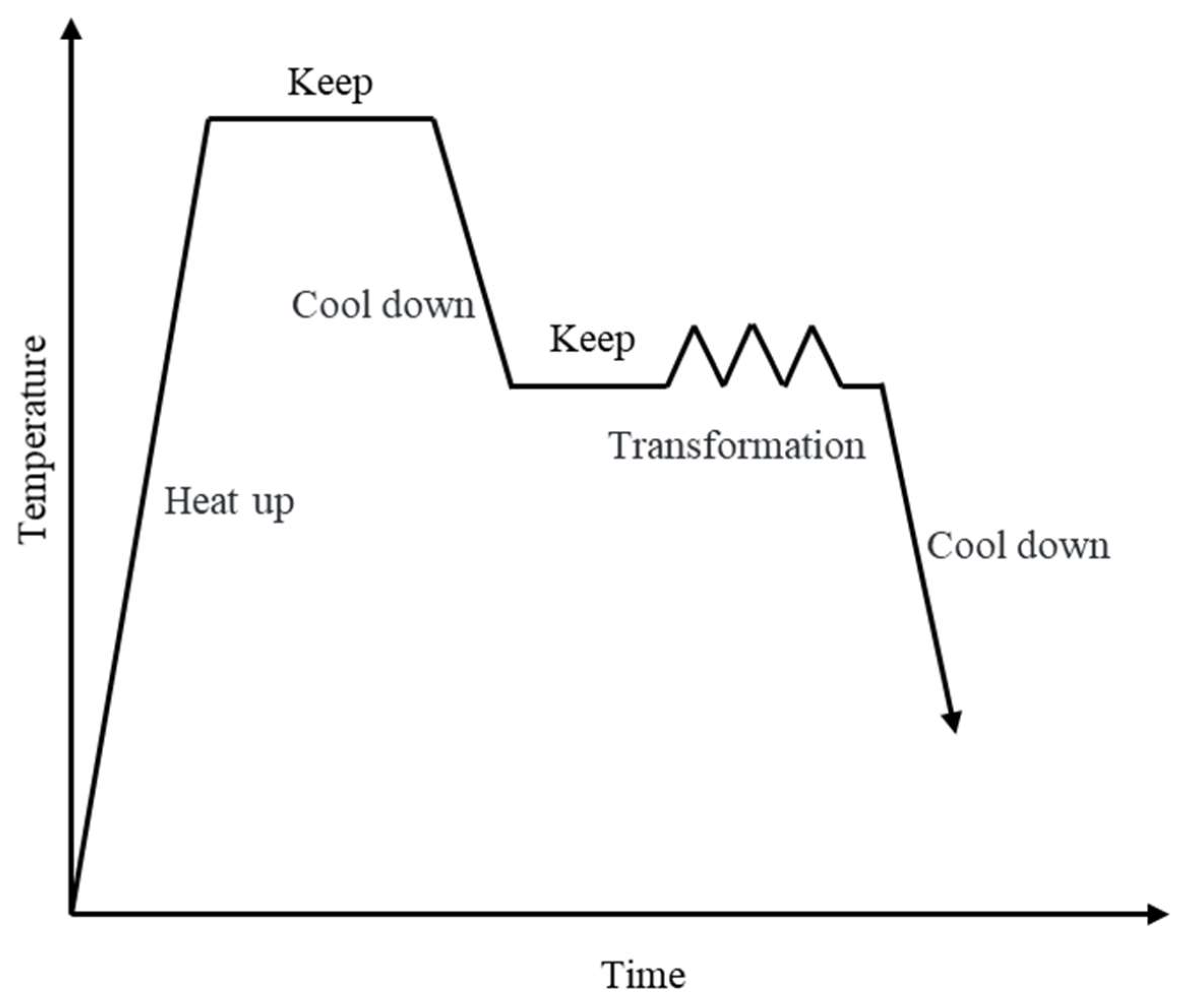
2.2. High-Temperature Compression Experiment
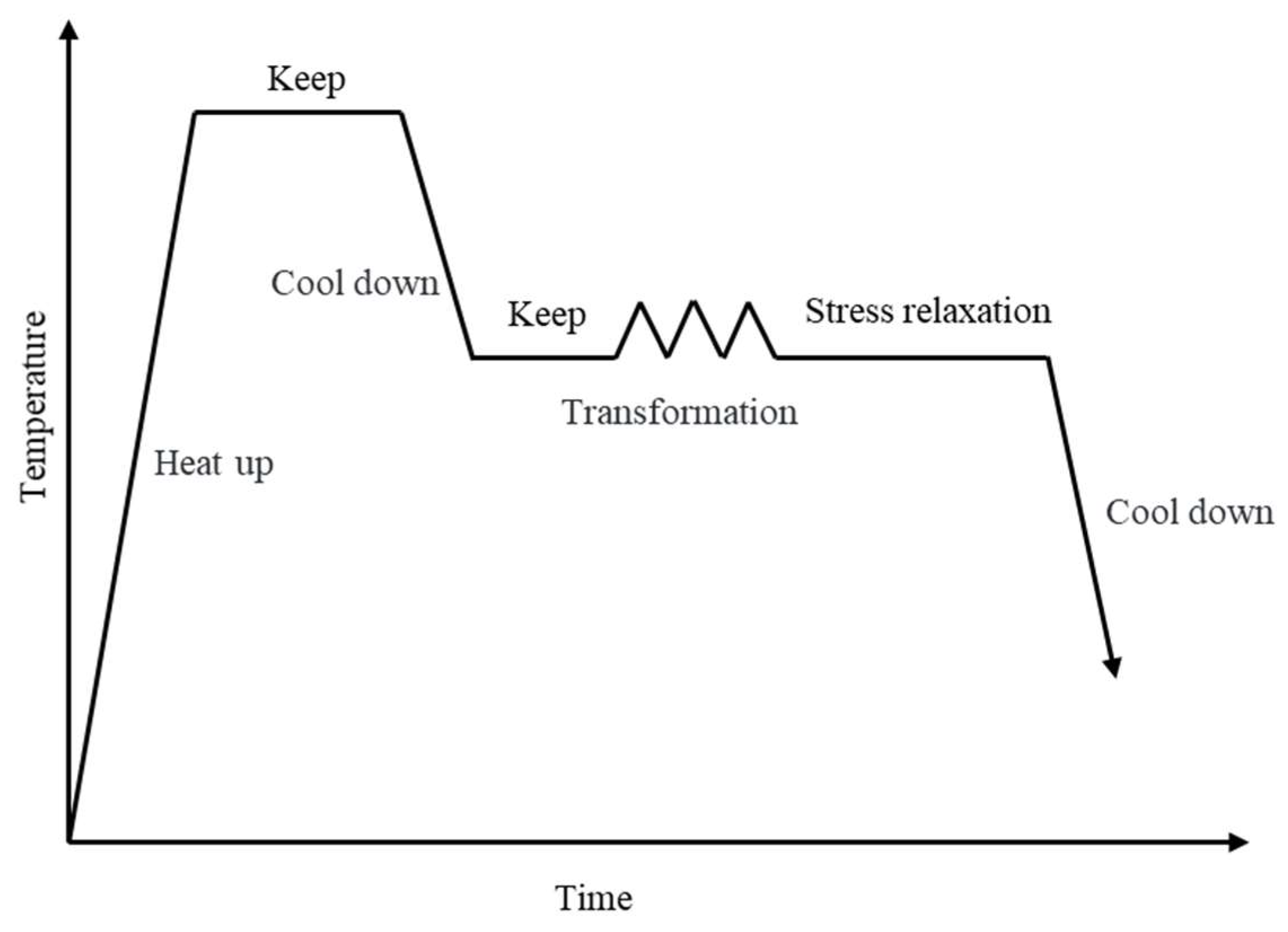
2.3. Stress Relaxation Experiment
2.4. Microscopic Observation and Analysis
3. Precipitation Theory Model
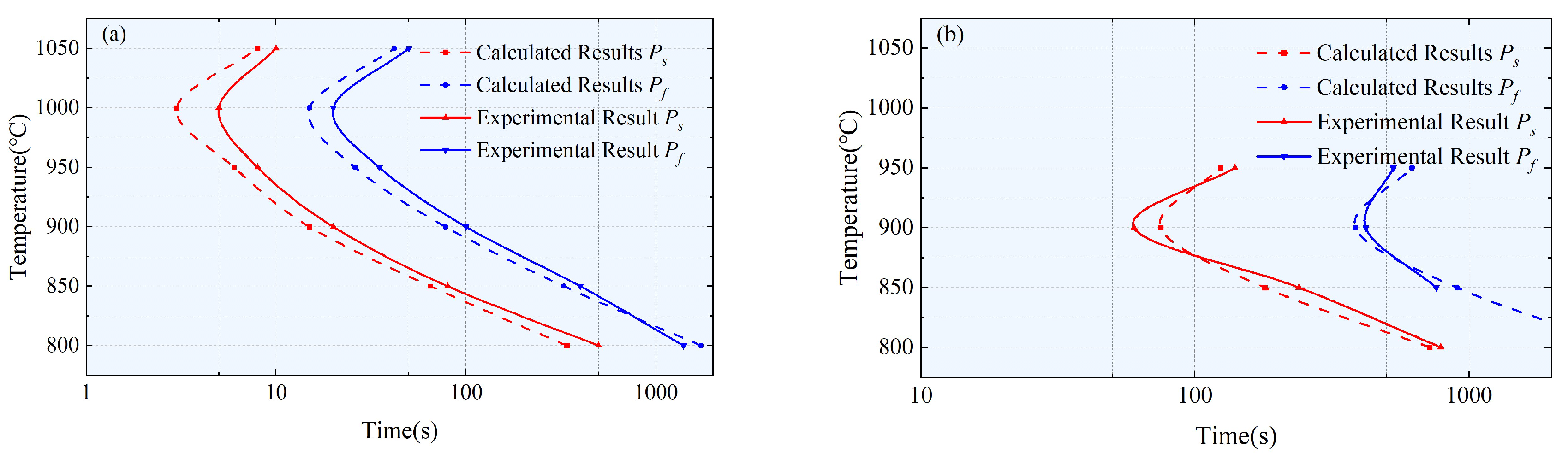
3.1. Precipitation Thermodynamic Model
3.2. Precipitation Kinetics Model
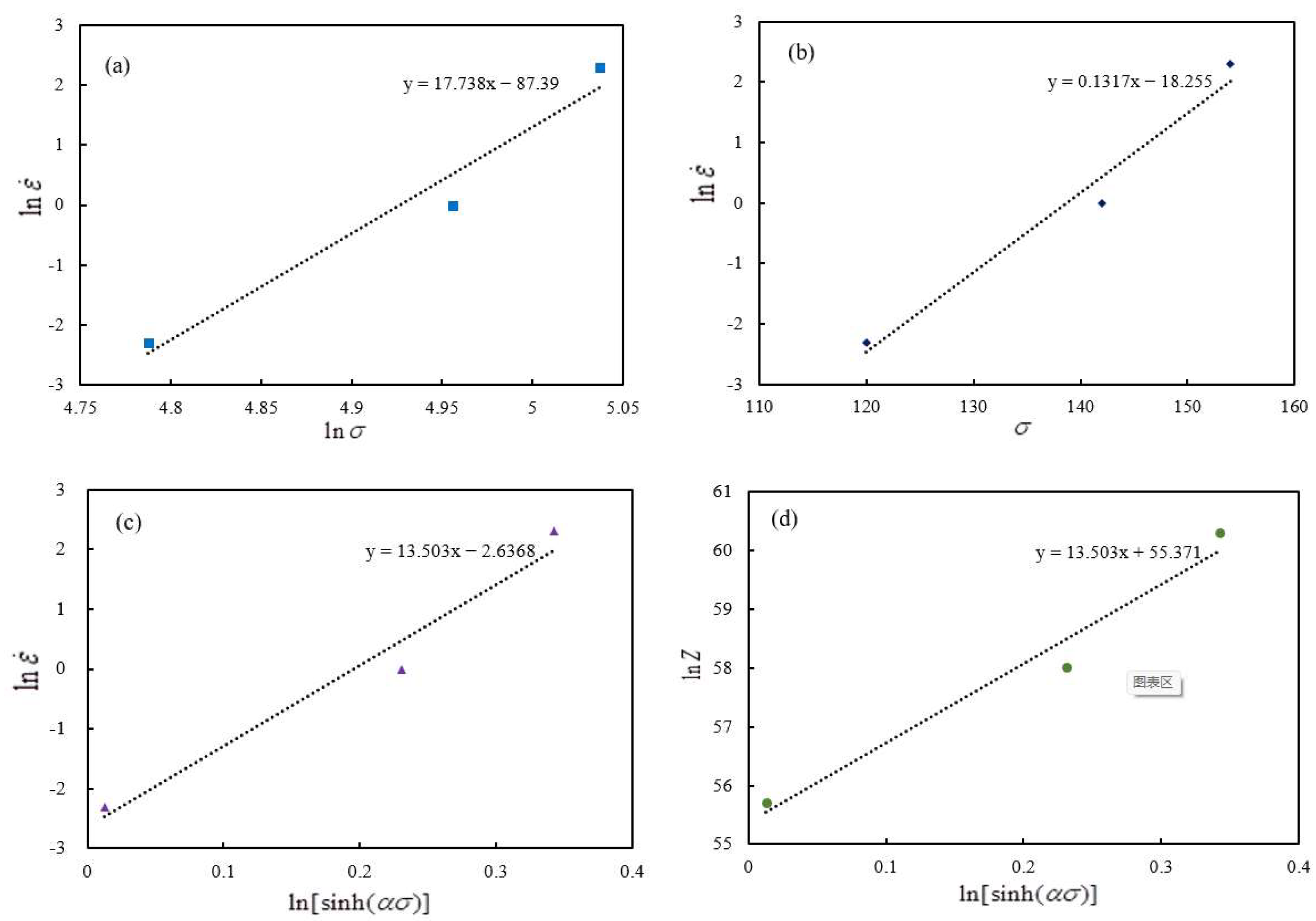
3.3. Precipitation Strengthening and High-Temperature Constitutive Models
4. Temperature Field and FEM Model
4.1. Construction of the Rolling Temperature Field
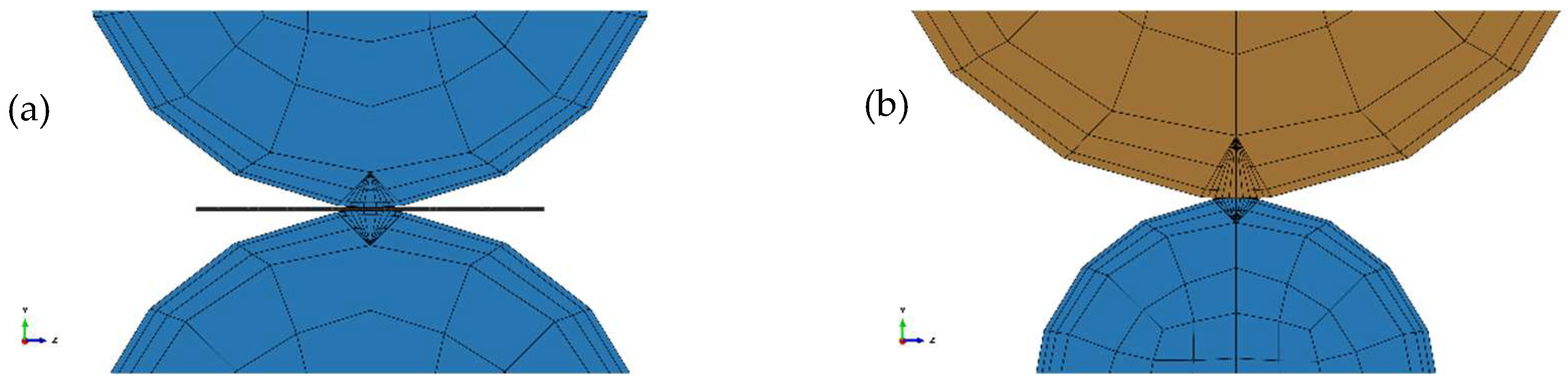
4.2. Construction of Elastic-Plastic FEM Model
4.3. Design of FEM Model Work Conditions
5. Results and Discussion
6. Conclusions
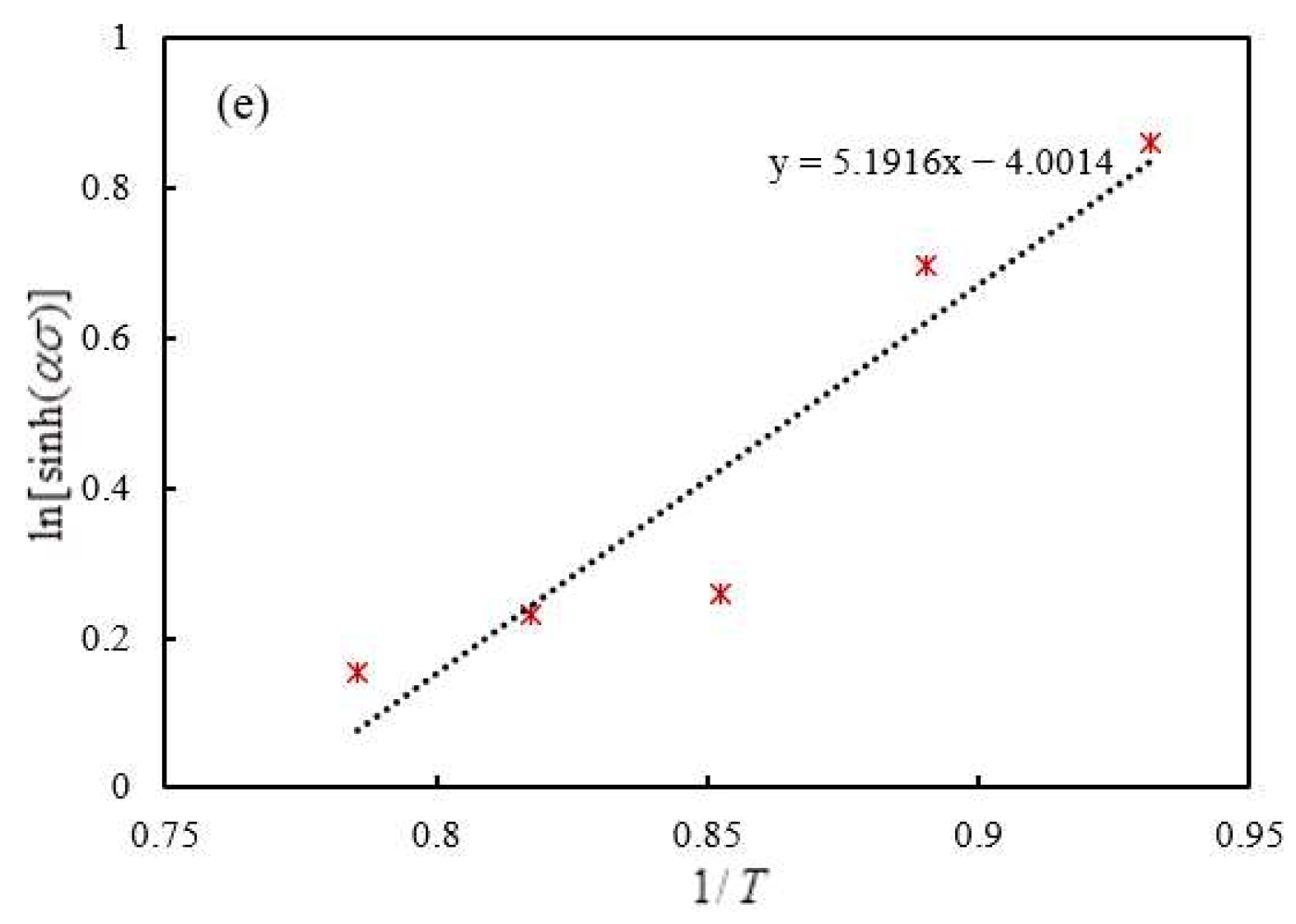
- From the high-temperature compression experiment, it is known that due to the large difference in Nb and Ti element content, sample 1# has a maximum true stress about 20% greater than sample 2#, and it exhibits greater deformation resistance during hot rolling.
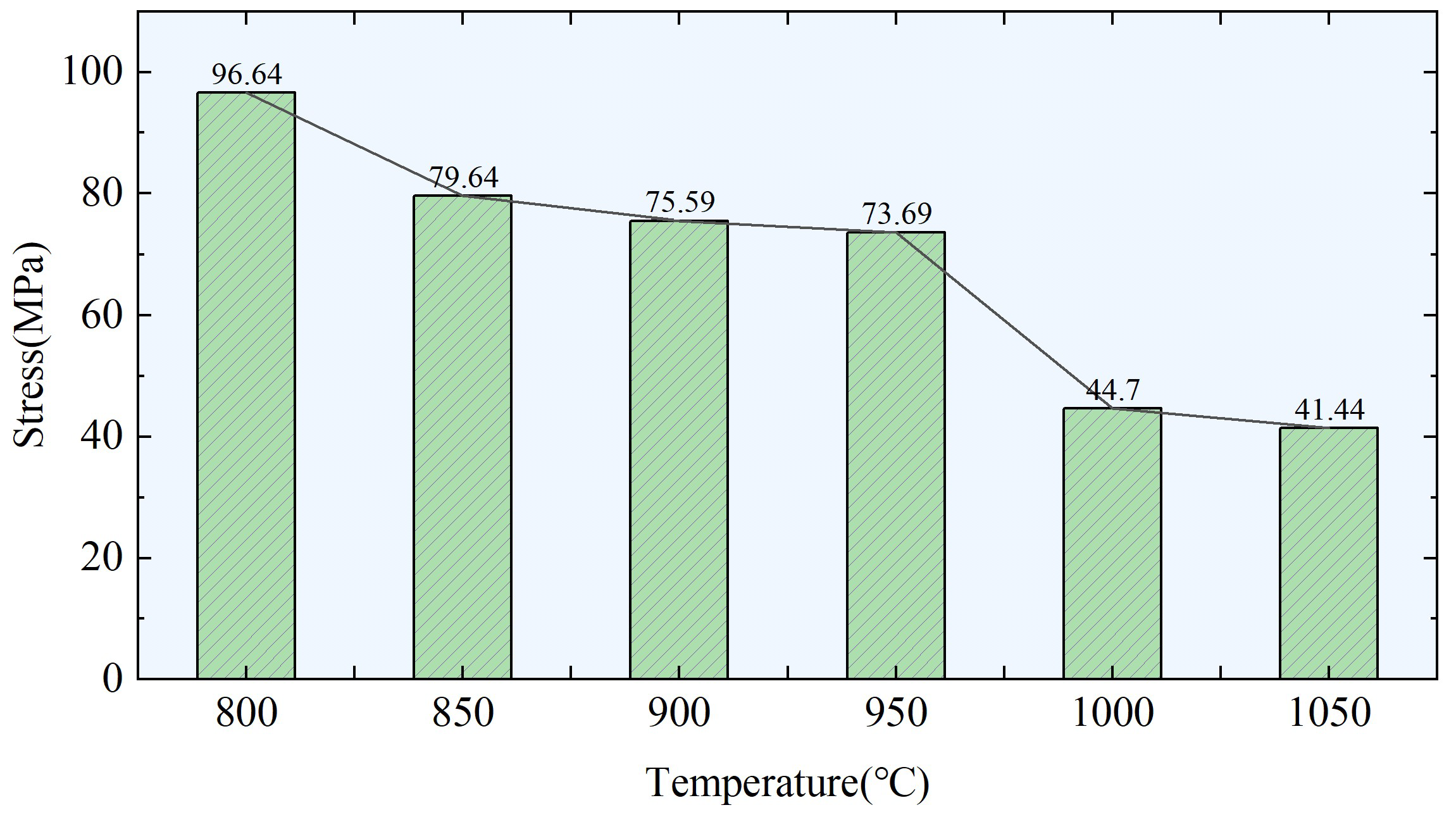
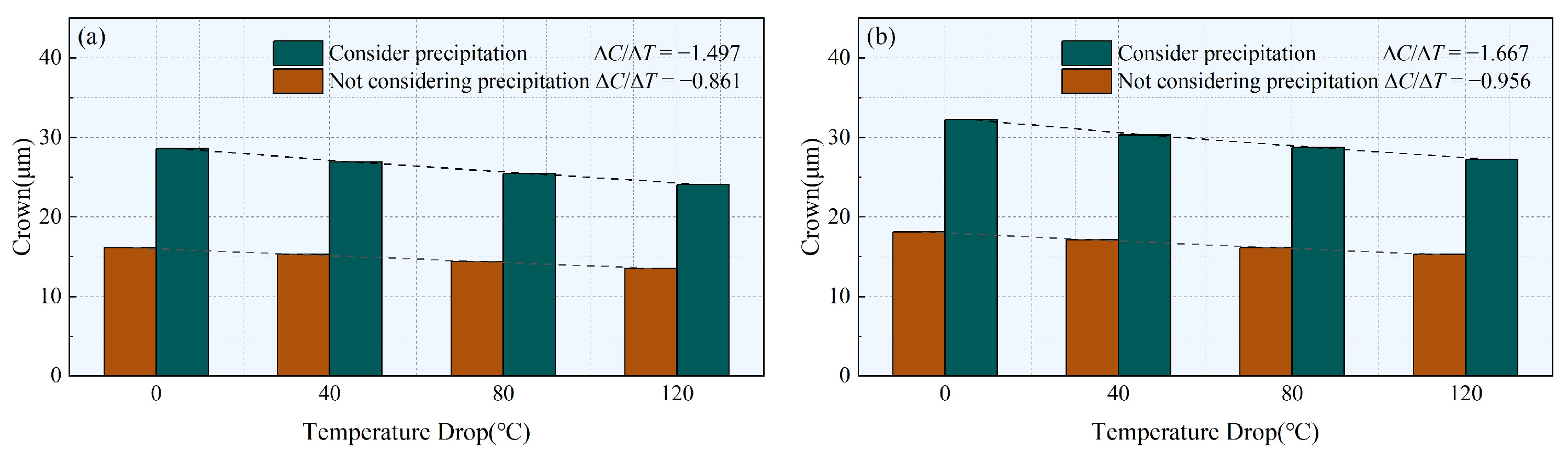
- After calculating the theoretical model of precipitation, it was known that the content of microalloying elements significantly affects the precipitation rate and the volume fraction of precipitates. The enhancement effect of precipitation on the strength in Sample 1# varies significantly, reaching a maximum of 96.6 MPa. By comparing with the control group, it can be concluded that precipitates are an important influencing factor for the shape of hot rolling strips in steel strips.
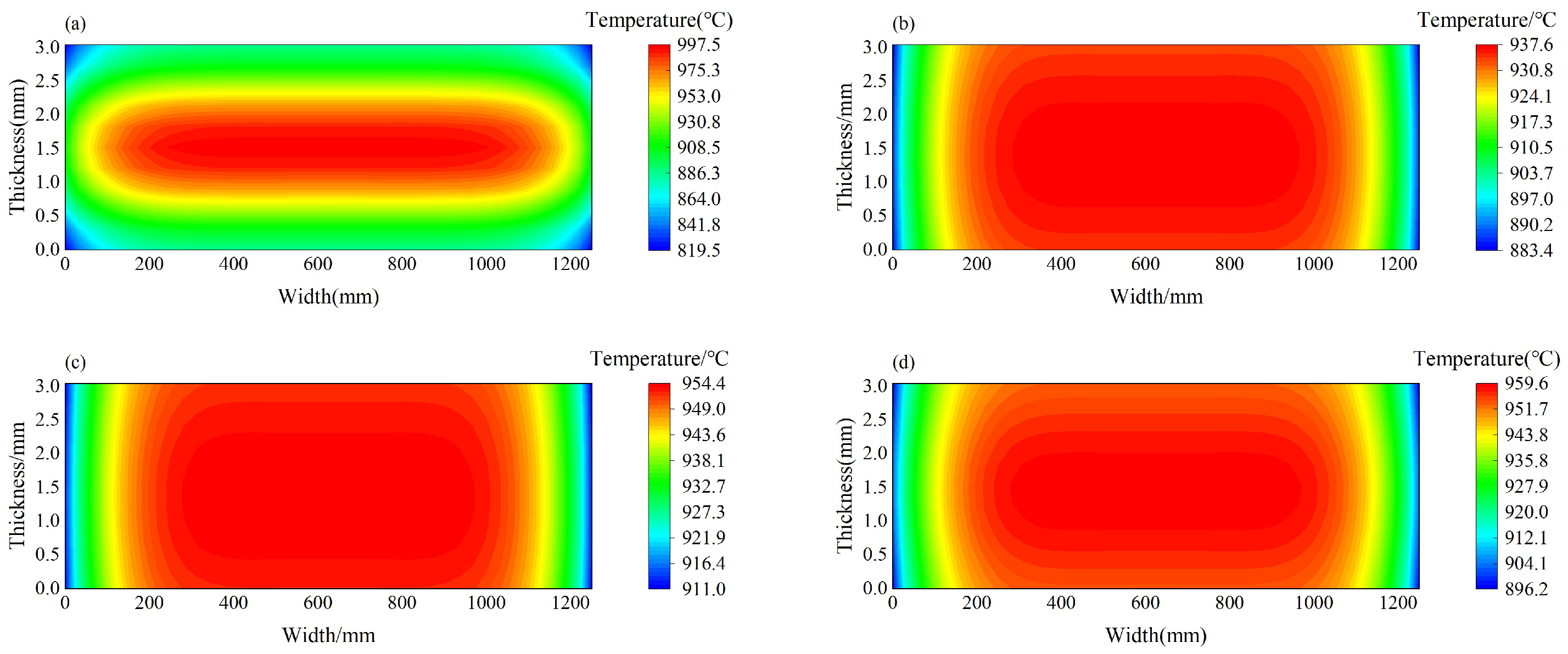
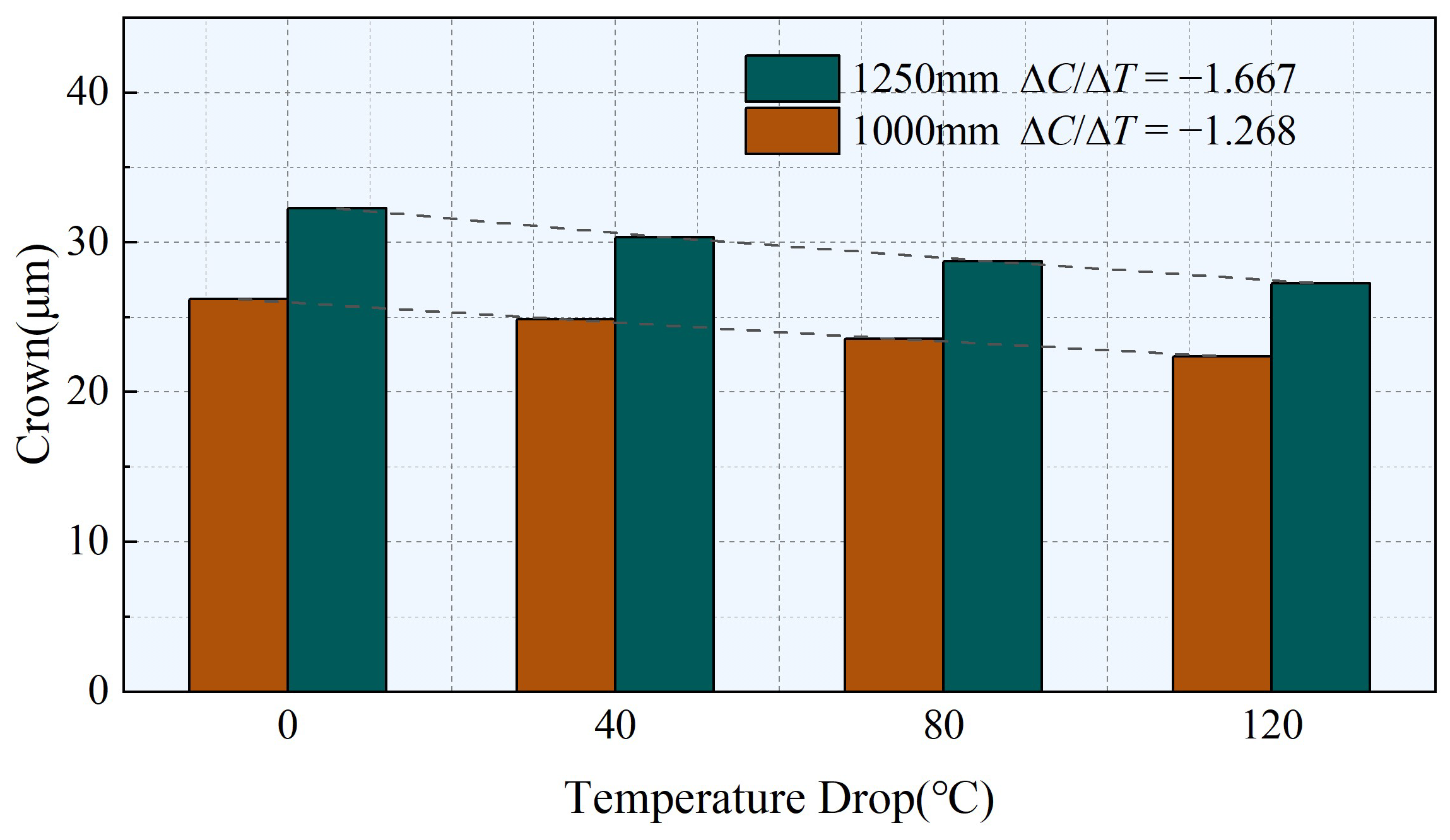
- The strip temperature decreases with the increase of the mill stand, and precipitation strengthening will exacerbate the uneven distribution of transverse strength of the strip, causing uneven thickness distribution and easy occurrence of strip shape problems. In addition, considering the sensitivity of crown to the overall temperature during precipitation, the sensitivity of crown to temperature drop decreases as the strip width decreases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skobir, D.A. High-strength low-alloy (HSLA) steels: Visokotrdna malolegirana (HSLA) konstrukcijska jekla. Mater. Tehnol. 2011, 45, 295–301. [Google Scholar]
- Singh, P.P.; Ghosh, S.; Mula, S. Strengthening behaviour and failure analysis of hot-rolled Nb+ V microalloyed steel processed at various coiling temperatures. Mater. Sci. Eng. A 2022, 859, 144210. [Google Scholar] [CrossRef]
- Chen, G.; Colin, S.; Fateh, F.; Michael, J.; Gaudet, M.J.; Jing, S.; Xiang, W.; Nabil, B.; Hatem, Z. Evolution of the microstructure and mechanical properties of a V-containing microalloyed steel during coiling. Mater. Sci. Eng. A 2023, 880, 145332. [Google Scholar]
- Hao, K.; Chain, L. A Review on Nano-Scale Precipitation in Steels. Technologies 2018, 6, 36. [Google Scholar]
- Vervynckt, S.; Verbeken, K.; Lopez, B.; Jonas, J. Modern HSLA steels and role of non-recrystallisation temperature. J. Int. Mater. Rev. 2012, 57, 187–207. [Google Scholar] [CrossRef]
- Sterjovski, Z.; Nolan, D.; Carpenter, K.R.; Dunne, D.P.; Norrish, J. Artificial neural networks for modelling the mechanical properties of steels in various applications. J. Mater. Process. Technol. 2005, 170, 536–544. [Google Scholar] [CrossRef]
- Bagheripoor, M.; Bisadi, H. Application of artificial neural networks for the prediction of roll force and roll torque in hot strip rolling process. Appl. Math. Model. 2013, 37, 4593–4607. [Google Scholar] [CrossRef]
- He, H.N.; Shao, J.; Wang, X.C.; Yang, Q.; Liu, Y.; Dong, X.; Sun, Y.Z. Research and application of approximate rectangular section control technology in hot strip mills. J. Iron Steel Res. Int. 2021, 28, 279–290. [Google Scholar] [CrossRef]
- Churyumov, A.Y.; Kazakova, A.A. Prediction of true stress at hot deformation of high manganese steel by artificial neural network Modeling. Materials 2023, 16, 1083. [Google Scholar] [CrossRef]
- Servin, R.; Arreola, S.A.; Calderón, I.; Perez, A.; San Miguel, S.M. Effect of crown shape of rolls on the distribution of stress and elastic deformation for rolling processes. Metals 2019, 9, 1222. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.; Yang, Q.; Wang, Q.; Wang, Y.; Li, W. Mechanism of lateral metal flow on residual stress distribution during hot strip rolling. J. Mater. Process. Technol. 2021, 288, 116838. [Google Scholar] [CrossRef]
- Lian, J.C.; Qi, X.D. Strip and Strip Rolling Theory and Strip Shape Control Theory; Machinery Industry Press: Beijing, China, 2013. [Google Scholar]
- Li, W.G.; Chen, S.X.; Liu, X.H. Rolling Force Model Considering Phase Transformation in the Precision Rolling Process of Hot Strip Steel. Northeast. Univ. Nat. Sci. 2013, 34, 1425–1429. [Google Scholar]
- Liu, C.; He, A.R.; Qiang, Y.; Guo, D. Effect of Phase Transformation and Latent Heat on Hot Rolling Deformation Behavior of Non-oriented Electrical Steel. ISIJ Int. 2017, 57, 5. [Google Scholar] [CrossRef]
- Stornelli, G.; Tselikova, A.; Mirabile Gattia, D.; Mortello, M.; Schmidt, R.; Sgambetterra, M.; Testani, T.; Zucca, G.; Di Schino, A. Influence of vanadium micro-alloying on the microstructure of structural high strength steels welded joints. Materials 2023, 16, 2897. [Google Scholar] [CrossRef]
- Pourasiabi, H.; Gates, J.D. Effects of niobium macro-additions to high chromium white cast iron on microstructure, hardness and abrasive wear behaviour. Mater. Des. 2021, 212, 110261. [Google Scholar] [CrossRef]
- Sauer, M.; Fabík, R.; Schindler, I.; Kawulok, P.; Opěla, P.; Kawulok, R.; Rusz, S. Analysis of the microstructure development of Nb-microalloyed steel during rolling on a heavy-section mill. Materials 2022, 16, 288. [Google Scholar] [CrossRef]
- Dutta, B.; Sellars, C.M. Effect of Composition and Process Variables on Nb(C,N) Precipitation in Niobium Microalloyed Austenite. Mater. Sci. Technol. 1987, 3, 197. [Google Scholar] [CrossRef]
- Liu, W.J. New Theory and kinetic modeling of strain-induced precipitation of Nb(C,N) in microalloyed austenite. Metall. Mater. Trans. A 1995, 26A, 1641–1657. [Google Scholar] [CrossRef]
- Dutta, B.; Palmiere, E.J.; Sellars, C.M. Modeling the kinetics of strain induced precipitation in Nb microalloyed steels. Acta Mater. 2001, 49, 785–794. [Google Scholar] [CrossRef]
- Benoit, M.J.; Tabaie, S.; Waqar, T.; Ganton, T.; Amirkhiz, B.S.; Hadadzadeh, A.; Nasiri, A. Effects of additive manufacturing processes and isothermal aging on the microstructure and properties of 13-8 Mo precipitation hardening martensitic stainless steel. Addit. Manuf. 2023, 72, 103615. [Google Scholar] [CrossRef]
- Wang, L.C.; Cai, H.N.; Meng, L.Q. Thermodynamic Analysis of the Influence of Microalloying Elements on Precipitation Phases in Austenitic Stainless Steel based on Thermo-Calc. Hot Work. Technol. 2021, 50, 39–43. [Google Scholar]
- Varanasi, R.S.; Gault, B.; Ponge, D. Effect of Nb micro-alloying on austenite nucleation and growth in a medium manganese steel during intercritical annealing. Acta Mater. 2022, 229, 117786. [Google Scholar] [CrossRef]
- Qu, J.B.; Wang, Z.D.; Liu, X.H.; Wang, G.D.; Xue, G.J.; Chen, G.; Cao, K.F.; Xu, J.G. Prediction Model of Microstructure and Properties for HSLA Steel in Controlled Rolling and Controlled Cooling Process. Iron Steel. 1999, 1, 37–40+32. [Google Scholar]
- Patra, P.K.; Sam, S.; Singhai, M.; Hazra, S.S.; Janaki Ram GD Bakshi, S.R. Effect of coiling temperature on the microstructure and mechanical properties of hot-rolled Ti–Nb microalloyed ultra high strength steel. Trans. Indian Inst. Met. 2017, 70, 1773–1781. [Google Scholar] [CrossRef]
- Adrian, H. Thermodynamic model for precipitation of carbonitrides in high strength low alloy steels containing up to three microalloying elements with or without additions of aluminum. Mater. Sci. Technol. 2013, 8, 406–420. [Google Scholar] [CrossRef]
- Vijay, V.A.; Santhy, K.; Sivakumar, G.; Rajasekaran, B. Thermal expansion and microstructure evolution of atmospheric plasma sprayed NiCrAlY bond coat using in-situ high temperature X-ray diffraction. Surf. Coat. Technol. 2023, 452, 129132. [Google Scholar] [CrossRef]
- Zhiping, X.; Ilana, T.; Elena, P. Clustering, nano-scale precipitation and strengthening of steels. Prog. Mater. Sci. 2020, 118, 100764. [Google Scholar]
- Szajewski, B.A.; Crone, J.C.; Knap, J. Analytic model for the Orowan dislocation-precipitate bypass mechanism. Materialia 2020, 11, 100671. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Chen, C.C.; Shao, J.; He, A.R. Research on Online Calculation Method of Temperature Field for Hot rolling Strip Steel. J. Mech. Eng. 2014, 50, 135–142. [Google Scholar] [CrossRef]
- Sadique, H.; Murtaza, Q. Heat transfer augmentation in microchannel heat sink using secondary flows: A review. Int. J. Heat Mass Transfer. 2022, 194, 123063. [Google Scholar] [CrossRef]







| Steel Sample | C | Si | Mn | Ti | S | Nb | P | N | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 1# | 0.0712 | 0.353 | 1.193 | 0.0026 | 0.0019 | 0.0513 | 0.011 | 0.0027 | Bal. |
| 2# | 0.0687 | 0.015 | 0.857 | 0.0008 | 0.0046 | 0.0136 | 0.009 | 0.0036 | Bal. |
| Parameter | F1 | F2 | F3 | F4 | F5 | F6 |
|---|---|---|---|---|---|---|
| Entry thickness (mm) | 42.95 | 17.81 | 11.33 | 7.62 | 4.37 | 3.25 |
| Exit thickness (mm) | 17.81 | 11.33 | 7.62 | 4.37 | 3.25 | 3.15 |
| Exit velocity (m/s) | 0.19 | 1.16 | 2.19 | 3.55 | 5.58 | 7.63 |
| Rolling force (kN) | 2034 | 2359 | 2555 | 2738 | 2092 | 1936 |
| Work roll diameter (mm) | 820 | 806 | 750 | 758 | 582 | 554 |
| Roll center distance (mm) | 5.5 | |||||
| Length of cooling water before and after rolling (mm) | 0.5 | |||||
| Length of cooling water between frames (mm) | 1 | |||||
| Width of cooling water between frames (mm) | 1500 | |||||
| Width(mm) | 1250 | |||||
| Strip | Working Roll | Supporting Roll | ||||
|---|---|---|---|---|---|---|
| Entry thickness | Exit thickness | Width | Diameter | Length | Diameter | Length |
| 5 mm | 3 mm | 1250/1000 mm | 850 mm | 2550 mm | 1600 mm | 2250 mm |
| Condition Code | Central Temperature (°C) | Strip Width (mm) | Temperature Drop (°C) |
|---|---|---|---|
| 1-Consider precipitation | 1000 | 1250 | 0/40/80/120 |
| 2-Consider precipitation | 950 | 1250 | 0/40/80/120 |
| 3-Consider precipitation | 950 | 1000 | 0/40/80/120 |
| 4-Not Consider Precipitation | 1000 | 1250 | 0/40/80/120 |
| 5-Not Consider Precipitation | 950 | 1250 | 0/40/80/120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Shao, J.; Yao, C.; Jia, P.; Xie, S.; Chen, D.; Xiao, M. Effect of Nb-Ti Microalloyed Steel Precipitation Behavior on Hot Rolling Strip Shape and FEM Simulation. Materials 2024, 17, 651. https://doi.org/10.3390/ma17030651
Li K, Shao J, Yao C, Jia P, Xie S, Chen D, Xiao M. Effect of Nb-Ti Microalloyed Steel Precipitation Behavior on Hot Rolling Strip Shape and FEM Simulation. Materials. 2024; 17(3):651. https://doi.org/10.3390/ma17030651
Chicago/Turabian StyleLi, Kaisheng, Jian Shao, Chihuan Yao, Pan Jia, Shuhao Xie, Desheng Chen, and Min Xiao. 2024. "Effect of Nb-Ti Microalloyed Steel Precipitation Behavior on Hot Rolling Strip Shape and FEM Simulation" Materials 17, no. 3: 651. https://doi.org/10.3390/ma17030651
APA StyleLi, K., Shao, J., Yao, C., Jia, P., Xie, S., Chen, D., & Xiao, M. (2024). Effect of Nb-Ti Microalloyed Steel Precipitation Behavior on Hot Rolling Strip Shape and FEM Simulation. Materials, 17(3), 651. https://doi.org/10.3390/ma17030651





