Next Article in Journal
Experimental and Numerical Study on Chloride Transport in Unsaturated Concrete: Highlighting Temperature, Humidity, and Mineral Admixtures
Previous Article in Journal
Nitrogen Removal from Landfill Leachate Using Biochar Derived from Wheat Straw
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 17
Issue 4
10.3390/ma17040929
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Superconductivity in Bi-Doped BaFe2As2 Single Crystals

by
Jiabin Si
1,†,
Jianfa Zhao
2,*,†,
Ying Liu
1,
Ying Liu
3,
Changqing Jin
2,
Jibing Liu
1 and
Lingyi Xing
1,*
1
College of Physics and Electronic Science, Hubei Normal University, Huangshi 435002, China
2
Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
3
Quantum Science Center of Guangdong-Hong Kong-Macao Greater Bay Area (Guangdong), Shenzhen 518045, China
*
Authors to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Materials 2024, 17(4), 929; https://doi.org/10.3390/ma17040929
Submission received: 22 January 2024 / Revised: 9 February 2024 / Accepted: 14 February 2024 / Published: 17 February 2024
Browse Figures
Versions Notes

Abstract

:
We have successfully synthesized a series of Bi-doped BaFe2As2 high-quality single crystals for the first time. X-ray diffraction (XRD) patterns show an expansion of lattice parameter c with Bi doping, indicating a negative pressure effect. By investigating the resistivity, a Fermi liquid (FL) to non-Fermi liquid (NFL) crossover is observed from normal state to antiferromagnetic order state, accompanied by three superconducting transitions labeled as SC I, SC II and SC III, which are supposed to be induced by three superconducting realms with various Bi concentrations. Thus, we propose that the NFL behavior is closely related to the presence of superconductivity. The magnetic susceptibility measurements further speculate that the SC I and SC III phases should exhibit filamentary superconductivity while the SC II exhibits a possible bulk superconductivity of TC~7 K.

1. Introduction

Since the discovery of TC = 26 K superconductivity in LaO1−xFxFeAs [1], iron-based superconductors (IBSC) have stimulated another round of interest in high-temperature superconductor research regarding cuprates [2]. Among them, the ‘122’ system AEFe2As2 (AE = Ba, Sr and Ca) with a ThCr2Si2-type structure has been heavily studied because of its easily grown, large, suitable and high-quality single crystals [3,4,5]. As for the BaFe2As2 parent compound [3], it exhibits an anomaly transition at 140 K which is attributed to a spin-density wave (SDW) and a tetragonal (I4/mmm) to orthorhombic (Fmmm) crystallographic structure transition. The superconductivity could eventually appear when the SDW transition is suppressed by applying physical pressure or chemical doping.
Compared with physical pressure, chemical doping has several alternative tuning modes, which can not only apply positive or negative chemical pressure but also introduce hole or electron carriers. For these reasons, it has been widely chosen as an effective method to investigate the superconductivity in BaFe2As2. For example, the superconductivity could be yielded by substituting isovalent P [6] or Ru [7] for As or Fe in order to introduce positive or negative chemical pressure, by substituting K for Ba to introduce hole carriers [3], and by substituting Co [8] or Ni [9] for Fe to introduce electron carriers. Unexpectedly, some other hole substitutions (Cr, Mn and V) at the Fe site could not induce superconductivity even though the SDW transition was also gradually suppressed [10,11,12]. The absence of hole carriers and a new competing G-type antiferromagnetic order has been proposed as a way to prevent the emergence of superconductivity in Mn- and Cr-doped BaFe2As2 [13,14]. However, even the strong hole-doping effect has been identified by Hall effect measurements in Ba(Fe1−xVx)2As2 [12], only local superconductivity along with coexisting magnetism is found to be consistent with the lack of bulk superconductivity [15]. This significant difference between hole doping and electron doping at the Fe site still provokes debate. Moreover, another much simpler correlation mechanism is proposed in a review article that suggests a decrease in c-lattice parameter is required to induce ‘in-plane’ (FeAs layer) superconductivity [16]. Based on this guideline, the bulk superconductivity induced by electron dopants at the Fe site and isovalent dopant at the As site with a smaller P element seems to be easily understood. Even for the isovalent Ru doping at the Fe site can be well interpreted, although the radius of the Ru ion is larger than the Fe ion, since it only expands lattice parameter a and the volume but indeed causes a decrease in lattice parameter c [7].
Recently, Jayalakshmi et al. theoretically proposed that the superconductivity is possible in (Ca,Sr,Ba)Fe2Bi2 compounds and BaFe2Bi2 might exhibit a higher TC (≈30 K) than other proposed materials [17,18]. However, the structural data show that lattice parameter c is larger than BaFe2As2, which is contrary to the previous prediction that c should be reduced for ‘in-plane’ bulk superconductivity. Further work must be performed in order to verify whether BaFe2As2 could become a superconductor by using isovalent Bi as a substitution for As to introduce a negative pressure and whether the relationship between the c decrease and bulk superconductivity is still satisfactory. In this work, we report the synthesis and investigation of Bi-doped BaFe2As2 single crystals experimentally for the first time. Two filamentary superconducting phases with TC~25 K (SC I) and 15 K (SC III), and another possible bulk superconducting phase (SC II) with TC~7 K, are found, which indirectly confirms the possible superconductivity of BaFe2Bi2; however, the reduction in lattice parameter c for ‘in-plane’ bulk superconductivity might be not sufficient.

2. Materials and Methods

The BaFe2(As1−xBix)2 single crystals were synthesized by self-flux method. FeAs1−xBix were prepared as precursors using the highly pure raw materials Fe, As and Bi by solid reaction method. The Fe, As and Bi powders were thoroughly mixed together and sealed in an evacuated quartz tube. The mixture was heated up to 750 °C and kept for 30 h. The obtained material was reground and sintered twice using the same heating procedure in order to make the Bi doping much more homogeneous. After we obtained the precursors, the Ba lump, as well as the FeAs and FeAs1−xBix powders, were loaded in the alumina oxide tube and sealed in the evacuated quartz tube according to the stoichiometry ratio 1:2:2. The quartz tube was heated up to 1150 °C for 20 h and then slowly cooled down to 1000 °C with a rate of 2 °C/h in order to grow single crystals. In the end, the high-quality single crystals with dimensions up to 8 mm × 6 mm × 0.1 mm were obtained, as shown in Figure 1a. All the synthesis manipulations were carried out in a glove box filled with high-purity nitrogen gas.
The surface morphology and actual chemical compositions of BaFe2(As1−xBix)2 single crystals were examined by a scanning electron microscope (SEM) equipped with energy dispersive X-ray spectroscopy (EDX). The X-ray diffraction (XRD) was conducted with 2θ range from 10° to 80° on a Rigaku X-ray diffractometer (SmartLab SE, Tokyo, Japan) using Cu Kα radiation (λ = 1.5406 Å) generated at 40 kV and 30 mA. Both the resistivity and DC magnetic susceptibility was measured by the Quantum Design’s Magnetic Property Measurement System (MPMS3, San Diego, CA, USA). The resistivity was measured using the standard four-probe method, while the DC magnetic susceptibility was measured using the zero-field-cooling (ZFC) and field-cooling (FC) modes with two fields H = 20 Oe and 1 T along the ab plane.

3. Results and Discussion

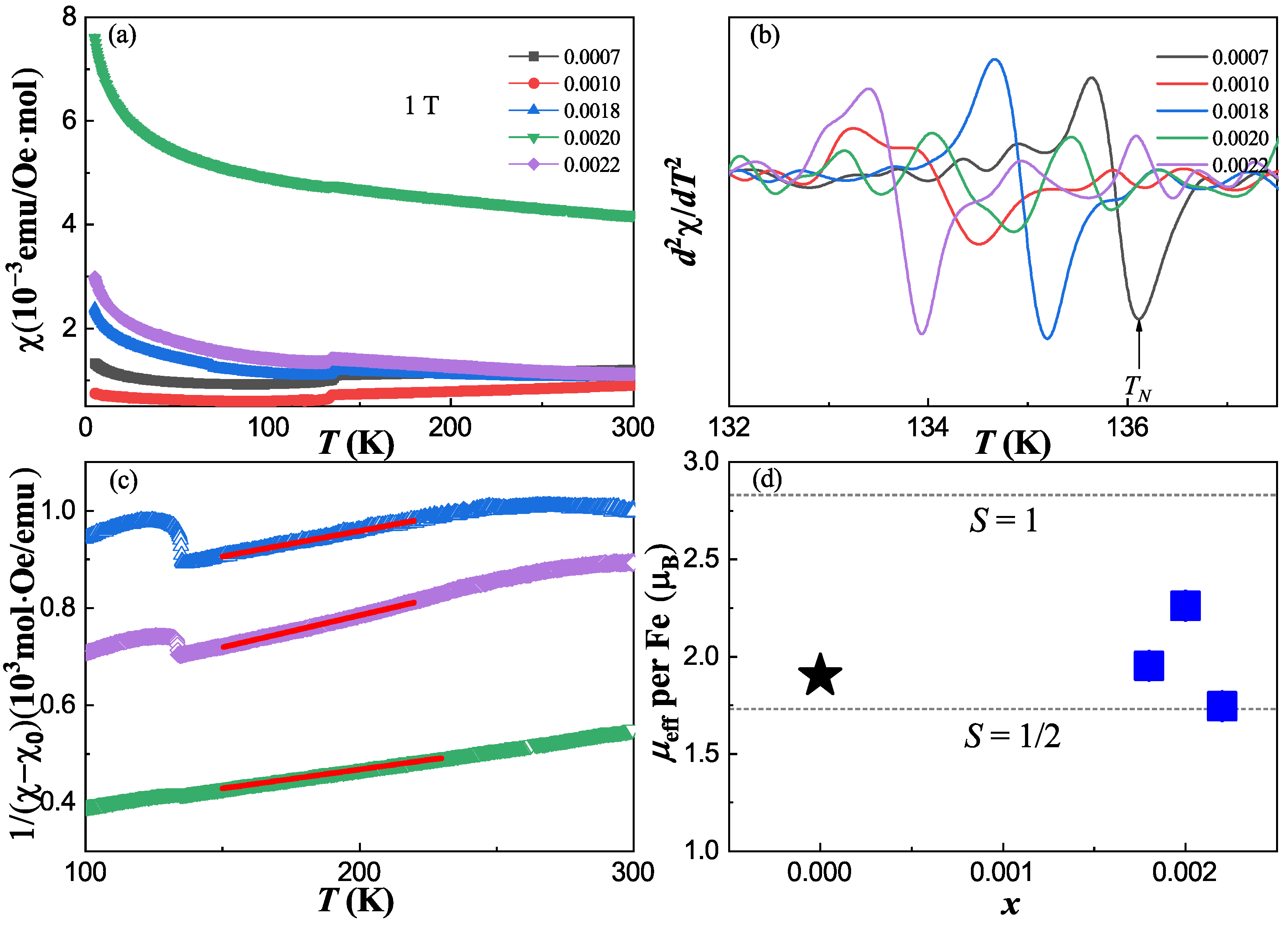
3.1. Actual Doping Concentration and Lattice Parameter c

We have successfully grown five batches of BaFe2(As1−xBix)2 single crystals for the first time. The typical photograph of the single crystals in Figure 1a shows a quite shiny and flat surface, and the surface morphology in Figure 1b taken by SEM clearly displays its layered structure; both reflect the high quality of our single crystals. In order to determine the actual Bi doping concentration, we conducted the EDX measurement. The single crystals were first cleaved in order to present a shiny surface. Then, three different regions were chosen to detect the concentration for each sample. Since the Bi-doping level was quite low, it was not homogeneous, which is also compatible with our later-proposed scenario in which there may exist three different realms in our sample (R I, R II and R III). Therefore, we took the averaged concentration as the actual concentration. The nominal and actual Bi concentration x are listed in Table 1, and the actual doping concentration x will be used to label the single crystals hereafter. We can find that the actual concentration of Bi is quite a bit lower than the nominal value and, with the increase in the nominal doping level, the actual concentration first increases slightly, but further decreases when nominal x is above 0.2. The highest actual doping level could only reach up to 0.22%. This indicates that it is quite difficult to dope the Bi into the As site, which may be a result of the solid solubility limit or an unstable phase.
Figure 1c shows the XRD patterns of BaFe2(As1−xBix)2 single crystals. Only sharp (00l) peaks can be reflected on the patterns, suggesting that the cleaved planes are perpendicular to the c-axis. The inset is the enlarged (004) peaks. The high intensity and the narrow full width at half maximum (FWHM) labeled in the inset (2θ~0.12°) again indicate the high quality of our single crystals. Meanwhile, the (004) peak shifts to the lower diffraction angle with the increase in Bi concentration x, indicating that the Bi element is indeed introduced into BaFe2As2. The lattice parameter c for each doping sample was calculated using the XRD patterns and was plotted as a function of concentration 100x in Figure 1d. When x is below 0.002, the lattice parameter c increases almost linearly with the doping evolution, which is consistent with Vegard’s law [19], and it begin to deviate above 0.002 with a step increase in lattice parameter c for the x = 0.0022 sample. Compared with P dopant, Bi substitution for As expands the c-axis, presenting a negative pressure effect which also matches the expectation since the radius of the Bi ion is larger than that of the As ion.

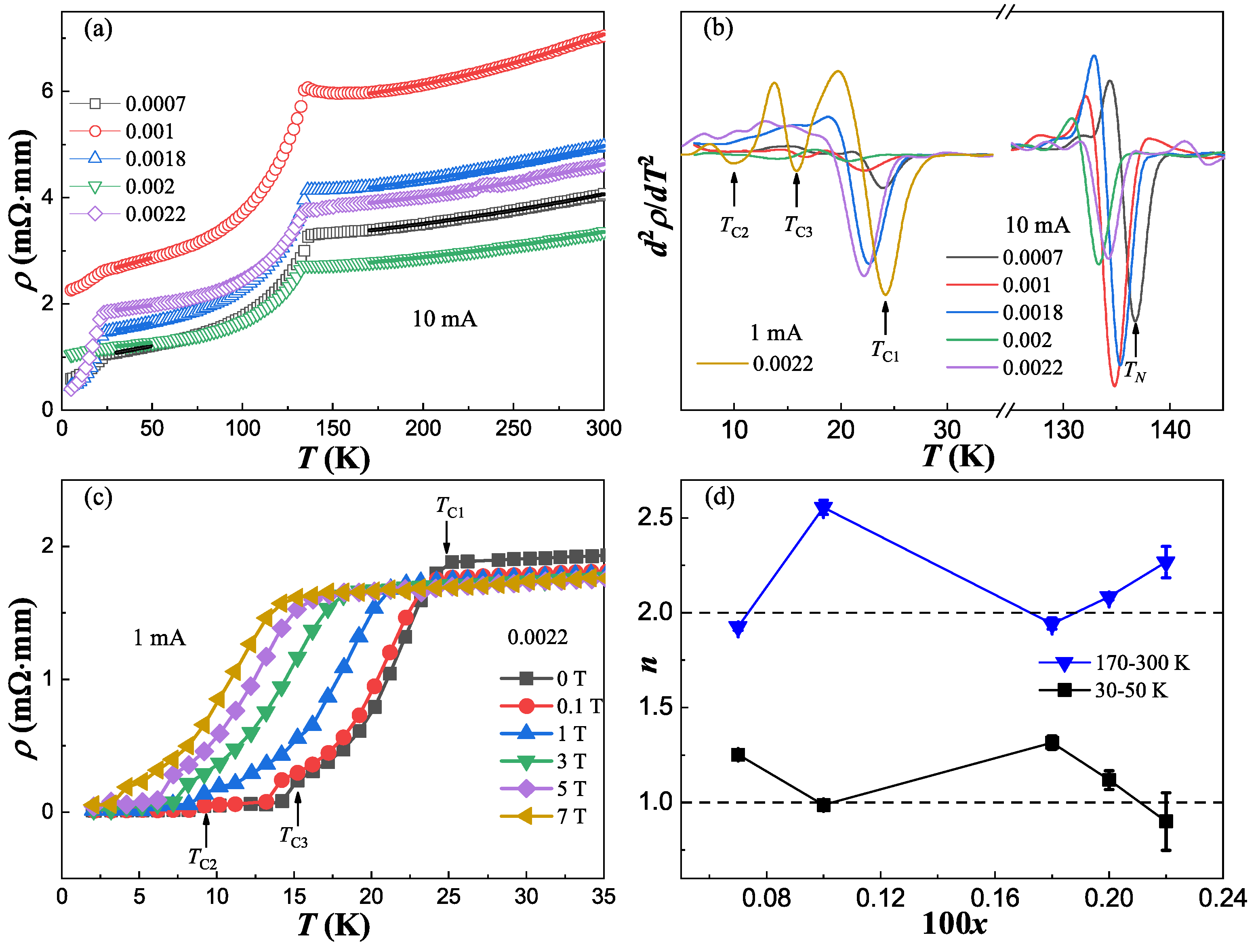
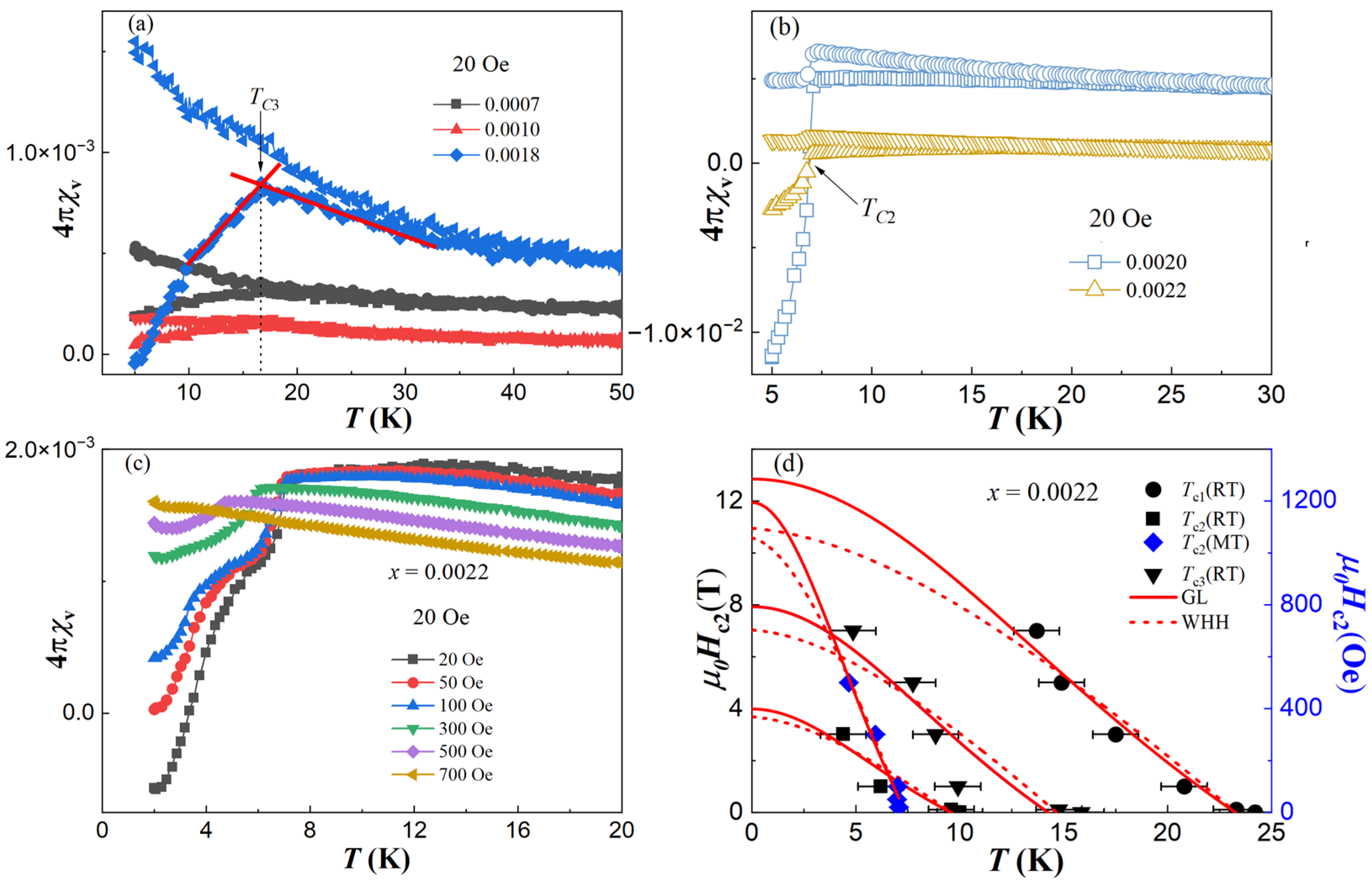
3.2. Superconducting Transitions and Non-Fermi Liquid Behavior

In order to investigate the superconducting properties, we first conducted resistivity measurements. Figure 2a displays the temperature dependence of resistivity down to 5 K measured with a 10 mA current for BaFe2(As1−xBix)2 single crystals. For all the samples, compared with the parent compound, a similar SDW transition around 135 K is found. But when temperature decreases to around 25 K, another transition happens with a drop of resistivity which may be associated with a superconducting transition. Actually, this kind of phenomenon is also observed in some BaFe2As2 [20,21], CaFe2As2 [22] and SrFe2As2 [23] parent compounds, as well as Ni-doped BaFe2As2 [24] and Pr-doped CaFe2As2 [25], which are proposed as filamentary superconducting transitions. For the x = 0.0022 sample, the percentage of resistivity dropping is highest: about 78%. Thus, we measured it again with lower 1 mA current and temperature down to 2 K, as shown in Figure 2c. Then, the zero resistivity was detected and, with the increase in the magnetic field, the transition temperature was suppressed gradually, confirming its superconducting properties. This significant dependence of resistivity on current is consistent with a more filamentary-natured superconductivity. To determine the antiferromagnetic (TN) and superconducting (TC) transitions, the temperature dependence of d2ρ/dT2 is plotted in Figure 2b and the minimum of d2ρ/dT2 is taken as the transition temperature marked by arrows. To our surprise, for the superconducting transition at low temperature, except for the one around 25 K (labeled as TC1), there seem to have been another two superconducting transitions around 15 K (labeled as TC3) and 10 K (labeled as TC2). These transitions are much clearer for the x = 0.0022 sample under 1 mA, which can also be identified easily by the naked eye, as marked by arrows in Figure 2c. Corresponding with the three temperatures, three superconducting phases are defined as SC I (TC1), SC II (TC2) and SC III (TC3).
The filamentary superconductivity (FL SC) has been argued to be attributed to the lattice distortion or strain [23], spin and orbital fluctuations [21], the antiphase domain walls [22] and the spontaneous electronic inhomogeneity at the nanoscale level [25]. Considering the average Bi concentration is quite low in our single crystals, we proposed our own scenario to interpret this behavior. We speculate that there might exist three kinds of realms in our sample: some realms (R I) are almost the same as the conditions found in the parent compound without any Bi dopants; some realms (R II) are highly Bi-doped; and the ratio of Bi doping in the rest of the realms (R III) is between the first two realms. The SC I with TC1, the SC II with TC2, and the SC III with TC3 originate from R I, R II and R III, respectively. The reasonable relationship between them will be discussed in detail later.
In iron pnictides, the normal state of resistivity has been extensively described by the power law formula ρ = ρ0 + ATn, where n is the temperature exponent, ρ0 is the residual resistivity, and A is a constant. Here, to avoid the antiferromagnetic (AFM) and superconducting transitions’ influence, the 30–50 K (above TC1 and below TN) and 170–300 K (above TN) ranges are chosen as two fitting regions. The solid lines shown in Figure 2a represent the perfect fitting results using the power law. The evolution of n with Bi doping is summarized in Figure 2d. There is no significant doping dependence of n for both regions. However, n is much closer to 2 above TN, thus corresponding to a Fermi-liquid (FL) ground state, while n is closer to 1 below TN before the emergence of superconductivity, thus corresponding to a non-Fermi-liquid (NFL) behavior. This anomalous NFL behavior has often been revealed just above the superconducting dome, which may be closely tied to superconductivity [26,27]. Moreover, a simultaneous disappearance of the superconductivity and the NFL transport is observed in CaFe2(As1−xPx)2 [28]. From our results, this explicit indication of a FL to NFL crossover from normal state to AFM order state confirms the idea that NFL behavior may play a crucial role in the presence of superconductivity.

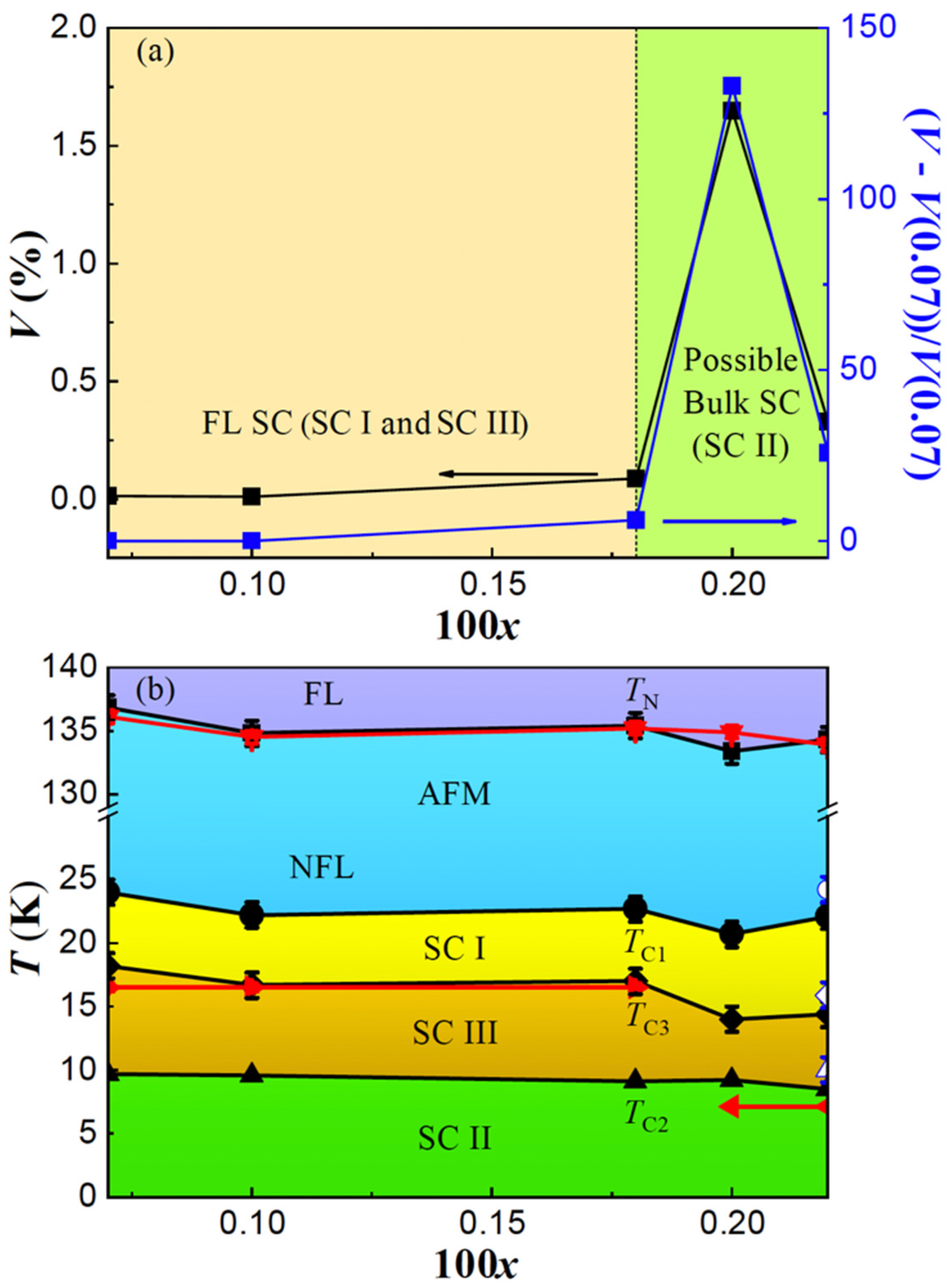
3.3. Superconducting Volume and Effective Moment

To further investigate the superconducting diamagnetism, the temperature dependence of magnetic susceptibility was measured using an H = 20 Oe magnetic field by the zero-field-cooling (ZFC) and field-cooling (FC) modes, as shown in Figure 3a–c. In contrast with the three superconducting transitions observed in resistivity, the one at TC1 could no longer be detected, while the one at TC3 was only detected in the low Bi-doping single crystals with x = 0.0007, 0.0010 and 0.0018 at 17 K, as shown in Figure 3a; the one at TC2 was only detected in the high Bi-doping single crystals with x = 0.0020 and 0.0022 at 7 K, as shown in Figure 3b. The absence of SC I in the magnetic susceptibility confirms its filamentary-natured superconductivity. Although the SC III is present, the superconducting transition is broad and the shielding signal magnitude is very weak, so that only the x = 0.0018 sample shows a diamagnetic property below 6 K, indicating a very small superconducting volume fraction. The absolute superconducting volume (SC V) is calculated by 4πχv(TC) − 4πχv(5 K), as shown in Figure 5a (left axis). The SC V for x = 0.0007, 0.0010 and 0.0018 is about 0.01%, 0.01% and 0.09%, respectively. This indicates that the SC III is not a bulk superconductor, but it does reflect that the superconductivity is less filamentary compared with SC I, and the SC V increases with the increase in Bi doping. Especially with the further increase in Bi concentration, a very sharp superconducting transition and a dramatically enhanced shielding signal are observed for SC II, as shown in Figure 3b. The SC V for x = 0.0020 and 0.0022 has increased significantly: up to about 1.65% and 0.34%. With the increase in Bi doping, the SC V changes by order of magnitude, crossing from 0 for SC I to 10−2 order for SC III and then to 10−1 or 1 order for SC II. Since the chemical substitution can create local, hence average, structural changes which would then greatly impact the electronic structure, the lattice effect of Bi doping could not be ignored. This suggests that these three superconducting phases and doping levels are mutually related. Therefore, the scenario we proposed previously regarding the relationship between the three superconducting phases (SC I, SC II and SC III) and the three realms (R I, R II and R III) has been shown to be reasonable and easily understood. This can also be reflected by the disappearance of the SC I and SC II for x = 0.0007, 0.0010 and 0.0018, as shown in Figure 3a. Although both of them are invisible, the reasons are different. For SC I, it is the result of its filamentary nature’s superconductivity property, which is related to the realm with almost no Bi doping, but for SC II, it is highly related to the Bi-doping level and its disappearance is attributed to the lack of Bi concentration. Moreover, compared with the SC V for x = 0.0007, the relative variation ratio (V − V(x = 0.0007))/V(x = 0.0007) is also plotted as a function of 100x, as shown in Figure 5a (right axis). Even though all of our single crystals show a non-bulk superconductivity with SC V, less than 2%, the relative variation ratio has a dramatic increase, up to 600%, 13,300% and 2565% for x = 0.0018, 0.0020 and 0.0022, respectively, clearly heralding the emergence of a possible bulk superconductivity (Bulk SC) for SC II. The reason why the bulk superconductivity was not shown in our sample is that the actual Bi concentration is still too low. We wonder if a true bulk superconductor could have emerged if the Bi concentration had been further increased. This idea is also supported by the theoretical calculation that the parent BaFe2Bi2 might hold TC~30 K superconductivity [18].
To study the upper critical field µ0HC2, the magnetic susceptibility for x = 0.0022 was measured again, down to 2 K, under various magnetic fields, up to 700 Oe, as shown in Figure 3c. As the field increases, the superconducting transition is gradually suppressed to a lower temperature, confirming its superconductivity properties. Combined with the resistivity and magnetic susceptibility, by taking the data from Figure 2c and Figure 3c, the TC value at each field is plotted as µ0HC2 versus T, as shown in Figure 3d. The dashed curves are fits to the Werthamer–Helfand–Hohenberg (WHH) relation [29], HC2(0) = −0.693TC(dHC2/dT)T=Tc, and the solid curves are fits to Ginzburg–Landau (GL) model: HC2(T) = HC2(0) [(1 − t2)/(1 + t2)], where t represents the normalized temperature T/TC. The obtained fitting parameters of TC and µ0HC2 are summarized in Table 2. The values of TC are consistent with each other while the values of µ0HC2(0) obtained from WHH are lower than GL, which is similar to those reported in other iron pnictide superconductors [30,31]. These values are much smaller than the nominal Pauli paramagnetic limit, which is roughly estimated by µ0HP = 1.84TC [32], indicating the orbital limit effect. The GL coherence length ξGL, shown in Table 2, is also calculated using the relation µ0HC2(0) = Φ0/(2π ξ G L 2 ), where Φ0 = 2.07 × 10−15 T·m2 is the flux quantum.
Magnetic susceptibility is also measured by applying the H = 1 T magnetic field, as shown in Figure 4a. The SDW transitions are observed for all the single crystals and the minimum of d2χ/dT2 plotted in Figure 4b is taken as the AFM transition temperature, which is consistent with the resistivity measurement. Above TN, the magnetic susceptibility shows a T-linear behavior for x = 0.0007 and 0.0010, which is universal in iron pnictides and is explained by the existence of a wide antiferromagnetic fluctuation [33]. When x > 0.0018, the deviation from T-linear behavior becomes obvious and gradually changes to a Curie–Weiss-like behavior. As shown in Figure 4c, the magnetic susceptibilities can be well fitted between 150 K and 220 K by the Curie–Weiss law 1/(χ − χ0) = (T − θCW)/C, where χ0 is the temperature-independent magnetic susceptibility, θCW is the Curie temperature and C is the Curie–Weiss constant. The extracted effective moment μeff per Fe is plotted in Figure 4d. The values are about 1.95μB, 2.26μB and 1.74μB for x = 0.0018, 0.0020 and 0.0022, corresponding to an effective spin close to S = ½, and comparable with a value of about 1.9μB for the parent compound BaFe2As2, as studied by inelastic neutron scattering [34]. It seems that the effective moment is almost independent from the Bi substitution. In contrast, the effective moment gradually decreases with increasing x for the other two isovalent substitution systems in BaFe2(As1−xPx)2 [35,36] and Ba(Fe1−xRux)2As2 [37,38]. Especially for the Ba(Fe1−xRux)2As2 system, Ru substitution also presents a negative pressure effect, but with a decrease in the c-axis. The dilution of the magnetic moment at the Fe site is contributed to a decrease in zAs, which is correlated with a decrease in the c-axis [38]. Therefore, the doping independence of effective moment in our BaFe2(As1−xBix)2 sample may be linked to the increase in the c-axis.

3.4. Superconducting Phase Diagram

Based on the resistivity and magnetic susceptibility data, we constructed a complete temperature-doping phase diagram of BaFe2(As1−xBix)2 which is presented in Figure 5b. One AFM phase and three superconducting phases labeled as SC I, SC II and SC III are well defined and coexistent. The TC is about 25 K, 15 K and 7 K for SC I, SC III and SC II, respectively. Attributed to the relatively low Bi concentration, the coexistence of the AFM state and superconductivity might only occur in the microscopic region. In addition, both the AFM and superconducting transition temperatures seem to be independent from the slight Bi variation. From the normal state to the AFM order state, a FL to NFL crossover is revealed and the NFL behavior appears right at the boundary of superconducting phases, which may be a significant factor driving the presence of superconductivity. The red data points in the superconducting region demonstrate that only the SC II and SC III could be detected by the diamagnetic signal. Combined with the dramatic enhancement of SC V in Figure 5a, we strongly suggest that these superconducting phases are closely correlated with the Bi concentration; the SC I and SC III should be filamentary superconductors, while the SC II should be a bulk superconductor.

4. Conclusions

In conclusion, a series of high-quality BaFe2(As1−xBix)2 single crystals were successfully grown for the first time. The highest doping level could only reach up to 0.22%, and the Bi doping enlarged lattice parameter c, showing a negative pressure effect. By investigating resistivity and magnetic susceptibility, a FL to NFL crossover from normal state to AFM state, and three superconducting phases labeled as SC I, SC II and SC III, were observed. We assume that the NFL behavior plays a crucial role in the presence of superconductivity. The evolution of SC V with Bi doping suggests that these superconducting phases should be highly related to the Bi doping concentration, and the SC II with TC~7 K is proposed as a possible bulk superconductor. Thus, the previous prediction regarding the superconductivity in parent BaFe2Bi2 is possible, and the reduction in lattice parameter c for ‘in-plane’ bulk superconductivity might be not sufficient. To further confirm our scenarios regarding the origin of the three superconducting phases, we recommend that scanning tunneling microscopy measurements be conducted for specific investigation in the future.

Author Contributions

Conceptualization and supervision, L.X.; investigation, J.S., J.Z., Y.L. (Ying Liu 1), C.J., J.L. and Y.L. (Ying Liu 2); formal analysis and writing—original draft preparation, L.X.; writing—review and editing, J.S., J.Z., Y.L. (Ying Liu 1), Y.L. (Ying Liu 2), C.J., J.L. and L.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (grant numbers 12004104 and 12204515) and the Young Elite Scientists Sponsorship Program by CAST (grant number 2022QNRC001).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are available upon request to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-based layered superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296. [Google Scholar] [CrossRef] [PubMed]
  2. Bednorz, J.G.; Muller, K.A. Possible high Tc superconductivity in the Ba−La−Cu−O system. Z. Fur Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
  3. Rotter, M.; Tegel, M.; Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1−xKx)Fe2As2. Phys. Rev. Lett. 2008, 101, 107006. [Google Scholar] [CrossRef]
  4. Sasmal, K.; Lv, B.; Lorenz, B.; Guloy, A.M.; Chen, F.; Xue, Y.Y.; Chu, C.W. Superconducting fe-based compounds (A1−xSrx)Fe2As2 with A = K and Cs with transition temperatures up to 37 K. Phys. Rev. Lett. 2008, 101, 107007. [Google Scholar] [CrossRef] [PubMed]
  5. Zhao, K.; Liu, Q.Q.; Wang, X.C.; Deng, Z.; Lv, Y.X.; Zhu, J.L.; Li, F.Y.; Jin, C.Q. Superconductivity above 33 K in (Ca1 −xNax)Fe2As2. J. Phys. Condens. Matter 2010, 22, 222203. [Google Scholar] [CrossRef] [PubMed]
  6. Jiang, S.; Xing, H.; Xuan, G.; Wang, C.; Ren, Z.; Feng, C.; Dai, J.; Xu, Z.A.; Cao, G. Superconductivity up to 30 K in the vicinity of the quantum critical point in BaFe2(As1−xPx)2. J. Phys. Condens. Matter 2009, 21, 382203. [Google Scholar] [CrossRef] [PubMed]
  7. Thaler, A.; Ni, N.; Kracher, A.; Yan, J.Q.; Bud’ko, S.L.; Canfield, P.C. Physical and magnetic properties of Ba(Fe1−xRux)2As2 single crystals. Phys. Rev. B 2010, 82, 014534. [Google Scholar] [CrossRef]
  8. Sefat, A.S.; Jin, R.Y.; McGuire, M.A.; Sales, B.C.; Singh, D.J.; Mandrus, D. Superconductivity at 22 K in Co-doped BaFe2As2 crystals. Phys. Rev. Lett. 2008, 101, 117004. [Google Scholar] [CrossRef]
  9. Li, L.J.; Luo, Y.K.; Wang, Q.B.; Chen, H.; Ren, Z.; Tao, Q.; Li, Y.K.; Lin, X.; He, M.; Zhu, Z.W.; et al. Superconductivity induced by Ni doping in BaFe2As2 single crystals. New. J. Phys. 2009, 11, 025008. [Google Scholar] [CrossRef]
  10. Thaler, A.; Hodovanets, H.; Torikachvili, M.S.; Ran, S.; Kracher, A.; Straszheim, W.; Yan, J.Q.; Mun, E.; Canfield, P.C. Physical and magnetic properties of Ba(Fe1−xMnx)2As2 single crystals. Phys. Rev. B 2011, 84, 144528. [Google Scholar] [CrossRef]
  11. Sefat, A.S.; Singh, D.J.; VanBebber, L.H.; Mozharivskyj, Y.; McGuire, M.A.; Jin, R.; Sales, B.C.; Keppens, V.; Mandrus, D. Absence of superconductivity in hole-doped BaFe2−xCrxAs2 single crystals. Phys. Rev. B 2009, 79, 224524. [Google Scholar] [CrossRef]
  12. Li, X.-G.; Sheng, J.-M.; Tian, C.-K.; Wang, Y.-Y.; Xia, T.-L.; Wang, L.; Ye, F.; Tian, W.; Wang, J.-C.; Liu, J.-J.; et al. Effects of vanadium doping on BaFe2As2. EPL 2018, 122, 67006. [Google Scholar] [CrossRef]
  13. Suzuki, H.; Yoshida, T.; Ideta, S.; Shibata, G.; Ishigami, K.; Kadono, T.; Fujimori, A.; Hashimoto, M.; Lu, D.H.; Shen, Z.X.; et al. Absence of superconductivity in the hole-doped Fe pnictide Ba(Fe1−xMnx)2As2: Photoemission and X-ray absorption spectroscopy studies. Phys. Rev. B 2013, 88, 100501. [Google Scholar] [CrossRef]
  14. Marty, K.; Christianson, A.D.; Wang, C.H.; Matsuda, M.; Cao, H.; VanBebber, L.H.; Zarestky, J.L.; Singh, D.J.; Sefat, A.S.; Lumsden, M.D. Competing magnetic ground states in nonsuperconducting Ba(Fe1−xCrx)2As2 as seen via neutron diffraction. Phys. Rev. B 2011, 83, 060509. [Google Scholar] [CrossRef]
  15. Sefat, A.S.; Nguyen, G.D.; Parker, D.S.; Fu, M.M.; Zou, Q.; Li, A.-P.; Cao, H.B.; Sanjeewa, L.D.; Li, L.; Gai, Z. Local superconductivity in vanadium iron arsenide. Phys. Rev. B 2019, 100, 104525. [Google Scholar] [CrossRef]
  16. Konzen, L.M.; Sefat, A.S. Lattice parameters guide superconductivity in iron-arsenides. J. Phys. Condens. Matter 2017, 29, 083001. [Google Scholar] [CrossRef]
  17. Sundareswari, M.; Jayalakshmi, D.S.; Viswanathan, E. A first principles study on newly proposed (Ca/Sr/Ba)Fe2Bi2 compounds with their parent compounds. Philos. Mag. 2016, 96, 511–523. [Google Scholar] [CrossRef]
  18. Jayalakshmi, D.S.; Sundareswari, M.; Viswanathan, E.; Hemanand, D.; Pranesh, V. Computational study on unconventional superconductivity and mechanical properties of novel antiferrromagnetic (Ca,Sr,Ba)Fe2Bi2 compounds. Int. J. Mod. Phys. B 2019, 33, 1950341. [Google Scholar] [CrossRef]
  19. Vegard, L. Die Konstitution der Mischkristalle und die Raumfüllung der Atome. Z. Phys. 1921, 5, 17–26. [Google Scholar] [CrossRef]
  20. Kim, J.S.; Blasius, T.D.; Kim, E.G.; Stewart, G.R. Superconductivity in undoped single crystals of BaFe2As2: Field and current dependence. J. Phys. Condens. Matter 2009, 21, 342201. [Google Scholar] [CrossRef]
  21. Xiao, H.; Hu, T.; He, S.K.; Shen, B.; Zhang, W.J.; Xu, B.; He, K.F.; Han, J.; Singh, Y.P.; Wen, H.H.; et al. Filamentary superconductivity across the phase diagram of Ba(Fe,Co)2As2. Phys. Rev. B 2012, 86, 064521. [Google Scholar] [CrossRef]
  22. Xiao, H.; Hu, T.; Dioguardi, A.P.; apRoberts-Warren, N.; Shockley, A.C.; Crocker, J.; Nisson, D.M.; Viskadourakis, Z.; Tee, X.; Radulov, I.; et al. Evidence for filamentary superconductivity nucleated at antiphase domain walls in antiferromagnetic CaFe2As2. Phys. Rev. B 2012, 85, 024530. [Google Scholar] [CrossRef]
  23. Saha, S.R.; Butch, N.P.; Kirshenbaum, K.; Paglione, J.; Zavalij, P.Y. Superconducting and ferromagnetic phases induced by lattice distortions in stoichiometric SrFe2As2 single crystals. Phys. Rev. Lett. 2009, 103, 037005. [Google Scholar] [CrossRef]
  24. Zhang, W.; Dai, Y.-M.; Xu, B.; Yang, R.; Liu, J.-Y.; Sui, Q.-T.; Luo, H.-Q.; Zhang, R.; Lu, X.-Y.; Yang, H.; et al. Magnetoresistivity and filamentary superconductivity in nickel-doped BaFe2As2. Chin. Phys. B 2016, 25, 047401. [Google Scholar] [CrossRef]
  25. Nguyen, G.D.; Fu, M.; Zou, Q.; Sanjeewa, L.D.; Li, A.P.; Sefat, A.S.; Gai, Z. Nanoscale Superconducting States in the Fe-Based Filamentary Superconductor of Pr-Doped CaFe2As2. Nanomaterials 2021, 11, 1019. [Google Scholar] [CrossRef]
  26. Hashimoto, K.K.; Cho, T.; Shibauchi, S.; Kasahara, Y.; Mizukami, R.; Katsumata, Y.; Tsuruhara, T.; Terashima, H.; Ikeda, M.A.; Tanatar, H.; et al. A Sharp Peak of the Zero-Temperature Penetration Depth at Optimal Composition in BaFe2(As1–xPx)2. Science 2012, 336, 1554. [Google Scholar] [CrossRef]
  27. Zhou, R.; Li, Z.; Yang, J.; Sun, D.L.; Lin, C.T.; Zheng, G.-Q. Quantum criticality in electron-doped BaFe2−xNixAs2. Nat. Commun. 2013, 4, 2265. [Google Scholar] [CrossRef]
  28. Kasahara, S.; Shibauchi, T.; Hashimoto, K.; Nakai, Y.; Ikeda, H.; Terashima, T.; Matsuda, Y. Abrupt recovery of Fermi-liquid transport following the collapse of the c axis in CaFe2(As1−xPx)2 single crystals. Phys. Rev. B 2011, 83, 060505. [Google Scholar] [CrossRef]
  29. Werthamer, N.R.; Helfand, E.; Hohenberg, P.C. Temperature and Purity Dependence of the Superconducting Critical Field,Hc2. III. Electron Spin and Spin-Orbit Effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
  30. Kumar, N.; Nagalakshmi, R.; Kulkarni, R.; Paulose, P.L.; Nigam, A.K.; Dhar, S.K.; Thamizhavel, A. Anisotropic magnetic and superconducting properties of CaFe2−xCoxAs2(x=0,0.06) single crystals. Phys. Rev. B 2009, 79, 012504. [Google Scholar] [CrossRef]
  31. Zhu, X.; Yang, H.; Fang, L.; Mu, G.; Wen, H.-H. Upper critical field, Hall effect and magnetoresistance in the iron-based layered superconductor LaFeAsO0.9F0.1−δ. Supercond. Sci. Technol. 2008, 21, 105001. [Google Scholar] [CrossRef]
  32. Clogston, A.M. Upper Limit for the Critical Field in Hard Superconductors. Phys. Rev. Lett. 1962, 9, 266–267. [Google Scholar] [CrossRef]
  33. Zhang, G.M.; Su, Y.H.; Lu, Z.Y.; Weng, Z.Y.; Lee, D.H.; Xiang, T. Universal linear-temperature dependence of static magnetic susceptibility in iron pnictides. EPL 2009, 86, 37006. [Google Scholar] [CrossRef]
  34. Harriger, L.W.; Liu, M.; Luo, H.; Ewings, R.A.; Frost, C.D.; Perring, T.G.; Dai, P. Temperature dependence of the paramagnetic spin excitations in BaFe2As2. Phys. Rev. B 2012, 86, 140403. [Google Scholar] [CrossRef]
  35. Allred, J.M.; Taddei, K.M.; Bugaris, D.E.; Avci, S.; Chung, D.Y.; Claus, H.; dela Cruz, C.; Kanatzidis, M.G.; Rosenkranz, S.; Osborn, R.; et al. Coincident structural and magnetic order in BaFe2(As1−xPx)2 revealed by high-resolution neutron diffraction. Phys. Rev. B 2014, 90, 104513. [Google Scholar] [CrossRef]
  36. Hu, D.; Lu, X.; Zhang, W.; Luo, H.; Li, S.; Wang, P.; Chen, G.; Han, F.; Banjara, S.R.; Sapkota, A.; et al. Structural and Magnetic Phase Transitions near Optimal Superconductivity in BaFe2(As1−xPx)2. Phys. Rev. Lett. 2015, 114, 157002. [Google Scholar] [CrossRef]
  37. Sharma, S.; Bharathi, A.; Chandra, S.; Reddy, V.R.; Paulraj, S.; Satya, A.T.; Sastry, V.S.; Gupta, A.; Sundar, C.S. Superconductivity in Ru-substituted polycrystalline BaFe2−xRuxAs2. Phys. Rev. B 2010, 81, 174512. [Google Scholar] [CrossRef]
  38. Sharma, S.; Bharathi, A.; Vinod, K.; Sundar, C.S.; Srihari, V.; Sen, S.; Ghosh, H.; Sinha, A.K.; Deb, S.K. Structural investigations in BaFe2−xRuxAs2 as a function of Ru and temperature. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2015, 71, 61–67. [Google Scholar] [CrossRef]
Materials 17 00929 g001
Figure 1. (a) The typical photograph, (b) the typical SEM surface morphology photograph, (c) the XRD patterns (inset is the enlarged (004) peaks and the FWHM is labeled) and (d) the concentration 100x dependence of lattice parameter c for BaFe2(As1−xBix)2 single crystals.
Figure 1. (a) The typical photograph, (b) the typical SEM surface morphology photograph, (c) the XRD patterns (inset is the enlarged (004) peaks and the FWHM is labeled) and (d) the concentration 100x dependence of lattice parameter c for BaFe2(As1−xBix)2 single crystals.
Materials 17 00929 g001
Materials 17 00929 g002
Figure 2. (a) The temperature dependence of resistivity measured with a 10 mA current for BaFe2(As1−xBix)2 single crystals. The solid lines are the fitting lines using the power law formula ρ = ρ0 + ATn between 30 K and 50 K, and between 170 K and 300 K. (b) The d2ρ/dT2 as a function of temperature according to the data from (a,c). (c) The temperature dependence of resistivity under different magnetic fields measured with a 1 mA current for the x = 0.0022 sample. (d) The concentration 100x dependence of fitting parameter n obtained from (a).
Figure 2. (a) The temperature dependence of resistivity measured with a 10 mA current for BaFe2(As1−xBix)2 single crystals. The solid lines are the fitting lines using the power law formula ρ = ρ0 + ATn between 30 K and 50 K, and between 170 K and 300 K. (b) The d2ρ/dT2 as a function of temperature according to the data from (a,c). (c) The temperature dependence of resistivity under different magnetic fields measured with a 1 mA current for the x = 0.0022 sample. (d) The concentration 100x dependence of fitting parameter n obtained from (a).
Materials 17 00929 g002
Materials 17 00929 g003
Figure 3. The temperature dependence of magnetic susceptibility for (a) BaFe2(As1−xBix)2 (x = 0.0007, 0.0010 and 0.0018) with H = 20 Oe magnetic field, (b) x = 0.0020 and 0.0022 with H = 20 Oe magnetic field, and (c) x = 0.0022 under different magnetic fields. (d) The temperature dependence of µ0Hc2 for x = 0.0022 sample. The black points corresponding to the left coordinate axis are obtained from resistivity data in Figure 2c, and the blue points corresponding to the right coordinate axis are from the magnetization data in (c). The red solid lines are the fitting lines according to GL function, and the red dash lines are according to WHH function.
Figure 3. The temperature dependence of magnetic susceptibility for (a) BaFe2(As1−xBix)2 (x = 0.0007, 0.0010 and 0.0018) with H = 20 Oe magnetic field, (b) x = 0.0020 and 0.0022 with H = 20 Oe magnetic field, and (c) x = 0.0022 under different magnetic fields. (d) The temperature dependence of µ0Hc2 for x = 0.0022 sample. The black points corresponding to the left coordinate axis are obtained from resistivity data in Figure 2c, and the blue points corresponding to the right coordinate axis are from the magnetization data in (c). The red solid lines are the fitting lines according to GL function, and the red dash lines are according to WHH function.
Materials 17 00929 g003
Materials 17 00929 g004
Figure 4. (a) The temperature dependence of magnetic susceptibility for BaFe2(As1−xBix)2 single crystals with H = 1 T magnetic field. (b) The d2χ/dT2 as a function of temperature according to the data from (a). (c) The temperature dependence of 1/(χ − χ0) for x = 0.0018, 0.0020 and 0.0022 samples. The red solid lines are fits to the Curie–Weiss law. (d) The effective moment per Fe site as a function of the doping concentration x. The blue square points are our results, and the black star point is from reference [34].
Figure 4. (a) The temperature dependence of magnetic susceptibility for BaFe2(As1−xBix)2 single crystals with H = 1 T magnetic field. (b) The d2χ/dT2 as a function of temperature according to the data from (a). (c) The temperature dependence of 1/(χ − χ0) for x = 0.0018, 0.0020 and 0.0022 samples. The red solid lines are fits to the Curie–Weiss law. (d) The effective moment per Fe site as a function of the doping concentration x. The blue square points are our results, and the black star point is from reference [34].
Materials 17 00929 g004
Materials 17 00929 g005
Figure 5. (a) The concentration 100x dependence of superconducting volume (left axis) and the relative variation ratio (V − V(x = 0.0007))/V(x = 0.0007) (right axis). (b) The phase diagram of BaFe2(As1−xBix)2 as a function of concentration 100x. The solid black (empty blue) points are derived from resistivity measured with 10 mA (1 mA) current. The solid red points are derived from magnetic susceptibility.
Figure 5. (a) The concentration 100x dependence of superconducting volume (left axis) and the relative variation ratio (V − V(x = 0.0007))/V(x = 0.0007) (right axis). (b) The phase diagram of BaFe2(As1−xBix)2 as a function of concentration 100x. The solid black (empty blue) points are derived from resistivity measured with 10 mA (1 mA) current. The solid red points are derived from magnetic susceptibility.
Materials 17 00929 g005
Table 1. The nominal and actual doping concentration of BaFe2(As1−xBix)2 single crystals.
Table 1. The nominal and actual doping concentration of BaFe2(As1−xBix)2 single crystals.
Nominal xActual x
0.010.0007
0.050.0020
0.100.0018
0.200.0022
0.350.0010
Table 2. The superconducting transition temperature TC, upper critical field µ0HC2 and GL coherence length ξGL parameters obtained from WHH and GL fits for the three superconducting phases derived from resistivity and magnetic susceptibility measurements for the x = 0.0022 sample.
Table 2. The superconducting transition temperature TC, upper critical field µ0HC2 and GL coherence length ξGL parameters obtained from WHH and GL fits for the three superconducting phases derived from resistivity and magnetic susceptibility measurements for the x = 0.0022 sample.
x = 0.0022WHH FitGL Fit
TC
(K)		µ0HC2
(T)		TC
(K)		µ0HC2
(T)		ξGL
(Å)
SC I (RT)23.310.9123.212.9051
SC II (RT)9.63.679.63.9891
SC II (MT)7.30.117.40.12524
SC III (RT)14.77.0114.37.9365
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Si, J.; Zhao, J.; Liu, Y.; Liu, Y.; Jin, C.; Liu, J.; Xing, L. The Superconductivity in Bi-Doped BaFe2As2 Single Crystals. Materials 2024, 17, 929. https://doi.org/10.3390/ma17040929

AMA Style

Si J, Zhao J, Liu Y, Liu Y, Jin C, Liu J, Xing L. The Superconductivity in Bi-Doped BaFe2As2 Single Crystals. Materials. 2024; 17(4):929. https://doi.org/10.3390/ma17040929

Chicago/Turabian Style

Si, Jiabin, Jianfa Zhao, Ying Liu, Ying Liu, Changqing Jin, Jibing Liu, and Lingyi Xing. 2024. "The Superconductivity in Bi-Doped BaFe2As2 Single Crystals" Materials 17, no. 4: 929. https://doi.org/10.3390/ma17040929

APA Style

Si, J., Zhao, J., Liu, Y., Liu, Y., Jin, C., Liu, J., & Xing, L. (2024). The Superconductivity in Bi-Doped BaFe2As2 Single Crystals. Materials, 17(4), 929. https://doi.org/10.3390/ma17040929

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop