Comparison of Dynamic Amplification Factor of Deflection and Bending Moment of Highway Continuous Box-Girder Bridges by Mode Superposition
Abstract
1. Introduction
2. Theoretical Analysis
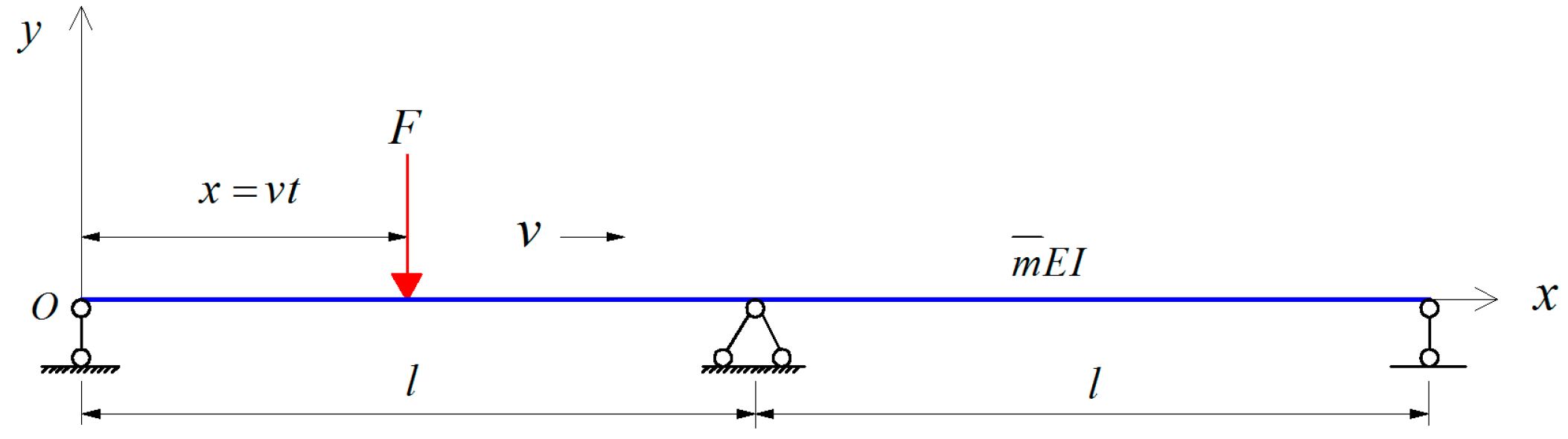
3. Vehicle-Bridge Interaction Models
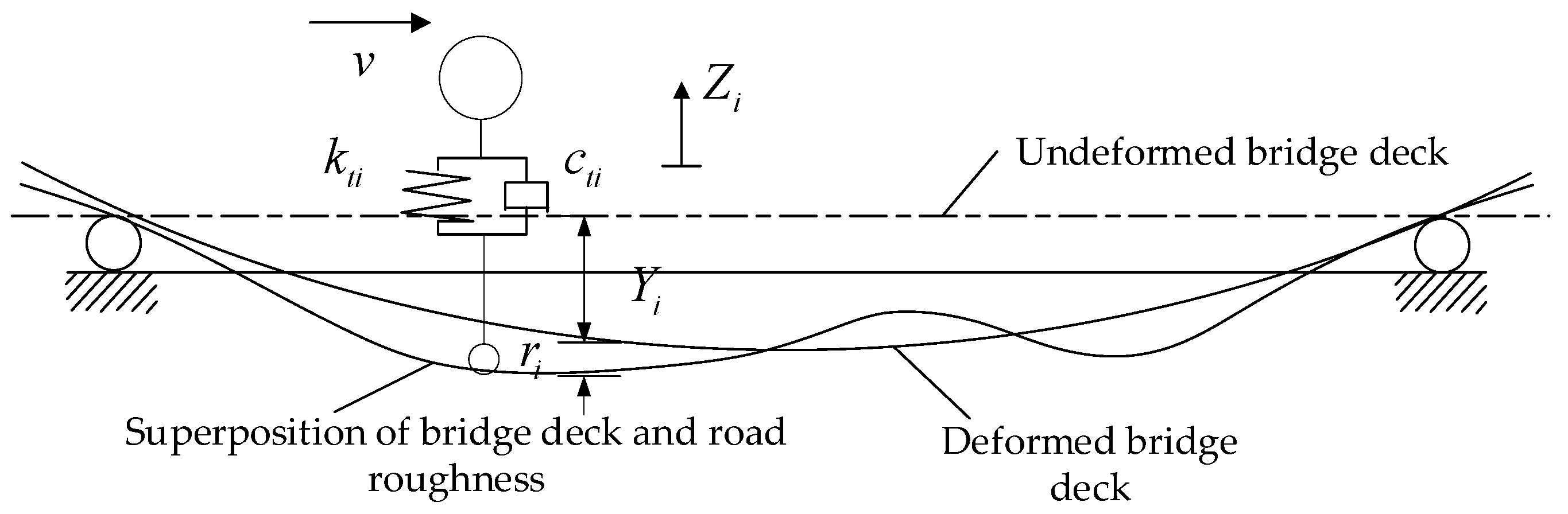
3.1. Vehicle and Bridge Vibration Equations
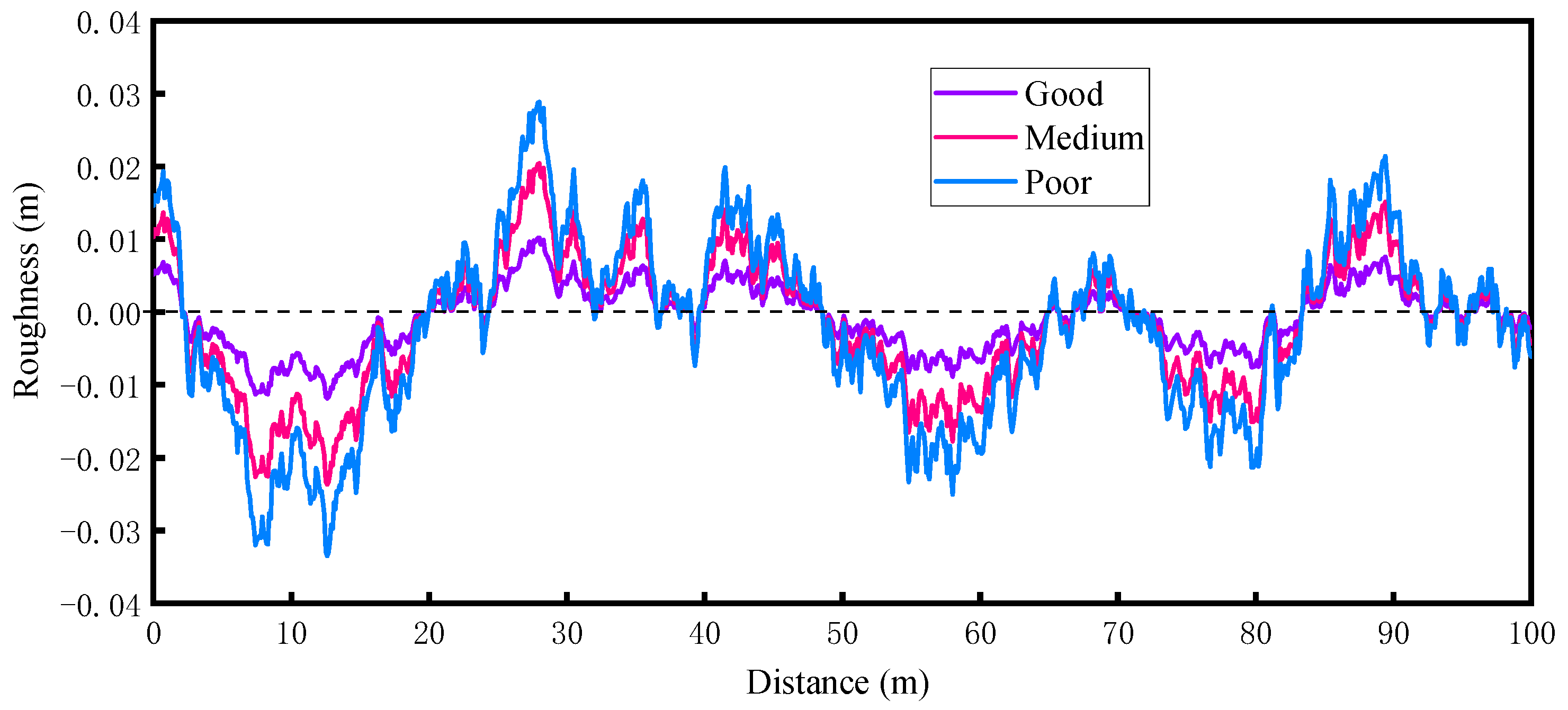
3.2. Road Surface Condition
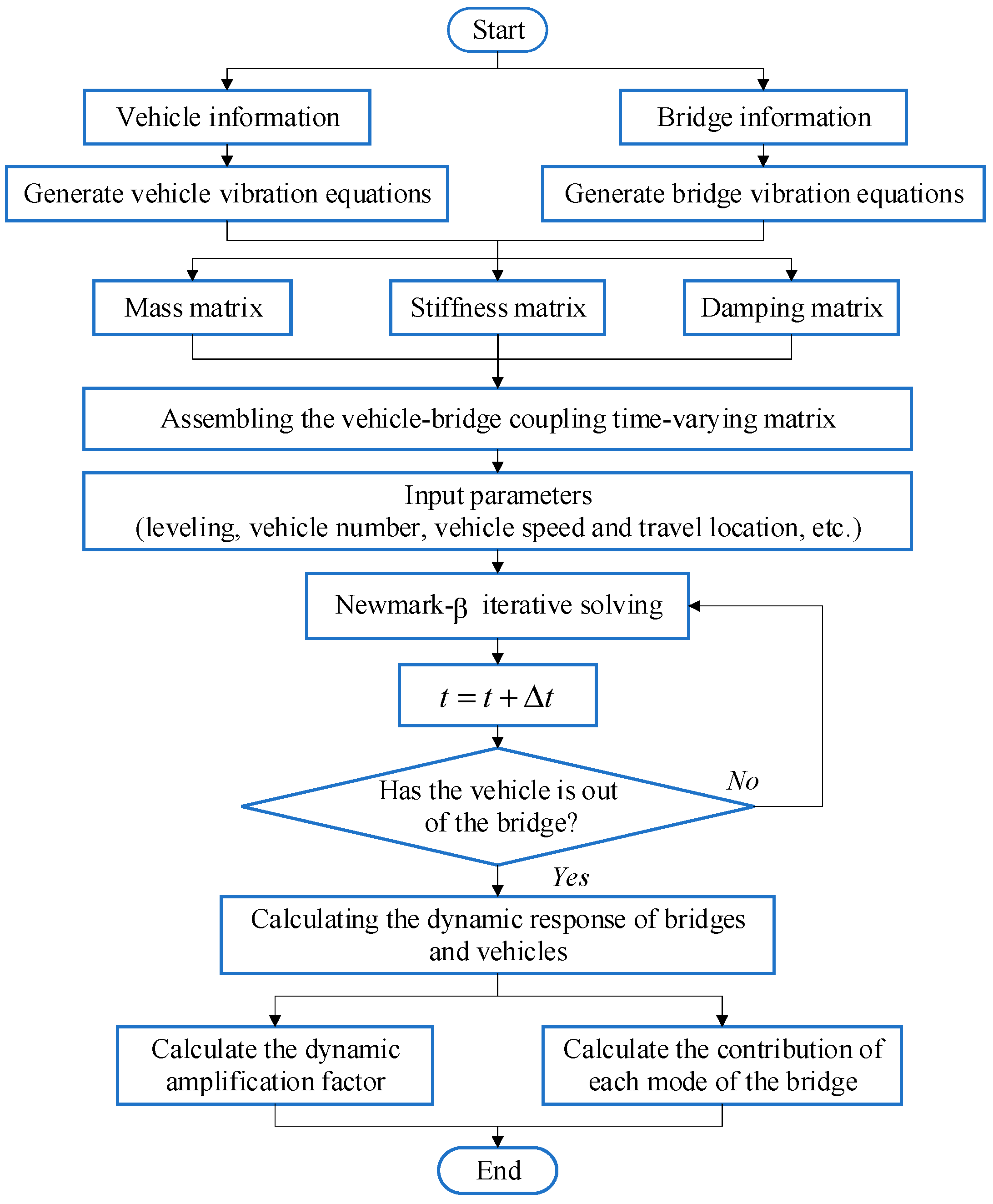
3.3. Vehicle-Bridge Interaction and Numerical Solution
4. Dynamic Analysis and Results
4.1. Prototype Bridges and Vehicle
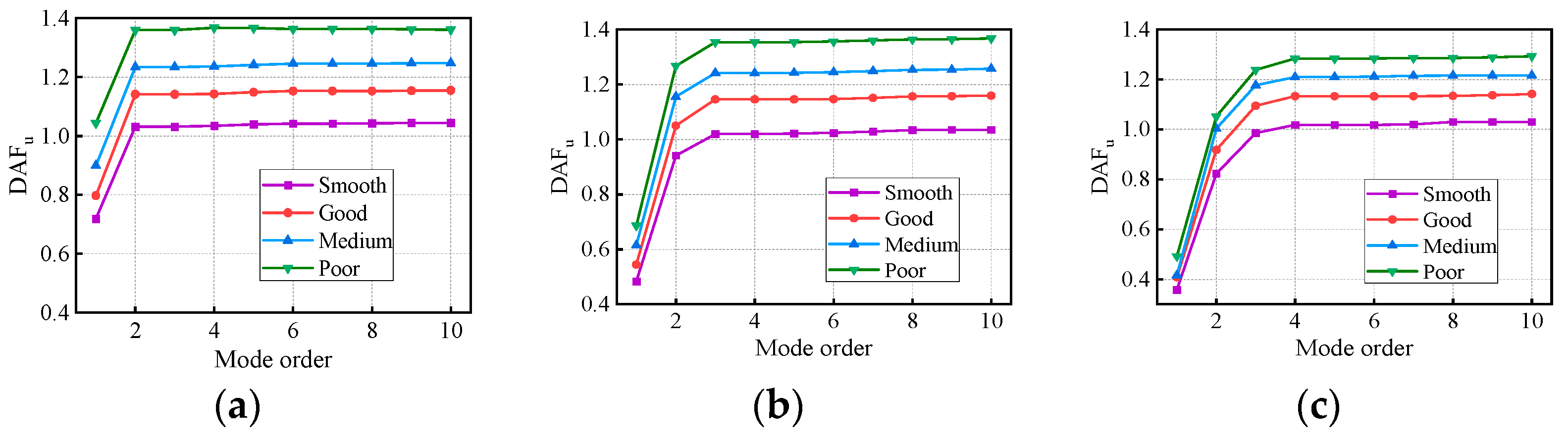
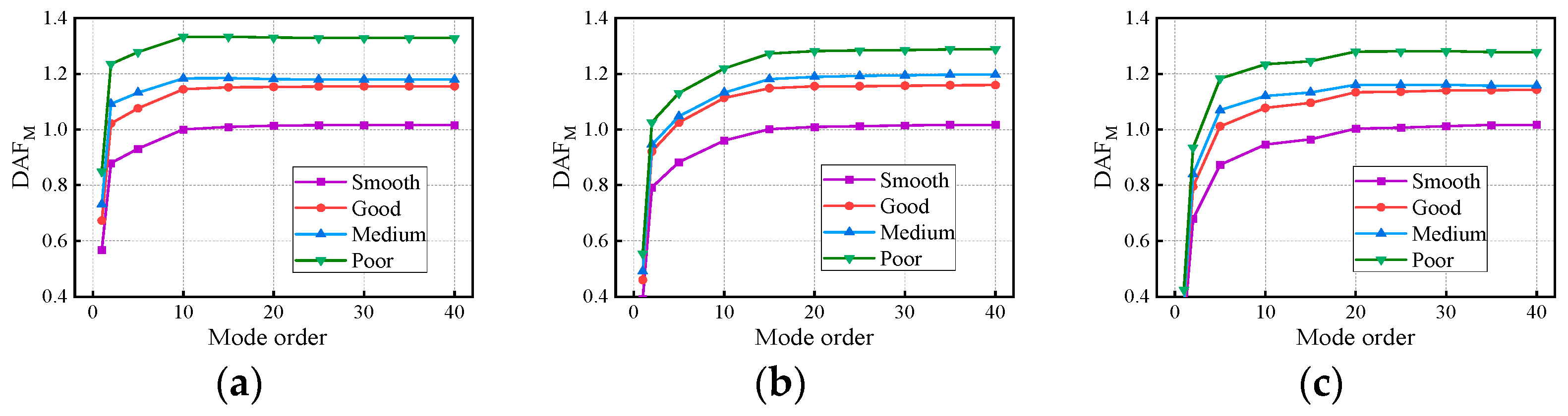
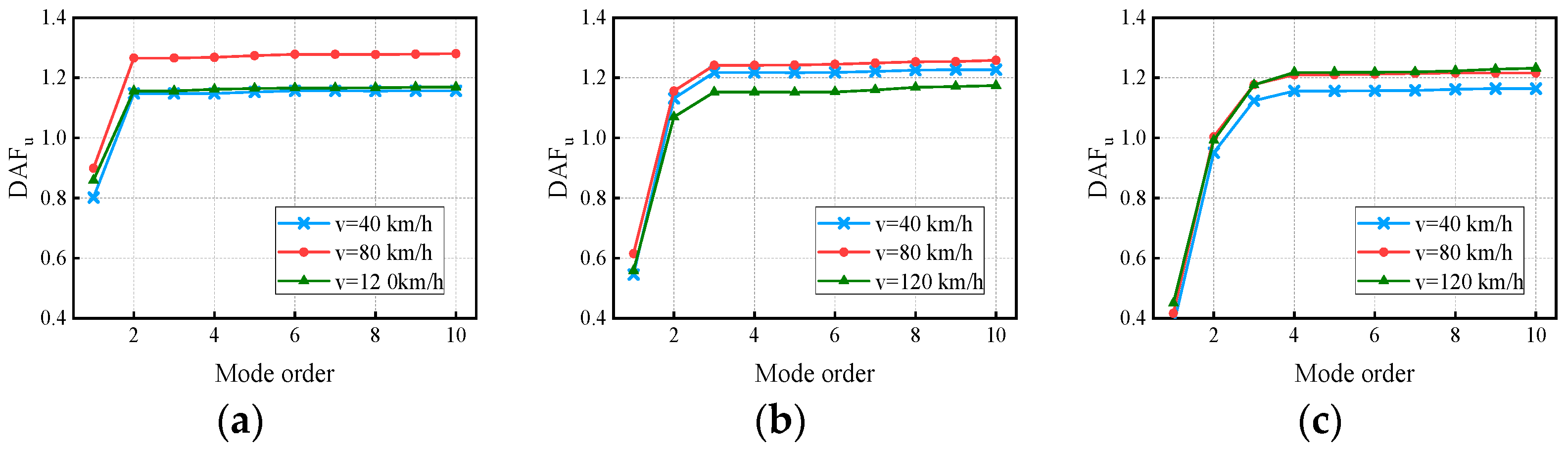
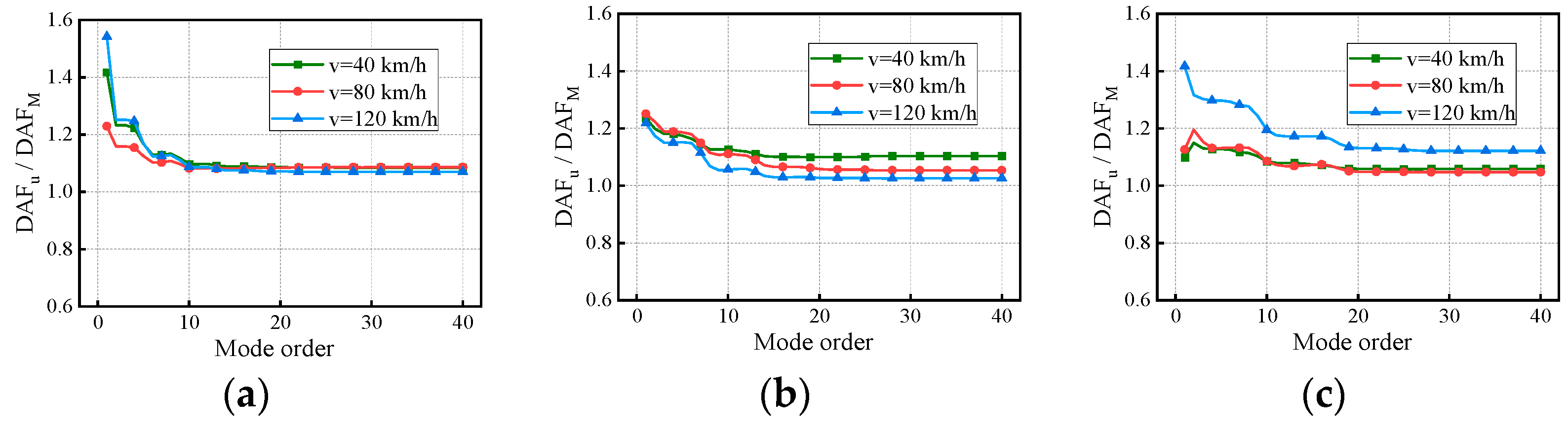
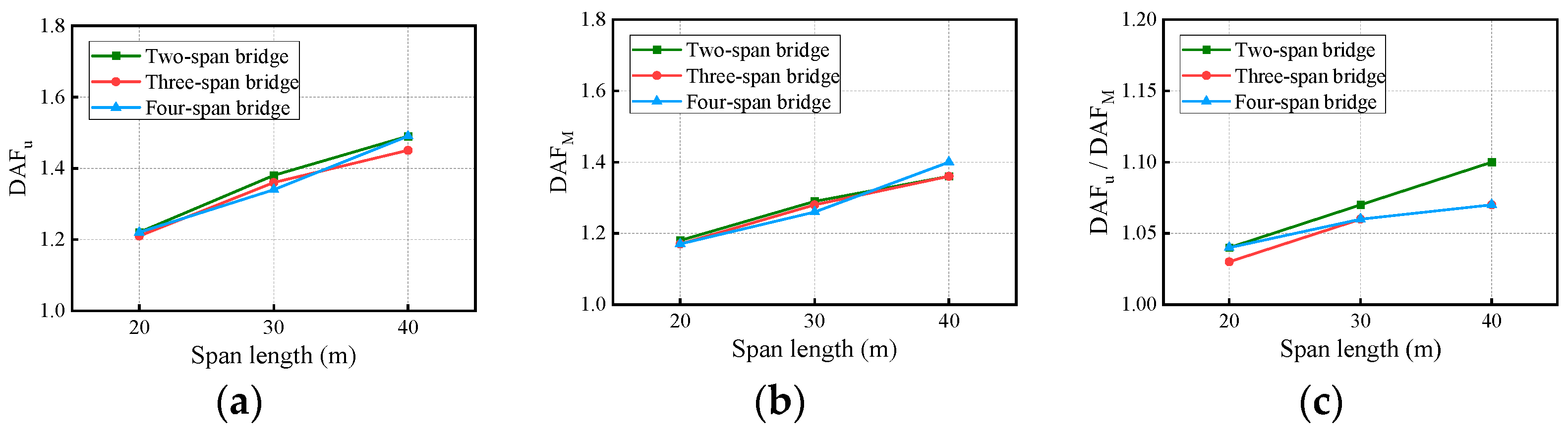
4.2. Comparison of Dynamic Amplification Factors
- (1)
- Road surface condition
- (2)
- Vehicle Speed
- (3)
- Span Length
- (4)
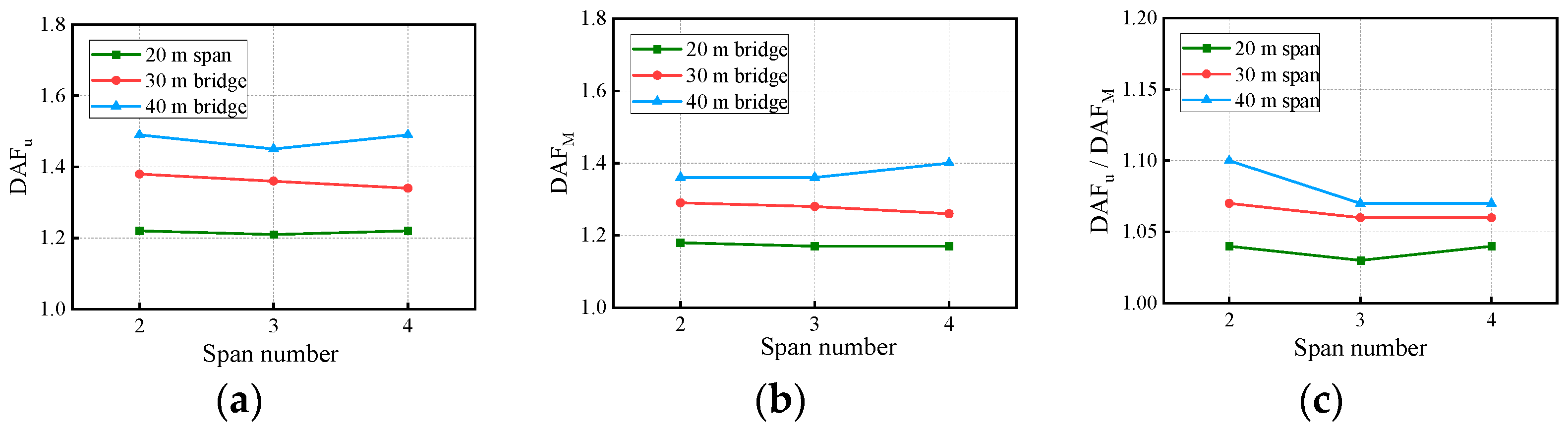
- Span Number
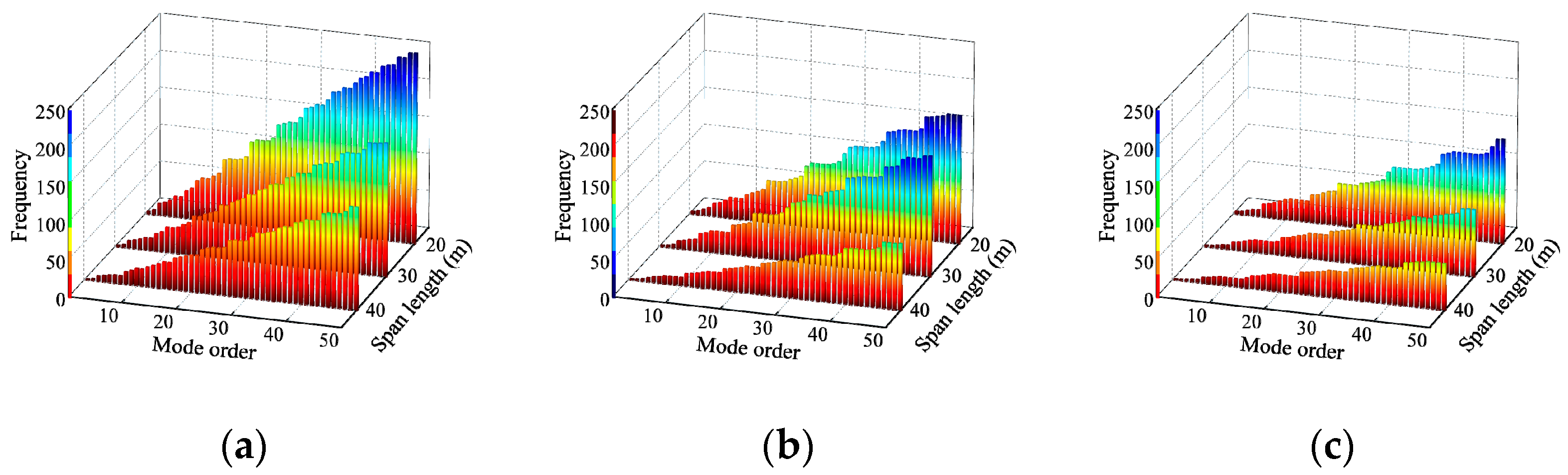
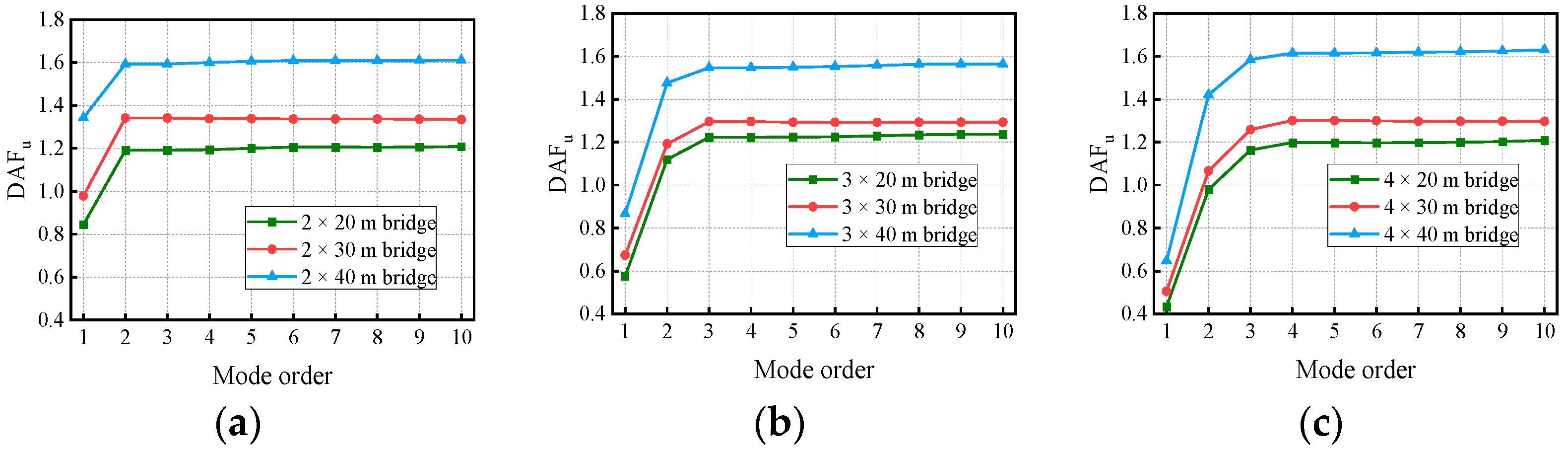
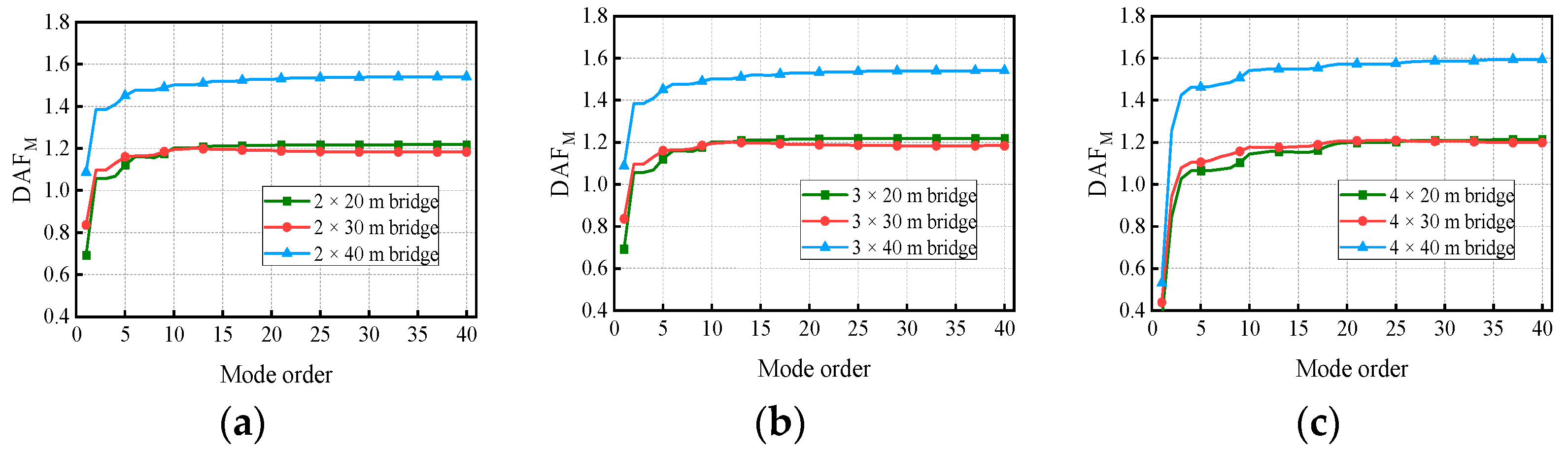
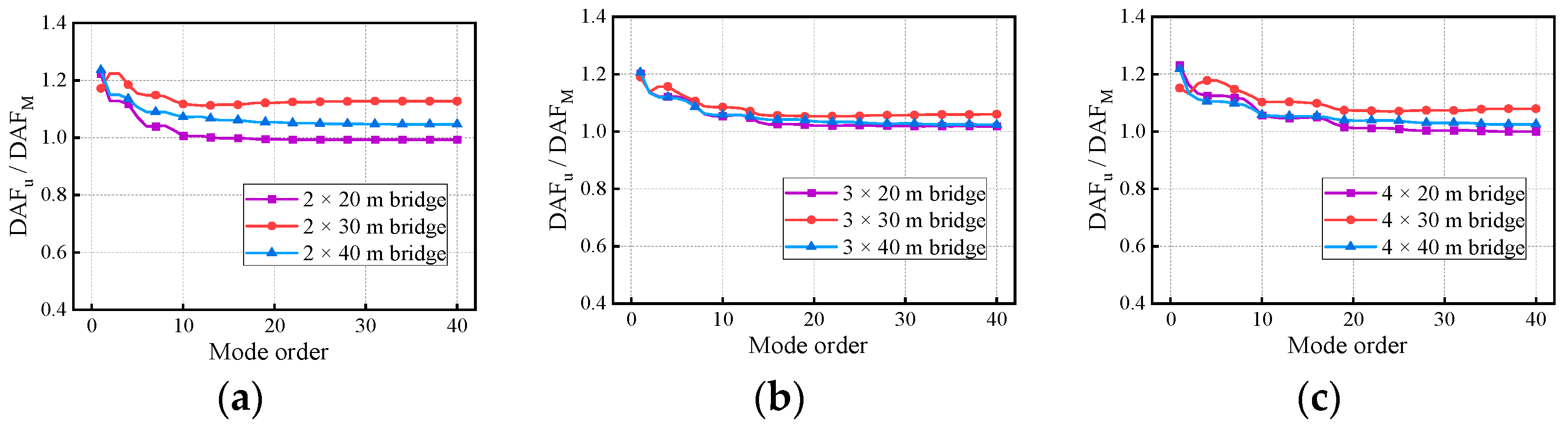
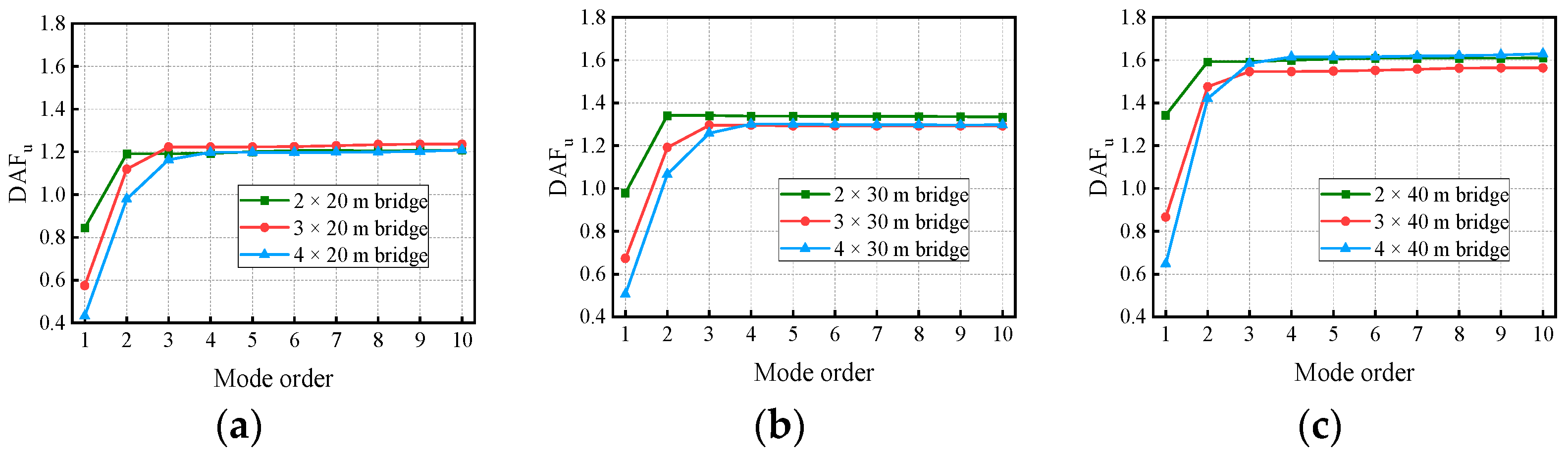
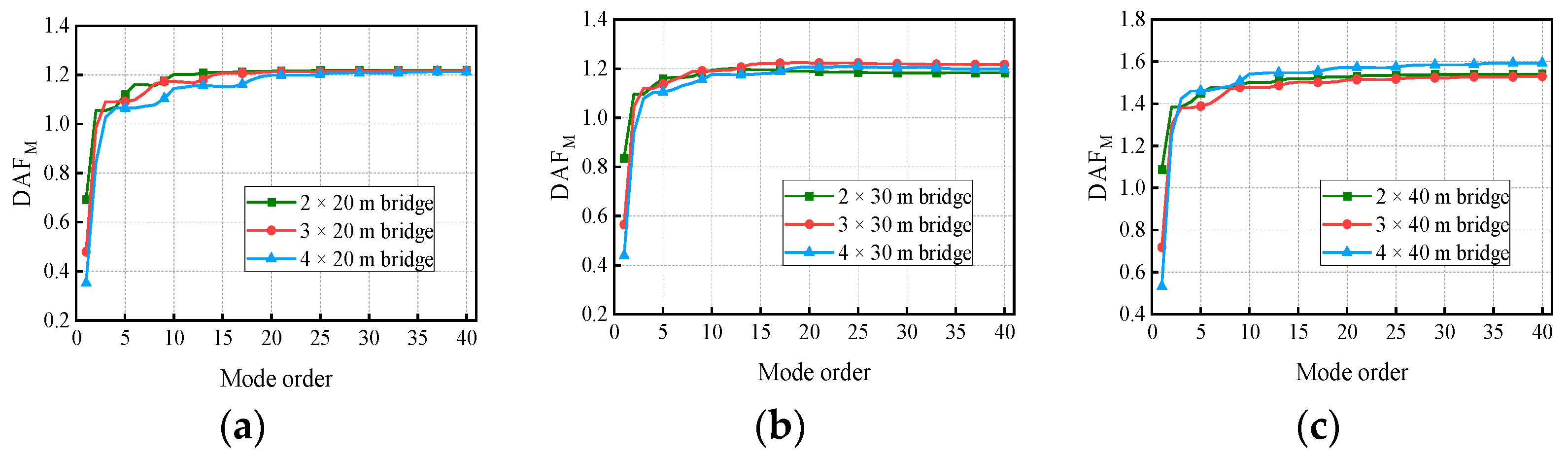
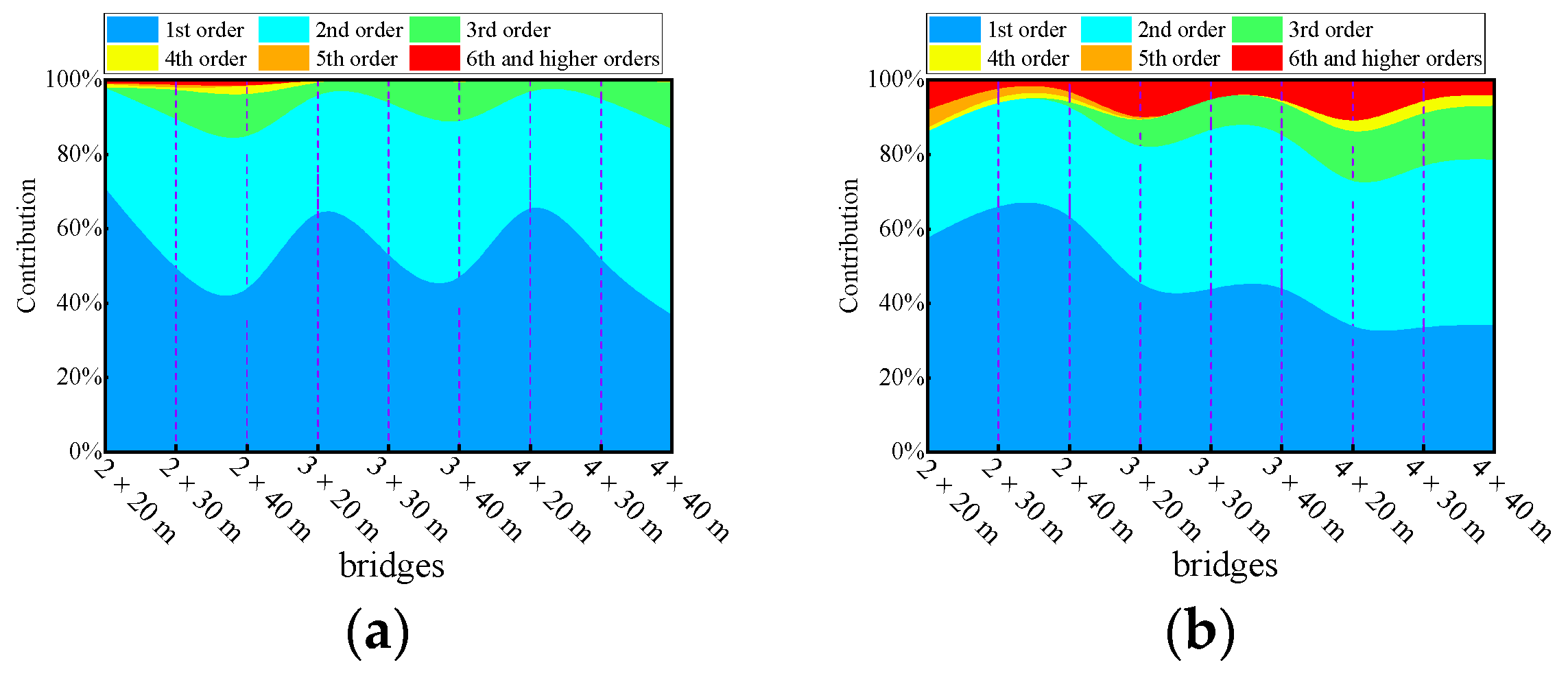
5. Cut-Off Modes for the Deflection and Bending Moment
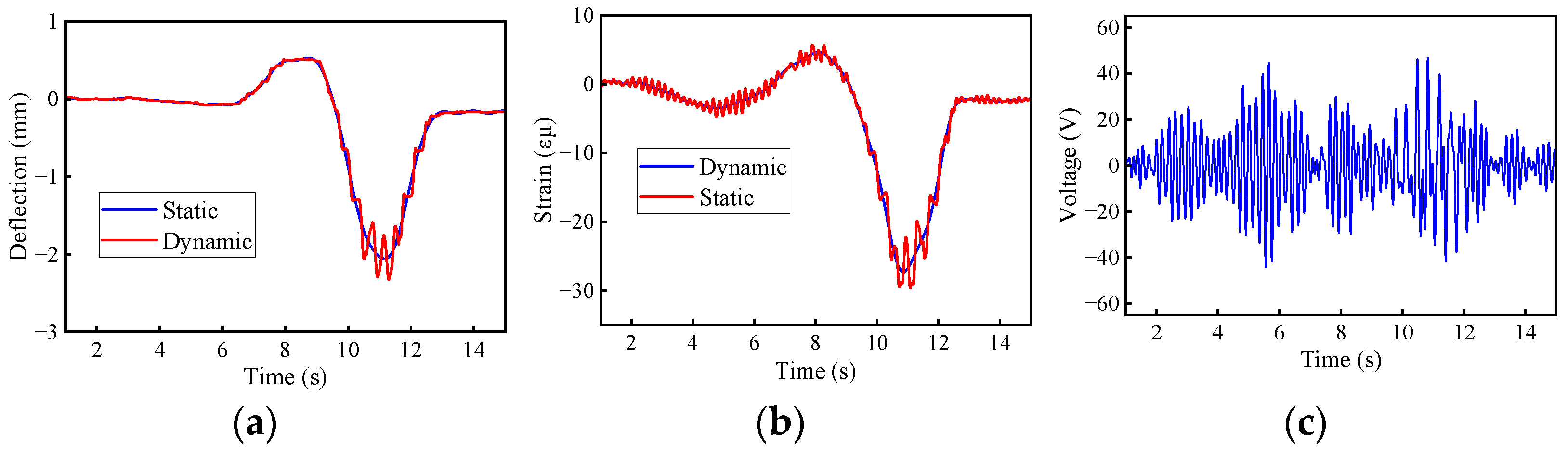
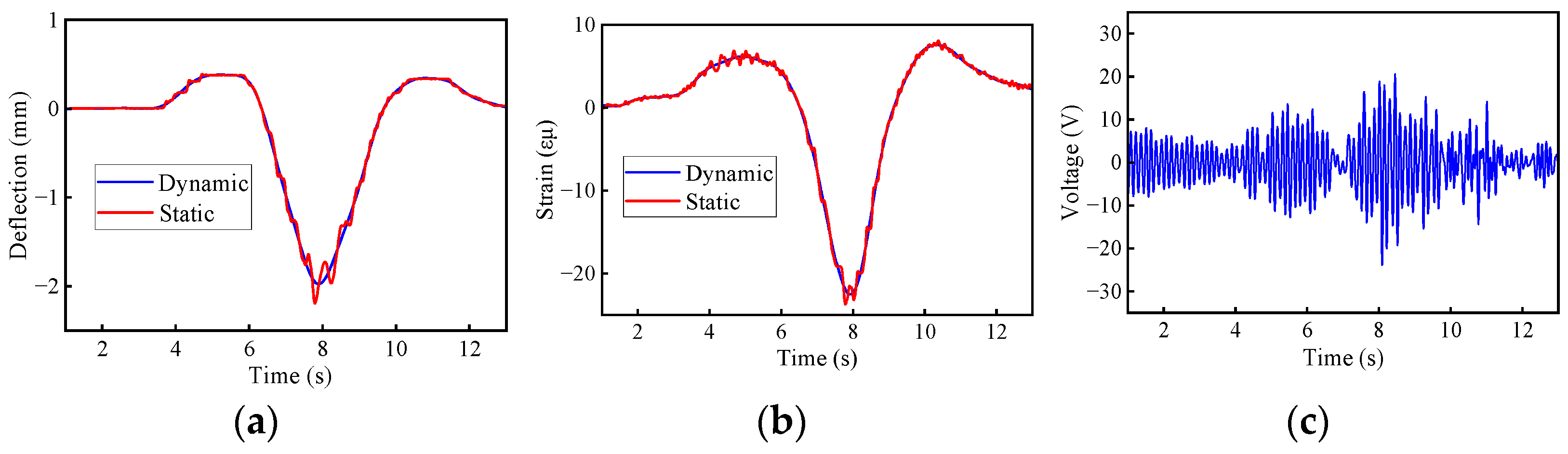
6. Experimental Investigation
7. Conclusions
- (1)
- Under varying conditions of travel speed, RSC, span length, and span number, the deflection DAF and positive bending moment DAF of the mid-span section of the continuous girder bridge increased rapidly with the modes and then stabilized. Under the influence of the above factors, the RDM decreased gradually with the number of modes but was greater than 1, indicating that the deflection DAF is always greater than the bending moment DAF.
- (2)
- The span length, RSC, vehicle speed, and span number have strong, strong, complicated, and weak associations with DAF, respectively. The RSC did not significantly change the contribution of each mode to the DAF and CM, but it had a significant effect on the bridges’ dynamic response and DAF. The vehicle speed altered the dynamic response, the DAF, and the contribution of each mode to the response. The span length had a greater effect on the modal contribution than did the span number.
- (3)
- The dominant vibration modes of continuous girder bridges were of the first two to four orders, and it is unreasonable to calculate the bridge deflection DAF and bending moment DAF by considering only the fundamental frequency. For precast continuous concrete box-girder bridges with four spans or less, the deflection DAF and bending moment DAF could be obtained with 95% accuracy after considering the first four orders and the first nine orders of modes, respectively.
- (4)
- In the field experiment, the RDMs of the mid-span section for the 4 × 30 m and 4 × 20 m continuous bridges were 1.04 and 1.05, respectively, demonstrating that the deflection DAF of the mid-span section of the bridges was greater than the strain (bending moment) results. After filtering at the cut-off mode frequency corresponding to the 95% accuracy index was considered, the maximum variation of the deflection DAF and bending moment DAF was 0.3%, proving the effectiveness of the cut-off mode in preserving signal fidelity.
- (5)
- In this paper, box-girder bridges were investigated. For precast bridges with other cross-sections (T-beam or hollow slab), the above conclusions are also applicable when the modes exhibit similar characteristics. Bridges with various structural types (skewed or curved) need further research. A comparative analysis was conducted on various parameters under the dynamic load test conditions of a single vehicle on the bridge. The vehicle number and driving position may have a greater influence on the results of the cut-off frequency compared to the bridge deck width, girder section, and girder number and, therefore, also need to be further investigated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pieraccini, M.; Miccinesi, L.; Abdorazzagh Nejad, A.; Naderi Nejad Fard, A. Experimental dynamic impact factor assessment of railway bridges through a radar interferometer. Remote Sens. 2019, 11, 2207. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Ma, Z.J.; Zhao, Y.; Shi, X.W.; He, S.H. Improved definition of dynamic load allowance factor for highway bridges. Struct. Eng. Mech. 2015, 54, 561–577. [Google Scholar] [CrossRef]
- Simoncelli, M.; Aloisio, A.; Zucca, M.; Venturi, G.; Alaggio, R. Intensity and location of corrosion on the reliability of a steel bridge. J. Constr. Steel Res. 2023, 206, 107937. [Google Scholar] [CrossRef]
- González, A.; Cantero, D.; OBrien, E.J. Dynamic increment for shear force due to heavy vehicles crossing a highway bridge. Comput. Struct. 2011, 89, 2261–2272. [Google Scholar] [CrossRef]
- Pourzeynali, S.; Zhu, X.; Ghari Zadeh, A.; Rashidi, M.; Samali, B. Comprehensive study of moving load identification on bridge structures using the explicit form of Newmark-β method: Numerical and experimental studies. Remote Sens. 2021, 13, 2291. [Google Scholar] [CrossRef]
- Yu, Y.; Deng, L.; Wang, W.; Cai, C.S. Local impact analysis for deck slabs of prestressed concrete box-girder bridges subject to vehicle loading. J. Vib. Control 2017, 23, 31–45. [Google Scholar] [CrossRef]
- O’Connor, C.; Pritchard, R.W. Impact studies on small composite girder bridge. J. Struct. Eng. 1985, 111, 641–653. [Google Scholar] [CrossRef]
- Aluri, S.; Jinka, C.; Gangarao, H.V. Dynamic response of three fiber reinforced polymer composite bridges. J. Bridge Eng. 2005, 10, 722–730. [Google Scholar] [CrossRef]
- Mohseni, I.; Ashin, A.; Choi, W.; Kang, J. Development of dynamic impact factor expressions for skewed composite concrete-steel slab-on-girder bridges. Adv. Mater. Sci. Eng. 2018, 2018, 4313671. [Google Scholar] [CrossRef]
- Szurgott, P.; Wekezer, J.; Kwasniewski, L.; Siervogel, J.; Ansley, M. Experimental assessment of dynamic responses induced in concrete bridges by permit vehicles. J. Bridge Eng. 2011, 16, 108–116. [Google Scholar] [CrossRef]
- Li, H.; Wekezer, J.; Kwasniewski, L. Dynamic response of a highway bridge subjected to moving vehicles. J. Bridge Eng. 2008, 13, 439–448. [Google Scholar] [CrossRef]
- Huang, D.Z. Dynamic analysis of steel curved box girder bridges. J. Bridge Eng. 2001, 6, 506–513. [Google Scholar] [CrossRef]
- Majka, M.; Hartnett, M. Effects of speed, load and damping on the dynamic response of railway bridges and vehicles. Comput. Struct. 2008, 86, 556–572. [Google Scholar] [CrossRef]
- Yang, Y.B.; Liao, S.S.; Lin, B.H. Impact formulas for vehicles moving over simple and continuous beams. J. Struct. Eng. 1995, 121, 1644–1650. [Google Scholar] [CrossRef]
- Fafard, M.; Laflamme, M.; Savard, M.; Bennur, M. Dynamic analysis of existing continuous bridge. J. Bridge Eng. 1998, 3, 28–37. [Google Scholar] [CrossRef]
- Senthilvasan, J.; Thambiratnam, D.; Brameld, G. Dynamic response of a curved bridge under moving truck load. Eng. Struct. 2002, 24, 1283–1293. [Google Scholar] [CrossRef]
- Huang, P.; Wang, J.; Han, W.S.; Yuan, Y.G. Study on impact factors of small-and medium-span bridges under the special-purpose vehicle load. Structures 2022, 43, 606–620. [Google Scholar] [CrossRef]
- Zeng, H.; Bert, C.W. Dynamic amplification of bridge/vehicle interaction: A parametric study for a skewed bridge. Int. J. Struct. Stab. Dyn. 2003, 3, 71–90. [Google Scholar] [CrossRef]
- Deng, L.; Yu, Y.; Zou, Q.L.; Cai, C.S. State-of-the-art review of dynamic impact factors of highway bridges. J. Bridge Eng. 2014, 20, 04014080. [Google Scholar] [CrossRef]
- Kemal, A.; Talukdar, S. Evaluation of impact factor parameters for T-girder concrete bridge considering multi-lane vehicle movement. Innov. Infrastruct. Solut. 2022, 7, 220. [Google Scholar] [CrossRef]
- Law, S.S.; Zhu, X.Q. Bridge dynamic responses due to road surface roughness and braking of vehicle. J. Sound Vibr. 2005, 282, 805–830. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wu, Y.S. A versatile element for analyzing vehicle-bridge interaction response. Eng. Struct. 2001, 23, 452–469. [Google Scholar] [CrossRef]
- Humar, J.L.; Kashif, A.M. Dynamic response of bridges under travelling loads. Can. J. Civ. Eng. 1993, 20, 287–298. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Xue, Y.X.; Gao, X.J.; Li, R.R.; Wang, Y.L.; Zhao, Y. Research on dynamie amplification factor of highway simply supportedgirder bridge based on modal superposition method. J. Traffic Transp. Eng. 2023, 23, 146–155. [Google Scholar]
- Zou, Q.; Deng, L.; Guo, T.; Yin, X. Comparative study of different numerical models for vehicle-bridge interaction analysis. Int. J. Struct. Stab. Dyn. 2016, 16, 1550057. [Google Scholar] [CrossRef]
- Li, S.; Ren, J. Investigation on three-directional dynamic interaction between a heavy-duty vehicle and a curved bridge. Adv. Struct. Eng. 2018, 21, 721–738. [Google Scholar] [CrossRef]
- Deng, L.; He, W.; Shao, Y. Dynamic impact factors for shear and bending moment of simply supported and continuous concrete girder bridges. J. Bridge Eng. 2015, 20, 04015005. [Google Scholar] [CrossRef]
- Wang, Y.L.; Tian, J.; Zhou, Y.J.; Zhao, Y.; Feng, W.; Mao, K.Q. Assessing dynamic load allowance of the negative bending moment in continuous girder bridges by weighted average method. Coatings 2022, 12, 1233. [Google Scholar] [CrossRef]
- Shao, Y.F.; Brownjohn, J.M.W.; Miao, C.Q.; Wang, M.M. A precise time-integration linear vehicle-bridge interaction method and dynamic sensitivity analysis. Structures 2021, 33, 4596–4603. [Google Scholar] [CrossRef]
- Shi, X.; Cai, C.S.; Chen, S. Vehicle induced dynamic behavior of short-span slab bridges considering effect of approach slab condition. J. Bridge Eng. 2008, 13, 83–92. [Google Scholar] [CrossRef]
- Huang, D.Z. Vehicle-induced vibration of steel deck arch bridges and analytical methodology. J. Bridge Eng. 2012, 17, 241–248. [Google Scholar] [CrossRef]
- Park, Y.S.; Shin, D.K.; Chung, T.J. Influence of road surface roughness on dynamic impact factor of bridge by full-scale dynamic testing. Can. J. Civ. Eng. 2005, 32, 825–829. [Google Scholar] [CrossRef]
- Broquet, C.; Bailey, S.F.; Fafard, M.; Brühwiler, E. Dynamic behavior of deck slabs of concrete road bridges. J. Bridge Eng. 2004, 9, 137–146. [Google Scholar] [CrossRef]
- Parida, S.; Talukdar, S. An insight to the dynamic amplification factor for steel truss girder bridge. Int. J. Steel Struct. 2020, 20, 1341–1354. [Google Scholar] [CrossRef]
- Aloisio, A.; Alaggio, R. Probabilistic comparative analysis of vehicle-bridge interaction models for predicting bridge response under moving vehicles. J. Eng. Mech. 2024, 150, 04023121. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, W.; Han, W.S.; Liu, J.X. Determining the dynamic amplification factor of multi-span continuous box girder bridges in highways using vehicle-bridge interaction analyses. Eng. Struct. 2019, 181, 47–59. [Google Scholar] [CrossRef]
- Mo, S.; Chen, K.; Huang, Z.; Zhang, W. Study on the spatial system dynamics of long-span arch bridge interacting with vehicles subjected to multiple vehicle loads. J. Vib. Eng. Technol. 2023, 6, 1–15. [Google Scholar] [CrossRef]
- Shen, H.M.; Xiao, X.B. Numerical method for vehicle-bridge coupled vibrations. J. Southwest Jiao Tong Univ. 2003, 38, 658–662. [Google Scholar]
- Tan, G.H.; Brameld, G.H.; Thambiratnam, D.P. Development of an analytical model for treating bridge-vehicle interaction. Eng. Struct. 1998, 20, 54–61. [Google Scholar] [CrossRef]
- Li, J.A.; Feng, D. A comparative study of vehicle-bridge interaction dynamics with 2D and 3D vehicle models. Eng. Struct. 2023, 292, 116493. [Google Scholar] [CrossRef]
- Deng, L.; Duan, L.L.; He, W.; Ji, W. Study on vehicle model for vehicle-bridge coupling vibration of highway bridges in China. China J. Highw. Transp. 2018, 31, 92–100. [Google Scholar]
- Gagarin, N.; Goulias, D.; Mekemson, J. Condition rating of bridge decks with fuzzy sets modeling for SF-GPR surveys. Remote Sens. 2023, 15, 3631. [Google Scholar] [CrossRef]
- Wang, B.; Xia, C.; Min, Q.; Zhu, S.; Li, Y. Dynamic amplification factors of an arch bridge under random traffic flows. Int. J. Struct. Stab. Dyn. 2023, 3, 2450064. [Google Scholar] [CrossRef]
- Moghimi, H.; Ronagh, H.R. Impact factors for a composite steel bridge using non-linear dynamic simulation. Int. J. Impact Eng. 2008, 35, 1228–1243. [Google Scholar] [CrossRef]
- Yin, X.; Liu, Y.; Kong, B.; Chen, S. Experimental and numerical studies of a damaged bridge considering stochastic traffic flows and road roughness. Int. J. Struct. Stab. Dyn. 2017, 17, 1750089. [Google Scholar] [CrossRef]
- Ling, T.; Deng, L.; He, W.; Cao, R.; Zhong, W. Determination of dynamic amplification factors for small-and medium-span highway bridges considering the effect of automated truck platooning loads. Mech. Syst. Signal Proc. 2023, 204, 110812. [Google Scholar] [CrossRef]
- Ashebo, D.B.; Chan, T.H.; Yu, L. Evaluation of dynamic loads on a skew box girder continuous bridge Part II: Parametric study and dynamic load factor. Eng. Struct. 2007, 29, 1064–1073. [Google Scholar] [CrossRef]
- Beben, D. Dynamic amplification factors of corrugated steel plate culverts. Eng. Struct. 2013, 46, 193–204. [Google Scholar] [CrossRef]

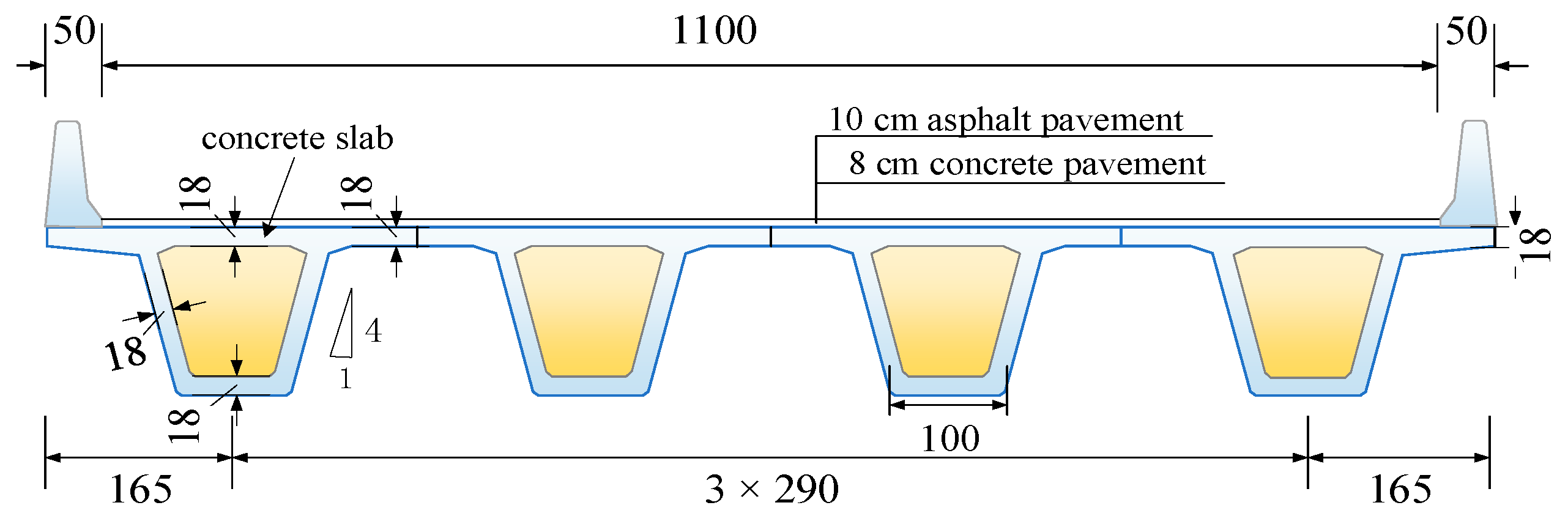

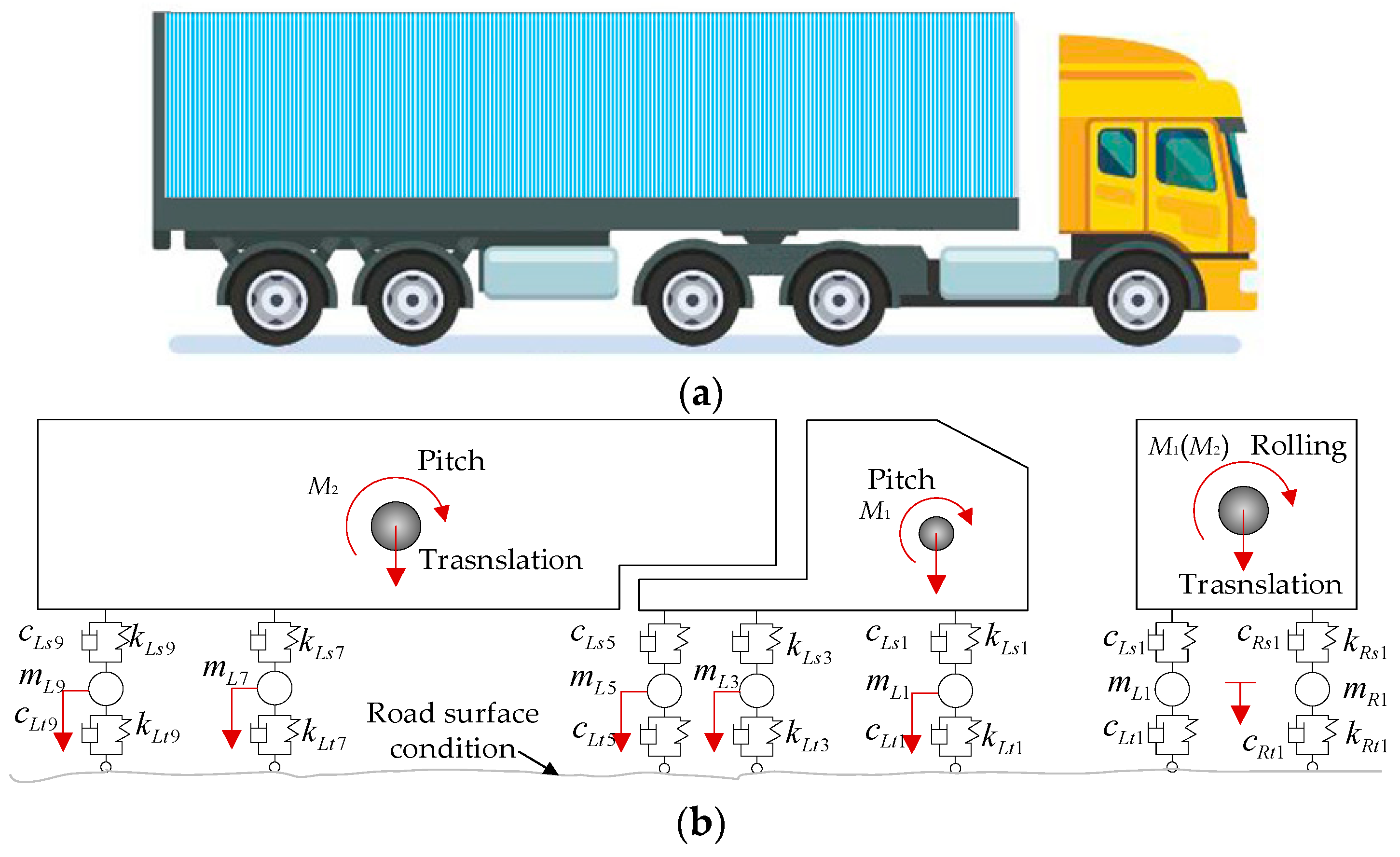





| Bridge Type | Span Length (m) | Span Number | Road Surface Condition | Vehicle Speed (km/h) (km/h) |
|---|---|---|---|---|
| Precast concrete continuous box-girder bridge | 20 | 2 | Smooth | 40 |
| 30 | 3 | Good | 80 | |
| 40 | 4 | Medium | 120 | |
| — | — | Poor | — |
| Cut-Off Mode Order | Deflection | Bending Moment | ||||
|---|---|---|---|---|---|---|
| Two-Span | Three-Span | Four-Span | Two-Span | Three-Span | Four-Span | |
| K1 | 3 | 3 | 4 | 7 | 8 | 9 |
| K2 | 6 | 7 | 8 | 15 | 20 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, Y.; Zhao, Y.; Zhao, Y.; Xue, Y.; Feng, W. Comparison of Dynamic Amplification Factor of Deflection and Bending Moment of Highway Continuous Box-Girder Bridges by Mode Superposition. Materials 2024, 17, 1041. https://doi.org/10.3390/ma17051041
Wang Y, Zhou Y, Zhao Y, Zhao Y, Xue Y, Feng W. Comparison of Dynamic Amplification Factor of Deflection and Bending Moment of Highway Continuous Box-Girder Bridges by Mode Superposition. Materials. 2024; 17(5):1041. https://doi.org/10.3390/ma17051041
Chicago/Turabian StyleWang, Yelu, Yongjun Zhou, Yang Zhao, Yu Zhao, Yuxin Xue, and Wei Feng. 2024. "Comparison of Dynamic Amplification Factor of Deflection and Bending Moment of Highway Continuous Box-Girder Bridges by Mode Superposition" Materials 17, no. 5: 1041. https://doi.org/10.3390/ma17051041
APA StyleWang, Y., Zhou, Y., Zhao, Y., Zhao, Y., Xue, Y., & Feng, W. (2024). Comparison of Dynamic Amplification Factor of Deflection and Bending Moment of Highway Continuous Box-Girder Bridges by Mode Superposition. Materials, 17(5), 1041. https://doi.org/10.3390/ma17051041






