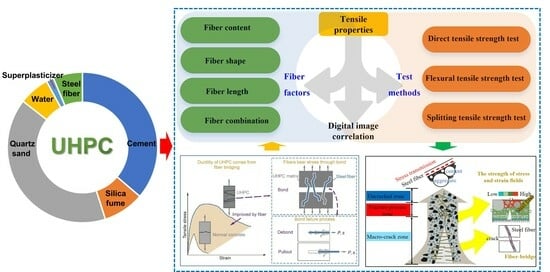
Effect of Steel Fibers on Tensile Properties of Ultra-High-Performance Concrete: A Review
Abstract
:1. Introduction
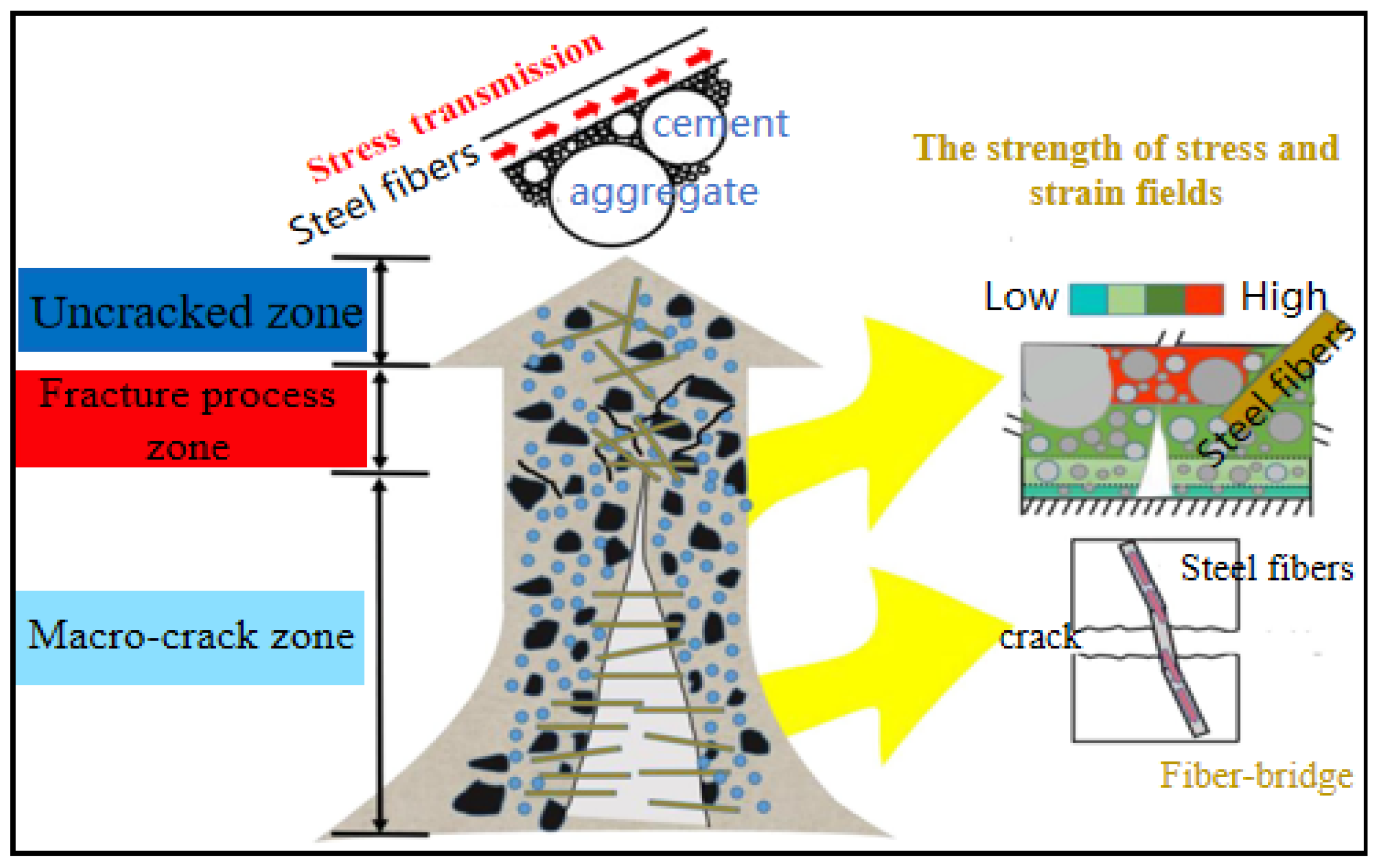
2. Advantages and Significance of Steel Fibers in Concrete
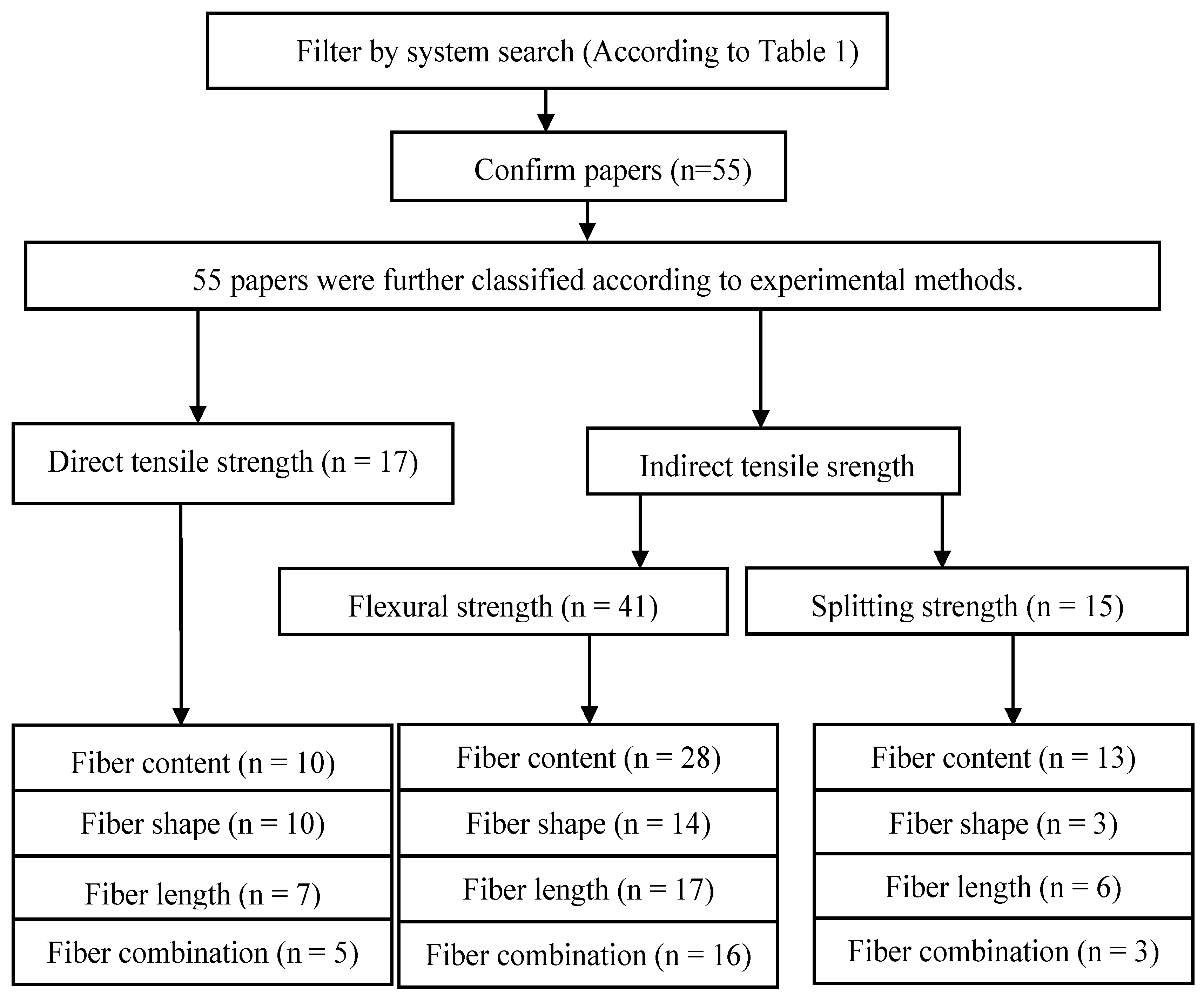
3. Research Methods
- (1)
- What experimental methods or standards are used to study the tensile properties of UHPC?
- (2)
- What are the effects of different fiber contents, shape, and hybrids on the tensile properties of UHPC?
4. Results and Discussion
4.1. Effect of Steel Fibers on Direct Tension Strength
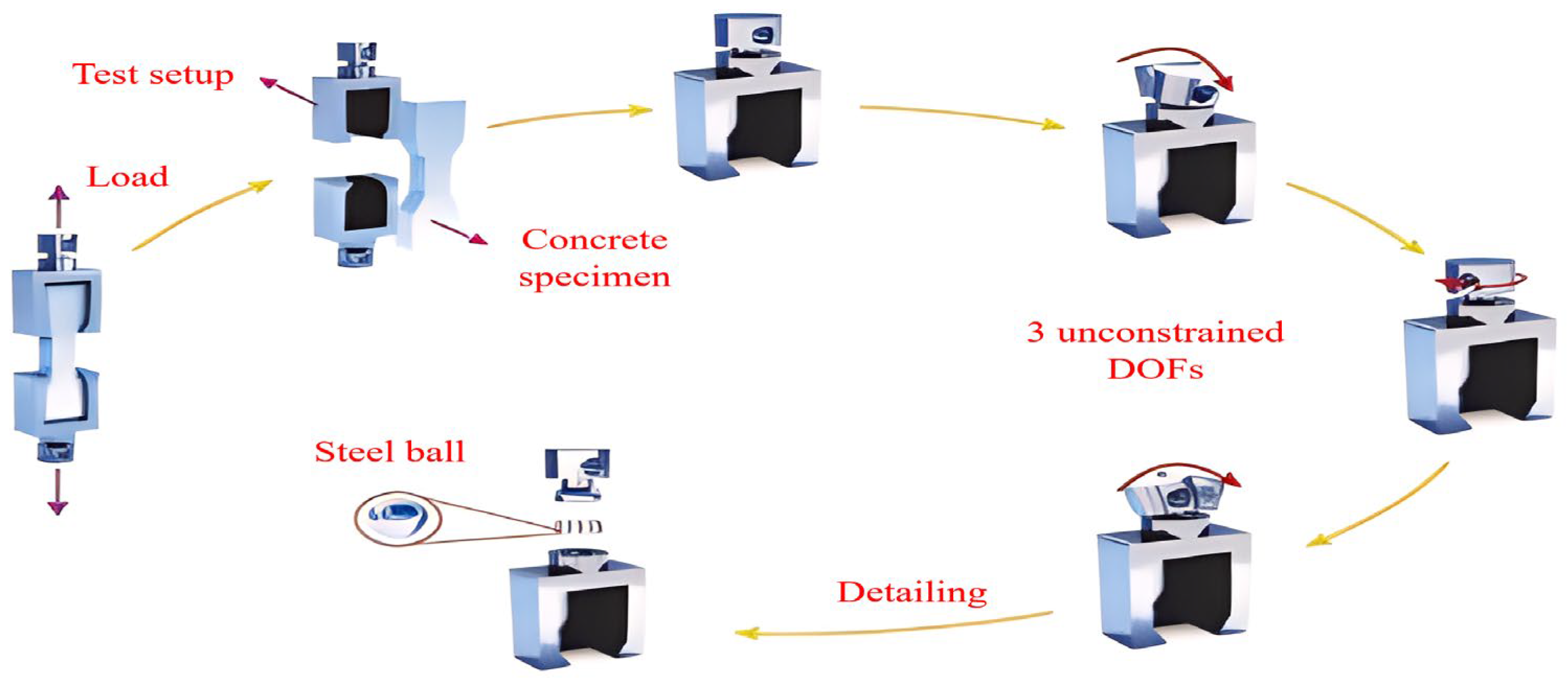
4.1.1. Test Setup for Direct Tensile Strength
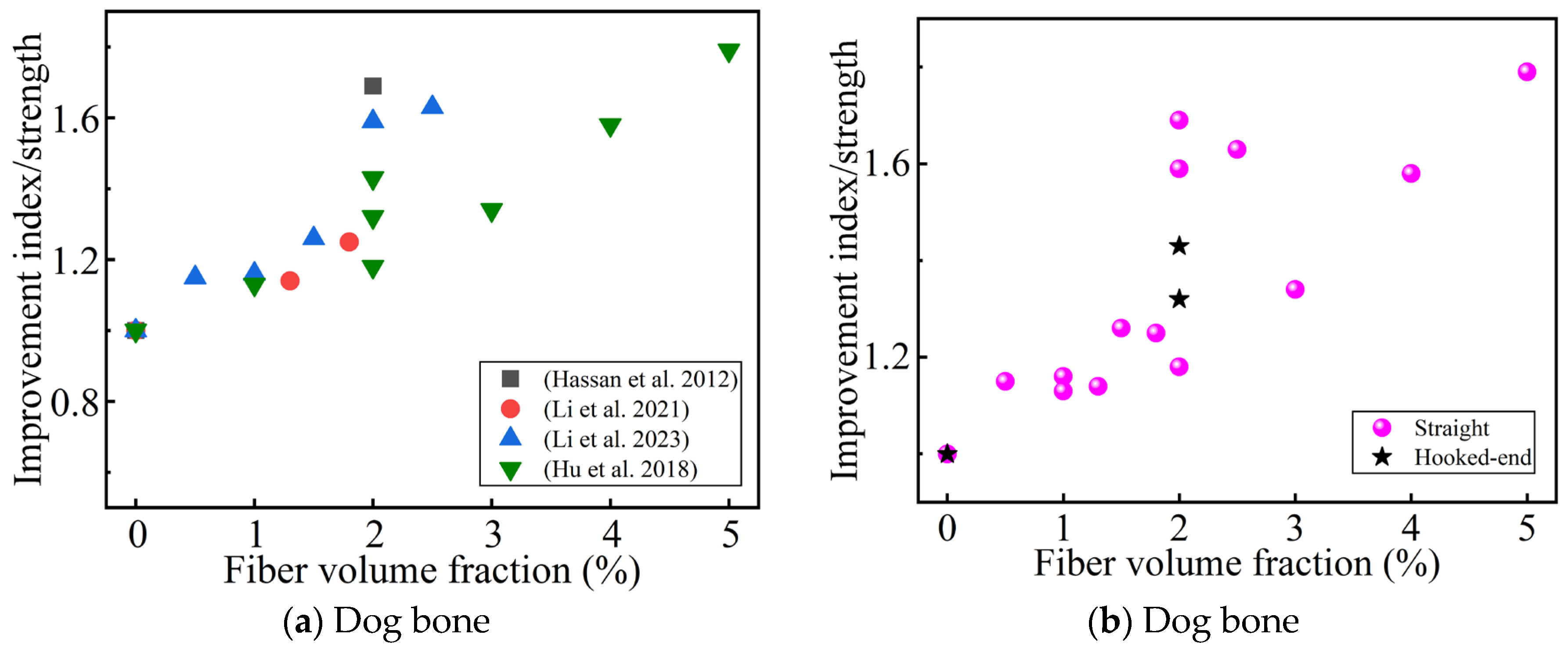
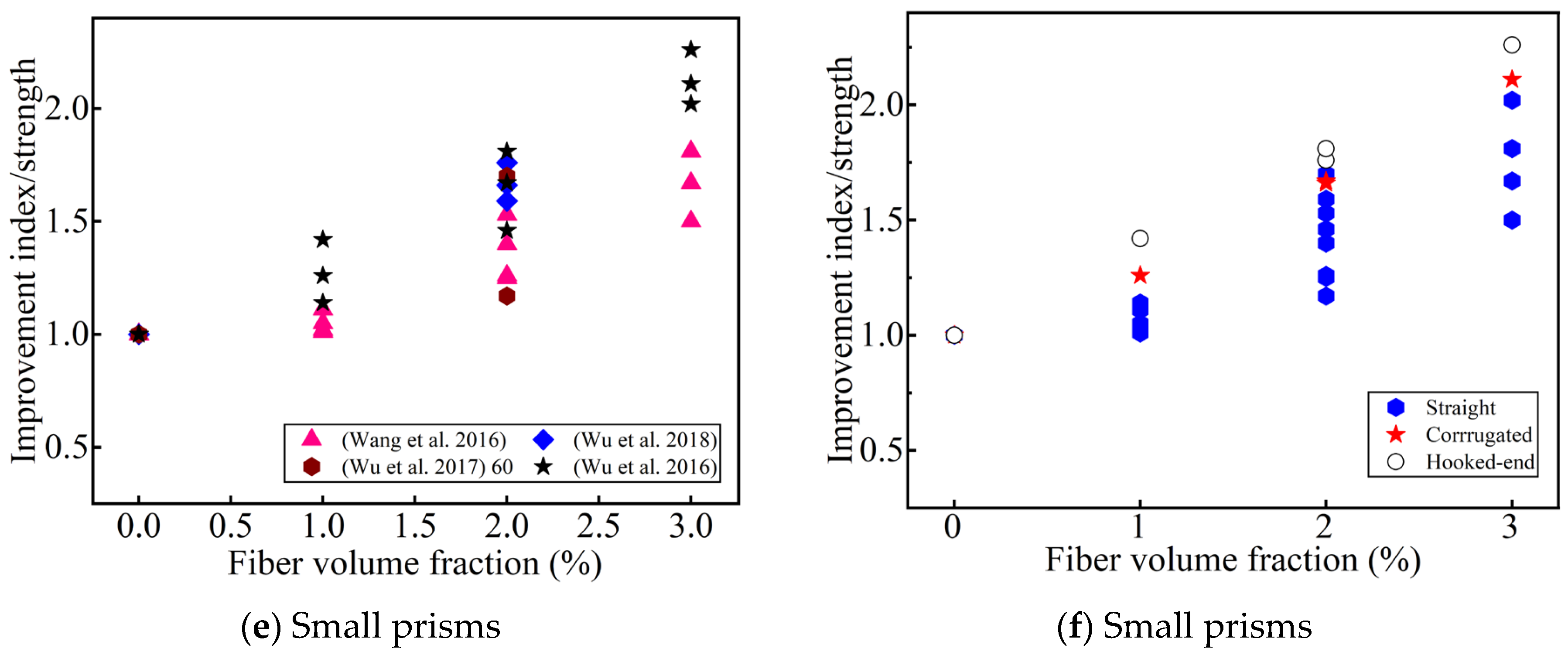
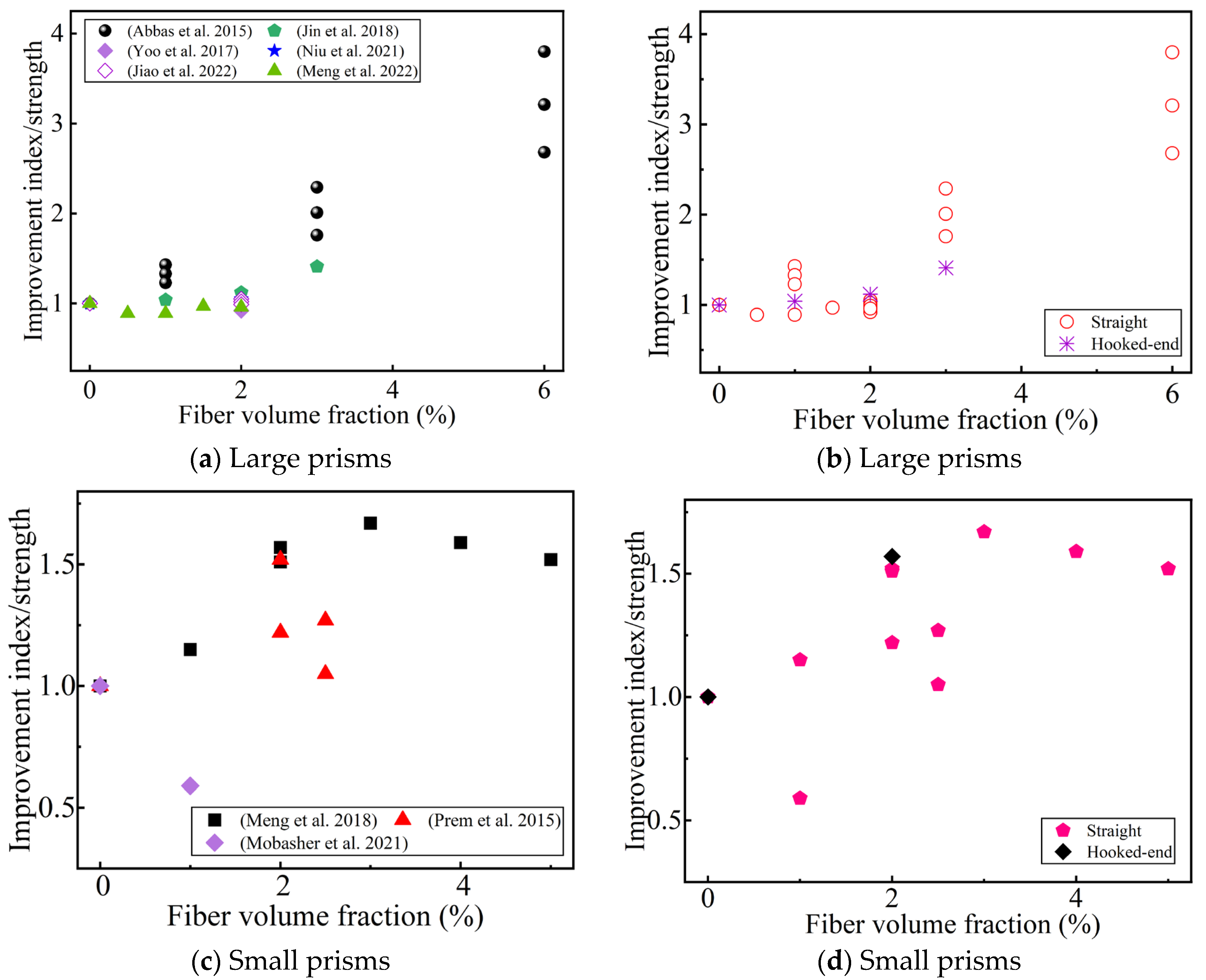
4.1.2. Effect of Steel Fiber Content and Shape on Direct Tensile Strength
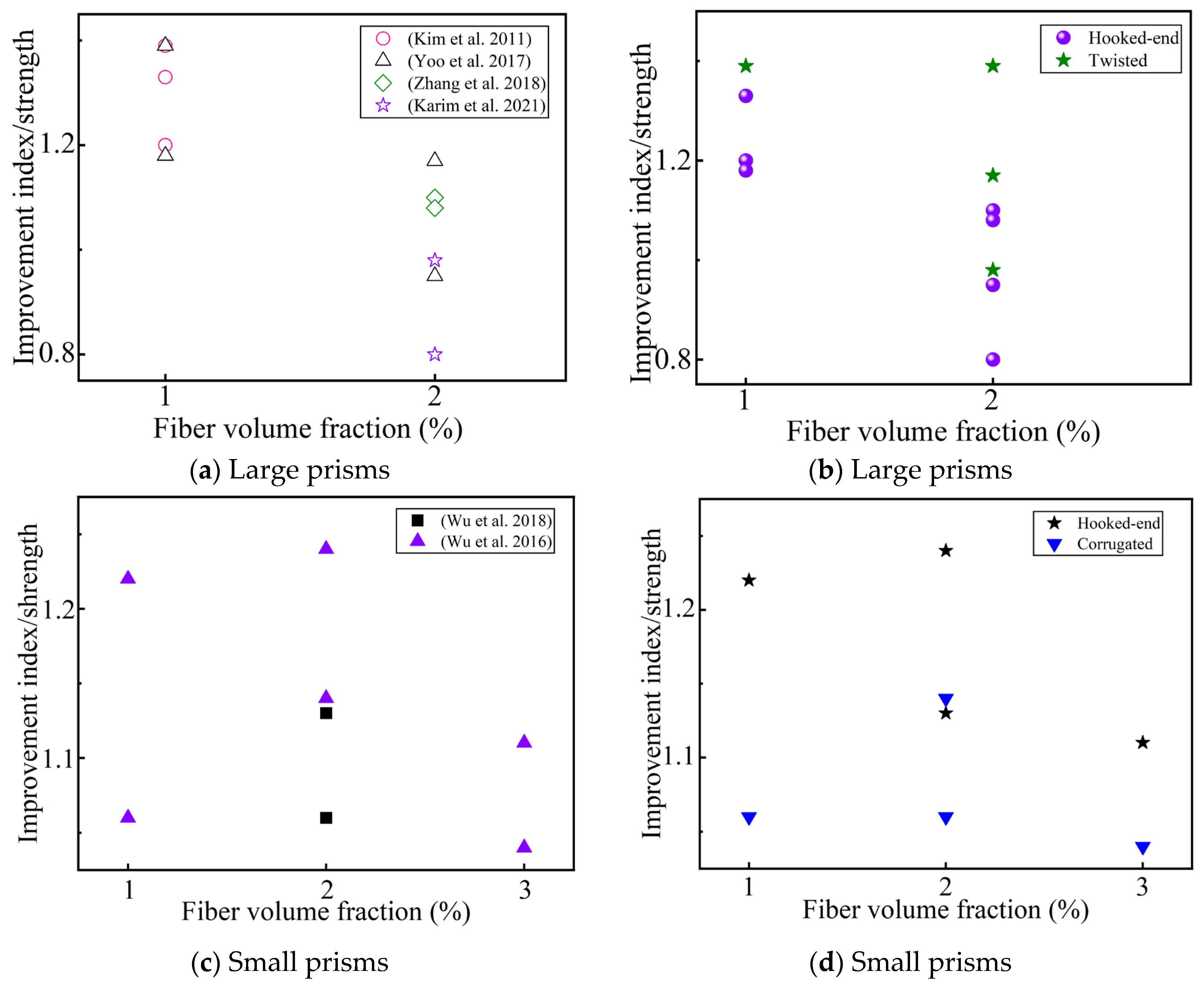
4.1.3. Effect of Steel Fiber Length and Hybrids on Direct Tensile Strength
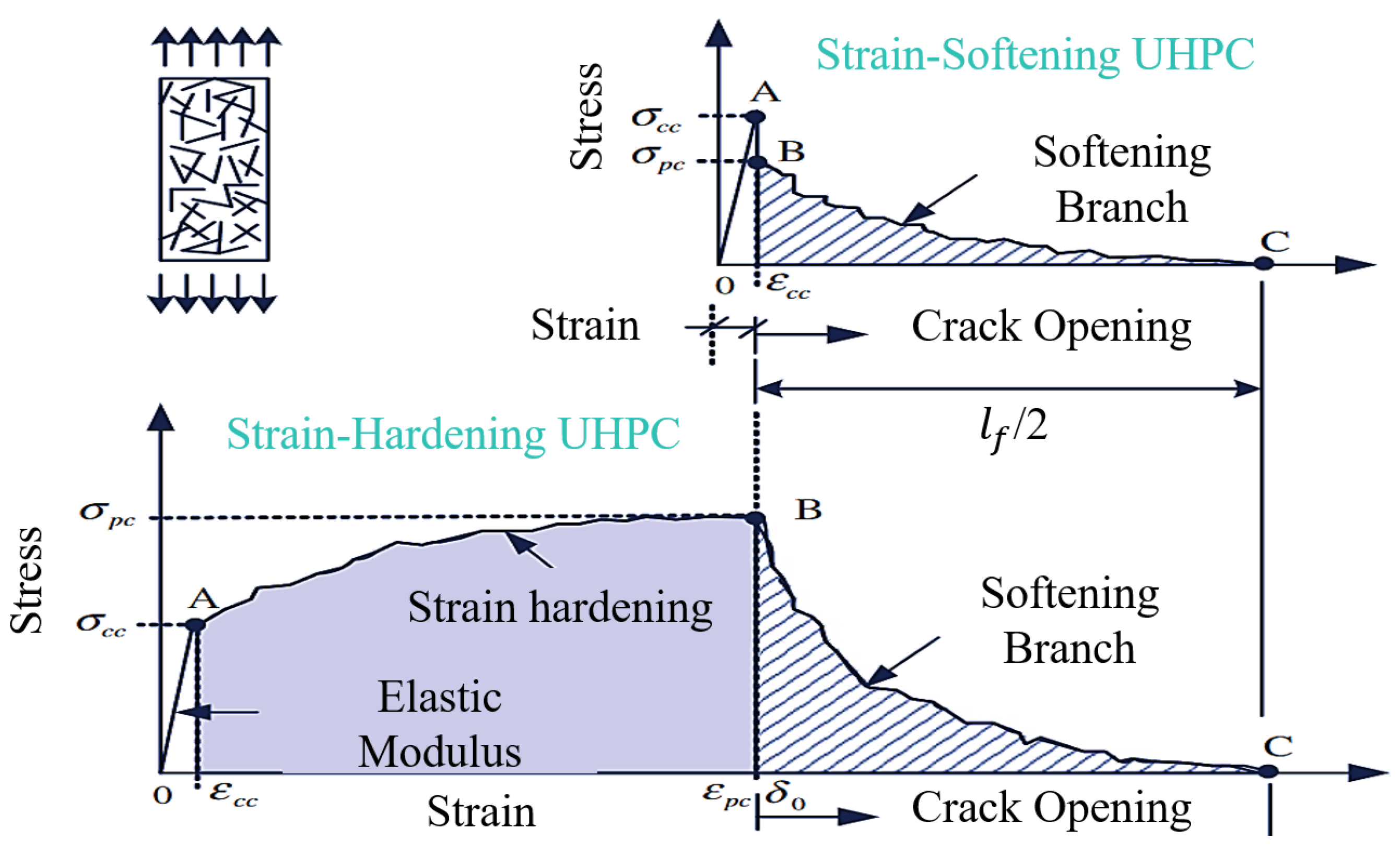
4.1.4. Stress–Strain Curve and Empirical Formula for Direct Tensile Strength
4.2. Effect of Steel Fibers on Flexural Strength
4.2.1. Test Setup for Flexural Tensile Strength
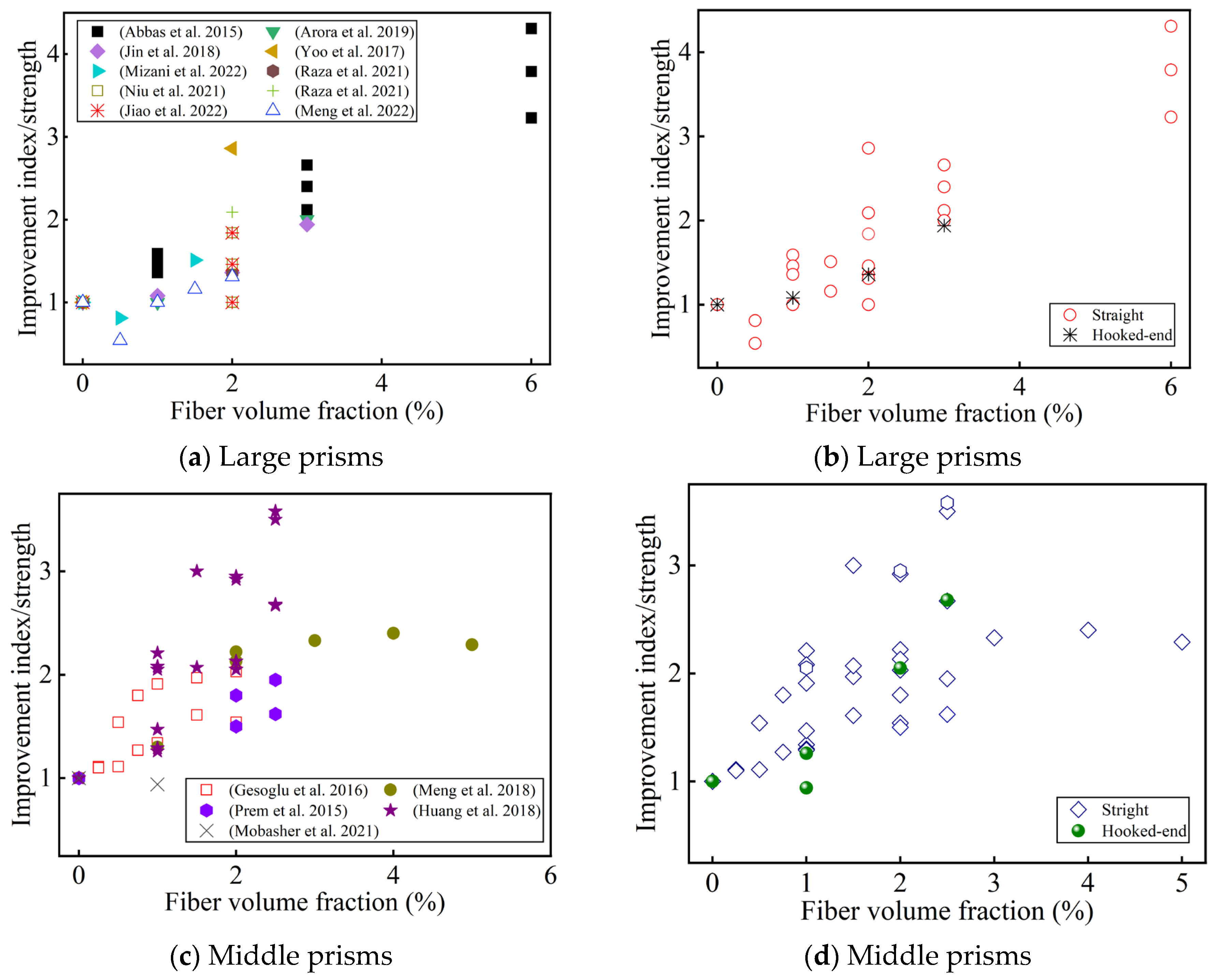
4.2.2. Effect of Steel Fiber Content and Type on Flexural Tensile Strength
4.2.3. Effect of Fiber Length and Hybrids on Flexural Tensile Strength
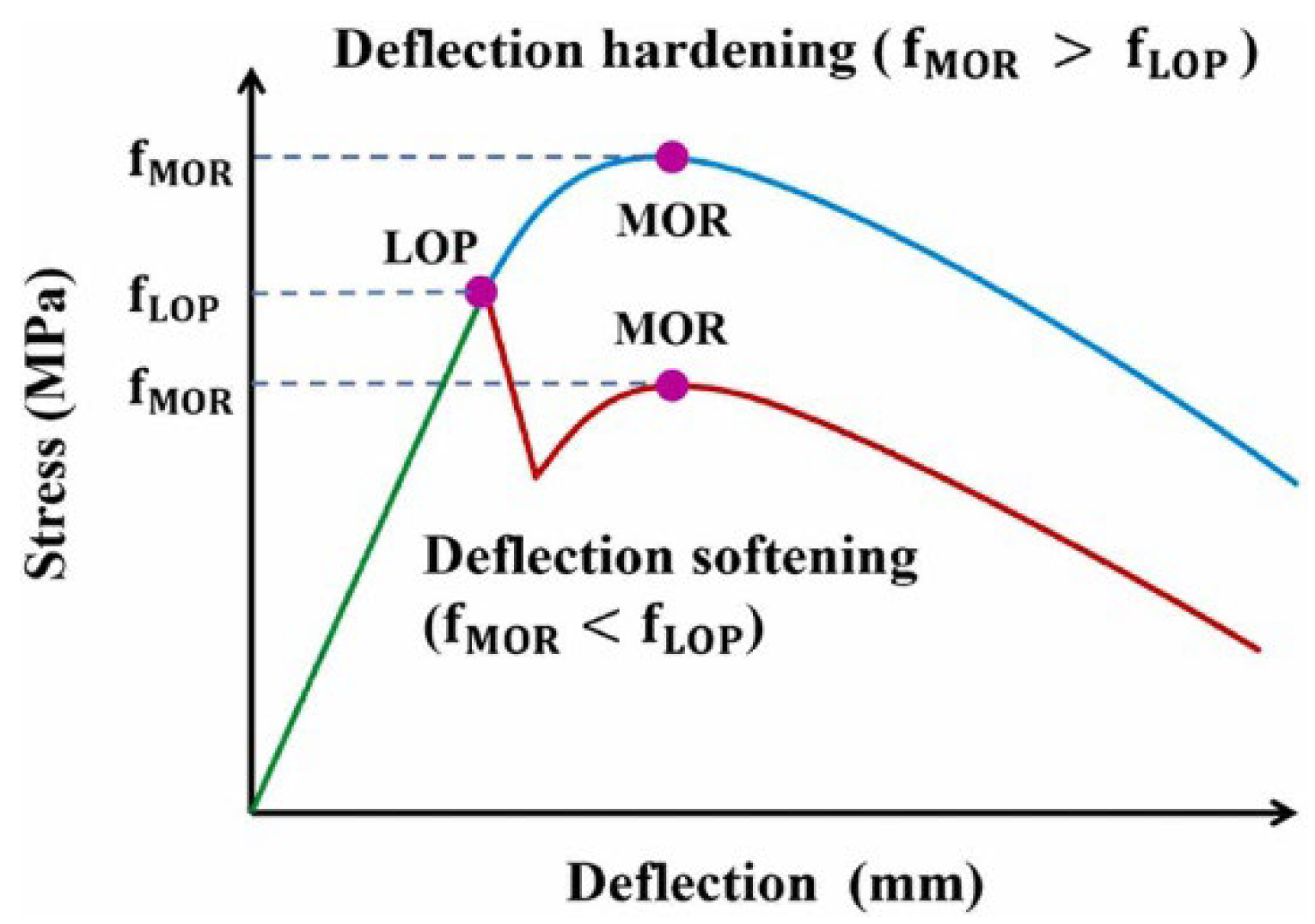
4.2.4. Load–Deflection Curve and Empirical Formula
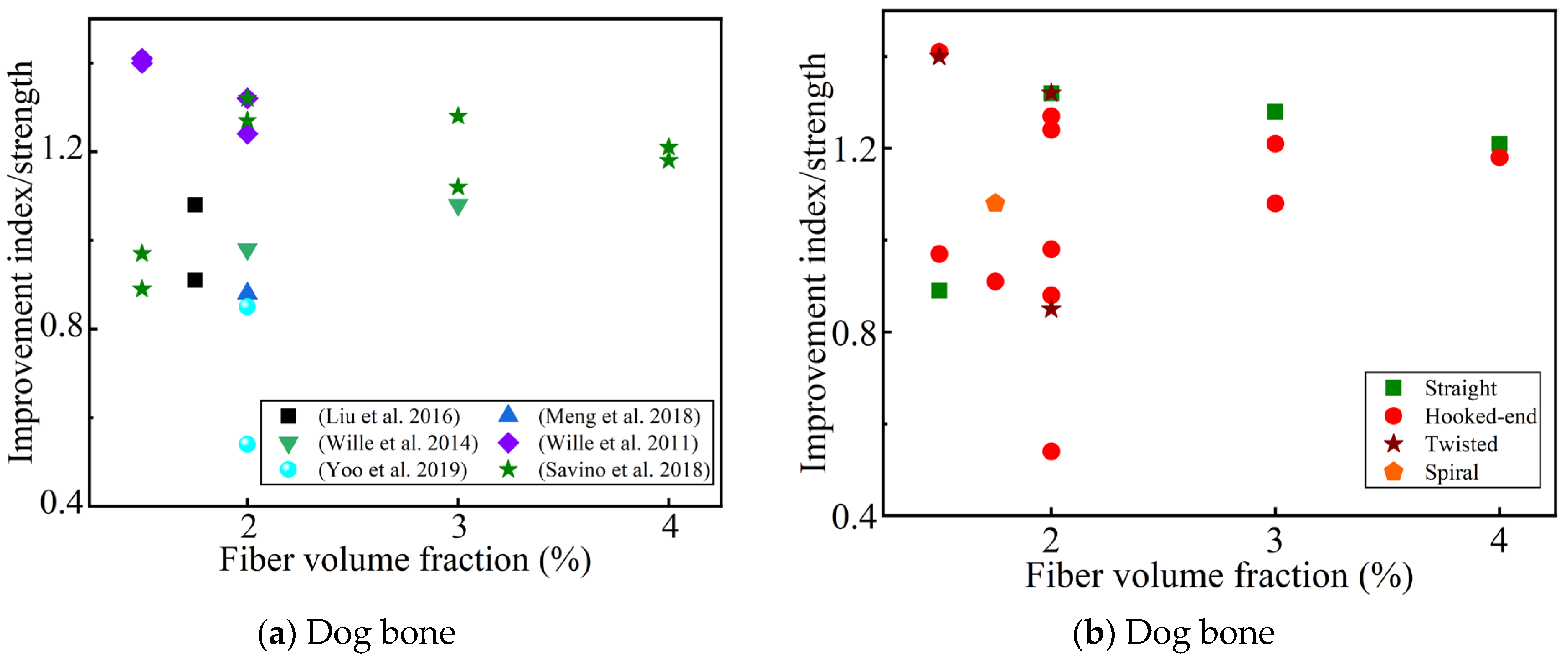
4.3. Effect of Steel Fibers on Splitting Tensile Strength
4.3.1. Test Setup for Splitting Tensile Strength
4.3.2. Effect of Fiber Content and Fiber Type on Splitting Tensile Strength
4.3.3. Effect of Fiber Length and Hybrids on Splitting Tensile Strength
4.3.4. Empirical Formulas for Splitting Tensile Strength
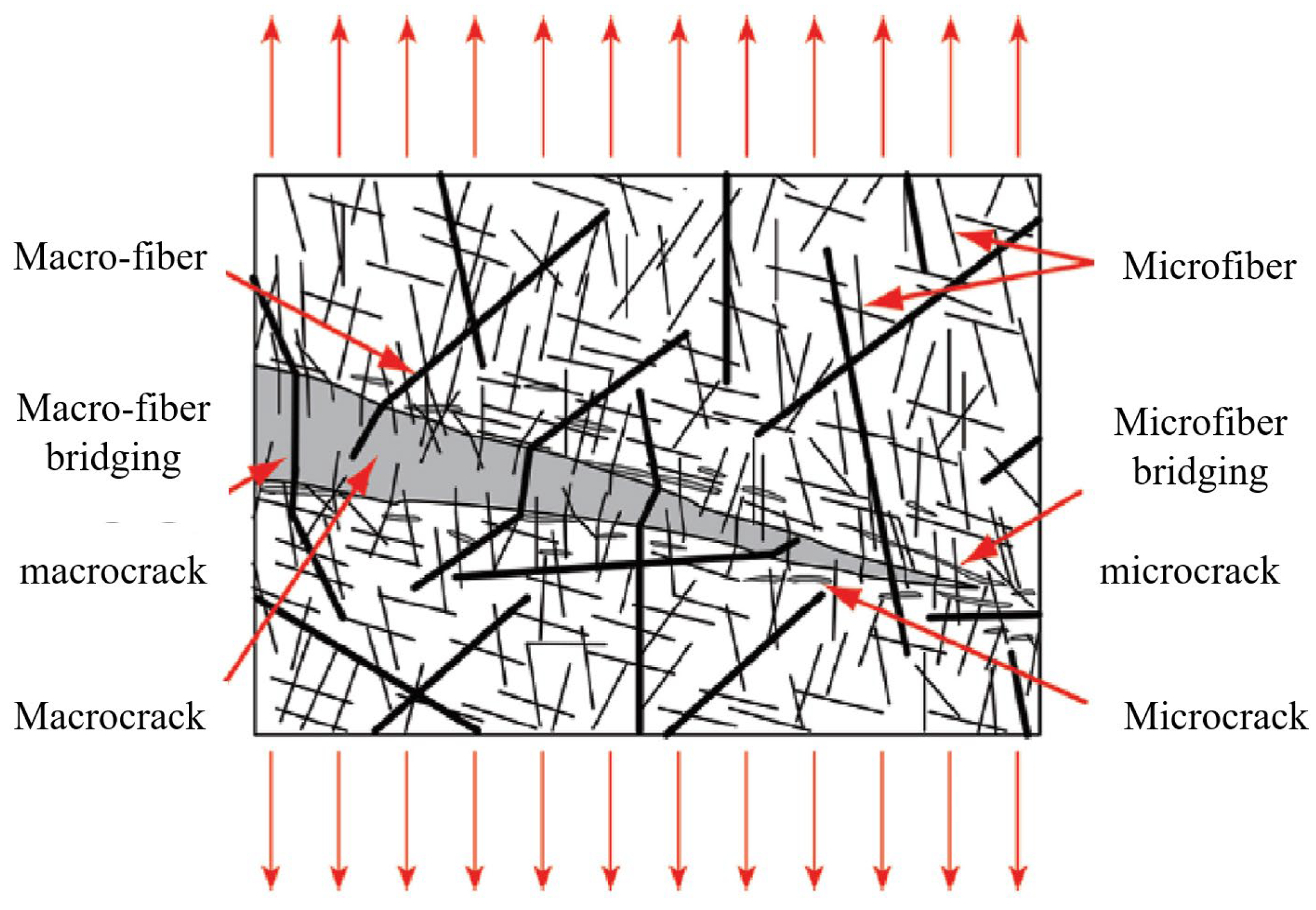
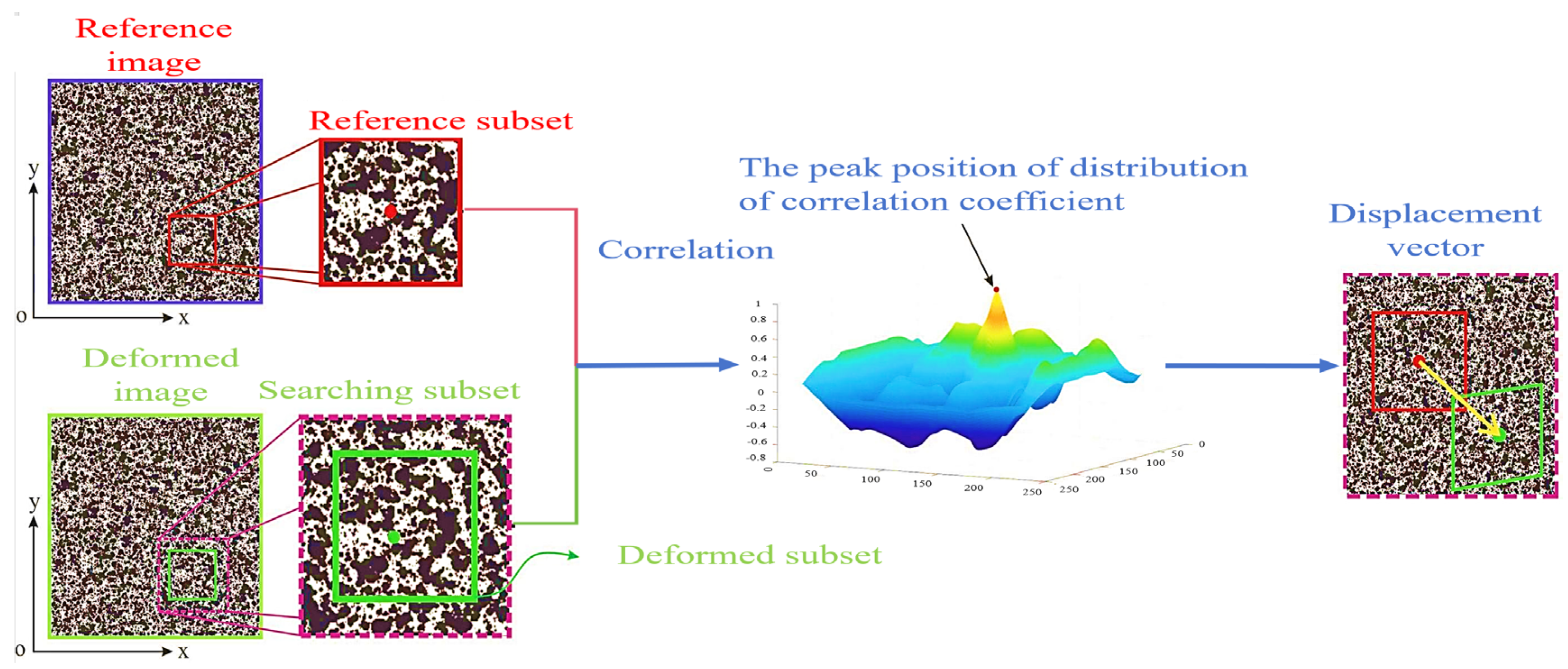
4.4. DIC Application to Tensile Properties of UHPC
4.4.1. The Basic Principle of DIC
4.4.2. The Role of DIC in the Tensile Properties of UHPC
5. Conclusions
- (1)
- The standard commonly used for flexural test is ASTMC1609, and the standard commonly used for splitting test is ATSMC496. These standards come from fiber concrete standards and ordinary concrete standards, respectively, and most of them do not refer to the relevant standards for the direct tension test.
- (2)
- In the study of the tensile properties of UHPC, deformed steel fibers (/ = 30/0.3) and straight steel fibers (/ = 13/0.2) are commonly used. Usually, the tensile strength of the steel fibers is greater than 2000 MPa, thus, avoiding the accidental fracture of the steel fiber.
- (3)
- Whether it is the direct tensile or indirect tensile test, the tensile strength is always proportional to the steel fiber content, and the optimal fiber content seems to be different for different tensile strength test methods. This is related to the shape and size of the specimen and the fiber type. The improvement in the tensile strength of deformed steel fibers is not always better than that of straight steel fibers, which also depends on the size of the steel fibers and the material composition of the UHPC.
- (4)
- Appropriately increasing the length of the steel fibers will help improve the tensile strength. The optimal fiber length is 13~20 mm, which is also related to the orientation of the fibers. The improvement in the tensile strength by hybrid steel fibers is uncertain, and it also depends on the effectiveness of the synergistic effect of the different fibers. It is generally believed that hybrid microfibers and macro steel fibers contribute to the improvement of the tensile strength.
- (5)
- Regarding the effect of steel fibers on the different tensile tests, the relationship between them is complex and nonlinear. Affected by the specimen size effect and cross-sectional stress gradient, the bending tensile test often obtains a tensile strength greater than the actual tensile strength of the UHPC. Direct tension can more intuitively observe the hardening behavior of the UHPC, so it is recommended to use direct tension testing to test the tensile strength of the UHPC.
- (6)
- DIC is promising for replacing traditional strain gauges and displacement gauges. At the same time, the use of DIC helps to evaluate the contribution of the steel fiber type to limiting the crack propagation of UHPC and deepens the understanding of tensile properties. It deserves further attention.
- (1)
- Although a large amount of research has been conducted on hybrid steel fibers, the synergistic effect of the different types of deformed steel fibers is not sufficiently understood, which is not conducive for further optimizing the mechanical properties and popularization of UHPC. This deserves further attention and optimization.
- (2)
- At present, there are still conflicting view about the improvement of tensile strength by steel fibers, partly due to the distribution and orientation of steel fibers. Although there have been some studies on this, most of them are based on straight steel fibers, and the predictions of the relevant mechanical models are mostly dependent on experimental results. Because of the different test standards and methods, they are not universally applicable. Therefore, a large amount of research must be conducted in order to obtain a constitutive model of general significance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mindess, S. Developments in the Formulation and Reinforcement of Concrete; Woodhead Publishing: Cambridge, UK, 2008. [Google Scholar]
- Lee, M.J.; Lee, M.G.; Huang, Y. The Study of UHPC Precast Concrete Containing Incinerator Fly Ash. J. Test. Eval. 2017, 46, 20160348. [Google Scholar] [CrossRef]
- Shi, C.; Wu, Z. A review on ultra high performance concrete: Part I. Raw materials and mixture design. Constr. Build. Mater. 2015, 10, 741–751. [Google Scholar] [CrossRef]
- Yoo, D.; Banthia, N. Mechanical properties of ultra-high-performance fiber-reinforced concrete: A review. Cem. Concr. Compos. 2016, 73, 267–280. [Google Scholar] [CrossRef]
- Garas, V.Y.; Kahn, L.F.; Kurtis, K.E. Tensile Creep Test of Fiber-Reinforced Ultra-High Performance Concrete. J. Test. Eval. 2010, 38, 102666. [Google Scholar] [CrossRef]
- Park, S.; Wu, S.; Liu, Z.C.; Pyo, S. The Role of Supplementary Cementitious Materials (SCMs) in Ultra High Performance Concrete (UHPC): A Review. Materials 2021, 14, 1472. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.; Jang, J.G.; Bansal, P.P. A comprehensive review on effects of mineral admixtures and fibers on engineering properties of ultra-high-performance concrete. J. Build. Eng. 2022, 45, 103314. [Google Scholar] [CrossRef]
- Tam, C.M.; Tam, V.W.; Ng, K.M. Assessing drying shrinkage and water permeability of reactive powder concrete produced in Hong Kong. Constr. Build. Mater. 2012, 26, 79–89. [Google Scholar] [CrossRef]
- Nilimaa, J.; Nilforoush, R. A Direct Tensile Strength Testing Method for Concrete from Existing Structures. CivilEng 2023, 4, 333–344. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, P.; Wang, J. Influence of fibers on the mechanical properties and durability of ultra-high-performance concrete: A review. J. Build. Eng. 2022, 52, 104370. [Google Scholar] [CrossRef]
- Shafieifar, M.; Farzad, M.; Azizinamini, A. Experimental and numerical study on mechanical properties of Ultra High Performance Concrete (UHPC). Constr. Build. Mater. 2017, 156, 402–411. [Google Scholar] [CrossRef]
- Yoo, D.; Shin, H.; Yoon, Y. Enhancing cracking resistance of ultra-high-performance concrete slabs using steel fibres. Mag. Concr. Res. 2015, 67, 487–495. [Google Scholar] [CrossRef]
- Zhao, B.; Li, X.; Pan, J. Strengthening mechanism of steel fiber in UHPC: A new fracture phase field model. J. Cent. South Univ. 2024, 31, 225–236. [Google Scholar] [CrossRef]
- Yoo, D.; Yoon, Y. Structural performance of ultra-high-performance concrete beams with different steel fibers. Eng. Struct. 2015, 102, 409–423. [Google Scholar] [CrossRef]
- Smarzewski, P.; Barnat-Hunek, D. Effect of Fiber Hybridization on Durability Related Properties of Ultra-High Performance Concrete. Int. J. Concr. Struct. Mater. 2017, 11, 315–325. [Google Scholar] [CrossRef]
- Ryu, G.; Kang, S.; Park, J. Evaluation of Fundamental UHPC Properties According to the Shape of Steel Fiber. Key Eng. Mater. 2010, 452–453, 717–720. [Google Scholar] [CrossRef]
- Kang, S.; Choi, J.; Koh, K. Hybrid effects of steel fiber and microfiber on the tensile behavior of ultra-high performance concrete. Compos. Struct. 2016, 145, 37–42. [Google Scholar] [CrossRef]
- Islam, M.M.; Zhang, Q.; Jin, Q. A review of existing codes and standards on design factors for UHPC placement and fiber orientation. Constr. Build. Mater. 2022, 345, 128308. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Banthia, N.; Yoon, Y.S. Recent development of innovative steel fibers for ultra-high-performance concrete (UHPC): A critical review. Cem. Concr. Compos. 2024, 145, 105359. [Google Scholar] [CrossRef]
- Dong, E.; Fan, D.; Ma, X. An Overview on the Dispersion of Steel Fiber in Ultra-High-Performance Concrete. J. Test. Eval. 2023, 52, 20230091. [Google Scholar] [CrossRef]
- Gong, J.; Ma, Y.; Fu, J. Utilization of fibers in ultra-high performance concrete: A review. Compos. B Eng. 2022, 241, 109995. [Google Scholar] [CrossRef]
- Larsen, I.; Thorstensen, R. The influence of steel fibres on compressive and tensile strength of ultra high performance concrete: A review. Constr. Build. Mater. 2020, 256, 119459. [Google Scholar] [CrossRef]
- Hung, C.; El-Tawil, S.; Chao, S. A Review of Developments and Challenges for UHPC in Structural Engineering: Behavior, Analysis, and Design. J. Struct. Eng. 2021, 147, 03121001. [Google Scholar] [CrossRef]
- Bahmani, H.; Mostofinejad, D. Microstructure of ultra-high-performance concrete (UHPC)—A review study. J. Build. Eng. 2022, 50, 104118. [Google Scholar] [CrossRef]
- Wang, D.; Shi, C.; Wu, Z. A review on ultra high performance concrete: Part II. Hydration, microstructure and properties. Constr. Build. Mater. 2015, 96, 368–377. [Google Scholar] [CrossRef]
- Akeed, M.H.; Qaidi, S.; Ahmed, H.U. Ultra-high-performance fiber-reinforced concrete. Part IV: Durability properties, cost assessment, applications, and challenges. Case Stud. Constr. Mater. 2022, 17, e01271. [Google Scholar] [CrossRef]
- Abbas, S.; Nehdi, M.L.; Saleem, M.A. Ultra-High Performance Concrete: Mechanical Performance, Durability, Sustainability and Implementation Challenges. Int. J. Concr. Struct. Mater. 2016, 10, 271–295. [Google Scholar] [CrossRef]
- Yang, J.; Chen, B.; Su, J. Effects of fibers on the mechanical properties of UHPC: A review. J. Traffic Trans. Eng. (Engl. Ed.) 2022, 9, 363–387. [Google Scholar] [CrossRef]
- Arbaoui, A.; Ouahabi, A.; Jacques, S.; Hamiane, M. Concrete Cracks Detection and Monitoring Using Deep Learning-Based Multiresolution Analysis. Electronics 2021, 10, 1772. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Yoon, Y.S. A review on structural behavior, design, and application of ultra-high-performance fiber-reinforced concrete. Int. J. Concr. Struct. Mater. 2016, 10, 125–142. [Google Scholar] [CrossRef]
- Pająk, M.; Ponikiewski, T. Flexural behavior of self-compacting concrete reinforced with different types of steel fibers. Constr. Build. Mater. 2013, 47, 397–408. [Google Scholar] [CrossRef]
- Banthia, N.; Sappakittipakorn, M. Toughness enhancement in steel fiber reinforced concrete through fiber hybridization. Cem. Concr. Res. 2007, 37, 1366–1372. [Google Scholar] [CrossRef]
- Pakravan, H.R.; Latifi, M.; Jamshidi, M. Hybrid short fiber reinforcement system in concrete: A review. Constr. Build. Mater. 2017, 142, 280–294. [Google Scholar] [CrossRef]
- Sridhar, R.; Prasad, R. Experimental and numerical study on damage evaluation of hybrid fiber-reinforced concrete. Asian J. Civ. Eng. 2019, 20, 745–758. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L. How do steel fibers improve the shear capacity of reinforced concrete beams without stirrups? Compos. Part B Eng. 2019, 175, 107079. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, Z.; Shi, C. Steel Fiber–Matrix Interfacial Bond in Ultra-High Performance Concrete: A Review. Engineering 2023, 22, 215–232. [Google Scholar] [CrossRef]
- Hannawi, K.; Bian, H.; William, P.A. Effect of different types of fibers on the microstructure and the mechanical behavior of Ultra-High Performance Fiber-Reinforced Concretes. Compos. Part B Eng. 2016, 86, 214–220. [Google Scholar] [CrossRef]
- Fang, C.; Ali, M.; Visintin, P. The influence of steel fibre properties on the shrinkage of ultra-high performance fibre reinforced concrete. Constr. Build. Mater. 2020, 242, 117993. [Google Scholar] [CrossRef]
- Ragalwar, K.; Heard, W.; Williams, B. On enhancing the mechanical behavior of ultra-high performance concrete through multi-scale fiber reinforcement. Cem. Concr. Compos. 2020, 105, 103422. [Google Scholar] [CrossRef]
- Hoang, A.; Fehling, E. Influence of steel fiber content and aspect ratio on the uniaxial tensile and compressive behavior of ultra high performance concrete. Constr. Build. Mater. 2017, 153, 790–806. [Google Scholar] [CrossRef]
- Abbas, S.; Soliman, A.; Nehdi, M. Exploring mechanical and durability properties of ultra-high performance concrete incorporating various steel fiber lengths and dosages. Constr. Build. Mater. 2015, 75, 429–441. [Google Scholar] [CrossRef]
- Arora, A.; Yao, Y. Fundamental insights into the compressive and flexural response of binder- and aggregate-optimized ultra-high performance concrete (UHPC). Cem. Concr. Compos. 2019, 98, 1–13. [Google Scholar] [CrossRef]
- Chun, B.; Yoo, D. Hybrid effect of macro and micro steel fibers on the pullout and tensile behaviors of ultra-high-performance concrete. Compos. B Eng. 2019, 162, 344–360. [Google Scholar] [CrossRef]
- Gesoglu, M.; Güneyisi, E. Strain hardening ultra-high performance fiber reinforced cementitious composites: Effect of fiber type and concentration. Compos. B Eng. 2016, 103, 74–83. [Google Scholar] [CrossRef]
- Hassan, A.; Jones, S.; Mahmud, G. Experimental test methods to determine the uniaxial tensile and compressive behaviour of ultra high performance fibre reinforced concrete (UHPFRC). Constr. Build. Mater. 2012, 37, 874–882. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, R. Experimental investigation on static and dynamic mechanical properties of steel fiber reinforced ultra-high-strength concretes. Constr. Build. Mater. 2018, 178, 102–111. [Google Scholar] [CrossRef]
- Kim, D.; Park, S. Comparative flexural behavior of Hybrid Ultra High Performance Fiber Reinforced Concrete with different macro fibers. Constr. Build. Mater. 2011, 25, 4144–4155. [Google Scholar] [CrossRef]
- Liu, J.; Han, F. Combined effect of coarse aggregate and fiber on tensile behavior of ultra-high performance concrete. Constr. Build. Mater. 2016, 121, 310–318. [Google Scholar] [CrossRef]
- Ma, R.; Guo, L. Influence of Hybrid Fiber Reinforcement on Mechanical Properties and Autogenous Shrinkage of an Ecological UHPFRCC. J. Mater. Civ. Eng. 2019, 31, 04019032. [Google Scholar] [CrossRef]
- Meng, W.; Khayat, K. Effect of Hybrid Fibers on Fresh Properties, Mechanical Properties, and Autogenous Shrinkage of Cost-Effective UHPC. J. Mater. Civ. Eng. 2018, 30, 04018030. [Google Scholar] [CrossRef]
- Park, J.; Yoo, D. Feasibility of Reducing the Fiber Content in Ultra-High-Performance Fiber-Reinforced Concrete under Flexure. Materials 2017, 10, 118. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Kim, D. Tensile behavior of Ultra High Performance Hybrid Fiber Reinforced Concrete. Cem. Concr. Compos. 2012, 34, 172–184. [Google Scholar] [CrossRef]
- Prem, P.; Murthy, A.; Bharatkumar, B. Influence of curing regime and steel fibres on the mechanical properties of UHPC. Mag. Concr. Res. 2015, 67, 988–1002. [Google Scholar] [CrossRef]
- Ryu, G.; Kang, S. Characteristic Evaluation of UHPC Flexural Behavior with Mixed-Use Hooked and Straight Type Fiber. Adv. Mater. Res. 2011, 368–373, 258–264. [Google Scholar] [CrossRef]
- Ryu, G.S.; Kang, S.T.; Park, J.J.; Koh, K.T.; Kim, S.W. Mechanical Behavior of UHPC (Ultra High Performance Concrete) According to Hybrid Use of Steel Fibers. Adv. Mater. Res. 2011, 287–290, 453–457. [Google Scholar] [CrossRef]
- Wang, R.; Gao, X. Relationship between Flowability, Entrapped Air Content and Strength of UHPC Mixtures Containing Different Dosage of Steel Fiber. Appl. Sci. 2016, 6, 216. [Google Scholar] [CrossRef]
- Wille, K.; El-Tawil, S.; Naaman, A. Properties of strain hardening ultra high performance fiber reinforced concrete (UHP-FRC) under direct tensile loading. Cem. Concr. Compos. 2014, 48, 53–66. [Google Scholar] [CrossRef]
- Wille, K.; Kim, D.; Naaman, A. Strain-hardening UHP-FRC with low fiber contents. Mater. Struct. 2011, 44, 583–598. [Google Scholar] [CrossRef]
- Wu, Z.; Khayat, K.; Shi, C. How do fiber shape and matrix composition affect fiber pullout behavior and flexural properties of UHPC? Cem. Concr. Compos. 2018, 90, 193–201. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W.; Wang, D. Static and dynamic compressive properties of ultra-high performance concrete (UHPC) with hybrid steel fiber reinforcements. Cem. Concr. Compos. 2017, 79, 148–157. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; Wu, L. Effects of steel fiber content and shape on mechanical properties of ultra high performance concrete. Constr. Build. Mater. 2016, 103, 8–14. [Google Scholar] [CrossRef]
- Yoo, D.; Kang, S.; Yoon, Y. Enhancing the flexural performance of ultra-high-performance concrete using long steel fibers. Compos. Struct. 2016, 147, 220–230. [Google Scholar] [CrossRef]
- Yoo, D.; Kim, M.; Park, J. Development of cost effective ultra-high-performance fiber-reinforced concrete using single and hybrid steel fibers. Constr. Build. Mater. 2017, 150, 383–394. [Google Scholar] [CrossRef]
- Yoo, D.; Kim, S. An experimental study on pullout and tensile behavior of ultra-high-performance concrete reinforced with various steel fibers. Constr. Build. Mater. 2019, 206, 46–61. [Google Scholar] [CrossRef]
- Yoo, D.; Kim, S.; Park, G. Effects of fiber shape, aspect ratio, and volume fraction on flexural behavior of ultra-high-performance fiber-reinforced cement composites. Compos. Struct. 2017, 174, 375–388. [Google Scholar] [CrossRef]
- Yoo, D.; Kim, S.; Park, J. Comparative flexural behavior of ultra-high-performance concrete reinforced with hybrid straight steel fibers. Constr. Build. Mater. 2017, 132, 219–229. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, J. Effect of Steel Fiber on Flexural Toughness and Fracture Mechanics Behavior of Ultrahigh-Performance Concrete with Coarse Aggregate. J. Mater. Civ. Eng. 2018, 30, 04018323. [Google Scholar] [CrossRef]
- Mizani, J.; Sadeghi, A.; Afshin, H. Experimental study on the effect of macro and microfibers on the mechanical properties of reactive powder concrete. Struct. Concr. 2022, 23, 240–254. [Google Scholar] [CrossRef]
- Raza, S.; Qureshi, L. Effect of different fibers (steel fibers, glass fibers, and carbon fibers) on mechanical properties of reactive powder concrete. Struct. Concr. 2021, 22, 334–346. [Google Scholar] [CrossRef]
- Karim, R.; Shafei, B. Flexural response characteristics of ultra-high performance concrete made with steel microfibers and macrofibers. Struct. Concr. 2021, 22, 3476–3490. [Google Scholar] [CrossRef]
- Huang, H.; Gao, X. Influence of fiber alignment and length on flexural properties of UHPC. Constr. Build. Mater. 2021, 290, 122863. [Google Scholar] [CrossRef]
- Huang, H.; Gao, X.; Khayat, K. Contribution of fiber alignment on flexural properties of UHPC and prediction using the Composite Theory. Cem. Concr. Compos. 2021, 118, 103971. [Google Scholar] [CrossRef]
- Al-Osta, M.; Sharif, A. Effect of hybridization of straight and hooked steel fibers and curing methods on the key mechanical properties of UHPC. J. Mater. Res. Technol. 2021, 15, 3222–3239. [Google Scholar] [CrossRef]
- Wei, J.; Li, J. Hybrid fibre reinforced ultra-high performance concrete beams under static and impact loads. Eng. Struct. 2021, 245, 112921. [Google Scholar] [CrossRef]
- Li, J.; Deng, Z. Tensile Behavior of Hybrid Fiber-Reinforced Ultra-High-Performance Concrete. Front. Mater. 2021, 8, 769579. [Google Scholar] [CrossRef]
- Mao, Z.; Zhang, J. Behavior evaluation of hybrid fibre-reinforced reactive powder concrete after elevated temperatures. Constr. Build. Mater. 2021, 306, 124917. [Google Scholar] [CrossRef]
- Niu, Y.; Wei, J.; Jiao, C. Crack propagation behavior of ultra-high-performance concrete (UHPC) reinforced with hybrid steel fibers under flexural loading. Constr. Build. Mater. 2021, 294, 123510. [Google Scholar] [CrossRef]
- Raza, S.; Qureshi, L. Effect of carbon fiber on mechanical properties of reactive powder concrete exposed to elevated temperatures. J. Build. Eng. 2021, 42, 102503. [Google Scholar] [CrossRef]
- Fang, H.; Gu, M. Effects of Steel Fiber and Specimen Geometric Dimensions on the Mechanical Properties of Ultra-High-Performance Concrete. Materials 2022, 15, 3027. [Google Scholar] [CrossRef]
- Li, J.; Deng, Z. Tensile behavior of ultra-high performance concrete reinforced with different hybrid fibers. Struct. Concr. 2023, 24, 1415–1435. [Google Scholar] [CrossRef]
- Jiao, C.; Ta, J.; Niu, Y. Analysis of the flexural properties of ultra-high-performance concrete consisting of hybrid straight steel fibers. Case Stud. Construct. Mater. 2022, 17, e01153. [Google Scholar] [CrossRef]
- Ashkezari, G.; Fotouhi, F.; Razmara, M. Experimental relationships between steel fiber volume fraction and mechanical properties of ultra-high performance fiber-reinforced concrete. J. Build. Eng. 2020, 32, 101613. [Google Scholar] [CrossRef]
- Huang, H.; Gao, X.; Li, L. Improvement effect of steel fiber orientation control on mechanical performance of UHPC. Constr. Build. Mater. 2018, 188, 709–721. [Google Scholar] [CrossRef]
- Dadmand, B.; Sadaghian, H. Studying the compressive, tensile and flexural properties of binary and ternary fiber-reinforced UHPC using experimental, numerical and multi-target digital image correlation methods. Case Stud. Construct. Mater. 2023, 18, e01865. [Google Scholar] [CrossRef]
- Abid, M.; Hou, X. Effect of Fibers on High-Temperature Mechanical Behavior and Microstructure of Reactive Powder Concrete. Materials 2019, 12, 329. [Google Scholar] [CrossRef] [PubMed]
- Meng, S.; Jiao, C. Effect of steel fiber-volume fraction and distribution on flexural behavior of Ultra-high performance fiber reinforced concrete by digital image correlation technique. Constr. Build. Mater. 2022, 320, 126281. [Google Scholar] [CrossRef]
- Voss, M.; Riding, K. Comparison between Direct Tension, Four-Point Flexure, and Simplified Double-Punch Tests for UHPC Tensile Behavior. J. Mater. Civ. Eng. 2022, 34, 04022229. [Google Scholar] [CrossRef]
- Savino, V.; Lanzoni, L. Simple and effective models to predict the compressive and tensile strength of HPFRC as the steel fiber content and type changes. Compos. B Eng. 2018, 137, 153–162. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, B. Multi-scale analysis on the tensile properties of UHPC considering fiber orientation. Compos. Struct. 2022, 280, 114835. [Google Scholar] [CrossRef]
- Teng, L.; Huang, H. Prediction of fiber orientation and flexural performance of UHPC based on suspending mortar rheology and casting method. Cem. Concr. Compos. 2021, 122, 104142. [Google Scholar] [CrossRef]
- Mobasher, B.; Anling, L. Characterization of toughening mechanisms in UHPC through image correlation and inverse analysis of flexural results. Cem. Concr. Compos. 2021, 122, 104157. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, H. Effects of steel fibers and concrete strength on flexural toughness of ultra-high performance concrete with coarse aggregate. Case Stud. Construct. Mater. 2022, 17, e01170. [Google Scholar] [CrossRef]
- Hu, A.; Liang, X.; Yu, J. Tensile characteristics of ultra-high-performance concrete. Mag. Concr. Res. 2018, 70, 314–324. [Google Scholar] [CrossRef]
- Wiemer, N.; Wetzel, A. Effect of Fibre Material and Fibre Roughness on the Pullout Behaviour of Metallic Micro Fibres Embedded in UHPC. Materials 2020, 13, 3128. [Google Scholar] [CrossRef]
- Zhou, Z.; Qiao, P. Direct Tension Test for Characterization of Tensile Behavior of Ultra-High Performance Concrete. J. Test. Eval. 2020, 48, 20170644. [Google Scholar] [CrossRef]
- JSCE. Recommendations for Design and Construction of Ultra High Performance Fiber Reinforced 19 Concrete Structures (Draft); Japan Society of Civil Engineers: Tokyo, Japan, 2004. [Google Scholar]
- AASHTO T 132-87; Standard Method of Test for Tensile Strength of Hydraulic Cement Mortars. American Association of State and Highway Transportation Officials: Washington, DC, USA, 2009.
- JSCE. Recommendations, for Design and Construction of High Performance Fiber Reinforced Cement Composites with Multiple Fine Cracks (HPFRCC); Japan Society of Civil Engineers: Tokyo, Japan, 2008. [Google Scholar]
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties, China. UDC China: Beijing, China, 2019.
- Zhao, J.; Shi, H.; Lu, X. Basic Properties and Test Methods of Ultra-High Performance Concrete; Building Materials Press: Beijing, China, 2019. [Google Scholar]
- Afnor, N.F. Specific Rules for Ultra-High Performance Fiber-Reinforced Concrete (UHPFRC); European Committee for Standardization: Brussels, Belgium, 2016; pp. P18–P710. [Google Scholar]
- Shen, R.; Cui, Q. New Fiber Reinforced Cement-Based Composites; Building Materials Industry Press: Beijing, China, 2004; Volume 7, pp. 61–66. [Google Scholar]
- Zhang, Z.; Shao, X. Axial Tensile Behavior Test of Ultra High Performance Concrete. China J. Highw. Transp. 2015, 28, 50–58. [Google Scholar]
- Li, L.; Zheng, W.Z.; Lu, S.S. Experimental study on mechanical properties of reactive powder concrete. J. Harbin Inst. Technol. 2010, 17, 795–800. [Google Scholar]
- Liao, W.C.; Chao, S.H.; Park, S.Y. Self-Consolidating High Performance Fiber Reinforced Concrete: SCHPFRC; Report; University of Michigan: Ann Arbor, MI, USA, 2006. [Google Scholar]
- Naaman, E. High Performance fiber reinforced cement composites. In Science and Applications; Taylor & Francis: Boca Raton, FL, USA, 2008; pp. 91–153. [Google Scholar]
- GB/T 17671-1999; Method of Testing Cements-Determination of Strength. Chinese National Standard: Beijing, China, 1999.
- ASTM C1609/C1609M; Standard Test Method for Flexural Performance of Fiber Reinforced Concrete (Using Beam with Third Point Loading). American Society for Testing and Materials: West Conshohocken, PA, USA, 2010.
- Fládr, J.; Bílý, P. Specimen size effect on compressive and flexural strength of high-strength fibre-reinforced concrete containing coarse aggregate. Compos. B Eng. 2018, 138, 77–86. [Google Scholar] [CrossRef]
- Yoo, D.; Banthia, N. Size effect in ultra-high-performance concrete beams. Eng. Fract. Mech. 2016, 157, 86–106. [Google Scholar] [CrossRef]
- RILEM TCS. Determination of fracture energy of mortar and concrete by means of three-point bend tests on notched beams. Mater. Struct. 1985, 18, 285e90. [Google Scholar]
- CECS 13: 2009; China Association for Engineering Construction Standardization; Standard Test Methods for Fiber Reinforced Concrete. China Planning Press: Beijing, China, 2009. (In Chinese)
- ASTM C 1018-97; Structural Test Method for Flexural Toughness and First Crack Strength of Fiber Reinforced Concrete (Using Beam with Third Point Loading). American Society of Testing and Materials: West Conshohocken, PA, USA, 1998.
- BSEN196-1-2005; Test Method for Cement. Part 4: Flexural Strength of Test Specimens. Chinese National Standard: Beijing, China, 2005.
- ASTM C293; Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Center Point Loading). ASTM International: West Conshohocken, PA, USA, 2016.
- Setra, A. Béton Fibrés à Ultra-Hautes Performences, Recommandations Provisoires; Fr. Janvier: Paris, France, 2002; p. 152. [Google Scholar]
- ASTM C348; Standard Test Method for Flexural Strength of Concrete. American Society of Testing and Materials: West Conshohocken, PA, USA, 2002.
- GT/B-50081; Standard for Test Method of Mechanical Properties in Ordinary Concrete. Chinese Standard: Beijing, China, 2016. (In Chinese)
- ASTM C1856-17; Standard Practice for Fabricating and Testing Specimens of Ultra-High Performance Concrete. ASTM: West Conshohocken, PA, USA, 2017.
- DIN EN 12390-5; Testing Hardened Concrete—Part 5: Flexural Strength of Test Specimens. Beuth Verlag GmbH: Berlin/Heidelberg, Germany, 2017.
- Hakeem, I.; Azad, A.; Ahmad, S. Effect of Steel Fibers and Thermal Cycles on Fracture Properties of Ultra-High-Performance Concrete. J. Test. Eval. 2013, 41, 20120182. [Google Scholar] [CrossRef]
- Larrard, F.; Sedran, T. Optimization of ultra-high-performance concrete by the use of a packing model. Cem. Conc. Res. 1994, 24, 997–1009. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.; Wu, C. Effects of steel fibres on dynamic strength of UHPC. Constr. Build. Mater. 2016, 114, 708–718. [Google Scholar] [CrossRef]
- JG/T 472-2015; Ministry of Housing and Urban-Rural Development of People’s Republic of China, Steel Fiber Reinforced Concrete. Standards Press of China: Beijing, China, 2015. (In Chinese)
- ACI 318-95; ACI Committee 318, Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 1995.
- ACI 363R-92; ACI Committee 363, State-of-the-Art Report on High-Strength Concrete. American Concrete Institute: Farmington Hills, MI, USA, 1992.
- ASTM C496/C496M; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. American Society for Testing and Materials: West Conshohocken, PA, USA, 2011.
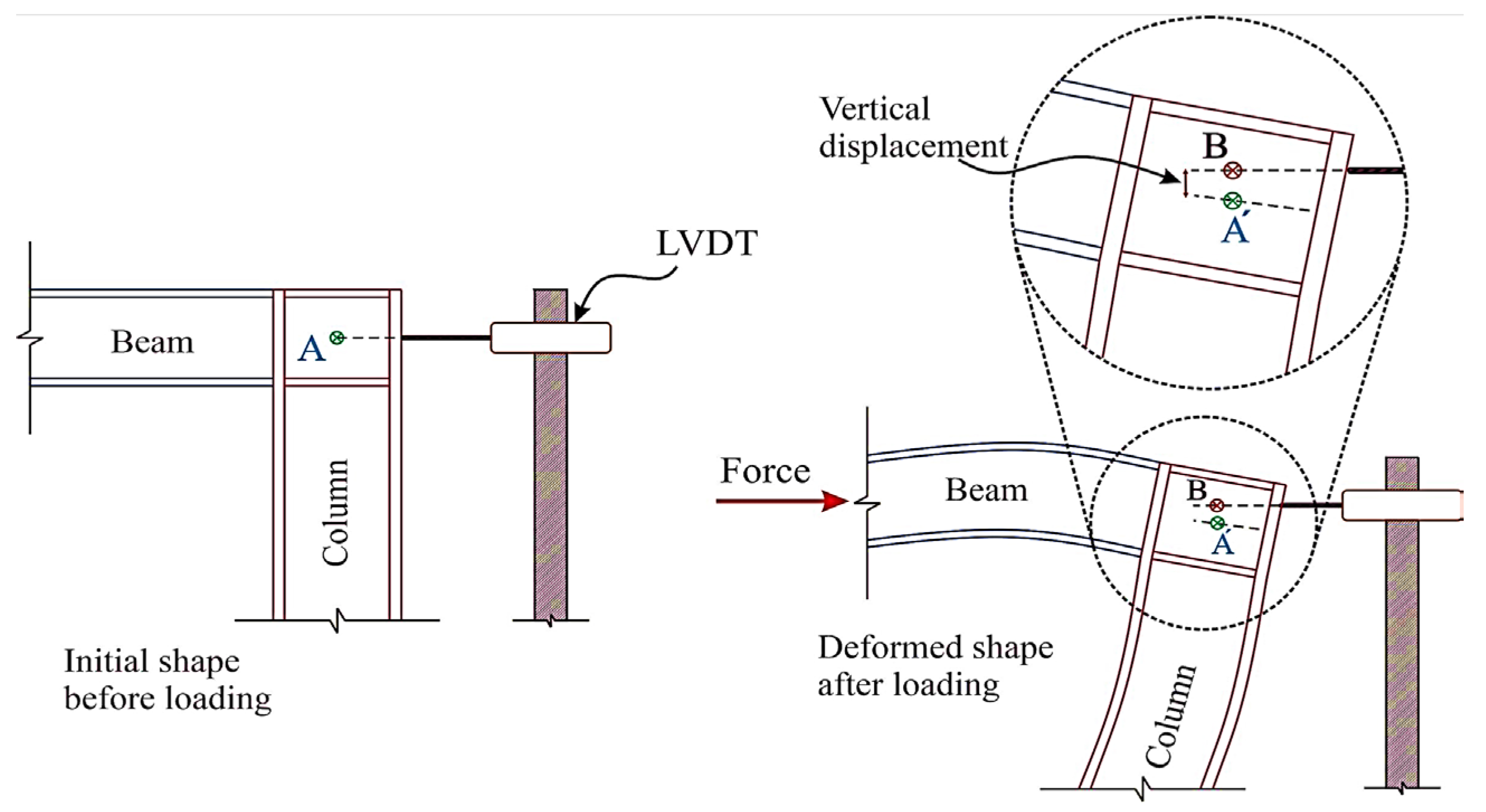
- Khalilzadehtabrizi, S.; Seifiasl, A.; Hoseinzadeh Asl, M. Measurement of deformation patterns in steel plate shear walls subjected to cyclic loading based on multi-target digital image correlation (MT-DIC). Structures 2021, 33, 2611–2627. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Hussein, H. Flexural strengthening of reinforced concrete beams or slabs using ultra-high performance concrete (UHPC): A state of the art review. Eng. Struct. 2020, 205, 110035. [Google Scholar] [CrossRef]
- Kang, S.T.; Kim, J.K. Investigation on the flexural behavior of UHPCC considering the effect of fiber orientation distribution. Constr. Build. Mater. 2012, 28, 5765. [Google Scholar] [CrossRef]
- Huang, Z.; Wu, W.; Niu, Y. Evaluation of crack propagation behavior of ultra-high performance concrete by 3D-DIC. Guangdong Build. Mater. 2021, 37, 9–14. [Google Scholar]



| Inclusion | Exclusion |
|---|---|
| (a) Steel fiber reinforcement. | (a) Non-steel fiber reinforcement. |
| (b) English language. | (b) Non-English language. |
| (c) Tensile strength (direct strength, flexural strength, spilling strength). | (c) Impact, blast, shear, fatigue. |
| (d) Journal or conference papers. | (d) Numerical or analytical studies. |
| (e) Experimental research papers. | (e) Structural members (beams, slabs, pillar). |
| Ref. | Test Properties | Fiber Combination | Fiber Types ( ) and Volume Fraction * | Fiber Tensile Strength [MPa] |
|---|---|---|---|---|
| [41] | Flexural strength, splitting strength | Single | SSF (8/0.2, 12/0.2, 16/0.2); 0%, 1%, 3%, 6%. | >2850 |
| [42] | Flexural strength | Single | SSF (13/0.2); 0%, 1%, 3%. | 1900 |
| [43] | Direct tensile strength | Single + Hybrid | SSF (13/0.2, 30/0.3), HSF (30/0.375), TSF (30/0.3); 2%. | 2428~2900 |
| [44] | Flexural strength, splitting strength | Single | SSF (6/0.16), HSF (30/0.55); 0%, 0.25%, 0.5%, 0.75%, 1%, 1.5%, 2%. | 1345~2250 |
| [45] | Direct tensile strength | Single | SSF (13/0.2); 0%, 2%. | - |
| [46] | Flexural strength, splitting strength | Single | HSF (30/0.6); 0%, 1%, 2%, 3%. | 1100 |
| [47] | Flexural strength | Single + Hybrid | SSF (13/0.2, 30/0.3), HSF (30/0.375, 62/0.775), TSF (30/0.3); 1%, 1.5%, 2%, 2.5%. | 1891~2788 |
| [40] | Direct tensile strength | Single | SSF (9/0.15, 13/0.175, 20/0.25); 0%, 1.5%, 3%. | 2500 |
| [48] | Direct tensile strength | Single | SSF (13/0.2), SPSF (13/0.2), HSF (13/0.2, 30/0.6); 0%, 1%, 1.75%, 2.5%. | 1890~2940 |
| [49] | Flexural strength | Single + Hybrid | SSF (13/0.22), HSF (13/0.22); 2.5%. | 2850 |
| [50] | Flexural strength, direct tensile strength | Single + Hybrid | SSF (13/0.2), HSF (30/0.5); 0%, 1%, 2%, 3%, 4%, 5%. | 1900 |
| [51] | Flexural strength | Single | SSF (13/0.2, 19.5/0.2, 30/0.3); 0.5%, 1%, 1.5%, 2%. | 2580~2788 |
| [52] | Direct tensile strength | Single + Hybrid | SSF (13/0.2, 30/0.3), HSF (30/0.375, 62/0.775), TSF (30/0.3); 1%, 1.5%, 2%, 2.5%. | 1891~2788 |
| [53] | Flexural strength, splitting strength | Single | SSF (6/0.16, 13/0.16); 0%, 2%, 2.5%. | 2000 |
| [54] | Flexural strength | Single + Hybrid | SSF (13/0.2, 16.3/0.2, 19.5/0.2), HSF (30/0.375); 2%. | 2311~2700 |
| [55] | Flexural strength | Single + Hybrid | SSF (13/0.2, 16.3/0.2, 19.5/0.2); 1.5%, 2%. | -- |
| [56] | Flexural strength | Single | SSF (13/0.2); 0%, 1%, 2%, 3%. | 2850 |
| [57] | Direct tensile strength | Single | SSF (13/0.2), HSF (30/0.38), TSF (18/0.3); 1.5%, 2%, 2.5%, 3%. | 2100~2900 |
| [58] | Direct tensile strength | Single | SSF (13/0.2), HSF (30/0.38), TSF (30/0.3); 1%, 1.5%, 2%, 2.5%. | 2100~3100 |
| [59] | Flexural strength | Single | SSF (13/0.2), HSF (13/0.2), CSF (13/0.2); 0%, 2%. | 2800 |
| [60] | Flexural strength | Single + Hybrid | SSF (6/0.2, 13/0.2); 0%, 2%. | 2800 |
| [61] | Flexural strength | Single | SSF (13/0.2), HSF (13/0.2), CSF (13/0.2); 0%, 1%, 2%, 3%. | 2800 |
| [62] | Flexural strength | Single | SSF (13/0.2, 16.3/0.2, 19.5/0.2); 2%. | 2500 |
| [63] | Flexural strength | Single + Hybrid | SSF (13/0.2, 19.5/0.2), HSF (30/0.38), TSF (30/0.3); 2%. | 2428~2788 |
| [64] | Direct tensile strength | Single | SSF (13/0.2), HSF (30/0.375, 25/0.375), TSF (30/0.3); 2%. | 2428~2900 |
| [65] | Flexural strength | Single | SSF (13/0.2, 19.5/0.2, 30/0.3), HSF (30/0.38), TSF (30/0.3); 0.5%, 1%, 1.5%, 2%. | 2428~2788 |
| [66] | Flexural strength | Single + Hybrid | SSF (13/0.2, 19.5/0.2, 30/0.2); 0%, 0.5%, 1%, 1.5%, 2%. | 2500~2788 |
| [67] | Flexural strength | Single + Hybrid | SSF (13/0.2), HSF (20/0.25, 20/0.35); 2%. | 2810~2940 |
| [68] | Flexural strength, splitting strength | Single + Hybrid | SSF (30/0.8, 13/0.2); 0%, 0.5%, 1.5%. | 700~2500 |
| [69] | Flexural strength, splitting strength | Single | SSF (15/0.6); 0%, 2%. | 1700 |
| [70] | Flexural strength | Single + Hybrid | SSF (13/0.2), TSF (25/0.5), HSF (34/0.54); 1%, 1.5%, 2%, 2.5%, 3%. | 1100~2000 |
| [71] | Flexural strength | Single | SSF (6/0.16, 13/0.2, 20/0.2); 2%. | 2850 |
| [72] | Flexural strength | Single | SSF (6/0.16, 13/0.2, 20/0.2); 1%, 2%, 3%. | 2850 |
| [73] | Flexural strength | Single + Hybrid | SSF (13/0.2), HSF (25/0.2); 2%. | 2500 |
| [74] | Flexural strength | Single + Hybrid | SSF (6/0.2, 10/0.2, 15/0.2); 2.5%. | >2850 |
| [75] | Direct tensile strength | Single | SSF (13/0.2); 0%,1.3%, 1.8%. | 2850 |
| [76] | Splitting strength | Single | SSF (13/0.22); 2%. | >2850 |
| [77] | Flexural strength, splitting strength | Single + Hybrid | SSF (6/0.2, 13/0.2, 20/0.2); 0%, 2%. | - |
| [78] | Flexural strength, splitting strength | Single | SSF (35/0.9); 0%, 2%. | 1250 |
| [79] | Flexural strength, splitting strength, direct tensile strength | Single | SSF (13/0.2), HSF (13/0.22, 16/0.22, 16/0.25); 0%, 1%, 2%, 3%. | 2500~2800 |
| [80] | Direct tensile strength | Single | SSF (13/0.2); 0%, 0.5%, 1%, 1.5%, 2%, 2.5%. | 2850 |
| [81] | Flexural strength, splitting strength | Single + Hybrid | SSF (6/0.2, 13/0.2, 20/0.2); 0%, 2%. | 2500~2788 |
| [82] | Flexural strength, splitting strength | Single | SSF (12/0.2); 0%, 0.5%, 1%, 1.5%, 2%, 2.5%, 3%. | 2850 |
| [83] | Flexural strength | Single | SSF (13/0.2); 0%, 1%, 2%, 2.5%. | 2850 |
| [84] | Flexural strength, direct tensile strength | Hybrid | SSF (13/0.16), HSF (30/0.76); 2%. | 1900~2700 |
| [85] | Flexural strength, splitting strength | Single | SSF (13/0.22); 2%. | 2850 |
| [86] | Flexural strength, splitting strength | Single | SSF (13/0.2); 0%, 0.5%, 1%, 1.5%, 2%. | - |
| [87] | Flexural strength, direct tensile strength | Single | SSF (13/0.2), TSF (13/0.5); 1%, 1.5%, 2%, 2.5%, 3%. | - |
| [88] | Direct tensile strength | Single | SSF (20/0.3, 13/0.175), HSF (35/0.75, 35/0.55, 30/0.35); 0%, 1.5%, 2%, 3%, 4%, 5%. | 1000~1250 |
| [89] | Direct tensile strength | Single | SSF (13/0.4); 0.75%, 1%, 1.5%, 2%. | - |
| [90] | Flexural strength | Single | SSF (13/0.2); 2%. | 1900 |
| [91] | Flexural strength | Single | SSF (13/0.2); 0%, 1%, 3%. | 1900 |
| [92] | Flexural strength, splitting strength | Single | SSF (13/0.2); 1.5%, 2%, 2.5%, 3%. | ≥2800 |
| [93] | Direct tensile strength | Single + Hybrid | SSF (7/0.18), HSF (13/0.22, 35/0.58); 0%, 1%, 2%, 3%, 4%, 5%. | ≥2850 |
| [94] | Flexural strength | Single | SSF (13/0.25, 17/0.25, 13/0.2, 17/0.2); 1%, 2.5%. | 1980~2000 |
| Schematic Diagram of Sample Shape | Cross-Sectional Testing Area [mm2] | Test Standard | Loading Rate | Ref. |
|---|---|---|---|---|
 | 30 × 13 | According to JSCE [99]. | 0.4 mm/min. | [43] |
 | 26 × 50 | No standard. | 0.4 mm/min. | [45] |
 | 40 × 40 (notched) | No standard. | 0.6 mm/min. and 0.3 mm/min. | [40] |
 | 100 × 100 | No standard. | 0.05 mm/min. | [48] |
 | 50 × 25 | No standard. | 0.05 mm/min. | [50] |
 | 50 × 100 | No standard. | 0.4 mm/min. | [52] |
 | 25 × 25 | According to AASHTO T 132–87 [96]. | 0.6 mm/min. | [57] |
 | 50.8 × 25.4 | No standard. | -- | [58] |
 | 30 × 13 | According to JSCE [99]. | 0.4 mm/min. | [64] |
 | 50 × 100 | According to GB/T 50081-2019 [97] and T/CBMF 37-2018 [100]. | 0.15 mm/min. | [75] |
 | 30 × 13 | According to JSCE [99]. | 0.5 mm/min. | [79] |
 | 100 × 100 | According to NF P 18-710 [101]. | 0.5 mm/min. | |
 | 50 × 100 | No standard. | 0.2 mm/min. | [80] |
 | 40 × 40 | No standard. | 0.1 mm/min. | [84] |
 | 51 × 51 | According to FHWA [98]. | 0.05 mm/min. | [87] |
 | 40 × - | No standard. | 0.1 mm/min. | [88] |
 | 50 × 50 | No standard. | 0.4 mm/min. | [89] |
 | 60 × 130 | No standard. | 0.05 mm/min. | [93] |
| Ref. | Prediction Formula | Fiber Shape | Fiber Volume Content | Eq. |
|---|---|---|---|---|
| [57] | Straight | 1.5~3% | (4) | |
| Hooked end | ||||
| Twisted | ||||
| [106] | - | - | (5) | |
| [40] | Straight | 1.5~3% | (6) | |
| [103] | Straight | 2~3.5% | (7) | |
| Hooked end | ||||
| Hooked end | 2~3.5% | (8) | ||
| Straight | ||||
| [104] | Straight | 2% | (9) | |
| [79] | Straight | 2% | (10) | |
| Hooked end | 0~3% | |||
| [105] | - | - | (11) | |
| [80] | Straight | 0.5~2.5% | (12) | |
| (13) | ||||
| [84] | Straight and hooked-end hybrid | 2% | (14) | |
| [88] | Straight | 0~4% | (15) | |
| Hooked end | 0~4% | (16) |
| Schematic Diagram of Sample Shape | Test Standard | Loading Rate | Specimen Size [mm3] | Ref. |
|---|---|---|---|---|
 | According to ASTM C1609 [108]. | 0.05 mm/min. | 100 × 100 × 400 | [41] |
 | According to ASTM C1609 [108]. | 0.5 mm/min. | 100 × 100 × 457 | [42] |
 | According to RILEM 50-FMC/198 [111]. | 0.02 mm/min. | 70 × 70 × 280 (notched) | [44] |
 | According to CECS 13:2009 [112]. | -- | 100 × 100 × 400 | [46] |
 | According to ASTM C1018-97 [113] and ASTM C 1609 [108]. | 0.4 mm/min. | 100 × 100 × 350 | [47] |
 | According to BS EN 196-1 (CEN 2005) [114]. | -- | 40 × 40 × 160 | [49] |
 | According to ASTM C1609 [108]. | -- | 76.2 × 76.2 × 304.8 | [50] |
 | According to ASTM C1609 [108]. | 0.4 mm/min. | 100 × 100 × 400 | [51] |
 | According to ASTM C1609 (ASTM, 2006) [108]. | -- | 70 × 70 × 350 (notched) | [53] |
 | No standard. | -- | [54] | |
 | No standard. | 0.2 mm/min. | -- | [55] |
 | According to GB/T 17671-1999 [107]. | -- | 40 × 40 × 160 | [56] |
 | No standard. | 1 mm/min. | 40 × 40 × 160 | [59] |
 | According to GB/T 17671-1999 [107]. | 40 × 40 × 160 | [60] | |
 | No standard. | 0.2 mm/min. | 40 × 40 × 160 | [61] |
 | According to ASTM C 1609/C 1609M [108]. | 0.4 mm/min. | 100 × 100 × 400 | [62] |
 | According to ASTM C1609 [108]. | 0.4 mm/min. | 100 × 100 × 400 | [63] |
 | According to ASTM C1609 [108]. | 0.4 mm/min. | 100 × 100 × 400 | [65] |
 | According to ASTM C1609 [108]. | 0.4 mm/min. | 100 × 100 × 400 | [66] |
 | According to ASTM C1609 [108]. | 0.1 mm/min. | 100 × 100 × 400 | [67] |
 | According to ASTM C1609 [108]. | 0.05 mm/min. | 100 × 100 × 450 | [68] |
 | According to ASTM C293 [115]. | 0.05 MPa/min. | 100 × 100 × 500 | [69] |
 | According to ASTM C1609 [108]. | 1.83 mm/min. | 100 × 100 × 350 | [70] |
 | No standard. | 0.4 mm/min. | 70 × 70 × 230 | [71] |
 | No standard. | 0.4 mm/min. | 70 × 70 × 230 | [72] |
 | According to French interim UHPC guideline annex [116]. | 0.5 mm/min. | 70 × 70 × 280 | [73] |
 | No standard. | 0.1 kN/s and 0.3 mm/min. | 100 × 100 × 400 | [74] |
 | No standard. | 0.1 kN/s and 0.3 mm/min. | 100 × 100 × 400 (notched) | |
 | According to ASTM C1609 [108]. | 0.2 mm/min. | 100 × 100 × 400 | [77] |
 | According to ASTM C1609 [108]. | 100 × 100 × 350 | [78] | |
 | According to NF P 18-710 [101]. | 0.2 mm/min. | 100 × 100 × 400 | [79] |
 | According to ASTM C1609 [108]. | 0.2 mm/min. | 100 × 100 × 400 | [81] |
 | According to ASTM C 348 [117]. | 40 × 40 × 160 | [82] | |
 | No standard. | 0.4 mm/min. | 70 × 70 × 230 | [83] |
 | According to ASTM C1609/C1609M [108]. | -- | 100 × 100 × 500 | [84] |
 | According to GB/T 50081 [118]. | 0.05 mm/min. | 70.7 × 70.7 × 220 | [85] |
 | According to ASTM C1609 [108]. | 0.05 mm/min. | 100 × 100 × 400 | [86] |
 | According to ASTM C1609 [108] and ASTM C1856 [119]. | -- | 102 × 102 × 356 | [87] |
 | According to ASTM C1609 [108]. | 0.1 mm/min. | 75 × 75 × 305 | [90] |
 | According to ASTM C1609 [108]. | 0.5 mm/min. | 64 × 51 × 381 | [91] |
| 100 × 100 × 457 | ||||
 | According to CECS (2013) [112]. | -- | 100 × 100 × 400 | [92] |
 | 100 × 100 × 400 (notched) | |||
 | According to DIN EN 12390-5 [120]. | 0.6 mm/min. | 40 × 40 × 160 | [94] |
| Ref. | Empirical Formula | Fiber Type | Fiber Content | Eq. |
|---|---|---|---|---|
| [46] | Hooked end | 0~3% | (21) | |
| [59] | Straight | 2% | (22) | |
| Hooked end | ||||
| Corrugated | ||||
| [66] | Straight | 0~2% | (23) | |
| [71] | Straight | 2% | (24) | |
| [72] | Straight | 1~3% | (25) | |
| [73] | * | Straight | 2% | (26) |
| Hooked end | ||||
| [82] | Straight | 0~3% | (27) | |
| [83] | Straight | 0~2.5% | (28) |
| Author(s), (Year) | Test Standard | Loading Rate | Shape and Size [mm3] | Ref. |
|---|---|---|---|---|
| Abbas et al. (2015) | According to ASTM C496/C496M [127]. | 0.025 mm/min. | Cylinder: 75 × 150 | [41] |
| Gesoglu et al. (2016) | According to ASTM C496 [127]. | -- | Cubes: 100 × 100 × 100 | [44] |
| Jin and Zhang et al. (2018) | According to CECS 13:2009 [112]. | -- | Cubes: 100 × 100 × 100 | [46] |
| Prem et al. (2015) | According to ASTM C1609 [108]. | 0.03 mm/min. | Prisms: 70 × 70 × 350 (notched) | [53] |
| Mizani and Sadeghi et al. (2022) | According to ASTM C496 [127]. | 1 MPa/min. | Cylinder: 150 × 300 | [68] |
| Raza et al. (2021) | According to ASTM C496 [127]. | -- | Cylinder: 100 × 200 | [69] |
| Mao et al. (2021) | According to GB/T 50081–2019 [97]. | 0.08 MPa/s. | Cubes: 100 × 100 × 100 | [76] |
| Niu et al. (2021) | No standard. | 1.2 MPa/s. | Cubes: 100 × 100 × 100 | [77] |
| Raza et al. (2021) | According to ASTM C496 [127]. | -- | Cylinder: 100 × 200 | [78] |
| Fang et al. (2022) | According to ASTM C496 [127]. | 1 kN/s. | Cylinder: 100 × 200 | [79] |
| Cylinder: 150 × 300 | ||||
| Jiao et al. (2022) | According to ASTM C496 [127]. | 1.2 MPa/s. | Cubes: 100 × 100 × 100 | [81] |
| Ashkezari et al. (2020) | According to ASTM C 496 [127]. | -- | Cylinder: 150 × 300 | [82] |
| Abid et al. (2019) | According to GB/T 50081 [118]. | 0.05 mm/min. | Cubes: 70.7 × 70.7 × 70.7 | [85] |
| Meng et al. (2022) | According to ASTM C1069 [108]. | 0.12 MPa/s. | Cubes: 100 × 100 × 100 | [86] |
| Wang et al. (2022) | According to CECS (2013) [112]. | -- | Cubes: 100 × 100 × 100 | [92] |
| Ref | Empirical Formula | Fiber Type | Fiber Content | Eq. |
|---|---|---|---|---|
| [46] | * | Hooked end | 0~3% | (32) |
| [82] | Straight | 0~3% | (33) | |
| Ref. | Fiber Combination | Fiber Shape | Application of DIC to UHPC |
|---|---|---|---|
| [42] | Single | Straight | (a) Characterize the main cracks and secondary cracks of the UHPC. (b) Analysis of the strain field at different load values. |
| [70] | Single + Hybrid | Hooked end | (a) Analysis of the strain field representing different deflections. (b) The maximum crack width of the UHPC reinforced with different steel fibers shapes. (c) Quantify the crack width within the depth range of the sample. |
| Twisted | |||
| Straight | |||
| [77] | Single + Hybrid | Straight | (a) Characterize the crack shape and strain distribution under different load values. (b) Quantify the crack width within the depth range of the sample. (c) Quantification of the crack growth rate. |
| [79] | Single | Straight | (a) Comparison of the strain cloud maps and failure patterns for the different specimens. |
| Hooked end | |||
| [81] | Single + Hybrid | Straight | (a) Characterize the crack shape and strain distribution under different load values. (b) Quantify the crack width within the depth range of the sample. |
| [86] | Single | Straight | (a) Characterization of horizontal displacement field of UHPC in different loading stages. (b) Changes in crack propagation in different loading stages. (c) Displacement of crack opening in different loading stages. |
| [91] | Single | Straight | (a) Comparison between DIC and traditional LVDT measurement methods. (b) Quantify crack width over a range of specimen heights. (c) Characterize the strain distribution under different load values. |
| [131] | Single | Straight | (a) Crack propagation in different loading stages. (b) Crack width in the range of sample depth under different loads. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, W.; Yu, F.; Qiu, L.; Guo, Y.; Wang, J.; Han, B. Effect of Steel Fibers on Tensile Properties of Ultra-High-Performance Concrete: A Review. Materials 2024, 17, 1108. https://doi.org/10.3390/ma17051108
Du W, Yu F, Qiu L, Guo Y, Wang J, Han B. Effect of Steel Fibers on Tensile Properties of Ultra-High-Performance Concrete: A Review. Materials. 2024; 17(5):1108. https://doi.org/10.3390/ma17051108
Chicago/Turabian StyleDu, Wanghui, Feng Yu, Liangsheng Qiu, Yixuan Guo, Jialiang Wang, and Baoguo Han. 2024. "Effect of Steel Fibers on Tensile Properties of Ultra-High-Performance Concrete: A Review" Materials 17, no. 5: 1108. https://doi.org/10.3390/ma17051108
APA StyleDu, W., Yu, F., Qiu, L., Guo, Y., Wang, J., & Han, B. (2024). Effect of Steel Fibers on Tensile Properties of Ultra-High-Performance Concrete: A Review. Materials, 17(5), 1108. https://doi.org/10.3390/ma17051108