Strength Characteristics, Ultrasonic Wave Velocity, and the Correlation between Them in Clay Bricks under Dry and Saturated Conditions
Abstract
:1. Introduction
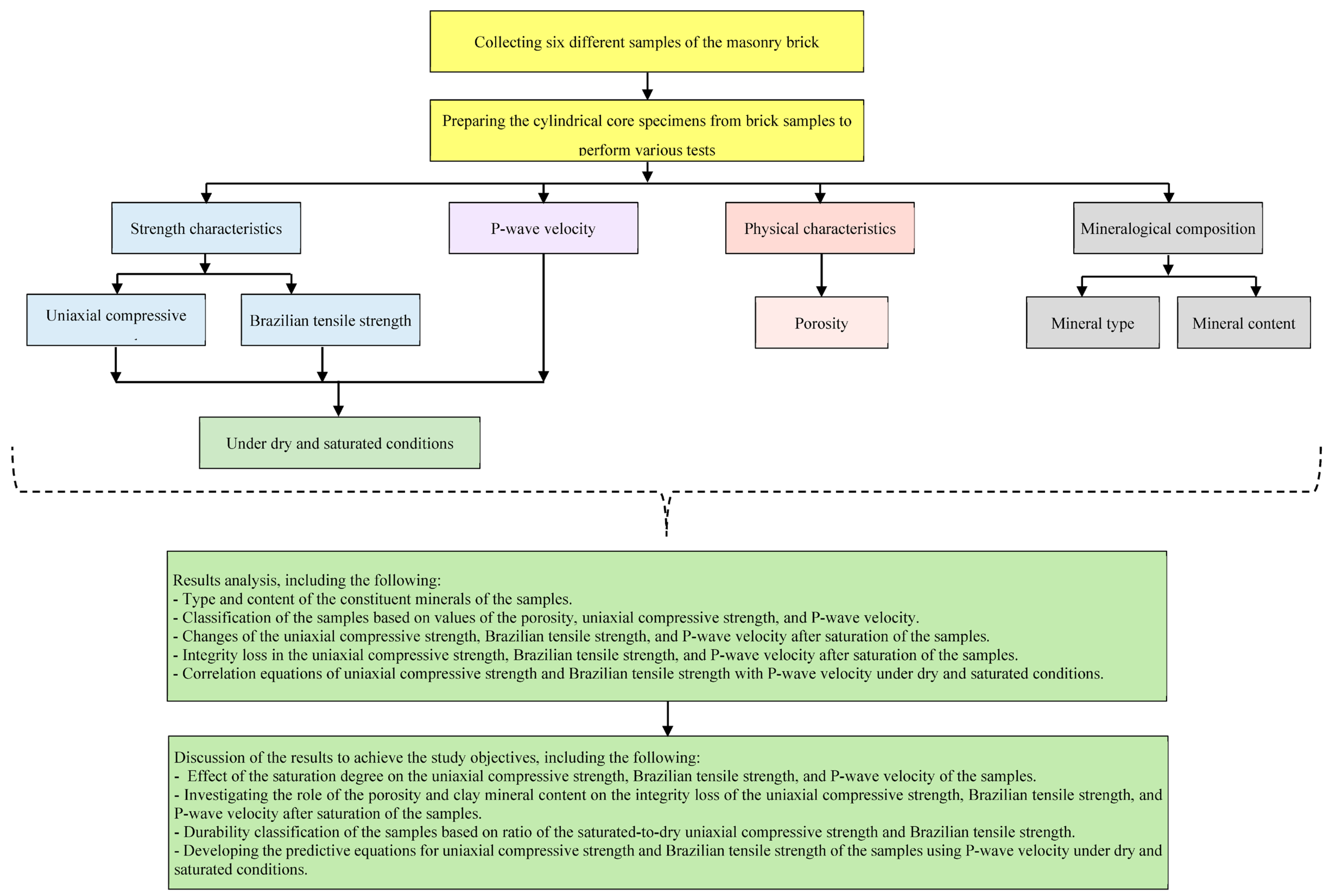
2. Materials and Methods
2.1. Mineralogical Composition
2.2. Physical Characteristics
2.3. Strength Characteristics
2.4. P-Wave Velocity
3. Results and Discussion
3.1. Mineralogical Composition and Porosity of the Samples
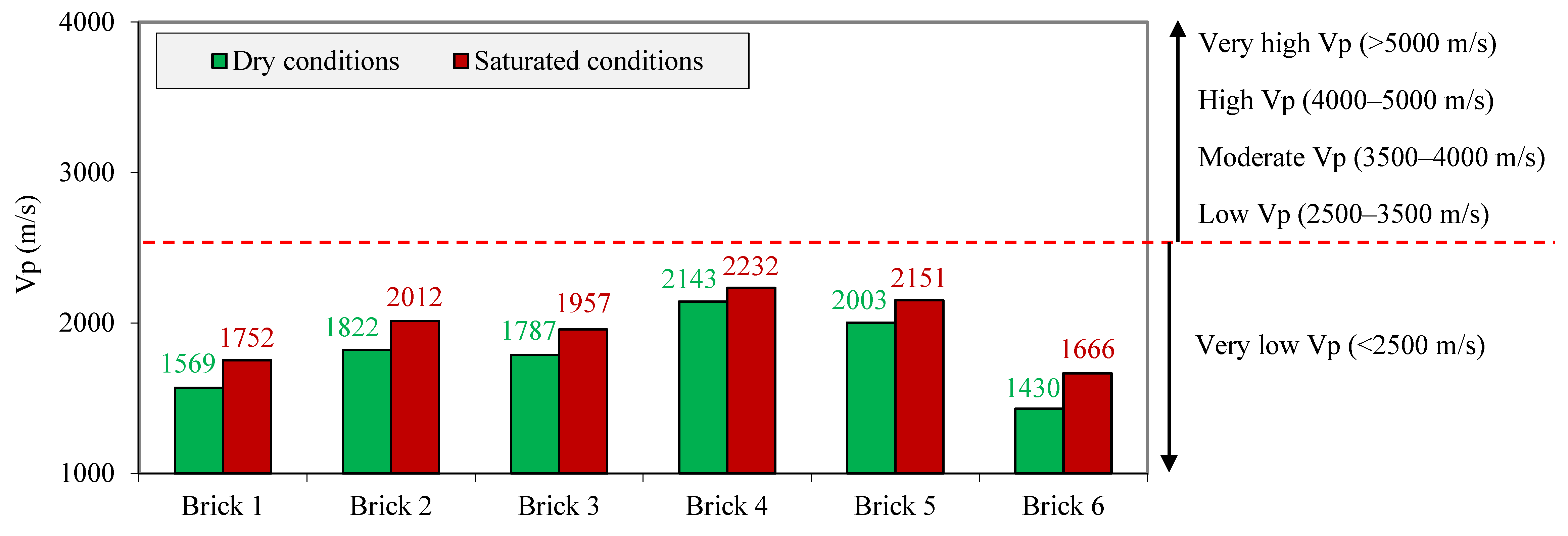
3.2. Strength Characteristics and Ultrasonic Wave Velocity of the Samples
3.3. Correlating the Strength Characteristics with Ultrasonic Wave Velocity
4. Conclusions
- After the saturation of the samples, significant reductions occurred in the UCS and BTS ranging from −7.95 to −40.91% and −15.60 to −48.15%, respectively, whereas an increase was observed for the Vp from 4.15 to 16.50%. The main reasons for the changes in the UCS and BTS and in the Vp were the softening and lubricating effects of water on the saturated samples.
- The change level of the UCS, BTS, and Vp after saturation of the samples was strongly affected by the n and clay minerals (CM). An increasing trend in the change intensity of the UCS, BTS, and Vp with the increasing n and CM of the sample was obtained.
- Based on values of the saturated-to-dry UCS and BTS, samples with lower n and CM have the highest durability against the softening and lubricating effects of water. An increase in the n and CM will lead to more intense integrity loss of the samples after their saturation.
- Good correlation equations with determination coefficients (R2) varying from 0.95 to 0.98 were obtained between the Vp and the UCS and BTS. The significance and performance of the equations were evaluated using a diagonal line, variance analysis, and statistics indices including coefficient values accounted for (VAF) and the root mean square error (RMSE). The results indicated that correlation equations are at a good accuracy level for predicting the UCS and BTS from the Vp for samples under both dry and saturated conditions.
- The predictive equations of the UCS and BTS from the Vp can be used for clay bricks from other buildings in the world with ranges of UCS, BTS, and Vp similar to the samples in the present study. As a result, in some cases where preparing test samples from a building is not possible for the direct measurement of the UCS and BTS, these equations can be used to avoid performing UCS and BTS tests. Such predictive equations can be developed for various bricks with a wide range of mineralogical compositions and physicomechanical characteristics. Therefore, further studies in this regard need to be undertaken by researchers in the future.
- It must be noted that clay bricks are notoriously variable and heterogeneous in their UCS, BTS, and Vp, which depend on the nature of their porous media such as the size distribution and shape of the pores and internal structure. Therefore, predictive equations for the UCS and BTS can be developed for various bricks with a wide range of mineralogical compositions and physicomechanical characteristics. In this regard, further studies need to be performed by researchers in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crespo-Lopez, L.; Benavente, D.; Morales-Ruano, S.; Vazquez-Vilchez, M.; Cultrone, G. Non-destructive techniques (NDT) and statistical analysis for the characterization of bricks made with added glass. Constr. Build. Mater. 2023, 408, 133583. [Google Scholar] [CrossRef]
- Ayala, D.D.; Aktas, Y.D. Moisture dynamics in the masonry fabric of historic buildings subjected to wind-driven rain and flooding. Build. Environ. 2016, 104, 208–220. [Google Scholar]
- Li, Y.; Kong, Z.; Xie, H.; Ma, Y.; Mu, B.; Hokoi, S. Construction type influences features of rising damp of blue-brick masonry walls. Constr. Build. Mater. 2021, 284, 122791. [Google Scholar] [CrossRef]
- Yue, J.; Li, Y.; Luo, Z.; Huang, X.; Kong, Q.; Wang, Z. Study on deterioration law and mechanism of Gray brick due to salt crystallization. Materials 2022, 15, 2936. [Google Scholar] [CrossRef] [PubMed]
- Jamshidi, A. Study of building stones durability against the freeze-thaw process: Current methods and recommendations for the future. J. Build. Eng. 2024, 86, 108772. [Google Scholar] [CrossRef]
- Seco, A.; Urmeneta, P.; Prieto, E.; Marcelino, S.; Garcia, B.; Miqueleiz, L. Estimated and real durability of unfired clay bricks: Determining factors and representativeness of the laboratory tests. Constr. Build. Mater. 2017, 131, 600–605. [Google Scholar] [CrossRef]
- Ikechukwu, A.F.; Shabangu, C. Strength and durability performance of masonry bricks produced with crushed glass and melted PET plastics. Case Stud. Constr. Mater. 2021, 14, e00542. [Google Scholar] [CrossRef]
- Ajalloeian, R.; Jamshidi, A.; Khorasani, R. Assessments of ultrasonic pulse velocity and dynamic elastic constants of granitic rocks using petrographic characteristics. Geotech. Geol. Eng. 2020, 38, 2835–2844. [Google Scholar] [CrossRef]
- Iyare, U.C.; Blake, O.O.; Ramsook, R. Estimating the uniaxial compressive strength of argillites using Brazilian tensile strength, ultrasonic wave velocities, and elastic properties. Rock Mech. Rock Eng. 2021, 54, 2067–2078. [Google Scholar] [CrossRef]
- Cobanoglu, I.; Celik, S.B. Estimation of uniaxial compressive strength from point load strength, Schmidt hardness and P-wave velocity. Bull. Eng. Geol. Environ. 2008, 67, 491–498. [Google Scholar] [CrossRef]
- Altindag, R. Correlation between P-wave velocity and some mechanical properties for sedimentary rocks. J. S. Afr. Inst. Min. Metall. 2012, 112, 229–237. [Google Scholar]
- Jamshidi, A.; Zamanian, H.; Zarei Sahamieh, R. The effect of density and porosity on the correlation between uniaxial compressive strength and P-wave velocity. Rock Mech. Rock Eng. 2018, 51, 1279–1286. [Google Scholar] [CrossRef]
- Bahrami, S.; Sarikhani, R.; Jamshidi, A.; Emami Mybodi, M.R. A comparative assessment of the effects of sodium and magnesium sulfates on the physico-mechanical characteristics of Abasabad Travertine, Mahallat, Urumieh-Dokhtar Magmatic Belt, Iran. Environ. Earth Sci. 2023, 82, 92. [Google Scholar] [CrossRef]
- Vasarhelyi, B.; Van, P. Influence of water content on the strength of rock. Eng. Geol. 2006, 84, 70–74. [Google Scholar] [CrossRef]
- Erguler, Z.A.; Ulusay, R. Water-induced variations in mechanical properties of clay-bearing rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 355–370. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Jong, M.C. Water saturation effects on the Brazilian tensile strength of gypsum and assessment of cracking processes using high-speed video. Rock Mech. Rock Eng. 2013, 47, 1103–1115. [Google Scholar] [CrossRef]
- Karakul, H. Investigation of saturation effect on the relationship between compressive strength and Schmidt hammer rebound. Bull. Eng. Geol. Environ. 2017, 76, 1143–1152. [Google Scholar] [CrossRef]
- Abdi, Y.; Khanlari, G.R.; Jamshidi, A. Correlation between mechanical properties of sandstones and P-wave velocity in different degrees of saturation. Geotech. Geol. Eng. 2024, 42, 665–674. [Google Scholar] [CrossRef]
- Jamshidi, A. An investigation on ultrasonic wave velocity of laminated sandstone under freeze-thaw and salt crystallization cycles: Insights from anisotropy effects. J. Build. Eng. 2023, 71, 106461. [Google Scholar] [CrossRef]
- Kahraman, S. The correlations between the saturated and dry P-wave velocity of rocks. Ultrasonics 2007, 46, 341–348. [Google Scholar] [CrossRef]
- Torok, A.; Vasarhelyi, B. The influence of fabric and water content on selected rock mechanical parameters of travertine, examples from Hungary. Eng. Geol. 2010, 115, 237–245. [Google Scholar] [CrossRef]
- Cobanoglu, I.; Celik, S.B. Determination of strength parameters and quality assessment of Denizli travertines (SW Turkey). Eng. Geol. 2012, 129–130, 38–47. [Google Scholar] [CrossRef]
- Karakul, H.; Ulusay, R. Empirical correlations for predicting strength properties of rocks from P-wave velocity under different degrees of saturation. Rock Mech. Rock Eng. 2013, 46, 981–999. [Google Scholar] [CrossRef]
- Kim, E.; Changani, H. Effect of water saturation and loading rate on the mechanical properties of red and buff sandstones. Int. J. Rock Mech. Min. Sci. 2016, 88, 23–28. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Cai, Y.T.; Huang, S.B.; Guo, Y.L.; Liu, G.F. Effect of water saturation on uniaxial compressive strength and damage degree of clay-bearing sandstone under freeze-thaw. Bull. Eng. Geol. Environ. 2020, 79, 2021–2036. [Google Scholar] [CrossRef]
- Khajevand, R. Determining dry and saturated strength of rocks by using the Schmidt hammer. Iran. J. Sci. 2023, 47, 779–790. [Google Scholar] [CrossRef]
- Arman, H.; Abdelghany, O.; Saima, M.A.; Aldahan, A.; Mahmoud, B.; Hussein, S.; Fowler, A.R. Petrological control on engineering properties of carbonate rocks in arid regions. Bull. Eng. Geol. Environ. 2021, 80, 4221–4233. [Google Scholar] [CrossRef]
- Jamshidi, A.; Sedaghatnia, M. The slake durability of argillaceous and non-argillaceous rocks: Insights from effects of the wetting–drying and rock lumps abrasion. Rock Mech. Rock Eng. 2023, 56, 5115–5131. [Google Scholar] [CrossRef]
- ISRM. Rock characterization, testing and monitoring. In ISRM Suggested Methods; Brown, E.T., Ed.; Pergamon Press: Oxford, UK, 1981. [Google Scholar]
- Sousa, L.M.O.; del Rio, L.M.S.; Calleja, L.; de Argandona, V.G.R.; Rey, A.R. Influence of microfractures and porosity on the physico-mechanical properties and weathering of ornamental granites. Eng. Geol. 2005, 77, 153–168. [Google Scholar] [CrossRef]
- Benavente, D.; Martinez-Martinez, J.; Cueto, N.; Ordonez, S.; Garcia-del-Cura, M.A. Impact of salt and frost weathering on the physical and durability properties of travertines and carbonate tufas used as building material. Environ. Earth Sci. 2018, 77, 147. [Google Scholar] [CrossRef]
- Torabi-Kaveh, M.; Mehrnahad, H.; Morshedi, S.; Jamshidi, A. Investigating the durability of weak rocks to forecast their long-term behaviors. Bull. Eng. Geol. Environ. 2022, 81, 8. [Google Scholar] [CrossRef]
- Chen, T.C.; Yeung, M.R.; Mori, N. Effect of water saturation on deterioration of welded tuff due to freeze–thaw action. Cold Reg. Sci. Technol. 2004, 38, 127–136. [Google Scholar] [CrossRef]
- Song, S.; Yu, H.; Ma, H. Influence of drying conditions on the durability of concrete subjected to the combined action of chemical attack and freeze–thaw cycles. Materials 2024, 17, 1131. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, F.M.; Lourenço, P.B.; Castro, F. Ancient Clay Bricks: Manufacture and Properties. In Materials, Technologies and Practice in Historic Heritage Structures; Dan Bostenaru, M., Ed.; Springer: Berlin, Germany, 2010; pp. 29–48. [Google Scholar]
- Livingston, R.A. Materials analysis of the masonry of the Hagia Sophia Basilica, Istanbul. In Proceedings of the Third International Conference on Structural Studies, Repairs and Maintenance of Historical Building, Bath, UK, 16–18 June 1993; pp. 15–31. [Google Scholar]
- Esbert, R.M.; Ordaz, J.; Alonso, J.; Montoto, M. Propriedades físicas. In Manual de Diagnosis y Tratamiento de Materiales Pétreos y Ceramicos; Collegi d’Aparelladors i Arquitectes de Barcelona: Barcelona, Spain, 1997; pp. 21–38. [Google Scholar]
- Maierhofer, C.; Leipold, S.; Schaurich, D.; Binda, L.; Saisi, A. Determination of the moisture distribution in the outside walls of S. Maria Rossa using radar. In Proceedings of the Seventh International Conference on Ground Penetrating Radar, Lawrence, KS, USA, 27–30 May 1998; pp. 509–514. [Google Scholar]
- Noor-E-Khuda, S.; Albermani, F. Mechanical properties of clay masonry units: Destructive and ultrasonic testing. Constr. Build. Mater. 2019, 219, 111–120. [Google Scholar] [CrossRef]
- IAEG. Classification of Rocks and Soils for Engineering Geological Mapping Part 1: Rock and Soil Materials. Bull. Int. Assoc. Eng. Geol. 1979, 19, 364–371. [Google Scholar] [CrossRef]
- Alvarez De Buergo, M.; Limon, T.G. Restauracion de Edificios Monumentales; Centro de Estudios y Experimentacion de Obras Publicas: Madrid, Spain, 1994. [Google Scholar]
- Pauri, M.; Stazi, A.; Mastrosanti, F.; D’orazio, M. The decay of ancient building masonry, a case study. In Proceedings of the Tenth International Brick/Block Masonry Conference, Calgary, AB, Canada, 5–7 July 1994; pp. 1295–1304. [Google Scholar]
- Koroth, S.R. Evaluation and Improvement of Frost Durability of Clay Bricks. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 1997. [Google Scholar]
- Kwon, Y.H.; Hong, S.G. Material characteristics of traditional bricks used in the Royal Tomb of King Muryeong, Gongju, Korea and its reproduction bricks. J. Conserv. Sci. 2014, 30, 287–298. [Google Scholar] [CrossRef]
- Kondekar, V.G.; Jaiswal, O.R.; Gupta, L.M. Ultrasonic pulse velocity testing of Gadhi Soil Adobe bricks. Int. J. Eng. Res. Mech. Civ. Eng. 2018, 3, 467–473. [Google Scholar]
- Grubesa, I.N.; Vracevic, M.; Ranogajec, J.; Vucetic, S. Influence of pore-size distribution on the resistance of clay brick to freeze–thaw cycles. Materials 2020, 13, 2364. [Google Scholar] [CrossRef]
- Azam, R.; Riaz, M.R.; Haq, E.U.; Shihata, A.; Zawam, M. Development of quality assessment criteria for burnt clay bricks of different ages based on ultrasonic pulse velocity test. Buildings 2022, 12, 1069. [Google Scholar] [CrossRef]
- Karaman, S.; Ersahin, S.; Gunal, H. Firing temperature and time influence on mechanical and physical properties of clay bricks. J. Sci. Ind. Res. 2006, 65, 153–159. [Google Scholar]
- Johari, I.; Said, S.; Hisham, B.; Bakar, A.; Ahmad, Z.A. Effect of the change of firing temperature on microstructure and physical properties of clay bricks from Beruas (Malaysia). Sci. Sinter. 2010, 42, 245–254. [Google Scholar] [CrossRef]
- Abbas, S.; Saleem, M.A.; Kazmi, S.M.S.; Munir, M.J. Production of sustainable clay bricks using waste fly ash: Mechanical and durability properties. J. Build. Eng. 2017, 14, 7–14. [Google Scholar] [CrossRef]
- Vatani Oskouei, A.; Afzali, M.; Madadipour, M. Experimental investigation on mud bricks reinforced with natural additives under compressive and tensile tests. Constr. Build. Mater. 2017, 142, 137–147. [Google Scholar] [CrossRef]
- Araujo, E.; Sousa, I.; Paz, R.; Costa, C.H.; Mesquita, E. Physical and mechanical characterization of traditional Brazilian clay bricks from different centuries. J. Build. Rehabil. 2020, 5, 22. [Google Scholar] [CrossRef]
- Chapagain, Y.P.; Sapkota, S.; Ghale, D.B.; Bohara, N.B.; Duwal, N.; Bhattarai, J. A case study on mineralogy and physico-mechanical properties of commercial bricks produced in Nepal. SN Appl. Sci. 2020, 2, 1856. [Google Scholar] [CrossRef]
- Rasanen, A.; Huuhka, S.; Pakkala, T.; Lahdensivu, J. Methods for evaluating the technical performance of reclaimed bricks. Case Stud. Constr. Mater. 2022, 17, e01504. [Google Scholar]
- Baronio, G.; Binda, L. Consolidation and durability of masonry materials: Mortars, bricks and plasters of the church of S. Lorenzo. In Proceedings of the 1st USA-Italy Workshop on Evaluation and Retrofit of Masonry Structures, Milan, Italy, 19–29 August 1987; pp. 61–69. [Google Scholar]
- Binda, L.; Saisi, A.; Tiraboschi, C. Investigation procedures for the diagnosis of historic masonries. Constr. Build. Mater. 2000, 14, 199–233. [Google Scholar] [CrossRef]
- Binda, L.; Tongini Folli, R.; Mirabella Roberti, G. Survey and investigation for the diagnosis of damaged masonry structures: The torrazzo of Cremona. In Proceedings of the 12th International Brick/Block Masonry Conference, Madrid, Spain, 25–28 June 2000; pp. 237–257. [Google Scholar]
- Fuenkajorn, K. Experimental assessment of long-term durability of some weak rocks. Bull. Eng. Geol. Environ. 2011, 70, 203–211. [Google Scholar] [CrossRef]
- Gautam, T.; Shakoor, A. Comparing the slaking of clay-bearing rocks under laboratory conditions to slaking under natural climatic conditions. Rock Mech. Rock Eng. 2016, 49, 19–31. [Google Scholar] [CrossRef]
- Cheng, K.; Heidari, Z. Combined interpretation of NMR and TGA measurements to quantify the impact of relative humidity on hydration of clay minerals. Appl. Clay Sci. 2017, 143, 362–371. [Google Scholar] [CrossRef]
- Zhao, M.; Zou, X.; Zou, P. Disintegration characteristics of red sandstone and its filling methods for highway roadbed and embankment. J. Mater. Civ. Eng. 2007, 19, 404–410. [Google Scholar] [CrossRef]
- Wangler, T.; Scherer, G.W. Clay swelling mechanism in clay-bearing sandstones. Environ. Geol. 2008, 56, 529–534. [Google Scholar] [CrossRef]
- Al-Shayea, N.A. The combined effect of clay and moisture content on the behavior of remolded unsaturated soils. Eng. Geol. 2001, 62, 319–342. [Google Scholar] [CrossRef]
- Vasarhelyi, B. Statistical analysis of the influence of water content on the strength of the Miocene limestone. Rock Mech. Rock Eng. 2005, 38, 69–76. [Google Scholar] [CrossRef]
- Hamzaban, M.T.; Buyuksagis, I.S.; Milad Manafi, M.; Touranchehzadeh, A. The effect of saturation on the physical and mechanical behavior of some rock samples. Civ. Eng. Limits 2021, 3, 23–31. [Google Scholar] [CrossRef]
- Zalooli, A.; Khamehchiyan, M.; Nikudel, M.R. Durability assessment of Gerdoi and red travertines from Azarshahr, East Azerbaijan province, Iran. Bull. Eng. Geol. Environ. 2019, 78, 1683–1695. [Google Scholar] [CrossRef]
- Huang, S.; Yu, S. Effect of water saturation on the strength of sandstones: Experimental investigation and statistical analysis. Bull. Eng. Geol. Environ. 2022, 81, 323. [Google Scholar] [CrossRef]
- Zalooli, A.; Khamehchiyan, M.; Nikudel, M.R. The quantification of total and effective porosities in travertines using PIA and saturation-buoyancy methods and the implication for strength and durability. Bull. Eng. Geol. Environ. 2018, 77, 1739–1751. [Google Scholar] [CrossRef]
- Akbay, D. Investigating the accuracy of specimen shape for point load index test in predicting the uniaxial compressive strength for rocks using regression analysis and machine learning. Min. Metall. Explor. 2023, 40, 2107–2115. [Google Scholar]
- Atici, U.; Ersoy, A. Correlation of specific energy of cutting saws and drilling bits with rock brittleness and destruction energy. J. Mater. Process Technol. 2009, 209, 2602–2612. [Google Scholar] [CrossRef]
- Jamshidi, A.; Nikudel, M.; Khamehchiyan, M.; Zalooli, A.; Yeganehfar, H. Estimating the mechanical properties of travertine building stones due to salt crystallization using multivariate regression analysis. J. Sci. Islam. Repub. Iran 2017, 28, 231–241. [Google Scholar]
- Kahraman, S.; Fener, M.; Gunaydin, O. Estimating the uniaxial compressive strength of pyroclastic rocks from the slake durability index. Bull. Eng. Geol. Environ. 2017, 76, 1107–1115. [Google Scholar] [CrossRef]




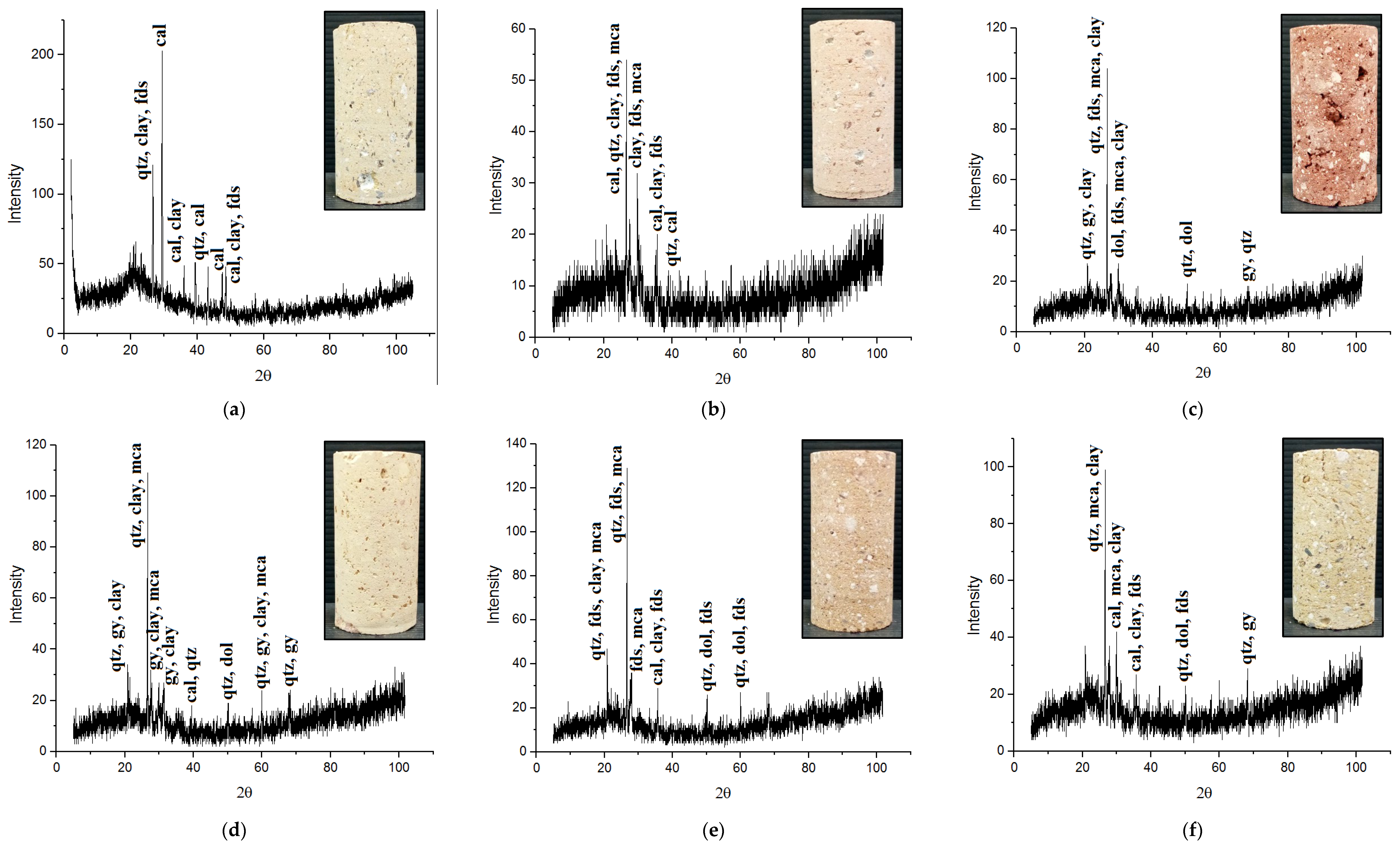
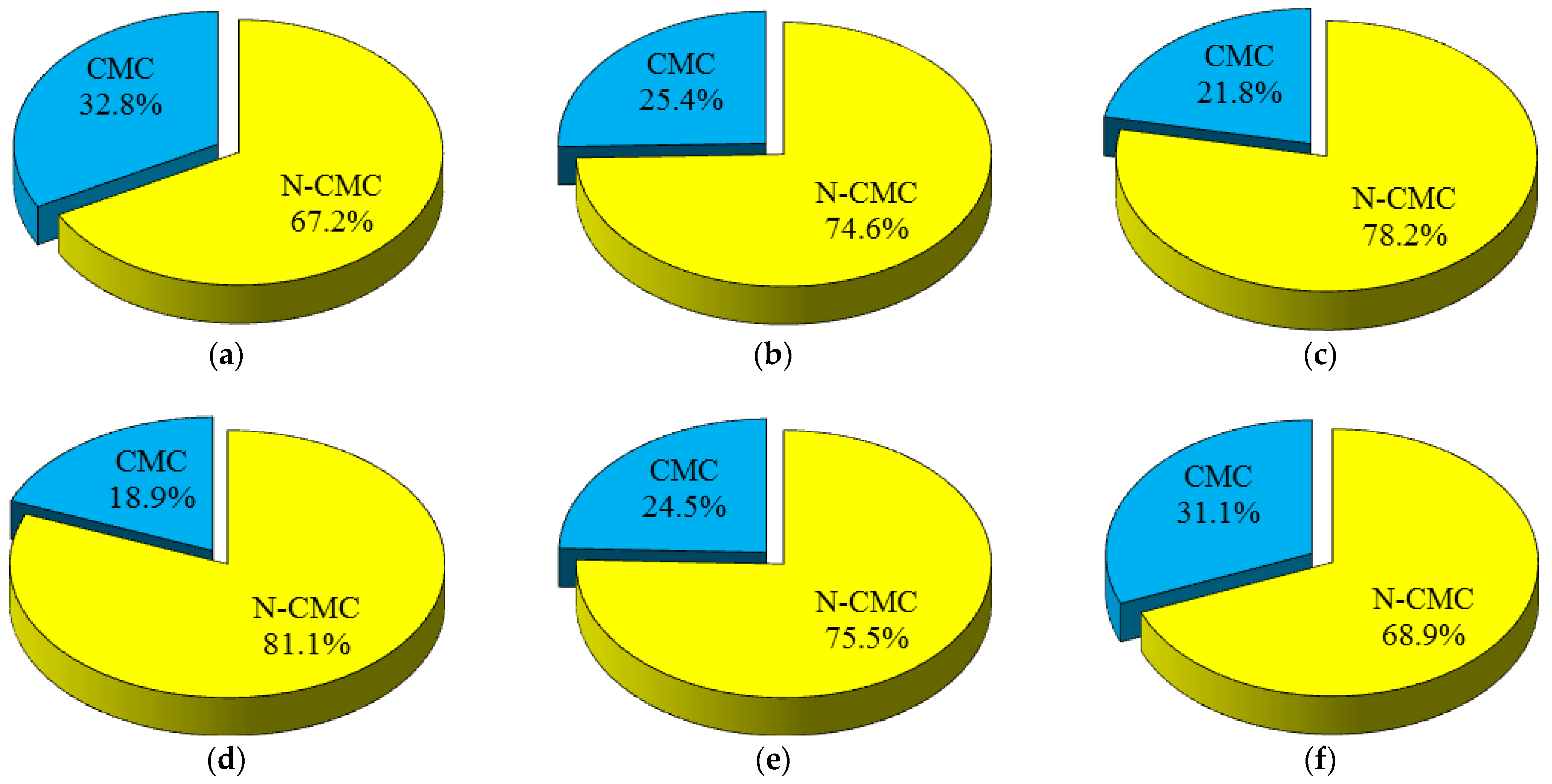


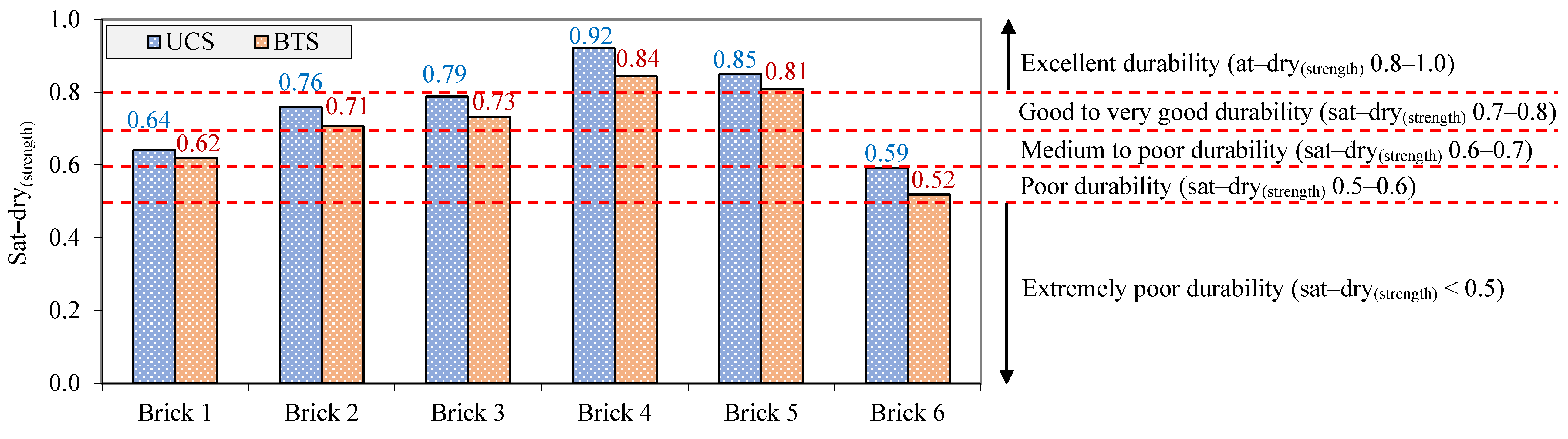
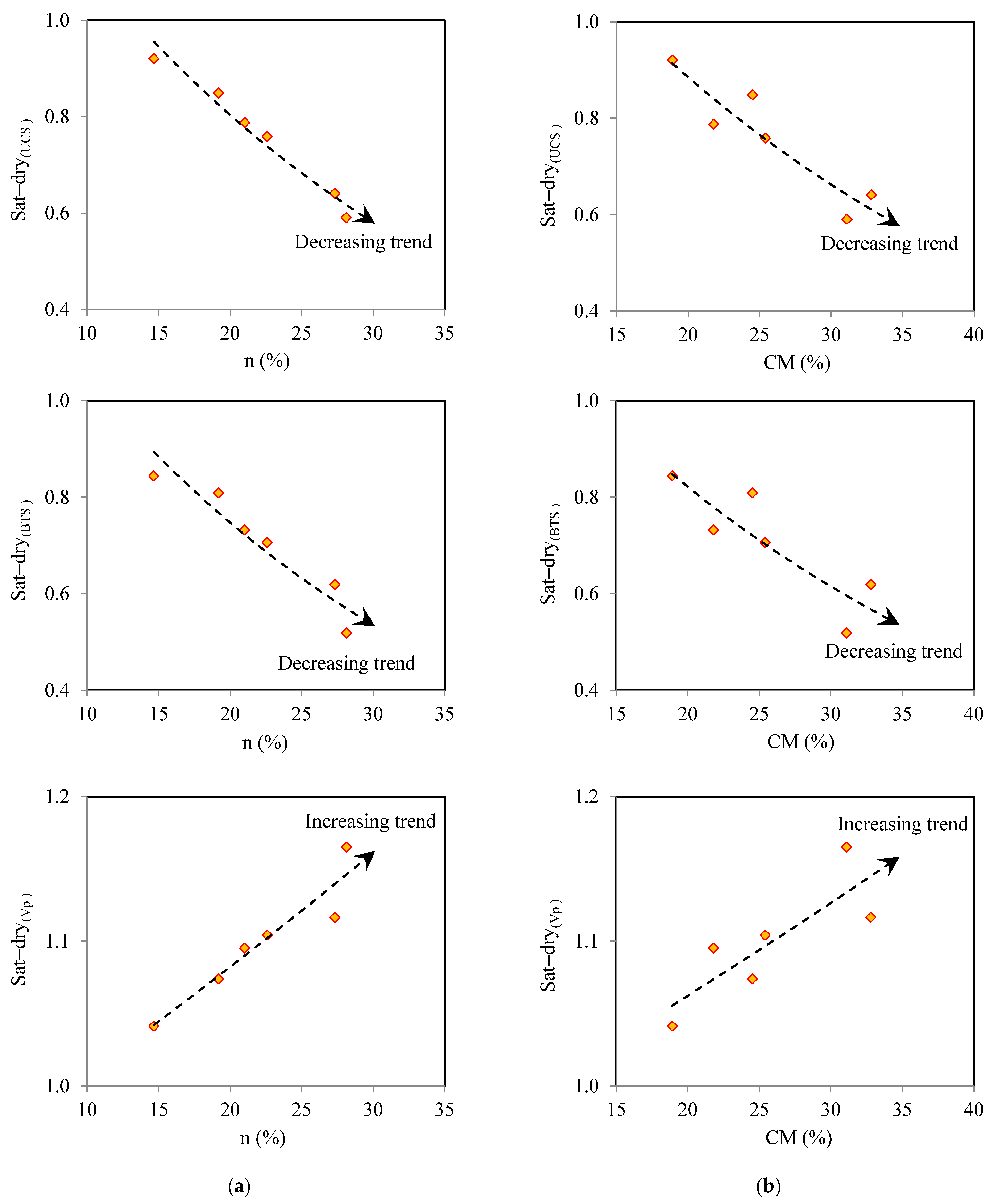
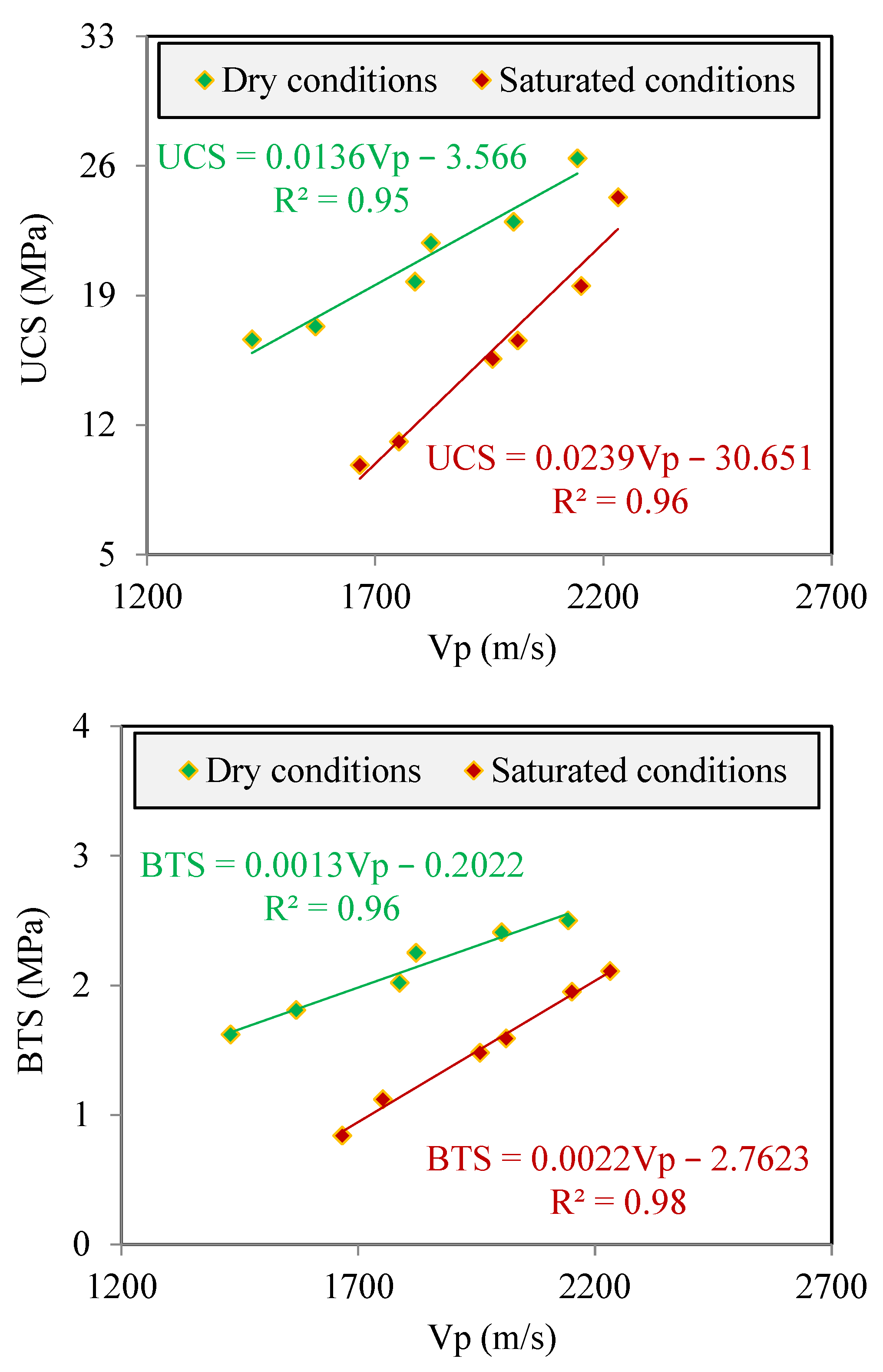

| Sample Code | Nonclay Minerals (N-CM) | Clay Minerals (CM) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quartz | Feldspar | Mica | Calcite | Dolomite | Gypsum | Chlorite | Kaolinite | Montmorillonite | Illite | |||
| Brick 1 | √ | √ | √ | √ | √ | √ | ||||||
| Brick 2 | √ | √ | √ | √ | √ | |||||||
| Brick 3 | √ | √ | √ | √ | √ | √ | √ | |||||
| Brick 4 | √ | √ | √ | √ | √ | √ | √ | |||||
| Brick 5 | √ | √ | √ | √ | √ | √ | ||||||
| Brick 6 | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||
| Sample Code | n (%) | * n Description | ||||
|---|---|---|---|---|---|---|
| VL | L | M | H | VH | ||
| Brick 1 | 27.32 | √ | ||||
| Brick 2 | 22.59 | √ | ||||
| Brick 3 | 21.02 | √ | ||||
| Brick 4 | 14.67 | √ | ||||
| Brick 5 | 19.18 | √ | ||||
| Brick 6 | 28.13 | √ | ||||
| Researcher/s | UCS (MPa) | Vp (m/s) |
|---|---|---|
| Crespo-Lopez et al. [1] | 6.4–72.6 | 1260–4625 |
| Noor-E-Khuda and Albermani [39] | 20.43–45.15 | 2507–3162 |
| Koroth [43] | 24.2–143.5 | 2201–4383 |
| Grubesa et al. [46] | ~27.0–56.0 | No data |
| Azam et al. [47] | ~5.0–24.0 | ~1380–3300 |
| Karaman et al. [48] | 8.5–31.4 | No data |
| Johari et al. [49] | 2.5–89.5 | No data |
| Abbas et al. [50] | ~23.0 | No data |
| Vatani Oskouei et al. [51] | 4.4 | No data |
| Araujo et al. [52] | 2.9–11.9 | 586–3520 |
| Chapagain et al. [53] | ~3.2–10.5 | No data |
| Rasanen et al. [54] | ~18.0–61.5 | ~1300–3500 |
| The present study | 9.82–26.40 | 1430–2232 |
| Equation No. | Correlation Equation | Sample Conditions | VAF (%) | RMSE | F Value | F Sig. | |
|---|---|---|---|---|---|---|---|
| Computed | Tabulated | ||||||
| (9) | Dry | 95.19 | 0.57 | 79.08 | 7.71 | 0.001 | |
| (10) | Saturated | 96.10 | 0.75 | 98.52 | 7.71 | 0.001 | |
| (11) | Dry | 96.29 | 0.05 | 104.15 | 7.71 | 0.001 | |
| (12) | Saturated | 99.38 | 0.04 | 647.78 | 7.71 | 0.000 | |
| Brick Code | Brick Age (year) | Measured Parameter | Predictive Equation | Predicted Parameter | a Error (%) | |
|---|---|---|---|---|---|---|
| Vp (m/s) | UCS (MPa) | UCS (MPa) | ||||
| H-series | 25–30 | 2703 | 18.00 | 33.19 | −84.4 | |
| W-series | 25–30 | 2723 | 28.54 | 33.47 | −17.3 | |
| O-series | 45–50 | 2340 | 16.18 | 28.26 | −74.6 | |
| S-series | 45–50 | 2385 | 18.00 | 28.87 | −60.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamshidi, A.; Sousa, L. Strength Characteristics, Ultrasonic Wave Velocity, and the Correlation between Them in Clay Bricks under Dry and Saturated Conditions. Materials 2024, 17, 1353. https://doi.org/10.3390/ma17061353
Jamshidi A, Sousa L. Strength Characteristics, Ultrasonic Wave Velocity, and the Correlation between Them in Clay Bricks under Dry and Saturated Conditions. Materials. 2024; 17(6):1353. https://doi.org/10.3390/ma17061353
Chicago/Turabian StyleJamshidi, Amin, and Luís Sousa. 2024. "Strength Characteristics, Ultrasonic Wave Velocity, and the Correlation between Them in Clay Bricks under Dry and Saturated Conditions" Materials 17, no. 6: 1353. https://doi.org/10.3390/ma17061353
APA StyleJamshidi, A., & Sousa, L. (2024). Strength Characteristics, Ultrasonic Wave Velocity, and the Correlation between Them in Clay Bricks under Dry and Saturated Conditions. Materials, 17(6), 1353. https://doi.org/10.3390/ma17061353







