Unraveling Broadband Near-Infrared Luminescence in Cr³⁺-Doped Ca₃Y₂Ge₃O₁₂ Garnets: Insights from First-Principles Analysis

Abstract

In this study, we conducted an extensive investigation into broadband near-infrared luminescence of Cr³⁺-doped Ca₃Y₂Ge₃O₁₂ garnet, employing first-principles calculations within the density functional theory framework. Our initial focus involved determining the site occupancy of Cr³⁺ activator ions, which revealed a pronounced preference for the Y³⁺ sites over the Ca²⁺ and Ge⁴⁺ sites, as evidenced by the formation energy calculations. Subsequently, the geometric structures of the excited states ²E and ⁴T₂, along with their optical transition energies relative to the ground state ⁴A₂ in Ca₃Y₂Ge₃O₁₂:Cr³⁺, were successfully modeled using the ΔSCF method. Calculation convergence challenges were effectively addressed through the proposed fractional particle occupancy schemes. The constructed host-referred binding energy diagram provided a clear description of the luminescence kinetics process in the garnet, which explained the high quantum efficiency of emission. Furthermore, the accurate prediction of thermal excitation energy yielded insights into the thermal stability of the compound, as illustrated in the calculated configuration coordinate diagram. More importantly, all calculated data were consistently aligned with the experimental results. This research not only advances our understanding of the intricate interplay between geometric and electronic structures, optical properties, and thermal behavior in Cr³⁺-doped garnets but also lays the groundwork for future breakthroughs in the high-throughput design and optimization of luminescent performance and thermal stability in Cr³⁺-doped phosphors.

1. Introduction

Among various crystalline solids that are used for optical applications, the compounds with the cubic garnet structure are of special importance and significance. This is a very large family of compounds, whose structure offers numerous opportunities for chemical composition alterations, such as creating solid solutions and/or introducing optically active impurity ions. The garnets can easily accommodate transition metal and rare earth ions, rendering them potential candidates for various optical applications. There has been a recent surge in interest in Cr³⁺-doped garnets due to their broadband near-infrared (NIR) luminescence, with potential applications in medical diagnostics, food analysis, horticultural lighting, night vision, etc. [1,2,3,4,5,6,7]. For instance, Ca₃Y₂Ge₃O₁₂: Cr³⁺, synthesized via the solid-state reaction method, exhibits a broadband NIR emission spanning from 700 to 1100 nm, with a peak centered at 800 nm [8]. This emission spectrum aligns perfectly with the absorption frequencies of hydrogen-containing groups X-H (where X=C, N and O), making it an ideal non-destructive testing tool for food safety applications [9]. Theoretical investigations that provide a comprehensive understanding of the luminescence mechanisms are necessary for enabling the next generation of highly efficient Cr³⁺-activated garnet phosphors.

Extensive systematic spectroscopic analyses have been conducted on garnet crystals doped with Cr³⁺ ions, utilizing the well-established Tanabe–Sugano energy level diagram for 3d³ ions in solids [10,11]. Additionally, the exchange charge model within the framework of semi-empirical crystal-field (CF) theory can provide valuable insights into the relationship between the spectroscopic properties of Cr³⁺ ions and their local coordination environments [12]. However, the number of first-principles studies focusing on Cr³⁺-doped garnets within the density functional theory (DFT) framework remains relatively small compared to experimental and semi-empirical theoretical papers on the same topic. This is primarily due to the rather complicated structure of garnets, characterized by a large number of atoms in a unit cell, thus incurring high computational costs. Moreover, most reported DFT calculations on Cr³⁺-doped compounds have predominantly concentrated on ground-state properties, as exemplified by the case of Ca₄ZrGe₃O₁₂: Cr³⁺ discussed in reference [13]. However, such studies are limiting since they fail to provide the knowledge of Cr³⁺ ions’ ²E and ⁴T₂ excited states, which are important in the design of new useful phosphors. Fortunately, Duan et al. [14,15,16] have successfully applied the ΔSCF-DFT method with non-Aufbau occupations on Kohn–Sham (KS) orbitals to model the excited states ²E and ⁴T₂ of Cr³⁺ ions doped in some oxides. However, such calculations probing Cr³⁺-doped garnets are lacking.

The main goal of the present work is to provide a deeper fundamental understanding of the excited states and the associated luminescence phenomena in Cr³⁺-doped garnets by integrating the first-principles ΔSCF-DFT technique. This integration is essential for addressing the aforementioned gaps in our knowledge. Specifically, we chose the garnet Ca₃Y₂Ge₃O₁₂: Cr³⁺ as a case study. In this paper, we conducted an extensive theoretical analysis of its structural, electronic, and optical properties. Special attention was devoted to factors such as the site occupancy, luminescence mechanism, and thermal stability of Cr³⁺ dopants within this garnet matrix. Furthermore, we delved into the challenge of achieving calculation convergence in modeling the excited ⁴T₂ state of Cr³⁺ ions, employing the approximation of the single-electron configuration t2 2ge1 g, utilizing either the DFT+U or hybrid DFT method. Notably, our previous investigation encountered a computational breakdown when describing the excited ⁴T₂ state of Mn⁴⁺ ions in K₂SiF₆ due to the significant mixing between the constrainedly occupied and unoccupied 3d KS orbitals in the hybrid DFT calculations [17]. Consequently, these predictive calculations and technique development can be readily applied to other systems doped with Cr³⁺ ions, thus offering potential for the high-throughput design of Cr³⁺-doped NIR materials.

This paper is organized as follows: Section 2 contains a description of the calculation method. Section 3 contains all obtained results and their analysis. Finally, the paper is concluded with a summary of our findings.

2. Method of Calculations

Our study employed first-principles calculations within the DFT framework, utilizing the Vienna ab initio simulation package (VASP, version 5.4.4.) [18]. Geometric structure relaxations and defect formation calculations were conducted using the Perdew–Burke–Ernzerhof (PBE) functional [19], incorporating an empirical U value (U_eff = 4.0 eV) specifically tailored for the Cr³⁺-3d orbitals [14,20]. The electronic structure and optical transitions of both neat and Cr³⁺-doped Ca₃Y₂Ge₃O₁₂ were calculated using the hybrid functional of PBE0 with an additional 25% Hartree–Fock exchange [21]. The treatment of semicore electrons for Ca (3s²3p⁶4s²), Y (4s²4p⁶5s²4d¹), Ge (4s²3d¹⁰4p²), O (2s²2p⁴), and Cr (3p⁶3d⁵4s¹) was explicitly addressed using the projector augmented-wave pseudopotentials [22,23]. Modeling Cr³⁺ defects in Ca₃Y₂Ge₃O₁₂ required a supercell containing 160 atoms, with one Y³⁺/Ca²⁺/Ge⁴⁺ ion substituted by a Cr³⁺ ion. Sampling the Brillouin zone involved a single k-point Γ for the total energy and relaxation calculations of the constructed supercell, while a 3 × 3 × 3 k-points mesh, based on the Monkhorst–Pack scheme [24], was employed for the host’s unit cell. For both the neat and doped systems, the closed-shell and spin-polarized DFT calculation forms were applied, respectively. A plane-wave basis cutoff energy of 520 eV was employed, with convergence criteria set at 10⁻⁶ eV for electronic energy minimization and 0.01 eV/Å for Hellman–Feynman forces on each atom.

The formation energy of a defect X in the charge state of q can be determined as follows [25]: $E^f\left(X^q\right)=E_{\mathrm{t}\mathrm{o}\mathrm{t}}\left[X^q\right]-E_{\mathrm{t}\mathrm{o}\mathrm{t}}\left[\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}\right]-\sum _i{n}_i{\mu }_i+q{E}_F$, where E_tot[X_q] and E_tot[bulk] represent the calculated total energies of the defective and perfect supercells, respectively. The variables n_i, μ_I, and E_F correspond to the change in the atom number of element i (added if n_i > 0 or removed if n_i < 0 with respect to the perfect supercell), the chemical potential of species i, and the Fermi energy level, respectively. To account for image charge interaction at periodic boundary conditions and changes in electrostatic potential caused by the defect, the total energies of charged defects were corrected using the method proposed by Durrant et al. [26]. The charge transition level of a defect X from its charged states q to q′ (where q > q′) can be assessed as ε(q/q′) = (E_tot[X_q′] − E_tot[X_q])/(q − q′) − E_VBM, where E_VBM represents the energy of the host’s valence band maximum (VBM).

The standard ΔSCF-DFT procedure [27,28] was employed to model the excited states ²E and ⁴T₂ of Cr³⁺ ions in Ca₃Y₂Ge₃O₁₂. These states correspond to a spin flip of one t_2g electron and a transition of the KS orbital from t_2g to e_g, respectively. Modeling the excited state ²E presented no challenges, although the ⁴A₂-²E optical transition energy required adjustment by a scaling factor of 1.5 compared to the DFT-generated value due to the spin contamination effect between the ground ⁴A₂ and excited ²E states [14]. However, it proved to be challenging to represent the excited state ⁴T₂ in Ca₃Y₂Ge₃O₁₂:Cr³⁺. The constrained separation of a pair of electrons and holes to the lowest e_g and the highest t_2g KS orbitals led to a significant calculation convergence issue in the DFT+U and hybrid DFT calculations. This is not surprising, given that the narrow t_2g-e_g energy gap of Cr³⁺ ions in Ca₃Y₂Ge₃O₁₂ intensifies the mixing between the lowest occupied e_g and the highest unoccupied t_2g KS orbitals, which pushes the calculations towards collapse. This problem is exacerbated by the fact that many Cr³⁺-doped garnets with broadband emission are associated with the weak CF case [29]. Considering that the structural disparity between the ground ⁴A₂ and excited ⁴T₂ states of Cr³⁺ ions primarily stems from the distinction in the electronic density profiles of the 3d-t_2g and e_g single-electron states, it is imperative to maintain the single-electron configuration t_2g²e_g¹ for modeling the excited state ⁴T₂ of the Cr³⁺ dopants. However, the two t_2g electrons can partially infiltrate into the highest empty t_2g KS orbitals to counteract the approach of the lowest occupied e_g KS orbital. Therefore, in this study, we proposed two sets of fractional particle occupancy schemes to characterize the geometric structure of the Cr^{3+ 4}T₂ excited state in Ca₃Y₂Ge₃O₁₂, as illustrated in Figure 1. In Scheme 1, one of the two t_2g electrons is uniformly distributed among the highest two t_2g KS orbitals, while the other occupies the lowest t_2g KS orbital entirely. In Scheme 2, the allocation of the two t_2g electrons is straightforward, with equal distribution among the three t_2g KS orbitals.

Slater’s transition-state method [30,31] was employed to estimate the ⁴A₂-⁴T₂ excitation and emission energies, respectively, at the equilibrium geometric structures of the ground ⁴A₂ and excited ⁴T₂ states. This process involves examining the disparities in energy between the lowest e_g and highest t_2g KS orbitals in the density of states (DOS) diagrams obtained from such calculations based on the single-electron configuration t_2g^2.5e_g^0.5, as depicted in Figure 1. The associated zero-phonon line (ZPL) energy can be readily determined by applying the Franck–Condon principle. Additionally, the Stokes shift energy can be calculated by evaluating the difference between the excitation and emission energies of the corresponding optical transitions.

3. Results and Discussion

3.1. Ground States of Both Neat and Cr³⁺-Doped Ca₃Y₂Ge₃O₁₂

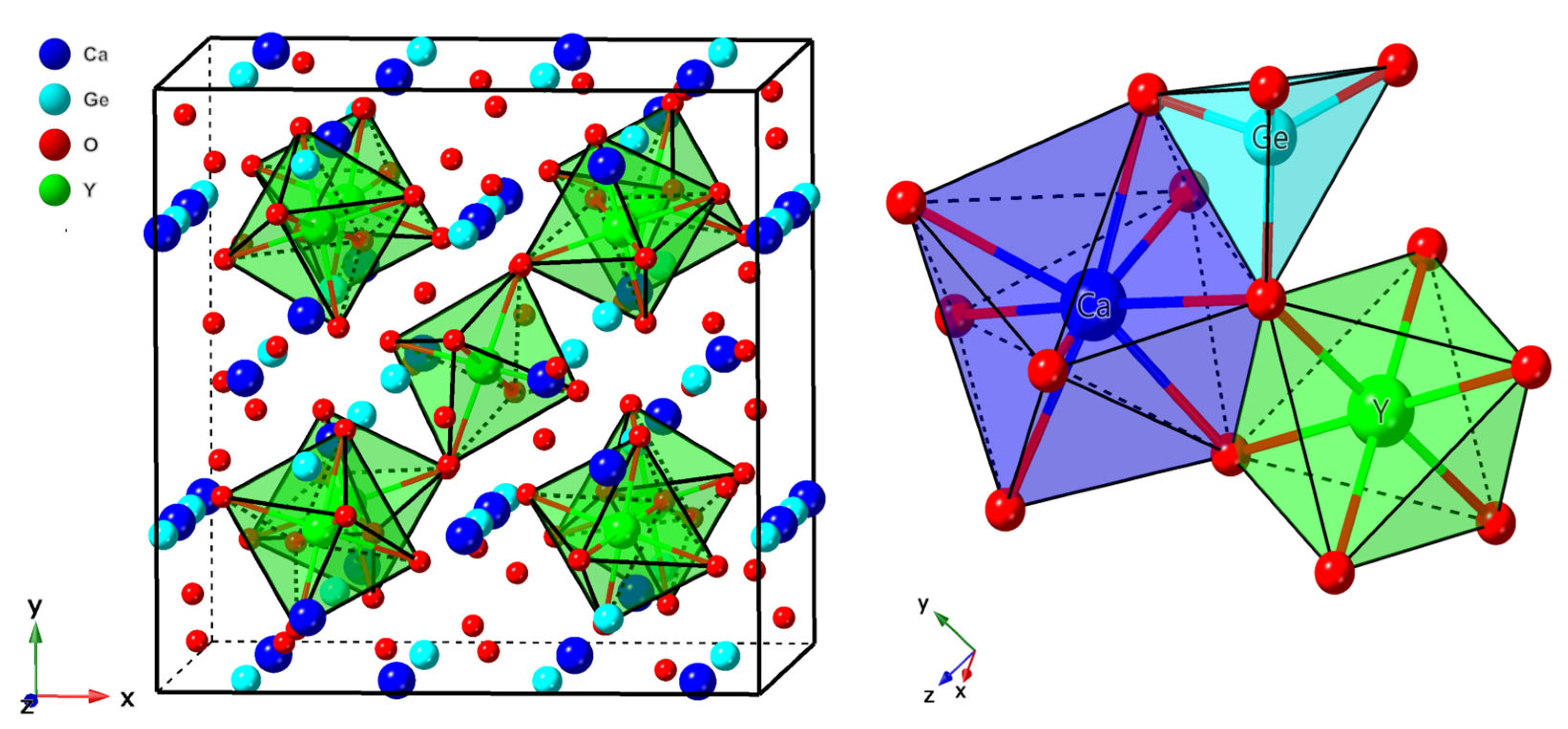
3.1.1. Structural Properties and Defect Site Occupancy

Ca₃Y₂Ge₃O₁₂ crystallizes in the conventional cubic garnet structure, with the $Ia\overline{3}d$ space group and an experimental lattice constant of 12.8059 Å [32]. Within this crystalline framework, the coordination environments of the constituent cations manifest intriguing symmetries and spatial arrangements, as shown in Figure 2. Specifically, the Y³⁺ ions occupy octahedral coordination sites, characterized by point group symmetry S₆, wherein each Y³⁺ ion is coordinated with six O²⁻ ions at an equidistant Y-O distance of 2.234 Å. In contrast, the Ge⁴⁺ ions reside in tetrahedral sites, displaying point group symmetry S₄, with a coordinated arrangement of four O²⁻ ions at an identical distance of 1.766 Å. Meanwhile, the Ca²⁺ ions are found within dodecahedral coordination environments, distinguished by point group symmetry D₂, each surrounded by eight neighboring O²⁻ ions. Notably, such a coordination environment results in two distinct Ca-O distances (2.469 and 2.560 Å).

The calculated structural data for the Ca₃Y₂Ge₃O₁₂ host, encompassing lattice constants, internal anion position, unit cell volume, and bond lengths of Y³⁺-O²⁻, Ge⁴⁺-O²⁻ and Ca²⁺-O²⁻, demonstrate substantial agreement with the earlier-discussed experimental descriptions, as outlined in

Table 1. Comparison of the calculated and experimental structural properties of both neat and Cr³⁺-doped Ca₃Y₂Ge₃O₁₂ in their ground states: lattice constants (a = b = c, in Å), non-dimensional coordinates of internal anion position (x, y, z), unit cell volume V before and after Cr³⁺ doping (in ų), and bond lengths of Y³⁺-O²⁻, Ge⁴⁺-O²⁻ and Ca²⁺-O²⁻ in the pure host, along with Cr³⁺-O²⁻ bond lengths upon Cr³⁺ doping at the three cationic sites (in Å).

System	Parameter	Calc.	Expt. a
Ca3Y2Ge3O12	a = b = c	12.9381	12.8059
	O (x, y, z)	0.9644, 0.0557, 0.1604	0.9637, 0.0567, 0.1609
	V(host)	2165.7508	2100.0533
	Y3+-6O2−	2.245	2.234
	Ge4+-4O2−	1.789	1.766
	Ca2+-4O(1)2−	2.486	2.469
	Ca2+-4O(2)2−	2.596	2.560
Ca3Y2Ge3O12:Cr3+	V(Cr3+/Y3+)	2155.4599	-
	Cr3+/Y3+-6O2−	2.062	-
	V(Cr3+/Ge4+)	2187.9207	-
	Cr3+/Ge4+-4O2−	1.932	-
	V(Cr3+/Ca2+)	2148.4651	-
	Cr3+/Ca2+-4O(1)2−	2.142	-
	Cr3+/Ca2+-4O(2)2−	2.576	-

Note: ^a Ref. [32].

. The observed slight overestimation is ascribed to the inherent characteristics of the generalized gradient approximation employed in the PBE functional. Considering the ionic radius difference between Cr³⁺ dopants and the three substitutional sites available [33], it is anticipated that the introduction of Cr³⁺ at the Y³⁺ and Ca²⁺ sites will induce a contraction in their local coordination environments, while the opposite effect is expected at the Ge⁴⁺ sites. The Cr³⁺-O²⁻ bond lengths and the unit cell volume changes upon Cr³⁺ doping at the three cationic sites, calculated using the PBE+U method, strongly corroborate this empirical conclusion, as evidenced by the data comparisons presented in Table 1. The experimentally refined unit cell volume after Cr³⁺ doping tends to decrease compared to the host case (refer to Figure 2c in the reference [8]). This, combined with the calculated findings, suggests a preference for Cr³⁺ dopants to substitute at Y³⁺ and Ca²⁺ sites over the Ge⁴⁺ sites. A further inference can be drawn, indicating that the Y³⁺ sites are more accommodating to Cr³⁺ ions than the Ca²⁺ sites, owing to the closer alignment of ionic radii between Y³⁺ and Cr³⁺ ions within a six-coordinated-ligand environment.

To conclusively determine the preferential site occupancy of Cr³⁺ ions in Ca₃Y₂Ge₃O₁₂, we calculated the formation energies of Cr dopants at the three cationic sites within the PBE+U framework. In this study, the chemical potential for oxygen atoms was established by considering a gas of O₂ molecules, expressed as ${\mu }_{\mathrm{O}}=\frac{1}{2}{E}_{{\mathrm{O}}_2\left[\mathrm{g}\mathrm{a}\mathrm{s}\right]}+\mathrm{\Delta }{\mu }_{\mathrm{O}}.$ Here, $E_{{\mathrm{O}}_2\left[\mathrm{g}\mathrm{a}\mathrm{s}\right]}$ represents the calculated total energy per formula unit for O₂ gas, and Δμ_O is related to the contribution arising from gas partial pressure (P) and sintering temperature (T). Under the specified experimental conditions (T = 1450 °C and P = 1 atm [8]), Δμ_O was determined as −2.051 eV, following the formula expression provided in the reference [34]. The chemical potentials of other atoms (Ca, Y, Ge, and Cr) were straightforwardly derived from the calculated total energies per formula unit of their respective bulk binary oxides, based on the obtained oxygen chemical potential. These are determined by the following equations: ${\mu }_{\mathrm{C}\mathrm{a}}=E_{\mathrm{C}\mathrm{a}\mathrm{O}\left[\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}\right]}-{\mu }_{\mathrm{O}}$, ${\mu }_{\mathrm{Y}}=1/2 (E_{{\mathrm{Y}}_2{\mathrm{O}}_3\left[\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}\right]}-3{\mu }_{\mathrm{O}})$, ${\mu }_{\mathrm{G}\mathrm{e}}=E_{\mathrm{G}\mathrm{e}{\mathrm{O}}_2\left[\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}\right]}-2{\mu }_{\mathrm{O}}$, and ${\mu }_{\mathrm{C}\mathrm{r}}=1/2 (E_{{\mathrm{C}\mathrm{r}}_2{\mathrm{O}}_3\left[\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}\right]}-3{\mu }_{\mathrm{O}})$. Figure 3 illustrates the formation energies of Cr ions substituting at the three cationic sites as a function of Fermi energy. Inspection of Figure 3 reveals that the charge state of Cr ions located at the Ge⁴⁺ sites undergoes a transition from “+4” to “+3” as the Fermi energy increases. This aligns with the common understanding in coordination chemistry, where transition metal ions with a 3d³ electronic configuration tend to be oxidized at a tetrahedral site in the absence of additional constraints from physics or chemistry. In contrast, those occupying the Ca²⁺ and Y³⁺ sites consistently maintain a “+3” charge state. Simultaneously, the formation energy of Cr³⁺ ions substituting the Y³⁺ sites consistently remains lower than those in the Ca²⁺ and Ge⁴⁺ sites. Consequently, defects involving Cr ions substituting at the Y³⁺ sites dominate, and the charge state of Cr ions is predominantly “+3” in Ca₃Y₂Ge₃O₁₂. This theoretical fact is fully confirmed by the experimental XRD analysis reported previously [8] and aligns with the calculated structural properties of Ca₃Y₂Ge₃O₁₂: Cr³⁺ discussed above. Hereafter, if not specifically emphasized, we exclusively focus on the case wherein Cr³⁺ ions occupy the Y³⁺ sites in Ca₃Y₂Ge₃O₁₂ for the description of the structural, electronic, and optical properties of Ca₃Y₂Ge₃O₁₂: Cr³⁺.

Despite the results obtained by Cui et al. [9], only the results for a single Cr³⁺ location in the host (at the Y³⁺ site) are shown here, which is based on the Cr³⁺ preference to occupy the octahedral sites in crystalline solids (see Figure 3).

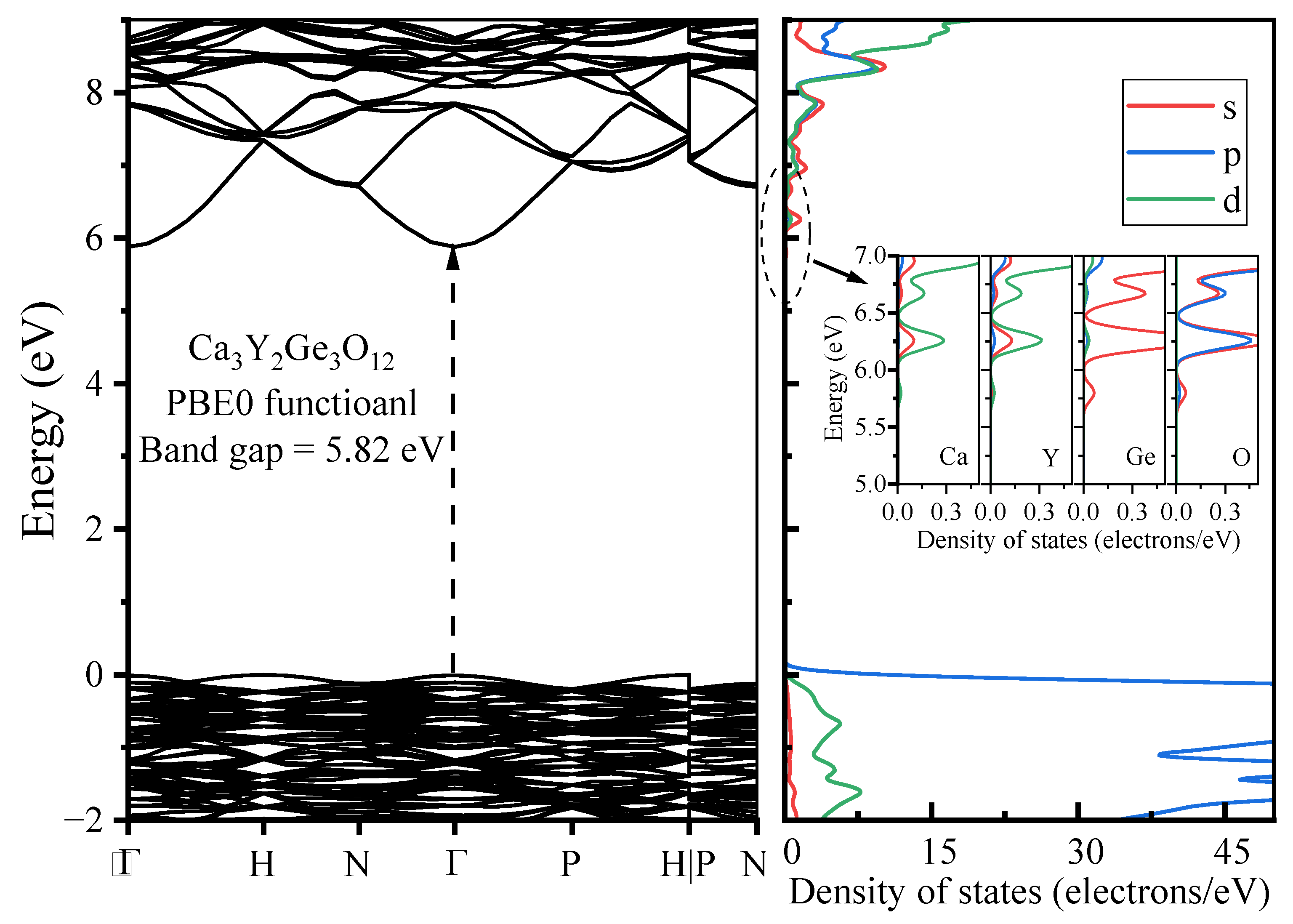
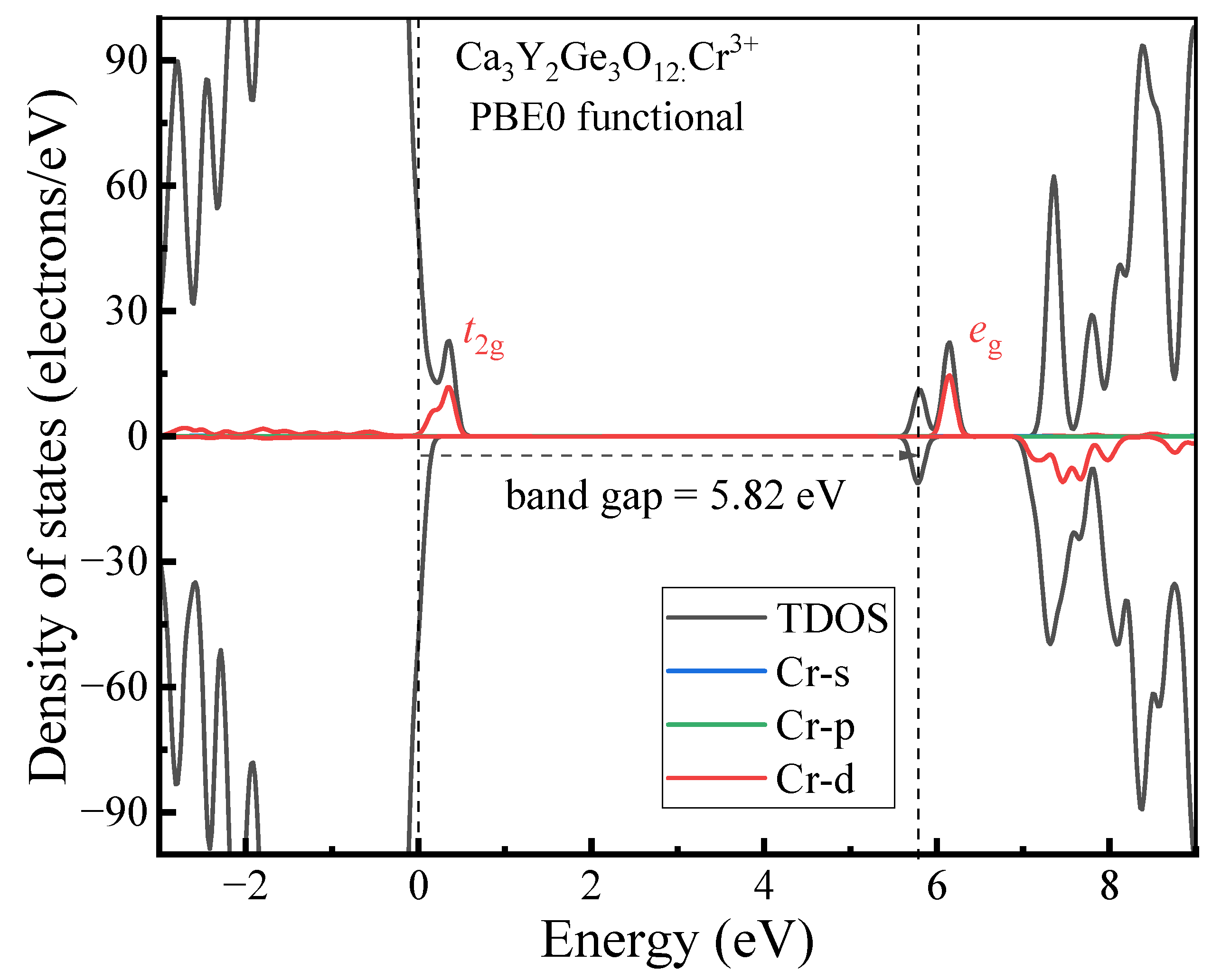
3.1.2. Electronic Properties

The band structure, along with the DOSs, were computed for pristine Ca₃Y₂Ge₃O₁₂ utilizing the PBE0 functional, taking into account the optimized geometric structure of the host, as illustrated in Figure 4. The calculated band gap displays a direct character and measures 5.82 eV, marking a significant improvement compared to the result of 3.32 eV obtained with the PBE functional. This closely aligns with the experimentally determined optical band gap of the host (5.71 eV), determined through the Kubelka–Munk function and the Tauc relation applied to the measured diffuse reflection spectra [8]. The top of the valence bands (VBs) appears relatively flat, similar to other oxygen-based garnets [35], while the bottom of the conduction bands (CBs) exhibits notable dispersion, with a single CB dipping down at the Γ point. This observation strongly suggests high electron mobility in the CBs and the localization behavior of holes in the VBs. The calculated DOS diagrams provide further insight into the composition of the band edges. The VBs’ top is predominantly influenced by the O-2p orbitals, whereas the CBs’ bottom is primarily composed of the Ca-3d, Y-4d, Ge-4s, and O-2sp orbitals.

Figure 5 depicts the DOS diagrams of Cr³⁺-doped Ca₃Y₂Ge₃O₁₂, obtained from the PBE0 calculations using the optimized geometric structure when Cr³⁺ ions occupy the Y³⁺ sites. As anticipated, new states associated with the Cr-3d orbitals emerge within the band gap. The lower Cr-3d-t_2g KS orbitals with spin up are observed to subtly split into two bands, positioned slightly above the top of the VBs. Meanwhile, the higher Cr-3d-e_g KS orbitals with spin up, localized in the CBs, remain as one band without any observable splitting. The calculated results fully align with the fundament knowledge in group theory: the triply degenerate t_2g transforms into a single-fold A and a doubly degenerate E, whereas the doubly degenerate e_g is maintained as E when Cr³⁺ ions occupy the Y³⁺ octahedral sites with the point group symmetry S₆ [36]. All the Cr-3d KS orbitals with spin down are deeply buried into the CBs.

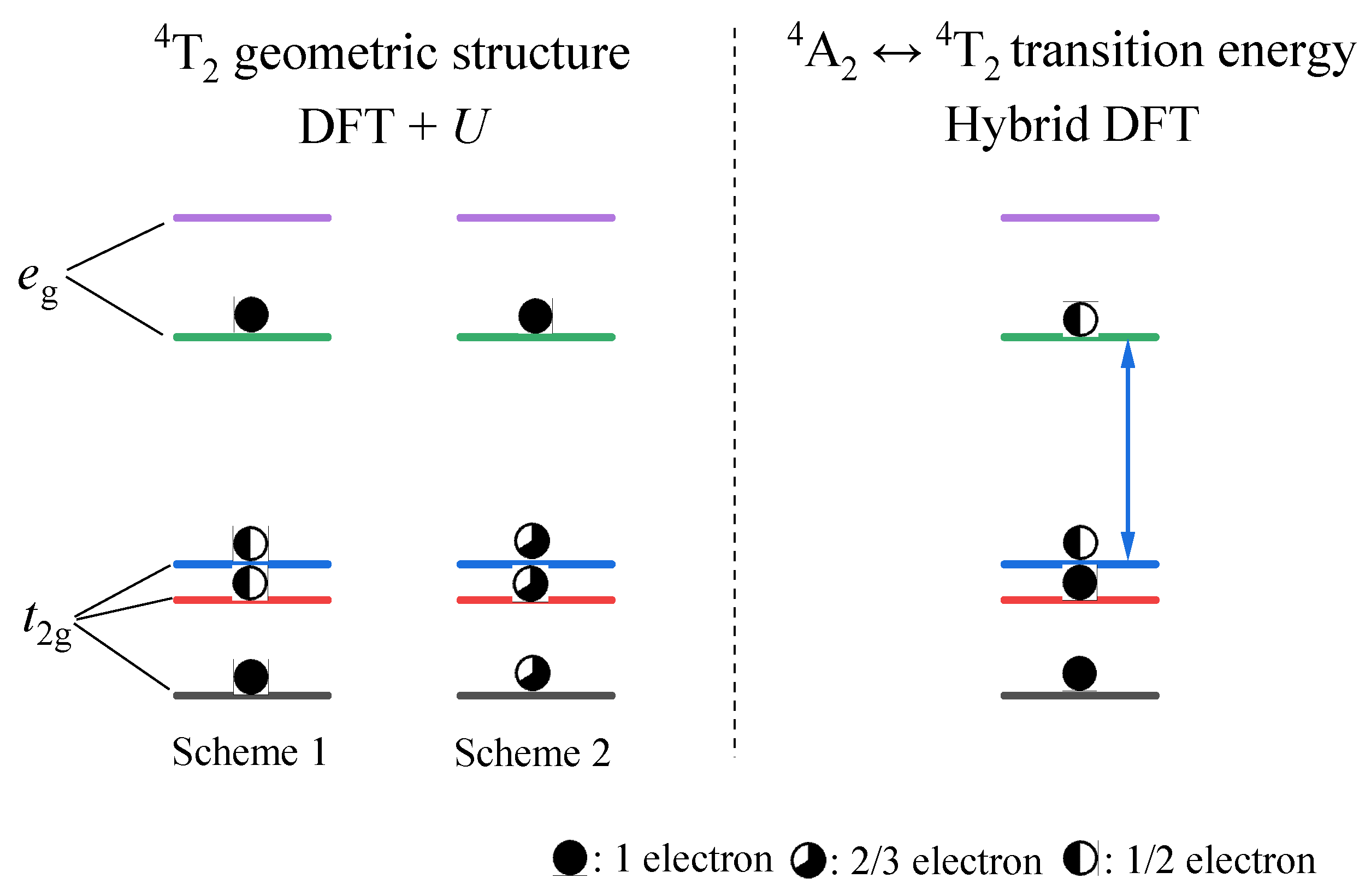
3.2. Excited States ²E and ⁴T₂ of Cr³⁺-Doped Ca₃Y₂Ge₃O₁₂

3.2.1. Structural Properties

The equilibrium geometric structures of the excited states ²E and ⁴T₂ of Cr³⁺ ions in Ca₃Y₂Ge₃O₁₂ were determined using the ΔSCF technique with the PBE+U method, as illustrated in Figure 6. In the case of the excited state ²E, the calculated local coordination environment of Cr³⁺ ions maintains the initial point group symmetry of S₆, with a slight bond length contraction of 0.007 Å in comparison to its ground state ⁴A₂. This minor change is anticipated since the ²E state is not associated with an orbital change but rather a spin flip when compared to ⁴A₂. In contrast, the optimized equilibrium geometric structures of the excited state ⁴T₂, utilizing two sets of fractional particle occupancy schemes tailored for the calculation convergence issues mentioned in the computational methodology section, undergo a significant Jahn–Teller distortion, resulting in a symmetry descent from S₆ to its subgroup C_i. This distortion involves a notable axial expansion (at least an increase of 0.15 Å) and a slight equatorial compression in the [CrO₆]⁹⁻ complex. And the Cr³⁺-O²⁻ bond lengths, initially identical, split into three groups. These calculation results align with semi-empirical CF analyses on the Jahn–Teller effect for 3d ions in solids [37]. Additionally, we considered the volume of the [CrO₆]⁹⁻ complex as an index to characterize the distortion level of the excited state ⁴T₂ with respect to the ground state ⁴A₂. The calculated results of 11.6742 (⁴A₂), 12.3496 (Scheme 1 for ⁴T₂), and 12.5107 (Scheme 2 for ⁴T₂) ų on this parameter indicate a potential over-relaxation risk in the equilibrium geometric structure obtained from the second fractional particle occupancy scheme, or an under-relaxation case for Scheme 1 (which will be discussed later).

3.2.2. Optical Properties and Luminescence Mechanism

Upon analysis of the obtained geometric structures for the ground state ⁴A₂ and excited states ²E and ⁴T₂ of Cr³⁺ in Ca₃Y₂Ge₃O₁₂, we conducted the PBE0 calculations to determine the excitation, emission, ZPL, and Stokes shift energies for the optical transitions ⁴A₂-²E and ⁴A₂-⁴T₂, employing the ΔSCF technique within Slater’s transition-state method. The resulting values, along with the available experimental data, are tabulated in

Table 2. Comparison of the calculated and experimental excitation, emission, ZPL, and Stokes shift energies of the optical transitions between the ⁴A₂ ground state and the excited states ²E and ⁴T₂ of Cr³⁺ in Ca₃Y₂Ge₃O₁₂ (all in eV).

	Excitation	Emission	ZPL	Stokes Shift
2E	1.80	1.78	1.79	0.02
4T2
Scheme 1	1.82	1.55	1.76	0.27
Scheme 2	1.82	1.39	1.71	0.43
Expt. a	1.83	1.55	-	0.28

Note: ^a Ref. [8].

. The observed comparison between the ZPL energies of the excited states ²E and ⁴T₂ and the ground state ⁴A₂ indicates a weak CF case in Ca₃Y₂Ge₃O₁₂: Cr³⁺. Consequently, the experimentally observed broad NIR emission should be attributed to the ⁴A₂-⁴T₂ optical transition, not solely due to its spin-allowed transition nature. Remarkably, the calculated excitation, emission, and Stokes shift energies for the ⁴A₂-⁴T₂ optical transition demonstrate excellent agreement with the experimental values, particularly when predicated on the ⁴T₂ geometric structure optimized with the first fractional particle occupancy scheme, as opposed to Scheme 2. An over-relaxation phenomenon is discerned in the ⁴T₂ geometric structure optimized by Scheme 2, manifesting through a markedly larger calculated Stokes shift energy. The superiority of Scheme 1 becomes apparent, as the chosen particle occupations on the three t_2g KS orbitals align aptly with their energy distribution corresponding to the combination of a single-fold A and a doubly degenerate E. Furthermore, the ⁴A₂-²E optical transition displays a negligible configuration coordinate change, evidenced by the calculated Stokes shift energy of 0.02 eV. This observation, in conjunction with the significantly larger Stokes shift energy of 0.27 eV observed in the optical transition of ⁴A₂-⁴T₂, receives robust support from the structural data presented in the previous section.

To understand the luminescence mechanism of the materials under investigation, we constructed a host-referred binding energy (HRBE) diagram for Cr³⁺-doped Ca₃Y₂Ge₃O₁₂ following Dorenbos’s standardization [38], as illustrated in Figure 7. The energy level position of the ground state ⁴A₂ of Cr dopants within the band gap was determined by employing the charge transition level ε(+1/0) (denoted as ε(Cr⁴⁺/Cr³⁺)), derived from the PBE0 total energy calculations. Simultaneously, the positions of the excited states ²E, ⁴T₂, and ⁴T₁ were ascertained by considering their calculated ZPL energies relative to the ground state ⁴A₂. It is worth noting that the estimation of the ⁴A₂-⁴T₁ ZPL energy involves the energy difference between the two experimentally observed ⁴A₂-⁴T₂ and ⁴A₂-⁴T₁ excitation energies (i.e., ~0.72 eV taken from reference [8]). Inspection of Figure 7 reveals three distinct excitation pathways that induce the luminescence: host absorption from VB to CB and the ⁴A₂ → ⁴T₁ and ⁴A₂ → ⁴T₂ transitions of Cr³⁺ dopants. Evidently, the excitation efficiency of the host absorption is the lowest, given the considerable separation of the ground ⁴A₂ and luminescent ⁴T₂ energy levels from the top of the VBs and the bottom of the CBs, respectively. The isolated nature of the luminescence, free from the interference of the host’s electronic structure, also ensures potentially excellent quantum efficiency for applications in NIR light sources. Both anticipated observations are substantiated by the experiments (refer to Figure 4 and see Section 3.4 in reference [8]).

3.2.3. Thermal Stability

The luminescent energy level observed in the investigated compound has been attributed to the excited state ⁴T₂ of Cr³⁺ dopants. Consequently, the thermal quenching effect in Cr³⁺-doped Ca₃Y₂Ge₃O₁₂ arises primarily from the thermally activated crossover between the potential surfaces of the ground ⁴A₂ and excited ⁴T₂ states [39]. It is crucial to note that the crossover between the potential surfaces of the ground ⁴A₂ and excited ²E states appears challenging due to a nearly negligible change in configuration coordinates relative to the ground state ⁴A₂. The thermal excitation energy (E_a) of Ca₃Y₂Ge₃O₁₂: Cr³⁺, a pivotal parameter for describing the thermal stability of materials, can be defined as the energy difference between the crossover point of the potential surfaces of the ground ⁴A₂ and excited ⁴T₂ states and the equilibrium structure point of the excited state ⁴T₂. To evaluate E_a, we constructed a configuration coordinate diagram of Cr³⁺ ions in Ca₃Y₂Ge₃O₁₂. This involved considering the equilibrium structure points of the ground ⁴A₂ and excited ⁴T₂ states (denoted as Q_g and Q_e, respectively), utilizing the calculated excitation, emission, and ZPL energies of the optical transition ⁴A₂-⁴T₂ (denoted as E_x., E_m. and E_ZPL, respectively), and applying a one-dimensional harmonic approximation for the potential surfaces of the ground ⁴A₂ and excited ⁴T₂ states, as illustrated in Figure 8.

By utilizing the calculated average Cr³⁺-O²⁻ bond lengths of the [CrO₆]⁹⁻ complex in the ground ⁴A₂ and excited ⁴T₂ states as the horizon coordinate values of the Q_g and Q_e points, respectively, the crossover point (denoted as Q_T) between the potential surfaces of the ground ⁴A₂ and excited ⁴T₂ states can be ascertained. Consequently, the thermal excitation energy E_a was determined to be 0.266 eV. This value closely aligns with the reported thermal excitation energy of 0.25 eV, derived by fitting a modified Arrhenius equation to the measured temperature dependence of the emission intensity of Ca₃Y₂Ge₃O₁₂: Cr³⁺ [8]. This good agreement between the calculated and experimentally estimated thermal barrier values serves as solid proof of the validity of the performed analysis and allows for a further investigation of the role of non-radiative processes in the deactivation of the excited electronic states. Such a prediction concerning thermal excitation energy holds significant value for the smart search for novel NIR Cr³⁺-doped phosphors with high thermal stability. Additionally, the energy differences between the two Q_g and Q_e points on the potential surfaces of the ground ⁴A₂ and excited ⁴T₂ states were assessed, yielding values of 0.21 and 0.06 eV, respectively (the sum of these values corresponds to the Stokes shift energy). This indicates that the primary energy loss during the luminescence kinetics process takes place in the ground-state relaxation following emission.

The reliable outcomes of the present paper validate the robustness of the fractional particle occupancy scheme developed in this study, effectively overcoming the calculation convergence challenges present in the DFT+U and hybrid DFT modeling of the excited ⁴T₂ state of 3d³ ions in solids. Additionally, this scheme can serve as a complement to an alternative approach quite recently proposed by Duan et al., which involves deactivating the 3d subspace diagonalization to address the same encountered problem [16]. Beyond enriching our fundamental understanding, this study establishes a foundation for future endeavors in the high-throughput design of novel Cr³⁺-doped phosphors, placing emphasis on both high thermal stability and the luminescent properties required for NIR applications.

4. Conclusions

In conclusion, our thorough investigation, employing first-principles calculations within the DFT framework, has successfully unraveled broadband NIR luminescence in Cr³⁺-doped Ca₃Y₂Ge₃O₁₂ garnets. This comprehensive exploration has provided valuable insights into the intricate interplay among geometric and electronic structures, optical properties, and thermal behavior. The findings are summarized below:

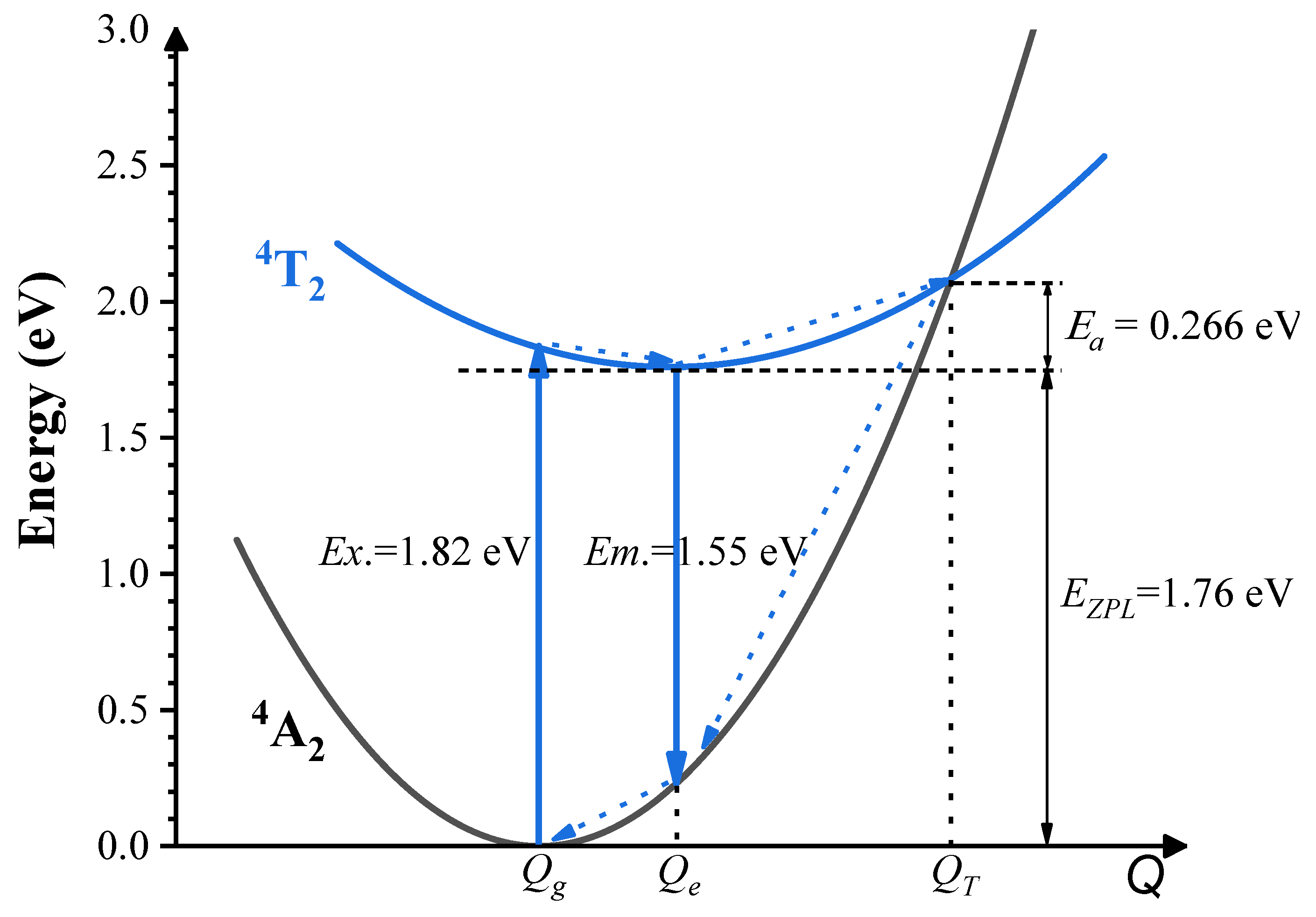
• The results from both the structural analysis and the defect formation energy calculations indicate a tendency for Cr³⁺ dopants to preferentially occupy Y³⁺ sites rather than Ca²⁺ and Ge⁴⁺ sites. Comparing the optimized geometric structure of the ground state ⁴A₂ of Cr³⁺ ions, the excited state ⁴T₂ exhibits a significant Jahn–Teller distortion, characterized by a notable axial expansion and a slight equatorial compression in the [CrO₆]⁹⁻ complex. In contrast, the excited state ²E primarily retains the initial ground-state structure, undergoing a negligible change.
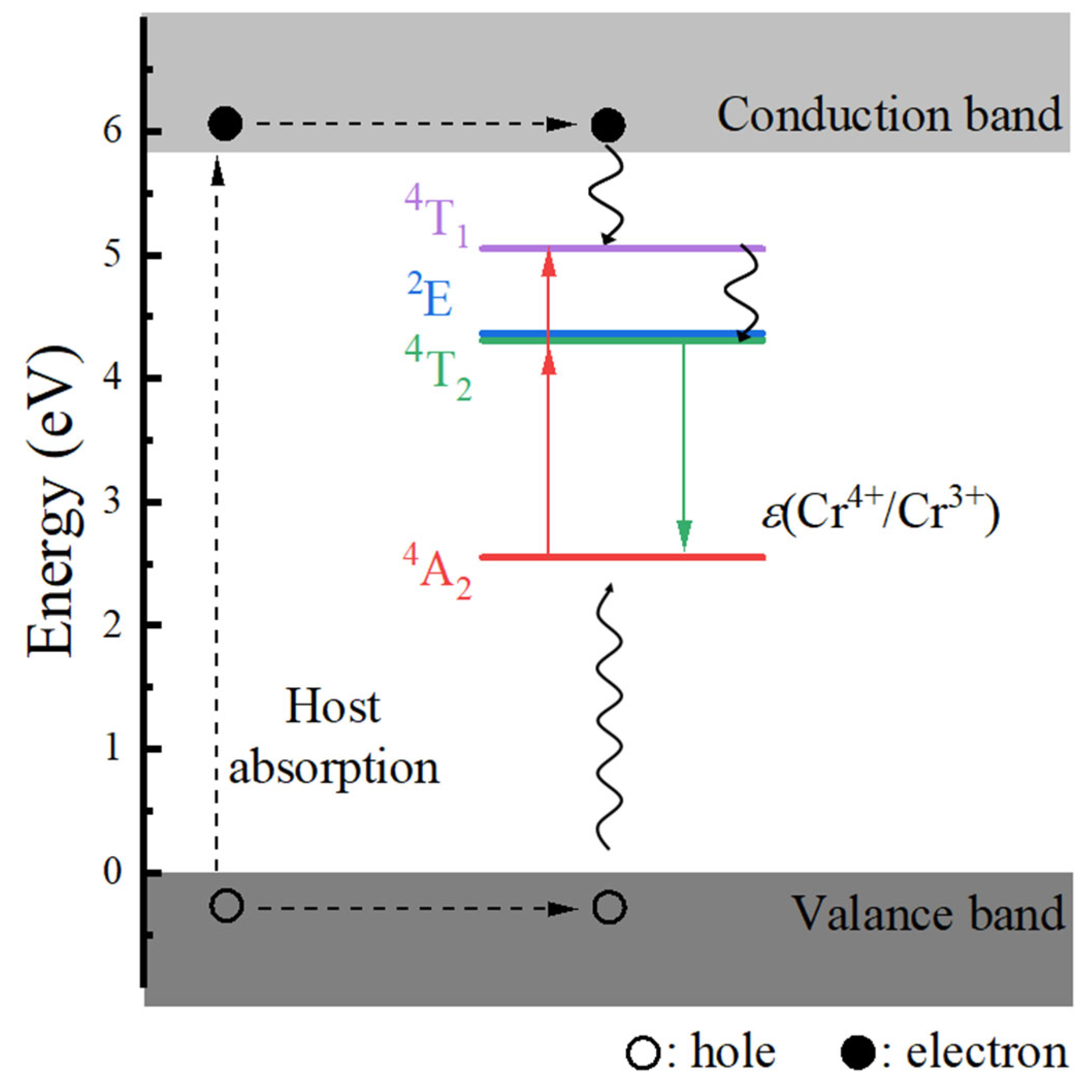
• The host material Ca₃Y₂Ge₃O₁₂ features a direct band gap of 5.82 eV, allowing sufficient space to accommodate the multiple energy levels of Cr³⁺ dopants. The calculated positions of the ground ⁴A₂ and excited ⁴T₂ energy levels within the band gap underscore the isolated nature of Cr³⁺ optical centers from the host’s electronic structure. This discovery further supports the observed higher quantum efficiency.
• The calculated energies for the excitation, emission, and Stokes shift associated with the optical transitions ⁴A₂-²E and ⁴A₂-⁴T₂ show a much better agreement with the experimental values. The energy comparison of the optical transitions ⁴A₂-²E and ⁴A₂-⁴T₂ indicates that Cr³⁺ ions are located in a weak CF. The identification of three distinct excitation pathways that induce the ⁴T₂→⁴A₂ luminescence suggests that the excitations of Cr³⁺ ions to the ⁴T₁ and ⁴T₂ states are more efficient.
• Our accurate prediction of thermal excitation energy has paved a direct path to providing fundamental analysis of the thermal quenching process in phosphors doped with 3d³ ions, using the configuration coordinate diagram.