AC Magnetic Susceptibility: Mathematical Modeling and Experimental Realization on Poly-Crystalline and Single-Crystalline High-Tc Superconductors YBa2Cu3O7−δ and Bi2−xPbxSr2Ca2Cu3O10+y
Abstract
:1. Introduction
2. Experimental Techniques and Materials
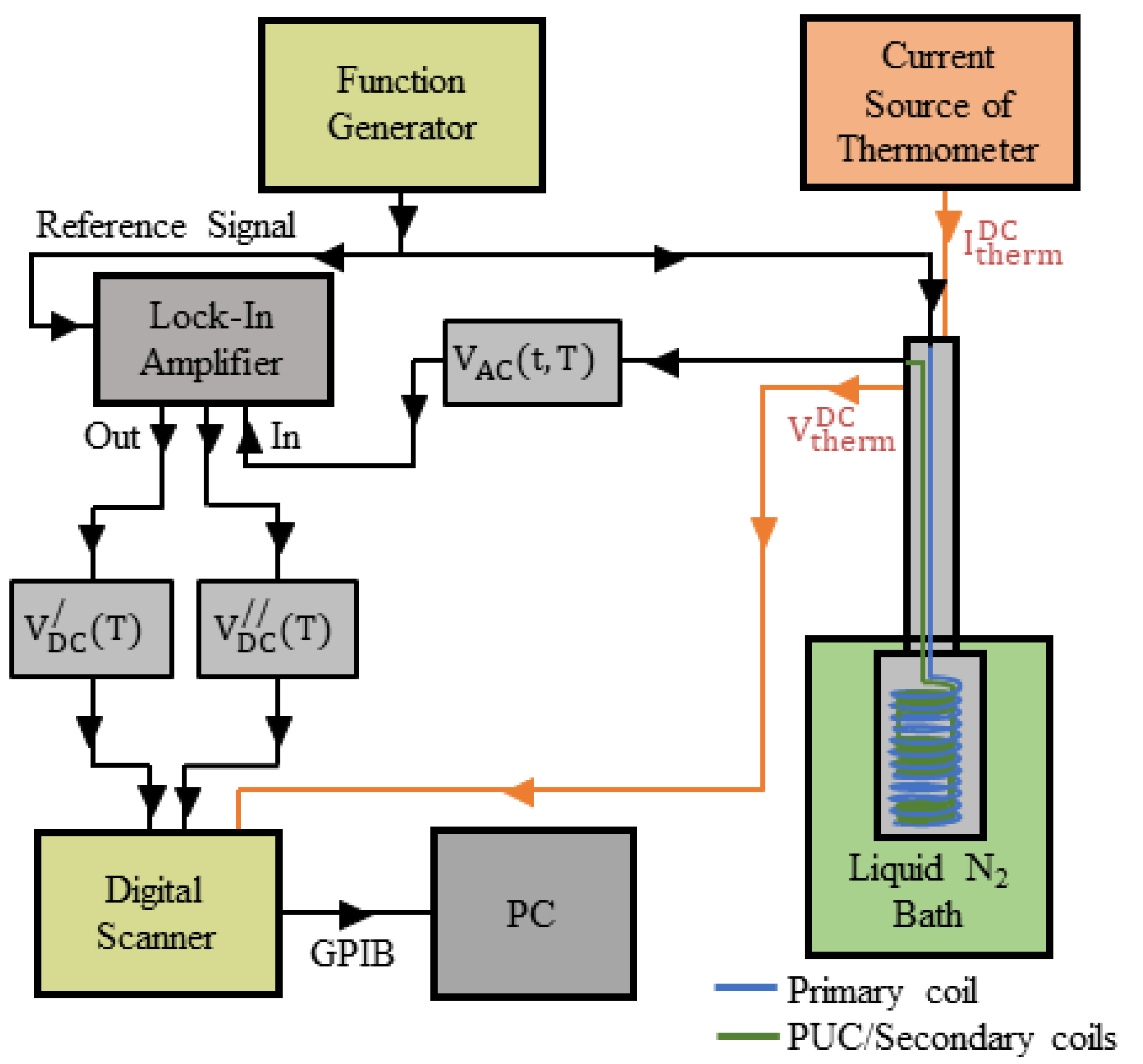
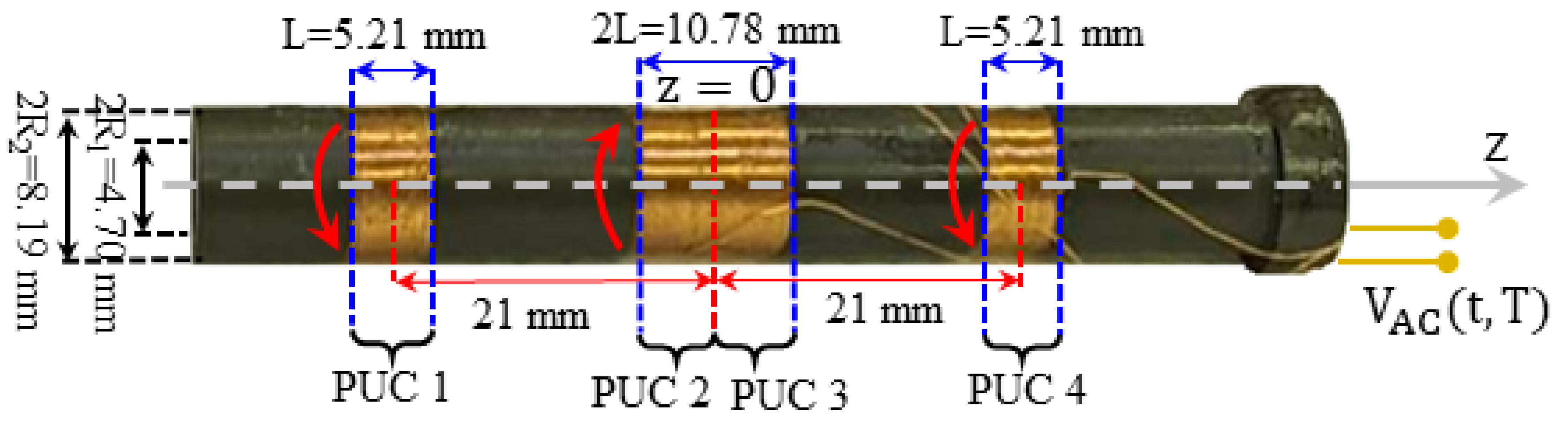
2.1. ACMS Experimental Set-Up
2.2. X-ray Diffractometer
2.3. Scanning Electron Microscopy
2.4. Materials
3. Mathematical Modeling of the ACMS Experimental Set-Up
4. Superconducting Cylinder—Complete Mathematical Modeling of the ACMS
5. Experimental Results
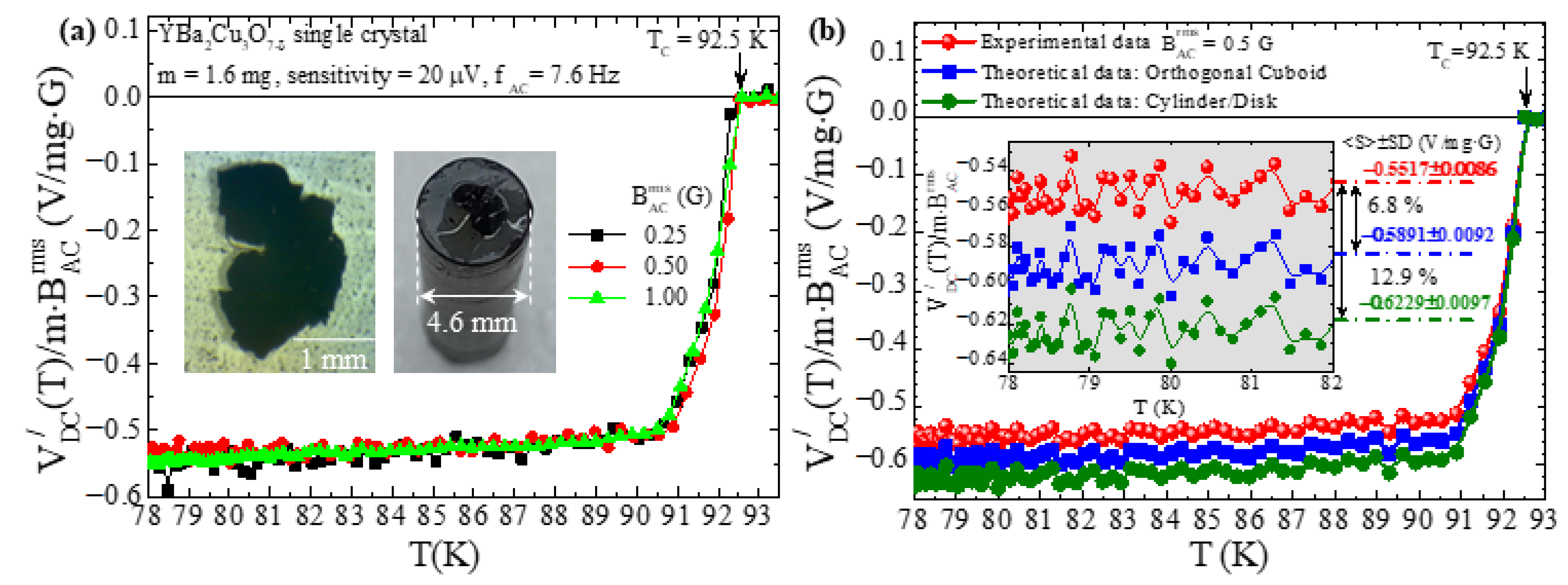
5.1. Poly-Crystalline Cylindrical Specimen of High-Tc YBa2Cu3O7−δ
5.2. Poly-Crystalline Cylindrical Specimen of High-Tc Bi2−xPbxSr2Ca2Cu3O10+y
5.3. Single-Crystalline Thin Plate of High-Tc YBa2Cu3O7−δ
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hein, R.A.; Francavilla, T.L.; Liebenberg, D.H. Magnetic Susceptibility of Superconductors and Other Spin Systems, 1st ed.; Plenum Press: New York, NY, USA, 1991. [Google Scholar]
- Ripka, P. Magnetic Sensors and Magnetometers; Artech House: Norwood, MA, USA, 2001. [Google Scholar]
- Moraitis, P.; Stamopoulos, D. Assemblies of Coaxial Pick-Up Coils as Generic Inductive Sensors of Magnetic Flux: Mathematical Modeling of Zero, First and Second Derivative Configurations. Sensors 2024. to be submitted. [Google Scholar]
- Stamenov, P.; Coey, J.M.D. Sample size, position, and structure effects on magnetization measurements using second-order gradiometer pickup coils. Rev. Sci. Instrum. 2006, 77, 015106. [Google Scholar] [CrossRef]
- Myers, W.; Slichter, D.; Hatridge, M.; Busch, S.; Mößle, M.; McDermott, R.; Trabesinger, A.; Clarke, J. Calculated signal-to-noise ratio of MRI detected with SQUIDs and Faraday detectors in fields from 10 μT to 1.5 T. J. Magn. Res. 2007, 186, 17337220. [Google Scholar] [CrossRef] [PubMed]
- Kodama, K. A new system for measuring alternating current magnetic susceptibility of natural materials over a wide range of frequencies. Geochem. Geophys. Geosyst. 2010, 11, Q11002. [Google Scholar] [CrossRef]
- Sawicki, M.; Stefanowicz1, W.; Ney, A. Sensitive SQUID magnetometry for studying nanomagnetism. Semicond. Sci. Technol. 2011, 26, 064006. [Google Scholar] [CrossRef]
- Buchner, M.; Höfler, K.; Henne, B.; Ney, V.; Ney, A. Tutorial: Basic principles, limits of detection, and pitfalls of highly sensitive SQUID magnetometry for nanomagnetism and spintronics. J. Appl. Phys. 2018, 124, 161101. [Google Scholar] [CrossRef]
- Chen, D.-X.; Skumryev, V.; Coey, J.M.D. Domain-wall dynamics in aligned bound Sm2Fe17. Phys. Rev. B 1996, 53, 9983297. [Google Scholar] [CrossRef] [PubMed]
- Topping, C.V.; Blundell, S.J. AC susceptibility as a probe of low-frequency magnetic dynamics. J. Phys. Condens. Matter 2018, 31, 013001. [Google Scholar] [CrossRef] [PubMed]
- Modestino, M.; Galluzzi, A.; Sarno, M.; Polichetti, M. The Effect of a DC Magnetic Field on the AC Magnetic Properties of Oleic Acid-Coated Fe3O4 Nanoparticles. Materials 2023, 16, 4246. [Google Scholar] [CrossRef]
- Botez, C.E.; Price, A.D. Ac-Susceptibility Studies of the Energy Barrier to Magnetization Reversal in Frozen Magnetic Nanofluids of Different Concentrations. Appl. Sci. 2023, 13, 9416. [Google Scholar] [CrossRef]
- Botez, C.E.; Mussslewhite, Z. Evidence of Individual Superspin Relaxation in Diluted Fe3O4/Hexane Ferrofluids. Materials 2023, 16, 4850. [Google Scholar] [CrossRef]
- Goldfarb, R.B.; Lelental, M.; Thomson, C.A. Alternating-Field Susceptometry and Magnetic Susceptibility of Superconductors; Plenum Press: New York, NY, USA, 1992. [Google Scholar]
- Nikolo, M. Superconductivity: A guide to alternating current susceptibility measurements and alternating current susceptometer design. Am. J. Phys. 1995, 63, 57. [Google Scholar] [CrossRef]
- Gömöry, F. Characterization of high-temperature superconductors by AC susceptibility measurements. Supercond. Sci. Technol. 1997, 10, 523. [Google Scholar] [CrossRef]
- Shamsodini, M.; Salamati, H.; Shakeripour, H.; Sarsari, I.A.; Esferizi, M.F.; Nikmanesh, H. Effect of using two different starting materials (nitrates and carbonates) and a calcination processes on the grain boundary properties of a BSCCO superconductor. Supercond. Sci. Technol. 2019, 32, 075001. [Google Scholar] [CrossRef]
- Barood, F.; Kechik, M.M.A.; Tee, T.S.; Kien, C.S.; Pah, L.K.; Hong, K.J.; Shaari, A.H.; Baqiah, H.; Karim, M.K.A.; Shabdin, M.K. Orthorhombic YBa2Cu3O7−δ Superconductor with TiO2 Nanoparticle Addition: Crystal Structure, Electric Resistivity, and AC Susceptibility. Coatings 2023, 13, 1093. [Google Scholar] [CrossRef]
- Lynnyk, A.; Puzniak, R.; Shi, L.; Zhao, J.; Jin, C. Superconducting State Properties of CuBa2Ca3Cu4O10+δ. Materials 2023, 16, 5111. [Google Scholar] [CrossRef] [PubMed]
- Buchkov, K.; Galluzzi, A.; Nazarova, E.; Polichetti, M. Complex AC Magnetic Susceptibility as a Tool for Exploring Nonlinear Magnetic Phenomena and Pinning Properties in Superconductors. Materials 2023, 16, 4896. [Google Scholar] [CrossRef] [PubMed]
- Ionescu, A.M.; Ivan, I.; Miclea, C.F.; Crisan, D.N.; Galluzzi, A.; Polichetti, M.; Crisan, A. Vortex Dynamics and Pinning in CaKFe4As4 Single Crystals from DC Magnetization Relaxation and AC Susceptibility. Condens. Matter 2023, 8, 93. [Google Scholar] [CrossRef]
- Goldfarb, R.B.; Minervini, J.V. Calibration of ac susceptometer for cylindrical specimens. Rev. Sci. Instrum. 1984, 55, 761. [Google Scholar] [CrossRef]
- Manual, DSP Lock-In Amplifier Model SR830; Stanford Research Systems: Sunnyvale, CA, USA, 2011.
- Chen, D.-X.; Brug, J.A.; Goldfarb, R.B. Demagnetizing factors for cylinders. IEEE Trans. Magn. 1991, 27, 3601. [Google Scholar] [CrossRef]
- Prozorov, R.; Giannetta, R.W.; Carrington, A.; Araujo-Moreira, F.M. Meissner-London state in superconductors of rectangular cross section in a perpendicular magnetic field. Phys. Rev. B 2000, 62, 115. [Google Scholar] [CrossRef]
- Brandt, E.H. Geometric edge barrier in the Shubnikov phase of type-II superconductors. Low Temp. Phys. 2001, 27, 723. [Google Scholar] [CrossRef]
- Prozorov, R.; Kogan, V.G. Effective Demagnetizing Factors of Diamagnetic Samples of Various Shapes. Phys. Rev. Appl. 2018, 10, 014030. [Google Scholar] [CrossRef]
- Prozorov, R. Meissner-London Susceptibility of Superconducting Right Circular Cylinders in an Axial Magnetic Field. Phys. Rev. Appl. 2021, 16, 024014. [Google Scholar] [CrossRef]
- Wu, M.K.; Ashburn, J.R.; Torng, C.J.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, Z.J.; Wang, Y.Q.; Chu, C.W. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure. Phys. Rev. Lett. 1987, 58, 908. [Google Scholar] [CrossRef] [PubMed]
- Liang, R.; Bonn, D.A.; Hardy, W.N. Growth of high quality YBCO single crystals using BaZrO3 Crucibles. Phys. C 1998, 304, 105. [Google Scholar] [CrossRef]
- Pissas, M.; Stamopoulos, D. Evidence for geometrical barriers in an untwinned YBa2Cu3O7−δ single crystal. Phys. Rev. B 2001, 64, 134510. [Google Scholar] [CrossRef]
- Liang, R.; Bonn, D.A.; Hardy, W.N. Evaluation of CuO2 plane hole doping in YBa2Cu3O6+x single crystals. Phys. Rev. B 2006, 73, 180505. [Google Scholar] [CrossRef]
- Djurek, D. Search for Novel Phases in Y-Ba-Cu-O Family. Condens. Matter 2024, 9, 10. [Google Scholar] [CrossRef]
- Stamopoulos, D. The ac Magnetic Susceptibility of Superconducting YBa2Cu3O7−δ Single Crystals in the Low Field Regime. unpublished results.
- Pissas, M.; Niarchos, D. Preparation of the 110 K high Tc superconductor Bi2Sr2Ca2Cu3Oy by Pb and Sb substitution. Phys. C 1989, 159, 643. [Google Scholar] [CrossRef]
- Pissas, M.; Niarchos, D.; Christides, C.; Anagnostou, M. The optimum percentage of Pb and the appropriate thermal procedure for the preparation of the 110 K Bi2−xPbxSr2Ca2Cu3Oy superconductor. Supercond. Sci. Technol. 1997, 3, 128. [Google Scholar] [CrossRef]
- Abdullah, S.N.; Kechik, M.M.A.; Kamarudin, A.N.; Talib, Z.A.; Baqiah, H.; Kien, C.S.; Pah, L.K.; Abdul Karim, M.K.; Shabdin, M.K.; Shaari, A.H.; et al. Microstructure and Superconducting Properties of Bi-2223 Synthesized via Co-Precipitation Method: Effects of Graphene Nanoparticle Addition. Nanomaterials 2023, 13, 2197. [Google Scholar] [CrossRef] [PubMed]
- Hai, Q.; Chen, H.; Sun, C.; Chen, D.; Qi, Y.; Shi, M.; Zhao, X. Green-Light GaN p-n Junction Luminescent Particles Enhance the Superconducting Properties of B(P)SCCO Smart Meta-Superconductors (SMSCs). Nanomaterials 2023, 13, 3029. [Google Scholar] [CrossRef] [PubMed]
- Stamopoulos, D. Evolution of the Superconducting Properties of Polycrystalline Bi1.6Pb0.4Sr1.6Ca2.0Cu2.8O9.2+x at Low Magnetic Fields. unpublished results.
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Poole, C.P., Jr. Handbook of Superconductivity; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Krabbes, G.; Fuchs, G.; Canders, W.R.; May, H.; Palka, R. High Temperature Superconductor Bulk Materials; Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar]
- Prozorov, R.; Giannetta, R.W. Magnetic penetration depth in unconventional superconductors. Supercond. Sci. Technol. 2006, 19, R41. [Google Scholar] [CrossRef]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists, 7th ed.; Academic Press: San Diego, CA, USA, 2013. [Google Scholar]
- Batygin, V.V.; Toptygin, I.N. Problems in Electrodynamics, 1st ed.; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Magnin, P.; Kahn, E. Superconductivity; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Chen, D.-X.; Nogues, J.; Rao, K.V. AC susceptibility and intergranular critical current density of high Tc superconductors. Cryogenics 1989, 29, 800. [Google Scholar] [CrossRef]
- Forkl, A. Magnetic Flux Distribution in Single Crystalline, Ceramic and Thin Film High-Tc-Superconductors. Phys. Scr. 1993, T49, 148. [Google Scholar] [CrossRef]
- Lortz, R.; Tomita, T.; Wang, Y.; Junod, A.; Schilling, J.S.; Masui, T.; Tajima, S. On the origin of the double superconducting transition in overdoped YBa2Cu3Ox. Phys. C 2006, 434, 194–198. [Google Scholar] [CrossRef]
- Salamati, H.; Kameli, P. AC susceptibility study of YBCO thin film and BSCCO bulk superconductors. J. Magn. Magn. Mat. 2004, 278, 237. [Google Scholar] [CrossRef]
- Hascicek, Y.S.; Testardi, L.R. Temperature-independent, constant E-J relation below T, in the current-induced resistive state of polycrystalline YBa2Cu3O7−x. Phys. Rev. B 1991, 43, 2853. [Google Scholar] [CrossRef]
- Dubson, M.A.; Herbert, S.T.; Calabrese, J.J.; Harris, D.C.; Patton, B.R.; Garland, J.C. Non-Ohmic dissipative regime in the superconducting transition of polycrystalline Y1Ba2Cu3Ox. Phys. Rev. Lett. 1998, 60, 1061. [Google Scholar] [CrossRef]
- Nikolo, M. Numerical modeling of AC susceptibility and induced nonlinear voltage waveforms of high-Tc granular superconductors. AIP Conf. Proc. 2018, 2025, 050004. [Google Scholar] [CrossRef]
- Garcia, J.; Rillo, C.; Lera, F.; Bartolome, J.; Navarro, R.; Blank, D.H.A.; Flokstra, J. Superconducting weak links in YBa2Cu3O7−σ an AC magnetic susceptibility study. J. Magn. Magn. Mat. 1987, 69, L225–L229. [Google Scholar] [CrossRef]
- Rani, P.; Jha, R.; Awana, V.P.S. AC Susceptibility Study of Superconducting YBa2Cu3O7:Agx Bulk Composites (x=0.0–0.20): The Role of Intra and Intergranular Coupling. J. Supercond. Nov. Magn. 2013, 26, 2347–2352. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moraitis, P.; Koutsokeras, L.; Stamopoulos, D. AC Magnetic Susceptibility: Mathematical Modeling and Experimental Realization on Poly-Crystalline and Single-Crystalline High-Tc Superconductors YBa2Cu3O7−δ and Bi2−xPbxSr2Ca2Cu3O10+y. Materials 2024, 17, 1744. https://doi.org/10.3390/ma17081744
Moraitis P, Koutsokeras L, Stamopoulos D. AC Magnetic Susceptibility: Mathematical Modeling and Experimental Realization on Poly-Crystalline and Single-Crystalline High-Tc Superconductors YBa2Cu3O7−δ and Bi2−xPbxSr2Ca2Cu3O10+y. Materials. 2024; 17(8):1744. https://doi.org/10.3390/ma17081744
Chicago/Turabian StyleMoraitis, Petros, Loukas Koutsokeras, and Dimosthenis Stamopoulos. 2024. "AC Magnetic Susceptibility: Mathematical Modeling and Experimental Realization on Poly-Crystalline and Single-Crystalline High-Tc Superconductors YBa2Cu3O7−δ and Bi2−xPbxSr2Ca2Cu3O10+y" Materials 17, no. 8: 1744. https://doi.org/10.3390/ma17081744




