Study of Anisotropic Behavior in Sheet Metal Forming
Abstract
:1. Introduction
2. Sheet Anisotropy Characterization Methods
2.1. Yld2000-2d Yield Criterion Anisotropy Characterization Capability
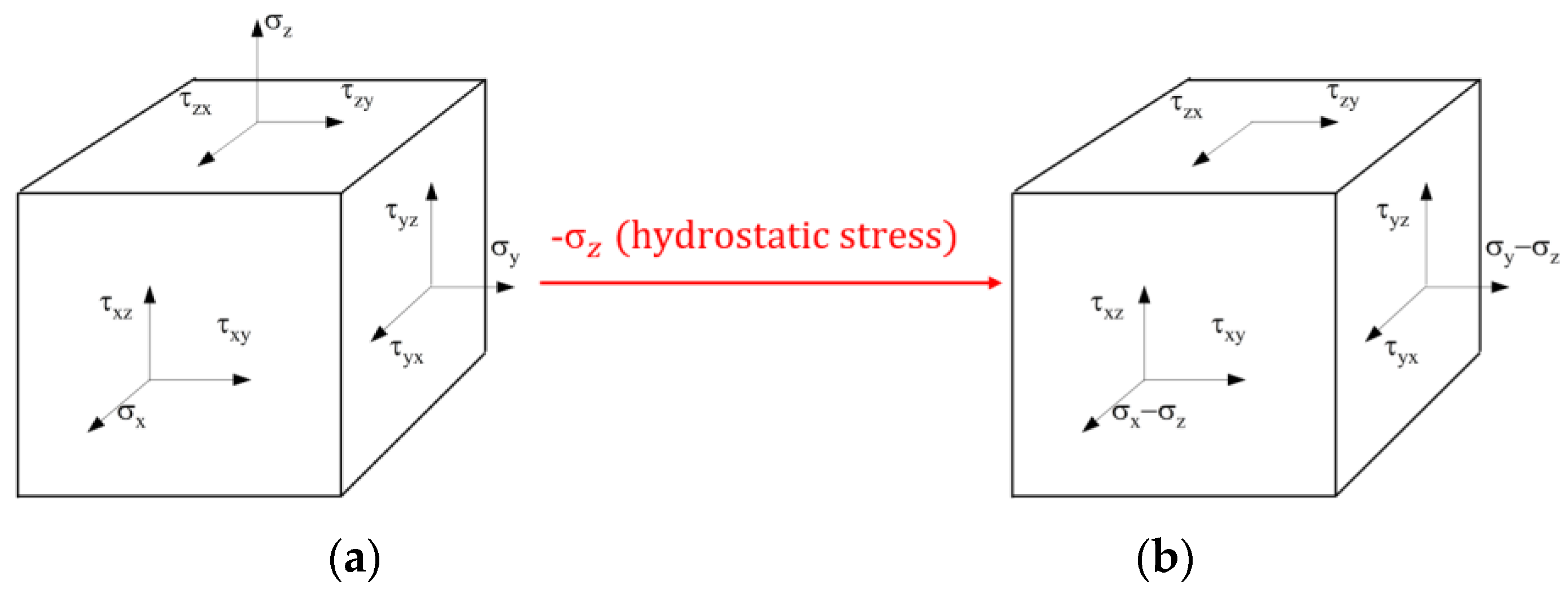
2.2. Prediction of Anisotropic Behavior of Materials in Three-Dimensional Stress State
3. Results and Discussion
3.1. Experimental and Material Data
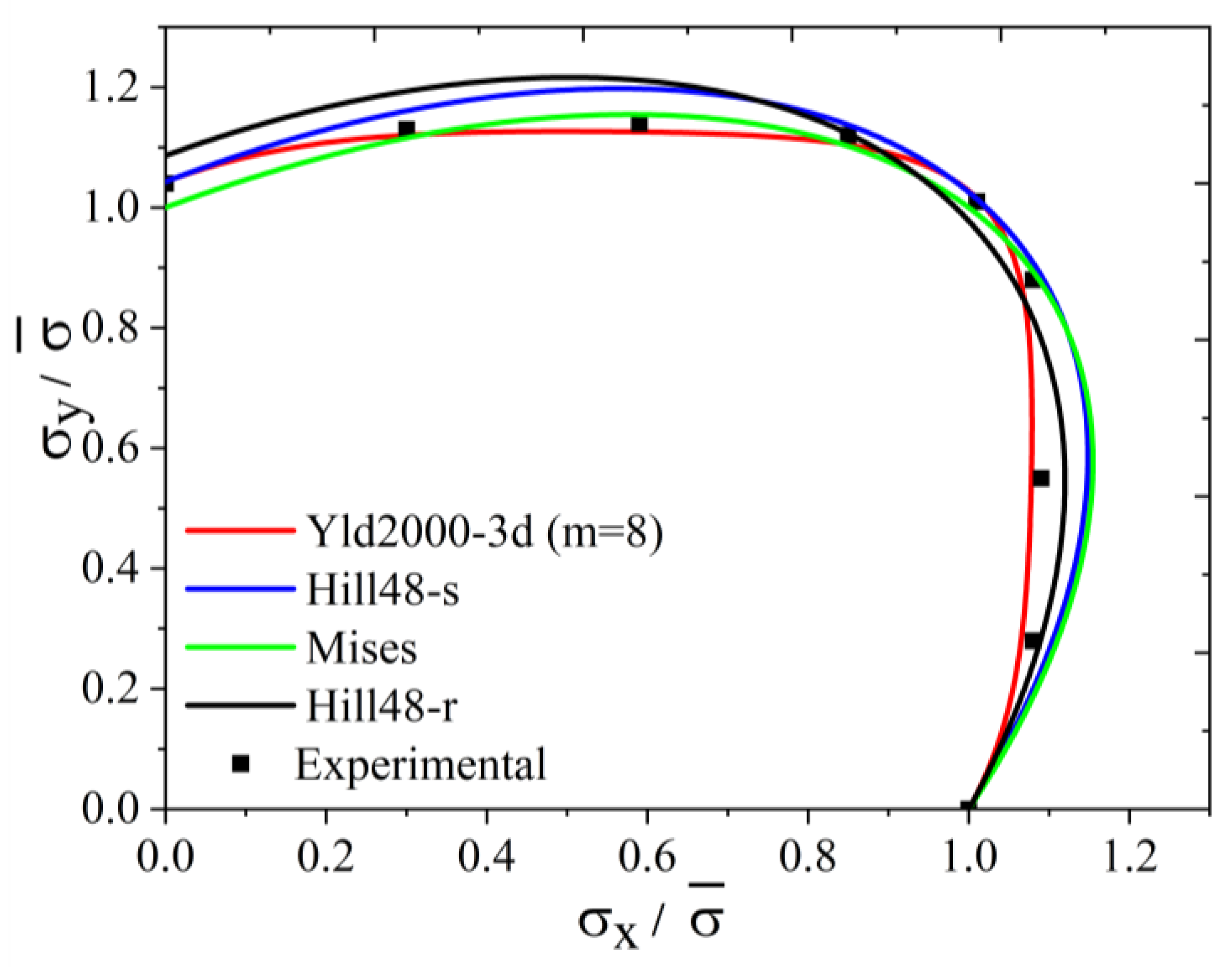
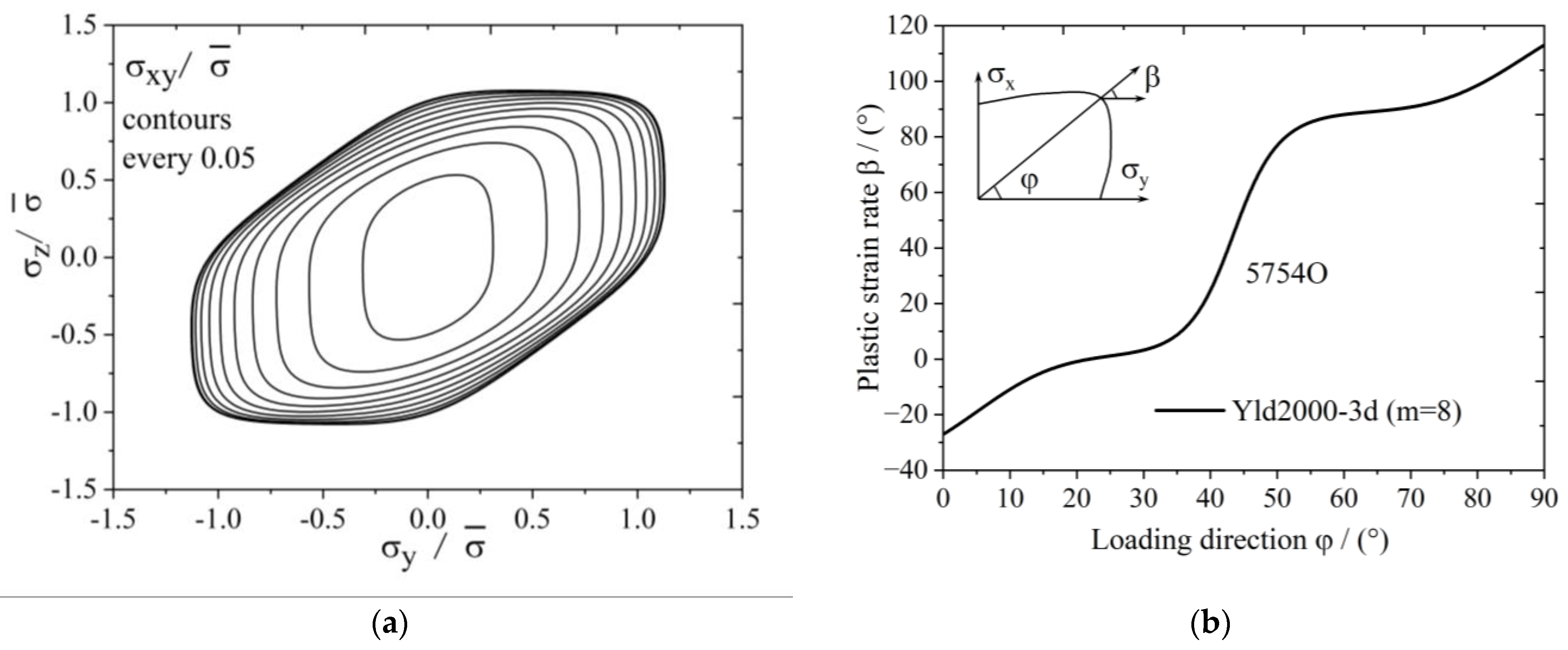
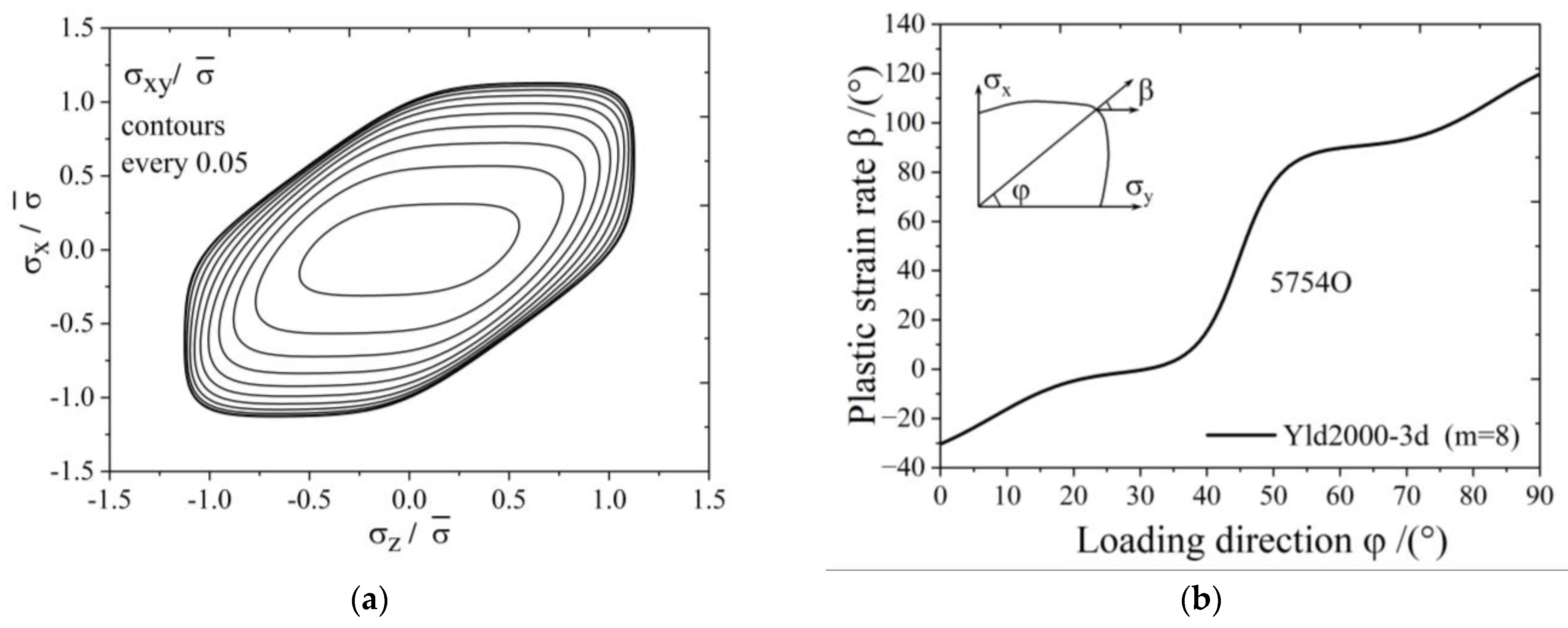
3.2. Three-Dimensional Stress State Material Anisotropy
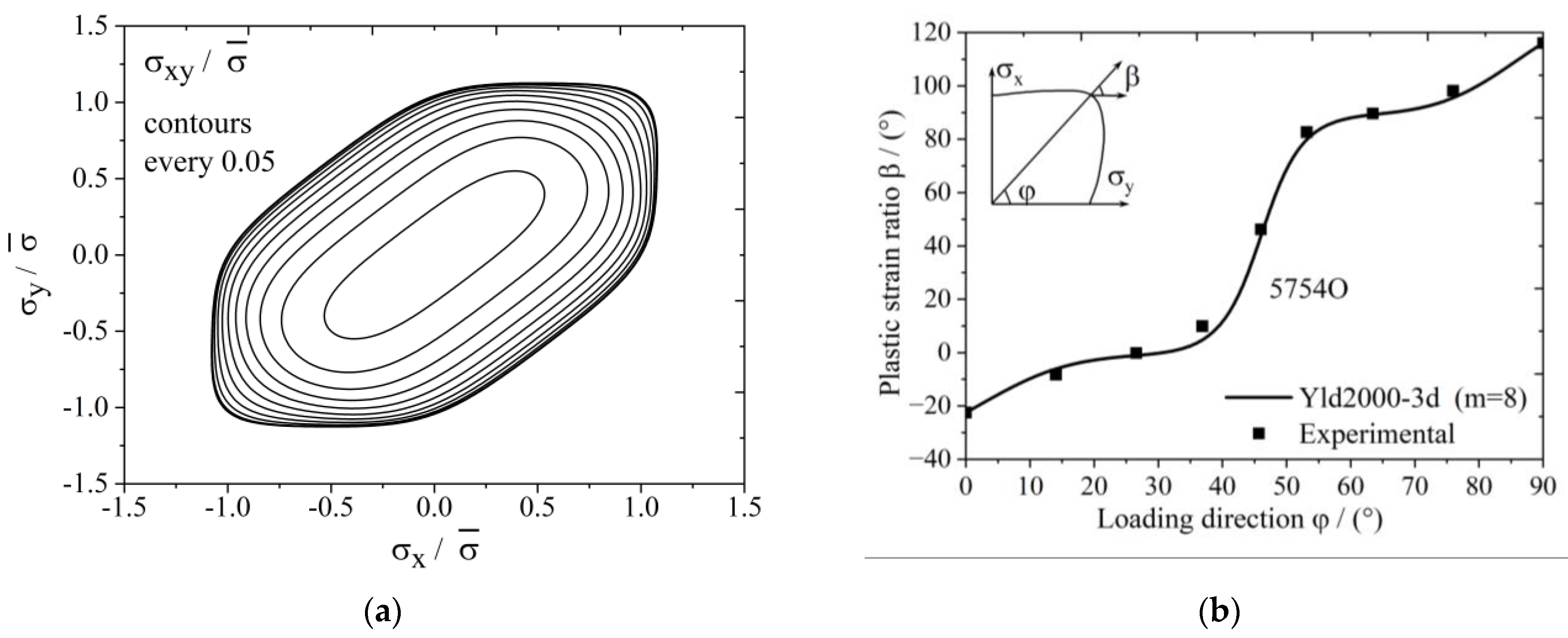
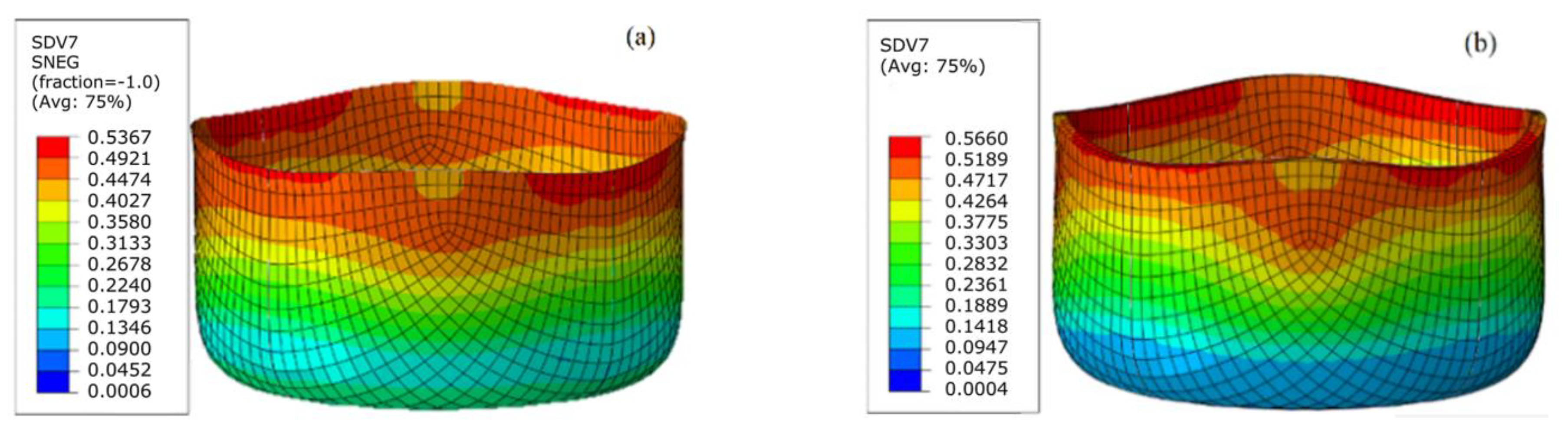
3.3. 5754O Aluminum Alloy Plate Anisotropy Prediction Verification
3.4. DP980 Steel Plate Anisotropy Prediction Verification
4. Conclusions
- (1)
- Considering that some actual sheet metal forming processes are under a three-dimensional stress condition, the Yld2000-2d anisotropic yield function is extended into three-dimensional space for hydrostatic-stress-independent materials; this extended function is named the Yld2000-3d yield function. Taking the 5754O aluminum sheet as an example, the yield surface and the plastic strain ratio diagram are drawn based on the Yld2000-3d three-dimensional stress yield function developed in this study. The results show that the developed Yld2000-3d anisotropic yield function can accurately describe the uniaxial and biaxial mechanical properties of 5754O aluminum alloy sheets, and it can predict the mechanical behaviors in YZ and XZ planes.
- (2)
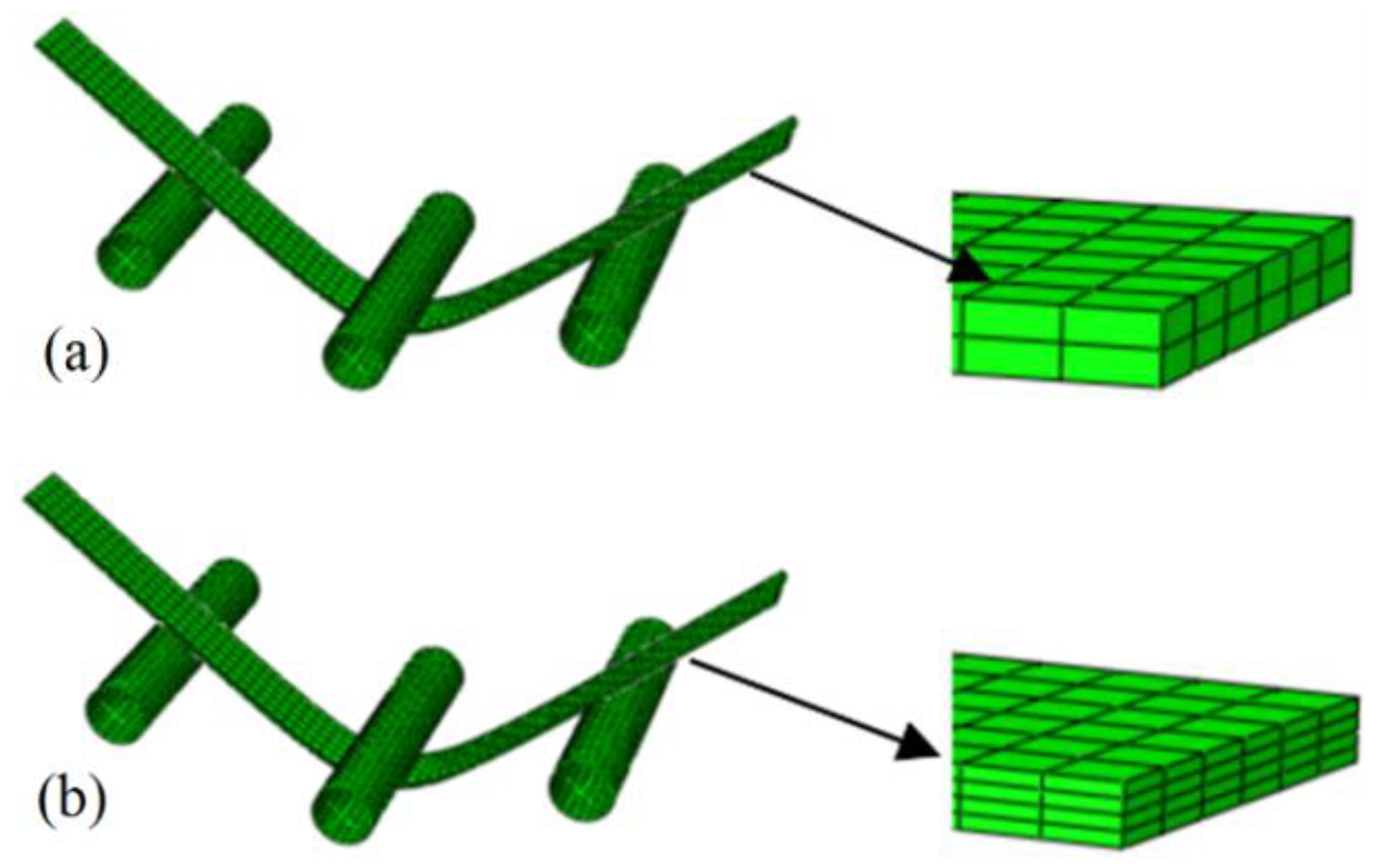
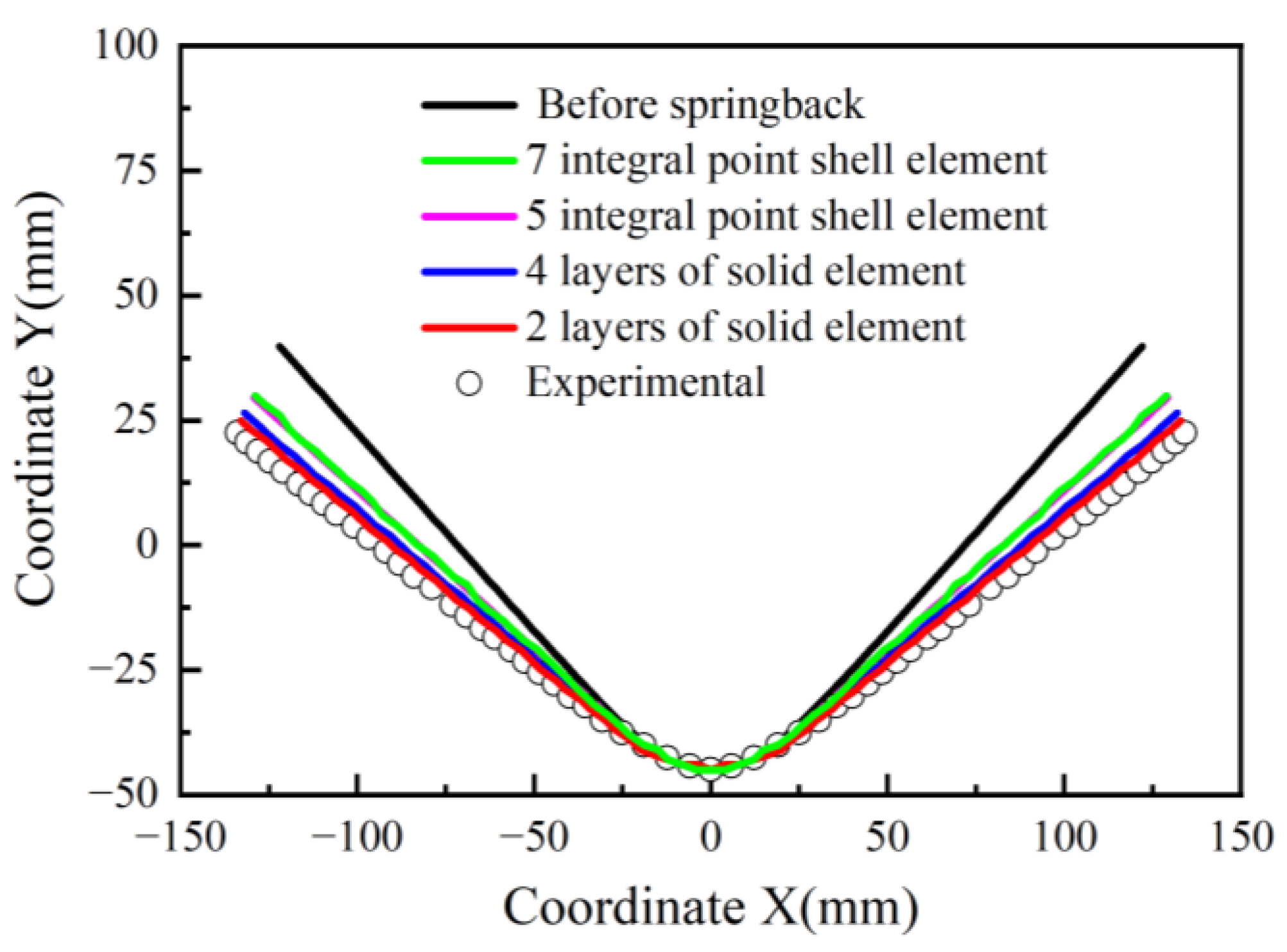
- The Yld2000-3d function developed in this study is implemented in ABAQUS software by using the UMAT (VUMAT) user subroutine. The three-points bending test of a 5754O aluminum alloy sheet is carried out and the corresponding FEM simulations are performed based on the Yld2000-2d and Yld2000-3d yield functions. It is shown that the simulated results of three-points bending based on the Yld2000-3d yield function with a solid element agree better with the experimental results than those based on the Yld2000-2d yield function with a shell element.
- (3)
- Further testing of other sheet metal forming processes was carried out by simulating deep drawing tests of DP980 steel plates using the Yld2000-3d, Yld2000-2d, Hill48, and Mises yield functions. The comparison between the simulated and experimental results of the deep drawing test shows that the Yld2000-3d yield function has the highest accuracy among them in predicting the earring profile.
- (4)
- Besides the advantages of the Yld2000-2d yield function, the stress components related to the thickness direction are also considered, and the Yld2000-3d yield function has high accuracy in describing the anisotropic behavior under a 3D stress state. Compared to the Yld2000-2d yield function, there is no additional parameter in the Yld2000-3d yield function, which makes it convenient in engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Wu, X. Research on the Plastic Deformation Behavior of Anisotropic Sheet Metal under Different Loading Paths; School of Mechanical Engineering and Automation, Beihang University: Beijing, China, 2004. [Google Scholar]
- Lee, S.; Lim, Y.; Galdos, L.; Lee, T. Gaussian process regression-driven deep drawing blank design method. Int. J. Mech. Sci. 2023, 265, 108898. [Google Scholar] [CrossRef]
- Basak, S.; Panda, S.K.; Lee, M.G. Formability and fracture in deep drawing sheet metals: Extended studies for pre-strained anisotropic thin sheets. Int. J. Mech. Sci. 2020, 170, 105346. [Google Scholar] [CrossRef]
- Kalina, M.; Schöne, V.; Spak, B.; Paysan, F.; Breitbarth, E.; Kästner, M. Fatigue crack growth in anisotropic aluminium sheets—Phase-field modelling and experimental validation. Int. J. Fatigue 2023, 176, 107874. [Google Scholar] [CrossRef]
- Hou, Y.; Min, J.Y.; El-Aty, A.A.; Han, H.N.; Lee, M.G. A new anisotropic-asymmetric yield criterion covering wider stress states in sheet metal forming. Int. J. Plast. 2023, 166, 103653. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. Ser. A 1948, 193, 281. [Google Scholar]
- Hill, R. Theoretical Plasticity of textured aggregates. Math. Proceeding Camb Philos. Soc. 1979, 85, 179. [Google Scholar] [CrossRef]
- Hill, R. Constitutive modeling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Hosford, W.F. On yield loci of anisotropic cubic metals. In Proceedings of the 7th North American Metalworking Research Conference, Ann Arbor, MI, USA, 13–16 May 1979; Volume 191. [Google Scholar]
- Barlat, F.; Becker, R.; Hayashida, Y.; Maeda, Y.; Yanagawa, M.; Chung, K.; Brem, J.; Lege, D.; Matsui, K.; Murtha, S.; et al. Yielding description for solution strengthened aluminum alloys. Int. J. Plast. 1997, 13, 385–401. [Google Scholar] [CrossRef]
- Barlat, F.; Maeda, Y.; Chung, K.; Yanagawa, M.; Brem, J.C.; Hayashida, Y.; Lege, D.J.; Matsui, K.; Murtha, S.J.; Hattori, S.; et al. Yield function development for aluminum alloy sheets. Mech. Phys. Solids 1997, 45, 1727–1763. [Google Scholar] [CrossRef]
- Barlat, F. Crystallographic textures anisotropic yield surfaces and forming limits of sheet metals. Mater. Sci. Eng. 1987, 91, 55–72. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Yan, Y. Capabilities of yield functions on predicting the anisotropic behaviors of DP600 steel sheet. J. Plast. Eng. 2015, 22, 45–50. [Google Scholar]
- Hosford, W.F. A generalized isotropic yield function. J. Appl. Mech. Trans. ASME 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dick, R.E.; Lege, D.J. Plane stress yield function for aluminum alloy sheets-part I: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Wang, H. Yielding and Hardening Behavior and Forming Limit for Sheet Metal under Complex Loading Paths; Beihang University: Beijing, China, 2009. [Google Scholar]
- Ryser, M.; Steffen, J.; Berisha, B.; Bambach, M. Integrating multiple samples into full-field optimization of yield criteria. Int. J. Mech. Sci. 2023, 265, 108880. [Google Scholar] [CrossRef]
- Raj, A.; Verma, R.K.; Singh, P.K.; Shamshoddin, S.; Biswas, P.; Narasimhan, K. Experimental and numerical investigation of differential hardening of cold rolled steel sheet under non-proportional loading using biaxial tensile test. Int. J. Plast. 2022, 154, 103297. [Google Scholar] [CrossRef]
- Wang, H.B.; Wan, M.; Wu, X.D.; Yan, Y. The equivalent plastic strain-dependent Yld2000-2d yield function and the experimental verification. Comput. Mater. Sci. 2009, 47, 12–22. [Google Scholar] [CrossRef]
- Li, Z.G.; Yang, H.F.; Liu, J.G.; Liu, F. An improved yield criterion characterizing the anisotropic and tension-compression asymmetric behavior of magnesium alloy. J. Magnes. Alloys 2022, 10, 569–584. [Google Scholar] [CrossRef]
- Ji, C.; Li, Z.G.; Liu, J.G. Development of an improved MMC-based fracture criterion characterizing the anisotropic and strain rate-dependent behavior of 6061-T5 aluminum alloy. Mech. Mater. 2020, 150, 103598. [Google Scholar] [CrossRef]
- Shen, F.; Münstermann, S.; Lian, J. An evolving plasticity model considering anisotropy, thermal softening and dynamic strain aging. J. Constr. Steel Res. 2020, 132, 102747. [Google Scholar] [CrossRef]
- He, Z.; Zhang, K.; Zhu, H.; Lin, Y.; Fu, M.W.; Yuan, S. An anisotropic constitutive model for forming of aluminum tubes under both biaxial tension and pure shear stress states. Int. J. Plast. 2022, 152, 103259. [Google Scholar] [CrossRef]
- Lee, H.R.; Lee, M.G.; Park, N. Incremental tube forming process with a novel free rotating bearing tool tip experiment and FE modeling with anisotropic plasticity. Model. Met. Mater. Int. 2022, 28, 2356–2370. [Google Scholar] [CrossRef]
- Min, J.; Guo, N.; Hou, Y.; Jiang, K.; Chen, X.; Carsley, J.E.; Lin, J. Effect of tension-compression testing strategy on kinematic model calibration and spring-back simulation of advanced high strength steels. Int. J. Mater. Form. 2021, 14, 435–448. [Google Scholar] [CrossRef]
- Gadallah, R.; Murakawa, H.; Shibahara, M. Investigation of thickness and welding residual stress effects on fatigue crack growth. J. Constr. Steel Res. 2023, 201, 107760. [Google Scholar] [CrossRef]
- Nixon, M.E.; Cazacu, O.; Lebensohn, R.A. Anisotropic response of high-purity alpha-titanium: Experimental characterization and constitutive modeling. Int. J. Plast. 2010, 26, 516–532. [Google Scholar] [CrossRef]
- Rouzbeh, A.; Hashemi, R.; Sedighi, M. Experimental and numerical study of microstructure, mechanical characteristics, and forming limit curve for Al 1050/ Mg-AZ31B two-layer sheets manufactured via roll bonding technique. J. Alloys Compd. 2023, 942, 169059. [Google Scholar] [CrossRef]
- Lian, J.; Baudelet, B. Forming limit diagram of sheet metal in the negative minor strain region. Mater. Sci. Eng. 1987, 86, 137–144. [Google Scholar] [CrossRef]
- Mu, Z.K.; Zhao, J.; Meng, Q.D.; Sun, H.L.; Yu, G.C. Anisotropic hardening and evolution of r-values for sheet metal based on evolving non-associated Hill48 model. Thin-Walled Struct. 2022, 171, 108791. [Google Scholar] [CrossRef]
- Rong, H.; Ying, L.; Hu, P.; Hou, W.B. Characterization on the thermal anisotropic behaviors of high strength AA7075 alloy with the Yld2004-18p yield function. J. Alloys Compd. 2021, 877, 159955. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.W.; Karabin, M.; Brem, J.C.; Dick, R. Linear transformation-based anisotropic yield functions. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, D.; Xu, J. Updated 5-parameters Barlat-Lian yield functions. J. Huazhong Univ. Sci. Technol. 2008, 129–132. [Google Scholar]
- Raemy, C.; Manopulo, N.; Hora, P. On the modelling of plastic anisotropy, asymmetry and directional hardening of commercially pure titanium: A planar Fourier series based approach. Int. J. Plast. 2017, 91, 182–204. [Google Scholar] [CrossRef]
- Yoshida, F.; Hamasaki, H.; Uemori, T. A user-friendly 3D yield function to describe anisotropy of steel sheets. Int. J. Plast. 2013, 45, 119–139. [Google Scholar] [CrossRef]
- Cazacu, O.; Plunkett, B.; Barlat, F. Orthotropic yield function for hexagonal closed packed metals. Int. J. Plast. 2006, 22, 1171–1194. [Google Scholar] [CrossRef]
- Lee, M.G.; Kim, D.; Kim, C.; Wenner, M.L.; Wagoner, R.H.; Chung, K. Spring-back evaluation of automotive sheets based on isotropic-kinematic hardening laws and non-quadratic anisotropic yield functions Part II: Characterization of material properties. Int. J. Plast. 2005, 21, 883–914. [Google Scholar]
- Lee, M.G.; Kim, D.; Kim, C.; Wenner, M.L.; Wagoner, R.H.; Chung, K. Spring-back evaluation of automotive sheets based on isotropic-kinematic hardening laws and non-quadratic anisotropic yield function part III: Applications. Int. J. Plast. 2005, 21, 915–953. [Google Scholar] [CrossRef]
- Wang, H.; Wan, M.; Yan, Y.; Wu, X. Correctness Verification of the implementation of yield functions into finite element software. J. Solid Mech. 2010, 2, 173–180. [Google Scholar]
- Cai, Z.; Diao, K.; Wu, X.; Wan, M. Constitutive modeling of evolving plasticity in high strength steel sheets. Int. J. Mech. Sci. 2016, 107, 43–57. [Google Scholar] [CrossRef]

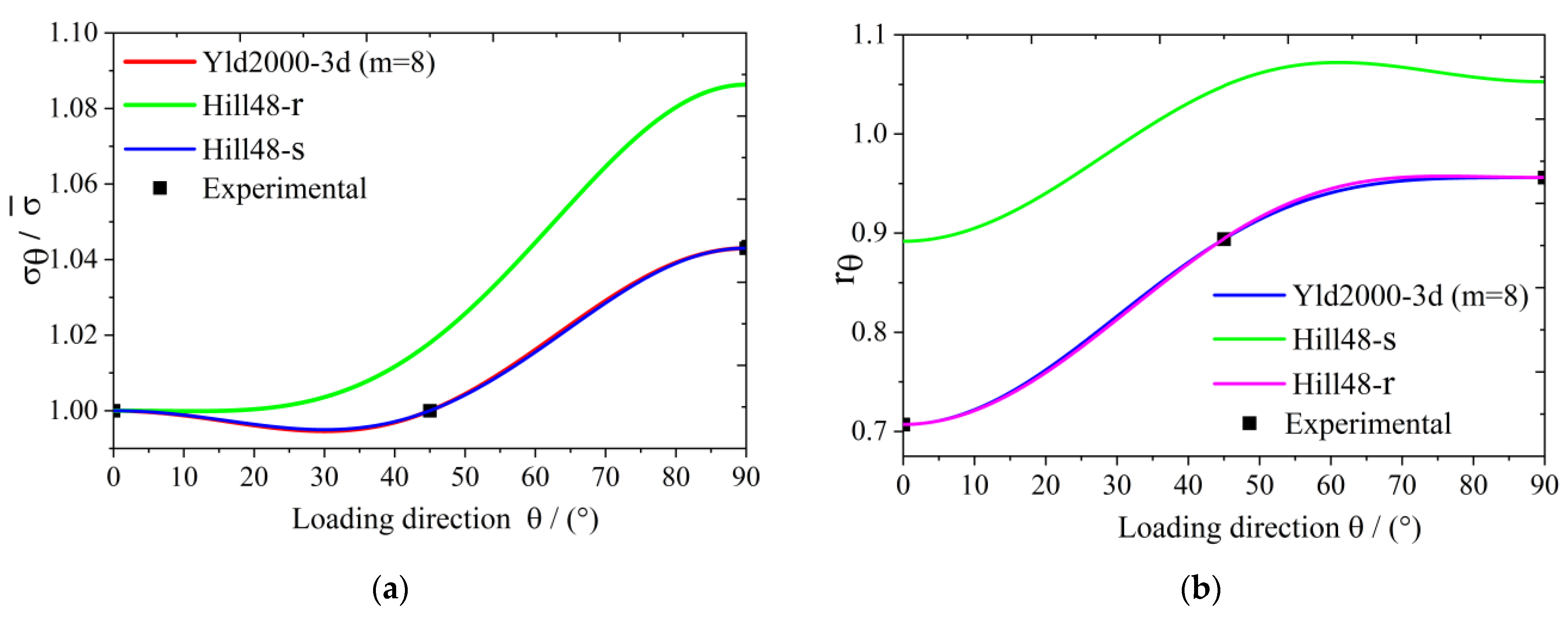



| Loading Direction to the Rolling Direction | Yield Stress (MPa) | r Value |
|---|---|---|
| 0° | 108.7 | 0.707 |
| 45° | 108.7 | 0.894 |
| 90° | 113.4 | 0.956 |
| Loading Ratios | Yield Stress Ratios | (o) |
|---|---|---|
| −22.5 | ||
| −8.25 | ||
| −0.13 | ||
| 7.93 | ||
| 47.21 | ||
| 98.18 | ||
| 89.67 | ||
| 82.69 | ||
| 116.05 |
| Materials | Direction from RD (deg) | (MPa) | (MPa) | r-Value |
|---|---|---|---|---|
| DP980 | 0 | 706.7 | 1023 | 0.609 |
| 45 | 685.6 | 991 | 0.914 | |
| 90 | 724.9 | 1048 | 0.749 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Niu, Q.; Yan, Y. Study of Anisotropic Behavior in Sheet Metal Forming. Materials 2024, 17, 2031. https://doi.org/10.3390/ma17092031
Wang H, Niu Q, Yan Y. Study of Anisotropic Behavior in Sheet Metal Forming. Materials. 2024; 17(9):2031. https://doi.org/10.3390/ma17092031
Chicago/Turabian StyleWang, Haibo, Qiang Niu, and Yu Yan. 2024. "Study of Anisotropic Behavior in Sheet Metal Forming" Materials 17, no. 9: 2031. https://doi.org/10.3390/ma17092031
APA StyleWang, H., Niu, Q., & Yan, Y. (2024). Study of Anisotropic Behavior in Sheet Metal Forming. Materials, 17(9), 2031. https://doi.org/10.3390/ma17092031





