Tuning the Piezoelectric Performance of K0.5Na0.5NbO3 through Li Doping: Insights from Structural, Elastic and Electronic Analyses
Abstract
:1. Introduction
2. Calculation Methods
3. Results and Discussion
3.1. Structural Properties
3.2. Formation Energy of Doped Systems
3.3. Elastic Properties
3.4. Piezoelectric Properties
3.5. The Born Effective Charge
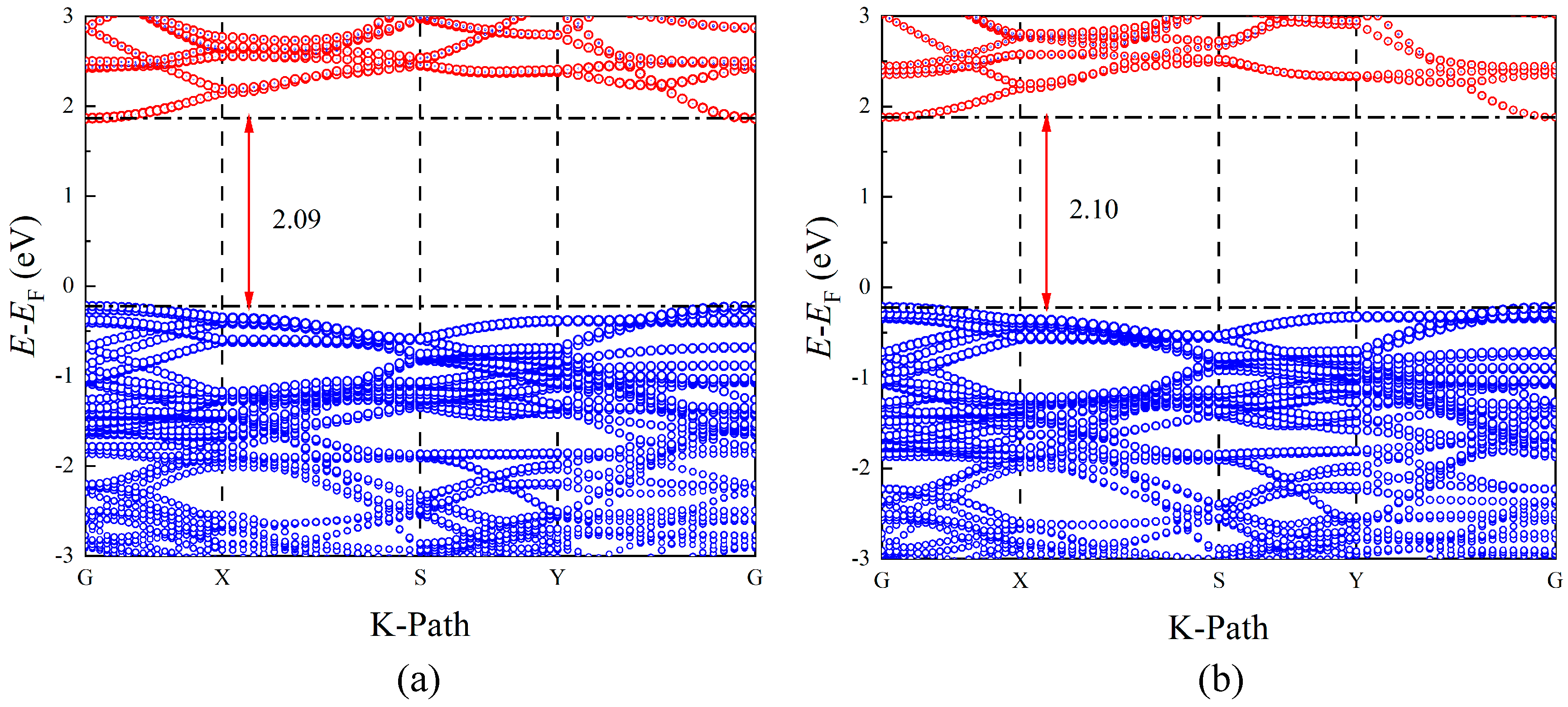
3.6. Band Structure
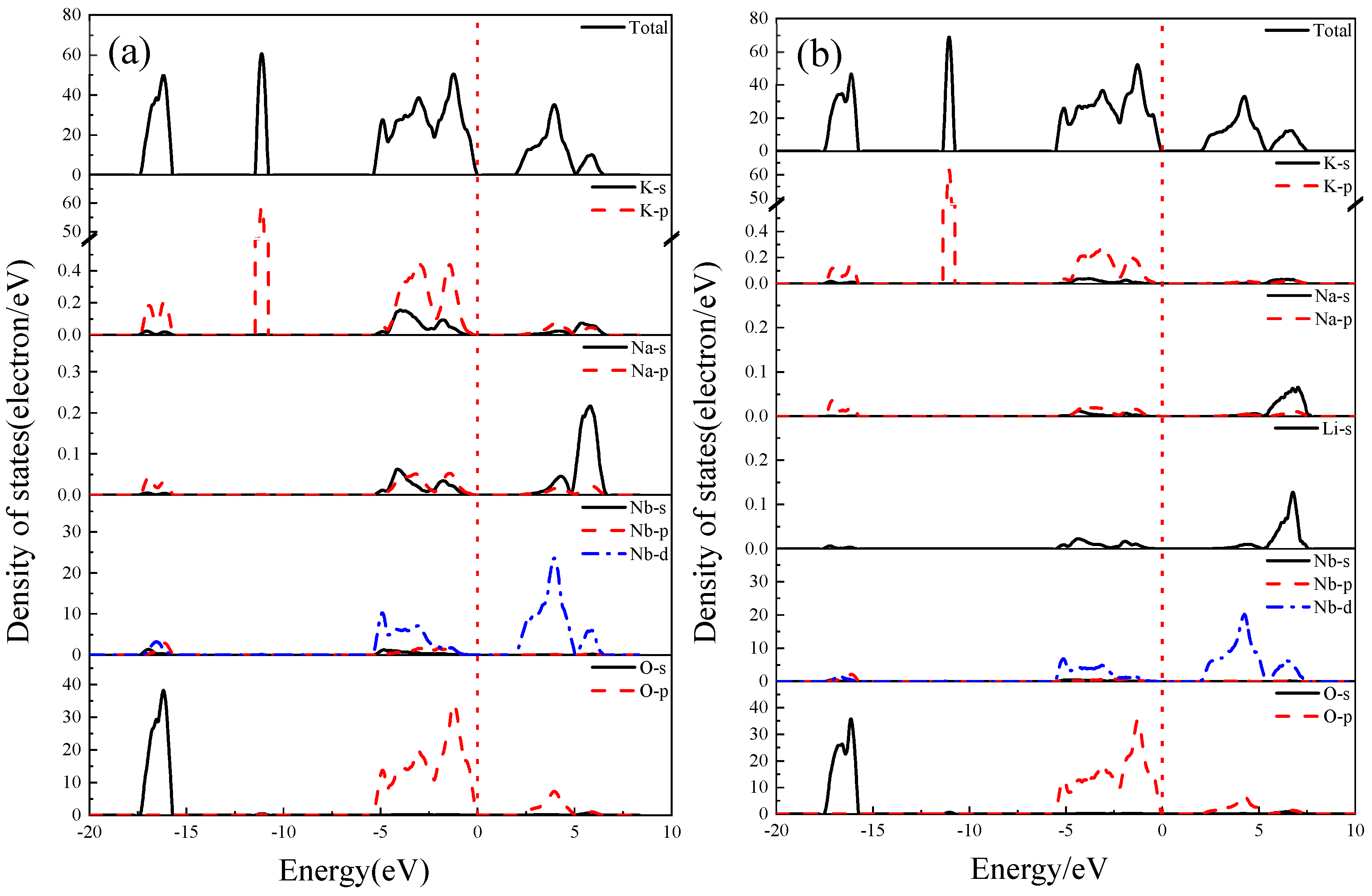
3.7. Density of States
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, T.; Wu, J.; Xiao, D.; Zhu, J. Recent development in lead-free perovskite piezoelectric bulk materials. Prog. Mater. Sci. 2018, 98, 552–624. [Google Scholar] [CrossRef]
- Yang, Z.; Du, H.; Jin, L.; Poelman, D. High-performance lead-free bulk ceramics for electrical energy storage applications: Design strategies and challenges. J. Mater. Chem. A 2021, 9, 18026–18085. [Google Scholar] [CrossRef]
- Yang, L.; Kong, X.; Li, F.; Hao, H.; Cheng, Z.; Liu, H.; Li, J.F.; Zhang, S. Perovskite lead-free dielectrics for energy storage applications. Prog. Mater. Sci. 2019, 102, 72–108. [Google Scholar] [CrossRef]
- Xu, K.; Li, J.; Lv, X.; Wu, J.; Zhang, X.; Xiao, D.; Zhu, J. Superior piezoelectric properties in potassium–sodium niobate lead-free ceramics. Adv. Mater. 2016, 28, 8519–8523. [Google Scholar] [CrossRef]
- Jie, X.; Zhi, T.; Ting, Z.; Jia-Gang, W.; Ding-Quan, X.; Jian-Guo, Z. Research progress of high piezoelectric activity of potassium sodium niobate based lead-free ceramics. Acta Phys. Sin. 2020, 69, 19. [Google Scholar]
- Wu, B.; Wu, H.; Wu, J.; Xiao, D.; Zhu, J.; Pennycook, S.J. Giant piezoelectricity and high Curie temperature in nanostructured alkali niobate lead-free piezoceramics through phase coexistence. J. Am. Chem. Soc. 2016, 138, 15459–15464. [Google Scholar] [CrossRef]
- Panda, P.K.; Sahoo, B.; Thejas, T.S.; Krishna, M. High d33 lead-free piezoceramics: A Review. J. Electron. Mater. 2022, 51, 938–952. [Google Scholar] [CrossRef]
- Panda, P.K.; Sahoo, B. PZT to Lead Free Piezo Ceramics: A Review. Ferroelectrics 2015, 474, 128–143. [Google Scholar] [CrossRef]
- Lv, X.; Zhu, J.; Xiao, D.; Zhang, X.X.; Wu, J. Emerging new phase boundary in potassium sodium-niobate based ceramics. Chem. Soc. Rev. 2020, 49, 671–707. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Ge, Y.; Zhang, X.; Zhao, Y.; Zhou, H.; Li, J.; Jin, H. Comprehensive investigation of Er2O3 doped (Li,K,Na)NbO3 ceramics rendering potential application in novel multifunctional devices. J. Alloy. Compd. 2016, 683, 171–177. [Google Scholar] [CrossRef]
- Guo, Y.; Kakimoto, K.I.; Ohsato, H. Phase transitional behavior and piezoelectric properties of (Na0.5K0.5)NbO3-LiNbO3 ceramics. Appl. Phys. Lett. 2004, 85, 4121–4123. [Google Scholar] [CrossRef]
- Song, H.C.; Cho, K.H.; Park, H.Y.; Ahn, C.W.; Nahm, S.; Uchino, K.; Park, S.H.; Lee, H.G. Microstructure and piezoelectric properties of (1−x)(Na0.5K0.5)NbO3–xLiNbO3 Ceramics. J. Am. Ceram. Soc. 2007, 90, 1812–1816. [Google Scholar] [CrossRef]
- Du, H.; Tang, F.; Liu, D.; Zhu, D.; Zhou, W.; Qu, S. The microstructure and ferroelectric properties of (K0.5Na0.5)NbO3–LiNbO3 lead-free piezoelectric ceramics. Mater. Sci. Eng. B 2007, 136, 165–169. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Li, Y.M.; Jiang, L.; Li, R.R.; Wang, Z.M.; Hong, Y.; Liao, R.H. Phase transition and electrical properties of LiNbO3-modified K0.49Na0.51NbO3 lead-free piezoceramics. J. Mater. Sci.-Mater. Electron. 2011, 22, 1071–1075. [Google Scholar] [CrossRef]
- Hao, J.; Li, W.; Zhai, J.; Chen, H. Progress in high-strain perovskite piezoelectric ceramics. Mater. Sci. Eng. R-Rep. 2019, 135, 1–57. [Google Scholar] [CrossRef]
- Machado, R.; Sepliarsky, M.; Stachiotti, M.G. Relative phase stability and lattice dynamics of NaNbO3 from first-principles calculations. Phys. Rev. B 2011, 84, 134107. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Wu, S.Y.; Zhang, L.J.; Wu, L.N.; Ding, C.C. First-principles study of structural, electronic, elastic, and optical properties of cubic KNbO3 and KTaO3 crystals. Phys. Status Solidi B 2017, 254, 1600620. [Google Scholar] [CrossRef]
- Zhou, S.L.; Zhao, X.; Jiang, X.P.; Han, X.D. Electronic and optical properties of KNbO3, NaNbO3 and K0.5Na0.5NbO3 in paraelectric cubic phase: A comparative first-principles study. Chin. J. Struct. Chem. 2012, 31, 1095–1104. [Google Scholar]
- Li, H.; Wang, L.; Xu, L.; Li, A.; Mao, P.; Wu, Q.; Xie, Z. First-principles study on the structural, elastic, piezoelectric and electronic properties of (BaTiO3, LiTaO3)-modified KNbO3. Mater. Today Commun. 2021, 26, 102092. [Google Scholar] [CrossRef]
- Li, H.; Wu, Q.; Zhou, T.; Wang, Y.; Qiu, Y.; Xu, K.; Zhao, X.; He, Z.; Yu, P. Elastic, piezoelectric, and electronic properties of K1-xMxNbO3 (M = Li, Na): A first-principles study. AIP Adv. 2023, 13, 075012. [Google Scholar] [CrossRef]
- Kresse, G. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Peng, Y.; Tan, Z.; An, J.; Zhu, J.; Zhang, Q. The tunable ferroelectricity and piezoelectricity of the KNN piezoceramics by Na concentrations: First-principles calculations. J. Eur. Ceram. Soc. 2019, 39, 5252–5259. [Google Scholar] [CrossRef]
- Katz, L.; Megaw, H.J.A.C. The structure of potassium niobate at room temperature: The solution of a pseudosymmetric structure by Fourier methods. Acta Crystallogr. 1967, 22, 639–648. [Google Scholar] [CrossRef]
- Hewat, A.W. Cubic-tetragonal-orthorhombic-rhombohedral ferroelectric transitions in perovskite potassium niobate: Neutron powder profile refinement of the structures. J. Phys. C Solid State Phys. 1973, 6, 2559. [Google Scholar] [CrossRef]
- Wang, Q.; Han, Y.; Liu, C.; Ma, Y.; Ren, W.; Gao, C. High-pressure electrical transport properties of KNbO3, Experimental and theoretical approaches. Appl. Phys. Lett. 2012, 100, 172905. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Kosec, M.; Bobnar, V.; Hrovat, M.; Bernard, J.; Malic, B.; Holc, J. New lead-free relaxors based on the K0.5Na0.5NbO3–SrTiO3 solid solution. J. Mater. Res. 2004, 19, 1849–1854. [Google Scholar] [CrossRef]
- Tellier, J.; Malic, B.; Dkhil, B.; Jenko, D.; Cilensek, J.; Kosec, M. Crystal structure and phase transitions of sodium potassium niobate perovskites. Solid State Sci. 2009, 11, 320–324. [Google Scholar] [CrossRef]
- Yang, D.; Wei, L.L.; Chao, X.L.; Yang, Z.P.; Zhou, X.Y. First-principles calculation of the effects of Li-doping on the structure and piezoelectricity of (K0.5Na0.5)NbO3 lead-free ceramics. Phys. Chem. Chem. Phys. 2016, 18, 7702–7706. [Google Scholar] [CrossRef]
- Egerton, L.; Dillon, D.M. Piezoelectric and dielectric properties of ceramics in the system potassium-sodium niobate. J. Am. Ceram. Soc. 1959, 42, 438–442. [Google Scholar] [CrossRef]
- Long, C.; Li, T.; Fan, H.; Wu, Y.; Zhou, L.; Li, Y.; Xiao, L.; Li, Y. Li-substituted K0.5Na0.5NbO3-based piezoelectric ceramics: Crystal structures and the effect of atmosphere on electrical properties. J. Alloys Compd. 2016, 658, 839–847. [Google Scholar] [CrossRef]
- Choi, M.; Oba, F.; Tanaka, I. First-principles study of native defects and lanthanum impurities in NaTaO3. Phys. Rev. B 2008, 78, 014115. [Google Scholar] [CrossRef]
- Li, C.; Xu, X.; Gao, Q.; Lu, Z. First-principle calculations of the effects of CaZrO3-doped on the structure of KNN lead-free ceramics. Ceram. Int. 2019, 45, 11092–11098. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Li, F.; Zhang, S.; Xu, Z.; Wei, X.; Luo, J.; Shrout, T.R. Investigation of electromechanical properties and related temperature characteristics in domain-engineered tetragonal Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 crystals. J. Am. Ceram. Soc. 2010, 93, 2731–2734. [Google Scholar] [CrossRef]
- Zgonik, M.; Bernasconi, P.; Duelli, M.; Schlesser, R.; Günter, P.; Garrett, M.H.; Rytz, D.; Zhu, Y.; Wu, X. Dielectric, elastic, piezoelectric, electro-optic, and elasto-optic tensors of BaTiO3 crystals. Phys. Rev. B 1994, 50, 5941. [Google Scholar] [CrossRef] [PubMed]

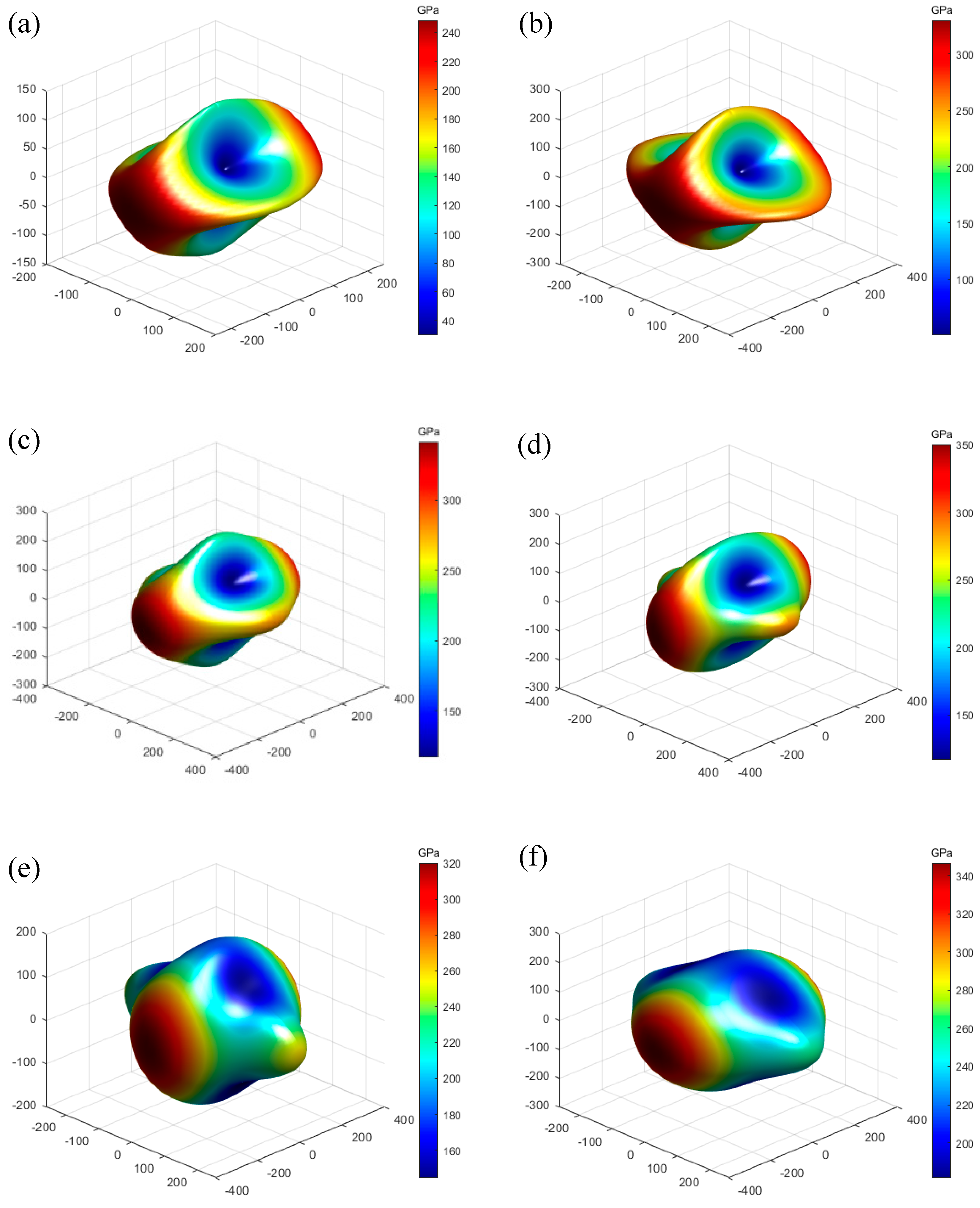
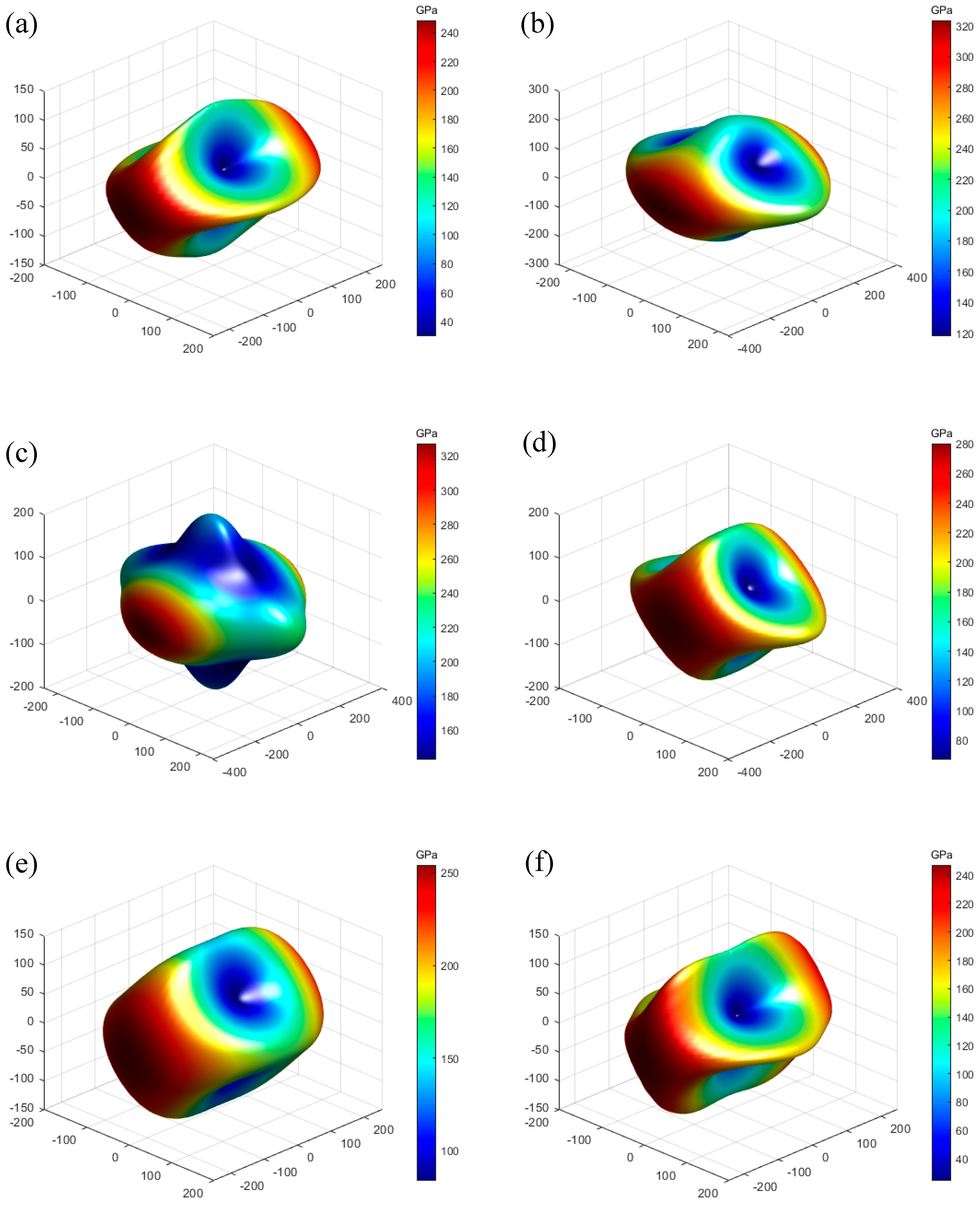
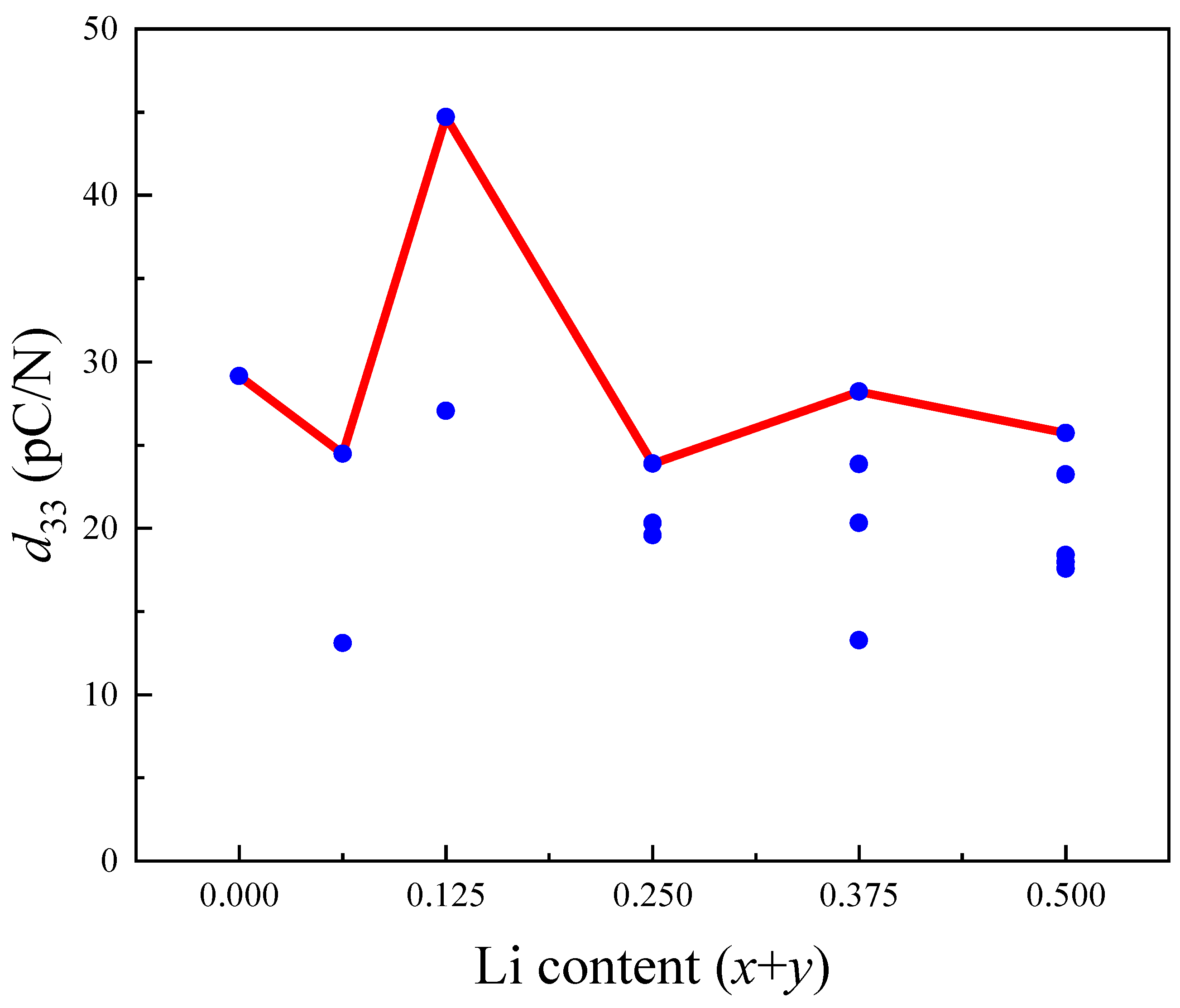
| Structure | a (Å) | b (Å) | c (Å) | V (Å3) | Ef (eV) | e33 | d33 | ||
|---|---|---|---|---|---|---|---|---|---|
| KNbO3 | Orthogonal (Bmm2) | Present | 5.842 | 4.017 | 5.886 | 138.1 | / | 3.00 | 23.74 |
| Calc [19] | 5.832 | 4.020 | 5.869 | / | / | 3.02 | 24.5 | ||
| Calc [27] | 5.789 | 3.991 | 5.822 | 134.5 | / | / | 23.25 | ||
| Expt [28] | 5.697 | 3.971 | 5.721 | 129.4 | / | / | / | ||
| Tetragonal (P4mm) | Present | 4.028 | 4.028 | 4.256 | 69.1 | / | 3.80 | 66.17 | |
| Calc [27] | 4.003 | 4.003 | 4.197 | 67.3 | / | / | 54.40 | ||
| Expt [29] | 3.996 | 3.996 | 4.063 | 64.9 | / | / | / | ||
| K0.5Na0.5NbO3 | Orthogonal (Bmm2) | Present | 5.764 | 3.992 | 5.838 | 134.3 | / | 3.96 | 29.15 |
| Expt. [30] | 5.657 | 4 | 4 | / | / | / | / | ||
| Calc [27] | / | / | / | / | / | / | 29.12 | ||
| Tetragonal (P4mm) | Present | 4.003 | 4.003 | 4.198 | 67.3 | / | 4.81 | 69.44 | |
| Calc. [31] | 3.978 | 3.978 | 3.931 | / | / | 4.14 | 149 | ||
| Expt. [32] | / | / | / | / | / | / | 80 | ||
| K0.5−xNa0.5−yLix+yNbO3 | x + y = 0.06 | Expt. [33] | 5.622 | 3.943 | 5.670 | 125.702 | / | / | 187 |
| x + y = 0.07 | Expt. [33] | 5.621 | 3.935 | 5.662 | 125.270 | / | / | / | |
| x + y = 0.0625 | x = 0.0625/y = 0 | 5.659 | 3.937 | 5.700 | 127.0 | −12.63 | 3.55 | 12.21 | |
| x = 0/y = 0.0625 | 5.675 | 3.946 | 5.707 | 127.8 | −12.97 | 5.29 | 24.49 | ||
| x + y = 0.125 | x = 0.125/y = 0 | 5.635 | 3.916 | 5.691 | 125.6 | −6.31 | 6.98 | 27.04 | |
| x = 0/y = 0.125 | 5.684 | 3.949 | 5.708 | 128.1 | −6.63 | 7.97 | 44.72 | ||
| x + y = 0.25 | x = 0.25/y = 0 | 5.596 | 3.887 | 5.687 | 123.7 | −6.42 | 5.10 | 20.33 | |
| x = 0/y = 0.25 | 5.690 | 3.948 | 5.746 | 129.1 | −6.85 | 3.72 | 19.58 | ||
| x = 0.125/y = 0.125 | 5.617 | 3.912 | 5.734 | 126.0 | −6.57 | 4.31 | 23.89 | ||
| x + y = 0.375 | x = 0.375/y = 0 | 5.592 | 3.839 | 5.651 | 121.3 | −6.90 | 4.22 | 20.33 | |
| x = 0/y = 0.375 | 5.701 | 3.962 | 5.765 | 130.2 | −7.28 | 4.26 | 28,20 | ||
| x = 0.125/y = 0.25 | 5.613 | 3.899 | 5.786 | 126.6 | −6.87 | 3.60 | 23.86 | ||
| x = 0.25/y = 0.125 | 5.605 | 3.898 | 5.696 | 124.5 | −6.67 | 2.71 | 13.26 | ||
| x +y = 0.5 | x = 0.5/y = 0 | 5.577 | 3.898 | 5.723 | 124.4 | −5.75 | 4.19 | 17.97 | |
| x = 0/y = 0.5 | 5.686 | 3.941 | 5.832 | 130.7 | −6.98 | 3.38 | 25.72 | ||
| x = 0.125/y = 0.375 | 5.653 | 3.926 | 5.752 | 127.7 | −6.64 | 3.64 | 23.23 | ||
| x = 0.375/y = 0.125 | 5.557 | 3.898 | 5.647 | 122.3 | −6.94 | 2.63 | 18.39 | ||
| x = 0.25/y = 0.25 | 5.667 | 3.933 | 5.723 | 127.6 | −6.77 | 3.48 | 17.56 | ||
| Li Content (x + y) | x and y | Elastic Stiffness Coefficients | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 | ||
| 0 | Present | 189.4 | 84.5 | 42.0 | 313.0 | 80.6 | 152.6 | 56.7 | 8.2 | 71.8 |
| Calc [27] | 189.5 | 80.5 | 33.1 | 327.7 | 72.9 | 149.2 | 66.8 | 12.2 | 77.1 | |
| 0.0625 | x = 0.0625/y = 0 | 313.3 | 104.6 | 94.7 | 386.7 | 105.0 | 278.8 | 100.5 | 13.6 | 108.0 |
| x = 0/y = 0.0625 | 275.4 | 111.3 | 85.1 | 391.8 | 105.6 | 244.7 | 85.2 | 37.3 | 95.3 | |
| 0.125 | x = 0.125/y = 0 | 307.3 | 78.5 | 71.1 | 376.2 | 76.5 | 249.8 | 91.8 | 36.1 | 103.4 |
| x = 0/y = 0.125 | 280.5 | 110.6 | 82.7 | 399.5 | 110.7 | 239.9 | 57.9 | 48.2 | 83.4 | |
| 0.25 | x = 0.25/y = 0 | 318.7 | 68.9 | 77.1 | 382.6 | 79.2 | 246.9 | 105.4 | 35.8 | 91.3 |
| x = 0/y = 0.25 | 240.9 | 91.9 | 79.9 | 347.1 | 107.2 | 211.5 | 80.0 | 19.4 | 87.3 | |
| x = 0.125/y = 0.125 | 259.1 | 55.2 | 52.9 | 335.3 | 72.8 | 191.9 | 90.3 | 29.5 | 78.8 | |
| 0.375 | x = 0.375/y = 0 | 285.2 | 65.8 | 64.4 | 343.7 | 54.2 | 200.9 | 92.2 | 49.5 | 82.0 |
| x = 0/y = 0.375 | 201.5 | 85.7 | 53.1 | 316.3 | 85.9 | 170.7 | 73.3 | 26.9 | 77.2 | |
| x = 0.125/y = 0.25 | 239.8 | 55.0 | 48.3 | 314.7 | 79.2 | 170.1 | 84.5 | 20.5 | 70.1 | |
| x = 0.25/y = 0.125 | 233.5 | 79.2 | 37.3 | 282.4 | 65.6 | 164.4 | 87.0 | 12.2 | 74.5 | |
| 0.5 | x = 0.5/y = 0 | 329.9 | 121.0 | 126.0 | 413.4 | 116.9 | 272.4 | 100.1 | 61.6 | 95.5 |
| x = 0/y = 0.5 | 199.9 | 82.1 | 47.0 | 310.2 | 83.1 | 151.2 | 70.8 | 6.6 | 67.7 | |
| x = 0.125/y = 0.375 | 208.5 | 34.5 | 51.1 | 225.6 | 49.2 | 168.3 | 74.2 | 12.5 | 71.6 | |
| x = 0.375/y = 0.125 | 133.9 | 39.9 | 3.4 | 144.7 | 16.3 | 147.8 | 80.6 | 42.3 | 85.1 | |
| x = 0.25/y = 0.25 | 232.1 | 101.7 | 83.9 | 317.9 | 84.6 | 201.8 | 73.8 | 11.1 | 81.8 | |
| Li Content (x + y) | x and y | BV | BR | BH | GV | GR | GH | E | ν | G/B |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | x = 0/y = 0 | 118.8 | 103.1 | 110.9 | 57.2 | 27.3 | 42.2 | 112.4 | 0.331 | 0.38 |
| 0.0625 | x = 0.0625/y = 0 | 176.4 | 172.2 | 174.3 | 89.4 | 44.0 | 66.7 | 177.4 | 0.330 | 0.38 |
| x = 0/y = 0.0625 | 168.4 | 160.1 | 164.2 | 84.2 | 71.1 | 77.7 | 201.3 | 0.296 | 0.47 | |
| 0.125 | x = 0.125/y = 0 | 153.9 | 149.7 | 151.8 | 93.4 | 76.0 | 84.7 | 214.2 | 0.265 | 0.56 |
| x = 0/y = 0.125 | 169.8 | 159.8 | 164.8 | 79.0 | 63.0 | 71.0 | 186.2 | 0.312 | 0.43 | |
| 0.25 | x = 0.25/y = 0 | 155.4 | 151.5 | 153.4 | 94.7 | 76.0 | 85.3 | 216.0 | 0.265 | 0.56 |
| x = 0/y = 0.25 | 150.8 | 143.2 | 147.0 | 72.0 | 50.1 | 61.1 | 160.9 | 0.318 | 0.42 | |
| x = 0.125/y = 0.125 | 127.6 | 121.1 | 124.3 | 80.1 | 63.2 | 71.6 | 180.3 | 0.258 | 0.58 | |
| 0.375 | x = 0.375/y = 0 | 133.2 | 127.1 | 130.1 | 87.8 | 79.3 | 83.6 | 206.5 | 0.236 | 0.64 |
| x = 0/y = 0.375 | 126.4 | 111.9 | 119.2 | 66.4 | 53.8 | 60.1 | 154.3 | 0.284 | 0.50 | |
| x = 0.125/y = 0.25 | 121.1 | 113.3 | 117.2 | 71.2 | 50.4 | 60.8 | 155.5 | 0.279 | 0.52 | |
| x = 0.25/y = 0.125 | 116.1 | 107.0 | 111.5 | 67.9 | 37.8 | 52.9 | 137.0 | 0.295 | 0.47 | |
| 0.5 | x = 0.5/y = 0 | 193.7 | 189.1 | 191.4 | 94.9 | 89.1 | 92.0 | 237.9 | 0.293 | 0.48 |
| x = 0/y = 0.5 | 120.6 | 106.2 | 113.4 | 59.0 | 23.8 | 41.4 | 110.6 | 0.337 | 0.36 | |
| x = 0.125/y = 0.375 | 96.9 | 88.4 | 92.7 | 62.8 | 34.0 | 48.4 | 123.7 | 0.278 | 0.52 | |
| x = 0.375/y = 0.125 | 60.6 | 59.1 | 59.9 | 66.0 | 60.7 | 63.4 | 140.5 | 0.109 | 1.06 | |
| x = 0.25/y = 0.25 | 143.6 | 137.9 | 140.8 | 65.5 | 35.2 | 50.3 | 134.8 | 0.340 | 0.36 |
| Materials | Species | ||||
|---|---|---|---|---|---|
| KN | K | 1.208 | 1.135 | 1.177 | 1.173 |
| Nb | 7.454 | 8.836 | 6.243 | 7.511 | |
| OI | −1.354 | −6.915 | −1.437 | −3.236 | |
| OII | −3.654 | −1.528 | −2.992 | −2.724 | |
| KNN | K | 1.169 | 1.150 | 1.170 | 1.163 |
| Na | 1.234 | 1.142 | 1.140 | 1.172 | |
| Nb | 7.664 | 8.740 | 6.473 | 7.625 | |
| OI | −1.378 | −7.068 | −1.430 | −3.292 | |
| OII | −3.779 | −1.469 | −3.117 | −2.788 | |
| KNN-L | K | 1.179 | 1.076 | 1.152 | 1.136 |
| Na | 1.342 | 1.324 | 1.320 | 1.329 | |
| Li | 1.067 | 1.056 | 0.993 | 1.039 | |
| Nb | 7.888 | 8.739 | 7.260 | 7.962 | |
| OI | −1.513 | −7.087 | −1.504 | −3.368 | |
| OII | −3.444 | −1.476 | −3.234 | −2.718 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhou, T.; Xu, K.; Wang, H.; Lu, W.; Liu, J. Tuning the Piezoelectric Performance of K0.5Na0.5NbO3 through Li Doping: Insights from Structural, Elastic and Electronic Analyses. Materials 2024, 17, 2118. https://doi.org/10.3390/ma17092118
Li H, Zhou T, Xu K, Wang H, Lu W, Liu J. Tuning the Piezoelectric Performance of K0.5Na0.5NbO3 through Li Doping: Insights from Structural, Elastic and Electronic Analyses. Materials. 2024; 17(9):2118. https://doi.org/10.3390/ma17092118
Chicago/Turabian StyleLi, Hui, Tianxiang Zhou, Kang Xu, Han Wang, Wenke Lu, and Jinyi Liu. 2024. "Tuning the Piezoelectric Performance of K0.5Na0.5NbO3 through Li Doping: Insights from Structural, Elastic and Electronic Analyses" Materials 17, no. 9: 2118. https://doi.org/10.3390/ma17092118
APA StyleLi, H., Zhou, T., Xu, K., Wang, H., Lu, W., & Liu, J. (2024). Tuning the Piezoelectric Performance of K0.5Na0.5NbO3 through Li Doping: Insights from Structural, Elastic and Electronic Analyses. Materials, 17(9), 2118. https://doi.org/10.3390/ma17092118






