Advances in Computational Methods for Modeling Photocatalytic Reactions: A Review of Recent Developments
Abstract
:1. Introduction
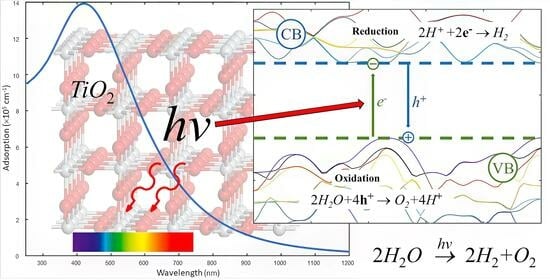
2. Basics of Photocatalysis
- Adsorption: The reactant molecule is adsorbed onto the semiconductor surface, creating a physical or chemical bond with the catalyst surface, which facilitates further interactions. This adsorption process is influenced by factors such as the catalyst’s surface area, charge, and affinity.
- Exciton(s) formation: The catalyst absorbs light within a specific wavelength range, typically in the UV or visible range, and then generates electron–hole pairs through a process known as exciton formation. The excited electrons transition from the valence band to the conduction band, leaving positive holes in the former. These electron–hole pairs, or excitons, exhibit high reactivity and a comparably short lifetime.
- Reaction: The electrons and/or holes react with the adsorbed molecule, either directly or indirectly. Direct reactions involve the transfer of electrons or holes from the catalyst to the molecule, resulting in oxidation or reduction. Indirect reactions involve the generation of reactive oxygen species (ROS), such as hydroxyl radicals, superoxide anions, or hydrogen peroxide, from the reaction of electrons or holes with water or oxygen. The ROS then attack the adsorbed molecule, causing its degradation or mineralization.
- Over-reaction: The reaction between the electrons or holes and the adsorbed molecule continues until the molecule is completely broken down into simple and harmless products, such as water, carbon dioxide, or inorganic ions. This process, also known as mineralization or complete oxidation, guarantees that no toxic intermediates remain in the solution.
- Desorption: The final step is the release of the reaction products from the surface, which frees up the active sites on the catalyst for new adsorption and reaction cycles. Desorption is influenced by factors such as the concentration of reactants, temperature, and pH.
3. Quantum Chemical Methods in Photocatalysis: Ab Initio, DFT, Semi-Empirical
- Detailed electronic structure analysis: These methods provide an accurate description of the electronic structure of molecules involved in photocatalysis, aiding in the prediction of absorption energy, charge transfer, and the dynamics of intermediate compounds during photochemical reaction [74,75,76].
- Quantitative prediction of reaction rates: First principles methods combined with kinetic models enable the prediction of reaction rates, aiding in the design of photocatalysts with improved performance [87].
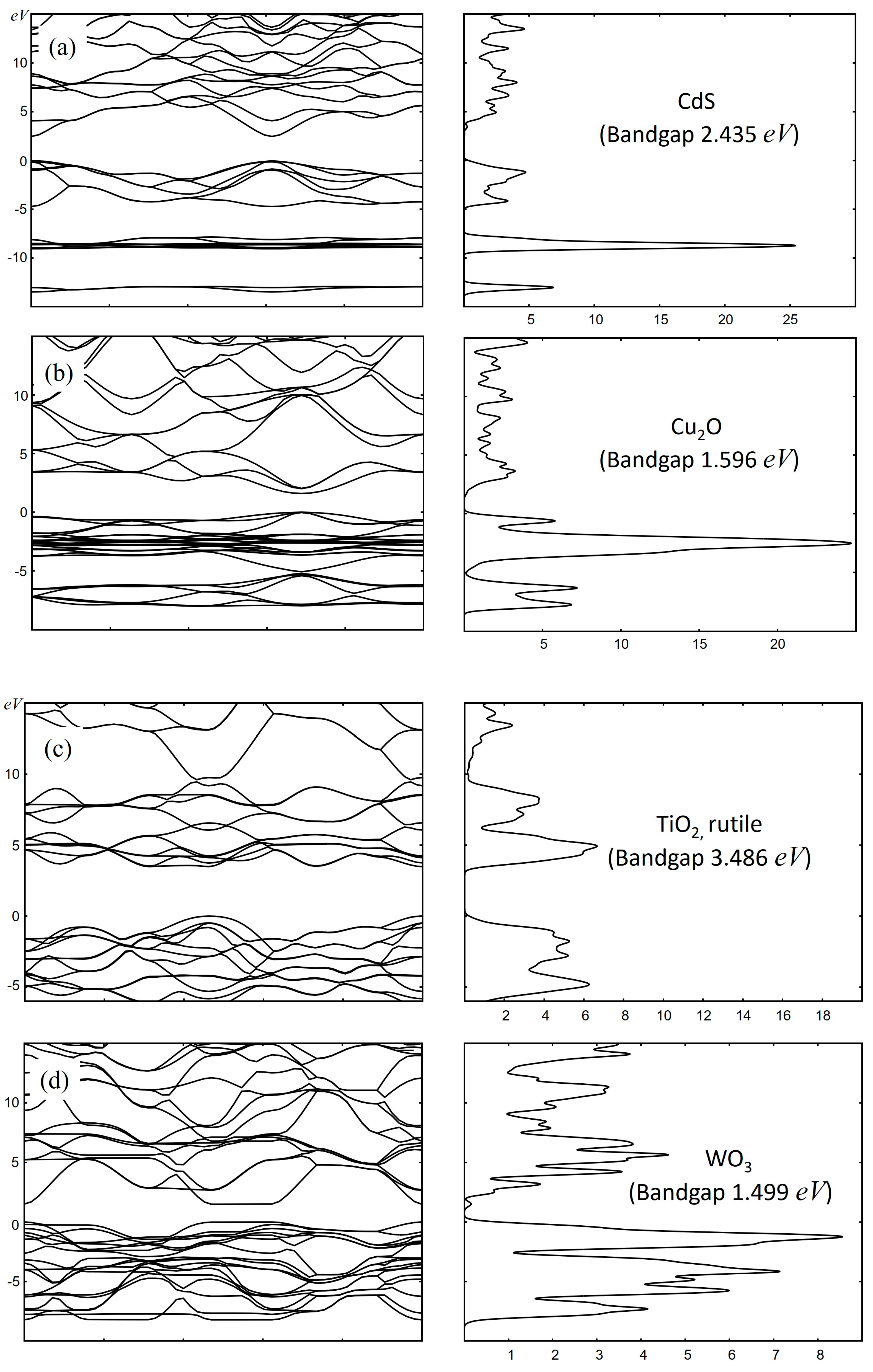
4. Example: Fundamental Properties Using Density Functional Theory
- Local density approximation (LDA): This functional depends only on the local density ρ(r) at a given point. This is the simplest and computationally the cheapest approximation, but it is often inaccurate for systems with strong electron–electron interactions or spatial variations in density. Some examples of such functionalities are VWN [121] and PWC [122].
- Gradient-corrected approximation (GGA): This functional depends on the local density ρ(r) and its gradient ∇ρ(r). This improves the accuracy of LDA by accounting for the non-uniformity of the electron density, but it still fails to capture some important effects such as dispersion or self-interaction. The most frequently used functionals of this type are PW91 [123], BLYP [124], and PBEsol [125].
- Hybrid: This functional combines some features of ab initio methods, such as Hartree–Fock, with some features of DFT methods. This enhances the accuracy of GGA by incorporating some exact exchange and correlation effects εx({φi}), but it also increases the computational cost and complexity because a large number of two-electron integrals are constructed from orbitals. Examples are B3LYP [126] and PBE0 [127].
- Meta-GGA: This functional depends on the local density, its gradient, and its kinetic energy τ(r) density (M11-L [128], revTPSS [129]). This improves the accuracy of GGA by accounting for the non-local effects of exchange and correlation, but it also introduces new parameters and challenges for the functional design, which also increases their functionality. Additionally, such functionals, like SCAN [130], satisfy all constraints [131], which makes them favorite candidates for electronic structure calculations.
- Range-separated hybrid: This functional split the exchange and correlation into short-range and long-range components and uses different approximations for each [132]. This improves the accuracy of hybrid methods by reducing the self-interaction error and the delocalization error, but it also requires the choice of a range-separation parameter that may depend on the system.
- Double hybrid: This functional combines a hybrid functional with a perturbative correction based on MP2 or similar methods [133]. This improves the accuracy of hybrid methods by including dynamic correlation effects, but it also makes the functional very expensive and sensitive to the basis set.
- Elastic constants of some crystals: LDA tends to over-bind atoms and predict stiffer bonds, which results in better agreement with experimental values of elastic constants for some materials, such as diamond or silicon. GGA, on the other hand, tends to underestimate elastic constants due to softer bonds and gradient corrections.
- Phase transitions of some metals: LDA is more accurate than GGA for predicting the critical pressures of structural phase transitions of some group IV, V, and VI elements, such as C, Si, Ge, Sn, S, Se, and Te. This is because LDA is exact for a uniform gas and works better for simple metals, while GGA introduces errors due to gradient corrections and the over-delocalization of the electrons. These are some examples of where LDA is more accurate than GGA, but they are not general rules. In most cases, GGA is preferred over LDA for studying the electronic structure and properties of many-body systems. However, even GGA may not be sufficient for some systems that require more advanced functionals, such as hybrid, meta-GGA, range-separated hybrid, or double-hybrid.
5. Software
6. Conclusions and Perspectives
- The further development of quantum chemical algorithms;
- The development of numerical algorithms;
- The exploitation of the structure of molecular systems;
- Parallelization and new computational hardware;
- New paradigms.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassaan, M.A.; El-Nemr, M.A.; Elkatory, M.R.; Ragab, S.; Niculescu, V.-C.; El Nemr, A. Principles of Photocatalysts and Their Different Applications: A Review. Top. Curr. Chem. 2023, 381, 31. [Google Scholar] [CrossRef]
- Sordello, F.; Calza, P.; Minero, C.; Malato, S.; Minella, M. More than One Century of History for Photocatalysis, from Past, Present and Future Perspectives. Catalysts 2022, 12, 1572. [Google Scholar] [CrossRef]
- Bessegato, G.G.; Guaraldo, T.T.; de Brito, J.F.; Brugnera, M.F.; Zanoni, M.V.B. Achievements and Trends in Photoelectrocatalysis: From Environmental to Energy Applications. Electrocatalysis 2015, 6, 415–441. [Google Scholar] [CrossRef]
- Ravelli, D.; Dondi, D.; Fagnoni, M.; Albini, A. A multi-faceted concept for green chemistry. Chem. Soc. Rev. 2009, 38, 1999–2011. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, A.M.; Aziz, F.; Mohtar, S.; Mhamad, S.; Ahmadu, B.; Nasir, M.; Aziz, M. A Review of Research Trends on the Usage of Photocatalysis for Wastewater Treatment: Bibliometric Analysis. Sustain. Water Resour. Manag. 2003, 9, 88. [Google Scholar] [CrossRef] [PubMed]
- Gaya, U.; Abdullah, A. Heterogeneous Photocatalytic Degradation of Organic Contaminants over Titanium Dioxide: A Review of Fundamentals, Progress and Problems. J. Photochem. Photobiol. C Photochem. Rev. 2008, 9, 1–12. [Google Scholar] [CrossRef]
- Yang, X.; Wang, D. Photocatalysis: From Fundamental Principles to Materials and Applications. ACS Appl. Energy Mater. 2018, 1, 6657–6693. [Google Scholar] [CrossRef]
- Subramanian, Y.; Dhanasekaran, A.; Omeiza, L.; Somalu, M.; Azad, A. A Review on Heteroanionic-based Materials for Photocatalysis Applications. Catalysts 2023, 13, 173. [Google Scholar] [CrossRef]
- Garrido, I.; Fenoll, J.; Flores, P.; Hellín, P.; Pérez-Lucas, G.; Navarro, S. Solar Photocatalysis as Strategy for On-site Reclamation of Agro-wastewater Polluted with Pesticide Residues on Farms Using a Modular Facility. Environ. Sci. Pollut. Res. 2021, 28, 23647–23656. [Google Scholar] [CrossRef]
- Gaur, N.; Dutta, D.; Singh, A.; Dubey, R.; Kamboj, D. Recent advances in the elimination of persistent organic pollutants by photocatalysis. Front. Environ. Sci. 2022, 10, 872514. [Google Scholar] [CrossRef]
- Adesina, A.A. Industrial exploitation of photocatalysis: Progress, perspectives and prospects. Catal. Surv. 2004, 8, 265–273. [Google Scholar] [CrossRef]
- Lee, H.; Gaharwar, A. Light-responsive Inorganic Biomaterials for Biomedical Applications. Adv. Sci. 2020, 7, 2000863–2000887. [Google Scholar] [CrossRef] [PubMed]
- Bokare, A.; Erogbogbo, F. Photocatalysis and Li-ion Battery Applications of {001} Faceted Anatase TiO2-based Composites. Multidiscip. Sci. J. 2021, 4, 500–530. [Google Scholar] [CrossRef]
- Rodriguez, J.; Puzenat, E.; Thivel, P.X. From solar photocatalysis to fuel-cell: A hydrogen supply chain. J. Environ. Chem. Eng. 2016, 4, 3001–3005. [Google Scholar] [CrossRef]
- Banerjee, T.; Podjaski, F.; Kröger, J.; Kröger, J.; Biswal, B.; Lotsch, B.; Lotsch, B. Polymer Photocatalysts for Solar-to-chemical Energy Conversion. Nat. Rev. Mater. 2021, 6, 168–190. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.; Qi, K.; Wang, C.; Zhang, Z. Photocatalysis and Electrocatalysis for Energy Conversion. Front. Chem. 2023, 10, 1128243. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Yun, N.; Zhang, Z. Recent Advances in Computational Photocatalysis: A Review. Can. J. Comp. Chem. 2019, 97, 1982–1998. [Google Scholar] [CrossRef]
- Khan, I.M.; Alam, K.; Alam, M.J. Exploring Charge Transfer Dynamics and Photocatalytic Behavior of Designed Donor-acceptor Complex: Characterization, Spectrophotometric and Theoretical Studies (DFT/TD-DFT). J. Mol. Liq. 2020, 310, 113213. [Google Scholar] [CrossRef]
- Lalithambika, K.C.; Shanmugapriya, K.; Sriram, S. Photocatalytic Activity of Mos 2 Nanoparticles: An Experimental and DFT Analysis. App. Phys. A 2019, 125, 817. [Google Scholar] [CrossRef]
- Wood, B.C.; Ogitsu, T.; Schwegler, E. Ab Initio Modeling of Water–semiconductor Interfaces for Photocatalytic Water Splitting: Role of Surface Oxygen and Hydroxyl. J. Photonics Energy 2011, 1, 016002. [Google Scholar] [CrossRef]
- Podolska, N.; Podolska, N.; Zhmakin, A. Semiconductor Nanostructure Properties. Molecular Dynamic Simulations. J. Phys. Conf. Ser. 2013, 461, 012004. [Google Scholar] [CrossRef]
- Zhidomirov, G.; Chuvylkin, N. Quantum-chemical Methods in Catalysis. Russ. Chem. Rev. 1986, 55, 153. [Google Scholar] [CrossRef]
- Thiel, W. Semiempirical Quantum-chemical Methods. Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 145–157. [Google Scholar] [CrossRef]
- Geerlings, P.; De Proft, F. Chemical Reactivity as Described by Quantum Chemical Methods. Int. J. Mol. Sci. 2010, 3, 276–309. [Google Scholar] [CrossRef]
- Lin, C.-H.; Rohilla, J.; Kuo, H.-H.; Chen, C.-Y.; Chang, T.-F.; Sone, M.; Ingole, P.; Lo, Y.-C.; Hsu, Y.-J. Density-Functional Theory Studies on Photocatalysis and Photoelectrocatalysis: Challenges and Opportunities. Solar RRL 2024. [Google Scholar] [CrossRef]
- Chiu, Y.-H.; Chang, T.-F.M.; Chen, C.-Y.; Sone, M.; Hsu, Y.-J. Mechanistic Insights into Photodegradation of Organic Dyes Using Heterostructure Photocatalysts. Catalysts 2019, 9, 430. [Google Scholar] [CrossRef]
- Deng, X.; Hao, M.; Li, Z. Engineering Metal-organic Frameworks (mofs) for Efficient Photocatalysis. Curr. Org. Chem. 2018, 22, 1825–1835. [Google Scholar] [CrossRef]
- Li, Y.; Xu, H.; Ouyang, S.; Ye, J.; Ye, J. Metal-organic Frameworks for Photocatalysis. Phys. Chem. Chem. Phys. 2016, 18, 7563–7572. [Google Scholar] [CrossRef] [PubMed]
- Boyjoo, Y.; Ang, M.; Pareek, V. Some Aspects of Photocatalytic Reactor Modeling Using Computational Fluid Dynamics. Chem. Eng. Sci. 2013, 101, 764–784. [Google Scholar] [CrossRef]
- Oliveira, G.; de Brito Lira, J.; Riella, H.; Soares, C.; Padoin, N. Modeling and Simulation of Reaction Environment in Photoredox Catalysis: A Critical Review. Front. Chem. Eng. 2022, 3, 788653. [Google Scholar] [CrossRef]
- Ziff, R.; Gulari, E.; Barshad, Y. Kinetic Phase Transitions in an Irreversible Surface-reaction Model. Phys. Rev. Lett. 1986, 56, 2553–2556. [Google Scholar] [CrossRef]
- Santen, R.A.; Niemantsverdriet, J.W. Chemical Kinetics and Catalysis; Twigg, M., Spencer, M., Eds.; Springer: New York, NY, USA, 1995. [Google Scholar]
- Mardirossian, N.; McClain, J.; Chan, G.-L. Lowering of the Complexity of Quantum Chemistry Methods by Choice of Representation. J. Chem. Phys. 2018, 148, 044106. [Google Scholar] [CrossRef]
- de Lazaro, S.R.; Ribeiro, R.A.P.; da Silveira Lacerda, L.H. Quantum Chemistry Applied to Photocatalysis with TiO2. In Titanium Dioxide; IntechOpen: London, UK, 2017. [Google Scholar]
- Ozaki, Y.; Ozaki, Y.; Beć, K.; Morisawa, Y.; Yamamoto, S.; Tanabe, I.; Huck, C.; Hofer, T. Advances, Challenges and Perspectives of Quantum Chemical Approaches in Molecular Spectroscopy of the Condensed Phase. Chem. Soc. Rev. 2021, 50, 10917–10954. [Google Scholar] [CrossRef]
- Guo, S.; Qian, W.; Zhu, W.; Zhang, C. A review of quantum chemical methods for treating energetic molecules. Energetic Mater. Front. 2021, 2, 292–305. [Google Scholar] [CrossRef]
- Pandya, S.B.; Socha, B.N.; Dubey, R.P.; Patel, U.H.; Patel, R.H.; Bhatt, S.B.; Thakor, P.; Bhakhar, S.; Vekariya, N.; Valand, J. Visible light-driven photocatalysts, quantum chemical calculations, ADMET-SAR parameters, and DNA binding studies of nickel complex of sulfadiazine. Sci. Rep. 2023, 13, 15275. [Google Scholar] [CrossRef]
- Weinan, E.; Engquist, B.; Li, X.; Ren, W.; Vanden-Eijnden, E. Heterogeneous multiscale methods: A review. Commun. Comput. Phys. 2007, 2, 367–450. [Google Scholar]
- Weinan, E. Principles of Multiscale Modeling; Princeton University Press: New Jersey, NJ, USA, 2011. [Google Scholar]
- Dral, P. Quantum Chemistry in the Age of Machine Learning. J. Phys. Chem. Lett. 2020, 11, 2336–2347. [Google Scholar] [CrossRef]
- Prezhdo, O.V. Advancing Physical Chemistry with Machine Learning. J. Phys. Chem. Lett. 2020, 11, 9656–9658. [Google Scholar] [CrossRef]
- Sugisaki, K.; Yamamoto, S.; Nakazawa, S.; Toyota, K.; Sato, K.; Shiomi, D.; Takui, T. Quantum Chemistry on Quantum Computers: A Polynomial-Time Quantum Algorithm for Constructing the Wave Functions of Open-Shell Molecules. J. Phys. Chem. A 2016, 120, 6459–6466. [Google Scholar] [CrossRef]
- Elm, J. Toward a Holistic Understanding of the Formation and Growth of Atmospheric Molecular Clusters: A Quantum Machine Learning Perspective. J. Phys. Chem. A 2021, 125, 895–902. [Google Scholar] [CrossRef]
- Naseri, M.; Gusarov, S.; Salahub, D.R. Quantum Machine Learning in Materials Prediction: A Case Study on ABO3 Perovskite Structures. J. Phys. Chem. Lett. 2023, 14, 6940–6947. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.B.; Sher, A. Band Structure Theory; Springer: Boston, MA, USA, 1995. [Google Scholar]
- Chong, M.N.; Jin, B.; Chow, C.W.; Saint, C. Recent Developments in Photocatalytic Water Treatment Technology: A Review. Water Res. 2010, 44, 2997–3027. [Google Scholar] [CrossRef] [PubMed]
- Serpone, N.; Emeline, A.V.; Horikoshi, S.; Kuznetsov, V.N.; Ryabchuk, V.K. On the Genesis of Heterogeneous Photocatalysis: A Brief Historical Perspective in the Period 1910 to the Mid-1980s. Photochem. Photobiol. Sci. 2012, 11, 1121–1150. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Zhu, S.; Wang, D. Photocatalysis: Basic Principles, Diverse Forms of Implementations and Emerging Scientific Opportunities. Adv. Energy Mater. 2017, 7, 1700841–1700864. [Google Scholar] [CrossRef]
- Bera, S.; Ghosh, S. Bandgap Engineering of Heterostructures for Visible Light-Driven Water Splitting, in Green Photocatalytic Semiconductors. In Green Chemistry and Sustainable Technology; Springer: Berlin, Germany, 2021; pp. 701–722. [Google Scholar]
- Katakis, D.; Mitsopoulou, C.; Konstantatos, J.; Vrachnou, E.; Falaras, P. Photocatalytic Splitting of Water. J. Photochem. Photobiol. A Chem. 1992, 68, 375–388. [Google Scholar] [CrossRef]
- Li, Y.; Tsang, S.C. Recent progress and strategies for enhancing photocatalytic water splitting, Mater. Today Sustain. 2020, 9, 100032. [Google Scholar]
- Kovačič, Ž.; Likozar, B.; Huš, M. Photocatalytic CO2 reduction: A review of ab initio mechanism, kinetics, and multiscale modeling simulations. ACS Catal. 2020, 10, 14984–15007. [Google Scholar] [CrossRef]
- Nishioka, S.; Osterloh, F.E.; Wang, X.; Mallouk, T.E.; Maeda, K. Photocatalytic water splitting. Nat. Rev. Methods Primers 2023, 3, 42. [Google Scholar] [CrossRef]
- Chowdhury, S.; Balasubramanian, R. Graphene/semiconductor Nanocomposites (gsns) for Heterogeneous Photocatalytic Decolorization of Wastewaters Contaminated with Synthetic Dyes: A Review. Appl. Catal. B. 2014, 160, 307–324. [Google Scholar] [CrossRef]
- Kim, J.; Hansora, D.; Sharma, P.; Jang, J.-W.; Lee, J. Toward Practical Solar Hydrogen Production—An Artificial Photosynthetic Leaf-to-farm Challenge. Chem. Soc. Rev. 2019, 48, 1908–1971. [Google Scholar] [CrossRef]
- Yan, Z.; Yin, K.; Xu, M.; Fang, N.; Yu, W.; Chu, Y.; Shu, S. Photocatalysis for synergistic water remediation and H2 production: A review. J. Chem. Eng. 2023, 472, 145066. [Google Scholar] [CrossRef]
- Eidsvåg, H.; Bentouba, S.; Vajeeston, P.; Yohi, S.; Velauthapillai, D. TiO2 as a Photocatalyst for Water Splitting—An Experimental and Theoretical Review. Molecules 2021, 26, 1687. [Google Scholar] [CrossRef]
- Krewald, V.; Retegan, M.; Pantazis, D.A. Principles of Natural Photosynthesis. In Solar Energy for Fuels; Springer: Berlin, Germany, 2015; Volume 371, pp. 23–48. [Google Scholar]
- Fang, S.; Rahaman, M.; Bharti, J.; Reisner, E.; Robert, M.; Ozin, G.A.; Hu, Y.H. Photocatalytic CO2 reduction. Nat. Rev. Methods Primers 2023, 3, 61. [Google Scholar] [CrossRef]
- Pahija, E.; Panaritis, C.; Gusarov, S.; Shadbahr, J.; Bensebaa, F.; Patience, G.; Boffito, D. Experimental and Computational Synergistic Design of Cu and Fe Catalysts for the Reverse Water-gas Shift: A Review. ACS Catal. 2022, 12, 6887–6905. [Google Scholar] [CrossRef]
- Gao, W.; Li, S.; He, H.; Li, X.; Cheng, Z.; Yang, Y.; Wang, J.; Shen, Q.; Wang, X.; Xiong, Y. Vacancy-defect Modulated Pathway of Photoreduction of CO2 on Single Atomically Thin Aginp2s6 Sheets into Olefiant Gas. Nat. Commun. 2021, 12, 4747. [Google Scholar] [CrossRef]
- Herrmann, J.-M. Photocatalysis Fundamentals Revisited to Avoid Several Misconceptions. Appl. Catal. B 2010, 99, 461–468. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering; Pearson Education: New Jersey, NJ, USA, 1986. [Google Scholar]
- Choudhary, T.V.; Banerjee, S.; Choudhary, V.R. Catalysts for combustion of methane and lower alkanes. Appl. Catal. A Gen. 2002, 234, 1–23. [Google Scholar] [CrossRef]
- Garg, S.; Chandra, A. Photocatalysis for Environmental Remediation and Energy Production; Springer: Berlin, Germany, 2023. [Google Scholar]
- Tahir, M.B.; Riaz, K.N. Nanomaterials and Photocatalysis in Chemistry, Mechanistic and Experimental Approaches; Springer: Berlin, Germany, 2021. [Google Scholar]
- Chen, Z.Y.; Huang, N.Y.; Xu, Q. Metal halide perovskite materials in photocatalysis: Design strategies and applications. Coord. Chem. Rev. 2023, 481, 215031. [Google Scholar] [CrossRef]
- Choon, S.; Lim, H.; Ibrahim, I.; Zainal, Z.; Tan, K.; Foo, C.; Ng, C. New potential materials in advancement of photovoltaic and optoelectronic applications: Metal halide perovskite nanorods. Renew. Sust. Energ. Rev. 2023, 171, 113037. [Google Scholar] [CrossRef]
- Li, A.; Zhang, Y.; Sun, Z.; Niu, Z.; Lan, G. Photosensitizing metal-organic layers for photocatalysis, artificial photosynthesis and fluorescence imaging. Sci. China Chem. 2023, 66, 3372–3382. [Google Scholar] [CrossRef]
- Song, X.-L.; Chen, L.; Gao, L.-J.; Ren, J.-T.; Yuan, Z.-Y. Engineering g-C3N4 based materials for advanced photocatalysis: Recent advances. Green Energy Environ. 2024, 2, 166–197. [Google Scholar] [CrossRef]
- Yuan, J.; Hu, L.; Huang, J.; Chen, J.; Qiao, S.; Xie, H. Photo/electrochemical urea synthesis via CO2 coupling with nitrogenous small molecules: Status and challenges for the development of mechanism and catalysts. Appl. Catal. B 2023, 339, 123146. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Abild-Pedersen, F.; Studt, F.; Bligaard, T. Density functional theory in surface chemistry and catalysis. Proc. Natl. Acad. Sci. USA 2011, 108, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Gurdal, Y.; Iannuzzi, M. DFT-based Theoretical Simulations for Photocatalytic Applications Using TiO2. In Titanium Dioxide; IntechOpen: London, UK, 2017. [Google Scholar]
- Tang, X.; Xue, Q.; Qi, X.; Cheng, C.; Yang, M.; Yang, T.; Chen, F.; Qiu, F.; Quan, X. DFT and experimental study on visible-light driven photocatalysis of rare-earth-doped TiO2. Vacuum 2022, 200, 110972. [Google Scholar] [CrossRef]
- Zhao, Z.; Gonçalves, R.; Gonçalves, R.; Barman, S.; Willard, E.; Byle, E.; Perry, R.; Wu, Z.; Huda, M.; Moulé, A. Electronic Structure Basis for Enhanced Overall Water Splitting Photocatalysis with Aluminum Doped Srtio3 in Natural Sunlight. Energy Environ. Sci. 2019, 12, 1385–1395. [Google Scholar] [CrossRef]
- Saafi, I.; Larbi, T.; Amlouk, A.; Amlouk, M. Physical investigations and DFT model calculation on Zn2SnO4-ZnO (ZTO-ZO) alloy thin films for wettability and photocatalysis purposes. Optik 2019, 187, 49–64. [Google Scholar] [CrossRef]
- Xie, L.; Lu, D.; Zeng, Y.; Kondamareddy, K.; Wu, Q.; Li, L.; Fan, H.; Ho, W. The mechanism insight for improved photocatalysis and interfacial charges transfer of surface-dispersed Ag0 modified layered graphite-phase carbon nitride nanosheets. Adv. Powder Technol. 2023, 34, 103936. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, F.; Wang, F.; Zhou, B.; Chen, H.; Yuan, R.; Liu, Y.; Chen, Y. Combined the Photocatalysis and Fenton-like Reaction to Efficiently Remove Sulfadiazine in Water Using g-C3N4/ag/γ-feooh: Insights into the Degradation Pathway from Density Functional Theory. Front. Chem. 2021, 9, 742459. [Google Scholar] [CrossRef] [PubMed]
- Rashid, J.; Parveen, N.; Iqbal, A.; Awan, S.; Iqbal, N.; Talib, S.; Hussain, N.; Akram, B.; Ulhaq, A.; Ahmed, B. Facile synthesis of g-C3N4(0.94)/CeO2(0.05)/Fe3O4(0.01) nanosheets for DFT supported visible photocatalysis of 2-Chlorophenol. Sci. Rep. 2019, 9, 10202. [Google Scholar] [CrossRef]
- Musho, T.; Wu, N. Ab initio calculation of electronic charge mobility in metal–organic frameworks. Phys. Chem. Chem. Phys. 2015, 17, 26160–26165. [Google Scholar] [CrossRef]
- Bertini, L.; Fantucci, P.; De Gioia, L.; Zampella, G. Excited State Properties of Diiron Dithiolate Hydrides: Implications in the Unsensitized Photocatalysis of H2 Evolution. Inorg. Chem. 2013, 52, 9826–9841. [Google Scholar] [CrossRef] [PubMed]
- Hendrickx, K.; Vanpoucke, D.; Leus, K.; Lejaeghere, K.; Van Yperen-De Deyne, A.; Van Speybroeck, V.; Van Der Voort, P.; Hemelsoet, K. Understanding Intrinsic Light Absorption Properties of Uio-66 Frameworks: A Combined Theoretical and Experimental Study. Inorg. Chem. 2015, 54, 10701. [Google Scholar] [CrossRef]
- Wu, X.; Gagliardi, L.; Truhlar, D. Cerium Metal-organic Framework for Photocatalysis. J. Am. Chem. Soc. 2018, 140, 7904–7912. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Liu, A.; Gao, L.; Zhang, C.; Yan, L.; Wen, S.; Ma, T. Computational screening of Cs based vacancy-ordered double perovskites for solar cell and photocatalysis applications. EcoMat 2022, 5, e12295. [Google Scholar] [CrossRef]
- Martsinovich, N.; Troisi, A. High-Throughput Computational Screening of Chromophores for Dye-Sensitized Solar Cells. J. Phys. Chem. C 2011, 115, 11781–11792. [Google Scholar] [CrossRef]
- Pyzer-Knapp, E.; Suh, C.; Gómez-Bombarelli, R.; Aguilera-Iparraguirre, J.; Aspuru-Guzik, A. What Is High-Throughput Virtual Screening? A Perspective from Organic Materials Discovery. Annu. Rev. Mater. Res. 2015, 45, 195–216. [Google Scholar] [CrossRef]
- Muñoz-Batista, M.J.; Kubacka, A.; Hungría, A.; Fernández-García, M. Heterogeneous Photocatalysis: Light-matter Interaction and Chemical Effects in Quantum Efficiency Calculations. J. Catal. 2015, 330, 154–166. [Google Scholar] [CrossRef]
- Xiong, R.; Honglei, Y.; Peng, Q.; Peng, Q.; Sa, B.; Sa, B.; Wen, C.; Wu, B.; Sun, Z. First-principle Investigation of Tcse2 Monolayer as an Efficient Visible Light Photocatalyst for Water Splitting Hydrogen Production. Res. Chem. Intermed. 2017, 43, 5271–5282. [Google Scholar] [CrossRef]
- Muchová, E.; Bezek, M.; Suchan, J.; Cibulka, R.; Slavíček, P. Molecular Dynamics and Metadynamics Simulations of [2 + 2] Photocycloaddition. Int. J. Quantum Chem. 2018, 118, 25534. [Google Scholar] [CrossRef]
- Nijamudheen, A.; Akimov, A. Quantum Dynamics Effects in Photocatalysis. In Visible Light—Active Photocatalysis; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2018; pp. 527–566. [Google Scholar]
- Ullah, H.N.; Rizwan, M.; Zahid, U.; Imran, A.; Cao, C. A Comprehensive DFT Study of Physical and Photocatalytic Properties of Sr1-xcdxtio3. Mater. Today Commun. 2022, 33, 104495. [Google Scholar] [CrossRef]
- Samanta, B.; Morales-García, Á.; Illas, F.; Goga, N.; Anta, J.; Calero, S.; Bieberle-Hütter, A.; Libisch, F.; Muñoz-García, A.; Pavone, M. Challenges of Modeling Nanostructured Materials for Photocatalytic Water Splitting. Chem. Soc. Rev. 2022, 51, 3794–3818. [Google Scholar] [CrossRef] [PubMed]
- Ri, M.-H.; Ri, H.-M.; Ri, U.-S.; Kim, K.-I.; Kim, N.-H.; Sin, Y.-S. Ab Initio Study of Photocatalytic Characteristics of Graphitic Carbon Nitride Assisted by Oxalic Acid. J. Mol. Model. 2021, 27, 258. [Google Scholar] [CrossRef] [PubMed]
- Di Valentin, C.; Wang, F.; Pacchioni, G. Tungsten Oxide in Catalysis and Photocatalysis: Hints from DFT. Top. Catal. 2013, 56, 1404–1419. [Google Scholar] [CrossRef]
- Friesner, R.A. Ab initio quantum chemistry: Methodology and applications. Proc. Natl. Acad. Sci. USA 2005, 102, 6648–6653. [Google Scholar] [CrossRef]
- McWeeny, R.; Sutcliffe, B.T. Methods of Molecular Quantum Mechanics. Phys. Today 1971, 24, 50. [Google Scholar] [CrossRef]
- Parr, R.; Weitao, Y. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Wang, J.; Cherevan, A.; Hannecart, C.; Hannecart, C.; Naghdi, S.; Nandan, S.; Gupta, T.; Eder, D. Ti-based MOFs: New insights on the impact of ligand composition and hole scavengers on stability, charge separation and photocatalytic hydrogen evolution. Appl. Catal. B. 2021, 283, 119626. [Google Scholar] [CrossRef]
- Zhang, R.; Jiao, L.; Yang, W.; Yang, W.; Wan, G.; Jiang, H.-L.; Jiang, H.-L. Single-atom catalysts templated by metal-organic frameworks for electrochemical nitrogen reduction. J. Mater. Chem. A 2019, 7, 26371–26377. [Google Scholar] [CrossRef]
- Bokarev, S.I.; Bokareva, O.; Kühn, N. A theoretical perspective on charge transfer in photocatalysis. The example of Ir-based systems. Coord. Chem. Rev. 2015, 304, 133–145. [Google Scholar] [CrossRef]
- Guo, C.; Ran, J.; Vasileff, A.; Qiao, S.-Z.; Qiao, S.-Z. Rational design of electrocatalysts and photo(electro)catalysts for nitrogen reduction to ammonia (NH3) under ambient conditions. Energy Environ. Sci. 2018, 11, 45–56. [Google Scholar] [CrossRef]
- Sharma, N.; Das, T.; Kumar, S.; Bhosale, R.; Kabir, M.; Ogale, S. Photocatalytic Activation and Reduction of CO2 to CH4 over Single Phase Nano Cu3SnS4: A Combined Experimental and Theoretical Study. ACS Appl. Energy Mater. 2019, 2, 5677–5685. [Google Scholar] [CrossRef]
- Malmqvist, P.A.; Roos, B.O. The CASSCF state interaction method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
- Roos, B.O.; Taylor, P.R.; Sigbahn, P.E. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Bernales, V.; Ortuño, M.; Truhlar, D.; Cramer, C.; Gagliardi, L. Computational Design of Functionalized Metal–Organic Framework Nodes for Catalysis. ACS Cent. Sci. 2018, 4, 5–19. [Google Scholar] [CrossRef] [PubMed]
- Treto-Suárez, M.A.; Schott, E.; Páez-Hernández, D.; Zarate, X.; Koivisto, B.; Mena-Ulecia, K.; Hidalgo-Rosa, Y. Tunning the optical properties of a photocatalytic metal–organic framework by means of molecular modelling. New J. Chem. 2022, 47, 3430–3444. [Google Scholar] [CrossRef]
- Malmqvist, P.-Å.; Rendell, A.; Roos, B. The restricted active space self-consistent-field method, implemented with a split graph unitary group approach. J. Phys. Chem. 1990, 14, 5477–5482. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863. [Google Scholar] [CrossRef] [PubMed]
- Čižek, J.; Paldus, J. Correlation problems in atomic and molecular systems III. Rederivation of the coupled-pair many-electron theory using the traditional quantum chemical methodst. Int. J. Quantum Chem. 1971, 5, 359–379. [Google Scholar] [CrossRef]
- Matsui, J.; Gutiérrez-Bonet, Á.; Rotella, M.; Alam, R.; Gutierrez, O.; Molander, G. Photoredox/Nickel-Catalyzed Single-Electron Tsuji-Trost Reaction: Development and Mechanistic Insights. Angew. Chem. 2018, 57, 15847–15851. [Google Scholar] [CrossRef] [PubMed]
- Whitten, J.L. Coulombic potential energy integrals and approximations. J. Chem. Phys. 1973, 58, 4496–4501. [Google Scholar] [CrossRef]
- Casida, M.E. Time-Dependent Density Functional Response Theory for Molecules. In Recent Advances in Density Functional Methods; World Scientific: Singapore, 1995; pp. 155–192. [Google Scholar]
- Roos, B. New method for large scale ci calculations. Chem. Phys. Lett. 1972, 15, 153–159. [Google Scholar] [CrossRef]
- Finley, J.; Malmqvist, P.; Roos, B.; Serrano-Andrés, L. The multi-state CASPT2 method. Chem. Phys. Lett. 1998, 288, 299–306. [Google Scholar] [CrossRef]
- Iftimie, R.; Minary, P.; Tuckerman, M. Ab Initio Molecular Dynamics: Concepts, Recent Developments, and Future Trends. Proc. Natl. Acad. Sci. USA 2005, 102, 6654–6659. [Google Scholar] [CrossRef]
- Shtoff, A.V.; Gusarov, S.; Dmitriev, Y.Y. Application of the Floquet Theory in Calculations of Higher-Order Nonlinear Optical Susceptibilities of Molecules. Opt. Spectrosc. 2000, 89, 192–194. [Google Scholar] [CrossRef]
- Schtoff, A.V.; Rérat, M.; Gusarov, S. Ab initio calculations of the second dynamic hyperpolarizability of LiH by means of Floquet theory approach. Eur. Phys. J. D 2001, 15, 199–208. [Google Scholar] [CrossRef]
- Casida, M.E.; Huix-Rotllant, M. Progress in Time-Dependent Density-Functional Theory. Annu. Rev. Phys. Chem. 2012, 63, 287–323. [Google Scholar] [CrossRef]
- Casida, M. Time-Dependent Density Functional Response Theory of Molecular Systems: Theory, Computational Methods, and Functionals. In Recent Developments and Applications of Modern Density Functional Theory; Elsevier: Amsterdam, The Netherlands, 1996; pp. 391–439. [Google Scholar]
- Koch, W.; Holthausen, M.C. A Chemist’s Guide to Density Functional Theory; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Perdew, J.P. Generalized gradient approximations for exchange and correlation: A look backward and forward. Physica B 1991, 172, 1–6. [Google Scholar] [CrossRef]
- Becke, A.D. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Perdew, J.; Ruzsinszky, A.; Csonka, G.; Vydrov, O.; Scuseria, G.; Constantin, L.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2009, 100, 136406. [Google Scholar] [CrossRef]
- Beke, A.D. Densityfunctional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. M11-L: A Local Density Functional That Provides Improved Accuracy for Electronic Structure Calculations in Chemistry and Physics. J. Phys. Chem. Lett. 2012, 3, 117–124. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Constantin, L.A.; Sun, J. Workhorse Semilocal Density Functional for Condensed Matter Physics and Quantum Chemistry. Phys. Rev. Lett. 2009, 106, 026403. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Sun, J.; Remsing, R.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 2016, 8, 831–836. [Google Scholar] [CrossRef]
- Ziegler, T.; Seth, M. Range-Separated Exchange Functionals with Slater-Type Functions. J. Chem. Theory Comput. 2012, 13, 901–907. [Google Scholar]
- Zhao, Y.; Lynch, B.; Truhlar, D. Doubly Hybrid Meta DFT: New Multi-Coefficient Correlation and Density Functional Methods for Thermochemistry and Thermochemical Kinetics. J. Phys. Chem. A 2004, 108, 4786. [Google Scholar] [CrossRef]
- Fujishima, A.; Zhang, X.; Tryk, D. TiO2 Photocatalysis and Related Surface Phenomena. Surf. Sci. Rep. 2008, 63, 515–582. [Google Scholar] [CrossRef]
- Xiong, J.; Xiong, J.; Di, J.; Di, J.; Xia, J.; Zhu, W.; Li, H. Surface Defect Engineering in 2D Nanomaterials for Photocatalysis. Adv. Funct. Mater. 2018, 28, 1801983. [Google Scholar] [CrossRef]
- Rapacioli, M.; Tarrat, N. Periodic DFTB for Supported Clusters: Implementation and Application on Benzene Dimers Deposited on Graphene. Computation 2022, 10, 39. [Google Scholar] [CrossRef]
- Kittel, C.; McEuen, P. Introduction to Solid State Physics; Willey: Hoboken, NJ, USA, 2004. [Google Scholar]
- Milman, V.; Winkler, B.; White, J.A.; Pickard, C.J.; Payne, M.C.; Akhmatskaya, E.V.; Nobes, R.H. Electronic structure, properties and phase stability of inorganic crystals: A pseudopotential plane-wave study. Int. J. Quantum Chem. 2000, 77, 895–910. [Google Scholar] [CrossRef]
- Levchenko, S.; Ren, X.; Wieferink, J.; Johanni, R.; Rinke, P.; Blum, V.; Scheffler, M. Hybrid Functionals for Large Periodic Systems in an All-electron, Numeric Atom-centered Basis Framework. Comput. Phys. Commun. 2015, 192, 60–69. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, G.; Si, Y.; Liu, M. Surface modeling of photocatalytic materials for water splitting. Phys. Chem. Chem. Phys. 2022, 24, 1237–1261. [Google Scholar] [CrossRef]
- Butera, V. Density functional theory methods applied to homogeneous and heterogeneous catalysis: A short review and a practical user guide. Phys. Chem. Chem. Phys. 2024, 26, 7950–7970. [Google Scholar] [CrossRef]
- Riaz, S.; Gul, M.; Khan, F.; Ahmad, I.; Ilyas, M. Effect of strain and stacking on electronic structure, optical and photocatalytic performance of monolayer XO2 (X = Ti, Ni and Ge). Appl. Phys. A 2023, 129, 589. [Google Scholar] [CrossRef]
- Yao, W.; Li, D.; Wei, S.; Liu, X.; Liu, X.; Wang, W. Density Functional Theory Study on the Enhancement Mechanism of the Photocatalytic Properties of the g-C3N4/BiOBr(001) Heterostructure. ACS Omega 2022, 7, 36479–36488. [Google Scholar] [CrossRef]
- He, X.; Zhang, C. Recent advances in structure design for enhancing photocatalysis. J. Mater. Sci. 2019, 54, 8831–8851. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sanchez, P.; Yang, W. Insights into Current Limitations of Density Functional Theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef]
- Möhle, T.; Bokareva, O.; Grell, G.; Kühn, O.; Bokarev, S. Tuned Range-Separated Density Functional Theory and Dyson Orbital Formalism for Photoelectron Spectra. J. Chem. Theory Comput. 2018, 14, 5870–5880. [Google Scholar] [CrossRef]
- Ortiz, J.V. Brueckner orbitals, Dyson orbitals, and correlation potentials. Int. J. Quant. Chem. 2004, 100, 1131–1135. [Google Scholar] [CrossRef]
- Rodríguez, S.; Hernandez-Fernández, E.; Vázquez, M.; Lagunas-Rivera, S. DFT Computational Analysis of Photophysical (Linear and Non-linear) and Photochemical Parameters for the Design of New Coumarins as Photocatalyst. Top Catal. 2024, 67, 520–529. [Google Scholar] [CrossRef]
- Peyghami, S.; Sharifi, S.; Rakhshanizadeh, F.; Alizadeh, K. Nonlinear optical properties of Rose Bengal: Effect of environment. J. Mol. Liq. 2017, 246, 157–165. [Google Scholar] [CrossRef]
- Srivastava, V.; Singh, P.S.A.; Sinha, S.; Singh, P. Recent Advances of Dicyanopyrazine (DPZ) in Photoredox Catalysis. Photochemistry 2021, 1, 237–246. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Shingu, H. A molecular orbital theory of reactivity in aromatic hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar] [CrossRef]
- Eddy, R.; Ukpe, P.; Ameh, G.R. Theoretical and experimental studies on photocatalytic removal of methylene blue (MetB) from aqueous solution using oyster shell synthesized CaO nanoparticles (CaONP-O). Environ. Sci. Pollut. Res. 2023, 30, 81417–81432. [Google Scholar] [CrossRef]
- Morell, C.; Grand, A.; Toro-Labbé, A. New dual descriptor for chemical reactivity. J. Phys. Chem. A 2005, 109, 205–212. [Google Scholar] [CrossRef]
- Martínez-Araya, J. Why is the dual descriptor a more accurate local reactivity descriptor than Fukui functions? J. Math. Chem. 2015, 53, 451–465. [Google Scholar] [CrossRef]
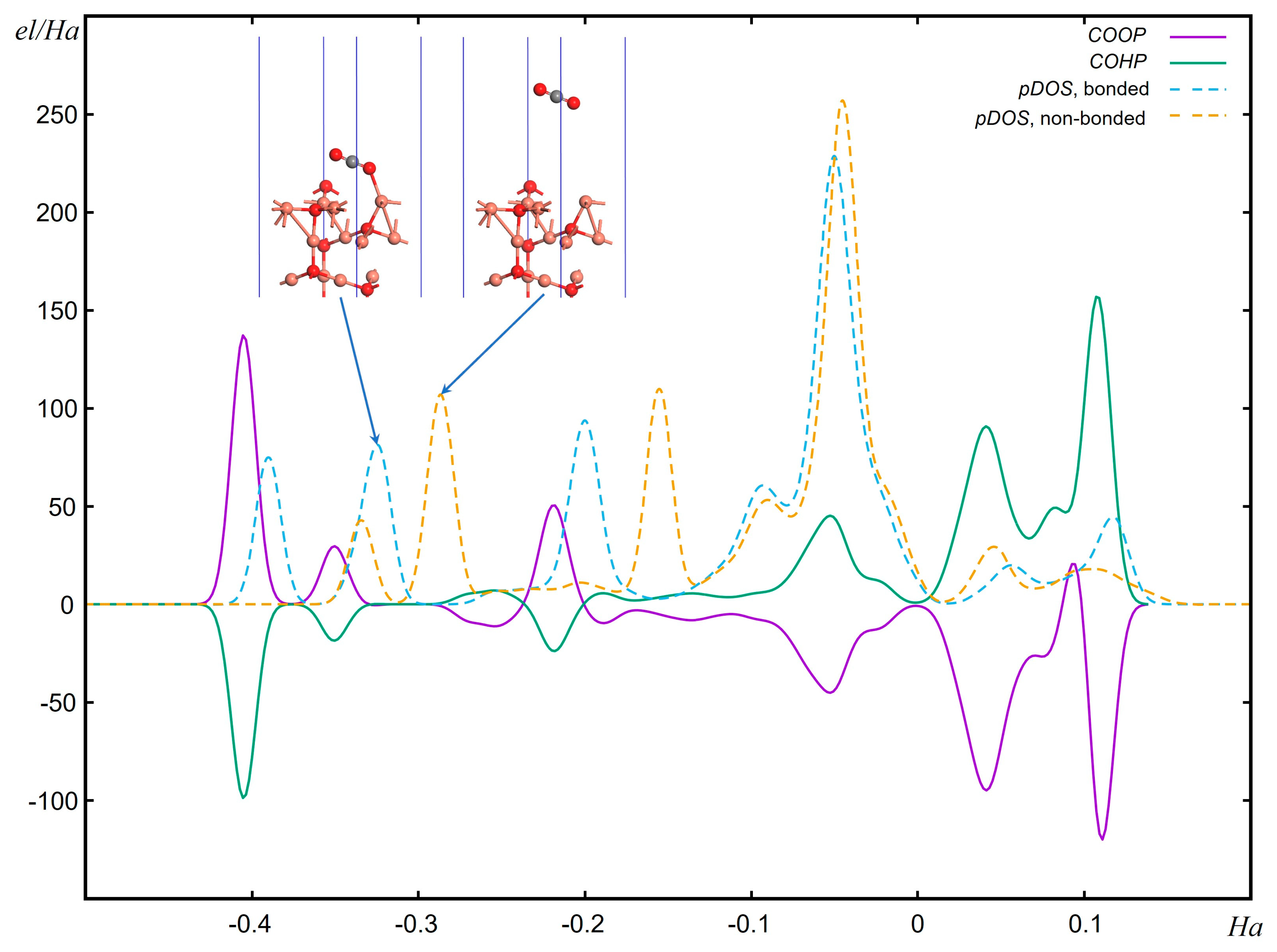
- Müller, C.; Ertural, J.; Hempelmann, D.R. Crystal Orbital Bond Index: Covalent Bond Orders in Solids. J. Phys. Chem. C 2021, 125, 7959–7970. [Google Scholar] [CrossRef]
- Dronskowski, R.; Bloechl, P.E. Crystal Orbital Hamilton Populations (COHP). Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Steinberg, S.; Dronskowski, R. The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds. Crystals 2018, 8, 225. [Google Scholar] [CrossRef]
- Li, S.-L.; Yin, H.; Kan, X.; Gan, L.-Y.; Gan, L.-Y.; Schwingenschlögl, U.; Zhao, Y. Potential of transition metal atoms embedded in buckled monolayer g-C3N4 as single-atom. Phys. Chem. Chem. Phys. 2017, 19, 30069–30077. [Google Scholar] [CrossRef]
- Hennefarth, M.; Hermes, M.; Truhlar, D.; Gagliardi, L. Analytic Nuclear Gradients for Complete Active Space Linearized Pair-Density Functional Theory. J. Chem. Theory Comput. 2024. [Google Scholar] [CrossRef]
- Lischka, H.; Nachtigallová, D.; Aquino, A.; Szalay, P.; Plasser, F.; Machado, F.; Barbatti, M. Multireference Approaches for Excited States of Molecules. Chem. Rev. 2018, 118, 7293–7361. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Baerends, T.; Ziegler, A.; Atkins, J.; Autschbach, O.; Baseggio, D.; Bashford, A.; Bérces, F.; Bickelhaupt, C.; Bo, P.; Boerrigter, E.; et al. ADF 2021.1, SCM; Vrije Universiteit: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Nesse, F. The ORCA program system, WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software Update: The ORCA Program System, version 4.0., WIREs. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Payne, M.; Teter, M.; Allan, D.; Arias, T.; Joannopoulos, J. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.; Pickard, C.; Hasnip, P.; Probert, M.; Refson, K.; Payne, M. First principles methods using CASTEP. Z. Krist. Cryst. Mater 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Delley, B. From molecules to solids with the DMol3 approach. J. Chem. Phys. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
- Boker, S.; Neale, M.; Maes, H.; Wilde, M.; Spiegel, M.; Brick, T.; Spies, J.; Estabrook, R.; Kenny, S.; Bates, T.; et al. OpenMX: An open source extended structural equation modeling framework. Psychometrika 2011, 76, 306–317. [Google Scholar] [CrossRef] [PubMed]
- Galván, I.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.; Bokarev, S.; Bogdanov, N.; Carlson, R.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef] [PubMed]
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafé, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.; Dumitric, T.; Dominguez, A.; et al. DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef] [PubMed]
- Kaye, P.; Laflamme, R.; Mosca, M. An Introduction to Quantum Computing; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Ryabinkin, I.G.; Yen, T.-C.; Genin, S.; Izmaylov, A. Qubit Coupled Cluster Method: A Systematic Approach to Quantum Chemistry on a Quantum Computer. J. Chem. Theory Comput. 2018, 14, 6317–6326. [Google Scholar] [CrossRef] [PubMed]
- Stair, N.H.; Huang, R.; Evangelista, F.A. A Multireference Quantum Krylov Algorithm for Strongly Correlated Electrons. Chem. Theory Comput. 2020, 16, 2236–2245. [Google Scholar] [CrossRef] [PubMed]
- Gomes, N.; Zhang, F.; Berthusen, N.F.; Wang, C.-Z.; Ho, K.-M.; Orth, P.P.; Yao, Y. Efficient Step-Merged Quantum Imaginary Time Evolution Algorithm for Quantum Chemistry. J. Chem. Theory Comput. 2020, 16, 6256–6266. [Google Scholar] [CrossRef]
- Lee, C.-K.; Hsieh, C.-Y.; Zhang, S.; Shi, L. Variational Quantum Simulation of Chemical Dynamics with Quantum Computers. J. Chem. Theory Comput. 2022, 18, 2105–2113. [Google Scholar] [CrossRef]
- Wang, Y.; Mulvihill, E.; Hu, Z.; Lyu, N.; Shivpuje, S.; Liu, Y.; Soley, M.B.; Geva, E.; Batista, V.S.; Kais, S. Simulating Open Quantum System Dynamics on NISQ Computers with Generalized Quantum Master Equations. J. Chem. Theory Comput. 2023, 19, 4851–4862. [Google Scholar] [CrossRef]
- Bauman, N.P.; Liu, H.; Bylaska, E.J.; Krishnamoorthy, S.; Low, G.H.; Granade, C.E.; Wiebe, N.; Baker, N.A.; Peng, B.; Roetteler, M.; et al. Toward Quantum Computing for High-Energy Excited States in Molecular Systems: Quantum Phase Estimations of Core-Level States. J. Chem. Theory Comput. 2021, 17, 201–210. [Google Scholar] [CrossRef]
- Jensen, W.K.; Kristensen, L.B.; Lavigne, C.; Aspuru-Guzik, A. Toward Quantum Computing with Molecular Electronics. J. Chem. Theory Comput. 2022, 18, 3318–3326. [Google Scholar] [CrossRef] [PubMed]
- Liepuoniute, I.; Motta, M.; Pellegrini, T.; Rice, J.; Gujarati, T.; Gil, S.; Jones, G. Simulation of a Diels-Alder Reaction on a Quantum Computer. arXiv 2024, arXiv:2403.08107. [Google Scholar]

| Method | Description | Strengths | Limitations | Extensions | Applications in Photocatalysis |
|---|---|---|---|---|---|
| Density functional theory (DFT) | Minimizes functional of electronic density, for which only approximate expressions are currently available. | Widely used for its efficiency and good balance between accuracy and computational cost. | May struggle with systems that have strong correlation effects or require accurate description of excited states. | New functionals (SCAN, Double hybrid, range separated, …), CASDFT, density fitting | Geometry optimization, orbital energies, TS, reaction barriers, DOS, band structure |
| Multiconfigurational and multireference methods (MRCI, CASSCF, RASSCF …) | Consider multi configurational states for a more accurate description of systems with significant electron correlation. | Provide a better treatment of systems with near-degeneracy and strong static correlation. | Computationally intensive and may not be suitable for very large systems. | Combination with DFT (CASDFT) and AI/ML, DMRG, resolution of identity, | Excitations, spectroscopy, accurate electronic density distributions |
| Perturbation theory (MP2, MBPT) | Account for electron correlation beyond the mean-field approximation by using perturbative corrections. | Can accurately describe quasiparticle excitations and excited states. | Requires high computational resources and expertise to apply correctly. | New GW and Green function approximations, combination with CAS (CASPT2) | Excitations, accurate adsorption energies, quasiparticle, and exciton binding modeling |
| Semiempirical methods (MNDO, AM3, PM6, PM7, DFTB, …) | Utilize empirical parameters obtained from experimental data or high-level calculations to account for electron correlation effects | Less computationally demanding, suitable for large systems and long time-scale simulations | Less accurate than ab initio methods; may not capture all relevant physical interactions; needs parametrization | New Hamiltonians, combinations with more accurate methods in QM/MM, ONIOM, … | Preliminary geometry optimization, modeling large systems, properties |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gusarov, S. Advances in Computational Methods for Modeling Photocatalytic Reactions: A Review of Recent Developments. Materials 2024, 17, 2119. https://doi.org/10.3390/ma17092119
Gusarov S. Advances in Computational Methods for Modeling Photocatalytic Reactions: A Review of Recent Developments. Materials. 2024; 17(9):2119. https://doi.org/10.3390/ma17092119
Chicago/Turabian StyleGusarov, Sergey. 2024. "Advances in Computational Methods for Modeling Photocatalytic Reactions: A Review of Recent Developments" Materials 17, no. 9: 2119. https://doi.org/10.3390/ma17092119
APA StyleGusarov, S. (2024). Advances in Computational Methods for Modeling Photocatalytic Reactions: A Review of Recent Developments. Materials, 17(9), 2119. https://doi.org/10.3390/ma17092119