Thermodynamic Modeling of the Au-Ge-X (X = In, Sb, Si, Zn) Ternary Systems
Abstract
:1. Introduction
2. Literature Information
2.1. The Au-Ge-In Ternary System
2.2. The Au-Ge-Sb Ternary System
2.3. The Au-Ge-Si Ternary System
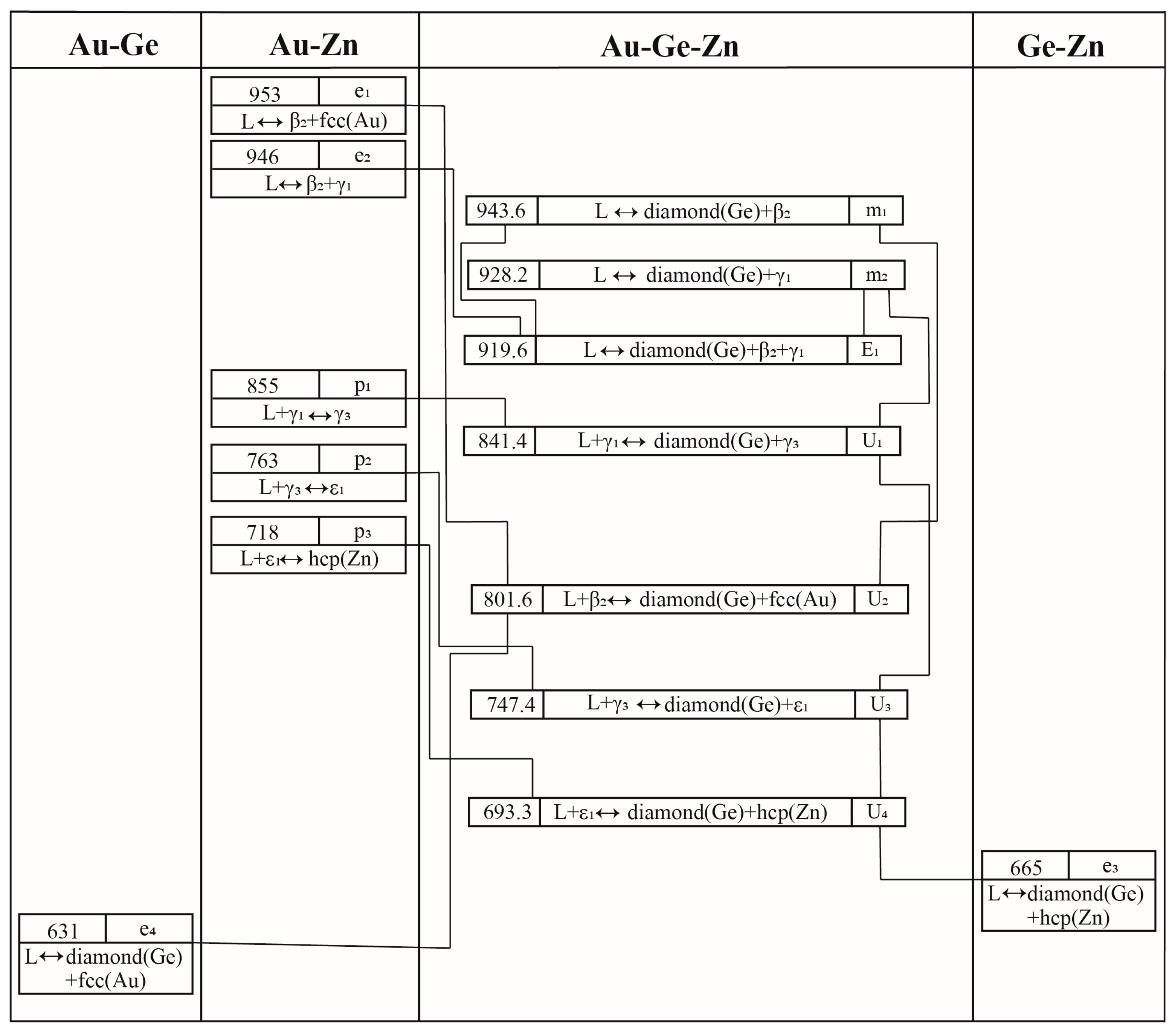
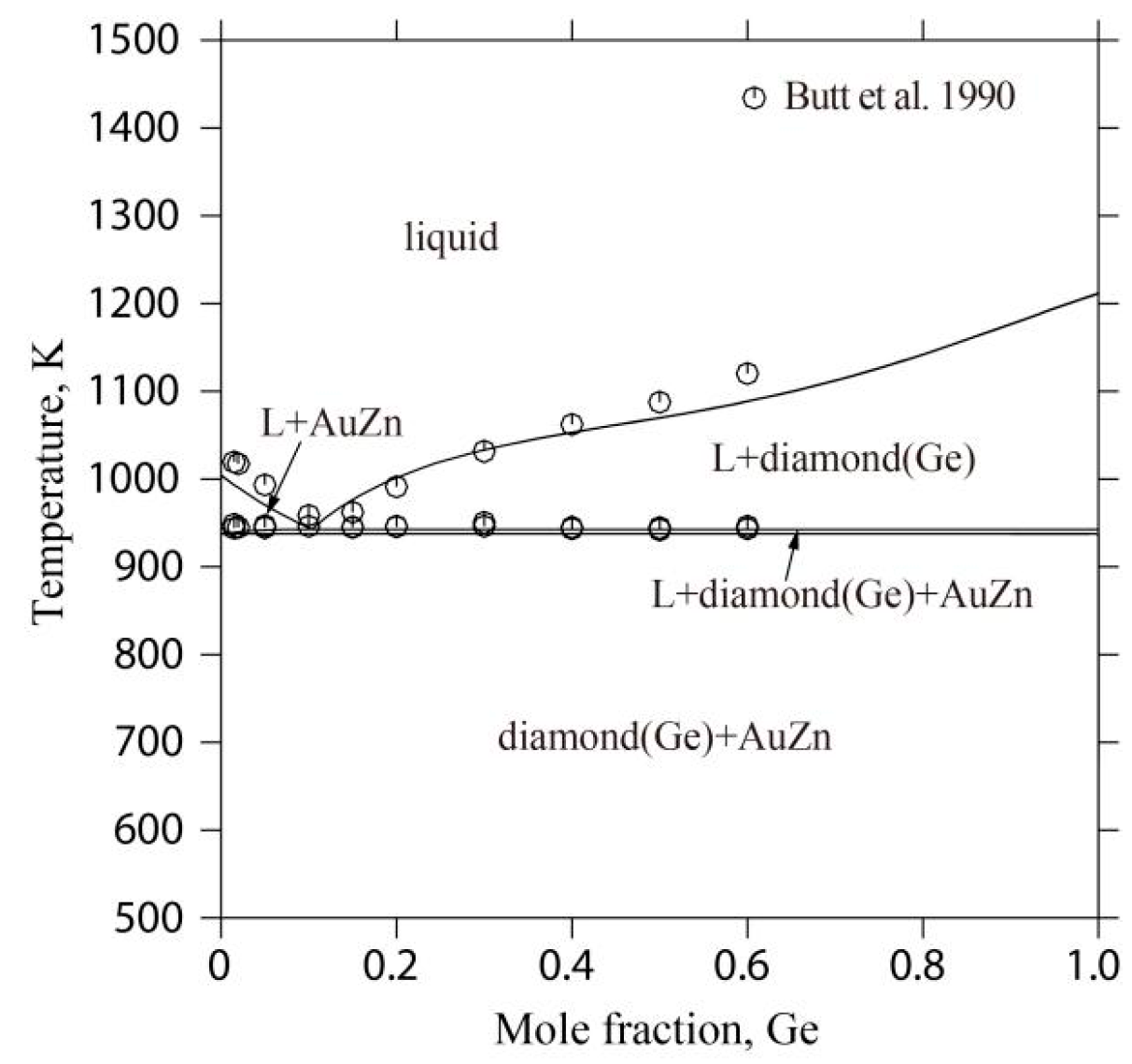
2.4. The Au-Ge-Zn Ternary System
3. Thermodynamic Models
3.1. Solution Phases
3.2. Intermetallic Compounds
4. Calculated Results and Discussion
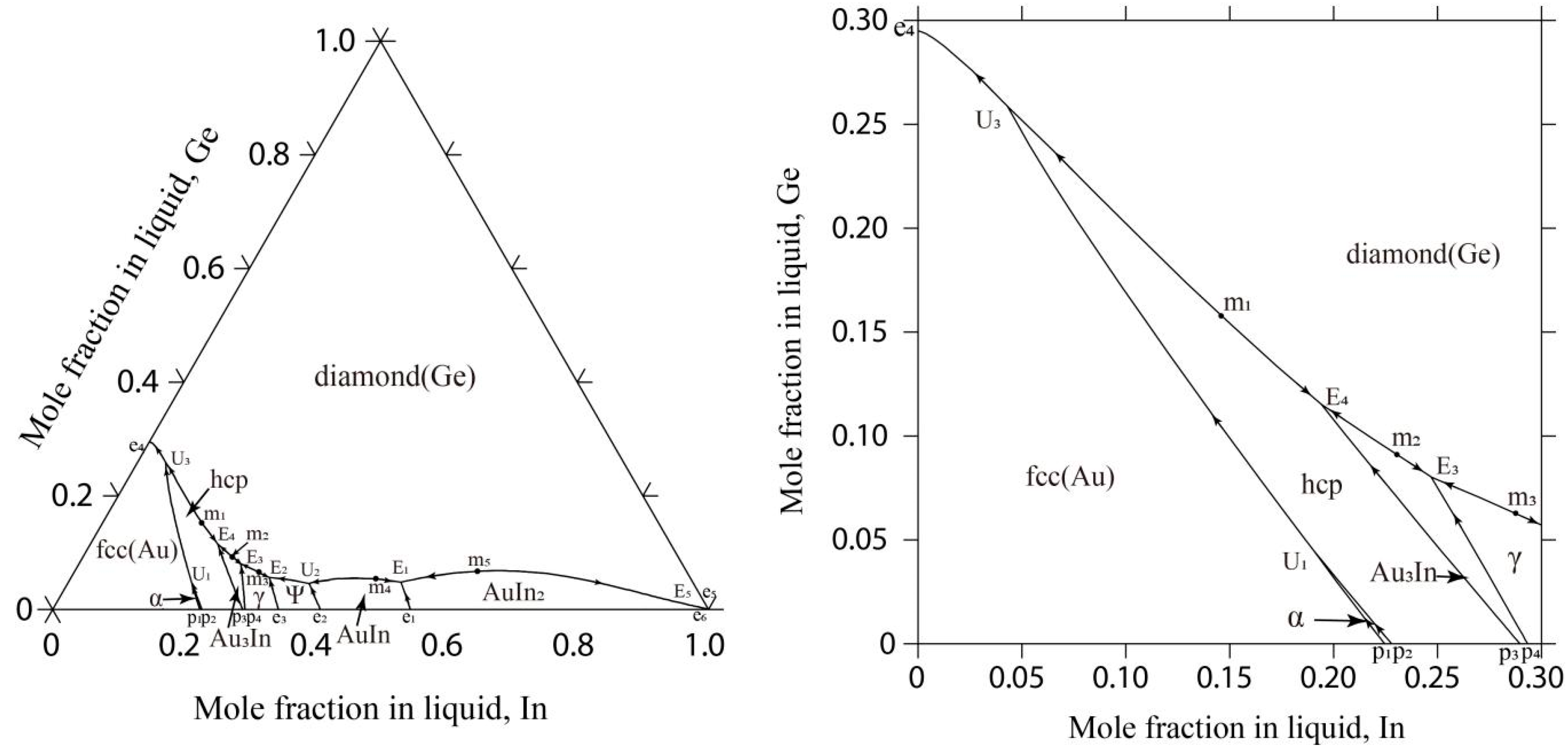
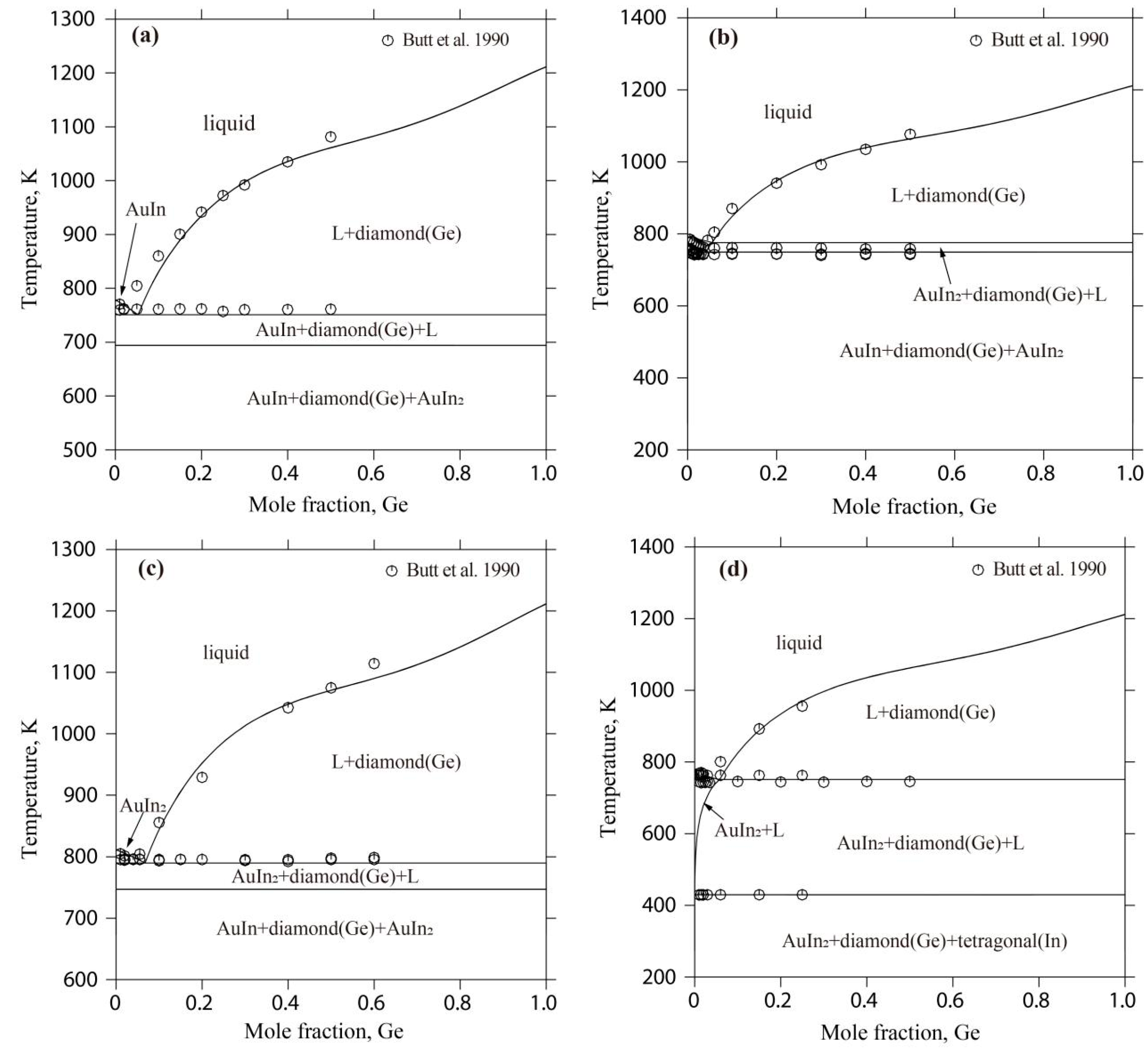
4.1. The Au-Ge-In System
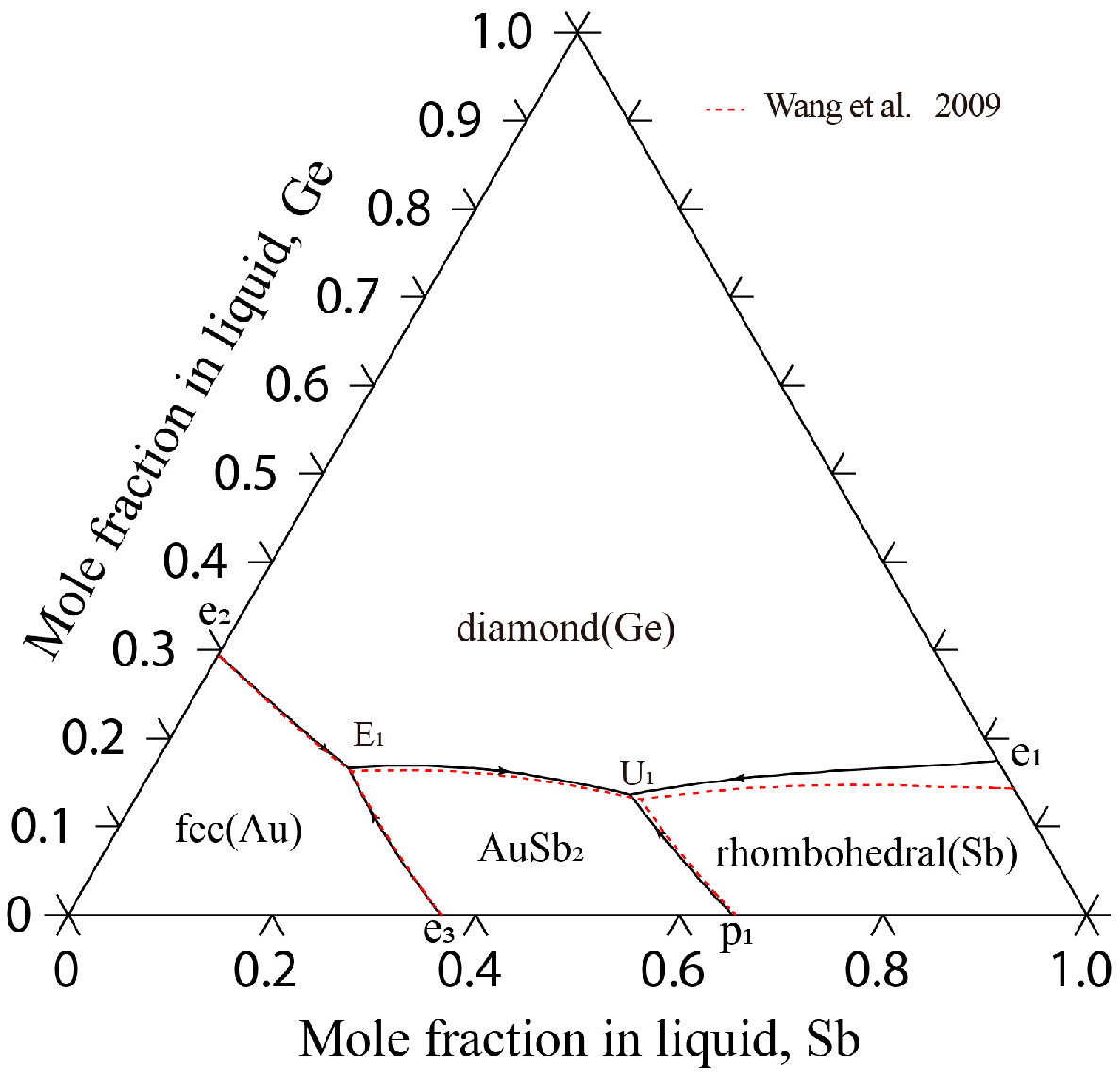
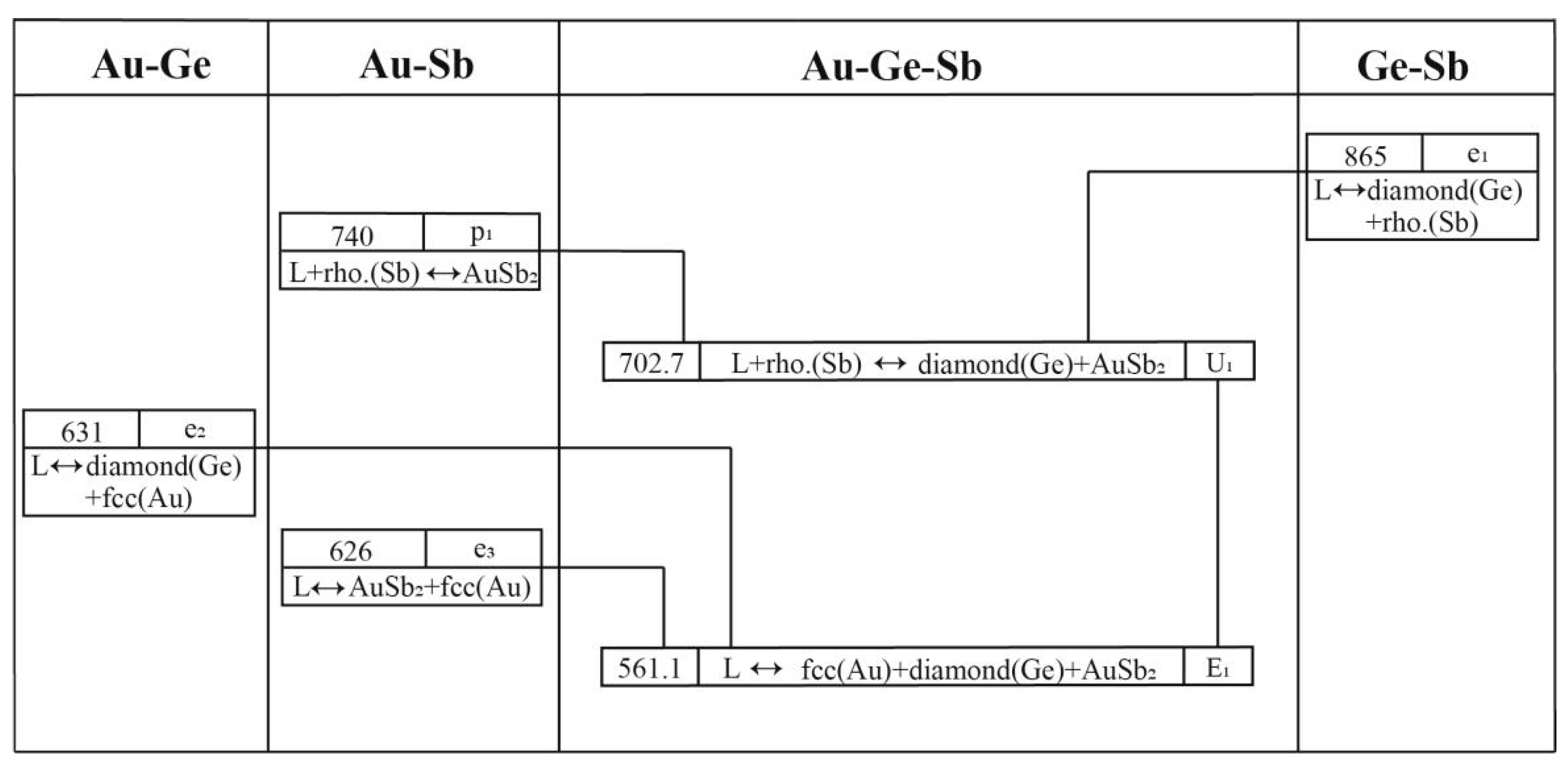
4.2. The Au-Ge-Sb System
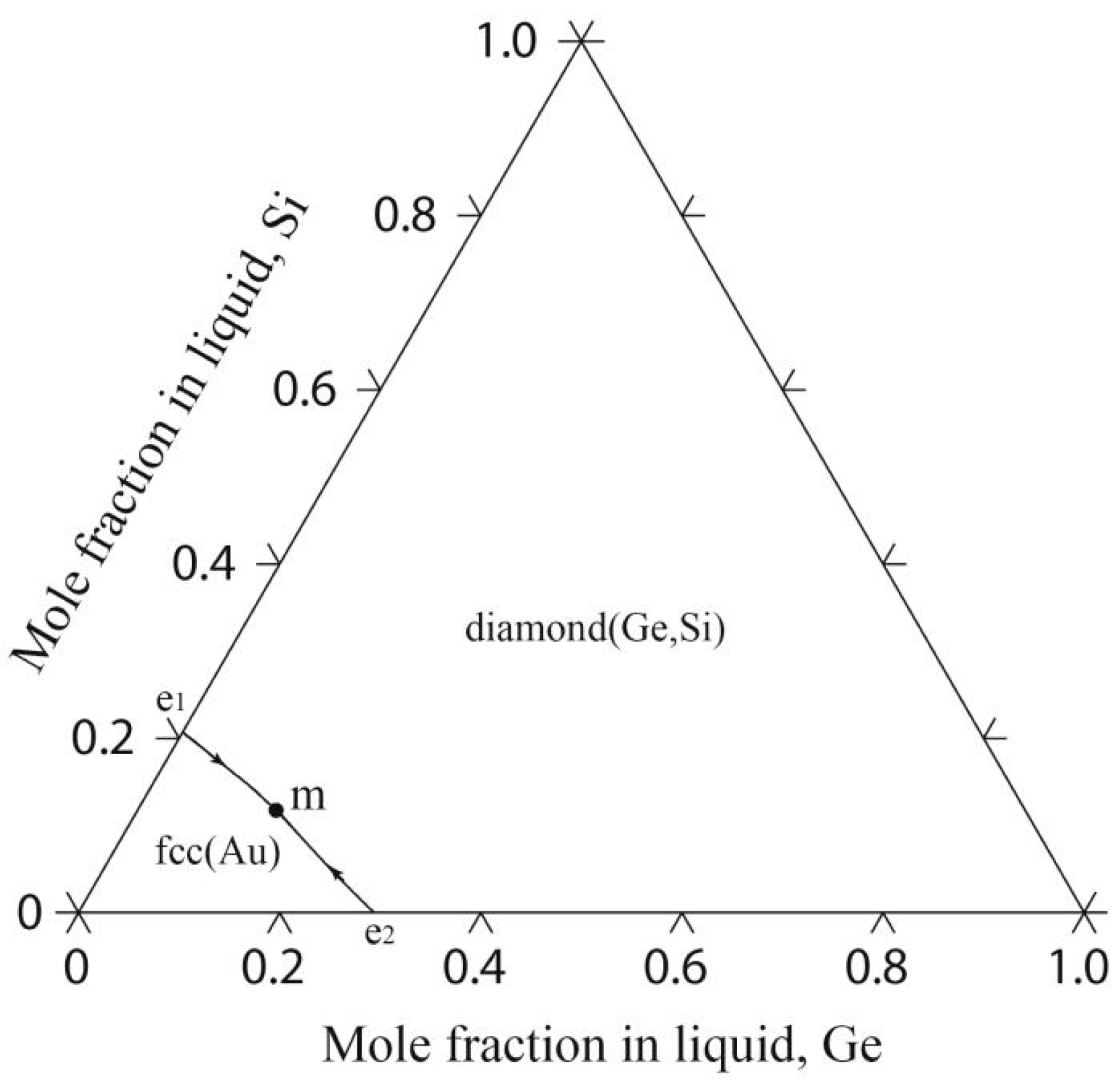
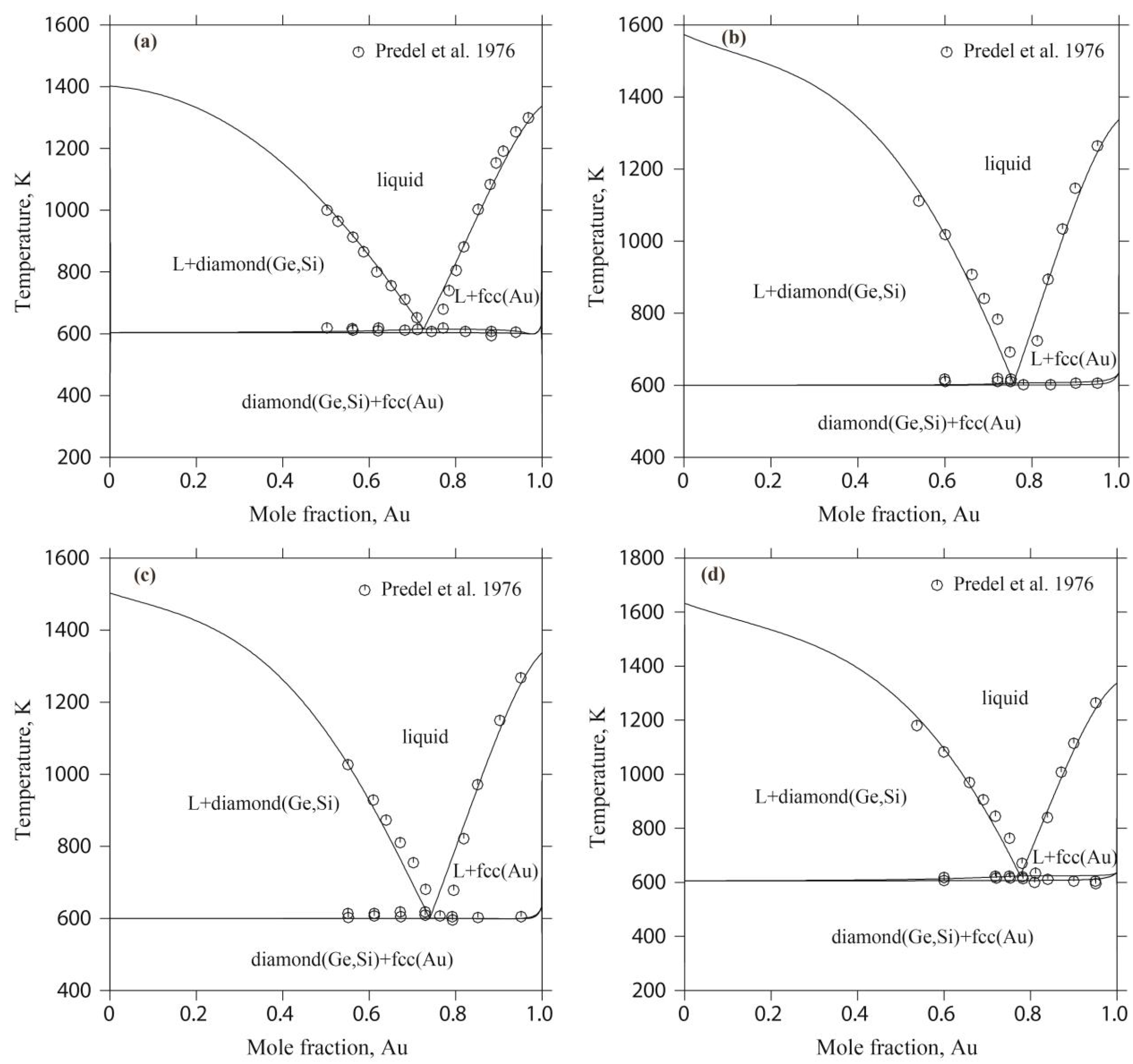
4.3. The Au-Ge-Si Ternary System
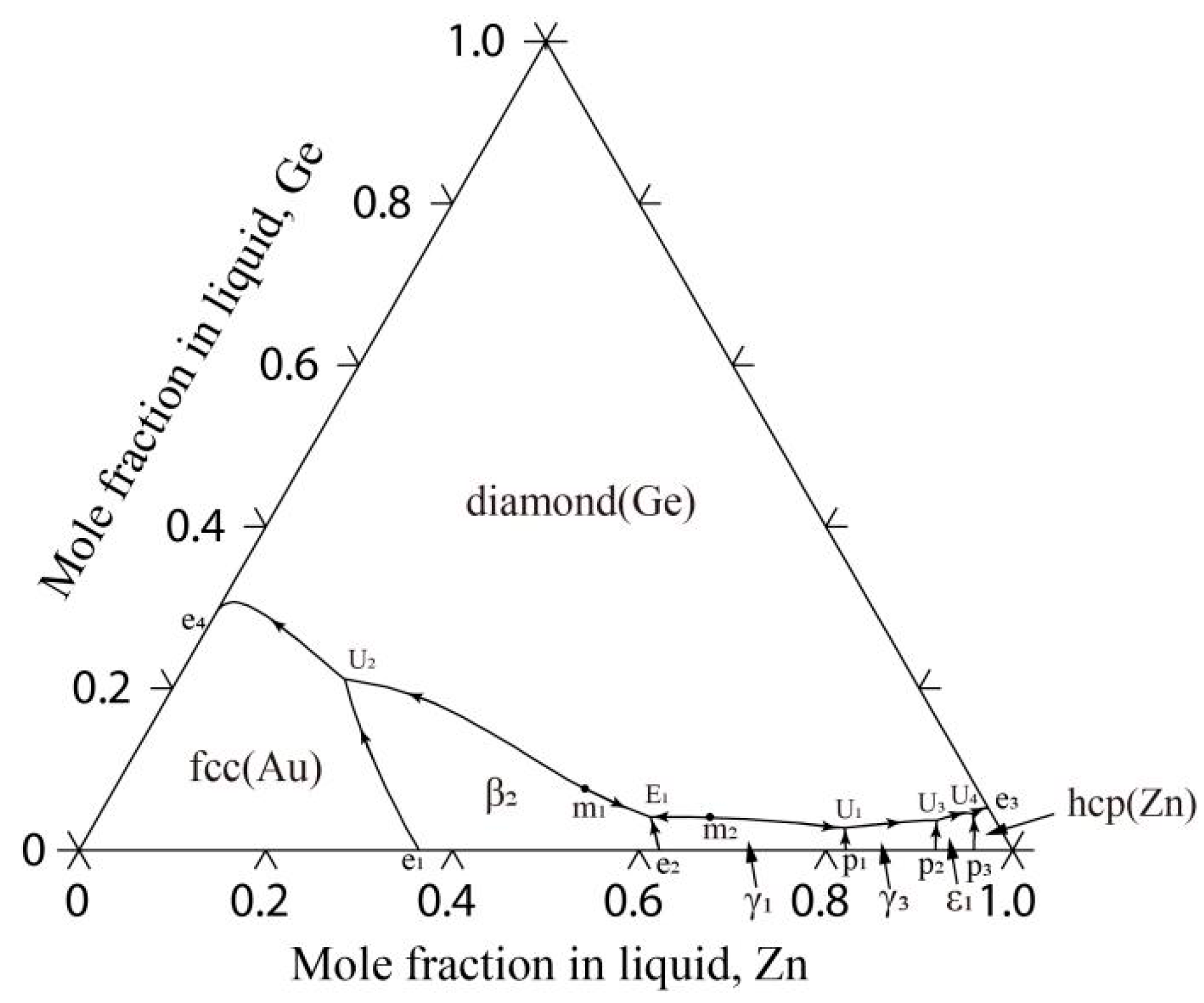
4.4. The Au-Ge-Zn Ternary System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Wu, M.; Pu, J.; Xue, S. Novel Au-based solder alloys: A Potential Answer for Electrical Packaging Problem. Adv. Mater. Sci. Eng. 2020, 2020, 4969647. [Google Scholar] [CrossRef]
- Wang, L.; Xue, S.; Liu, H.; Lin, Y.; Chen, H. Research Progress of Au-20Sn Solder for Electronic Packaging. Cailiao Daobao 2019, 33, 2483–2489. [Google Scholar]
- Zhang, H.; Minter, J.; Lee, N.C. A brief review on high-temperature, Pb-free die-attach materials. J. Electron. Mater. 2019, 48, 201–210. [Google Scholar] [CrossRef]
- Larsson, A.; Tollefsen, T.A.; Løvvik, O.M.; Aasmundtveit, K.E. A review of eutectic Au-Ge solder joints. Metall. Mater. Trans. A 2019, 50, 4632–4641. [Google Scholar] [CrossRef]
- Rerek, T.; Skowronski, L.; Kobierski, M.; Naparty, M.K.; Derkowska-Zielinska, B. Microstructure and opto-electronic properties of Sn-rich Au-Sn diffusive solders. Appl. Surf. Sci. 2018, 451, 32–39. [Google Scholar] [CrossRef]
- Živković, D.; Ćubela, D.; Manasijević, D.; Balanović, L.; Gigović-Gekić, A.; Gomidželović, L.; Štrbac, N.; Mitovski, A. Thermal and structural characteristics of a eutectic Au-Ge alloy. Mater. Test. 2017, 59, 118–122. [Google Scholar] [CrossRef]
- Kobayashia, T.; Ando, T. Recent development of joining and conductive materials for electronic components. Mater. Trans. 2021, 62, 1270–1276. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Li, M.L. Structure and properties of Au-Sn lead-free solders in electronic packaging. Mater. Trans. 2022, 63, 93–104. [Google Scholar] [CrossRef]
- Larsson, A.; Aamundtveit, K.E. On the Microstructure of Off-Eutectic Au-Ge Joints: A High-Temperature Joint. Metall. Mater. Trans. A 2020, 51, 740–749. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.S.; Liu, L.B.; Jin, Z.P. Thermodynamic description of Au-Ag-Si ternary system. Trans. Nonferrous Met. Soc. China 2007, 17, 1405–1411. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.S.; Liu, L.B.; Jin, Z.P. Thermodynamic description of the Sn-Ag-Au ternary system. Calphad 2007, 31, 545–552. [Google Scholar] [CrossRef]
- Wang, J.; Meng, F.G.; Rong, M.H.; Liu, L.B.; Jin, Z.P. Thermodynamic description of the Au-Ag-Pb ternary system. Thermochim. Acta 2010, 505, 79–85. [Google Scholar] [CrossRef]
- Wang, J.; Meng, F.G.; Liu, H.S.; Liu, L.B.; Jin, Z.P. Thermodynamic modeling of the Au-Bi-Sb ternary system. J. Electron. Mater. 2007, 36, 568–577. [Google Scholar] [CrossRef]
- Wang, J.; Leinenbach, C.; Roth, M. Thermodynamic modeling of the Au-Ge-Sn ternary system. J. Alloys Compd. 2009, 481, 830–836. [Google Scholar] [CrossRef]
- Wang, J.; Leinenbach, C.; Roth, M. Thermodynamic description of the Au-Ge-Sb ternary system. J. Alloys Compd. 2009, 485, 577–582. [Google Scholar] [CrossRef]
- Jin, S.; Duarte, L.I.; Leinenbach, C. Experimental study and thermodynamic description of the Au-Cu-Ge system. J. Alloys Compd. 2014, 588, 7–16. [Google Scholar] [CrossRef]
- Jin, S.; Duarte, L.I.; Huang, G.; Leinenbach, C. Experimental investigation and thermodynamic modeling of the Au-Ge-Ni system. Monatshefte Für Chem.-Chem. Mon. 2012, 143, 1263–1274. [Google Scholar] [CrossRef]
- Liu, H.S.; Liu, C.L.; Ishida, K.; Jin, Z.P. Thermodynamic modeling of the Au-In-Sn system. J. Electron. Mater. 2003, 32, 1290–1296. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.J.; Liu, L.B.; Zhou, H.Y.; Jin, Z.P. Thermodynamic modeling of the Au-Sb-Si ternary system. J. Alloys Compd. 2011, 509, 3057–3064. [Google Scholar] [CrossRef]
- Meng, F.G.; Liu, H.S.; Liu, L.B.; Jin, Z.P. Thermodynamic description of the Au-Si-Sn system. J. Alloys Compd. 2007, 431, 292–297. [Google Scholar] [CrossRef]
- Liu, J.; Guo, C.; Li, C.; Du, Z. Thermodynamic optimization of the Ge-Sb and Ge-Sb-Sn systems. Thermochim. Acta 2011, 520, 38–47. [Google Scholar] [CrossRef]
- Okamoto, H.; Massalski, T.B. The Au-Ge (gold-germanium) system. Bull. Alloy Phase Diagr. 1984, 5, 601–610. [Google Scholar] [CrossRef]
- Chevalier, P.Y. A thermodynamic evaluation of the Au-Ge and Au-Si systems. Thermochim. Acta 1989, 141, 217–226. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Ansara, I.; Nabot, J.P. A thermodynamic assessment of the Au-In system. Thermochim. Acta 1988, 129, 89–97. [Google Scholar] [CrossRef]
- Liu, H.S.; Cui, Y.; Ishida, K.; Jin, Z.P. Thermodynamic reassessment of the Au-In binary system. Calphad 2003, 27, 27–37. [Google Scholar] [CrossRef]
- Chewvalier, P.Y. A thermodynamic evaluation of the Ge-In, Ge-Pb, Ge-Sb, Ge-Tl and Ge-Zn systems. Thermochim. Acta 1989, 155, 227–240. [Google Scholar] [CrossRef]
- Butt, M.T.Z. Study of Gold-Based Alloy Phase Diagrams. Ph.D. Thesis, Brunel University School of Engineering and Design, London, UK, 1990. [Google Scholar]
- Chevalier, P.Y. A thermodynamic evaluation of the Au-Sb and Au-Tl systems. Thermochim. Acta 1989, 155, 211–225. [Google Scholar] [CrossRef]
- Kim, J.H.; Jeong, S.W.; Lee, H.M. A thermodynamic study of phase equilibria in the Au-Sb-Sn solder system. J. Electron. Mater. 2002, 31, 557–563. [Google Scholar] [CrossRef]
- Liu, H.S.; Liu, C.L.; Wang, C.; Jin, Z.P.; Ishida, K. Thermodynamic modeling of the Au-In-Sb ternary system. J. Electron. Mater. 2003, 32, 81–88. [Google Scholar] [CrossRef]
- Gierlotka, W. Thermodynamic description of the binary Au-Sb and ternary Au-In-Sb systems. J. Alloys Compd. 2013, 579, 533–539. [Google Scholar] [CrossRef]
- Zwingmann, G. Das Dreistofisystem Gold-Antimon-Germanium. Z. Fuer Met. 1964, 55, 192–194. [Google Scholar] [CrossRef]
- Prince, A.; Raynor, G.V.; Evans, D.S. Phase Diagrams of Ternary Gold Alloys; The Institute of Metals: London, UK, 1990; pp. 7–42. [Google Scholar]
- Olesinski, R.W.; Abbaschian, G.J. The Ge-Si (germanium-silicon) system. Bull. Alloy Phase Diagr. 1984, 5, 180–183. [Google Scholar] [CrossRef]
- Bergman, C.; Chastel, R.; Castanet, R. Thermodynamic investigation on the Si-Ge binary system by calorimetry and Knudsen cell mass spectrometry. J. Phase Equilibria 1992, 13, 113–118. [Google Scholar] [CrossRef]
- Predel, B.; Bankstahl, H.; Gödecke, T. Die Zustandsdiagramme Silber-Germanium-Silizium und Gold-Germanium-Silizium. J. Less-Common Met. 1976, 44, 39–49. [Google Scholar] [CrossRef]
- Okamoto, H.; Massalski, T.B. The Au-Sn (Gold-tin) system. Bull. Alloy Phase Diagr. 1984, 5, 492–503. [Google Scholar] [CrossRef]
- Ipser, H.; Krachler, R. The AuZn melting diagram in the range of the β′-AuZn phase. Scr. Metall. 1988, 22, 1651–1654. [Google Scholar] [CrossRef]
- Liu, H.S.; Ishida, K.; Jin, Z.P.; Du, Y. Thermodynamic assessment of the Au-Zn binary system. Intermetallics 2003, 11, 987–994. [Google Scholar] [CrossRef]
- Butt, M.T.Z.; Bodsworth, C.; Prince, A. The AuZn-Ge section of the Au-Ge-Zn ternary system. Scr. Metall. 1989, 23, 1105–1107. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A.T. Thermodynamics of nonelectrolyte solutions. Ind. Eng. Chem. 1948, 40, 341–345. [Google Scholar] [CrossRef]
- Muggianu, M.Y.; Gambino, M.; Bros, J.P. Enthalpies of formation of liquid alloys bismuth-gallium-tin at 723k-choice of an analytical representation of integral and partial thermodynamic functions of mixing for this ternary-system. J. Chim. Phys. Phys.-Chim. Biol. 1975, 72, 83–88. [Google Scholar] [CrossRef]
- Sundman, B.; Jansson, B.; Andersson, J.O. The thermo-calc databank system. Calphad 1985, 9, 153–190. [Google Scholar] [CrossRef]


| Phase | Prototype | Space Group | Pearson Symbol | Thermodynamic Model | Reference |
|---|---|---|---|---|---|
| fcc (Au) | Cu | Fmm | cF4 | (Au) | [26] |
| diamond (Ge/Si) | Diamond | Fdm | cF8 | (Ge)/(Si) | [35] |
| tetragonal (In) | In | I4/mmm | tI2 | (In) | [26] |
| rhombohedral (Sb) | As | Rm | hR6 | (Sb) | [31] |
| hcp (Zn) | Mg | P63/mmc | hP2 | (Zn) | [40] |
| hcp (Au, In) | Mg | P63/mmc | hP2 | (Au, In) | [26] |
| α (Au, In) | Ni3Ti | P63/mmc | hP16 | (Au, In) | [26] |
| β-Au4In | Cu11Sb3 | Amm2 | — | (Au)0.785: (In)0.215 | [26] |
| β′-Au4In | Cu10Sb3 | — | — | (Au)0.77778: (In)0.22222 | [26] |
| γ-Au9In4 | Cu9Al4 | P3m | cP52 | (Au)0.69231: (Au, In)0.23077: (In)0.07692 | [26] |
| γ′-Au7In3 | Au7In3 | P3 | hP60 | (Au)0.7: (In)0.3 | [26] |
| ψ-Au3In2 | Ni2Al3 | P3m1 | hP5 | (Au)0.5: (Au, In)0.33333: (In)0.16667 | [26] |
| Au3In | Cu3Ti | Pmmn | oP8 | (Au)0.75: (In)0.25 | [26] |
| AuIn | — | — | — | (Au)0.5: (In)0.5 | [26] |
| AuIn2 | CaF2 | Fmm | cF12 | (Au)0.33333: (In)0.66667 | [26] |
| AuSb2 | FeS2 | Pa3 | cP12 | (Au)0.3333: (Sb)0.6667 | [31] |
| α1-Au3Zn | Ag3Mg | — | — | (Au)0.6: (Au, Zn)0.2: (Zn)0.2 | [40] |
| α2-Au3Zn | — | Abam (Cmca) | oC32 | (Au)0.75: (Zn)0.25 | [40] |
| α3-Au3Zn | Cu3Pd | Pn2n/Pnmn | — | (Au)0.64286: (Au, Zn)0.25: (Zn)0.10714 | [40] |
| ε1-Au3Zn17 | Mg | P63/mmc | hP2 | (Au, Zn) | [40] |
| ε2-Au3Zn17 | — | — | — | (Au)0.15: (In)0.85 | [40] |
| β1-AuZn | CsCl | Pmm | cP2 | (Au, Zn)0.5: (Au, Zn)0.5 | [40] |
| Au5Zn3 | — | Ibam | — | (Au)0.625: (Zn)0.375 | [40] |
| δ1-Au11Zn14 | — | — | — | (Au)0.44: (Zn)0.56 | [40] |
| γ1-AuZn3 | Cu5Zn8 | — | — | (Au, Zn)0.15385: (Au)0.15385: (Au, Zn)0.23077: (Zn)0.46153 | [40] |
| γ2-AuZn3 | H3U | Pnm | cP32 | (Au)0.25: (Zn)0.75 | [40] |
| γ3-AuZn3 | — | — | — | (Au)0.12: (Au, Zn)0.16: (Zn)0.72 | [40] |
| Phase | Thermodynamic Parameters | Reference |
|---|---|---|
| liquid (Au, Ge, In) | [14] | |
| [14] | ||
| [26] | ||
| [26] | ||
| [26] | ||
| This work | ||
| fcc (Au, Ge, In) | [14] | |
| [26] | ||
| [26] | ||
| diamond(Ge) | cited from SGTE database | [14] |
| tetragonal(In) | cited from SGTE database | [26] |
| hcp(Au, In) | [26] | |
| α(Au, In) | [26] | |
| β-Au4In | [26] | |
| β′-Au4In | [26] | |
| γ-Au9In4 | [26] | |
| [26] | ||
| [26] | ||
| γ′-Au7In3 | [26] | |
| ψ-Au3In2 | [26] | |
| [26] | ||
| [26] | ||
| Au3In | [26] | |
| AuIn | [26] | |
| AuIn2 | [26] |
| Phase | Thermodynamic Parameters | Reference |
|---|---|---|
| liquid (Au, Ge, Sb) | [14] | |
| [14] | ||
| [31] | ||
| [31] | ||
| [21] | ||
| This work | ||
| This work | ||
| This work | ||
| fcc (Au, Ge, Sb) | [14] | |
| [31] | ||
| diamond (Ge, Sb) | [21] | |
| rhombohedral (Ge, Sb) | [31] | |
| [21] | ||
| AuSb2 | [31] |
| Phase | Thermodynamic Parameters | Reference |
|---|---|---|
| liquid (Au, Ge, Si) | [14] | |
| [14] | ||
| [14] | ||
| [20] | ||
| [20] | ||
| [20] | ||
| [35] | ||
| This work | ||
| This work | ||
| This work | ||
| fcc (Au, Ge, Si) | [14] | |
| [20] | ||
| diamond (Au, Ge, Si) | [20] | |
| [35] |
| Phase | Thermodynamic Parameters | Reference |
|---|---|---|
| liquid (Au, Ge, Zn) | , | [14] |
| , | [40] | |
| , | [27] | |
| , , | This work | |
| fcc (Au, Ge, Zn) | [14] | |
| , | [40] | |
| Diamond (Ge, Zn) | [27] | |
| hcp(Au, Zn) | , | [40] |
| α1-Au3Zn | [40] | |
| [40] | ||
| [40] | ||
| α2-Au3Zn | [40] | |
| α3-Au3Zn | [40] | |
| [40] | ||
| [40] | ||
| ε1-Au3Zn17 | , | [40] |
| ε2-Au3Zn17 | [40] | |
| β1-AuZn | [40] | |
| [40] | ||
| Au5Zn3 | [40] | |
| δ1-Au11Zn14 | [40] | |
| γ1-AuZn3 | [40] | |
| [40] | ||
| [40] | ||
| [40] | ||
| , | [40] | |
| γ2-AuZn3 | [40] | |
| γ3-AuZn3 | [40] | |
| [40] | ||
| [40] |
| Invariant Reactions | Type | T (K) | Composition | Reference | |
|---|---|---|---|---|---|
| L + α(Au, In) ↔ fcc(Au) + hcp(Au, In) | U1 | 863 | 0.765 | 0.045 | This work |
| L ↔ diamond(Ge) + AuIn + AuIn2 | E1 | 747 | 0.444 | 0.048 | This work |
| 744 | 0.433 | 0.035 | [28] | ||
| L + AuIn ↔ diamond(Ge) +ψ-Au3In2 | U2 | 964 | 0.586 | 0.046 | This work |
| L ↔ diamond(Ge) + γ-Au9In4 +ψ-Au3In2 | E2 | 671 | 0.641 | 0.056 | This work |
| L ↔ diamond(Ge) + γ-Au9In4 + Au3In | E3 | 667 | 0.673 | 0.080 | This work |
| L ↔ diamond(Ge) + hcp(Au, In) + Au3In | E4 | 665 | 0.691 | 0.115 | This work |
| L + hcp(Au, In) ↔ diamond(Ge) + fcc(Au) | U3 | 654 | 0.698 | 0.259 | This work |
| L ↔ diamond(Ge) + AuIn2 + tetragonal(In) | E5 | 429 | 0.001 | 0.001 | This work |
| 429 | — | — | [28] | ||
| L ↔ diamond(Ge) + hcp(Au, In) | m1 | 667 | 0.696 | 0.158 | This work |
| L ↔ diamond(Ge) + Au3In | m2 | 668 | 0.679 | 0.091 | This work |
| L ↔ diamond(Ge) + γ-Au9In4 | m3 | 673 | 0.649 | 0.063 | This work |
| L ↔ diamond(Ge) + AuIn | m4 | 751 | 0.474 | 0.053 | This work |
| L ↔ diamond(Ge) + AuIn2 | m5 | 790 | 0.310 | 0.067 | This work |
| Invariant Reactions | Type | T (K) | Composition | Reference | |
|---|---|---|---|---|---|
| L + rhombohedral (Sb) ↔ diamond (Ge) + AuSb2 | U1 | 703 | 0.350 | 0.140 | [33] |
| 702 | 0.383 | 0.137 | [15] | ||
| 703 | 0.379 | 0.137 | This work | ||
| L ↔ diamond (Ge) + fcc (Au) + AuSb2 | E1 | 561 | 0.680 | 0.150 | [33] |
| 560 | 0.639 | 0.166 | [15] | ||
| 561 | 0.641 | 0.166 | This work | ||
| Invariant Reactions | Type | T (K) | Composition | Reference | |
|---|---|---|---|---|---|
| L ↔ β2-AuZn + diamond (Ge) + γ1-AuZn3 | E1 | 920 | 0.368 | 0.041 | This work |
| L + γ1-AuZn3 ↔ diamond (Ge) + γ3-AuZn | U1 | 841 | 0.166 | 0.028 | This work |
| L +β2-AuZn ↔ diamond (Ge) + fcc (Au) | U2 | 802 | 0.610 | 0.211 | This work |
| L + γ3-AuZn ↔ diamond (Ge) + ε1-Au3Zn17 | U3 | 747 | 0.063 | 0.037 | This work |
| L + ε1-Au3Zn17 ↔ diamond (Ge) + hcp (Zn) | U4 | 693 | 0.020 | 0.045 | This work |
| L ↔ diamond (Ge) + β2-AuZn | m1 | 944 | 0.440 | 0.094 | This work |
| L ↔ diamond (Ge) + γ1-AuZn3 | m2 | 928 | 0.319 | 0.041 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Tong, Q.; Rong, M.; Tan, C.; Liu, X.; Li, M.; Wang, J. Thermodynamic Modeling of the Au-Ge-X (X = In, Sb, Si, Zn) Ternary Systems. Materials 2024, 17, 2137. https://doi.org/10.3390/ma17092137
Bai Y, Tong Q, Rong M, Tan C, Liu X, Li M, Wang J. Thermodynamic Modeling of the Au-Ge-X (X = In, Sb, Si, Zn) Ternary Systems. Materials. 2024; 17(9):2137. https://doi.org/10.3390/ma17092137
Chicago/Turabian StyleBai, Yuchen, Qingsong Tong, Maohua Rong, Cong Tan, Xingyu Liu, Man Li, and Jiang Wang. 2024. "Thermodynamic Modeling of the Au-Ge-X (X = In, Sb, Si, Zn) Ternary Systems" Materials 17, no. 9: 2137. https://doi.org/10.3390/ma17092137
APA StyleBai, Y., Tong, Q., Rong, M., Tan, C., Liu, X., Li, M., & Wang, J. (2024). Thermodynamic Modeling of the Au-Ge-X (X = In, Sb, Si, Zn) Ternary Systems. Materials, 17(9), 2137. https://doi.org/10.3390/ma17092137






