Development of a Stable Process for Wire Embedding in Fused Filament Fabrication Printing Using a Geometric Correction Model
Abstract
1. Introduction
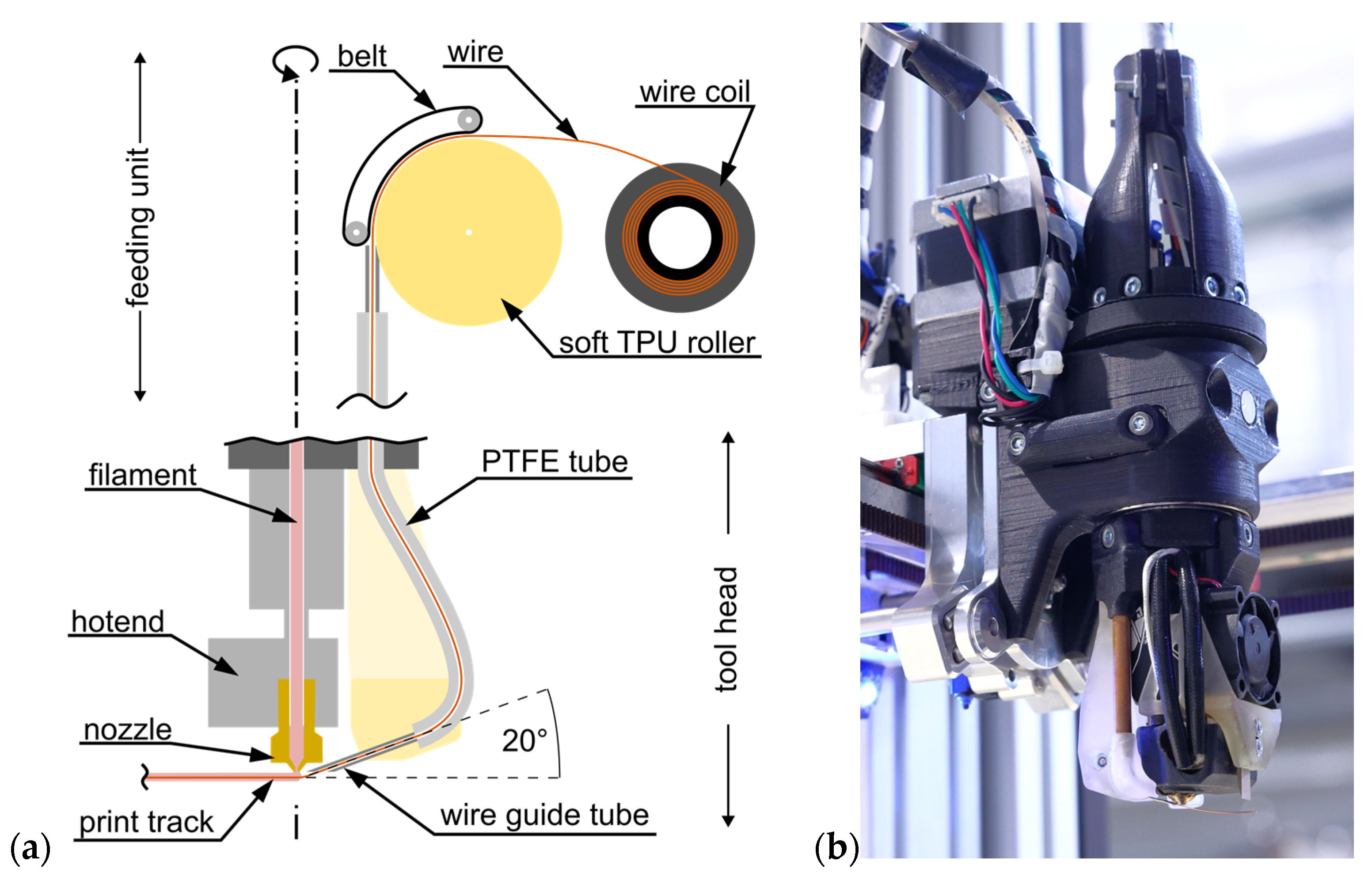
2. Wire-Encapsulating Additive Manufacturing (WEAM)
3. Correction Model
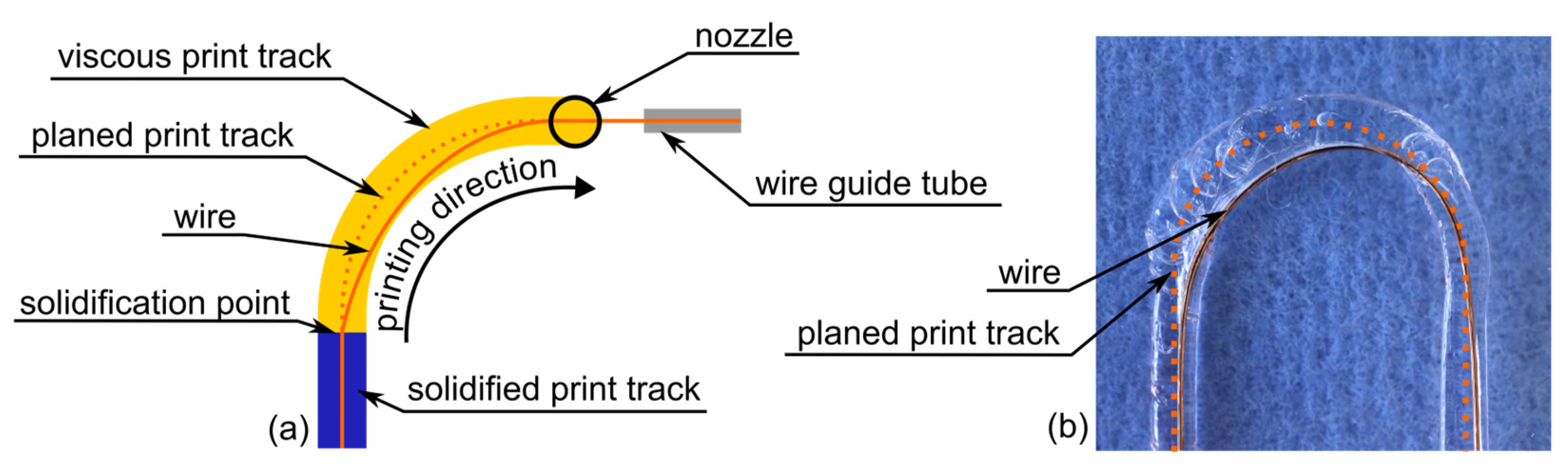
3.1. Deviations of the Wire Position
3.2. Fundamental Idea
- Opening the offset;
- Passing through the arc while holding a constant offset;
- Closing the offset at the end of the arc.
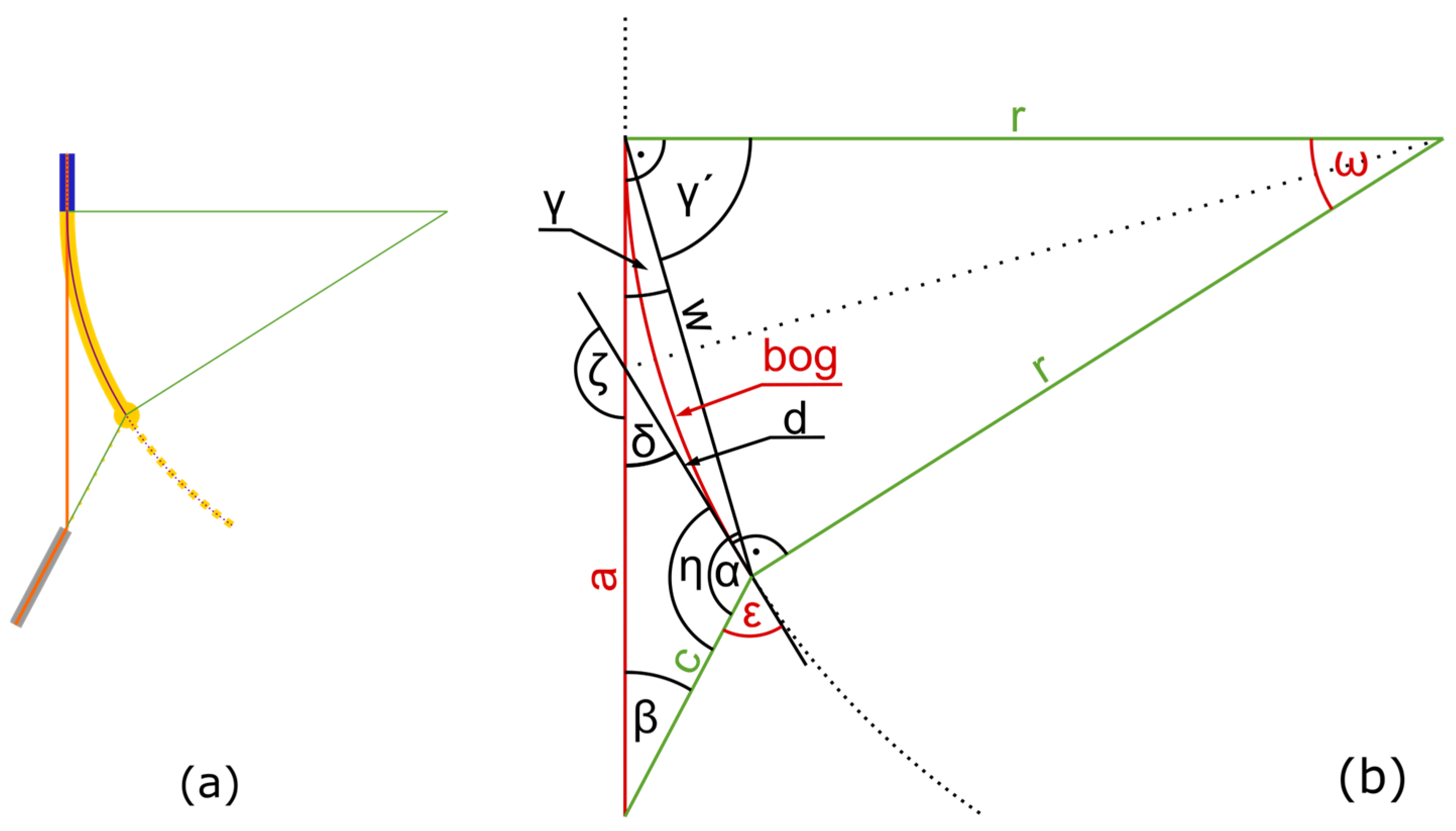
3.3. Mathematical Description
- Offset angle from the wire guide tube ε to define the offset of the rotation of the wire guide tube.
- Distance between the wire guide tube and solidification point a to define the length of the wire.
- Arc length between the nozzle and solidification point bog to define the amount of the deposited polymer track.
- Position of the nozzle in relation to the solidification point via ω to describe the position of the nozzle.
- Distance between the nozzle and the wire guide tube c.
- Start, end, and center points of the arc in x and y.
- Radius of the planed print track r.
- Rate of movement (also called feed rate of the machine) F.
4. Materials and Methods
4.1. Materials
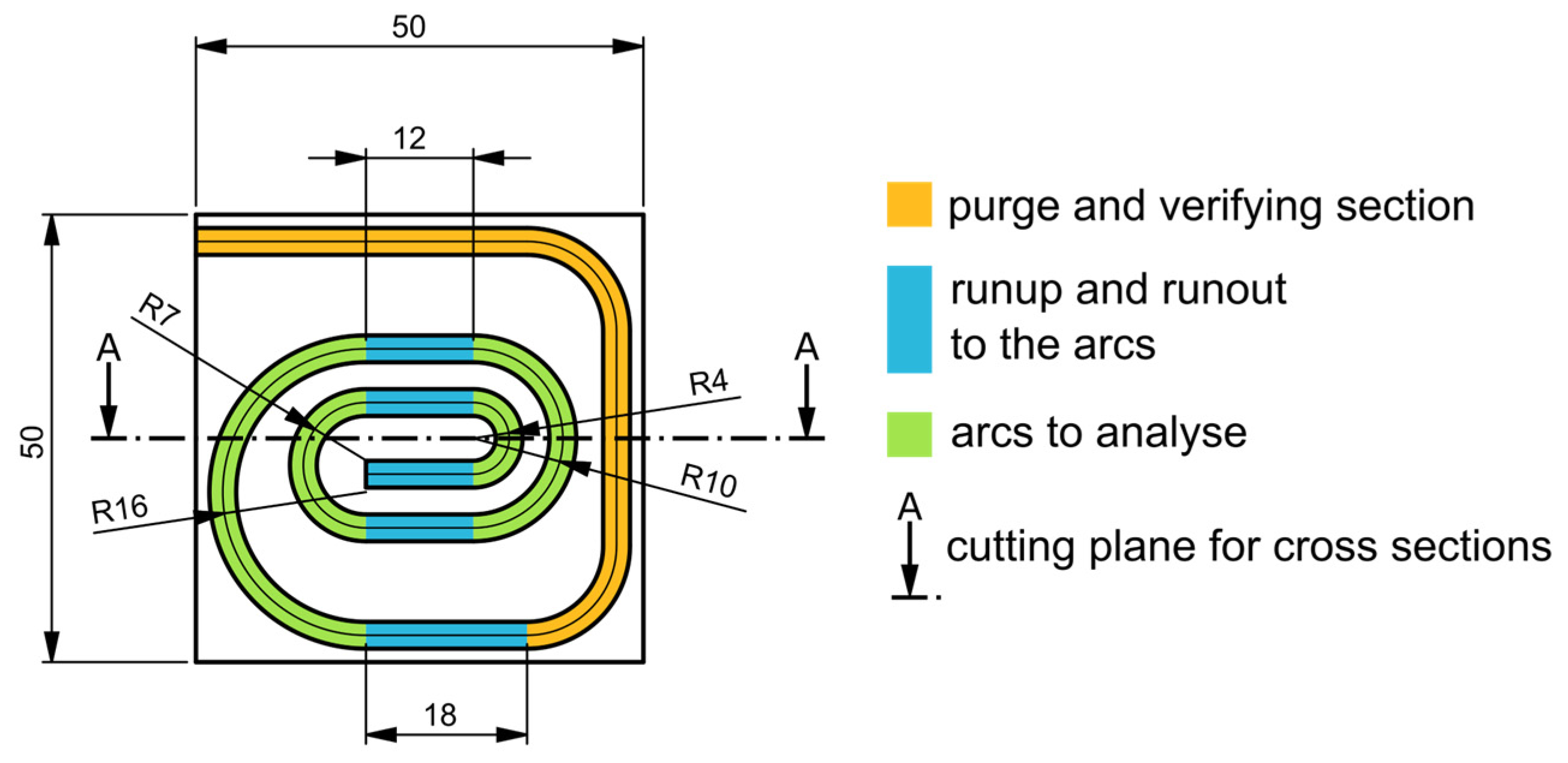
4.2. Test Samples
4.3. Experimental Determination of Cooling Time
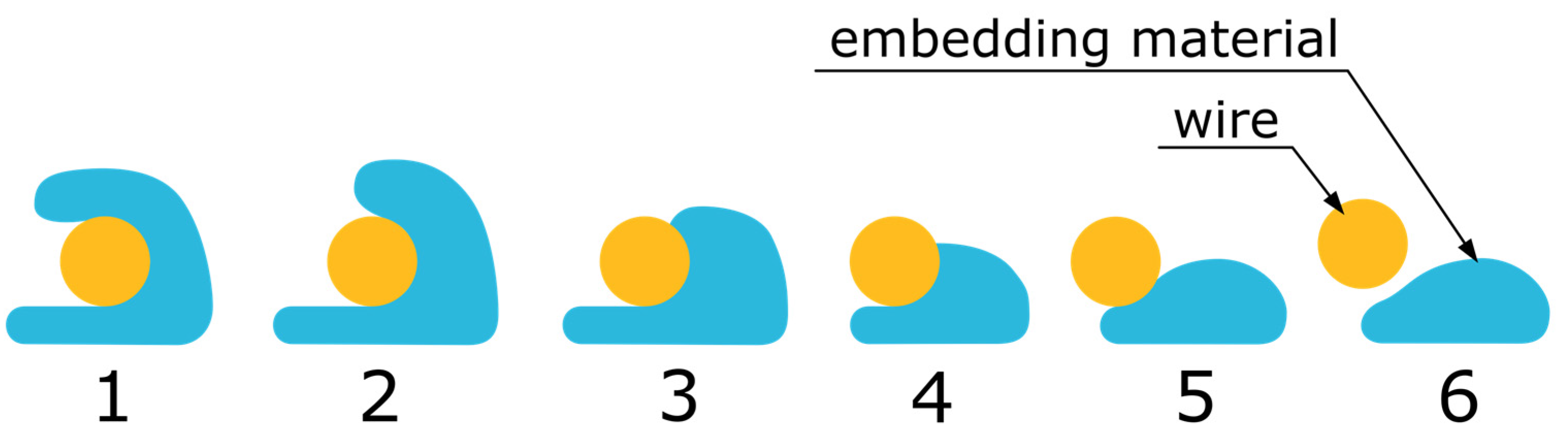
4.4. Determination of the Embedding Quality
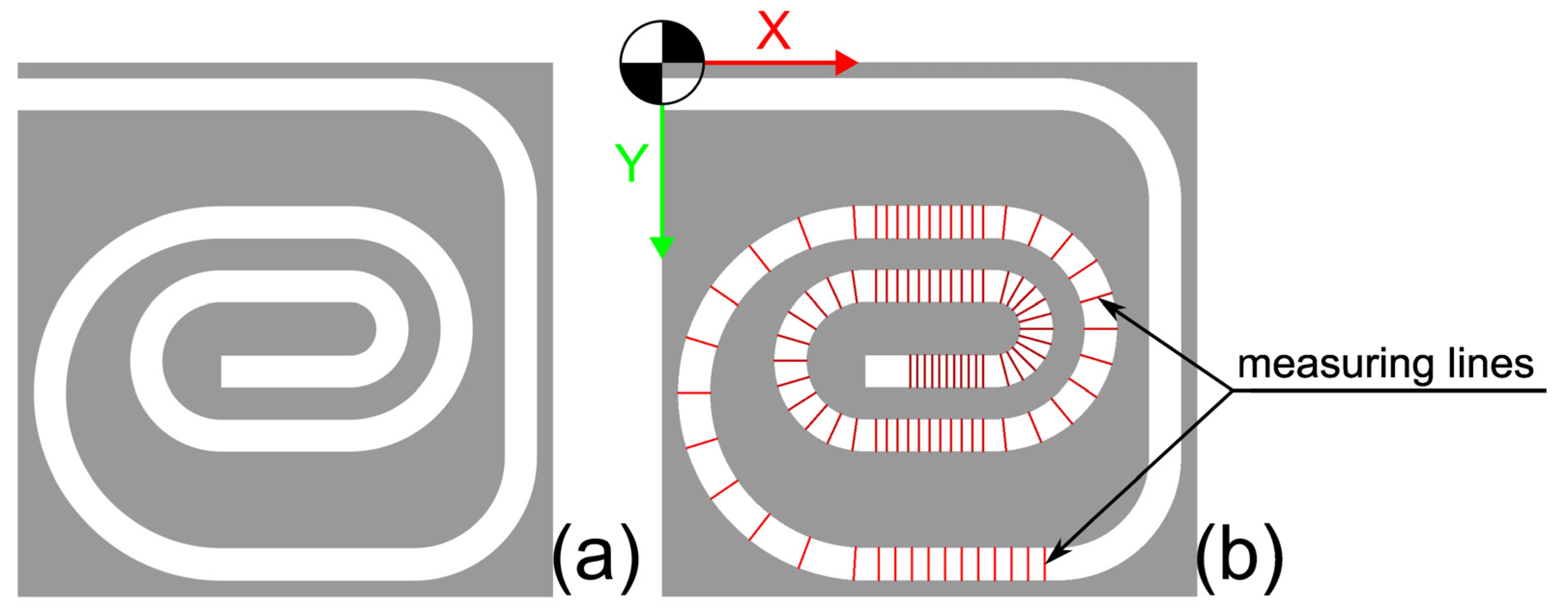
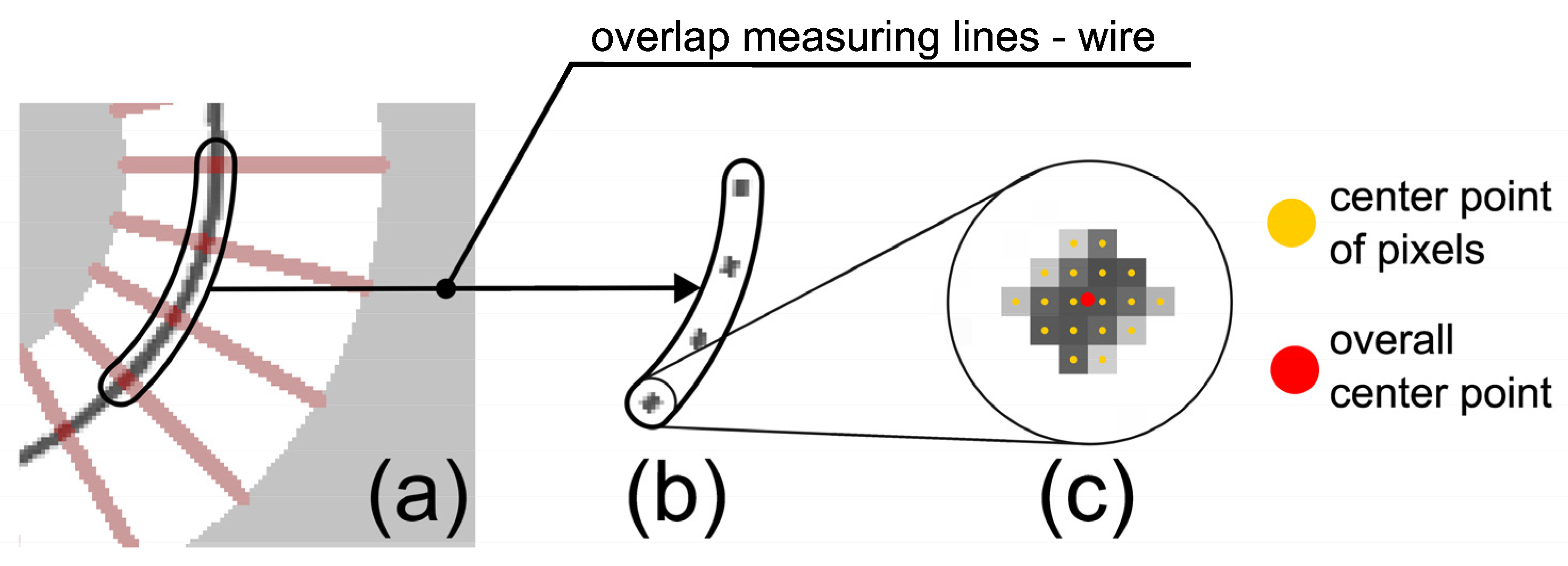
4.5. Determination of the Wire Position
- Separation of base part and wire based on the color value (the wire has a darker shade of gray compared to the thin copper filament layer) (Figure 10).
- Aligning the base part to a mask from CAD (Figure 11), resulting in a displacement matrix.
- Aligning the wire according to the displacement matrix obtained from Step 2.
- Calculation of the deviation of the measured points from the planned wire position.
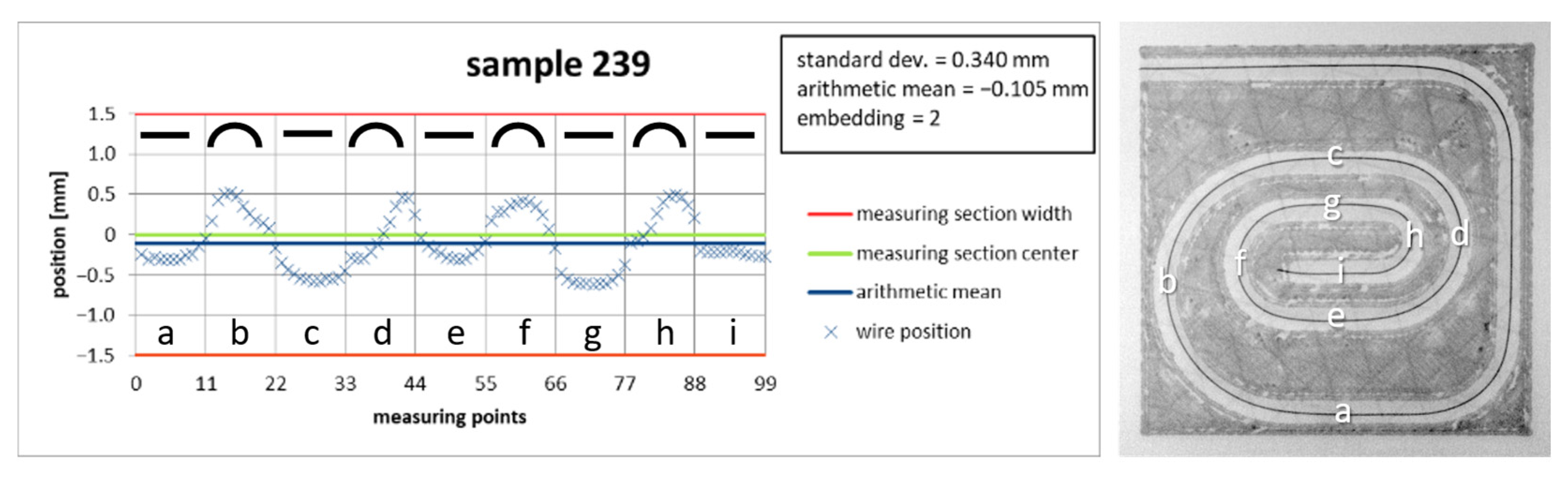
- Generation of a diagram of the wire position, as well as calculation of the characteristic values: standard deviation and mean value (Figure 13).
5. Results
5.1. Validation of the Model
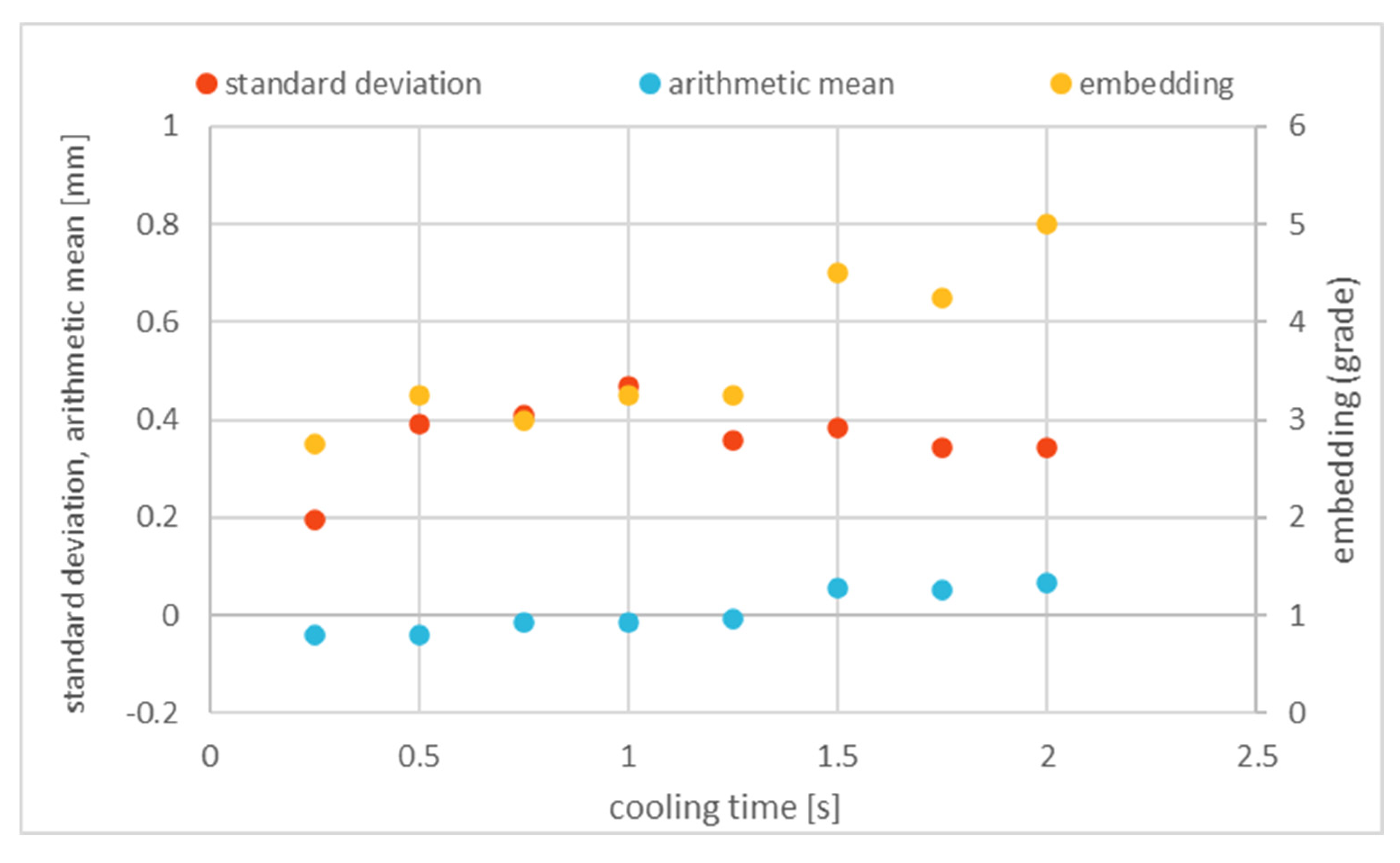
5.2. Cooling Time
5.3. Process Optimization
5.4. Material Variation
6. Discussion
- In the automotive sector, due to its high standards as a replacement for conventional cable harnesses to reduce assembly costs.
- In the aviation and aerospace industry, for the integration of accurate sensor structures into the base components to reduce weight.
- In consumer electronics, for efficient integrated antenna coils for cost-effective on-demand production
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing |
| CFF | Continuous Fiber Fabrication |
| CT | Computed tomography |
| IWU | Institute for Machine Tools and Forming Technology |
| PETG | Polyethylene terephthalate glycol |
| PLA | Polylactide |
| WEAM | Wire-encapsulating additive manufacturing |
Appendix A
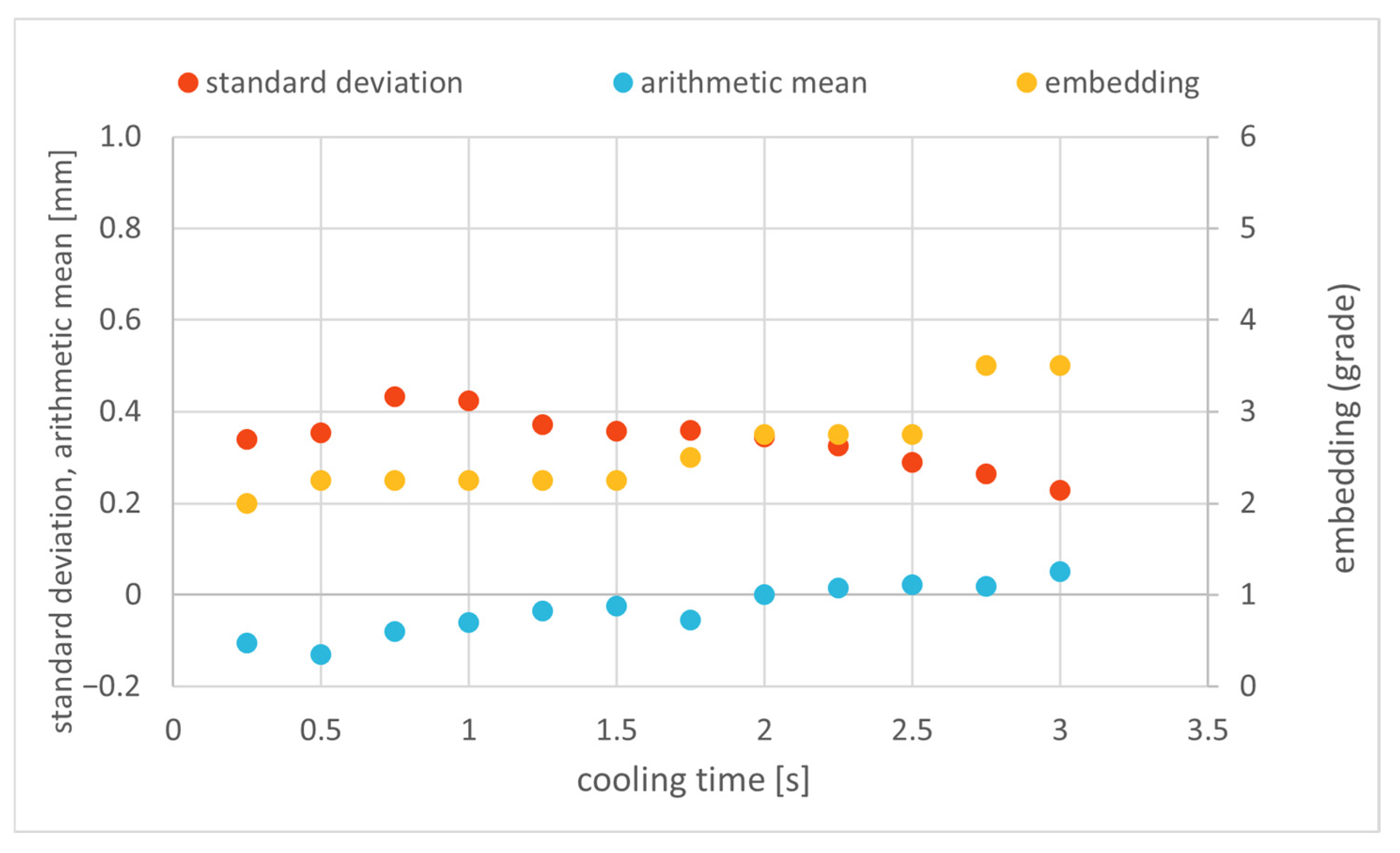
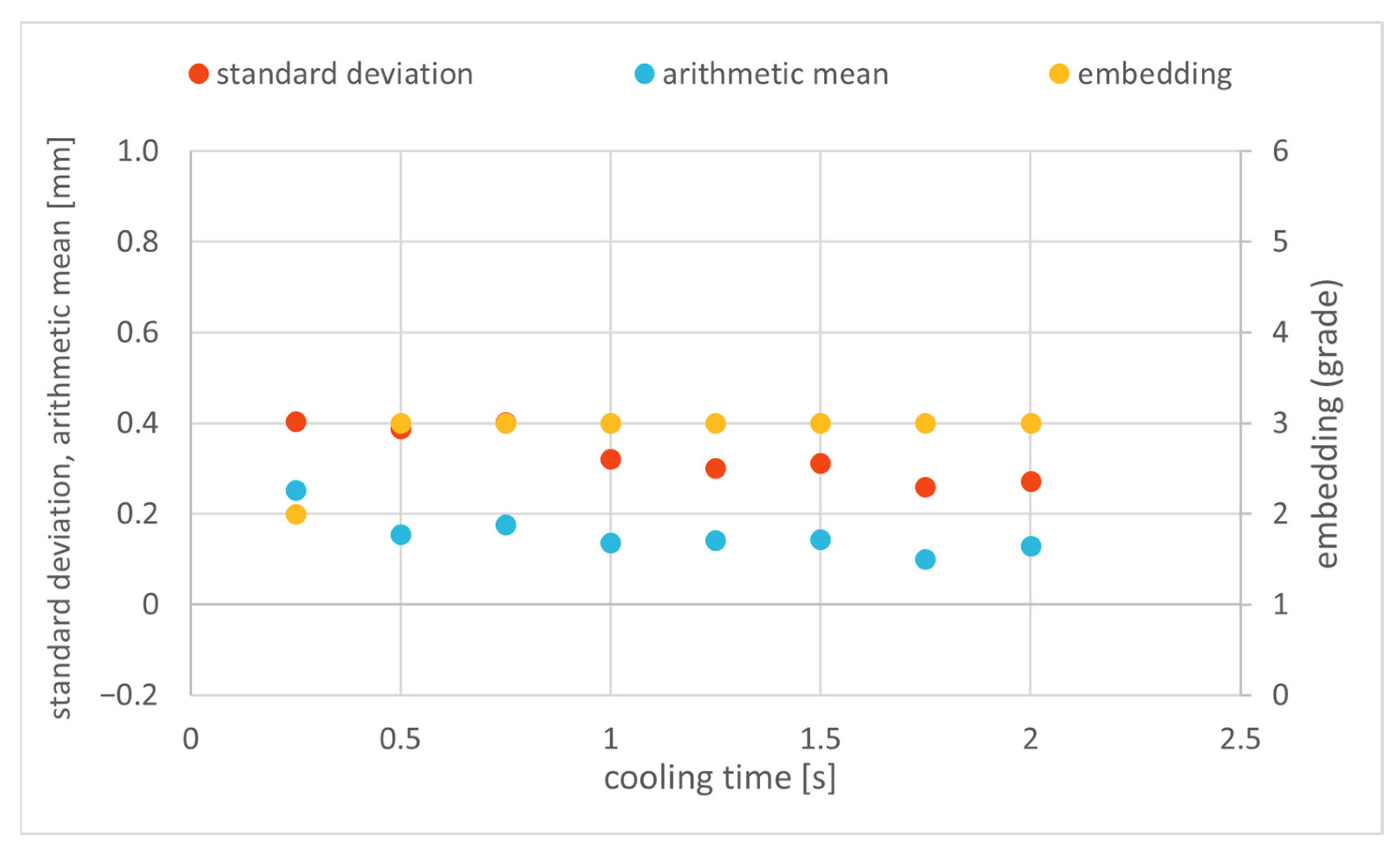
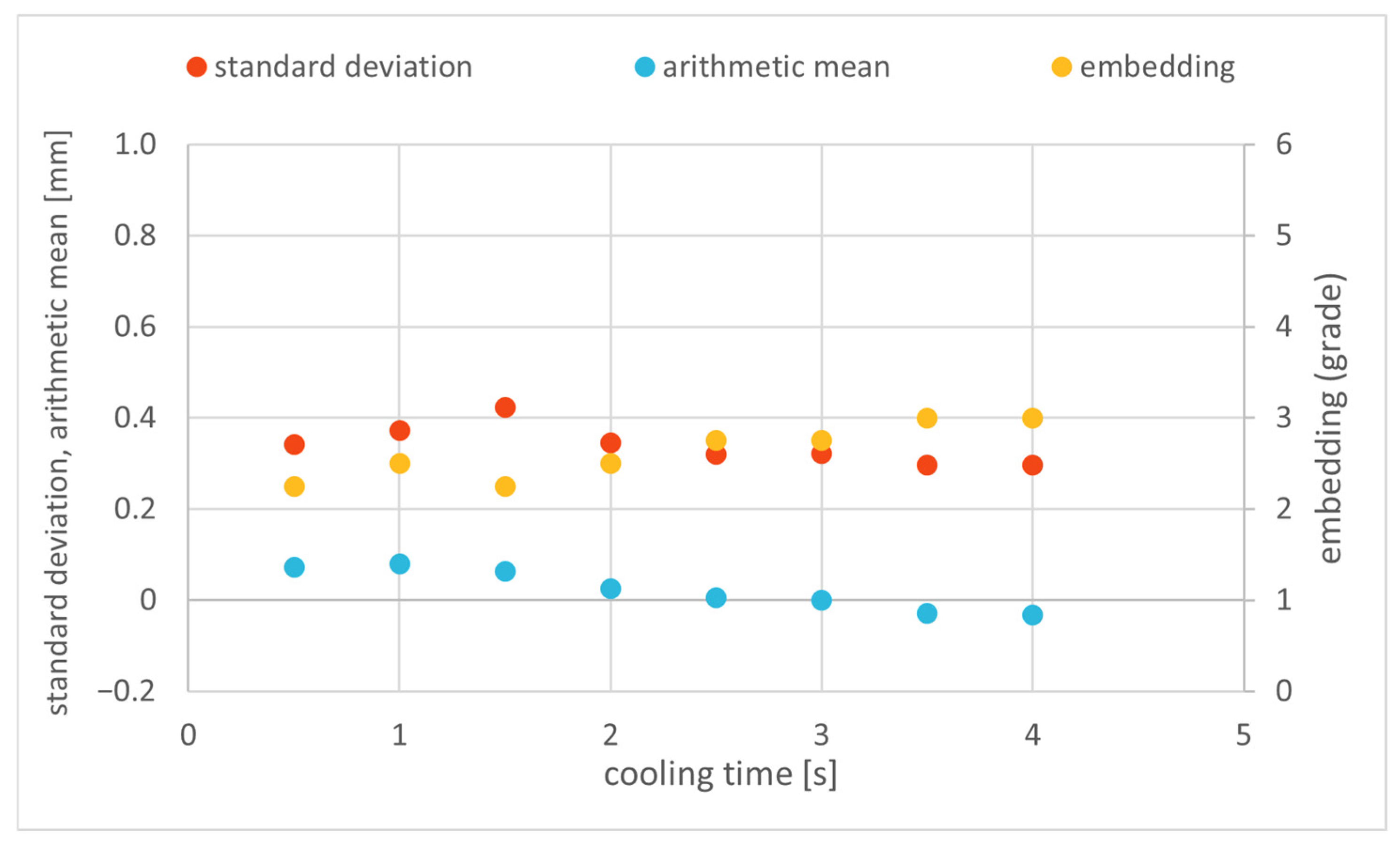
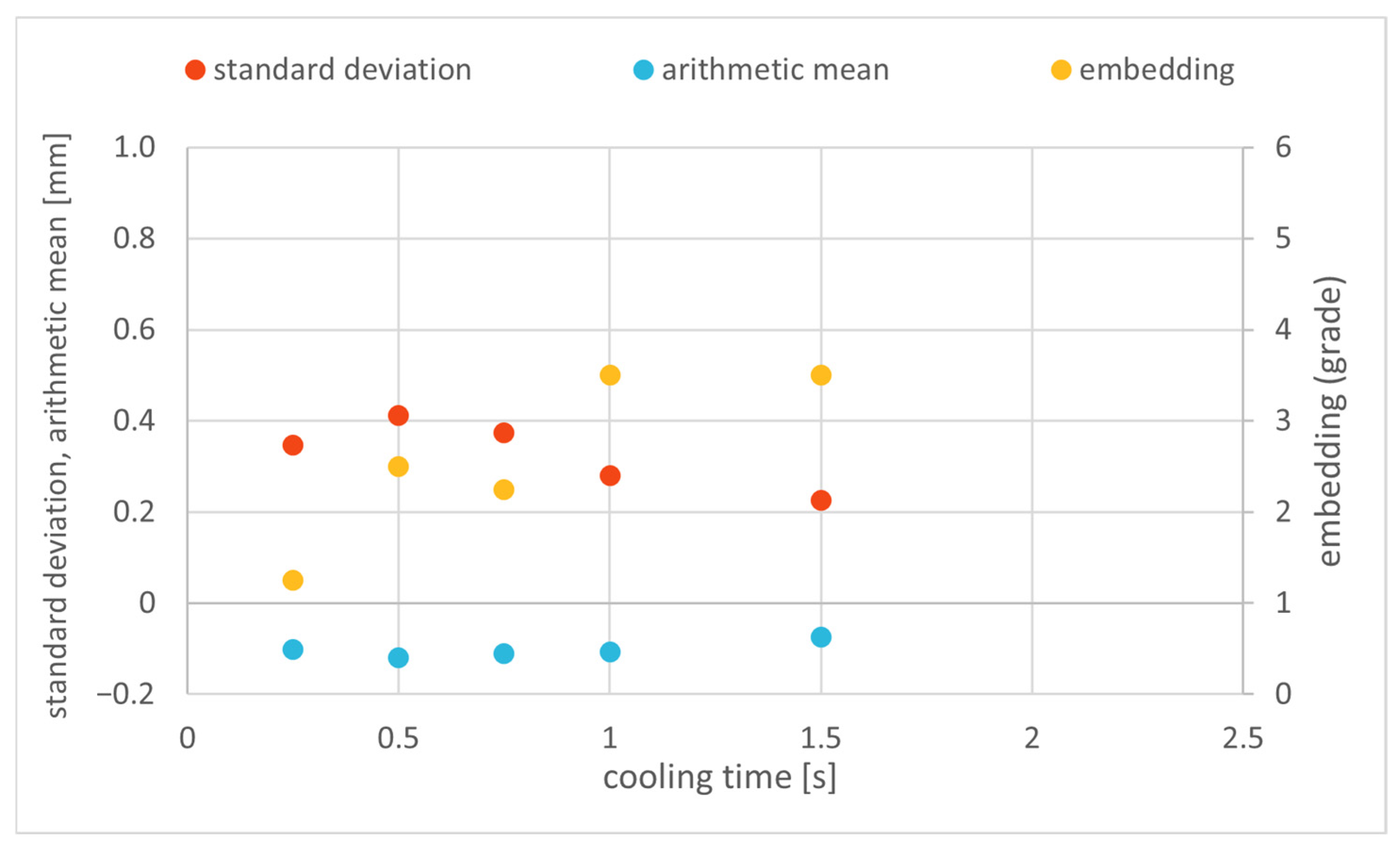
Appendix B
- G1/G3—Movement command
- X/Y/Z—Linear axes
- U/V—Rotary axes
- W—Wire feed axis (absolute)
- E—Filament feed axis (relative)
- I/J—Relative coordinates of the circle center point
- F—Feed speed
- Without the correction, the arc can be printed with one command:
- Straight before:
- G1 X-5 Y-24 U0 V0 W131.708 E19.2 F200;
- Arc:
- G3 X5 Y-24 I5 J0 U-180 V-180 W147.416 E6.283 F150;
- Straight after:
- G1 X5 Y24 U-180 V-180 W195.416 E19.2 F200.
- With the correction, the arc is divided up into multiple commands:
- Straight before:
- G1 X-5 Y-24 U0 V0 W131.708 E28.8 F200;
- Opening phase:
- G3 X-4.564 Y-26.043 I5 J0 U7.165 V7.165 W133.724 E1.263 F141.2
- G3 X-4.140 Y-26.804 I4.564 J2.043 U14.228 V14.228 W134.405 E0.523 F141.2
- G3 X-3.729 Y-27.331 I4.140 J2.804 U21.299 V21.299 W134.800 E0.401 F141.2
- G3 X-3.33 Y-27.730 I3.729 J3.331 U28.498 V28.498 W135.014 E0.338 F141.2
- G3 X-2.944 Y-28.042 I3.33 J3.730 U35.984 V35.984 W135.082 E0.298 F141.2;
- Holding phase:
- G3 X5 Y-24 I2.944 J4.042 U-90.082 V-90.082 W146.083 E6.601 F141.2;
- Closing phase:
- G1 X5 Y-23.695 U-98.932 V-98.932 W146.580 E0.183 F141.2
- G1 X5 Y-23.348 U-109.050 V-109.050 W147.144 E0.209 F141.2
- G1 X5 Y-22.925 U-121.173 V-121.173 W147.813 E0.254 F141.2
- G1 X5 Y-22.343 U-137.324 V-137.324 W148.685 E0.349 F141.2
- G1 X5 Y-20.626 U-180 V-180 W150.790 E1.030 F141.2;
- Straight after:
- G1 X5 Y24 U-180 V-180 W195.416 E28.8 F200.
References
- Xu, Y.; Wu, X.; Guo, X.; Kong, B.; Zhang, M.; Qian, X.; Mi, S.; Sun, W. The Boom in 3D-Printed Sensor Technology. Sensors 2017, 17, 1166. [Google Scholar] [CrossRef]
- Espalin, D.; Muse, D.W.; MacDonald, E.; Wicker, R.B. 3D Printing multifunctionality: Structures with electronics. Int. J. Adv. Manuf. Technol. 2014, 72, 963–978. [Google Scholar] [CrossRef]
- Ziervogel, F. Custom-Printed Actuator Coils. Available online: https://www.iwu.fraunhofer.de/en/projects/custom-printed-actuator-coils.html (accessed on 27 November 2024).
- Ibrahim, Y. 3D Printing of Continuous Wire Polymer Composite for Mechanical and Thermal Applications. Master’s Thesis, York University, Toronto, ON, Canada, 2019. [Google Scholar]
- Kwok, S.W.; Goh, K.H.H.; Tan, Z.D.; Tan, S.T.M.; Tjiu, W.W.; Soh, J.Y.; Ng, Z.J.G.; Chan, Y.Z.; Hui, H.K.; Goh, K.E.J. Electrically conductive filament for 3D-printed circuits and sensors. Appl. Mater. Today 2017, 9, 167–175. [Google Scholar] [CrossRef]
- Zymelka, D.; Yamashita, T.; Sun, X.; Kobayashi, T. Printed Strain Sensors Based on an Intermittent Conductive Pattern Filled with Resistive Ink Droplets. Sensors 2020, 20, 4181. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Yu, A.J.; Simonton, J.; Yang, G.; Dohrmann, Y.; Kang, Z.; Li, Y.; Mo, J.; Zhang, F.-Y. An inkjet-printed capacitive sensor for water level or quality monitoring: Investigated theoretically and experimentally. J. Mater. Chem. A 2017, 5, 17841–17847. [Google Scholar] [CrossRef]
- Hedges, M.; Marin, A.B. 3D Aerosol jet printing-Adding electronics functionality to RP/RM. In Proceedings of the DDMC 2012 Conference, Berlin, Germany, 14–15 March 2012; pp. 1–5. [Google Scholar]
- Ansell, T.Y. Current Status of Liquid Metal Printing. J. Manuf. Mater. Process. 2021, 5, 31. [Google Scholar] [CrossRef]
- Saari, M. Design and Control of Fiber Encapsulation Additive Manufacturing. Ph.D. Thesis, Southern Methodist University, Dallas, TX, USA, 2019. [Google Scholar]
- Löffler, D.; Dani, I.; Meltke, R.; Knobloch, M. Vorrichtung zum Dreidimensionalen Ab- oder Verlegen von Mit Einer Ummantelung Versehenen Filamenten. DE102019206539A1, 7 May 2019. [Google Scholar]
- Ziervogel, F.; Boxberger, L.; Bucht, A.; Drossel, W.-G. Expansion of the Fused Filament Fabrication (FFF) Process Through Wire Embedding, Automated Cutting, and Electrical Contacting. IEEE Access 2021, 9, 43036–43049. [Google Scholar] [CrossRef]
- Mauersberger, V. Process Investigation for the Integration of Wires in the FFF Process, as well as the Production of Functionally Integrative Components. Master’s Thesis, Hochschule Mittweida University of Applied Sciences, Mittweida, Germany, 2022. [Google Scholar]
- APS Tech-Solutions. Wizard 480+. Available online: https://rimaag.ch/download.php?id=106 (accessed on 26 August 2022).
- E3D. ToolChanger & Motion System Bundle. Available online: https://e3d-online.com/blogs/news/tc-discontinued (accessed on 3 January 2023).
- Raise3D. Raise3D Premium PLA Technical Data Sheet. Available online: https://s1.raise3d.com/2022/07/Raise3D_Premium_PLA_TDS_V5_EN.pdf (accessed on 1 September 2022).
- filamentworld. Filamentworld–PETG Filament–Glasklar–1.75 mm. Available online: www.filamentworld.de/shop/special-filament/petg-filament/petg-filament-1-75-mm-glasklar/ (accessed on 3 January 2023).
- Latko-Durałek, P.; Dydek, K.; Boczkowska, A. Thermal, Rheological and Mechanical Properties of PETG/rPETG Blends. J. Polym. Environ. 2019, 27, 2600–2606. [Google Scholar] [CrossRef]
- Farid, T.; Herrera, V.N.; Kristiina, O. Investigation of crystalline structure of plasticized poly (lactic acid)/Banana nanofibers composites. IOP Conf. Ser. Mater. Sci. Eng. 2018, 369, 12031. [Google Scholar] [CrossRef]
- filamentworld. Formfutura–MetalFil–PLA Filament–Classic Copper|Kupfer–1.75 mm–0.75 kg. Available online: www.filamentworld.de/shop/special-filament/metall-filament/metalfil-175-mm-classic-copper-kupfer/ (accessed on 3 January 2023).
- Slice Engineering®. Mosquito® Hotend. Available online: https://www.sliceengineering.com/collections/hotends-upgrades/products/the-mosquito-hotend (accessed on 26 November 2024).







| Wire | Application Examples |
|---|---|
| Copper ø 0.2 | Coils, antennas, signal conductors |
| Copper ø 0.4 | Power transmission |
| Constantan ø 0.2 | Heating elements, sensors |
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Wire embedded in full u shape | Polymer in u shape, wire not fully covered | Wire not covered, polymer higher than wire | Wire not covered, polymer lower than wire | Wire not covered but resting on polymer | Wire detached |
| A | B | |
|---|---|---|
| Extrusion coefficient | 0.4 | 0.2 |
| Feed [mm/min] | 1000 | 3000 |
| Nozzle height [mm] | 1 | 0.6 |
| Cooling time [s] | 0.25 | 0.075 |
| Embedding grade | 2.75 | 2.5 |
| Arithmetic mean [mm] | −0.039 | 0.027 |
| Standard deviation [mm] | 0.197 | 0.267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mauersberger, V.W.; Ziervogel, F.; Weisheit, L.; Boxberger, L.; Drossel, W.-G. Development of a Stable Process for Wire Embedding in Fused Filament Fabrication Printing Using a Geometric Correction Model. Materials 2025, 18, 41. https://doi.org/10.3390/ma18010041
Mauersberger VW, Ziervogel F, Weisheit L, Boxberger L, Drossel W-G. Development of a Stable Process for Wire Embedding in Fused Filament Fabrication Printing Using a Geometric Correction Model. Materials. 2025; 18(1):41. https://doi.org/10.3390/ma18010041
Chicago/Turabian StyleMauersberger, Valentin Wilhelm, Fabian Ziervogel, Linda Weisheit, Lukas Boxberger, and Welf-Guntram Drossel. 2025. "Development of a Stable Process for Wire Embedding in Fused Filament Fabrication Printing Using a Geometric Correction Model" Materials 18, no. 1: 41. https://doi.org/10.3390/ma18010041
APA StyleMauersberger, V. W., Ziervogel, F., Weisheit, L., Boxberger, L., & Drossel, W.-G. (2025). Development of a Stable Process for Wire Embedding in Fused Filament Fabrication Printing Using a Geometric Correction Model. Materials, 18(1), 41. https://doi.org/10.3390/ma18010041







