Experimental Study on Seismic Performance of Dovetail Profiled Steel Concrete Composite Shear Walls with Self-Tapping Screw Connections
Abstract
1. Introduction
2. Test Program
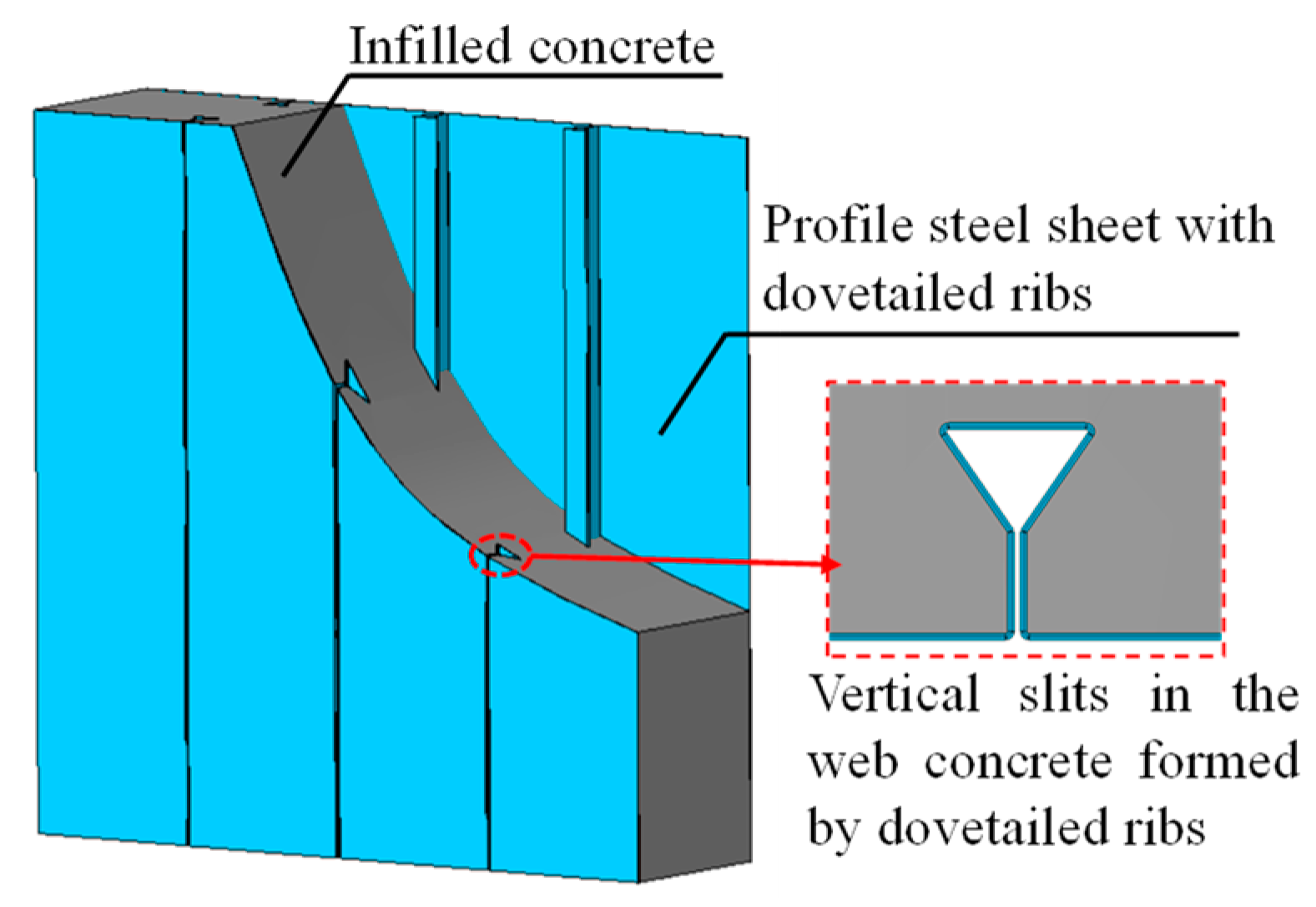
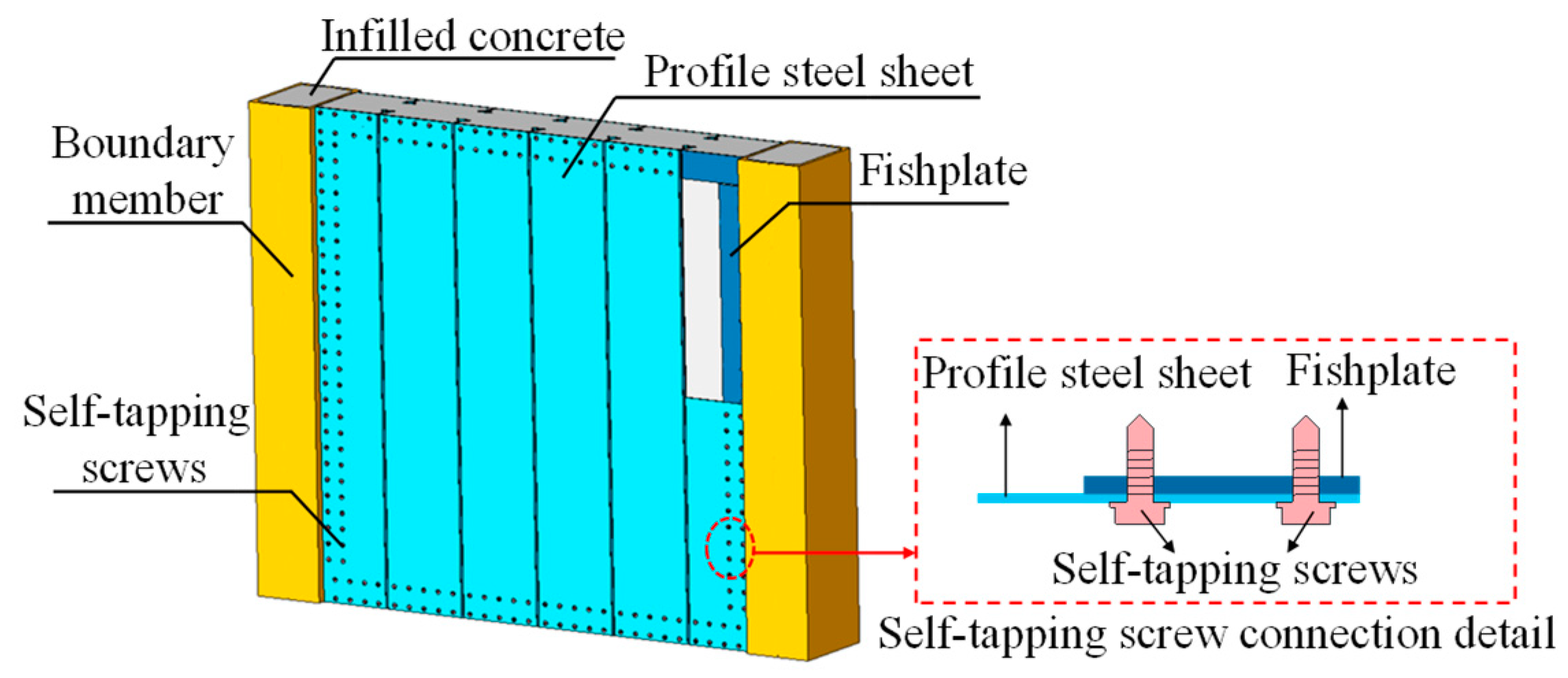
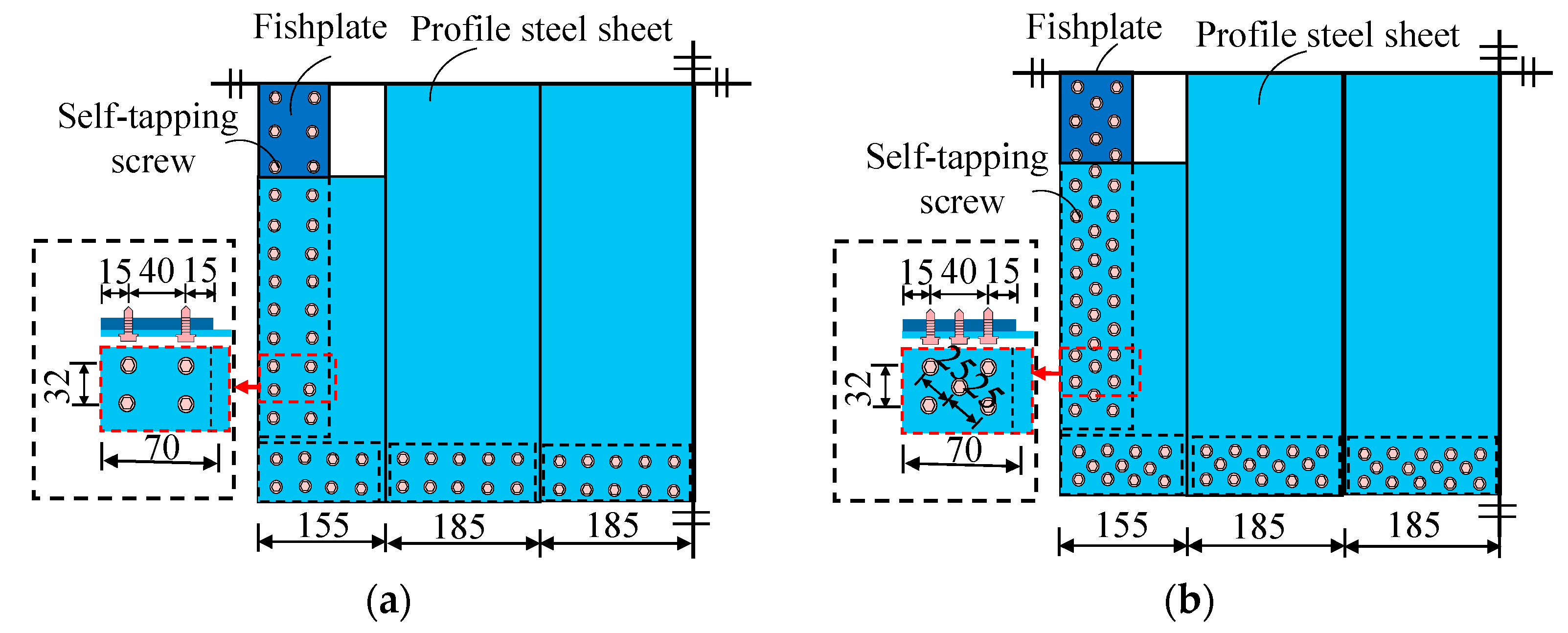
2.1. Specimen Design
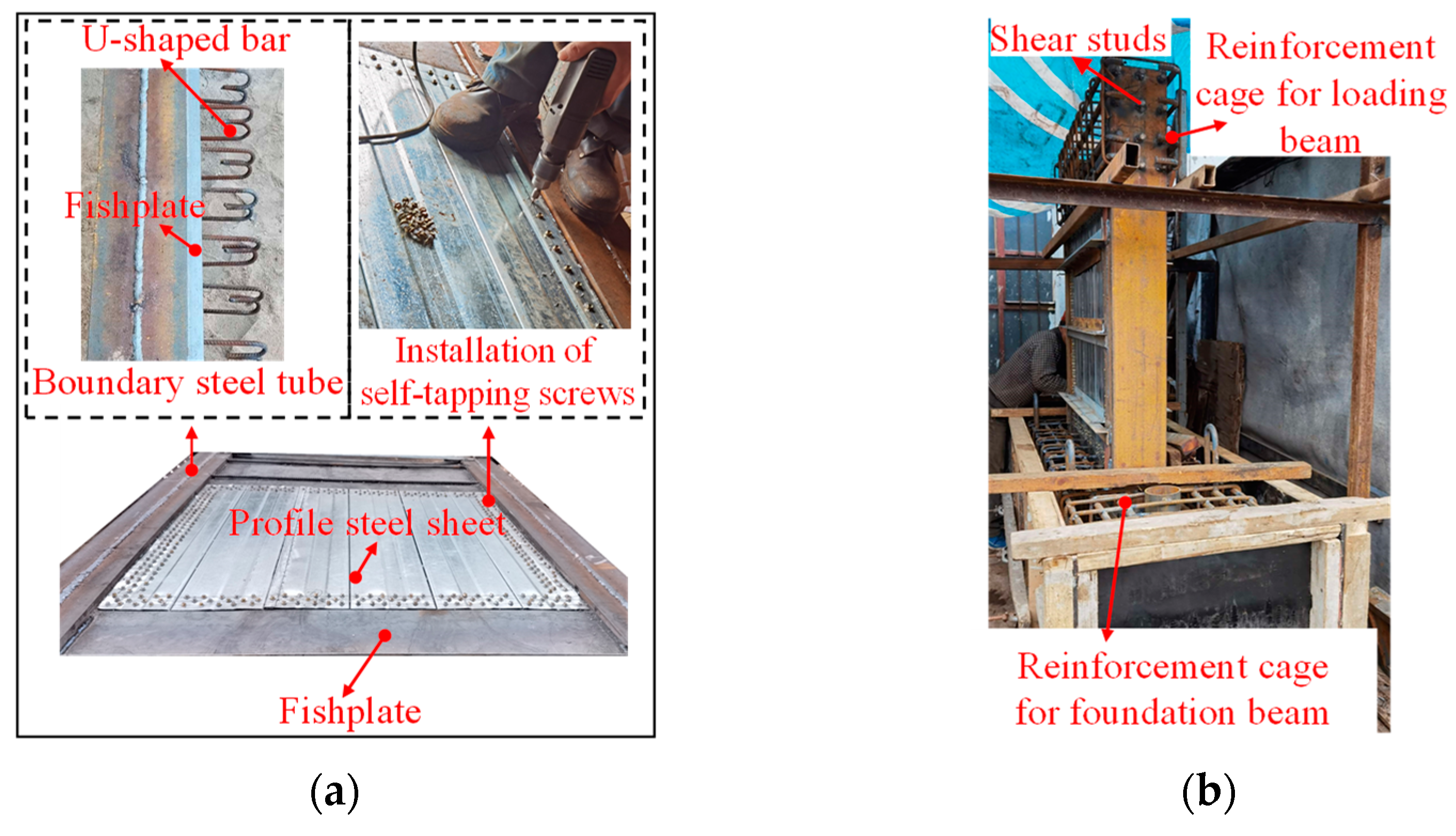
2.2. Specimen Fabrication
2.3. Material Properties
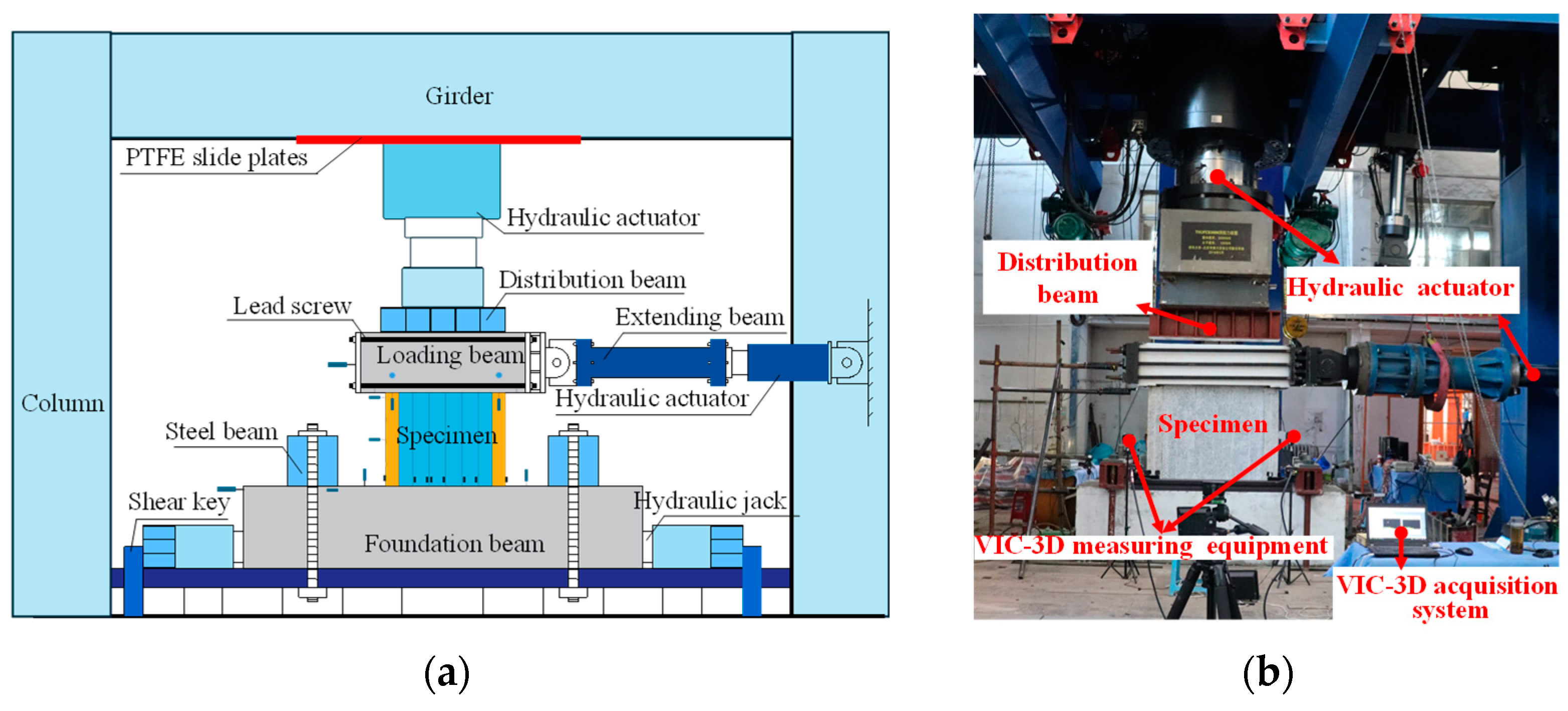
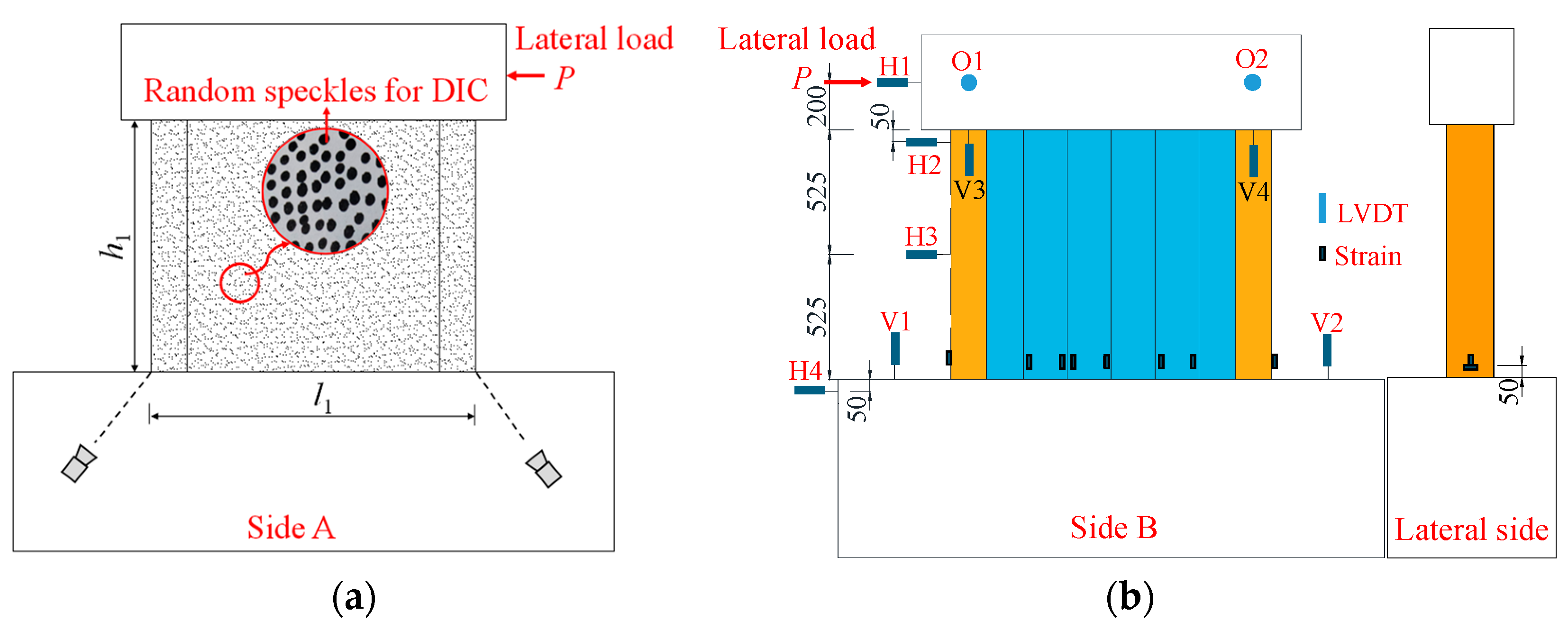
2.4. Test Set-Up and Instrumentation
2.5. Loading Scheme
3. Test Results and Discussion
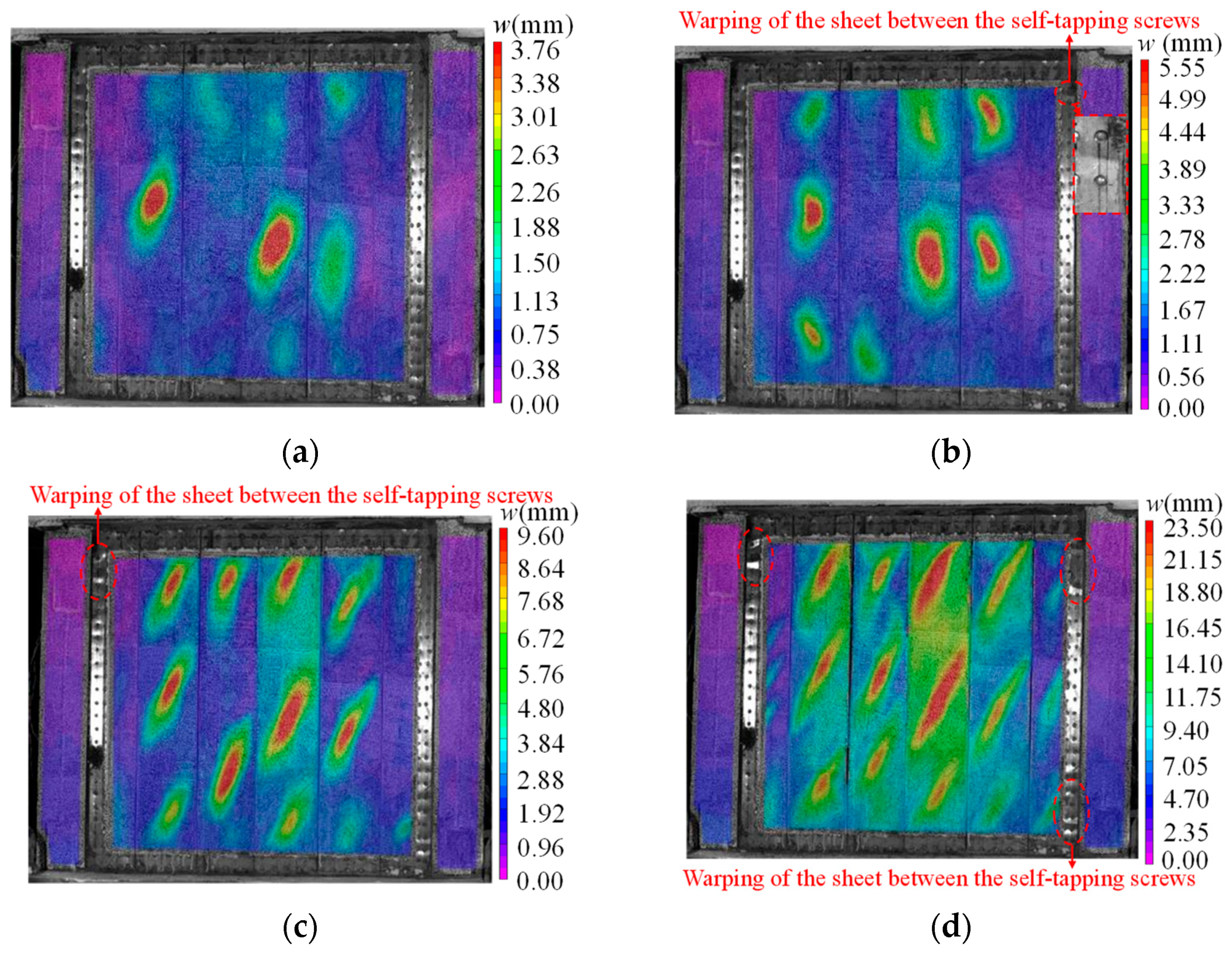
3.1. Experimental Phenomenon
3.2. Failure Mode
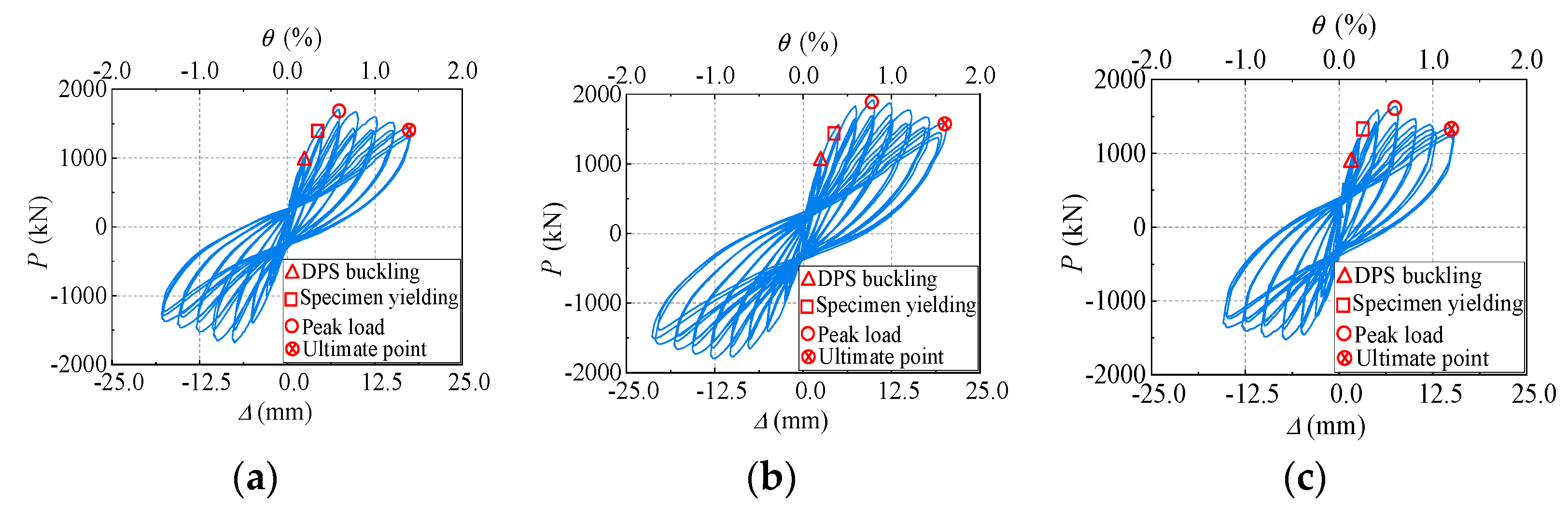
3.3. Lateral Load-Displacement Hysteretic Response
3.4. Ductility
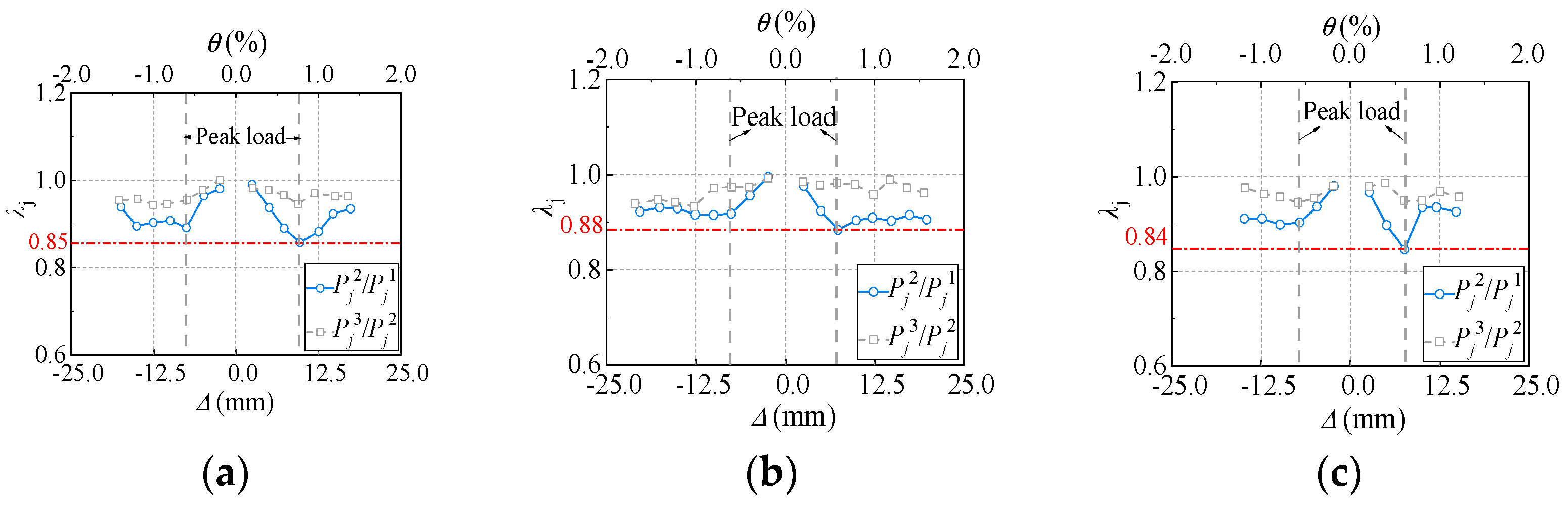
3.5. Stiffness and Strength Degradation
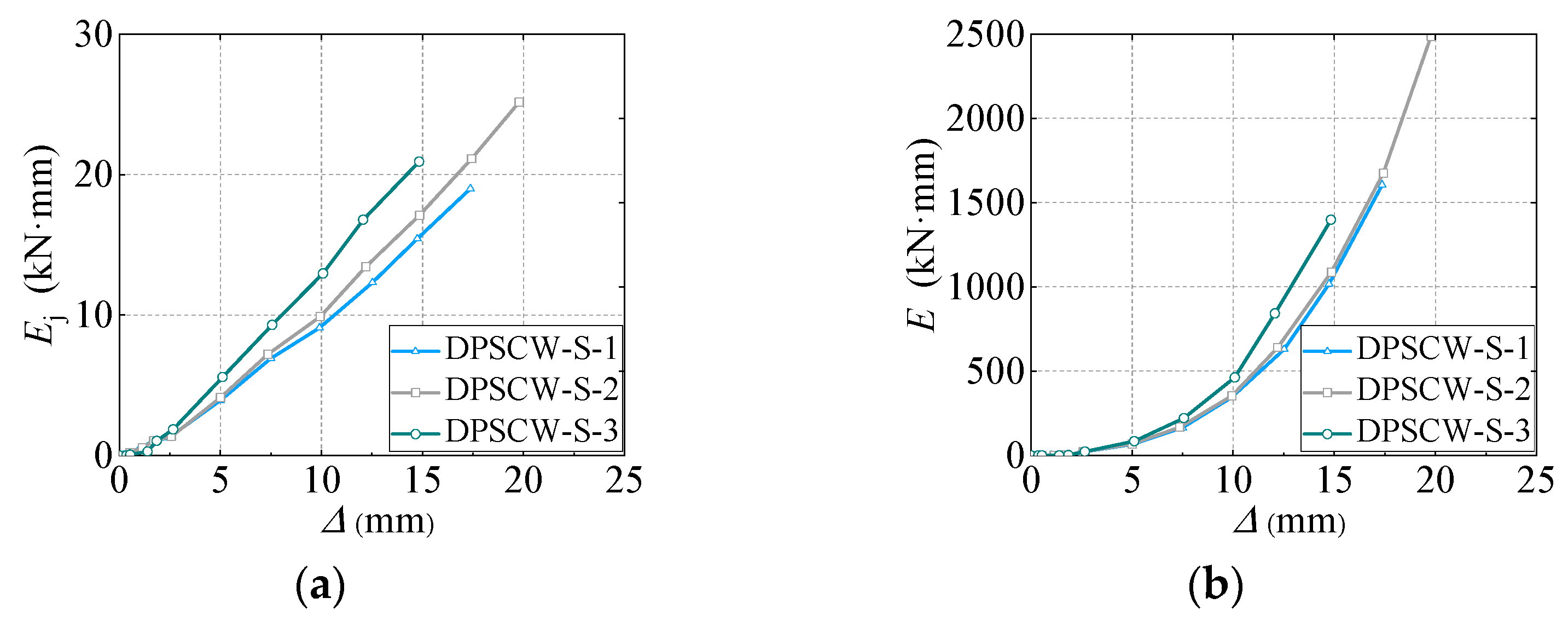
3.6. Energy Dissipation
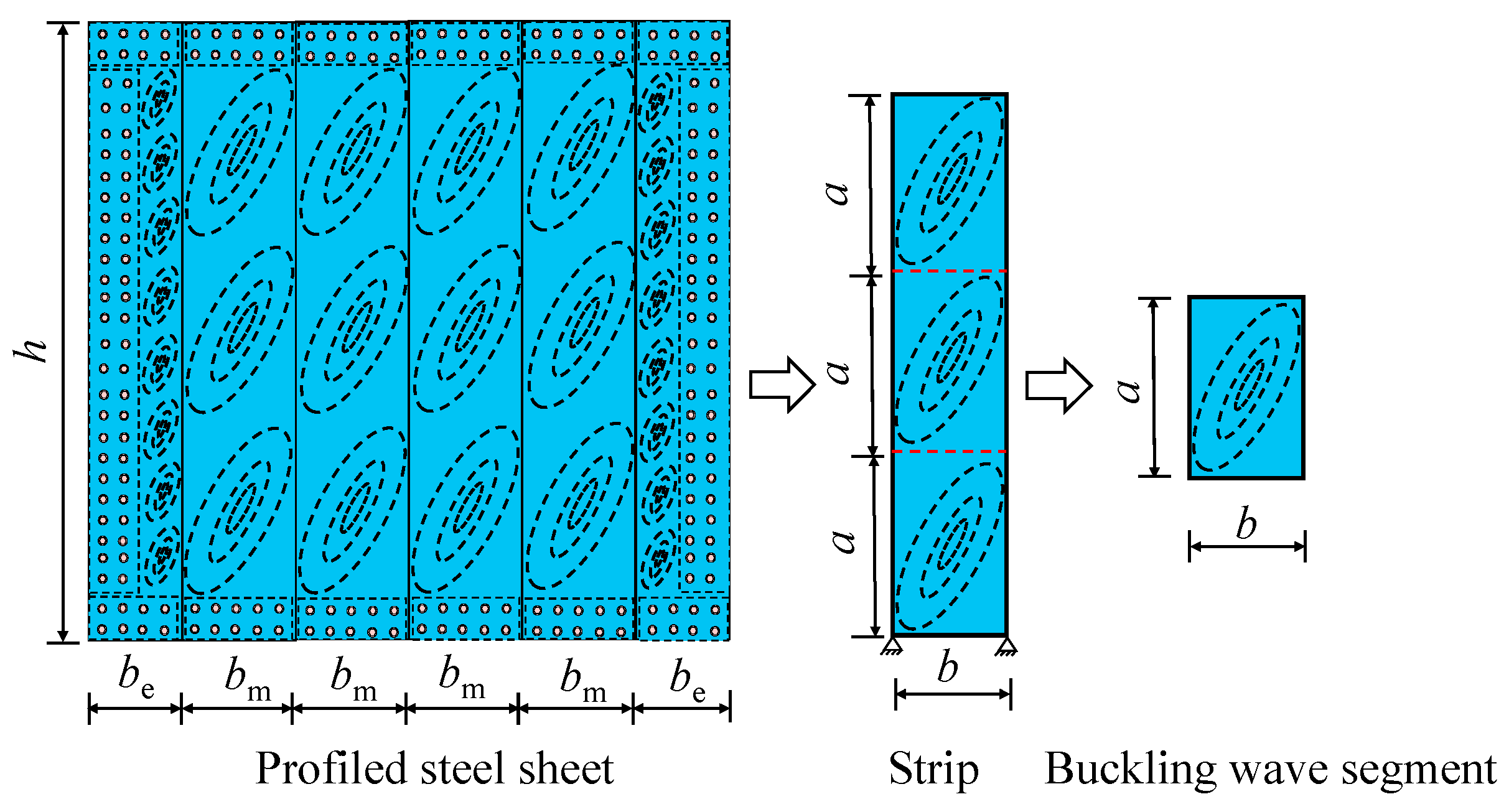
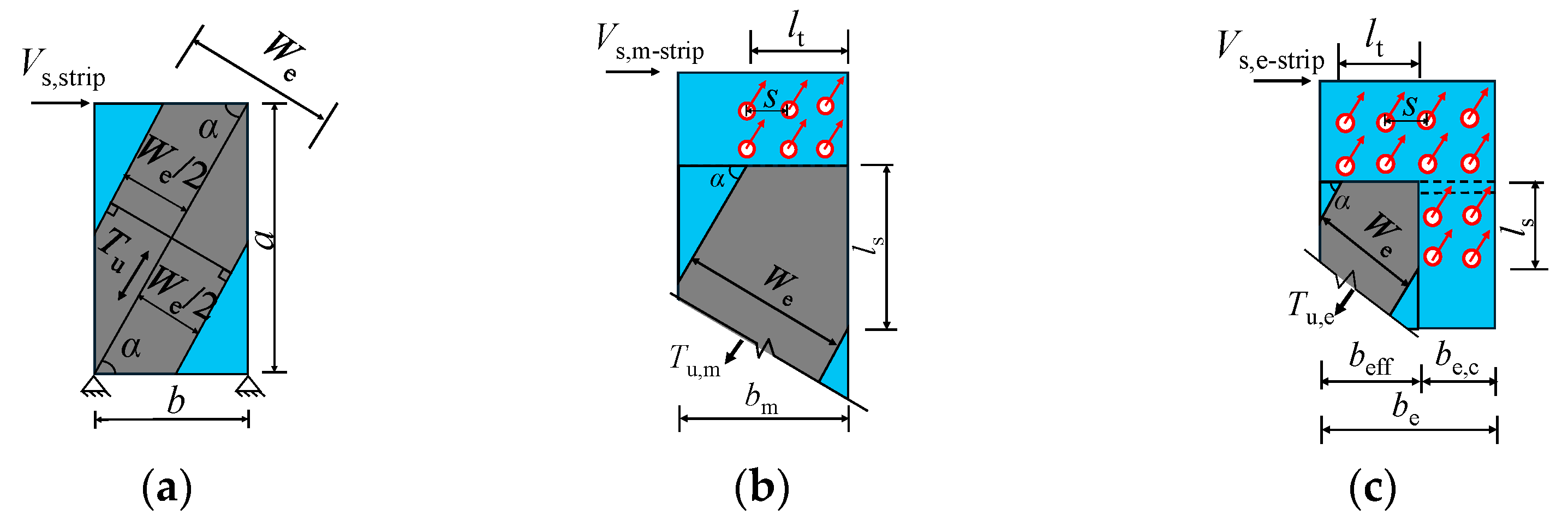
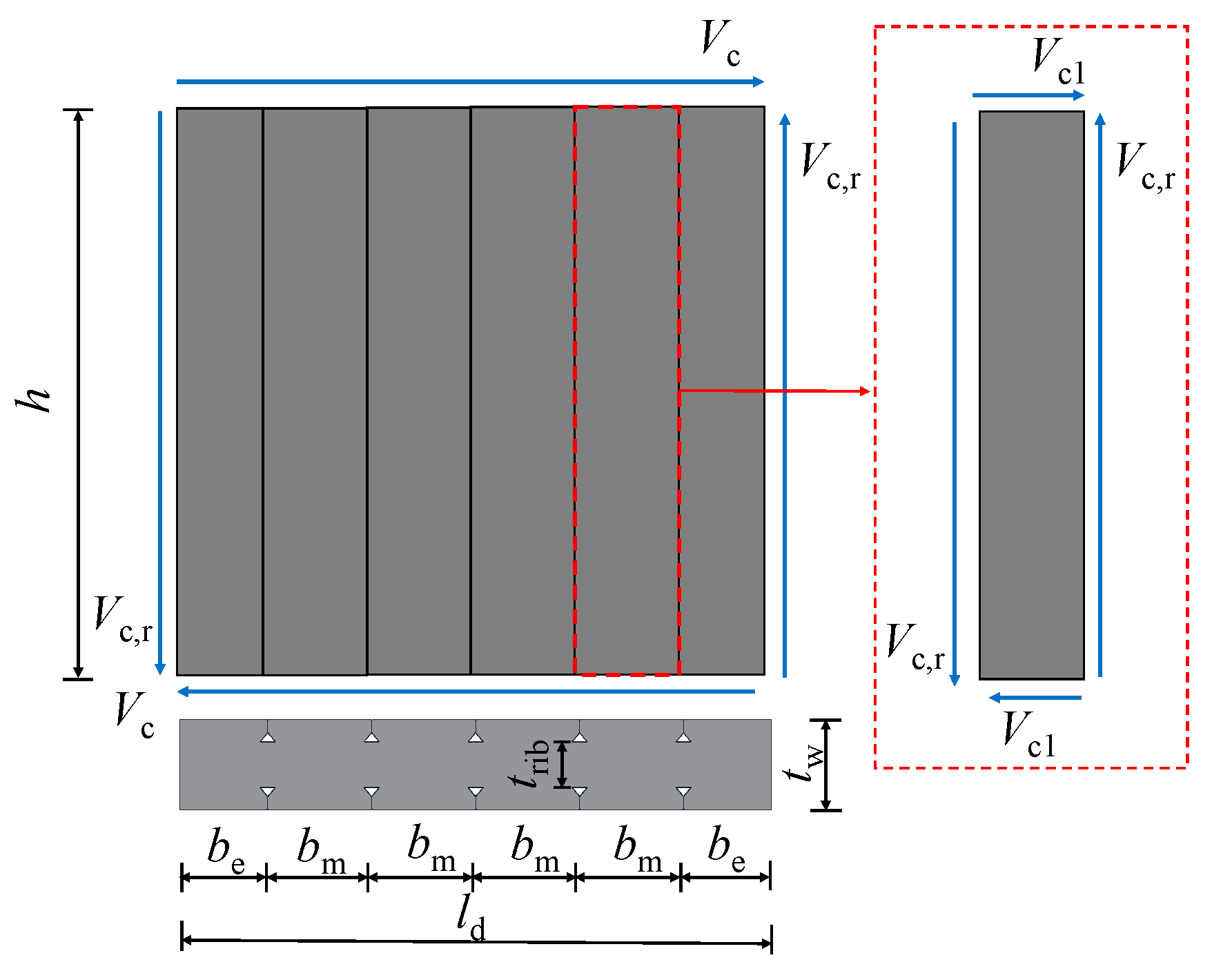
4. Design Method for the Self-Tapping Screw Connections in DPSCWs
5. Conclusions
- (1)
- The self-tapping screw-connected DPSCW specimens exhibited a failure progression starting with local shear buckling of the strips, followed by inclined tension fields anchored by the concrete-embedded ribs. The wall concrete experienced compression-bending failure in several concrete columns, while the self-tapping screw connections remained intact with no significant damage.
- (2)
- The specimens achieved yield drift ratios of 1/286 to 1/225, ultimate drift ratios of 1/63 to 1/94, and ductility coefficients of 3.09 to 3.51, all meeting the deformation capacity requirements in the “Code for Seismic Design of Buildings”. This confirms the effectiveness of self-tapping screw connections in ensuring reliable force transfer between the profiled steel plates and boundary members.
- (3)
- Increasing the number of self-tapping screws by 40% slightly increased peak load capacity by 9.5%, ultimate drift ratio by 23%, and ductility factor by 6%, with minimal impact on initial stiffness.
- (4)
- Increasing the axial compression ratio from 0.2 to 0.5 resulted in a 13% increase in initial stiffness. However, the peak load capacity, ultimate drift ratio, and ductility coefficient decreased by 14%, 33%, and 12%, respectively.
- (5)
- An analytical model for the shear capacity of profiled steel sheets connected by self-tapping screws in DPSCWs was developed based on the effective strip method, with the error between the calculated and experimental results within 12%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uy, B.; Wright, H.; Bradford, M. Combined axial and flexural strength of profiled composite walls. P. I. Civ. Eng-Str. B. 2001, 146, 129–139. [Google Scholar] [CrossRef]
- Wright, H. Local stability of filled and encased steel sections. J. Struct. Eng. 1995, 121, 1382–1388. [Google Scholar] [CrossRef]
- Tong, J.; Pan, W.; Shen, M. Performance of double-skin composite walls with re-entrant profiled faceplates under eccentric compression. J. Build. Eng. 2020, 28, 101010. [Google Scholar] [CrossRef]
- Yu, C.; Tong, J. Compressive behavior of slender profiled double-skin composite walls. J. Constr. Steel Res. 2021, 182, 106657. [Google Scholar] [CrossRef]
- Xu, L.; Guo, Z.; Guo, Y. Experimental study on seismic behavior of low-aspect-ratio concrete filled funnel-shaped profiled steel sheet composite shear walls. J. Build. Struc. 2023, 44, 119–128. (In Chinese) [Google Scholar]
- Huang, Z.; Sun, Z.; Zhang, S. Mechanical behavior of dove-tail-shaped profiled steel concrete composite shear walls under axial compression. J. Build. Struc. 2019, 40, 84–90. (In Chinese) [Google Scholar]
- Zhang, S.; Huang, Z.; Guo, L. Performance of dovetail profiled steel concrete composite sandwich walls under axial compression. Constr. Build. Mater. 2021, 309, 125090. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, Z.; Guo, L. Hysteretic performance of dovetail profiled steel-concrete composite sandwich shear walls. Eng. Struct. 2022, 256, 113994. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, S.; Guo, L. Cyclic behavior of low shear-span ratio dovetailed profiled steel-concrete composite shear walls. J. Build. Eng. 2022, 59, 105094. [Google Scholar] [CrossRef]
- Li, Y.; Shuai, Y.; Shen, Z. Experimental study on tension behavior of self-drilling screw connections for cold-formed thin-walled steel structures. J. Build. Struc. 2015, 36, 143–152. (In Chinese) [Google Scholar]
- Roy, K.; Lau, H.; Tina, C. Experiments and finite element modelling of screw pattern of self-drilling screw connections for high strength cold-formed steel. Thin Wall Struct. 2019, 145, 106393. [Google Scholar] [CrossRef]
- Huynh, M.; Cao, H.; Hancock, G. Design of screwed connections in cold-formed steels in shear. Thin Wall Struct. 2020, 154, 106817. [Google Scholar] [CrossRef]
- Lu, L.; Wang, D.; Wang, W. Shear bearing capacity of Self-drilling screw group connections of CFS sheets. Structures 2022, 35, 160–171. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z.; Qian, F. Finite element analysis of the shear capacity of stainless-steel screw connections. Structures 2022, 41, 957–968. [Google Scholar] [CrossRef]
- Liu, W.; Deng, L.; Zhong, W. Parametric study on the pull-out performance of screw connections in cold-formed thin walled steel structures. Eng. Struct. 2023, 274, 115007. [Google Scholar] [CrossRef]
- Cai, K.; Yuan, H. Testing, numerical and analytical modelling of self-drilling screw connections between thin steel sheets in shear. Thin Wall Struct. 2023, 182, 110292. [Google Scholar] [CrossRef]
- Zhou, X.; Shi, Y.; Zhou, T. Experimental study of the shear resistance of cold-formed steel stud walls. Chin. Civil. Eng. J. 2010, 43, 38–44. (In Chinese) [Google Scholar]
- Yu, C. Shear resistance of cold-formed steel framed shear walls with 0.686 mm, 0.762 mm, and 0.838 mm steel sheet sheathing. Eng. Struct. 2010, 32, 1522–1529. [Google Scholar] [CrossRef]
- Chen, W.; Ye, J.; Xu, Y. Shear experiments of load-bearing cold-formed thin-walled steel wall system lined with sandwich panels. J. Build. Struc. 2017, 38, 85–92. (In Chinese) [Google Scholar]
- Zhang, W.; Mandavian, M.; Yu, C. Lateral strength and deflection of cold-formed steel shear walls using corrugated sheathing. J. Constr. Steel Res. 2018, 148, 399–408. [Google Scholar] [CrossRef]
- Chao, S.; Lu, L.; Wu, H. Shearing Bearing Capacity of Screwed Connections of Thin Steel Sheets. Int. J. Steel Struct. 2019, 19, 577–590. [Google Scholar] [CrossRef]
- GB50018-2002; Technical Code of Cold-Formed Thin-Walled Steel Structures. China Planning Publishing House: Beijing, China, 2010. (In Chinese)
- Nie, J.; Hu, H.; Fan, J.; Tao, M. Experimental study on seismic behavior of high-strength concrete filled double-steel-plate composite walls. J. Constr. Steel Res. 2013, 88, 206–219. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, Y.; Tian, Y. Cyclic behavior of corrugated double-skin composite walls with different aspect ratios. J. Struct. Eng. ASCE 2020, 146, 04020214. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical and Mechanical Properties. China Architecture & Building Press: Beijing, China, 2019. (In Chinese)
- GB/T 228. 1-2010; Metallic Materials: Tensile Testing: Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2021. (In Chinese)
- JGJ/T 101-2015; Specification for Seismic Test of Buildings. China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Feng, P.; Qiang, H.; Ye, L. Discussion and definition on yield points of materials, members and structures. Eng. Mech. 2017, 34, 36–46. (In Chinese) [Google Scholar]
- Park, R. State of the art report ductility evaluation from laboratory and analytical testing. In Proceedings of the Ninth World Conference on Earthquake Engineering, Tokyo/Kyoto, Japan, 2–9 August 1988; pp. 605–616. [Google Scholar]
- GB 50011-2010; Code for Seismic Design of Buildings. China Construction Industry Press: Beijing, China, 2010. (In Chinese)
- ASCE/SEI 41-13; Seismic Evaluation and Retrofit of Existing Buildings. American Society of Civil Engineers: Reston, VA, USA, 2017.
- AISI S213-07w/S1-09; North American Standard for Cold Formed Steel Framing-Lateral Design with Supplement 1. American Iron and Steel Institute: Washington, DC, USA, 2012.
- AISI S400-15; North American Standard for Seismic Design of Cold-Formed Steel Structural Systems. American Iron and Steel Institute: Washington, DC, USA, 2015.
- Xie, Z.; Zhang, A.; Yan, W.; Zhang, Y.; Mu, T.; Yu, C. Study on shear performance and calculation method for self-pierce riveted joints in galvanized steel sheet. Thin Wall Struct. 2021, 161, 74–90. [Google Scholar] [CrossRef]
- Yanagi, N.; Yu, C. Effective Strip Method for the Design of Cold-Formed Steel Framed Shear Wall with Steel Sheet Sheathing. J. Struct. Eng. 2014, 140, 04013101. [Google Scholar] [CrossRef]
- JGJ 138-2016; Code for Design of Composite Structures. China Architecture & Building Press: Beijing, China, 2016. (In Chinese)







| Specimen | Number of Self-Tapping Screws | Design Axial Compression Ratio | Applied Axial Force N (kN) |
|---|---|---|---|
| DPSCW-S-1 | 56 (2 rows) | 0.20 | 2000 |
| DPSCW-S-1 | 78 (3 rows) | 0.20 | 2000 |
| DPSCW-S-3 | 78 (3 rows) | 0.50 | 5000 |
| Specimen | fcu (MPa) | fcp (MPa) | Ec (GPa) | ʋc |
|---|---|---|---|---|
| DSCW-S-1 | 28.25 | 26.33 | 27.9 | 0.19 |
| DSCW-S-2 | 30.07 | 28.87 | 29.8 | 0.20 |
| DSCW-S-3 | 27.11 | 22.63 | 26.9 | 0.20 |
| Components | Measured Thickness or Diameter (mm) | fy (MPa) | εy | fu (MPa) | Es (GPa) | ʋs |
|---|---|---|---|---|---|---|
| YXB40-185-740 | 1.17 | 331 | 0.0018 | 382 | 200 | 0.28 |
| Fishplate | 2.96 | 325 | 0.0017 | 372 | 195 | 0.29 |
| Channel steel | 8.95 | 341 | 0.0018 | 490 | 199 | 0.26 |
| Longitudinal rebar | 27.40 | 467 | 0.0023 | 648 | 182 | - |
| Specimen | Load Direction | Initial Stiffness | Yield of DPSCW | Peak Lateral Load | Ultimate Displacement | Ductility Coefficient | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K0/(kN/mm) | Py/kN | Δy/mm | θy | Pm/kN | Δm/mm | θm | Pu/kN | Δu/mm | θu | μ = Δu/Δy | ||
| DPSCW-S-1 | Puch | 1063 | 1454 | 4.80 | 1/263 | 1709 | 7.30 | 1/172 | 1453 | 16.18 | 1/78 | 3.38 |
| Pull | 1025 | 1438 | 4.94 | 1/250 | 1680 | 7.52 | 1/167 | 1428 | 15.97 | 1/78 | 3.23 | |
| Average | 1044 | 1446 | 4.87 | 1/257 | 1695 | 7.41 | 1/170 | 1441 | 16.07 | 1/78 | 3.31 | |
| DPSCW-S-2 | Puch | 1072 | 1617 | 5.48 | 1/227 | 1876 | 9.94 | 1/125 | 1628 | 19.52 | 1/64 | 3.56 |
| Pull | 1061 | 1507 | 5.89 | 1/213 | 1810 | 12.62 | 1/99 | 1587 | 20.35 | 1/61 | 3.45 | |
| Average | 1066 | 1562 | 5.69 | 1/225 | 1843 | 11.28 | 1/111 | 1608 | 19.94 | 1/63 | 3.51 | |
| DPSCW-S-3 | Puch | 1340 | 1385 | 4.14 | 1/294 | 1627 | 7.5 | 1/167 | 1391 | 13.05 | 1/94 | 3.15 |
| Pull | 1238 | 1355 | 4.49 | 1/278 | 1535 | 7.09 | 1/175 | 1348 | 13.58 | 1/93 | 3.02 | |
| Average | 1289 | 1370 | 4.32 | 1/286 | 1581 | 7.30 | 1/167 | 1369 | 13.32 | 1/94 | 3.09 | |
| Specimen | Tested Lateral Load Pm (kN) | Tested Shear Capacity of Profiled Steel Sheets Vs,exp (kN) | Calculated Shear Capacity of Profiled Steel Sheets Vs,cal (kN) | Vs,cal/Vs,exp |
|---|---|---|---|---|
| DPSCW-S-1 | 1695 | 359 | 331 | 0.92 |
| DPSCW-S-2 | 1843 | 437 | 389 | 0.89 |
| DPSCW-S-3 | 1581 | 346 | 389 | 1.12 |
| Average | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Tan, Y.; Zhong, Z.; Zhang, S.; Guo, L.; Wang, Y. Experimental Study on Seismic Performance of Dovetail Profiled Steel Concrete Composite Shear Walls with Self-Tapping Screw Connections. Materials 2025, 18, 49. https://doi.org/10.3390/ma18010049
Huang Z, Tan Y, Zhong Z, Zhang S, Guo L, Wang Y. Experimental Study on Seismic Performance of Dovetail Profiled Steel Concrete Composite Shear Walls with Self-Tapping Screw Connections. Materials. 2025; 18(1):49. https://doi.org/10.3390/ma18010049
Chicago/Turabian StyleHuang, Zhenfeng, Youwen Tan, Zheng Zhong, Sumei Zhang, Lanhui Guo, and Yunhe Wang. 2025. "Experimental Study on Seismic Performance of Dovetail Profiled Steel Concrete Composite Shear Walls with Self-Tapping Screw Connections" Materials 18, no. 1: 49. https://doi.org/10.3390/ma18010049
APA StyleHuang, Z., Tan, Y., Zhong, Z., Zhang, S., Guo, L., & Wang, Y. (2025). Experimental Study on Seismic Performance of Dovetail Profiled Steel Concrete Composite Shear Walls with Self-Tapping Screw Connections. Materials, 18(1), 49. https://doi.org/10.3390/ma18010049






