Experimental-Theoretical Investigation of the Strength and Deformability of Full-Scale Second-Generation Profiled Sheeting Samples
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Experimental Stand, Sheeting Specimens, and Testing Procedure
2.2. Theoretical Calculations of Strength and Deformability of Profiled Sheeting Specimens
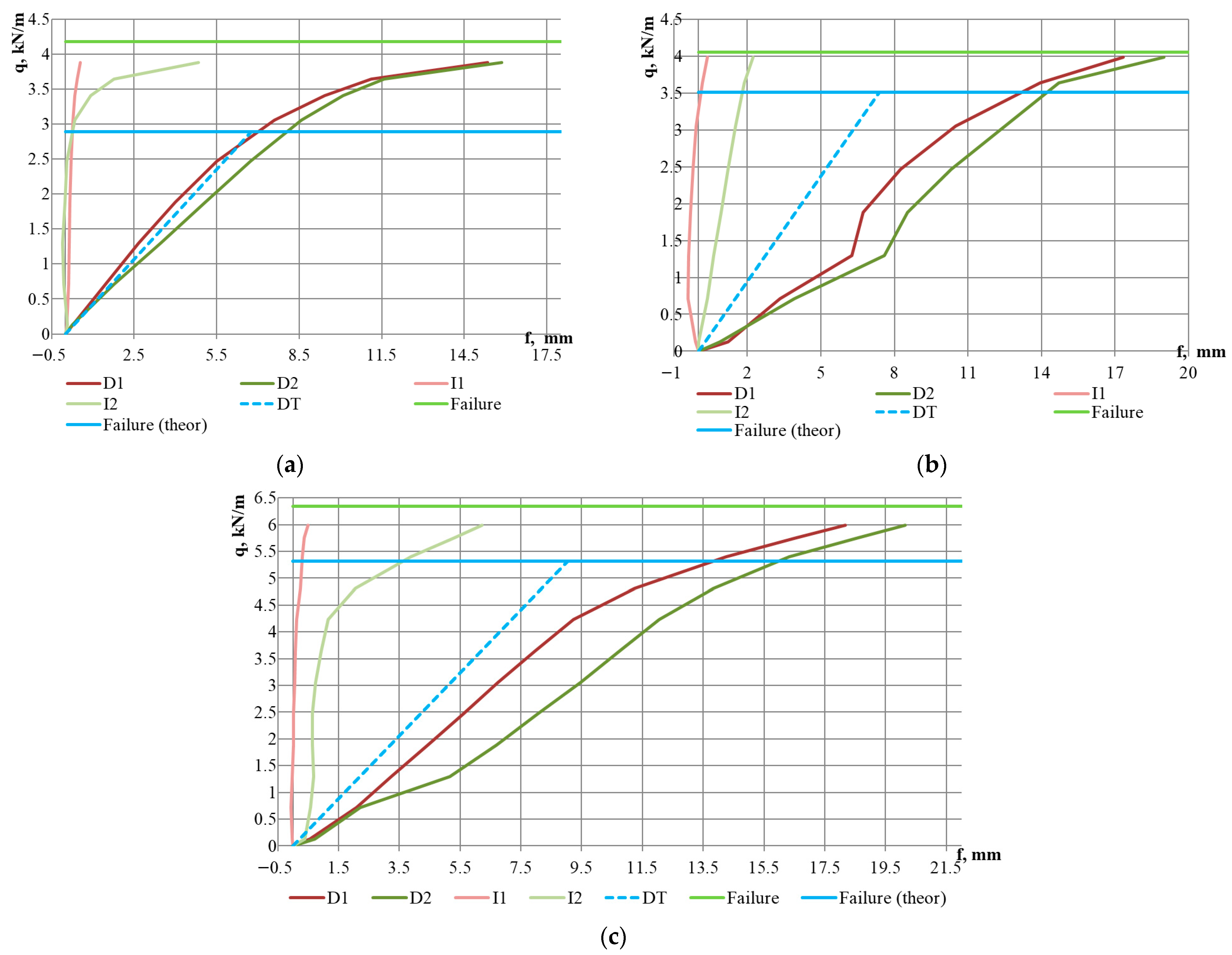
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EN 1993-1-3:2024; Eurocode 3: Design of Steel Structures. Part 1-3: Cold-Formed Members and Sheeting. CEN: Brussels, Belgium, 2024.
- EN 1993-1-3:2006; Eurocode 3: Design of Steel Structures. Part 1-3: General Rules. Supplementary Rules for Cold-Formed Members and Sheeting. CEN: Brussels, Belgium, 2006.
- Hofmeyer, H.; Kerstens, J.G.M.; Snijder, H.H.; Bakker, M.C.M. Combined web crippling and bending moment failure of first-generation trapezoidal steel sheeting. J. Constr. Steel Res. 2002, 58, 1509–1529. [Google Scholar] [CrossRef]
- Rzeszut, K.; Szumigała, T. Optimal design methods of trapezoidal steel sheets. AIP Conf. Proc. 2019, 2060, 020011. [Google Scholar] [CrossRef]
- Franco, J.M.S.; de Batista, E.M. Buckling behavior and strength of thin-walled stiffened trapezoidal CFS under flexural bending. Thin-Walled Struct. 2017, 117, 268–281. [Google Scholar] [CrossRef]
- Biegus, A.; Czepiżak, D. Research on the interactive resistance of corrugated sheets under combined bending and contact pressure. Thin-Walled Struct. 2006, 44, 825–831. [Google Scholar] [CrossRef]
- Biegus, A.; Czepiżak, D. Experimental investigations on combined resistance of corrugated sheets with strengthened cross-sections under bending and concentrated load. Thin-Walled Struct. 2008, 46, 303–309. [Google Scholar] [CrossRef]
- Hofmeyer, H.; Bakker, M.C.M. Sheeting interaction failure, from yield-line to two-strip model. Thin-Walled Struct. 2008, 46, 839–847. [Google Scholar] [CrossRef]
- Hofmeyer, H.; Geers, S.W.A.; Snijder, H.H.; Schafer, B.W. The Direct Strength Method for first generation trapezoidal steel sheeting under Interior One Flange and Interior Two Flange web crippling. Thin-Walled Struct. 2022, 180, 109795. [Google Scholar] [CrossRef]
- Willems, D.W.C.; Hofmeyer, H.; Snijder, H.H.; Schafer, B.W. The direct strength method for combined bending and web crippling of second-generation trapezoidal steel sheeting. Thin-Walled Struct. 2021, 167, 108149. [Google Scholar] [CrossRef]
- Zakhimi, H.; Hofmeyer, H.; Snijder, H.H.; Mahendran, M. Explicit and interaction direct strength methods for combined web crippling and bending moment failure of first-generation trapezoidal steel sheeting. Thin-Walled Struct. 2020, 157, 106927. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, X.; Wang, W.; Wang, J.; Yang, Y. Research on the Flexural Behavior of Profiled Steel Sheet–Hollow Concrete Composite Floor Slab. Buildings 2025, 15, 2140. [Google Scholar] [CrossRef]
- Heweidak, M.; Kafle, B.; Al-Ameri, R. Shear-Bond Behaviour of Profiled Composite Slab Incorporated with Self-Compacted Geopolymer Concrete. Appl. Sci. 2022, 12, 8512. [Google Scholar] [CrossRef]
- Far, H.; Nejadi, S.; Al-Hunaity, S.A. Structural Behaviour and Mechanical Characteristics of BlueDeck Profiled Steel Sheeting for Use in Composite Flooring Systems. Buildings 2024, 14, 3204. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R.; Pavese, A. Mechanical model for seismic response assessment of lightly reinforced concrete walls. Earthq. Struct. 2016, 11, 461–481. [Google Scholar] [CrossRef]
- Al-Rifaie, H.; Studziński, R.; Gajewski, T.; Malendowski, M.; Sumelka, W.; Sielicki, P.W. A New Blast Absorbing Sandwich Panel with Unconnected Corrugated Layers—Numerical Study. Energies 2021, 14, 214. [Google Scholar] [CrossRef]
- Studziński, R.; Gajewski, T.; Malendowski, M.; Sumelka, W.; Al-Rifaie, H.; Peksa, P.; Sielicki, P.W. Blast Test and Failure Mechanisms of Soft-Core Sandwich Panels for Storage Halls Applications. Materials 2021, 14, 70. [Google Scholar] [CrossRef] [PubMed]
- Budescu, M.; Ciongradi, I.; Roşca, O. Theoretical and experimental studies of a class of steel roof profiles. In Proceedings of the International Symposium “Computational Civil Engineering. 2004”, Iaşi, Romania, 11 June 2004. [Google Scholar]
- Casafont, M.; Marimon, F.; Bové, O.; Ferrer, M.; Centelles, X. Local buckling of cold-formed steel trapezoidal sheets: Data for finite element model validation. Data Brief 2024, 53, 110075. [Google Scholar] [CrossRef] [PubMed]
- Szumigała, T.; Rzeszut, K. Does standard test of trapezoidal sheets allow for a reliable assessment of their load-bearing capacity in real structures? In Proceedings of the XXVIII LSCE 2022: Lightweight Structures in Civil Engineering: Contemporary Problems, Poznan, Poland, 1–2 December 2022. [Google Scholar]
- Szumigała, T. Experimental tests of second generation trapezoidal sheets. In Modern Trends in Research on Steel, Aluminium and Composite Structures, 1st ed.; Giżejowski, M.A., Kozłowski, A., Chybiński, M., Rzeszut, K., Studziński, R., Szumigała, M., Eds.; Routledge: London, UK, 2021; pp. 192–198. [Google Scholar] [CrossRef]
- Tarasiuk, V.; Zharko, L.; Ovchar, V.; Tsymbal, S.; Belokon, A. Load test of the structural profiled sheeting of BTR 160.250.750 type produced by Balex Metal LLC for coverings. Sci. Constr. 2016, 1, 42–47. (In Ukrainian) [Google Scholar]
- Belov, I.; Vabischevich, M.; Dedov, O.; Krivenko, O. Testing of Experimental Samples of Profiled Decking by an Experimental Stand. Manag. Dev. Complex Syst. 2022, 49, 52–58. (In Ukrainian) [Google Scholar] [CrossRef]
- Bródka, J.; Garncarek, R.; Miłaczewski, K. Blachy Fałdowe w Budownictwie Stalowym; Arkady: Warszawa, Poland, 1999. (In Polish) [Google Scholar]
- European Convention for Constructional Steelwork. Worked Examples According to EN 1993-1-3, Eurocode 3, Part 1.3, 1st ed.; №. 123; ECCS European Convention for Constructional Steelwork: Brussels, Belgium; Multicomp Lda: Mem Martins, Portugal, 2008. [Google Scholar]
- European Convention for Constructional Steelwork. European Recommendations for Steel Constructions: The Design of Profiled Sheeting; №. 040; ECCS European Convention for Constructional Steelwork: Brussels, Belgium, 1986. [Google Scholar]
- GRISPE. Test Report of Steel Trapezoidal Sheeting With and Without Embossments and Outward Stiffeners, Annex, 31.10.2014, Deliverable D 1.3 (Rev03. 29. June 2015). Available online: http://www.grispeplus.eu/wp-content/uploads/2017/09/D-1.3-Test-report_annex-23112015.pdf (accessed on 16 September 2025).
- Dubina, D.; Ungureanu, V.; Landolfo, R. Design of Cold-Formed Steel Structures, 1st ed.; ECCS European Convention for Constructional Steelwork: Brussels, Belgium; Multicomp Lda: Mem Martins, Portugal, 2012. [Google Scholar]
- Semko, V.; Semko, P. Experimental studies of the profiled steel decks collaborative work. In Proceedings of the XXVIII LSCE 2022: Lightweight Structures in Civil Engineering: Contemporary Problems, Poznan, Poland, 1–2 December 2022. [Google Scholar]
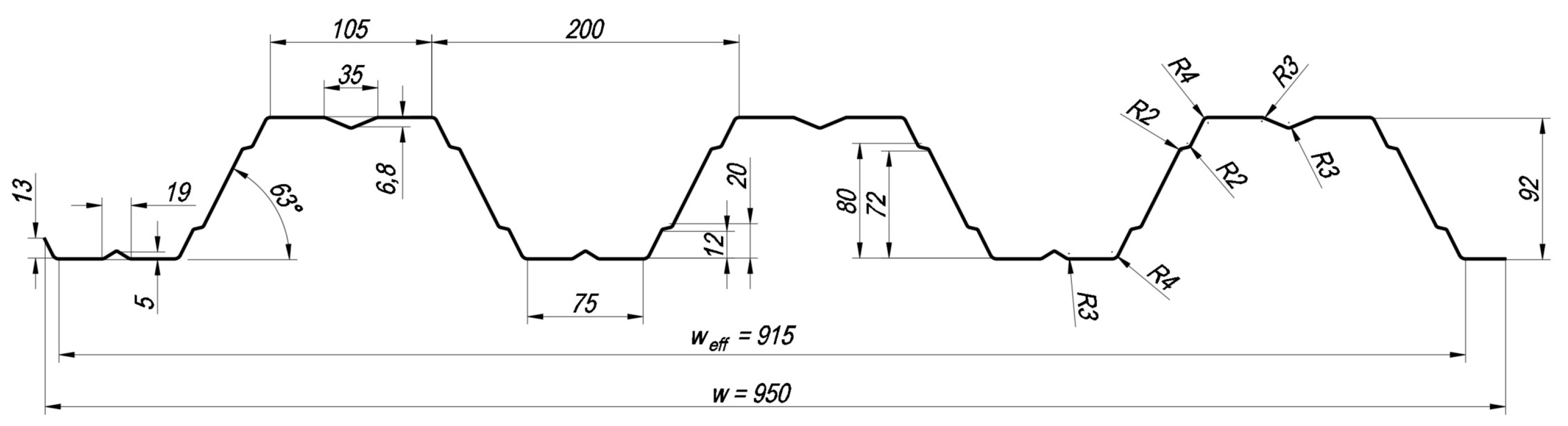
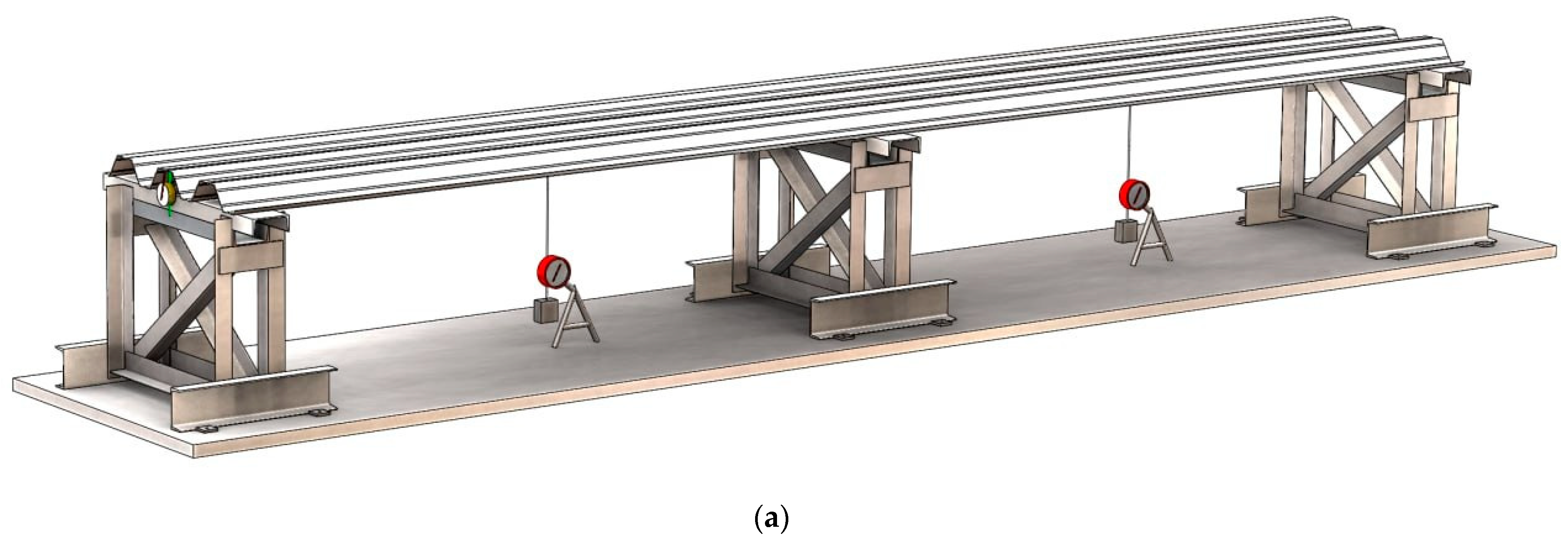



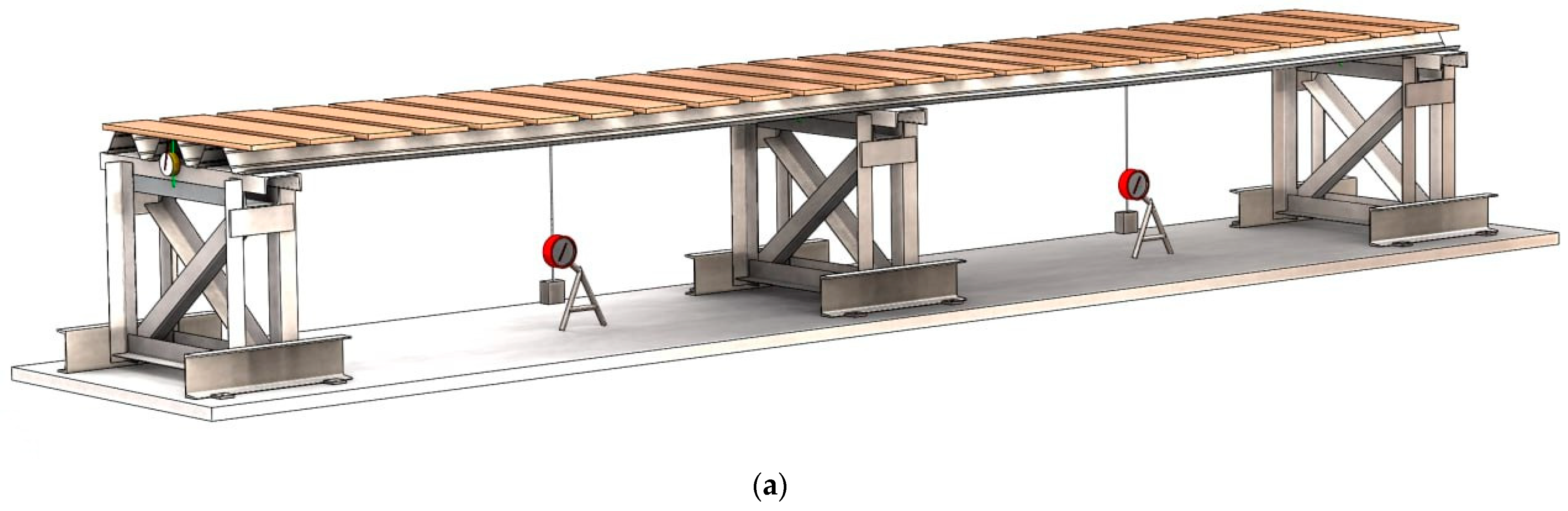

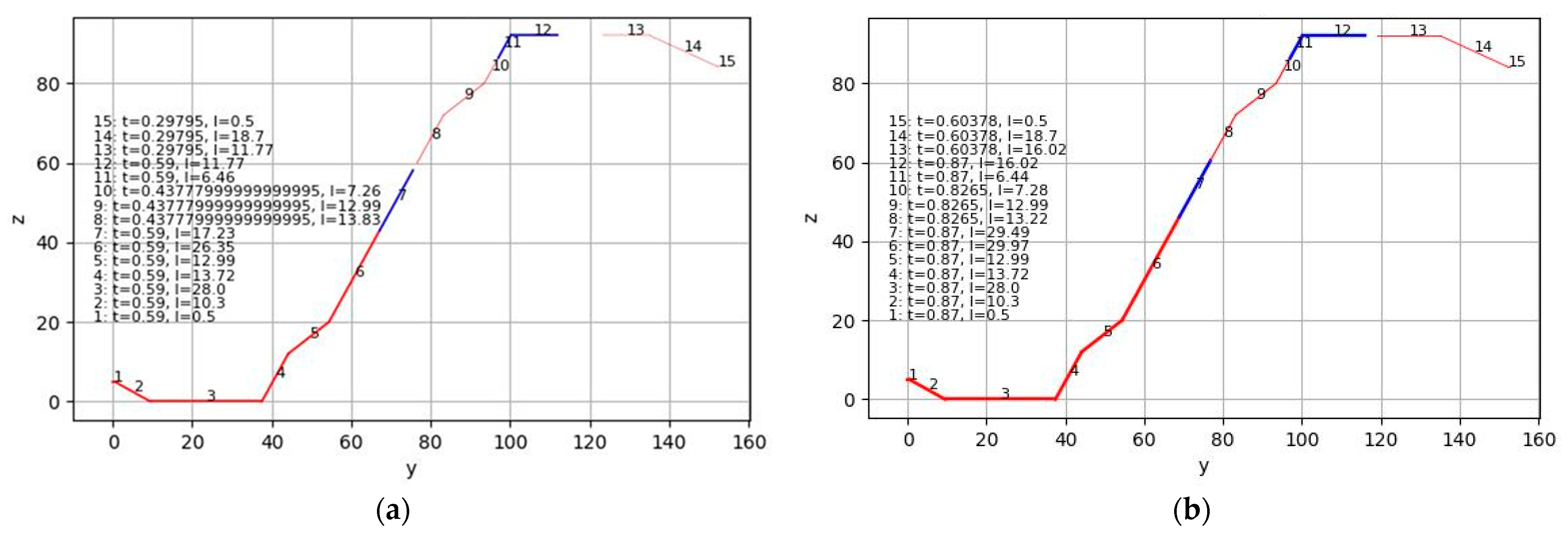



| Specimen | Mark of the Specimen | Span, mm | Core Thickness t, mm | Width of the Support (Edge/Intermediate), mm | Steel Grade |
|---|---|---|---|---|---|
| S01 | T92-2P-0.63 | 3000 | 0.59 | 150/200 | S320GD |
| S02 | T92-2P-0.7 | 3000 | 0.66 | 150/200 | S320GD |
| S03 | T92-2P-0.88 | 3000 | 0.84 | 150/200 | S320GD |
| S04 | 4T92-2P-0.63 | 4000 | 0.59 | 150/200 | S320GD |
| S05 | 4T92-2P-0.7 | 4000 | 0.66 | 150/200 | S320GD |
| S06 | 4T92-2P-0.88 | 4000 | 0.84 | 150/200 | S320GD |
| S07 | 4H-92-2P-0.88-1 | 4000 | 0.87 | 120/120 | DX51 |
| S08 | 4H-92-2P-0.88-2 | 4000 | 0.87 | 120/120 | DX51 |
| S09 | 4H-92-2P-0.88-3 | 4000 | 0.87 | 120/120 | DX51 |
| S10 | 4.5T92-2P-0.7 | 4500 | 0.66 | 150/200 | S320GD |
| S11 | 4.5T92-2P-0.88 | 4500 | 0.84 | 150/200 | S320GD |
| S12 | 5T92-2P-0.88 | 5000 | 0.84 | 150/200 | S320GD |
| t, mm | fy, N/mm2 | Vb, kN | Rw,end, kN | Rw,end, kN | Mp, kNm | Mn, kNm | Ieff, mm4 |
|---|---|---|---|---|---|---|---|
| 0.59 | 320 | 21.54 | 4.2 | 21.54 | 4.53 | 4.35 | 864,188 |
| 0.66 | 320 | 26.65 | 5.28 | 26.65 | 5.61 | 5.22 | 992,937 |
| 0.84 | 320 | 41.72 | 8.53 | 41.72 | 8.11 | 7.75 | 1,309,142 |
| 0.87 | 293 | 34.79 | 10.55 | 34.79 | 8.05 | 7.58 | 1,371,806 |
| Specimen | qmax, kN/m | fmax, mm | Specimen | qmax, kN/m | fmax, mm |
|---|---|---|---|---|---|
| S01 | 2.88 | 6.76 | S07 | 3.06 | 19.33 |
| S02 | 3.51 | 7.39 | S08 | 3.06 | 19.33 |
| S03 | 5.32 | 9.05 | S09 | 3.06 | 19.33 |
| S04 | 1.81 | 16.02 | S10 | 1.80 | 23.54 |
| S05 | 2.19 | 17.51 | S11 | 2.71 | 25.82 |
| S06 | 3.31 | 20.4 | S12 | 2.26 | 31.88 |
| Specimen | qpl, kN/m | qtheor, kN/m | qexp, kN/m | (qpl/qtheor) × 100% | (qpl/qexp) × 100% | (qtheor/qexp) × 100% |
|---|---|---|---|---|---|---|
| S01 | 3.056 | 2.887 | 4.172 | 105.9 | 73.3 | 69.2 |
| S02 | 3.056 | 3.511 | 4.053 | 87.0 | 75.4 | 86.6 |
| S03 | 4.227 | 5.32 | 6.34 | 79.5 | 66.7 | 83.9 |
| S04 | 1.72 | 1.805 | 2.525 | 95.3 | 68.1 | 71.5 |
| S05 | 1.839 | 2.191 | 2.88 | 83.9 | 63.9 | 76.1 |
| S06 | 2.406 | 3.309 | 4.127 | 72.7 | 58.3 | 80.2 |
| S07 | 2.796 | 3.06 | 3.509 | 91.4 | 79.7 | 87.2 |
| S08 | 2.915 | 3.06 | 3.462 | 95.3 | 84.2 | 88.4 |
| S09 | 2.915 | 3.06 | 3.391 | 95.3 | 86.0 | 90.2 |
| S10 | 1.299 | 1.797 | 2.177 | 72.3 | 59.7 | 82.5 |
| S11 | 2.118 | 2.709 | 3.294 | 78.2 | 64.3 | 82.2 |
| S12 | 1.811 | 2.261 | 2.599 | 80.1 | 69.7 | 87.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semko, V.; Mahas, N.; Semko, P.; Skliarenko, S.; Rabenseifer, R. Experimental-Theoretical Investigation of the Strength and Deformability of Full-Scale Second-Generation Profiled Sheeting Samples. Materials 2025, 18, 4365. https://doi.org/10.3390/ma18184365
Semko V, Mahas N, Semko P, Skliarenko S, Rabenseifer R. Experimental-Theoretical Investigation of the Strength and Deformability of Full-Scale Second-Generation Profiled Sheeting Samples. Materials. 2025; 18(18):4365. https://doi.org/10.3390/ma18184365
Chicago/Turabian StyleSemko, Volodymyr, Nataliia Mahas, Pavlo Semko, Serhii Skliarenko, and Roman Rabenseifer. 2025. "Experimental-Theoretical Investigation of the Strength and Deformability of Full-Scale Second-Generation Profiled Sheeting Samples" Materials 18, no. 18: 4365. https://doi.org/10.3390/ma18184365
APA StyleSemko, V., Mahas, N., Semko, P., Skliarenko, S., & Rabenseifer, R. (2025). Experimental-Theoretical Investigation of the Strength and Deformability of Full-Scale Second-Generation Profiled Sheeting Samples. Materials, 18(18), 4365. https://doi.org/10.3390/ma18184365










